Fig. C.1
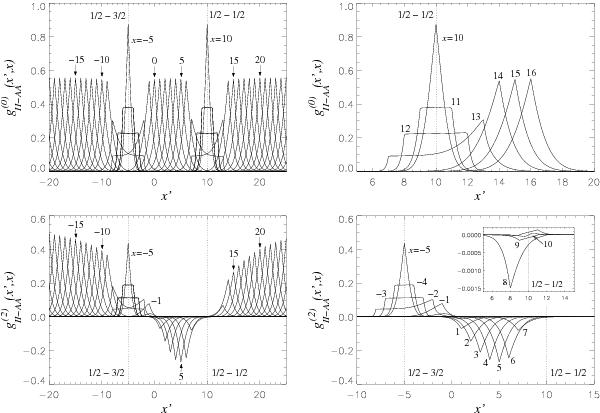
Upper left: plot of the
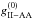 redistribution function defined in Eq. (61), as a function of the reduced frequency of the incoming photons
(x′). Each curve corresponds to a
different (integer) value of the reduced frequency of the outgoing photon
(x).
For some curves, the value of x is indicated in the plot. The reduced
frequencies x and x′ are
defined with respect to the frequency ν0 corresponding to the energy
separation between the centers of gravity of the two terms (x = (ν0 − ν)/ΔνD,
x′ = (ν0 − ν′)/ΔνD).
We consider a 2S − 2P
transition, the two fine-structure components having a separation of 15 Doppler
widths (the energies of the upper levels are calculated according to the
L − S coupling scheme). We
assume an Einstein coefficient Auℓ = 108
s-1, a
Doppler width ΔλD = 60 mÅ, and we accordingly
calculate the damping constant as a = Auℓ/(4πΔνD) ≈ 10-3
(collisional broadening is neglected, and the conversion of the Doppler width from
wavelength units to frequency units is made assuming that the transitions fall at
5000 Å). Upper right: same as upper left, but
considering only a few values of x (indicated in the plot). Lower
left: same as upper left, but for the
redistribution function defined in Eq. (61), as a function of the reduced frequency of the incoming photons
(x′). Each curve corresponds to a
different (integer) value of the reduced frequency of the outgoing photon
(x).
For some curves, the value of x is indicated in the plot. The reduced
frequencies x and x′ are
defined with respect to the frequency ν0 corresponding to the energy
separation between the centers of gravity of the two terms (x = (ν0 − ν)/ΔνD,
x′ = (ν0 − ν′)/ΔνD).
We consider a 2S − 2P
transition, the two fine-structure components having a separation of 15 Doppler
widths (the energies of the upper levels are calculated according to the
L − S coupling scheme). We
assume an Einstein coefficient Auℓ = 108
s-1, a
Doppler width ΔλD = 60 mÅ, and we accordingly
calculate the damping constant as a = Auℓ/(4πΔνD) ≈ 10-3
(collisional broadening is neglected, and the conversion of the Doppler width from
wavelength units to frequency units is made assuming that the transitions fall at
5000 Å). Upper right: same as upper left, but
considering only a few values of x (indicated in the plot). Lower
left: same as upper left, but for the
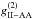 redistribution function. Lower right: same as lower
left, but considering only a few values of x (indicated in the
plot). The inset panel is a zoom of the line core region of the
1/2–1/2 transition, showing in more details the curves obtained for values of
x
close to x = 10 (the frequency position of the 1/2–1/2
transition).
redistribution function. Lower right: same as lower
left, but considering only a few values of x (indicated in the
plot). The inset panel is a zoom of the line core region of the
1/2–1/2 transition, showing in more details the curves obtained for values of
x
close to x = 10 (the frequency position of the 1/2–1/2
transition).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


