Velocity evolution of broad-lined type-Ic supernovae with and without gamma-ray bursts

Home

All issues

Volume 700 (August 2025)

A&A, 700 (2025) A200

Full HTML

Open Access

Table C.2.

Best-fit parameters for power law and broken power law fits for different time shifts.

	Power law fit		Broken power law fit				Best-fit stats.
Time-shift	a	b	t_b	α₁	α₂	A	F-stat.	p-value	Best-fit
[days]	[km/s]		[days]			[km/s]
-6	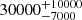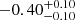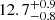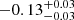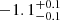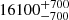$30000_{- 7000}^{+ 10000}$ ${30000_{-7000}^{+10000}}$	$- 0 . 40_{- 0.10}^{+ 0.10}$ ${-0.40_{-0.10}^{+0.10}}$	$12 . 7_{- 0.8}^{+ 0.9}$ ${12.7_{-0.8}^{+0.9}}$	$- 0 . 13_{- 0.03}^{+ 0.03}$ ${-0.13_{-0.03}^{+0.03}}$	$- 1 . 1_{- 0.1}^{+ 0.1}$ ${-1.1_{-0.1}^{+0.1}}$	$16100_{- 700}^{+ 700}$ ${16100_{-700}^{+700}}$	74.824	0.0028	BPL
-5	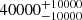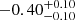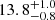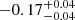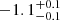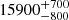$40000_{- 10000}^{+ 10000}$ ${40000_{-10000}^{+10000}}$	$- 0 . 40_{- 0.10}^{+ 0.10}$ ${-0.40_{-0.10}^{+0.10}}$	$13 . 8_{- 0.8}^{+ 1.0}$ ${13.8_{-0.8}^{+1.0}}$	$- 0 . 17_{- 0.04}^{+ 0.04}$ ${-0.17_{-0.04}^{+0.04}}$	$- 1 . 1_{- 0.1}^{+ 0.1}$ ${-1.1_{-0.1}^{+0.1}}$	$15900_{- 800}^{+ 700}$ ${15900_{-800}^{+700}}$	76.968	0.0026	BPL
-4	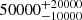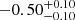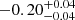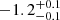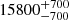$50000_{- 10000}^{+ 20000}$ ${50000_{-10000}^{+20000}}$	$- 0 . 50_{- 0.10}^{+ 0.10}$ ${-0.50_{-0.10}^{+0.10}}$	$14 . 8_{- 0.8}^{+ 1.0}$ ${14.8_{-0.8}^{+1.0}}$	$- 0 . 20_{- 0.04}^{+ 0.04}$ ${-0.20_{-0.04}^{+0.04}}$	$- 1 . 2_{- 0.1}^{+ 0.1}$ ${-1.2_{-0.1}^{+0.1}}$	$15800_{- 700}^{+ 700}$ ${15800_{-700}^{+700}}$	75.161	0.0027	BPL
-3	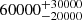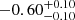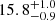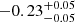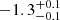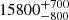$60000_{- 20000}^{+ 30000}$ ${60000_{-20000}^{+30000}}$	$- 0 . 60_{- 0.10}^{+ 0.10}$ ${-0.60_{-0.10}^{+0.10}}$	$15 . 8_{- 0.9}^{+ 1.0}$ ${15.8_{-0.9}^{+1.0}}$	$- 0 . 23_{- 0.05}^{+ 0.05}$ ${-0.23_{-0.05}^{+0.05}}$	$- 1 . 3_{- 0.1}^{+ 0.1}$ ${-1.3_{-0.1}^{+0.1}}$	$15800_{- 800}^{+ 700}$ ${15800_{-800}^{+700}}$	68.606	0.0031	BPL
-2	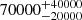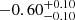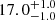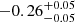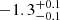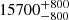$70000_{- 20000}^{+ 40000}$ ${70000_{-20000}^{+40000}}$	$- 0 . 60_{- 0.10}^{+ 0.10}$ ${-0.60_{-0.10}^{+0.10}}$	$17 . 0_{- 1.0}^{+ 1.0}$ ${17.0_{-1.0}^{+1.0}}$	$- 0 . 26_{- 0.05}^{+ 0.05}$ ${-0.26_{-0.05}^{+0.05}}$	$- 1 . 3_{- 0.1}^{+ 0.1}$ ${-1.3_{-0.1}^{+0.1}}$	$15700_{- 800}^{+ 800}$ ${15700_{-800}^{+800}}$	64.125	0.0035	BPL
-1	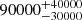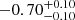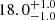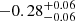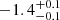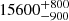$90000_{- 30000}^{+ 40000}$ ${90000_{-30000}^{+40000}}$	$- 0 . 70_{- 0.10}^{+ 0.10}$ ${-0.70_{-0.10}^{+0.10}}$	$18 . 0_{- 1.0}^{+ 1.0}$ ${18.0_{-1.0}^{+1.0}}$	$- 0 . 28_{- 0.06}^{+ 0.06}$ ${-0.28_{-0.06}^{+0.06}}$	$- 1 . 4_{- 0.1}^{+ 0.1}$ ${-1.4_{-0.1}^{+0.1}}$	$15600_{- 900}^{+ 800}$ ${15600_{-900}^{+800}}$	56.881	0.0041	BPL
0	$110000_{- 30000}^{+ 40000}$ ${110000_{-30000}^{+40000}}$	$- 0 . 70_{- 0.10}^{+ 0.10}$ ${-0.70_{-0.10}^{+0.10}}$	$19 . 0_{- 1.0}^{+ 1.0}$ ${19.0_{-1.0}^{+1.0}}$	$- 0 . 31_{- 0.07}^{+ 0.07}$ ${-0.31_{-0.07}^{+0.07}}$	$- 1 . 4_{- 0.1}^{+ 0.1}$ ${-1.4_{-0.1}^{+0.1}}$	$15600_{- 900}^{+ 900}$ ${15600_{-900}^{+900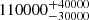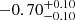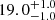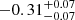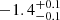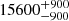}}$	52.735	0.0046	BPL
1	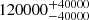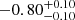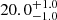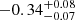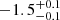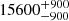$120000_{- 40000}^{+ 40000}$ ${120000_{-40000}^{+40000}}$	$- 0 . 80_{- 0.10}^{+ 0.10}$ ${-0.80_{-0.10}^{+0.10}}$	$20 . 0_{- 1.0}^{+ 1.0}$ ${20.0_{-1.0}^{+1.0}}$	$- 0 . 34_{- 0.07}^{+ 0.08}$ ${-0.34_{-0.07}^{+0.08}}$	$- 1 . 5_{- 0.1}^{+ 0.1}$ ${-1.5_{-0.1}^{+0.1}}$	$15600_{- 900}^{+ 900}$ ${15600_{-900}^{+900}}$	44.667	0.0059	BPL
2	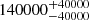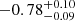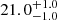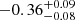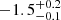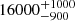$140000_{- 40000}^{+ 40000}$ ${140000_{-40000}^{+40000}}$	$- 0 . 78_{- 0.09}^{+ 0.10}$ ${-0.78_{-0.09}^{+0.10}}$	$21 . 0_{- 1.0}^{+ 1.0}$ ${21.0_{-1.0}^{+1.0}}$	$- 0 . 36_{- 0.08}^{+ 0.09}$ ${-0.36_{-0.08}^{+0.09}}$	$- 1 . 5_{- 0.1}^{+ 0.2}$ ${-1.5_{-0.1}^{+0.2}}$	$16000_{- 900}^{+ 1000}$ ${16000_{-900}^{+1000}}$	36.955	0.0077	BPL
3	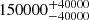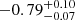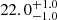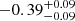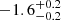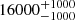$150000_{- 40000}^{+ 40000}$ ${150000_{-40000}^{+40000}}$	$- 0 . 79_{- 0.07}^{+ 0.10}$ ${-0.79_{-0.07}^{+0.10}}$	$22 . 0_{- 1.0}^{+ 1.0}$ ${22.0_{-1.0}^{+1.0}}$	$- 0 . 39_{- 0.09}^{+ 0.09}$ ${-0.39_{-0.09}^{+0.09}}$	$- 1 . 6_{- 0.2}^{+ 0.2}$ ${-1.6_{-0.2}^{+0.2}}$	$16000_{- 1000}^{+ 1000}$ ${16000_{-1000}^{+1000}}$	31.043	0.0099	BPL
4	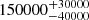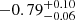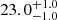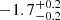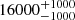$150000_{- 40000}^{+ 30000}$ ${150000_{-40000}^{+30000}}$	$- 0 . 79_{- 0.06}^{+ 0.10}$ ${-0.79_{-0.06}^{+0.10}}$	$23 . 0_{- 1.0}^{+ 1.0}$ ${23.0_{-1.0}^{+1.0}}$	$- 0 . 40_{- 0.10}^{+ 0.10}$ ${-0.40_{-0.10}^{+0.10}}$	$- 1 . 7_{- 0.2}^{+ 0.2}$ ${-1.7_{-0.2}^{+0.2}}$	$16000_{- 1000}^{+ 1000}$ ${16000_{-1000}^{+1000}}$	26.984	0.0121	BPL
5	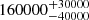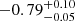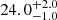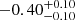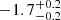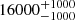$160000_{- 40000}^{+ 30000}$ ${160000_{-40000}^{+30000}}$	$- 0 . 79_{- 0.05}^{+ 0.10}$ ${-0.79_{-0.05}^{+0.10}}$	$24 . 0_{- 1.0}^{+ 2.0}$ ${24.0_{-1.0}^{+2.0}}$	$- 0 . 40_{- 0.10}^{+ 0.10}$ ${-0.40_{-0.10}^{+0.10}}$	$- 1 . 7_{- 0.2}^{+ 0.2}$ ${-1.7_{-0.2}^{+0.2}}$	$16000_{- 1000}^{+ 1000}$ ${16000_{-1000}^{+1000}}$	25.628	0.013	BPL
6	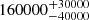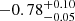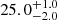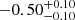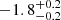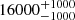$160000_{- 40000}^{+ 30000}$ ${160000_{-40000}^{+30000}}$	$- 0 . 78_{- 0.05}^{+ 0.10}$ ${-0.78_{-0.05}^{+0.10}}$	$25 . 0_{- 2.0}^{+ 1.0}$ ${25.0_{-2.0}^{+1.0}}$	$- 0 . 50_{- 0.10}^{+ 0.10}$ ${-0.50_{-0.10}^{+0.10}}$	$- 1 . 8_{- 0.2}^{+ 0.2}$ ${-1.8_{-0.2}^{+0.2}}$	$16000_{- 1000}^{+ 1000}$ ${16000_{-1000}^{+1000}}$	25.731	0.0129	BPL
7	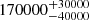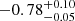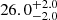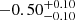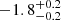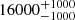$170000_{- 40000}^{+ 30000}$ ${170000_{-40000}^{+30000}}$	$- 0 . 78_{- 0.05}^{+ 0.10}$ ${-0.78_{-0.05}^{+0.10}}$	$26 . 0_{- 2.0}^{+ 2.0}$ ${26.0_{-2.0}^{+2.0}}$	$- 0 . 50_{- 0.10}^{+ 0.10}$ ${-0.50_{-0.10}^{+0.10}}$	$- 1 . 8_{- 0.2}^{+ 0.2}$ ${-1.8_{-0.2}^{+0.2}}$	$16000_{- 1000}^{+ 1000}$ ${16000_{-1000}^{+1000}}$	27.953	0.0115	BPL
8	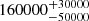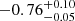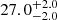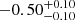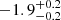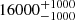$160000_{- 50000}^{+ 30000}$ ${160000_{-50000}^{+30000}}$	$- 0 . 76_{- 0.05}^{+ 0.10}$ ${-0.76_{-0.05}^{+0.10}}$	$27 . 0_{- 2.0}^{+ 2.0}$ ${27.0_{-2.0}^{+2.0}}$	$- 0 . 50_{- 0.10}^{+ 0.10}$ ${-0.50_{-0.10}^{+0.10}}$	$- 1 . 9_{- 0.2}^{+ 0.2}$ ${-1.9_{-0.2}^{+0.2}}$	$16000_{- 1000}^{+ 1000}$ ${16000_{-1000}^{+1000}}$	30.732	0.01	BPL
9	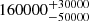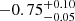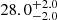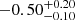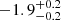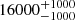$160000_{- 50000}^{+ 30000}$ ${160000_{-50000}^{+30000}}$	$- 0 . 75_{- 0.05}^{+ 0.10}$ ${-0.75_{-0.05}^{+0.10}}$	$28 . 0_{- 2.0}^{+ 2.0}$ ${28.0_{-2.0}^{+2.0}}$	$- 0 . 50_{- 0.10}^{+ 0.20}$ ${-0.50_{-0.10}^{+0.20}}$	$- 1 . 9_{- 0.2}^{+ 0.2}$ ${-1.9_{-0.2}^{+0.2}}$	$16000_{- 1000}^{+ 1000}$ ${16000_{-1000}^{+1000}}$	34.483	0.0085	BPL
10	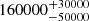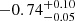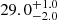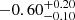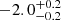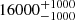$160000_{- 50000}^{+ 30000}$ ${160000_{-50000}^{+30000}}$	$- 0 . 74_{- 0.05}^{+ 0.10}$ ${-0.74_{-0.05}^{+0.10}}$	$29 . 0_{- 2.0}^{+ 1.0}$ ${29.0_{-2.0}^{+1.0}}$	$- 0 . 60_{- 0.10}^{+ 0.20}$ ${-0.60_{-0.10}^{+0.20}}$	$- 2 . 0_{- 0.2}^{+ 0.2}$ ${-2.0_{-0.2}^{+0.2}}$	$16000_{- 1000}^{+ 1000}$ ${16000_{-1000}^{+1000}}$	37.033	0.0077	BPL

Notes. Values shown are the median and 16th and 84th percentile uncertainties. The BPL results for a time-shift of 0 days agree within uncertainties with the parameters of the generating function shown in Table C.1.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.