Scintillometry of fast radio bursts - Resolution effects in two-screen models

Home

All issues

Volume 700 (August 2025)

A&A, 700 (2025) A99

Full HTML

Open Access

Table 1.

Comparison of formulas proposed to constrain the distance between the FRB source and host galaxy screen.

Study	Distance estimation formula	D_{h,FRB 20190520B}	D_{h,FRB 20201124A}	D_{h,FRB 20221022A}
Main et al. (2022)	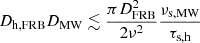$D_{h,FRB} D_{MW} ≲ \frac{π D_{FRB}^{2}}{2 ν^{2}} \frac{ν_{s,MW}}{τ_{s,h}}$ $D_{\text{h,FRB}}D_{\text{MW}} \lesssim \frac{\pi D_{\text{FRB}}^2}{2 \nu^2}\frac{\nu_{\text{s,MW}}}{\tau_{\text{s,h}}}$	≲1.1 kpc	≲34 kpc	≲135 kpc
Ocker et al. (2022)	$D_{h,FRB} D_{MW} ≲ \frac{D_{FRB}^{2}}{2 π ν^{2}} \frac{ν_{s,MW}}{τ_{s,h}}$ $D_{\text{h,FRB}}D_{\text{MW}} \lesssim \frac{D_{\text{FRB}}^2}{2 \pi \nu^2} \frac{\nu_{\text{s,MW}}}{ \tau_{\text{s,h}} }$	≲0.11 kpc	≲3.4 kpc	≲14 kpc
Nimmo et al. (2025)
Sammons et al. (2023)	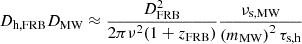$D_{h,FRB} D_{MW} \approx \frac{D_{FRB}^{2}}{2 π ν^{2} (1 + z_{FRB})} \frac{ν_{s,MW}}{{(m_{MW})}^{2} τ_{s,h}}$ $D_{\text{h,FRB}}D_{\text{MW}} \approx \frac{D_{\text{FRB}}^2}{2 \pi \nu^2 (1+z_{\text{FRB}})} \frac{\nu_{\text{s,MW}}}{\left(m_{\text{MW}}\right)^2 \tau_{\text{s,h}}}$	(≈0.088 kpc)	≈9.0 kpc	≈22 kpc
This work	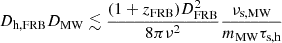$D_{h,FRB} D_{MW} ≲ \frac{(1 + z_{FRB}) D_{FRB}^{2}}{8 π ν^{2}} \frac{ν_{s,MW}}{m_{MW} τ_{s,h}}$ $D_{\text{h,FRB}}D_{\text{MW}} \lesssim \frac{(1 + z_{\text{FRB}}) D_{\text{FRB}}^2}{8 \pi \nu^2 } \frac{\nu_{\text{s,MW}}}{m_{\text{MW}} \tau_{\text{s,h}}}$	(≲0.034 kpc)	≲1.6 kpc	≲4.5 kpc

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.