Cosmology with supernova Encore in the strong lensing cluster MACS J0138−2155 - Photometry, cluster members, and lens mass model

Home

All issues

Volume 702 (October 2025)

A&A, 702 (2025) A157

Full HTML

Open Access

Table C.1.

Model parameter priors and inferred values from observed image positions and stellar velocity dispersion measurements.

Parameter	Description	Prior	`iso_halo`	`PL_halo`	`iso_halo+sheet`	`iso_halo+ell_BCG`	`baseline`
Scaling relation (ID_phot = 115)

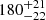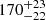σ_v, 115 [km/s]	velocity dispersion	𝒢(206,25)	$180_{- 22}^{+ 21}$ $180_{-22}^{+21}$	180 ± 21	170 ± 21	$180_{- 22}^{+ 20}$ $180_{-22}^{+20}$	$170_{- 22}^{+ 23}$ $170_{-22}^{+23}$
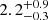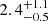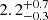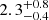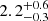r_t, 115 [″]	truncation radius	flat(1.8,40)	$2 . 2_{- 0.3}^{+ 0.9}$ $2.2_{-0.3}^{+0.9}$	$2 . 4_{- 0.5}^{+ 1.1}$ $2.4_{-0.5}^{+1.1}$	$2 . 2_{- 0.3}^{+ 0.7}$ $2.2_{-0.3}^{+0.7}$	$2 . 3_{- 0.4}^{+ 0.8}$ $2.3_{-0.4}^{+0.8}$	$2 . 2_{- 0.3}^{+ 0.6}$ $2.2_{-0.3}^{+0.6}$

BCG

(x_BCG, y_BCG) [″]	centroid	exact	(0, 0)	(0, 0)	(0, 0)	(0, 0)	(0, 0)
q_BCG	axis ratio	exact or flat(0.4,1)	1	1	1	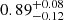$0 . 89_{- 0.12}^{+ 0.08}$ $0.89_{-0.12}^{+0.08}$	1
ϕ_BCG [°]	position angle	flat(0,360)	—	—	—	36 ± 63	—
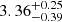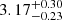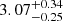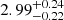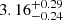θ_{E, ∞, BCG} [″]	Einstein radius	𝒢(3.08,0.32)^†	$3 . 36_{- 0.39}^{+ 0.25}$ $3.36_{-0.39}^{+0.25}$	$3 . 17_{- 0.23}^{+ 0.30}$ $3.17_{-0.23}^{+0.30}$	$3 . 07_{- 0.25}^{+ 0.34}$ $3.07_{-0.25}^{+0.34}$	$2 . 99_{- 0.22}^{+ 0.24}$ $2.99_{-0.22}^{+0.24}$	$3 . 16_{- 0.24}^{+ 0.29}$ $3.16_{-0.24}^{+0.29}$
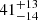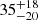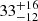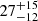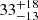r_t, BCG [″]	truncation radius	flat(1,50)	$41_{- 14}^{+ 13}$ $41_{-14}^{+13}$	$35_{- 20}^{+ 18}$ $35_{-20}^{+18}$	$33_{- 12}^{+ 16}$ $33_{-12}^{+16}$	$27_{- 12}^{+ 15}$ $27_{-12}^{+15}$	$33_{- 13}^{+ 18}$ $33_{-13}^{+18}$

Cluster member not in scaling relation

(x₁₁₆, y₁₁₆) [″]	centroid	exact	(0.314, 9.819)	(0.314, 9.819)	(0.314, 9.819)	(0.314, 9.819)	(0.314, 9.819)
q₁₁₆	axis ratio	exact	1	1	1	1	1
θ_{E, ∞, 116} [″]	Einstein radius G1	𝒢(1.67,0.19)^†	1.6 ± 0.2	1.6 ± 0.2	1.6 ± 0.2	1.6 ± 0.2	1.6 ± 0.2
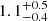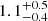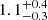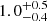r_t, 116 [″]	truncation radius	flat(0.05,10)	$1 . 1_{- 0.4}^{+ 0.5}$ $1.1_{-0.4}^{+0.5}$	1.1 ± 0.4	$1 . 1_{- 0.4}^{+ 0.5}$ $1.1_{-0.4}^{+0.5}$	$1 . 1_{- 0.3}^{+ 0.4}$ $1.1_{-0.3}^{+0.4}$	$1 . 0_{- 0.4}^{+ 0.5}$ $1.0_{-0.4}^{+0.5}$

Jellyfish galaxies

(x_JF1, y_JF1) [″]	centroid	exact	(19.094, −13.361)	(19.094, −13.361)	(19.094, −13.361)	(19.094, −13.361)	(19.094, −13.361)
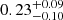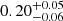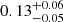θ_{E, ∞, JF1} [″]	Einstein radius	flat(0.01,10)	0.25 ± 0.07	0.25 ± 0.08	$0 . 23_{- 0.10}^{+ 0.09}$ $0.23_{-0.10}^{+0.09}$	$0 . 20_{- 0.06}^{+ 0.05}$ $0.20_{-0.06}^{+0.05}$	$0 . 13_{- 0.05}^{+ 0.06}$ $0.13_{-0.05}^{+0.06}$
r_t, JF1 [″]	truncation radius	exact	5	5	5	5	5
(x_JF2, y_JF2) [″]	centroid	exact	(−5.114, 6.941)	(−5.114, 6.941)	(−5.114, 6.941)	(−5.114, 6.941)	(−5.114, 6.941)
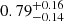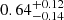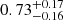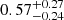θ_{E, ∞, JF2} [″]	Einstein radius	flat(0.01,10)	$0 . 79_{- 0.14}^{+ 0.16}$ $0.79_{-0.14}^{+0.16}$	$0 . 64_{- 0.14}^{+ 0.12}$ $0.64_{-0.14}^{+0.12}$	0.63 ± 0.14	$0 . 73_{- 0.16}^{+ 0.17}$ $0.73_{-0.16}^{+0.17}$	$0 . 57_{- 0.24}^{+ 0.27}$ $0.57_{-0.24}^{+0.27}$
r_t, JF2 [″]	truncation radius	exact	5	5	5	5	5

(x_JF3, y_JF3) [″]	centroid	exact	(−1.649, 2.597)	(−1.649, 2.597)	(−1.649, 2.597)	(−1.649, 2.597)	(−1.649, 2.597)
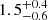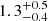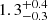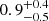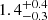θ_{E, ∞, JF3} [″]	Einstein radius	flat(0.01,10)	$1 . 5_{- 0.6}^{+ 0.4}$ $1.5_{-0.6}^{+0.4}$	$1 . 3_{- 0.4}^{+ 0.5}$ $1.3_{-0.4}^{+0.5}$	$1 . 3_{- 0.3}^{+ 0.4}$ $1.3_{-0.3}^{+0.4}$	$0 . 9_{- 0.5}^{+ 0.4}$ $0.9_{-0.5}^{+0.4}$	$1 . 4_{- 0.3}^{+ 0.4}$ $1.4_{-0.3}^{+0.4}$
r_t, JF3 [″]	truncation radius	exact	5	5	5	5	5

Foreground galaxy

(x_fg, y_fg) [″]	centroid	exact	(−0.868, −16.564)	(−0.868, −16.564)	(−0.868, −16.564)	(−0.868, −16.564)	(−0.868, −16.564)
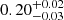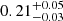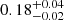θ_{E, ∞, fg} [″]	Einstein radius	flat(0.1,10)	$0 . 20_{- 0.03}^{+ 0.02}$ $0.20_{-0.03}^{+0.02}$	0.24 ± 0.04	$0 . 21_{- 0.03}^{+ 0.05}$ $0.21_{-0.03}^{+0.05}$	0.20 ± 0.03	$0 . 18_{- 0.02}^{+ 0.04}$ $0.18_{-0.02}^{+0.04}$
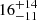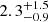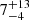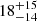r_t, fg [″]	truncation radius	flat(0.1,40)	$16_{- 11}^{+ 14}$ $16_{-11}^{+14}$	$2 . 3_{- 0.9}^{+ 1.5}$ $2.3_{-0.9}^{+1.5}$	$7_{- 4}^{+ 13}$ $7_{-4}^{+13}$	$18_{- 14}^{+ 15}$ $18_{-14}^{+15}$	$8_{- 7}^{+ 28}$ $8_{-7}^{+28}$

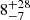Background galaxy

(x_bkg, y_bkg) [″]	centroid	exact	(6.871, 3.843)	(6.871, 3.843)	(6.871, 3.843)	(6.871, 3.843)	(6.871, 3.843)
θ_{E, ∞, bkg} [″]	Einstein radius	𝒢(1.66,0.10)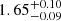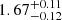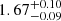^†	$1 . 65_{- 0.09}^{+ 0.10}$ $1.65_{-0.09}^{+0.10}$	$1 . 67_{- 0.12}^{+ 0.11}$ $1.67_{-0.12}^{+0.11}$	$1 . 67_{- 0.09}^{+ 0.10}$ $1.67_{-0.09}^{+0.10}$	1.67 ± 0.09	1.64 ± 0.10
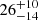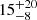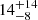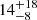r_t, bkg [″]	truncation radius	flat(0.1,40)	$26_{- 14}^{+ 10}$ $26_{-14}^{+10}$	22 ± 12	$15_{- 8}^{+ 20}$ $15_{-8}^{+20}$	$14_{- 8}^{+ 14}$ $14_{-8}^{+14}$	$14_{- 8}^{+ 18}$ $14_{-8}^{+18}$

Dark matter halos

x_DM1 [″]	x centroid	flat(−20,20)	−0.1 ± 0.3	−0.2 ± 0.3	−0.1 ± 0.3	−0.3 ± 0.3	0.1 ± 0.3
y_DM1 [″]	y centroid	flat(−20,20)	−1.2 ± 0.5	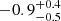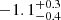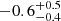$- 0 . 9_{- 0.5}^{+ 0.4}$ $-0.9_{-0.5}^{+0.4}$	$- 1 . 1_{- 0.4}^{+ 0.3}$ $-1.1_{-0.4}^{+0.3}$	$- 0 . 6_{- 0.4}^{+ 0.5}$ $-0.6_{-0.4}^{+0.5}$	−1.1 ± 0.4
q_DM1	axis ratio	flat(0.2,1)	0.64 ± 0.02	0.64 ± 0.02	0.63 ± 0.02	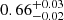$0 . 66_{- 0.02}^{+ 0.03}$ $0.66_{-0.02}^{+0.03}$	0.63 ± 0.02
ϕ_DM1 [°]	position angle	flat(0,360)	43 ± 1	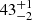$43_{- 2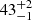}^{+ 1}$ $43_{-2}^{+1}$	44 ± 2	$43_{- 1}^{+ 2}$ $43_{-1}^{+2}$	45 ± 2
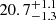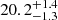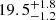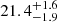θ_{E, ∞, DM1} [″]	Einstein radius	flat(0,50)	$20 . 7_{- 1.3}^{+ 1.1}$ $20.7_{-1.3}^{+1.1}$	—	$20 . 2_{- 1.3}^{+ 1.4}$ $20.2_{-1.3}^{+1.4}$	$19 . 5_{- 1.2}^{+ 1.8}$ $19.5_{-1.2}^{+1.8}$	$21 . 4_{- 1.9}^{+ 1.6}$ $21.4_{-1.9}^{+1.6}$
E [″]	halo strength	flat(0,50)	—	13 ± 2	—	—	—
r_c, DM1 [″]	core radius	flat(0,50)	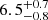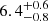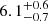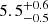$6 . 5_{- 0.8}^{+ 0.7}$ $6.5_{-0.8}^{+0.7}$	$6 . 4_{- 0.8}^{+ 0.6}$ $6.4_{-0.8}^{+0.6}$	$6 . 1_{- 0.7}^{+ 0.6}$ $6.1_{-0.7}^{+0.6}$	$5 . 5_{- 0.5}^{+ 0.6}$ $5.5_{-0.5}^{+0.6}$	6.6 ± 0.8
γ	radial slope	flat(0.,2.)	—	0.51 ± 0.03	—	—	—

x_DM2 [″]	x centroid	flat(−30,30)	$25_{- 5}^{+ 4}$ $25_{-5}^{+4}$	$20_{- 5}^{+ 6}$ $20_{-5}^{+6}$	$21_{- 8}^{+ 6}$ $21_{-8}^{+6}$	$18_{- 3}^{+ 8}$ $18_{-3}^{+8}$	$19_{- 6}^{+ 9}$ $19_{-6}^{+9}$
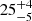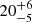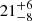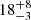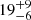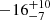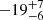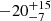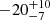y_DM2 [″]	y centroid	flat(−30,30)	$- 16_{- 7}^{+ 10}$ $-16_{-7}^{+10}$	$- 19_{- 6}^{+ 7}$ $-19_{-6}^{+7}$	$- 20_{- 7}^{+ 15}$ $-20_{-7}^{+15}$	−22 ± 4	$- 20_{- 7}^{+ 10}$ $-20_{-7}^{+10}$
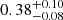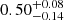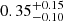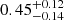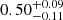q_DM2	axis ratio	flat(0.2,1)	$0 . 38_{- 0.08}^{+ 0.10}$ $0.38_{-0.08}^{+0.10}$	$0 . 50_{- 0.14}^{+ 0.08}$ $0.50_{-0.14}^{+0.08}$	$0 . 35_{- 0.10}^{+ 0.15}$ $0.35_{-0.10}^{+0.15}$	$0 . 45_{- 0.14}^{+ 0.12}$ $0.45_{-0.14}^{+0.12}$	$0 . 50_{- 0.11}^{+ 0.09}$ $0.50_{-0.11}^{+0.09}$
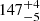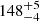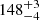ϕ_DM2 [°]	position angle	flat(0,360)	$147_{- 5}^{+ 4}$ $147_{-5}^{+4}$	145 ± 3	$148_{- 4}^{+ 5}$ $148_{-4}^{+5}$	141 ± 4	$148_{- 4}^{+ 3}$ $148_{-4}^{+3}$
θ_{E, ∞, DM2} [″]	Einstein radius	flat(0,50)	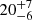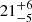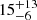$20_{- 6}^{+ 7}$ $20_{-6}^{+7}$	$21_{- 5}^{+ 6}$ $21_{-5}^{+6}$	$15_{- 6}^{+ 13}$ $15_{-6}^{+13}$	23 ± 6	$25_{- 6}^{+ 8}$ $25_{-6}^{+8}$
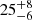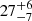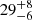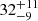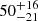r_c, DM2 [″]	core radius	flat(0,70)	$27_{- 7}^{+ 6}$ $27_{-7}^{+6}$	$29_{- 6}^{+ 8}$ $29_{-6}^{+8}$	$32_{- 9}^{+ 11}$ $32_{-9}^{+11}$	24 ± 5	$50_{- 21}^{+ 16}$ $50_{-21}^{+16}$

Mass sheet

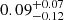κ₀	mass sheet	flat(−1,1)	—	—	$0 . 09_{- 0.12}^{+ 0.07}$ $0.09_{-0.12}^{+0.07}$	—	—

Notes. Columns 1 and 2 are the parameter and description. Column 3 is the prior on the parameter, where the letter 𝒢 denotes a Gaussian prior, with its center and 1σ width in parentheses. The Gaussian priors on the Einstein radii with a ^† symbol are based on the first version of velocity dispersion measurements from Granata et al. (2025) using an older version of stellar template libraries; the final velocity dispersion measurements change by ≲1 km s⁻¹, which has negligible effect on the modeling results. Columns 4 to 7 list the inferred parameter values of the corresponding mass models indicated in the header line. Parameter values that have no uncertainties are parameters that are fixed with priors listed as ‘exact’. A dashed line in the parameter value indicates that the parameter is not present in the particular mass model. Position angles are measured east of north in degrees.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.