Fig. 1.
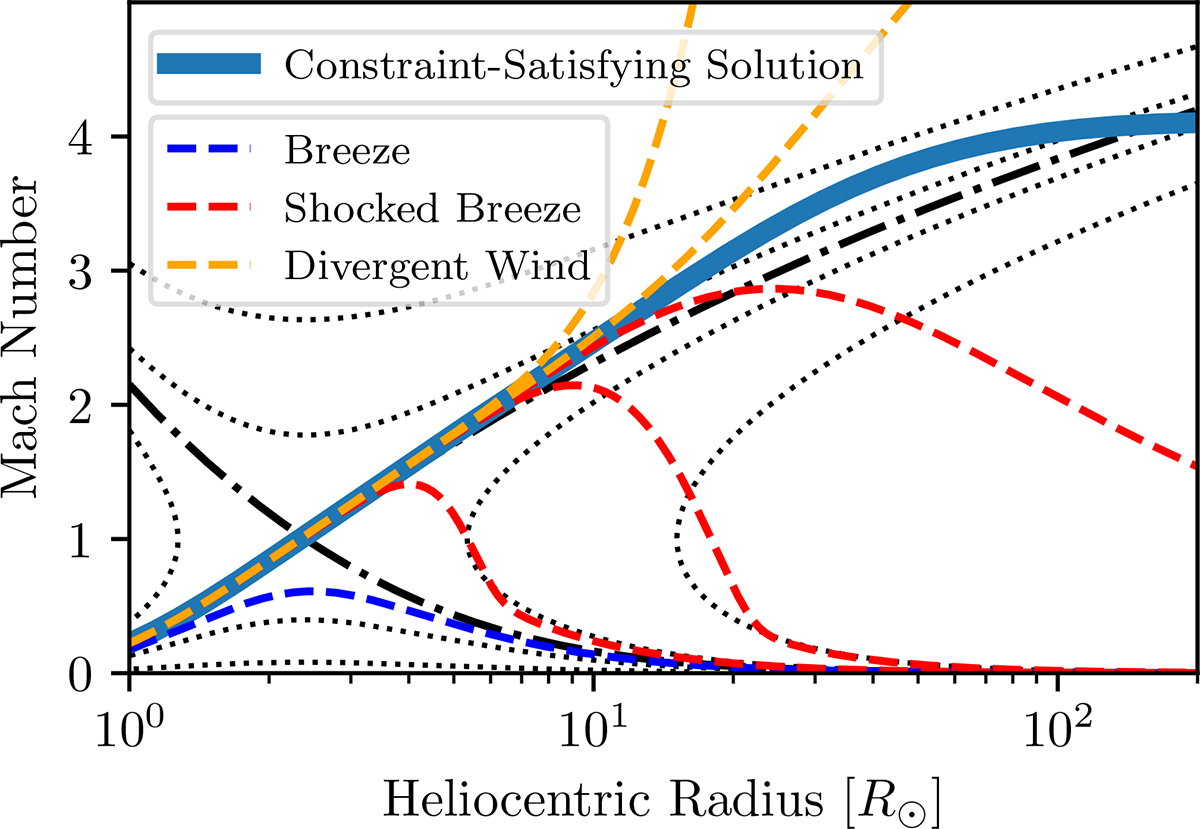
Download original image
Comparison of the viscous isothermal solutions to the analytical (inviscid) Parker solution. The black curves represent contours of De Leval’s Equation (32). Of these, only the black dashed-dotted curve(s) exhibits a sonic point at the allowed critical point, consistent with Parker’s description of a transonic solar wind. The variously colored blue, yellow, and red curves are numerical solutions to the viscous isothermal equations. The dashed blue curve is a subsonic breeze solution for which to u → 0 as s → ∞. The dashed yellow (divergent wind) and red (shocked breeze) curves are transonic solutions that exhibit either u → ∞ or u → 0, respectively, as s → ∞. The constraint matching solution (solid teal curve) satisfies the boundary condition σ(s = 1 AU) = 0.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


