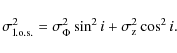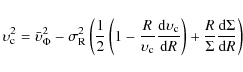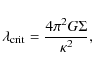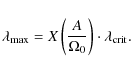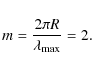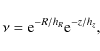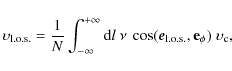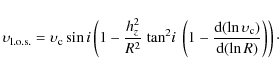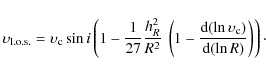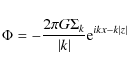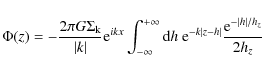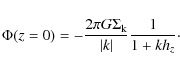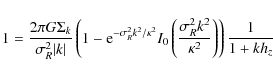On the nature of IC 3328, an early-type dwarf galaxy with weak spiral structure

T. Lisker; B. Fuchs

doi:10.1051/0004-6361/200811331

Home

All issues

Volume 501 / No 2 (July II 2009)

A&A, 501 2 (2009) 429-435

Full HTML

Free Access

Issue		A&A Volume 501, Number 2, July II 2009


Page(s)		429 - 435
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361/200811331
Published online		13 May 2009

On the nature of IC 3328, an early-type dwarf galaxy with weak spiral structure

T. Lisker - B. Fuchs

Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstraße 12-14, 69120 Heidelberg, Germany

Received 11 November 2008 / Accepted 13 March 2009

Abstract
Various early-type dwarf galaxies with disk features have been identified in the Virgo cluster, including objects that display weak grand-design spiral arms despite being devoid of gas. Are these still related to the classical dEs, or are they a continuation of ordinary spiral galaxies? Kinematical information of acceptable quality is available for one of these galaxies, IC 3328. We investigated its dynamical configuration, taking the effect of asymmetric drift into account, and using the Toomre parameter, as well as density wave considerations. The derived mass-to-light ratios and rotational velocities indicate a significant dynamically hot component in addition to the disk. However, any unambiguous conclusions will need to await further data for this and other early-type dwarfs with spiral structure.

Key words: galaxies: dwarf - galaxies: elliptical and lenticular, cD - galaxies: fundamental parameters - galaxies: kinematics and dynamics - galaxies: spiral - galaxies: structure

1 Introduction

As the most numerous type of galaxy in clusters and the possible descendants of the building blocks in hierarchical structure formation, early-type dwarf (dE) galaxies play a key role toward understanding galaxy cluster evolution. Initially believed to be spheroidal objects having old stellar populations and preferring the high-density regions of clusters, today's picture of dEs is far more diverse. In the Virgo cluster, several subclasses with significantly different characteristics exist (Lisker et al. 2007), and these are correlated with environmental density. Those dEs that populate less dense cluster regions partly have younger stellar populations (Lisker et al. 2006a,2008), flatter shapes (Lisker et al. 2007; Ferguson & Sandage 1989; Lisker et al. 2006b), and clustering properties not like giant ellipticals but similar to spiral galaxies (Lisker et al. 2007).

Among them is the ``dE(di)'' subclass, characterised by weak disk features - like spiral arms or bars - that could only be seen through unsharp masks or by subtracting a model of the smooth galaxy light (Lisker et al. 2006b). The first discovery of spiral structure in a dE was reported by Jerjen et al. (2000) for the galaxy IC 3328 (VCC 856), which is also the focus of the work presented here (Fig. 1). The dE(di)s are not a negligible species, but they make up one third of the brighter (M_B<-16) Virgo cluster dEs, reaching a fraction of 50% at the bright end. For those showing spiral substructure, the arm opening angles are inconsistent with being the mere remainders of late-type progenitor galaxies (Lisker et al. 2006b; Jerjen et al. 2000), and the arms do not show up in colour maps that would indicate stellar population differences (Lisker et al. 2006b).

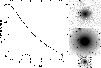$\begin{figure} \par\resizebox{9cm}{!}{\rotatebox{0}{\includegraphics{1331fig1.eps}}} \end{figure}$

Figure 1:

Appearance and light profile of IC 3328. Surface brightness in SDSS-r versus radius, adopting a distance modulus m-M=31.0 mag (d=15.85 Mpc, van den Bergh 1996), corresponding to a scale of 77 pc/ $^{\prime \prime }$ . The half-light radius $r_{\rm e}$ , as well as 2.2 scalelengths h (using $r_{\rm e}=1.68h$ ), are indicated by the vertical dotted lines. The images shown on the right are, from top to bottom, the SDSS r-band image, a deep white-filter image obtained with ESO 2.2m/WFI (program 077.B-0785), and an unsharp mask image of the latter, revealing the spiral arm structure. The half-light aperture is indicated in the SDSS and unsharp mask image.

Open with DEXTER

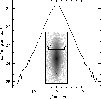$\begin{figure} \par\resizebox{9cm}{!}{\rotatebox{0}{\includegraphics{1331fig2.eps}}} \end{figure}$

Figure 2:

Light profile in z-direction of IC 3435. SDSS r-band image (inset) of IC 3435, and the intensity profile obtained by collapsing the outlined box-shaped region along the galaxy's major axis. The box has a side length corresponding to the major axis of the half-light elliptical isophote, or equivalently, three times its minor axis. Smearing due to seeing effects can occur in the innermost $\sim$ $\pm$ $1.5\hbox {$^{\prime \prime }$ }$ .

Open with DEXTER

An indication that the dE(di)s might have been formed out of infalling disk galaxies is that spiral arms and bar structures in dEs also arise in N-body simulations of galaxy harassment (Mastropietro et al. 2005), in which late-type galaxies accreted by the cluster experience a violent structural transformation (Moore et al. 1996; also see Kormendy et al. 2009). Alternatively, the dE(di)s - being compact, gas-poor disk galaxies - might simply constitute the low-luminosity counterpart to normal S0/Sa galaxies, with a few ``dwarf-like'' S0/Sa galaxies possibly bridging the gap to the more luminous systems (Lisker et al. 2006a).

Do the dE(di)s have a significant dynamically hot component, which would be expected for dEs with embedded disks, or are they consistent with being pure disk galaxies? A first assessment can be provided by examining an apparently edge-on dE(di), IC 3435 (VCC 1304, Fig. 2, Lisker et al. 2006b). Its axis ratio of 0.33 equals the estimate for the intrinsic axis ratio of the dE(di)s from Lisker et al. (2007). While it is, of course, not known whether this galaxy hosts similar spiral structure to IC 3328, it still appears worth examining whether a thin disk component is visible in the vertical light profile, i.e. perpendicular to the disk. However, from the SDSS r-band image, no such component is seen (Fig. 2), and the profile appears perfectly consistent with a single exponential decline.

In this context, it would be obvious to ask about the kinematical properties of the dE(di)s with spiral arms. Unfortunately, useful kinematical data is only available for one of these enigmatic objects, namely IC 3328, and only along its major axis (Simien & Prugniel 2002). Here we attempt to draw conclusions on the nature of IC 3328 from these data.

2 Data

2.1 Structural measurements

Total magnitude, half-light radius, and ellipticity of IC 3328 were measured from r-band images of the Sloan Digital Sky Survey (Adelman-McCarthy et al. 2007), as outlined in Lisker et al. (2008). The ellipticity of 0.87, measured at the half-light radius, is consistent with the ellipticity that could be derived from the spiral structure only, as illustrated in Fig. 1. This yields an inclination $i=30^{\circ}$ . The radial surface brightness profile in r, shown in Fig. 1, was measured from annuli of fixed elliptical shape, using IRAF/ellipse (Tody 1993). Out to the radial extent of the rotation curve (Fig. 3) it would be compatible with an exponential profile, i.e. a straight line. Nevertheless, a change in the profile slope is seen at larger radii. This is included in the discussion (Sect. 4).

2.2 Stellar mass-to-light ratio

From the analysis of SDSS multicolour photometry for Virgo dEs (Lisker et al. 2008), we can derive an estimate of the stellar mass-to-light ratio (M/L) of IC 3328, using the g-r and i-z colours measured within the half-light radius. With stellar population synthesis models of Bruzual & Charlot (2003), ``Padova 1994'' isochrones (Bertelli et al. 1994), a Chabrier (2003) initial mass function, and an exponentially declining star formation rate (decay time $\tau=1$ Gyr), we derive luminosity-weighted age and metallicity values of 7.5 Gyr (time since the onset of star formation) and Z=0.004 (corresponding to ${\rm [Fe/H]}=-0.64$ ). When using simple stellar population (SSP) models instead, the age changes to 5.9 Gyr. This perfectly agrees with the spectroscopic results from the Lick index analysis of Michielsen et al. (2008), who find 6.0 Gyr and ${\rm [Fe/H]}=-0.64$ using the SSP models of Vazdekis et al. (1996). It also agrees with a preliminary spectroscopic analysis of ESO VLT/FORS2 spectra (Paudel et al., in prep.).

The corresponding stellar M/L in V is (M/L)_V=1.4. Despite the good agreement of age and metallicity from different sources, we use the rather large age uncertainties given by Michielsen et al. (2008) ( 6⁺⁹_-4 Gyr) to obtain M/L uncertainties ( 1.4^+1.4_-0.8). This conservative approach is also supposed to cover any potential M/L uncertainties inherent to the modelling process.

2.3 Kinematical data

A rotation and velocity dispersion curve of IC 3328 was published by Simien & Prugniel (2002), obtained from major-axis long-slit spectroscopy taken at the Observatoire de Haute-Provence. For the analysis presented here, the average of published velocity data points at opposite sides of the centre was taken, and errors propagated accordingly. We correct for the inclination (Sect. 2.1) and consider the effect of finite disk thickness on the line-of-sight velocity distribution (Appendix A), yielding the rotation curve shown in Fig. 3. With the adopted intrinsic axis ratio of 0.33 (Lisker et al. 2007), the resulting velocity correction is negligible (< $3\%$ ) for radii beyond 0.5 disk scalelengths. The rotation curve published by Geha et al. (2003) is not used due to its significantly smaller radial extent.

$\begin{figure} \par\resizebox{18cm}{!}{\rotatebox{0}{\includegraphics{1331fig3.eps}}} \end{figure}$

Figure 3:

Rotation curve and the effect of asymmetric drift. Large filled circles are the inclination-corrected measurements from Simien & Prugniel (2002). The lower solid curve is a fit of $f(r)=a(1-{\rm e}^{-\frac{r}{b}})$ to them. Taking the asymmetric drift into account (see text) results in the small filled circles, along with the corresponding fit using the same function (upper solid curve). In the left panel, we use $\sigma _{R}=45$ km s^-1, while 71 km s^-1 is used in the right panel. The inclination-corrected measurements from Geha et al. (2003) are shown as filled squares in the left panel.

Open with DEXTER

3 Kinematical analysis

Our approach is to analyse the kinematical data of IC 3328 with the assumption of a pure disk, as implied by the vertical light profile of IC 3435 (Sect. 1). We then discuss whether a two-component galaxy would be more likely based on the results.

3.1 Velocity dispersion

The observed line-of-sight velocity dispersion $\sigma_{\rm {l.o.s.}}$ is more or less constant with radius, within the measurement uncertainties (Simien & Prugniel 2002), at 35 km s^-1. For major axis spectra, it can be expressed in terms of the angular and the vertical velocity dispersion as

$\begin{displaymath} \sigma_{\rm {l.o.s.}}^2 = \sigma_{\Phi}^2\sin^2i + \sigma_{\rm z}^2\cos^2i {.} \end{displaymath}$

(1)

Following Gerssen (2000), we adopt $\sigma_{z}=0.8\sigma_{R}$ as our ``working value'', but also perform our analysis using factors of 0.4 and 0.9 instead. This range covers the values found for galaxies of type T=1 to 5. For $\sigma_{\Phi}$ , we have

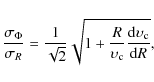$\begin{displaymath}\frac{\sigma_{\Phi}}{\sigma_{R}} = \frac{1}{\sqrt{2}}\sqrt{1+... ...\upsilon_{\rm c}}\frac{{\rm d}\upsilon_{\rm c}}{{\rm d}R}} {,} \end{displaymath}$

(2)

which we estimate to be between 0.7 and 1. With the above range of factors, this yields values for $\sigma_{\rm {l.o.s.}}$ between 0.5 and 0.9 times $\sigma_{R}$ , leading to $38\la \sigma_{R}\lesssim 71$ km s¹, with our working value being 45 km s^-1.

3.2 Asymmetric drift

While the asymmetric drift has a minor effect on the observed rotation curves of normal spiral galaxies, it can be much more significant for dwarf galaxies. The true orbital velocity at a given radius, $\upsilon_{\rm c}(R)$ , and the observed velocity, $\bar{\upsilon}_{\rm\Phi}$ , are related by the radial Jeans equation as follows (Binney & Tremaine 1987):

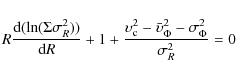$\begin{displaymath}R\frac{{\rm d}(\ln(\Sigma\sigma_{R}^2))}{{\rm d}R}+1+\frac{\u... ...\bar{\upsilon}_{\rm\Phi}^2-\sigma_{\rm\Phi}^2}{\sigma_{R}^2}=0 \end{displaymath}$

(3)

with $\upsilon_{\rm c}-\bar{\upsilon}_{\rm\Phi}$ the asymmetric drift velocity. (We neglect here the tilt of the velocity ellipsoid.) Adopting d $\sigma_{R}/{\rm d}R=0$ , this leads to

$\begin{displaymath} \upsilon_{\rm c}^2=\bar{\upsilon}_{\rm\Phi}^2-\sigma_{\rm R... ...}R}\right)+\frac{R}{\Sigma}\frac{\rm d\Sigma}{{\rm d}R}\right) \end{displaymath}$

(4)

with the surface mass density $\Sigma$ .

Since we do not want to impose any kinematical model on the analysis, we adopt the following simple method to derive d $\upsilon_{\rm c}/{\rm d}R$ and determine $\upsilon_{\rm c}(R)$ . The observed, inclination-corrected rotation curve is fitted with $f(r)=a(1-{\rm e}^{-\frac{r}{b}})$ , and its derivative is used as initial estimate for d $\upsilon_{\rm c}/{\rm d}R$ at each data point. The thus derived first iteration for $\upsilon_{\rm c}(R)$ is then also fitted with f(r), and the derivative is now used as a better estimate for d $\upsilon_{\rm c}/{\rm d}R$ , applying Eq. (4). Here, the surface mass density $\Sigma$ is taken to be the observed luminosity density, which is obtained from the surface brightness profile (Fig. 1) and the adopted distance of 15.85 Mpc. No specific M/L value needs to be assumed for the conversion, since it occurs in both the enumerator and the denominator of the last term of Eq. (4), thus cancelling out. In this and all following steps, we exclude data points at $R<3\hbox{$^{\prime\prime}$ }$ , since the luminosity density is only reliable for radii significantly larger than the SDSS seeing FWHM ( $\approx$ $1.5\hbox {$^{\prime \prime }$ }$ ).

This leads to the second iteration on $\upsilon_{\rm c}(R)$ , and is repeated one more time. The resulting data points for $\upsilon_{\rm c}(R)$ are then also fitted with f(r), yielding a rotation curve instead of discrete data points alone. The differences between the last and second-last iterations are very small ( $\lesssim$ 2 km s^-1). In this procedure we always set $\upsilon_{\rm c}(0)=0$ . The resulting curves are shown in the left panel of Fig. 3 for our working value $\sigma _{R}=45$ km s^-1 (Sect. 3.1), and in the right panel for the extreme case of $\sigma _{R}=71$ km s. These are the rotation curves that enter the calculations of the following sections.

3.3 Toomre stability parameter

Table 1: Mass-to-light ratio in V, using the colour transformation V=r+0.27 (Smith et al. 2002).

An important diagnostic of the dynamics of a galactic disk is the Toomre (1964) stability parameter:

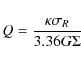$\begin{displaymath}Q=\frac{\kappa\sigma_{R}}{3.36G\Sigma} \end{displaymath}$

(5)

where $\Sigma$ is the surface density and $\kappa$ the epicyclic frequency. The value of Q for a thin disk must lie in the range $1<Q\la 2$ , to ensure that the disk is not only stable against local Jeans instabilities, but also able to develop spiral arms (Fuchs 2001). By choosing a value for Q, the mass density $\Sigma$ can be obtained, yielding a mass-to-light ratio when combined with the observed luminosity density.

To properly consider the disk thickness (adopted intrinsic axis ratio 0.33, see Sects. 1 and 2), we calculate how much more mass a thicker disk contains per surface area if it has the desired properties for spiral arm development (Appendix B). This is equivalent to using an ``effective Q'' value that is lower than the actual one for a thin disk. The above range of $1<Q\la 2$ thus changes to $0.62<Q_{\rm eff}\la 1.24$ for the case $\sigma _{R}=45$ km s^-1, and $0.64<Q_{\rm eff}\la 1.28$ for $\sigma _{R}=71$ km s^-1.

Table 1 shows the resulting values for M/L at the half-light radius when choosing Q=1.0,1.5,2.0 (i.e., $Q_{\rm eff}=0.62,0.93,1.24$ for $\sigma_{\rm R}=45$ km s^-1, etc.). These are compared to the stellar M/L from Sect. 2.2.

The thus derived mass density at the half-light radius can be used to predict the rotational velocity for an exponential disk model and for a Mestel disk. These values are listed in Table 2 and illustrated in Fig. 4, again for the three Q values.

3.4 Density wave theory

An alternative estimate for the mass density can be obtained from density wave theory. It predicts the circumferential wavelength $\lambda_{\rm max}$ at which density waves mainly grow. In terms of the critical wavelength (Toomre 1964),

$\begin{displaymath} \lambda_{\rm crit}=\frac{4\pi^2G\Sigma}{\kappa^2} , \end{displaymath}$

(6)

the preferred wavelength is given by (Toomre 1981; Athanassoula et al. 1987)

$\begin{displaymath} \lambda_{\rm max}= X\left(\frac{A}{\Omega_0}\right)\cdot\lambda_{\rm crit} . \end{displaymath}$

(7)

The coefficient X depends on the shape of the rotation curve, measured by Oort's constant A, with

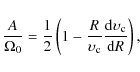$\begin{displaymath}\frac{A}{\Omega_0} = \frac{1}{2}\left(1-\frac{R}{\upsilon_{\rm c}}\frac{{\rm d}\upsilon_{\rm c}}{{\rm d}R}\right) , \end{displaymath}$

(8)

and is given in Fuchs (2001). The number of spiral arms, m, is given by how often $\lambda_{\rm max}$ fits onto the annulus (Fuchs 2008):

$\begin{displaymath} m=\frac{2\pi R}{\lambda_{\rm max}}=2 . \end{displaymath}$

(9)

From Eqs. (6), (7), and (9), we have

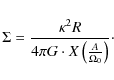$\begin{displaymath}\Sigma = \frac{\kappa^2 R}{4\pi G \cdot X\left(\frac{A}{\Omega_0}\right)} \cdot \end{displaymath}$

(10)

In contrast to the Toomre parameter, this involves no velocity dispersion. An approximation for taking the actual thickness of the disk into account yields a 15% lower value for the coefficient X (see Appendix C), which we use in the calculation of the resulting M/L values at the half-light radius (Table 1, labelled `` $\lambda =\lambda _{\rm max}$ ''). Like above for the Toomre parameter, rotational velocities can be predicted for an exponential and a Mestel disk (Table 2 and Fig. 4).

4 Discussion

The analysis of IC 3328 by Jerjen et al. (2000) shows that the spiral structure holds clues to its dynamical configuration. However, no rotation curve had been obtained then. With the now available kinematical data from Simien & Prugniel (2002), a more detailed investigation was possible.

While the mass-to-light ratios derived with the Toomre criterion clearly exceed the stellar M/L (Table 1), the value derived using density wave theory is still compatible with the stellar value. The predicted rotation curve of the exponential model from $\lambda =\lambda _{\rm max}$ provides good agreement with the measured, asymmetric-drift-corrected curve (Fig. 4). However, as for the M/L, the curves derived from the Toomre criterion lie at velocities that are too high, implying that the picture of a pure disk is probably too simple.

For the case of a very high velocity dispersion, the M/L values are substantially higher (columns labelled `` $\sigma _{R}=71$ km s^-1'' in Tables 1 and 2), and now the value from $\lambda =\lambda _{\rm max}$ is also incompatible with the observed stellar range. The velocities show the same relative behaviour as for the lower velocity dispersion: the model velocities from the Toomre criterion are higher than those from $\lambda =\lambda _{\rm max}$ , which agree with the measured curve. However, the high M/L values might indicate that the actual velocity dispersion is indeed lower than in this extreme case. Of course one could argue that a significant amount of dark matter is present as well; and yet, Geha et al. (2002) conclude that dark matter does not contribute significantly within the half-light radius for their (admittedly small) Virgo dE sample.

The M/L values from $\lambda =\lambda _{\rm max}$ are thus the only ones that are at least partly consistent with the inferred stellar value. A major difference between the Toomre criterion and the density wave approach is that velocity dispersion does not enter the latter directly - only implicitly through the asymmetric drift correction - but it does enter the Toomre parameter directly, which yields M/L values that are too high. This might hint at a significant dynamically hot component being present in addition to the disk. If such a component contributed substantially to the measured velocity dispersion, the disk component's own velocity dispersion would be significantly smaller. This would reduce the surface mass density inferred from the Toomre criterion towards the value derived from $\lambda =\lambda _{\rm max}$ .

Table 2: Rotational velocity, with values at the half-light radius for an exponential disk and a Mestel disk, using the same cases as in Table 1.

$\begin{figure} \par\resizebox{9cm}{!}{\rotatebox{0}{\includegraphics{1331fig4.eps}}} \end{figure}$	Figure 4: Measured versus predicted rotational velocities. The black lines are the same as in the left panel of Fig. 3, i.e. for $\sigma _{R}=45$ km s^-1. The exponential ( left) and Mestel ( right) model velocities are shown for the cases given in Tables 1 and 2, i.e. Q=1,1.5,2 as well as $\lambda =\lambda _{\rm max}$ .
Open with DEXTER

As for the rotational velocity, since the contribution of the asymmetric drift is directly related to the disk's velocity dispersion, its contribution would be much smaller in the case just described. This would lower both the observational and model velocities, again with particular relevance to the Toomre criterion.

We illustrate this possibility by repeating our analysis with a significantly lower velocity dispersion of $\sigma_{R}=10$ km s^-1and a smaller half-light radius of 0.9 kpc. The latter represents only the ``inner'' component of a double-exponential fit to the light profile of Fig. 1, which yielded a ratio of the two components' scalelengths of 3:10, with a central intensity ratio of 33:2. Obviously, the asymmetric drift contribution is much smaller in this scenario. The choice of $\sigma_{R}=10$ km s^-1 is such that the two approaches, $\lambda =\lambda _{\rm max}$ and the Toomre criterion, agree with each other in the predicted rotational velocities and also the mass-to-light ratios (Tables 1 and 2, rightmost column). In this case, the derived M/L values appear to be somewhat lower than the inferred stellar M/L - but, given that now the disk contributes only part of the light that is used for the calculation, the values are very compatible. The model rotational velocities also agree with the measured value. This leads to a coherent picture, in which IC 3328 consists of a dynamically hot component with an embedded thin disk.

Nevertheless, this interpretation must be regarded with some caution, given the measurement uncertainties, the moderate radial extent of the kinematical data, and the number of assumptions and simplifications made in the analysis. Clearly, it would be desirable to obtain kinematical data of higher quality, in order to decrease the measurement errors and to trace the curve to larger radii. Furthermore, minor axis data would be desirable for pinning down the velocity anisotropy.

Finally, we mention again that no thin disk component is seen in the vertical light profile of the apparently edge-on dE(di) IC 3435 (see Sect. 1). It is of course not known whether this galaxy hosts similar spiral structure. Nevertheless, if indeed IC 3328 had a thin disk surrounded by a hotter component, then IC 3435 would not be an edge-on version of the same kind of object.

5 Summary

We attempted to gain insight into the actual nature of early-type dwarf galaxies with weak spiral structure by analysing the kinematical data of IC 3328, the prototype of this galaxy population. To our knowledge, no other object of this kind has kinematical data of sufficient quality. Based on mass-to-light ratios derived with different methods, we find that the observed velocity dispersion of IC 3328 cannot be fully attributed to a stellar disk, but that a distinct dynamically hot component is present. An unambiguous conclusion is, however, not possible, due to the moderate radial coverage and the lack of minor-axis kinematical data. We thus see our study as motivation to increase the amount of good-quality kinematical observations for dEs.

Acknowledgements

We thank Eva Grebel for initiating this collaboration, and the referee, Albert Bosma, for constructive suggestions. T.L. is supported within the framework of the Excellence Initiative by the German Research Foundation (DFG) through the Heidelberg Graduate School of Fundamental Physics (grant number GSC 129/1). This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France, and of NASA's Astrophysics Data System Bibliographic Services.

Appendix A: Finite disk thickness correction of the observed rotation curve

To obtain a first-order correction for the finite thickness of the disk, we approximate the density profile of the galaxy with a double exponential,

$\begin{displaymath} \nu={\rm e}^{-R/h_{R}}{\rm e}^{-z/h_{z}} , \end{displaymath}$

(A.1)

and then integrate along the line of sight over the density-weighted rotational velocity:

$\begin{displaymath} \upsilon_{\rm {l.o.s.}}=\frac{1}{N}\int^{+\infty}_{-\infty}{... ...\vec{e}_{\rm {l.o.s.}},\vec{\rm e}_{\phi})~ \upsilon_{\rm c} , \end{displaymath}$

(A.2)

with N the normalization factor, $R=\sqrt{x^2+y^2}$ , and $l=\sqrt{y^2+z^2}$ , such that the x-direction is perpendicular to the line of sight. The unit vectors $\vec{e}_{\rm {l.o.s.}}$ and $\vec{e}_{\phi}$ are defined in the direction of the line of sight and the direction of the (cylindrically assumed) circular rotation of the galaxy, respectively.

We assume that the vertical scalelength h_z is much shorter than the radial scalelength h_R, and perform a Taylor expansion of the integrand about z=0 to second order. After the integration, we neglect terms higher than second order in h_z, yielding

$\begin{displaymath} \upsilon_{\rm {l.o.s.}}=\upsilon_{\rm c}\sin{i} \left(1-\fra... ... d}(\ln \upsilon_{\rm c})}{{\rm d}(\ln R)}\right)\right) \cdot \end{displaymath}$

(A.3)

Adopting h_R/h_z=3 (Lisker et al. 2006b) and using the inclination $i=30^{\circ}$ (Sect. 2.1), this results in

$\begin{displaymath} \upsilon_{\rm {l.o.s.}}=\upsilon_{\rm c}\sin{i} \left(1-\fra... ... d}(\ln \upsilon_{\rm c})}{{\rm d}(\ln R)}\right)\right) \cdot \end{displaymath}$

(A.4)

Appendix B: The Toomre stability criterion corrected for the finite thickness of galactic disks

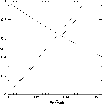$\begin{figure} \par\resizebox{9cm}{!}{\rotatebox{0}{\includegraphics{1331fig5.eps}}} \end{figure}$	Figure B.1: The Toomre Q parameter corrected for the finite thickness $h_{z} / \lambda _{\rm crit}$ of a galactic disk. The right dashed line represents the case $\sigma _{R}=45$ km s^-1, and the left dashed line is for $\sigma _{R}=71$ km s^-1. See the text of Appendix B for details.
Open with DEXTER

The gravitational potential of a Fourier component of the surface density of an infinitesimally thin disk is given by

$\begin{displaymath} \Phi=-\frac{2\pi G \Sigma_{k}}{\vert k\vert}{\rm e}^{ikx-k\vert z\vert} \end{displaymath}$

(B.1)

where k denotes the wave number of the Fourier term. Following Toomre (1964) we consider a disk of finite thickness as a superposition of infinitesimally thin disks,

$\begin{displaymath} \Phi(z)=-\frac{2\pi G \Sigma_{\rm k}}{\vert k\vert}{\rm e}^... ...-k\vert z-h\vert}\frac{{\rm e}^{-\vert h\vert/h_{ z}}}{2h_{z}} \end{displaymath}$

(B.2)

which leads at the midplane to

$\begin{displaymath} \Phi(z=0)=-\frac{2\pi G \Sigma_{\rm k}}{\vert k\vert}\frac{1}{1+kh_{z}} \cdot \end{displaymath}$

(B.3)

In the following we use the reduction term (1+kh_z)^-1, which is slightly different from that adopted by Toomre (1964), to modify the diagnostics of the dynamical state of a galactic disk for finite thickness.

Fuchs & von Linden (1998) show in their Appendix A1 how such a correction term must be applied to the dispersion relation for ring-like perturbations of the disk. In their analysis, Fuchs & von Linden (1998) adopted an exponential velocity distribution. If we switch back to a Schwarzschild distribution as assumed by Toomre (1964), we find for the line separating exponentially growing perturbations from neutrally stable perturbations in the space spanned by $\sigma_{R} k_{\rm crit}/\kappa$ (or Q) and the wavenumber,

$\begin{displaymath} 1=\frac{2\pi G \Sigma_{k}}{\sigma_{R}^2\vert k\vert} \left(... ...c{\sigma_{R}^2k^2}{\kappa^2}\right)\right) \frac{1}{1+kh_{z}} \end{displaymath}$

(B.4)

where $I_{\rm0}$ denotes the modified Bessel function. Equation B.4 is a modified version of Eq. (62) of Toomre (1964).

When Q is drawn as a function of $\lambda=2\pi/k$ , we always find a lower limit for Q, above which perturbations are stable on all wavelengths. This is illustrated as a solid line in Fig. B.1. As can be seen from the figure, the allowed Q values are lower than one, which means that a disk of finite thickness can be significantly more massive than an infinitesimally thin disk, but still be dynamically stable. However, it needs to be taken into account that the vertical scale height h_z in units of $\lambda_{\rm crit}$ enters into the calculation. Therefore, if one increases the disk surface density, Q will drop, but $h_{z} / \lambda _{\rm crit}$ drops as well. Thus the most massive, but still dynamically stable disk model is reached when Q (originally Q=1) has dropped by the same fraction as the originally calculated $h_{z} / \lambda _{\rm crit}$ . These models are indicated by the intersections of the solid line and the dashed lines in Fig. B.1.

Appendix C: Density wave theory analysis with a correction for finite thickness

We use the same reduction factor as derived in Appendix B to correct the prediction of density wave theory for finite thickness of the disk. Since we follow ``swing-amplification'' theory (Toomre 1981), we can straightforwardly use the formalism of Fuchs (2001). We multiplied the kernel $\mathcal{K}$ of his Eq. (68) by the reduction factor $\left(1+h_{z}\sqrt{k_{x}^2+k_{y}^2}\right)^{-1}$ and again solved the Volterra integral equation. The main result is that the operation characteristics of the swing-amplifier mechanism, i.e. at which k_y and $k_{x}^{\rm eff}$ amplification peaks, are hardly affected by this correction, the effect being of the order of 15%. Only the amplification amplitude is much reduced as compared to infinitesimally thin disks. This shows again that disks of finite thickness are dynamically more stable than razor-thin disks.

References

Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2007, ApJS, 172, 634 [NASA ADS] [CrossRef] (In the text)
Athanassoula, E., Bosma, A., & Papaioannou, S. 1987, A&A, 179, 23 [NASA ADS]
Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS] (In the text)
Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton, NJ: Princeton University Press), 747 (In the text)
Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] (In the text)
Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] (In the text)
Ferguson, H. C., & Sandage, A. 1989, ApJ, 346, L53 [NASA ADS] [CrossRef]
Fuchs, B. 2001, A&A, 368, 107 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Fuchs, B. 2008, Invited contribution to Galactic and Stellar Dynamics in the era of high resolution surveys, Strasbourg, March 16-20 [arXiv:0810.3503] (In the text)
Fuchs, B., & von Linden, S. 1998, MNRAS, 294, 513 [NASA ADS] [CrossRef] (In the text)
Geha, M., Guhathakurta, P., & van der Marel, R. P. 2002, AJ, 124, 3073 [NASA ADS] [CrossRef] (In the text)
Geha, M., Guhathakurta, P., & van der Marel, R. P. 2003, AJ, 126, 1794 [NASA ADS] [CrossRef] (In the text)
Gerssen, J. 2000, Stellar kinematics in disk galaxies (Groningen: Proefschrift, Rijksuniversiteit) (In the text)
Jerjen, H., Kalnajs, A., & Binggeli, B. 2000, A&A, 358, 845 [NASA ADS] (In the text)
Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJS, 182, 216 [NASA ADS] [CrossRef] (In the text)
Lisker, T., Glatt, K., Westera, P., & Grebel, E. K. 2006a, AJ, 132, 2432 [NASA ADS] [CrossRef]
Lisker, T., Grebel, E. K., & Binggeli, B. 2006b, AJ, 132, 497 [NASA ADS] [CrossRef]
Lisker, T., Grebel, E. K., & Binggeli, B. 2008, AJ, 135, 380 [NASA ADS] [CrossRef]
Lisker, T., Grebel, E. K., Binggeli, B., & Glatt, K. 2007, ApJ, 660, 1186 [NASA ADS] [CrossRef]
Mastropietro, C., Moore, B., Mayer, L., et al. 2005, MNRAS, 364, 607 [NASA ADS] (In the text)
Michielsen, D., Boselli, A., Conselice, C. J., et al. 2008, MNRAS, 385, 1374 [NASA ADS] [CrossRef] (In the text)
Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] (In the text)
Simien, F., & Prugniel, P. 2002, A&A, 384, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Smith, J. A., Tucker, D. L., Kent, S., et al. 2002, AJ, 123, 2121 [NASA ADS] [CrossRef] (In the text)
Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, ASP Conf. Ser., 52, 173 (In the text)
Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] (In the text)
Toomre, A. 1981, in Structure and Evolution of Normal Galaxies, ed. S. M. Fall, & D. Lynden-Bell (Cambridge: CUP), 111
van den Bergh, S. 1996, PASP, 108, 1091 [NASA ADS] [CrossRef] (In the text)
Vazdekis, A., Casuso, E., Peletier, R. F., & Beckman, J. E. 1996, ApJS, 106, 307 [NASA ADS] [CrossRef] (In the text)

Footnotes

... structure: Partly based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere, Chile, for program 077.B-0785.
... IRAF/ellipse: IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.
...Fuchs (2001): Actually, 1/X is given there.
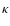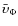... dispersion: Since these calculations are performed based on the asymmetric-drift-corrected rotation curve, a dependence on velocity dispersion is implicitly included through $\kappa$ , since the derivation of $\upsilon_{\rm c}$ from the observed $\bar{\upsilon}_{\rm\Phi}$ involves 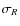$\sigma_{R}$ (see Eq. (4)).
... column): Following Sect. 3.3 and Appendix B, we use here an ``effective Q'' range of 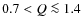$0.7<Q\la 1.4$ , corresponding to an intrinsic disk axis ratio of 0.1.

All Tables

Table 1: Mass-to-light ratio in V, using the colour transformation V=r+0.27 (Smith et al. 2002).

Table 2: Rotational velocity, with values at the half-light radius for an exponential disk and a Mestel disk, using the same cases as in Table 1.

All Figures

$\begin{figure} \par\resizebox{9cm}{!}{\rotatebox{0}{\includegraphics{1331fig1.eps}}} \end{figure}$	Figure 1: Appearance and light profile of IC 3328. Surface brightness in SDSS-r versus radius, adopting a distance modulus m-M=31.0 mag (d=15.85 Mpc, van den Bergh 1996), corresponding to a scale of 77 pc/ $^{\prime \prime }$ . The half-light radius $r_{\rm e}$ , as well as 2.2 scalelengths h (using $r_{\rm e}=1.68h$ ), are indicated by the vertical dotted lines. The images shown on the right are, from top to bottom, the SDSS r-band image, a deep white-filter image obtained with ESO 2.2m/WFI (program 077.B-0785), and an unsharp mask image of the latter, revealing the spiral arm structure. The half-light aperture is indicated in the SDSS and unsharp mask image.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\rotatebox{0}{\includegraphics{1331fig2.eps}}} \end{figure}$	Figure 2: Light profile in z-direction of IC 3435. SDSS r-band image (inset) of IC 3435, and the intensity profile obtained by collapsing the outlined box-shaped region along the galaxy's major axis. The box has a side length corresponding to the major axis of the half-light elliptical isophote, or equivalently, three times its minor axis. Smearing due to seeing effects can occur in the innermost $\sim$ $\pm$ $1.5\hbox {$^{\prime \prime }$ }$ .
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{18cm}{!}{\rotatebox{0}{\includegraphics{1331fig3.eps}}} \end{figure}$	Figure 3: Rotation curve and the effect of asymmetric drift. Large filled circles are the inclination-corrected measurements from Simien & Prugniel (2002). The lower solid curve is a fit of $f(r)=a(1-{\rm e}^{-\frac{r}{b}})$ to them. Taking the asymmetric drift into account (see text) results in the small filled circles, along with the corresponding fit using the same function (upper solid curve). In the left panel, we use $\sigma _{R}=45$ km s^-1, while 71 km s^-1 is used in the right panel. The inclination-corrected measurements from Geha et al. (2003) are shown as filled squares in the left panel.
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\rotatebox{0}{\includegraphics{1331fig4.eps}}} \end{figure}$	Figure 4: Measured versus predicted rotational velocities. The black lines are the same as in the left panel of Fig. 3, i.e. for $\sigma _{R}=45$ km s^-1. The exponential ( left) and Mestel ( right) model velocities are shown for the cases given in Tables 1 and 2, i.e. Q=1,1.5,2 as well as $\lambda =\lambda _{\rm max}$ .
Open with DEXTER
In the text

$\begin{figure} \par\resizebox{9cm}{!}{\rotatebox{0}{\includegraphics{1331fig5.eps}}} \end{figure}$	Figure B.1: The Toomre Q parameter corrected for the finite thickness $h_{z} / \lambda _{\rm crit}$ of a galactic disk. The right dashed line represents the case $\sigma _{R}=45$ km s^-1, and the left dashed line is for $\sigma _{R}=71$ km s^-1. See the text of Appendix B for details.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.