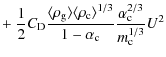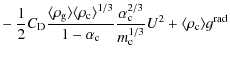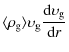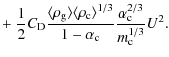EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A50 Full HTML
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A50
Number of page(s) 6
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200912872
Published online 31 March 2010
A&A 512, A50 (2010)

X-ray temperatures and their radial distributions from winds of O-type supergiants: the effects of clumps

J. H. Guo1,2

1 - National Astronomical Observatories/Yunnan Observatory, Chinese Academy of Science, PR China
2 - Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, PR China

Received 13 July 2009 / Accepted 15 December 2009

Abstract
Context. Based on the multiphase hydrodynamical flows and the clump model, a two-fluid model of the O stars $\zeta $ Ori A and $\zeta $ Pup is investigated, in which the flow is described by a set of two components.
Aims. I investigate the influence of clumps on the production of X-ray and derive wind parameters from a comparison with the X-ray temperature distributions in the wind of O-type supergiants.
Methods. The velocity structure of the clump is assumed to be beta law, thus the transonic velocity structure of the ambient wind can be attained via the shooting method.
Results. The mass, filling factor, and velocity structure of the clump are very sensitive to the post-shock temperatures. I find that the filling factor must be about 0.01 for fitting the observed X-ray temperatures. The mass of the clump cannot be smaller than 1018 g. A clump carries about $10^{-4}~\dot{M}$ and $10^{-5}~\dot{M}$ for $\zeta $ Ori A and $\zeta $ Pup, respectively. The model with the exponent of clump velocity $\beta=0.5{-}0.6$ for O-type supergiants fits the observations better than one with the exponent $\beta=0.8$.
Conclusions. These results indicate that the forward shock scenario can explain the X-ray emission, except for the hottest X-ray lines for O-type supergiants. Theoretical and observable evidence shows that a low velocity law should be applied to O-type supergiants.

Key words: stars: early type - stars: individual: $\zeta $ Ori A - stars: individual: $\zeta $ Pup - stars: winds, outflows - X-ray: stars

1 Introduction

Stellar winds have a strong effect on the evolution of massive stars. Hot stars of spectral O and B have been observed with X-ray emission. Most of the X-ray emission with temperatures of several million degrees from early-type stars appears to originate in their winds (Waldron & Cassinelli 2000, 2007). Solar-type coronal emission was first assumed to explain X-ray emission (Cassinelli & Olson 1979), but the observations did not show the expected large attenuation by the cold winds in the soft X-ray band. The X-ray emissions in normal OB stars are generally explained in terms of shock heating of the supersonic, radiation-driven winds (Lucy & White 1980; Lucy 1982; Cohen et al. 2006). Shocks are distributed throughout their winds and are most likely formed from instabilities of line-driven flow (Lucy & Solomon 1970; Owicki et al. 1988). An important implication of line-driven flow instabilities suggests that the outer winds of OB stars develop extensive structure that is a mixture of rarefied regions and dense ``clumps'' (Feldmeier et al. 1997a; Owocki & Puls 1999), which are typically an order of magnitude denser than the ambient wind.

With the launching of Chandra and XMM-Newton, high-resolution X-ray emission lines have been detected. By analyzing their profiles, a direct constraint is available to the wind-shock model. Much research has shown that the hot, X-ray emitting plasma is distributed throughout winds (Kramer et al. 2003; Leutenegger et al. 2006a; Cohen et al. 2006). The locations and temperatures of the X-ray sources have been measured in terms of the high-resolution X-ray emission lines (Waldron & Cassinelli 2000, 2007; Cohen et al. 2003). Waldron (2005) shows that the X-ray temperature distributions decline outward through the winds for OB supergiants. Such steady decrease outward from 10 MK (even higher) to 2 MK does not seem predicted by shock models. Moreover, Waldron & Cassinelli (2007) find that the X-ray temperatures of supergiants show a tight correlation with radii. They find a one-to-one correspondence between  $R_{\rm fir}$ and their associated X-ray continuum optical depth unity radii ( $R_{\tau=1}$) when the traditional mass-loss rates were adopted, and explain this as density dependence. The detailed hydrodynamic numerical simulation predicted that the winds are permeated by forward and reverse shocks (Feldmeier et al. 1997a; Owocki & Puls 1999; Runacres & Owocki 2002). A high temperature may be created at low radii if photospheric turbulence is included.

Lucy & White (1980) developed a phenomenological model to explain the X-ray emission in which the wind is described in terms of a two-component structure, where one is for the dense clumps and the other for the interclump gas. This model assumes that clumps are driven by a radiative force while the ambient gas is pushed along by the drag of these blobs. Therefore, there are a lot of strong forward shocks in their model. The model can account for the X-ray luminosity of $\zeta $ Puppis, but fails for B-type star $\tau$ Scorpii. (In fact, Lucy & White did not consider the effect of clump on the mass-loss rate, which could result in a smaller attenuation for X-ray luminosity.) An alternative situation is considered by Howk et al. (2000). In their model, the clumps move outward(inward) with a velocity below that of the ambient wind. Thus, a higher relative velocity can be attained when these clumps fall back towards the star, producing higher X-ray temperatures. This can explain the hard X-ray emission in $\tau$ Scorpii.

The previous studies by Lucy & White (1980) seem to be supported in part by the following facts. First, numerical simulations of the line-driven flow show that the most of flow is composed of``clump'' separated by an almost void interclump medium. Second, the nonlinear interaction from clump collisions result little net velocity-density correlation, which suggests that there is a roughly equal mixture of forward and reverse shocks in the outer wind (Runacres & Owocki 2002).

The main aim of this paper is to investigate the X-ray temperatures and locations of two O stars $\zeta $ Ori and $\zeta $ Pup. I have chosen to use a basic shock model, namely, the forward shock model. Hydrodynamic simulation predicts that there are reverse shocks in the inner region of the wind. Thus, a full picture of shocks in the winds should include both forward and reverse shocks. However, it is still useful to consider the assumption of forward shock. First, the X-ray temperature distributions depend on the square of the relative velocity so that it is difficult to distinguish the forward with reverse shock from the observed X-ray temperatures. Second, the density contrast between the clump and interclump medium is high, which is supported by both observations and hydrodynamic simulations (Bouret et al. 2003, 2005; Fullerton et al. 2006; Feldmeier et al. 1997a). The interclump medium is almost void so the velocity law determined from observations should be the effect of clumps. Those observations show that the velocity structure of clump is consistent with the theoretic prediction. Thus, it is not unreasonable to assume that clumps are driven by radiative force (Thus, a $\beta$ velocity law is used.). On the assumption that the clumps move outward with a velocity below that of the ambient wind, the motion of clump depends on the drag force of gas. Howk et al. (2000) show that the drag force is proportional to the density of the interclump medium and is inversely proportional to  $\rho_{\rm clump}^{2/3}$. A direct consequence is that the dense clump could fall back toward the star or move outward with a low velocity, which is not supported by the observations of O-type supergiants. And third, by fitting the observed X-ray temperature distributions, we can determine the extent to which the applying forward shock model for O-type supergiants may explain the X-ray temperatures of observations.

On the assumption that the velocity of the clump is calculated using a $\beta$ velocity law throughout the wind (Sect. 2.1), which results in a low relative velocity near the star, the model cannot predict a very high temperature near the star. However, 107 K temperatures is observed by Waldron & Cassinelli (2007) and predicted by hydrodynamic simulations. A suitable complement for this model is to include reverse shocks or magnetic confinement in the inner wind. Cassinelli et al. (2008) suggest that the bow shocks can be produced when the stellar wind impacts on the clumps. Their results show that the temperature distribution is a function of the impact parameter for an adiabatic bow shock and that a high temperature can be produced at the apex of the shock. In this paper, I only discuss the forward-shock model. A full description of the forward and reverse shocks (magnetic confinement)is beyond the scope of this paper.

On the assumption of forward shocks, the radiation from stars exerting on the ambient gas is weak because it must first penetrate those clumps. The motion of the ambient gas is mainly controlled by friction between the clumps and the ambient gas. Therefore the main component of the mass loss is more likely clumped and those clumps embedded in smooth gas. The stellar continuum radiation in spectral lines force the clumps to flow away from the star. Lucy & White (1980) solved the two-phase equations of clumps and interclump media; however, they assumed an arbitrary initial value condition. In this model I complement the calculation with a critical transonic solution that yields subsonic velocity at the base of the wind and increases with the critical point outward (also see Guo 2008). Therefore, this paper represents a natural extension of the previous studies by Lucy & White (1980).

The hydrodynamic equations are present in Sect. 2.1. I briefly discuss the numerical method in Sect. 2.2. In Sect. 3 I provide a summary of X-ray observations for $\zeta $ Ori A and $\zeta $ Pup. The numerical results are shown in Sect. 4 and discussed in Sect. 5, and in Sect. 6 I draw the conclusions.

2 The model

2.1 Construction of equations

For the multiphase hydrodynamical flows, Pistinner & Shaviv (1993) present a formalism with the concept of spatial averages. The advantages of the technique are that the equations can be formulated in a straightforward physical interpretation. I just present the results, but for details, the reader can refer to Pistinner & Shaviv (1993) (cf. Eqs. (45)-(49)). I assume the flow is steady, spherical and symmetric. Thus, the terms of time are neglected. I also assume that the wind is isothermal. The exchange of mass between the clump and the interclump gas is also neglected. The smooth gas and clumps are coupled by friction. These clumps are accelerated by stellar radiation and slowed down by gravity and friction. The interclump gas is accelerated in terms of drag between the clump and interclump gas. Thus the mass and momentum equations for the two-phase flow can be written as

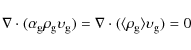
\begin{displaymath}% \nabla \cdot(\alpha_{\rm g}\rho_{\rm g}\upsilon_{\rm g})=\nabla\cdot(\langle \rho_{\rm g} \rangle \upsilon_{\rm g})=0 \end{displaymath} (1)

and

\begin{displaymath}% \nabla\cdot(\alpha_{\rm c}\rho_{\rm c}\upsilon_{\rm c})=\nabla\cdot(\langle \rho_{\rm c} \rangle \upsilon_{\rm c})=0 \end{displaymath} (2)

with the constraint

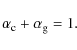
\begin{displaymath}% \alpha_{\rm c}+\alpha_{\rm g}=1. \end{displaymath} (3)

In these equations, $\rho_{\rm g}$ and $\rho_{\rm c}$ are gas and clump densities averaged over the volume occupied by gas and the clump, $\upsilon_{\rm g}$ and  $\upsilon_{\rm g}$ are the gas and clump velocities, $\langle \rho_{\rm g} \rangle$ and  $\langle \rho_{\rm c} \rangle$ are gas and clump densities averaged over the control volume, $\alpha_{\rm g}$ and  $\alpha_{\rm c}$ are volume filling factor for gas and clump, respectively.
          $\displaystyle % \nabla\cdot[\langle \rho_{\rm g} \rangle \upsilon_{\rm g}\upsilon_{\rm g}]$ = $\displaystyle -(1-\alpha_{\rm c})\nabla P_{\rm g}+ \langle \rho_{\rm g} \rangle g(1-\Gamma)$  
    $\displaystyle + ~\frac{1}{2}C_{\rm D}\frac{\langle \rho_{\rm g} \rangle \langle... ...rangle ^{1/3}}{1-\alpha_{\rm c}}\frac{\alpha^{2/3}_{\rm c}}{m_{\rm c}^{1/3}}U^2$ (4)


               $\displaystyle % \nabla\cdot[\langle \rho_{\rm c} \rangle \upsilon_{\rm c}\upsilon_{\rm c}]$ = $\displaystyle -\alpha_{\rm c}\nabla P_{\rm g}+ \langle \rho_{\rm c} \rangle g(1-\Gamma)$  
    $\displaystyle - ~\frac{1}{2}C_{\rm D}\frac{\langle \rho_{\rm g} \rangle \langle... ...a^{2/3}_{\rm c}}{m_{\rm c}^{1/3}}U^2 + \langle \rho_{\rm c} \rangle g^{\rm rad}$ (5)

where $g^{\rm rad}$ is the acceleration due to radiation from star. Here, U = $\upsilon_{\rm c}-\upsilon_{\rm g}$, $m_{\rm c}$ is the mass of the clump, and $C_{\rm D}$ is the drag coefficient, which denotes the efficiency of the momentum transfer to the gas. In this work, I assumed the $C_{\rm D}=2$ (see Howk et al. 2000). In these equations $P_{\rm g}$ is gas pressure. The state equation for the gas can be written as

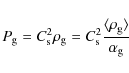
\begin{displaymath}% P_{\rm g}=C_{\rm s}^{2}\rho_{\rm g}=C_{\rm s}^{2}\frac{\langle \rho_{\rm g} \rangle}{\alpha_{\rm g}} \end{displaymath} (6)

with $c_{\rm s}$ = $\frac{\kappa T_{0}}{\mu m_{\rm H}}$, where T0 is the constant gas temperature, $\mu$ mean atomic weight, $\kappa$ the Boltzmann constant, $m_{\rm H}$ the mass of a hydrogen atom, $\Gamma$ = $\frac{\sigma_{\rm e}L}{4\pi cgM_{*}}$ Eddington factor, and $C_{\rm s}$ the sound velocity. For the equation of momentum conservation, the drag acceleration per unit mass is given by Lucy & White (1980).

To solve the set of coupled nonlinear differential equations, we need a powerful numerical method. However, I only consider the motion of the interclump gas. The velocity structure of the clump is assumed to be $\beta$ law

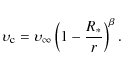
\begin{displaymath}% \upsilon_{\rm c}=\upsilon_{\infty}\left(1-\frac{R_{*}}{r}\right)^{\beta}. \end{displaymath} (7)

Thus I only solve Eqs. (1) and (4). In the spherical coordinates, Eqs. (1) and (4) can be written as

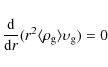
\begin{displaymath}% \frac{{\rm d}}{{\rm d}r}(r^{2} \langle \rho_{\rm g} \rangle \upsilon_{\rm g})=0 \end{displaymath} (8)

and
              $\displaystyle % \langle \rho_{\rm g} \rangle \upsilon_{\rm g}\frac{{\rm d}\upsilon_{\rm g}}{{\rm d}r}$ = $\displaystyle -(1-\alpha_{\rm c})\nabla P_{\rm g}+ \langle \rho_{\rm g} \rangle g(1-\Gamma)$  
    $\displaystyle + ~ \frac{1}{2}C_{\rm D}\frac{\langle \rho_{\rm g} \rangle \langl... ...angle ^{1/3}}{1-\alpha_{\rm c}}\frac{\alpha^{2/3}_{\rm c}}{m_{\rm c}^{1/3}}U^2.$ (9)

Hydrodynamic equations for the interclumpt gas are described by Eqs. (8) and (9).

2.2 Numerical solution

The solution of the differential Eqs. (8) and (9) can be obtained by a numerical method. I selected the Newton-Raphson method to solve the question. The method requests initialization to both velocity and density. According to Eqs. (3), (6), (8), and (9), we obtain

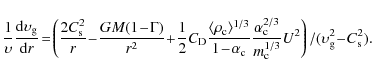
\begin{displaymath}% \frac{1}{\upsilon}\frac{{\rm d}\upsilon_{\rm g}}{{\rm d}r} ... ...^{1/3}}U^2 \right)/(\upsilon^{2}_{\rm g}\!-\!C^{2}_{\rm s}).~~ \end{displaymath} (10)

The equation considered here essentially has the similar structure as the solar wind. The velocity structure is independent of the density. The momentum equation has a singularity at the point where $\upsilon_{\rm g}=C_{\rm s}$. This singularity is important because the transonic solution is the only one that can yield flows from subsonic velocity at the base of the wind to supersonic velocity at the outside of the singularity. The position of singularity is determined when both numerator and denominator go to zero simultaneously. To perform the condition, a suitable lower boundary condition is necessary. I apply a shooting method to find the lower boundary condition, the idea of which is to guess a lower boundary condition and to iterate the gas equation outwards. If the solution converges, then the initial lower boundary condition will be modified until the solution satisfies the singularity condition. If the method fails to converge, the first estimate must be changed until the procedure converges. Then I start to calculate the solution at the outer part of singularity.

To account for the influence of wind clumping, the method described by Abbott (1981) is adopted. The mass-loss rate is defined from the mean density,

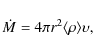
\begin{displaymath}% \dot{M}=4\pi r^{2} \langle \rho \rangle \upsilon, \end{displaymath} (11)

and

\begin{displaymath}% \langle \rho \rangle =\frac{1}{\triangle V}\int[\alpha_{\rm c}\rho_{\rm c}+(1-\alpha_{\rm c})\rho_{\rm g}]{\rm d}V, \end{displaymath} (12)

where $\rho_{\rm c}$ and $\rho_{\rm g}$ denote the density of the clump and interclump gases, respectively. Since the measure of mass-loss rate depends on $\tau_{\nu}\propto \langle \rho^{2} \rangle = \langle \rho \rangle ^{2}[\alpha_{\rm c}+(1-\alpha_{\rm c})x^{2}]/[\alpha_{\rm c}+(1-\alpha_{\rm c})x]^{2}$, the clumped wind can produce the same emission measure as a smooth wind but with a factor  $\sqrt{\alpha_{\rm c}}$ less than $\dot{M}$ if the density ratio $x=\rho_{\rm g}/\rho_{\rm c}\rightarrow 0$ in the extreme condition of a zero density interclump region. In fact, hydrodynamic numerical simulations have shown that the density of the clump is typically 1-2 order of magnitude denser than for the ambient wind. Therefore, the most contribution of the mass-loss rates comes from the component of clumps. In the model, the mass-loss rates are used to multiply by the factor  $\sqrt{\alpha_{\rm c}}$ when the filling factor  $\alpha_{\rm c}$ is specified.

To calculate the velocity structure of the interclump gas the inner boundary densities for both component have to be set. I assume that the inner velocity of the clump is the sound velocity. The inner boundary density, $\rho_{\rm c}$, is determined by the velocity at the inner boundary and $\dot{M}*\sqrt{\alpha_{\rm c}}$. The density of the gas is assumed to be a factor 10 lower than that of the clump.

3 X-ray

The typical O-type stars $\zeta $ Ori A and $\zeta $ Pup are ideal candidates for testing models about X-ray emission because they have been studied in detail (Feldmeier et al. 1997b; Waldron & Cassineli 2000; Cassineli et al. 2001; Leutenegger et al. 2006b; Pollock 2007; Raassen et al. 2008). An important test for this model is to compare the X-ray temperatures. To estimate the postshock temperature, I take $T_{\rm s}=1.44$ $\times$ $10^5 \left(\frac{U}{100~{\rm km~s}^-1}\right)^2~{\rm K}$, where U is the relative velocity between the interclump gas and the clump. In fact, shocks can only exist in supersonic flows. Thus, in this model I used the above formula to calculate the post-shock temperatures when the relative velocity between the clump and the gas is higher than the sound velocity. The observed temperatures and locations of X-ray sources are obtained from Waldron & Cassinelli (2007). (An Erratum about the paper was published in ApJ, 680, 1595, so I used the revised data.) The radii  $R_{\rm fir}$, which were determined by using the He-like ions, denote the local radii in which the emission lines of different elements are formed. One might be problematic for the radii whether these thin shells can represent the range in which each element is formed. In generally, the spectral lines seem to be formed over a large range. However, the line emission is proportional to $\rho^{2}$, so the observed lines should be dominated by the densest regions. Thus, it is reasonable to depict a characteristic radius to each element line. The X-ray temperatures determined by the H-like-to-He-like line ratios can represent the average temperatures of the He-like ions and H-like ions for these element. The temperatures should be somewhat higher than those of He-like ions. The lack of observed data forced me to use the average temperatures to denote the temperatures of He-like ions. In fact, the final results of this model should be corrected for this discordance. For both stars $\zeta $ Ori A and $\zeta $ Pup, the X-ray temperatures for the sulfur are greater than 10 MK. However, there is no definite observational data in Waldron & Cassinelli (2007). Thus, I neglect to fit the temperature for sulfur. In fact, such high temperature is incompatible with wind shocks. Schulz et al. (2003) have revealed similar phenomena in young stars  $\theta^{1}$ Ori A, C, and E. The hottest X-ray lines appear to originate closest to the stars since the observed HWHM values are significantly lower than the wind terminal velocity. (The HWHMs for $\tau$ Scorpii are also found to be essentially identical to the HWHMs observed in late-type stars.) Schulz et al. (2003) show that these hottest lines are the likely result of magnetic confinement. Some magnetic confined models have been considered by Babel & Montmerle (1997), Ud-Doula & Owocki (2002), and Mullan & Waldron (2006).

Table 1:   Line widths of the program stars.

4 Numerical results

Stellar parameters were taken from Table 1 of Feldmeier et al. (1997b). The mass-loss rates are not corrected for the clumping.

For searching the best fits between the observed and theoretical X-ray locations and temperatures, I used a $\chi^2$ method to match the observations. To demonstrate the sensitivity of the motion of the interclump gas to these parameters, I tested a number of possible cases. For each individual star, I computed the X-ray temperatures with the values of $\beta$ chosen in the range of 0.5-1. The mass of the clump was chosen from a wide range. Moreover, these models were calculated with the constant filling factors throughout the winds. For completeness, the observed MEG, HEG, and their average X-ray temperatures are plotted in Figs. 1 and 2. By finding the minimum differences with the average values, the best-fit parameters were determined for individual objects.

Figure 1 shows that the model with $m=10^{19}~{\rm g}$, $\beta=0.5$, and $\alpha_{\rm c}=0.015$ is the best-fit model for O-type supergiant $\zeta $ Ori A, but it produces a lower temperature for Silicon. Waldron & Cassinelli (2000) find that the Si XIII line originates in the base of the wind ( $R\approx 1.1~R_{*}$) and suggest that the velocity there is too low to produce the shock jump. However, Leutenegger et al. (2006a) report a very different value of 2.1 R*, which does not agree with the result of Waldron & Cassinelli (2007). In theirs multi-temperature calculations, Raassen et al. (2008) show that the X-ray temperatures were in the range of 0.85-6.4 Mk. This is in good agreement with our results. In the model, the maximum relative velocity between the clump and interclump gas is about 710  $\rm km~s^{-1}$ at R=1.95 R*, which is high enough to produce the higher temperature at the base of the wind. The model with m=5 $\times$ $10^{18}~{\rm g}$, $\beta=0.5$, and $\alpha_{\rm c}=0.01$ produces higher temperature distributions at the region of low-temperature regions (see dashed line). Evidently, model with $m=10^{18}~{\rm g}$, $\beta=0.8$, and $\alpha_{\rm c}=0.01$predicted flatter temperature distributions in the majority of the winds (see dotted line). If the mass of the clump is greater than $m=10^{19}~{\rm g}$, the X-ray temperatures predicted by this model will produce a higher temperature distribution in the whole wind.

\begin{figure} \par\includegraphics[width=7.5cm,clip]{12872fg1.eps} \end{figure} Figure 1:

The X-ray temperature distributions with different value of the mass, velocity law, and filling factor of the clump for $\zeta $ Ori A. A circle represents the observed MEG value, and a square represents the observed HEG value. The averaged value is denoted by a black triangle.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.5cm,clip]{12872fg2.eps} \end{figure} Figure 2:

The X-ray temperature distributions with different velocity law of the clump for $\zeta $ Pup. A circle represents the observed MEG value, and a square represents the observed HEG value. The averaged value is denoted by a black triangle.

Open with DEXTER

For $\zeta $ Pup, the best-fit model is $m=10^{18}~{\rm g}$, $\beta=0.6$, and $\alpha_{\rm c}=0.01$ (Fig. 2). For indicating the influence of velocity structure of the clump on the X-ray temperature distributions, the models with different values of $\beta$ are also shown in Fig. 2. These models with higher $\beta$ predict the reasonable X-ray temperatures of elements except for silicon. On the previous analysis for the X-ray luminosity $L_{\rm x}$, Lucy & White (1980) estimated the mass of the clump is about $m = 10^{15}~{\rm g}$, which is different with the result of this model. However, as pointed by Lucy & White (1980): ``$L_{\rm x}$ is gratifyingly insensitive to m ...''. Thus, the mass of the clump could not be constrained well by their model. In this model, the the highest post-shock temperature is $T_{\rm X}=7$ $\times$ $10^{6}~{\rm K}$, and the corresponding velocity difference is 700  $\rm km~s^{-1}$ at R=1.99 R* while Lucy & White (1980) predicted a maximum relative velocity $U=363~{\rm km~s}^{-1}$, and the corresponding highest temperature is 1.4 $\times$ $10^{6}~{\rm K}$ at R=1.31 R*. The result is significantly different from that of this model and is lower than that of observations.

The clump masses cannot be determined by observations. Thus, I redefine the clump masses by the mass-loss rate. The mass-flow rate in a clump is  $m_{\rm c}/\tau$, where $\tau \sim r/v$ is the flow time. For our program stars, the flow time can be estimated by  $R_{*}/v_{\infty}$; therefore, a clump carries about $10^{-4}~\dot{M}$ for $\zeta $ Ori A and $10^{-5}~\dot{M}$ for $\zeta $ Pup.

Leutenegger et al. (2006a) present a comparison of their measurements to those of Waldron & Cassinelli (2000) and Cassinelli et al. (2001). Table 6 of Leutenegger et al. (2006a) show that the minimum radius extends to nearly the surface of the star. The shock jump required for S XV should be higher than that of Si XIII. This hints that either a steeper velocity structure or a higher mass for the clump, or both, are needed to fit the emission of sulfur. A velocity law with $\beta$ < 0.5 does not seem to be supported by observations. In our numerical experience, the models with a higher mass of the clump cannot fit the temperatures for other elements. Thus, the fits of the S XV emission lines can place a strong constraint on future modeling efforts.

5 Discussion

As evident in Figs. 1 and 2, the filling factor, mass, and velocity structure of the clump may significantly affect the X-ray temperature distributions. The post-shock temperature is determined by the relative velocity between the clumps and ambient wind. Equation (5) shows that the drag force between the two components is controlled by the mass, velocity law, and filling factor of the clump, as discussed below.

5.1 Parameters

For clumps with the lower mass, the outward drag force is much greater than gravity at the base of the wind. Thus, the sound point is very close to the stellar surface. In fact, the velocity structure of gas is steeper if the sound point appears near the star. This suggests that the difference in velocity remains relatively small. If there is no relative motion between the interclump gas and the clump, the post-shock gas temperature is zero. I tested the models with different masses of clumps. The clumps with lower mass produce lower X-ray temperature distributions. The model with $m=10^{12}~{\rm g}$ produces the X-ray temperature distributions, which are almost zero. The model with $m = 10^{15}~{\rm g}$ improves the X-ray temperature distributions, but they are much lower than for observations.

The model with higher $\beta$ will produce a flatter velocity structure than that with $\beta=0.5$. We find that at the base (1-4 R*) of the wind, the fast accelerated clumps result in a greater velocity difference than slow accelerated clumps. For normal OB stars, the determination of velocity law from observations is described by $\beta \approx 0.5{-}1$ (Garmany et al. 1981; Groenewegen & Lamers 1989). By fitting the far-ultraviolet line P v, Fullerton et al. (2006) obtained $\beta=1.0$ for $\zeta $ Ori A and 0.5 for $\zeta $ Pup. Their results are very close to the value of this model for $\zeta $ Pup, but different from that of $\zeta $ Ori A. In fact, if the winds are composed of two components, the observed value of $\beta$ should be greater than 0.5 because it is a weighted average of the clumps and ambient gas.

A small filling factor implies that the mass-loss rates are decreased a large factor. In this model the filling factor of the best-fit models for $\zeta $ Ori A is 0.015 and $\zeta $ Pup is 0.01. The X-ray temperatures are very sensitive to the filling factor of the clump,  $\alpha_{\rm c}$. The increase in filling factor by a factor 3 can result in a lower X-ray temperature distribution.

In this paper, I used a constant filling factor. In fact, the filing factor may be variable with the radius. In the quantitative spectral analysis for O stars HD 190429 and HD 96715 Bouret et al. (2005) use an exponentially degressive filling factor. However, Puls et al. (2006) have found the lower clumping factor (the clumping factor is inversely proportional to the volume filling factor, namely, $f_{\rm c}\propto \frac{1}{\alpha_{\rm c}}$) in the outmost than the inner wind. Moreover, hydrodynamic simulation (Runacres & Owocki 2002) predict that the clumping factor is variable with time. Thus, constraining the filling factor from theoretical model becomes an important issue.

Waldron & Cassinelli (2007) find a one-to-one correspondence between  $R_{\rm fir}$ and their associated X-ray continuum optical depth unity radii ( $R_{\tau=1}$) when the traditional mass-loss rates were adopted, and explained this as density dependence. For completeness, I also calculated the dependence of mass-loss rates on X-ray temperature distributions. The model with a higher mass-loss rate underestimates the X-ray temperature distributions, reflecting the consistency between observation and theory, meaning that the mass loss rate should be decreased.

5.2 X-ray emission lines

I also compared the widths of the X-ray emission lines. In Table 1, I list the line widths for O VII, Ne IX, Mg XI, and Si XIII. I used a half of the local velocity to represent the theoretical value. The fact that the theoretical line widths increase outward through the wind indicates that the lines occur in the accelerated region of the wind. I also notice that the observed widths are very different for the different authors. Cohen et al. (2006) determine the value of the line widths of $\zeta $ Ori, which are 500+120-70 and 1360+160-150  $\rm km~s^{-1}$ for O VII and Ne Ix; however, the values measured by Waldron & Cassinelli (2000) are 900 $\pm$ $200~{\rm km~s}^{-1}$. The theoretical results agree with the values of Waldron & Cassinelli (2000). It is not clear why the theoretical results contradict the observations of Cohen et al. (2006). In fact, the emission line analysis of $\zeta $ Ori from Cohen et al. shows that there is significant blueshift, but Waldron & Cassinelli find that the lines are almost symmetric, and the velocity dispersions for all X-ray line are in the range 900 $\pm$ $200~{\rm km~s}^{-1}$. Thus, another observation may be needed to distinguish the contradiction.

For the spectrum of $\zeta $ Pup, there are no corresponding values for ions O VII, Ne IX, Mg XI, and Si XIII from the published literature. In the XMM spectrum of $\zeta $ Pup (Kahn et al. 2001), the high Z lines have characteristic widths ${\thicksim}1000~{\rm km~s}^{-1}$. In their Table 2 Cassinelli et al. (2001) list the line widths of some ions, with the HWHM of $610{-}1570~{\rm km~s}^{-1}$. These values are comparable to the theoretical results.

6 Conclusion

The spatial X-ray temperature distributions show that the temperature decreases with the increase in radius of supergiants. The model predicted the trend and fitted the observed X-ray temperatures. In fact, the theoretic X-ray temperatures are determined by the mass, filling factor, and velocity structure of the clump. The model shows that the range in mass of clump is about $10^{18}{-}10^{19}~{\rm g}$; otherwise, the model cannot predict significant X-ray temperatures. The results are also sensitive to the velocity law. The models with the exponent of the clump velocity $\beta=0.5{-}0.6$ can produce a large shock jump near the stellar surface and fit the observations. For the whole wind, a flatter velocity structure is possible because of the counteraction of velocity structure of the clump and interclump gas. Compared with the smooth-wind models, this model also shows that the winds of O-type suergiants are strongly clumped and the mass loss rates could decrease by a factor of 8-10. The model also predicts the line widths of O VII, Ne IX, Mg XI, and Si XIII for the $\zeta $ Pup and the $\zeta $ Ori A. The theoretical results are consistent with the values of observations.

Acknowledgements
I am grateful to the referee for a constructive suggestion that lead to substantive improvements in this work. This work was supported by the National Natural Science Foundation of China (Nos. 10803018); the Knowledge Innovation Program of Chinese Academy of Sciences (07ACX21001), and Western Light Talent Culture Project of The Chinese Academy of Sciences (08AXB31001).

References

  1. Abbott, D. C., Bieging, J. H., & Churchwell, E. 1981, ApJ, 250, 645 [NASA ADS] [CrossRef] [Google Scholar]
  2. Babel, J. 1997, A&A, 323, 121 [NASA ADS] [Google Scholar]
  3. Bouret, J. C., Lanz, T., Hillier, D. J., et al. 2003, ApJ, 595, 1182 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bouret, J. C., Lanz, T., & Hillier, D. J. 2005, A&A, 438, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Cassinelli, J. P., & Olson, G. L. 1979, ApJ, 229, 304 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cassinelli, J. P., Miller, N. A., Waldron, W. L., et al. 2001, ApJ, 554, L55 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cassinelli, J. P., Ignace, R., Waldron, W. L., et al. 2008, ApJ, 683, 1052 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cohen, D. H., de Messières, G. E., MacFarlane, J. J., et al. 2003, ApJ, 586, 495 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cohen, D. H., Leutenegger, M. A., Grizzard, K. T., et al. 2006, MNRAS, 368, 1905 [NASA ADS] [CrossRef] [Google Scholar]
  10. Feldmeier, A., Puls, J., & Pauldrach, W. A. 1997a, A&A, 322, 878 [NASA ADS] [Google Scholar]
  11. Feldmeier, A., Kudritzki, R. P., Palsa, R., et al. 1997b, A&A, 320, 899 [NASA ADS] [Google Scholar]
  12. Fullerton, A. W., Massa, D. L., & Prinja, R. K. 2006, ApJ, 637, 1025 [NASA ADS] [CrossRef] [Google Scholar]
  13. Garmany, C. D., Olson, G. L., & van Steenberg, M. E. 1981, ApJ, 250, 660 [NASA ADS] [CrossRef] [Google Scholar]
  14. Groenewegen, M. A. T., & Lamers, H. J. G. L. M. 1989, A&AS, 79, 359 [NASA ADS] [Google Scholar]
  15. Guo, J. H. 2008, IAUS, 252, 341 [NASA ADS] [CrossRef] [Google Scholar]
  16. Howk, J. C., Cassinelli, J. P., Bjorkman, J. E., & Lamers, H. J. G. L. M. 2000, ApJ, 534, 348 [NASA ADS] [CrossRef] [Google Scholar]
  17. Kahn, S. M., Leutenegger, M. A., Cottam, J., et al. 2001, A&A, 365, L312 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Kramer, R., Cohen, D. H., & Owocki, S. P. 2006, ApJ, 592, 532 [Google Scholar]
  19. Leutenegger, M. A., Paerels, F. B. S., Kahn, S. M., & Cohen, D. H. 2006a, ApJ, 650, 1096 [NASA ADS] [CrossRef] [Google Scholar]
  20. Leutenegger, M. A., Owocki, S. P., Kahn, S. M., & Paerels, B. S. 2006b, ApJ, 659, 642 [Google Scholar]
  21. Lucy, L. B. 1982, ApJ, 255, 284 [Google Scholar]
  22. Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 [NASA ADS] [CrossRef] [Google Scholar]
  23. Lucy, L. B., & White, R. L. 1980, ApJ, 241, 300 [NASA ADS] [CrossRef] [Google Scholar]
  24. Mullan, D. J., & Waldron, W. L. 2006, ApJ, 637, 506 [NASA ADS] [CrossRef] [Google Scholar]
  25. Owocki, S. P., & Cohen, D. H. 2006, ApJ, 648, 565 [NASA ADS] [CrossRef] [Google Scholar]
  26. Owocki, S. P., & Puls, J. 1999, ApJ, 510, 355 [NASA ADS] [CrossRef] [Google Scholar]
  27. Owocki, S. P., Castor, J. I., & Rybicki, G. B. 1988, ApJ, 335, 914 [NASA ADS] [CrossRef] [Google Scholar]
  28. Pollock, A. M. T. 2007, A&A, 463, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Pistinner, S., & Shaviv, G. 1993, ApJ, 414, 612 [NASA ADS] [CrossRef] [Google Scholar]
  30. Puls, J., Markova, N., Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Raassen, A. J. J., van der Hucht, K. A., Millier, N. A., & Cassinelli, J. P. 2008, A&A, 478, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Runacres, M. C., & Owocki, S. P. 2002, A&A, 381, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Schulz, N. S., Canizares, C., Huenemoerder, D., & Tibbets, K. 2003, ApJ, 595, 365 [NASA ADS] [CrossRef] [Google Scholar]
  34. ud-Doula, A., & Owocki, S. P. 2002, ApJ, 576, 413 [NASA ADS] [CrossRef] [Google Scholar]
  35. Waldron, W. L. 2005, in ITAMP Workshop: X-ray Diagnostics of Astrophysical plasma (New York: AIP), AIP Conf. Ser., 774, 353 [Google Scholar]
  36. Waldron, W. L., & Cassinelli, J. P. 2000, ApJ, 548, L45 [Google Scholar]
  37. Waldron, W. L., & Cassinelli, J. P. 2007, ApJ, 668, 456 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1:   Line widths of the program stars.

All Figures

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{12872fg1.eps} \end{figure} Figure 1:

The X-ray temperature distributions with different value of the mass, velocity law, and filling factor of the clump for $\zeta $ Ori A. A circle represents the observed MEG value, and a square represents the observed HEG value. The averaged value is denoted by a black triangle.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{12872fg2.eps} \end{figure} Figure 2:

The X-ray temperature distributions with different velocity law of the clump for $\zeta $ Pup. A circle represents the observed MEG value, and a square represents the observed HEG value. The averaged value is denoted by a black triangle.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.