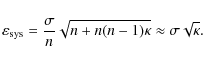| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 19 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200913007 | |
| Published online | 30 March 2010 | |
Searching for chameleon-like scalar
fields with the ammonia method![[*]](/icons/foot_motif.png)
S. A. Levshakov1,2 - P. Molaro1 - A. V. Lapinov3 - D. Reimers4 - C. Henkel5 - T. Sakai6
1 - INAF - Osservatorio Astronomico di Trieste, via G. B. Tiepolo 11,
34131 Trieste, Italy
2 - Ioffe Physical - Technical Institute, Polytekhnicheskaya Str. 26,
194021 St. Petersburg, Russia
3 - Institute for Applied Physics, Uljanov Str. 46, 603950 Nizhny
Novgorod, Russia
4 - Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029
Hamburg, Germany
5 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121
Bonn, Germany
6 - Institute of Astronomy, The University of Tokyo, Osawa, Mitaka,
Tokyo 181-0015, Japan
Received 29 July 2009 / Accepted 18 November 2009
Abstract
Aims. We probe the dependence of the
electron-to-proton mass ratio,
![]() ,
on the ambient matter density by means of radio astronomical
observations.
,
on the ambient matter density by means of radio astronomical
observations.
Methods. The ammonia method, which has been proposed
to explore the electron-to-proton mass ratio, is applied to nearby dark
clouds in the Milky Way. This ratio, which is measured in different
physical environments of high (terrestrial) and low (interstellar)
densities of baryonic matter is supposed to vary in chameleon-like
scalar field models, which predict strong dependences of both masses
and coupling constant on the local matter density. High resolution
spectral observations of molecular cores in lines of NH3
(J,K)
= (1,1), HC3N
J = 2-1, and N2H+
J = 1-0 were performed at three radio telescopes to
measure the radial velocity offsets,
![]() ,
between the inversion transition of NH3 (1,1)
and the rotational transitions of other molecules with different
sensitivities to the parameter
,
between the inversion transition of NH3 (1,1)
and the rotational transitions of other molecules with different
sensitivities to the parameter
![]()
![]() .
.
Results. The measured values of ![]() exhibit a statistically significant velocity offset of
exhibit a statistically significant velocity offset of
![]() m s-1 .
When interpreted in terms of the electron-to-proton mass ratio
variation, this infers that
m s-1 .
When interpreted in terms of the electron-to-proton mass ratio
variation, this infers that
![]() =
=
![]() .
If only a conservative upper bound is considered, then the maximum
offset between ammonia and the other molecules is
.
If only a conservative upper bound is considered, then the maximum
offset between ammonia and the other molecules is
![]() m s-1 .
This provides the most accurate reference point at z
= 0 for
m s-1 .
This provides the most accurate reference point at z
= 0 for ![]() of
of ![]() .
.
Key words: line: profiles - ISM: molecules - radio lines: ISM - techniques: radial velocities
1 Introduction
Testing the variability of dimensionless physical constants is an important topic in contemporary laboratory and astrophysical experiments. The physical constants are not supposed to vary in the Standard Model (SM) of particle physics but do vary quite naturally in grand unification theories, multidimensional theories, and whenever there is a coupling between light scalar fields and baryonic matter. In particular, light scalar fields have been widely discussed in the context of dark energy, since they provide negative pressure that may be responsible for the cosmic acceleration detected at low redshifts, z<1(Caldwell et al. 1998; Peebles & Rata 2003). If this scalar field does exist, then a question arises: why has it not been detected in local tests of the equivalence principle or fifth force searches? A solution was suggested using the so-called ``chameleon'' models (Khoury & Weltman 2004; Brax et al. 2004; Mota & Shaw 2007). These models assume that a light scalar field acquires both an effective potential and effective mass because of its coupling to matter that strongly depends on the ambient matter density. In this way, this scalar field may evade local tests of the equivalence principle and fifth force experiments since the range of the scalar-mediated fifth force for the terrestrial matter densities is too small to be detected. This is not the case for space-based tests, where the matter density is considerably lower, an effective mass of the scalar field is negligible, and an effective range for the scalar-mediated force is large. The present paper deals with one such astronomical test based on spectral observations of molecular clouds in the Milky Way disk. Additional tests employing polarization of the light from the stars and a modification of the Sunyaev-Zel'dovich effect in the cosmic microwave background due to a coupling between a chameleon-like scalar field and photons are described, respectively, in Burrage et al. (2009) and Davis et al. (2009).
Astronomical spectroscopy can probe the physical constants
that describe
atomic and molecular discrete spectra: the fine-structure constant,
![]() ,
and the electron-to-proton mass ratio,
,
and the electron-to-proton mass ratio,
![]() .
In GUTs, these constants mediate the strength of fundamental
forces:
.
In GUTs, these constants mediate the strength of fundamental
forces: ![]() is the coupling constant of the electromagnetic interaction,
is the coupling constant of the electromagnetic interaction,
![]() is related
to the vacuum expectation value of the Higgs field, namely
to the scale of the weak nuclear force, and
is related
to the vacuum expectation value of the Higgs field, namely
to the scale of the weak nuclear force, and ![]() is proportional to the
quantum chromodynamics scale.
We note that the predicted variabilities of the fine-structure constant
and the electron-to-proton mass ratio
are not independent and that the variations in
is proportional to the
quantum chromodynamics scale.
We note that the predicted variabilities of the fine-structure constant
and the electron-to-proton mass ratio
are not independent and that the variations in ![]() may exceed those of
may exceed those of ![]() (Calmet
& Fritzsch 2002;
Langacker et al. 2002;
Dine et al. 2003;
Flambaum et al. 2004).
Thus, a hypothetical variation in
(Calmet
& Fritzsch 2002;
Langacker et al. 2002;
Dine et al. 2003;
Flambaum et al. 2004).
Thus, a hypothetical variation in ![]() is expected to be easier to detect than that in
is expected to be easier to detect than that in ![]() .
.
Despite many efforts,
the variability in ![]() and
and ![]() has never been detected.
Data obtained from high precision frequency measurements in laboratory
experiments with atomic clocks and from astronomical observations
provide only upper limits.
For example, laboratory experiments have delivered the following
results:
fractional temporal variations in
has never been detected.
Data obtained from high precision frequency measurements in laboratory
experiments with atomic clocks and from astronomical observations
provide only upper limits.
For example, laboratory experiments have delivered the following
results:
fractional temporal variations in ![]() are restricted to a level of
are restricted to a level of
![]() yr-1
(Shelkovnikov et al. 2008), and
yr-1
(Shelkovnikov et al. 2008), and
![]() yr-1
(Blatt et al. 2008),
whereas the current level for
yr-1
(Blatt et al. 2008),
whereas the current level for ![]() is
is
![]() yr-1
(Rosenband et al. 2008).
Here
yr-1
(Rosenband et al. 2008).
Here ![]() and
and ![]() are the relative changes between the values measured at two different
epochs.
are the relative changes between the values measured at two different
epochs.
The most stringent upper limits to
![]() and
and ![]() obtained from astronomical observations of extragalactic objects are
restricted by a few units of ppm (1 ppm = 10-6).
Here
obtained from astronomical observations of extragalactic objects are
restricted by a few units of ppm (1 ppm = 10-6).
Here
![]() ,
where
,
where ![]() denote the values of the fine-structure constant in the laboratory and
the specific absorption/emission line system of a Galactic or
extragalactic object (the same definition is applied to
denote the values of the fine-structure constant in the laboratory and
the specific absorption/emission line system of a Galactic or
extragalactic object (the same definition is applied to
![]() ).
However, there are claims of a variability in both
).
However, there are claims of a variability in both ![]() and
and ![]() at the 5
at the 5![]() and 4
and 4![]() confidence levels, respectively, although they are in contrast to other
null results and the whole issue is highly controversial.
The current observational status is the following.
confidence levels, respectively, although they are in contrast to other
null results and the whole issue is highly controversial.
The current observational status is the following.
From the measurements of the relative radial velocity shifts
of different absorption lines (e.g., Mg II,
Si II, Fe II,
Zn II) of 143 QSO absorption
systems obtained with the Keck/HIRES in the redshift range
0.2 < z < 4.2, Murphy et al.
(2004)
claimed that
![]() ppm. On the other hand, Chand et al. (2004)
using VLT/UVES spectra of bright QSOs analyzed 23 absorption systems,
which are not
in common with those studied by the Keck telescope, and failed to
reproduce Murphy et al.'s result. At first, they claimed a
very stringent limit of
ppm. On the other hand, Chand et al. (2004)
using VLT/UVES spectra of bright QSOs analyzed 23 absorption systems,
which are not
in common with those studied by the Keck telescope, and failed to
reproduce Murphy et al.'s result. At first, they claimed a
very stringent limit of
![]() ppm, but Murphy et al. (2008a)
demonstrated convincingly that the error estimate of Chand
et al. (2004)
is underestimated. When these errors are properly accounted for, the
new weighted mean becomes
ppm, but Murphy et al. (2008a)
demonstrated convincingly that the error estimate of Chand
et al. (2004)
is underestimated. When these errors are properly accounted for, the
new weighted mean becomes
![]() ppm.
The new value has a scatter that is larger than the quoted errors
implying that there are systematic errors that are comparable or even
larger
than the statistical ones. However, Srianand et al. (2008) showed
that excluding two systems that deviate
from the mean at the 3
ppm.
The new value has a scatter that is larger than the quoted errors
implying that there are systematic errors that are comparable or even
larger
than the statistical ones. However, Srianand et al. (2008) showed
that excluding two systems that deviate
from the mean at the 3![]() level when reanalyzing VLT/UVES systems
leads to
level when reanalyzing VLT/UVES systems
leads to
![]() ppm.
We note that the only claimed non-zero measurement of
ppm.
We note that the only claimed non-zero measurement of
![]() corresponds to an uncertainty
in the wavelength scale calibration smaller 100 m s-1 .
This precise
calibration of the Keck/HIRES spectra is difficult to achieve as shown
by Griest et al. (2010).
Using iodine exposures to calibrate the normal Th-Ar Keck data pipeline
output, they found absolute wavelength offsets of
500 m s-1 to
1000 m s-1 with
drifts of more than 500 m s-1 over
a single night, and drifts of nearly 2000 m s-1 over
several nights. Their conclusion is that these systematic uncertainties
make it difficult to use Keck/HIRES QSO spectra to constrain the change
in the fine structure constant at the 10-6
level.
The most stringent constraint on
corresponds to an uncertainty
in the wavelength scale calibration smaller 100 m s-1 .
This precise
calibration of the Keck/HIRES spectra is difficult to achieve as shown
by Griest et al. (2010).
Using iodine exposures to calibrate the normal Th-Ar Keck data pipeline
output, they found absolute wavelength offsets of
500 m s-1 to
1000 m s-1 with
drifts of more than 500 m s-1 over
a single night, and drifts of nearly 2000 m s-1 over
several nights. Their conclusion is that these systematic uncertainties
make it difficult to use Keck/HIRES QSO spectra to constrain the change
in the fine structure constant at the 10-6
level.
The most stringent constraint on
![]() ppm was found from the Fe II lines at z
= 1.15 towards the bright quasar HE 0515-4414 (Quast
et al. 2004;
Levshakov et al. 2005;
Molaro et al. 2008).
ppm was found from the Fe II lines at z
= 1.15 towards the bright quasar HE 0515-4414 (Quast
et al. 2004;
Levshakov et al. 2005;
Molaro et al. 2008).
Bounds on ![]() variations are most effectively obtained from observations of the
Werner and Lyman
series of the molecular hydrogen H2 in damped Ly-
variations are most effectively obtained from observations of the
Werner and Lyman
series of the molecular hydrogen H2 in damped Ly-![]() systems (DLA). The electron-vibro-rotational transitions have
different dependences on the reduced mass and can be used to constrain
the variability of
systems (DLA). The electron-vibro-rotational transitions have
different dependences on the reduced mass and can be used to constrain
the variability of ![]() (Thompson 1975;
Varshalovich & Levshakov 1993).
The measurements of
(Thompson 1975;
Varshalovich & Levshakov 1993).
The measurements of ![]() rely on the same H2 systems observed with
VLT/UVES and claim a variability of
rely on the same H2 systems observed with
VLT/UVES and claim a variability of
![]() ppm (Reinhold et al. 2006)
or no variability with
ppm (Reinhold et al. 2006)
or no variability with
![]() ppm (Levshakov et al. 2002),
ppm (Levshakov et al. 2002),
![]() ppm
(Wendt & Reimers 2008),
ppm
(Wendt & Reimers 2008),
![]() ppm (King et al. 2008),
and
ppm (King et al. 2008),
and
![]() ppm
(Thompson et al. 2009).
Radio astronomical observations place constraints on
ppm
(Thompson et al. 2009).
Radio astronomical observations place constraints on ![]() -variations
of
-variations
of ![]() ppm at redshift z = 0.68 (Murphy et al. 2008b),
and
ppm at redshift z = 0.68 (Murphy et al. 2008b),
and ![]() ppm at z = 0.89 (Henkel et al. 2009).
ppm at z = 0.89 (Henkel et al. 2009).
One should keep in mind, however, that laboratory experiments and spectra of extragalactic objects probe very different time-scales and different regions of the universe, and the connection between them is quite model dependent (Mota & Barrow 2004).
Astronomical measurements of the dimensionless constants are
based on the comparison
of the line centers in the absorption/emission spectra of astronomical
objects
and the corresponding laboratory values. To distinguish the line shifts
due to the radial motion of the object from those caused by
the variability of constants, lines with different
sensitivity coefficients, Q, to the variations in ![]() and/or
and/or ![]() should be employed. Unfortunately, the observable optical lines have
very close sensitivity coefficients with differences of
should be employed. Unfortunately, the observable optical lines have
very close sensitivity coefficients with differences of
![]() that do not exceed 0.05. Combined with the resolving power of
spectrographs at modern optical telescopes, this small difference leads
to an upper limit on
that do not exceed 0.05. Combined with the resolving power of
spectrographs at modern optical telescopes, this small difference leads
to an upper limit on ![]() and
and ![]() of
of ![]() 1 ppm,
the optimal value achievable in observations of extragalactic objects
with existing facilities.
However, one can probe the values of fundamental constants at a
considerably more
accurate level if, firstly, nearby objects in the Milky Way are
observed and, secondly,
spectral lines from other frequency ranges, infrared and radio, are
employed.
This statement is based on the following considerations.
1 ppm,
the optimal value achievable in observations of extragalactic objects
with existing facilities.
However, one can probe the values of fundamental constants at a
considerably more
accurate level if, firstly, nearby objects in the Milky Way are
observed and, secondly,
spectral lines from other frequency ranges, infrared and radio, are
employed.
This statement is based on the following considerations.
As mentioned above, the scalar field models suggest
a coupling between the scalar fields and baryonic matter. This coupling
results in a functional dependence of ![]() and
and ![]() on
on ![]() ,
the local matter density (Olive & Pospelov 2008).
This coupling alone may prevent a positive detection of the variations
in
,
the local matter density (Olive & Pospelov 2008).
This coupling alone may prevent a positive detection of the variations
in ![]() and
other dimensionless constants in laboratory studies, since they are
performed under the
same terrestrial conditions and the effective range of the
scalar-field-mediated force is smaller than 1 mm at terrestrial matter
densities (Olive & Pospelov 2008). On the
other hand, the density in cold molecular clouds is only
103-105 particles per cm3,
i.e.,
and
other dimensionless constants in laboratory studies, since they are
performed under the
same terrestrial conditions and the effective range of the
scalar-field-mediated force is smaller than 1 mm at terrestrial matter
densities (Olive & Pospelov 2008). On the
other hand, the density in cold molecular clouds is only
103-105 particles per cm3,
i.e., ![]() 1019
times lower than in terrestrial environments.
Because of this extremely large difference between the matter
densities non-zero values of
1019
times lower than in terrestrial environments.
Because of this extremely large difference between the matter
densities non-zero values of
![]() and
and ![]() are predicted. It is very important to compare the above ratio of
are predicted. It is very important to compare the above ratio of ![]() 1019
with the differences in
1019
with the differences in ![]() between molecular clouds themselves, to find that
they are negligible, i.e., at most one or two orders of magnitude for a
given tracer. In the context of
between molecular clouds themselves, to find that
they are negligible, i.e., at most one or two orders of magnitude for a
given tracer. In the context of
![]() (or
(or ![]() )
this means that
measurements of all dense molecular clouds are identical irrespective
of their location in space and time (redshift). Thus, nearby Galactic
molecular clouds can be observed to ensure a strong signal, i.e., that
the line profiles can be centered with high accuracy.
)
this means that
measurements of all dense molecular clouds are identical irrespective
of their location in space and time (redshift). Thus, nearby Galactic
molecular clouds can be observed to ensure a strong signal, i.e., that
the line profiles can be centered with high accuracy.
Molecular lines originating in these clouds are mainly
observed in cm and mm radio bands. An advantage of radio observations
is that very narrow spectral lines (of line widths ![]() 100 m s-1 )
arising in cold molecular cores can be observed with extremely high
spectral resolution,
100 m s-1 )
arising in cold molecular cores can be observed with extremely high
spectral resolution, ![]() m s-1 .
In optical observations of extragalactic objects, we have in general
broader sources,
m s-1 .
In optical observations of extragalactic objects, we have in general
broader sources,
![]() km s-1 ,
and use lower resolution spectrographs,
km s-1 ,
and use lower resolution spectrographs,
![]() km s-1
(Levshakov et al. 2007).
Taking into account that the uncertainty in the line position is
roughly 1/10th of the pixel size, this infers a gain of about two
orders of magnitude in the accuracy of the measurements of
km s-1
(Levshakov et al. 2007).
Taking into account that the uncertainty in the line position is
roughly 1/10th of the pixel size, this infers a gain of about two
orders of magnitude in the accuracy of the measurements of
![]() and/or
and/or ![]() if radio spectra of the local interstellar objects are used.
if radio spectra of the local interstellar objects are used.
Complementary to this, differences in the sensitivity
coefficients for lines from the microwave, far IR, and radio ranges are
much larger than those from optical and UV ranges.
For example, the difference between the sensitivity coefficient of the
(J,K)=(1,1)
inversion transition of ammonia (NH3) and that
of any rotational transition in another molecule is
![]() (Flambaum
& Kozlov 2007).
When compared with UV transitions, this infers a gain of about
70 times in the sensitivity of the line positions to the change
in
(Flambaum
& Kozlov 2007).
When compared with UV transitions, this infers a gain of about
70 times in the sensitivity of the line positions to the change
in ![]() .
.
Our preliminary study of cold molecular clouds (Levshakov
et al. 2008a,
hereafter LMK)
was based on published results of high quality spectral radio
observations obtained with the 100-m Green Bank telescope (Rosolowsky
et al. 2008;
Rathborne et al. 2008)
and the 45-m Nobeyama radio telescope (Sakai et al. 2008).
Comparison of the relative radial velocities of the NH3
(J,K)
= (1,1) inversion
transition and CCS JN
= 21-10 rotational
transition measured a systematic shift of
![]() m s-1 ,
which when interpreted in terms of the electron-to-proton mass ratio
variation infers that
m s-1 ,
which when interpreted in terms of the electron-to-proton mass ratio
variation infers that ![]()
![]() .
We also noted that a similar offset between N2H+
and NH3 measured by
Pagani et al. (2009)
in the cold dark cloud L183 could have a similar physical origin
(Molaro et al. 2009).
.
We also noted that a similar offset between N2H+
and NH3 measured by
Pagani et al. (2009)
in the cold dark cloud L183 could have a similar physical origin
(Molaro et al. 2009).
In this paper, we present results of our own spectral observations of cold and compact molecular cores in the Taurus giant molecular complex obtained with the Medicina 32-m telescope, the Effelsberg 100-m telescope, and the Nobeyama 45-m telescope.
2 The ammonia method
Narrow molecular lines observed in cold dark clouds provide a sensitive
spectroscopic tool to study relative shifts of the order of a few
10 m s-1 between
radial velocities of different molecular transitions.
Among numerous molecules detected in the interstellar medium,
ammonia (NH3) is of particular interest
because of the high
sensitivity of the inversion frequency to a change in ![]() .
The inversion vibrational mode of NH3 is
described by a double-well
potential, the first two vibrational levels lying below the barrier.
The quantum mechanical tunneling splits these two levels into inversion
doublets providing a transition frequency that falls in the microwave
range
(Ho & Townes 1983).
.
The inversion vibrational mode of NH3 is
described by a double-well
potential, the first two vibrational levels lying below the barrier.
The quantum mechanical tunneling splits these two levels into inversion
doublets providing a transition frequency that falls in the microwave
range
(Ho & Townes 1983).
For the ammonia isotopologue 15ND3,
van Veldhoven et al. (2004)
first showed that the inversion frequency of the
(J,K)
= (1,1) level varies as![]()
i.e., the inversion transition is an order of magnitude more sensitive to
The sensitivity coefficient of the inversion transition
(J,K)
= (1,1) in NH3 (
![]() GHz) was calculated
by Flambaum & Kozlov (2007)
from the numerical integration of the Schrödinger equation for
different
values of
GHz) was calculated
by Flambaum & Kozlov (2007)
from the numerical integration of the Schrödinger equation for
different
values of ![]() ,
and from the analytical
Wentzel-Kramers-Brillouin (WKB) approximation of the
inversion frequency. Both methods provide similar results giving
,
and from the analytical
Wentzel-Kramers-Brillouin (WKB) approximation of the
inversion frequency. Both methods provide similar results giving
Here
The rotational frequency scales as
![]() and, thus,
and, thus,
By comparing the observed inversion frequency of NH3 (1, 1) with a suitable rotational frequency of another molecule produced co-spatially with ammonia, a limit on the spatial variation of
In radio astronomical observations, any frequency shift
![]() is related
to the radial velocity shift
is related
to the radial velocity shift
![]() (
(![]() is the line-of-sight projection of the velocity vector)
is the line-of-sight projection of the velocity vector)
where V0 is the reference radial velocity, and
From Eq. (5), we can estimate the limiting accuracy of
where
From this equation it is seen that the measurability of the signal (
2.1 Molecules appropriate for
 measurements
measurements
The observed molecular transitions should as far as possible share the
same volume elements
to have similar Doppler velocity shifts.
The ammonia inversion transitions are usually detected
in dense molecular cores (
![]() cm-3 ),
which are represented in the
Milky Way disk by a large variety of types and physical
properties (Di Francesco et al. 2007).
Mapping of the dense molecular cores in different molecular lines shows
that
there is a good correlation between the ammonia NH3,
N2H+, and HC3N
distributions (e.g., Fuller & Myers 1993; Hotzel
et al. 2004;
Tafalla et al. 2004;
Pagani et al. 2009).
However, in some clouds NH3 is not traced by HC3N.
The most striking case is the dark cloud TMC-1, where peaks of line
emission are offset by 7 arcmin (Olano et al. 1988).
cm-3 ),
which are represented in the
Milky Way disk by a large variety of types and physical
properties (Di Francesco et al. 2007).
Mapping of the dense molecular cores in different molecular lines shows
that
there is a good correlation between the ammonia NH3,
N2H+, and HC3N
distributions (e.g., Fuller & Myers 1993; Hotzel
et al. 2004;
Tafalla et al. 2004;
Pagani et al. 2009).
However, in some clouds NH3 is not traced by HC3N.
The most striking case is the dark cloud TMC-1, where peaks of line
emission are offset by 7 arcmin (Olano et al. 1988).
Table 1: Target list.
In general,
N-bearing molecules such as NH3 and N2H+
trace the inner cores, where the density approaches 105
cm-3 . At the same time, the
carbon-chain molecules disappear from the gas-phase
because of freeze-out onto dust grains (Tafalla et al. 2004).
HC3N, as well as other C-bearing molecules, are
usually distributed in the outer parts of the cores. The mutual
distribution of NH3 and HC3N
is affected
by chemical differentiation in the process of the dynamical evolution
of the core. HC3N is abundant in the early
evolutional stage of the star-forming regions (Lee et al. 1996), when the
fractional abundance of HC3N remains almost
constant and the spatial distributions of the N- and C-bearing
molecules match each other quite well (Suzuki et al. 1992).
As the gas density increases and at dust temperatures
![]() K,
these distributions diverge because of adsorption of the heavy
molecules (e.g., HC3N) from the gas phase
onto grain mantles (Flower et al. 2006).
In the later stages of the protostellar collapse, carbon
chain molecules are destroyed
by high velocity outflows and radiation from protostars, whereas the
same
processes favor the desorption of ammonia from dust grains (Suzuki
et al. 1992).
K,
these distributions diverge because of adsorption of the heavy
molecules (e.g., HC3N) from the gas phase
onto grain mantles (Flower et al. 2006).
In the later stages of the protostellar collapse, carbon
chain molecules are destroyed
by high velocity outflows and radiation from protostars, whereas the
same
processes favor the desorption of ammonia from dust grains (Suzuki
et al. 1992).
The chemical differentiation and velocity gradients within the
molecular core are the main sources of the unavoidable Doppler noise in
Eq. (6).
Additional scatter in the ![]() values is caused by the different optical depths of the hyperfine
structure transitions. However, all of these effects lead to the radial
velocity shifts detected
between NH3 and other molecules (HC3N,
N2H+), which may be
random from core to core. Thus, being averaged over a large sample of
targets, the Doppler noise component
values is caused by the different optical depths of the hyperfine
structure transitions. However, all of these effects lead to the radial
velocity shifts detected
between NH3 and other molecules (HC3N,
N2H+), which may be
random from core to core. Thus, being averaged over a large sample of
targets, the Doppler noise component
![]() in Eq. (6)
should be canceled out.
in Eq. (6)
should be canceled out.
3 Observations
For relative velocity measurements, the molecular lines
of NH3, HC3N, and N2H+
were chosen. From the published data,
we selected 41 molecular cores with compact morphology,
i.e., the cores whose geometrical structure can be represented by a
central
region of nearly constant density and a surrounding envelope
with a density that decreases as a power law.
For the dark clouds in the Taurus molecular complex,
a typical size of the central core is
![]() (e.g., Daniel et al. 2007).
The selection was based on narrow and sufficiently strong
molecular lines that correspond to
individual hyperfine transitions: NH3
(J,K)
= (1,1), HC3N J=2-1, and N2H+
J=1-0. This suggests that the selected cores have
low kinetic temperatures (
(e.g., Daniel et al. 2007).
The selection was based on narrow and sufficiently strong
molecular lines that correspond to
individual hyperfine transitions: NH3
(J,K)
= (1,1), HC3N J=2-1, and N2H+
J=1-0. This suggests that the selected cores have
low kinetic temperatures (
![]() K) and are located
at distances below 250 pc. The kinetic temperature is known to
be surprisingly uniform in dark
clouds (e.g., Dickman 1975;
Walmsley & Ungerechts 1983).
The list of sources is given in Table 1.
Observations were performed with radio telescopes in Medicina,
Effelsberg, and Nobeyama between November 2008
and April 2009.
K) and are located
at distances below 250 pc. The kinetic temperature is known to
be surprisingly uniform in dark
clouds (e.g., Dickman 1975;
Walmsley & Ungerechts 1983).
The list of sources is given in Table 1.
Observations were performed with radio telescopes in Medicina,
Effelsberg, and Nobeyama between November 2008
and April 2009.
Medicina. Observations at the
Medicina 32-m telescope![]() were carried out on November 24-28, 2008.
Both available digital spectrometers ARCOS (ARcetri COrrelation
Spectrometer)
and MSpec0 (high resolution digital spectrometer) were used
with channel separations of 4.88 kHz and 2 kHz,
respectively.
For ARCOS, this corresponds to 62 m s-1
at the position of the ammonia inversion transition (23 GHz)
and 80 m s-1 at the
rotational HC3N (2-1) line (18 GHz).
For MSpec0, it is 25 m s-1
and 32 m s-1 at the
corresponding frequencies. Only a few brightest objects (marked by a
symbol m in Table 1) were observed. The
Medicina 32-m telescope angular resolution is
were carried out on November 24-28, 2008.
Both available digital spectrometers ARCOS (ARcetri COrrelation
Spectrometer)
and MSpec0 (high resolution digital spectrometer) were used
with channel separations of 4.88 kHz and 2 kHz,
respectively.
For ARCOS, this corresponds to 62 m s-1
at the position of the ammonia inversion transition (23 GHz)
and 80 m s-1 at the
rotational HC3N (2-1) line (18 GHz).
For MSpec0, it is 25 m s-1
and 32 m s-1 at the
corresponding frequencies. Only a few brightest objects (marked by a
symbol m in Table 1) were observed. The
Medicina 32-m telescope angular resolution is ![]() 1.6' at 23 GHz and
1.6' at 23 GHz and ![]() 2.1' at
18 GHz. The pointing accuracy was superior to 25''.
Spectra were taken in a position switching mode with a typical
integration time
of 5 min for both ON- and OFF-source scans.
The OFF position was taken to be approximately five beam widths to the
west of the source position. Typically, 10-20 ON/OFF pairs
were taken,
depending on the frequency and source flux.
Unfortunately, because of poor weather conditions not all observations
studied both NH3 and HC3N
transitions.
Standard data reduction was performed using the CLASS reduction
package
2.1' at
18 GHz. The pointing accuracy was superior to 25''.
Spectra were taken in a position switching mode with a typical
integration time
of 5 min for both ON- and OFF-source scans.
The OFF position was taken to be approximately five beam widths to the
west of the source position. Typically, 10-20 ON/OFF pairs
were taken,
depending on the frequency and source flux.
Unfortunately, because of poor weather conditions not all observations
studied both NH3 and HC3N
transitions.
Standard data reduction was performed using the CLASS reduction
package![]() .
.
Effelsberg. The (J,K)
= (1,1) inversion line of ammonia (NH3) and the J
= 2-1 rotation line of cyanoacetylene (HC3N)
were also observed with the 100-m telescope
at Effelsberg![]() on
February 20-22, 2009. The corresponding targets are marked by
symbol e in Table 1.
The lines were measured with a K-band HEMT (high
electron mobility transistor) dual channel receiver, yielding spectra
with angular resolutions of
40'' (NH3) and 50'' (HC3N)
in two orthogonally
oriented linear polarizations. Averaging the emission from both
channels, typical system temperatures are 100-150 K for NH3and
80-100 K for HC3N on a main beam
brightness temperature scale.
on
February 20-22, 2009. The corresponding targets are marked by
symbol e in Table 1.
The lines were measured with a K-band HEMT (high
electron mobility transistor) dual channel receiver, yielding spectra
with angular resolutions of
40'' (NH3) and 50'' (HC3N)
in two orthogonally
oriented linear polarizations. Averaging the emission from both
channels, typical system temperatures are 100-150 K for NH3and
80-100 K for HC3N on a main beam
brightness temperature scale.
The measurements were carried out in frequency switching mode
using a frequency throw of ![]() 5 MHz.
The backend was an FFTS
(fast fourier transform spectrometer), operated with its minimum
bandwidth of 20 MHz, providing simultaneously
16 384 channels
for each polarization. The resulting channel widths are 15.4 and
20.1 m s-1 for NH3
and HC3N, respectively. We note,
however, that the true velocity resolution is about twice as large.
5 MHz.
The backend was an FFTS
(fast fourier transform spectrometer), operated with its minimum
bandwidth of 20 MHz, providing simultaneously
16 384 channels
for each polarization. The resulting channel widths are 15.4 and
20.1 m s-1 for NH3
and HC3N, respectively. We note,
however, that the true velocity resolution is about twice as large.
Observations started by measuring the continuum emission of
calibration sources (NGC 7027, W3(OH), 3C 286) and
continued by
performing pointing measurements toward a source close to the
spectroscopic
target. Spectral line measurements were interspersed with pointing
measurements at least once per hour. The calibration is estimated
to be accurate to ![]() 15%
and the pointing accuracy to be superior to
10 arcsec. The CLASS reduction package was used for standard
data reduction.
15%
and the pointing accuracy to be superior to
10 arcsec. The CLASS reduction package was used for standard
data reduction.
Table 2: Hyperfine components of the NH3 (J,K) = (1,1) transition.
Nobeyama. The NH3
(J, K)
= (1, 1) line
at 23 GHz and the N2H+ J
= 1-0 line at 93 GHz
were observed with the Nobeyama Radio Observatory (NRO)
45-m telescope![]() on April 8-10,
2009. We used a low-noise HEMT receiver, H22,
for the NH3 observations and the two
sideband-separating SIS
(Superconductor-Insulator-Superconductor)
receiver, T100 (Nakajima et al. 2008), for the
N2H+ observations.
Both of them are dual polarization receivers. We observed two
polarizations simultaneously. The 45-m radio telescope angular
resolution
is about 73 and 17 arcsec at 23 and 93 GHz, respectively, and
the main beam efficiency is 0.84 at 23 GHz, and 0.53
at 93 GHz. Autocorrelators were employed as a backend with
bandwidth and channel separation of 4 MHz and 4.375 kHz,
respectively. This corresponds to channel widths of
57 m s-1 at
23 GHz, and 14 m s-1
at 93 GHz.
on April 8-10,
2009. We used a low-noise HEMT receiver, H22,
for the NH3 observations and the two
sideband-separating SIS
(Superconductor-Insulator-Superconductor)
receiver, T100 (Nakajima et al. 2008), for the
N2H+ observations.
Both of them are dual polarization receivers. We observed two
polarizations simultaneously. The 45-m radio telescope angular
resolution
is about 73 and 17 arcsec at 23 and 93 GHz, respectively, and
the main beam efficiency is 0.84 at 23 GHz, and 0.53
at 93 GHz. Autocorrelators were employed as a backend with
bandwidth and channel separation of 4 MHz and 4.375 kHz,
respectively. This corresponds to channel widths of
57 m s-1 at
23 GHz, and 14 m s-1
at 93 GHz.
The telescope pointing was checked by observing nearby SiO
maser
sources every 1-2 h. The pointing accuracy was ![]() 5''. The
line intensities were calibrated using the
chopper wheel method, and the observations were carried out in position
switching mode. The data reduction was performed partly with the
AIPS-based software package NewStar developed at NRO.
5''. The
line intensities were calibrated using the
chopper wheel method, and the observations were carried out in position
switching mode. The data reduction was performed partly with the
AIPS-based software package NewStar developed at NRO.
4 Data analysis
4.1 V
 calculation
calculation
The radial velocities, ![]() ,
are determined from the spectral line analysis.
Each individual exposure was first visually analyzed and corrupted data
were excluded. Individual exposures were then coadded to increase the
signal-to-noise
(S/N) ratio. Before coadding, a baseline was removed from each
spectrum. To define the baseline,
spectral intervals without emission lines and/or noise spikes were
selected and the mean signal Ti
along with
its rms uncertainty
,
are determined from the spectral line analysis.
Each individual exposure was first visually analyzed and corrupted data
were excluded. Individual exposures were then coadded to increase the
signal-to-noise
(S/N) ratio. Before coadding, a baseline was removed from each
spectrum. To define the baseline,
spectral intervals without emission lines and/or noise spikes were
selected and the mean signal Ti
along with
its rms uncertainty ![]() were calculated for each interval. A set of pairs
were calculated for each interval. A set of pairs
![]() was used to find a baseline (regression line) by minimizing
was used to find a baseline (regression line) by minimizing ![]() .
This baseline was typically linear but was in some cases quadratic or
cubic.
Since individual rms uncertainties
.
This baseline was typically linear but was in some cases quadratic or
cubic.
Since individual rms uncertainties ![]() were of the same order of magnitude, their mean value
were of the same order of magnitude, their mean value ![]() was assigned to the whole spectrum. The resulting spectra were coadded
with weights that are inversionally proportional to their variances,
was assigned to the whole spectrum. The resulting spectra were coadded
with weights that are inversionally proportional to their variances, ![]() .
.
The line parameters such as the total optical depth in the
transition, ![]() ,
the radial velocity,
,
the radial velocity, ![]() ,
the line broadening Doppler parameter, b, and the
amplitude, A, were estimated by fitting
a one-component Gaussian model to the observed spectra. The model was
defined by
,
the line broadening Doppler parameter, b, and the
amplitude, A, were estimated by fitting
a one-component Gaussian model to the observed spectra. The model was
defined by
where
where ai, vi is, respectively, the relative intensity of the ith hyperfine component and its velocity separation from the reference frequency. The sum in Eq. (9) runs over the k hyperfine structure (hfs) components of the transition. The physical parameters ai, and vi for the NH3 (1,1), HC3N (2-1), and N2H+ (1-0) transitions are listed in Tables 2-4, respectively.
Table 3: Hyperfine components of the HC3N J = 2-1 transition.
Table 4: Hyperfine components of the N2H+ J = 1-0 transition.
Table 5:
Radial velocities, ![]() ,
Doppler parameters, b, and corresponding
,
Doppler parameters, b, and corresponding
![]() values normalized per degree
of freedom.
values normalized per degree
of freedom.
Table 6:
Radial velocities, ![]() ,
Doppler parameters, b, and corresponding
,
Doppler parameters, b, and corresponding
![]() values normalized per degree of freedom.
values normalized per degree of freedom.
The fitting parameters
![]() were determined by means of a
were determined by means of a ![]() -minimization procedure.
For optically thin transitions, Eq. (8) transforms into
-minimization procedure.
For optically thin transitions, Eq. (8) transforms into
which prevents the independent estimation of A and
Since we are mostly interested in the model parameters
![]() and b, their values are listed in Tables 5 and 6. The
and b, their values are listed in Tables 5 and 6. The ![]() errors of
errors of
![]() and b were estimated from the diagonal elements of
the covariance matrix calculated for the minimum of
and b were estimated from the diagonal elements of
the covariance matrix calculated for the minimum of ![]() .
The error in
.
The error in ![]() was also estimated independently by the
was also estimated independently by the
![]() method (e.g., Press
et al. 1992)
to control
both results. When two estimates differed, the larger error was
adopted.
method (e.g., Press
et al. 1992)
to control
both results. When two estimates differed, the larger error was
adopted.
4.2 Uncertainties in the rest-frequencies
Molecular lines observed in cold dark clouds of
![]() K
can
be extremely narrow with a thermal broadening of
K
can
be extremely narrow with a thermal broadening of
![]() m s-1
for NH3 or even lower for heavier
molecules. They provide a sensitive spectroscopic measurement of
shallow velocity gradients in molecular clouds (Lapinov 2006).
At high spectral resolution (
m s-1
for NH3 or even lower for heavier
molecules. They provide a sensitive spectroscopic measurement of
shallow velocity gradients in molecular clouds (Lapinov 2006).
At high spectral resolution (
![]() m s-1 ),
the uncertainty in the line position measurement from radio
astronomical observations can be
as small as 1 m s-1
which is comparable to the precision available for laboratory
rest-frame frequencies of the NH3
(J,K)
= (1,1) transition (Kukolich 1967;
Hougen 1972).
The physical parameters of the observed hfs components of NH3
are listed in
Table 2.
Column 1 indicates the group numbers shown in the upper panel
of Fig. 2.
The errors in the line positions given in parentheses in
Col. 7 are
smaller than 1 m s-1
with a mean of
m s-1 ),
the uncertainty in the line position measurement from radio
astronomical observations can be
as small as 1 m s-1
which is comparable to the precision available for laboratory
rest-frame frequencies of the NH3
(J,K)
= (1,1) transition (Kukolich 1967;
Hougen 1972).
The physical parameters of the observed hfs components of NH3
are listed in
Table 2.
Column 1 indicates the group numbers shown in the upper panel
of Fig. 2.
The errors in the line positions given in parentheses in
Col. 7 are
smaller than 1 m s-1
with a mean of ![]() m s-1 .
However, laboratory uncertainties for other molecules used in the
present observations are significantly larger.
m s-1 .
However, laboratory uncertainties for other molecules used in the
present observations are significantly larger.
The analysis of all available laboratory data about HC3N
carried out
by Müller et al. (2005)
and independently by Lapinov (2008, private comm.) shows good
agreement,
the latter results being of slightly higher precision (
![]() m s-1 ).
The physical parameters of the hfs components of the J
= 2-1 transition
are presented in Table 3.
The line identification numbers from Col. 1
are depicted in the middle panel of Fig. 2.
m s-1 ).
The physical parameters of the hfs components of the J
= 2-1 transition
are presented in Table 3.
The line identification numbers from Col. 1
are depicted in the middle panel of Fig. 2.
The rest-frame frequencies for the third molecule N2H+
(Table 4)
were taken from the Cologne Database for Molecular Spectroscopy (CDMS)
described in
Müller et al. (2005).
The group numbers from Table 4,
Col. 1 are also shown in Fig. 2, lower panel.
The CDMS data have a factor of two smaller errors than
the hyperfine frequencies estimated from observations
of the molecular core L1512 in both N2H+
(93 GHz)
and C3H2
(85 GHz). It is again assumed that these molecules are
co-spatially distributed (Caselli et al. 1995).
The error in ![]() m s-1
(
m s-1
(![]() 4 kHz)
reported in Table 4
corresponds to the CDMS data.
The mean offset between the data from Caselli et al. and the
CDMS is
4 kHz)
reported in Table 4
corresponds to the CDMS data.
The mean offset between the data from Caselli et al. and the
CDMS is
![]() m s-1 .
m s-1 .
We do not correct the N2H+
frequencies for a 40 m s-1
offset as by
Pagani et al. (2009),
who used the rest-frame frequencies of Caselli et al.. The
offset of 40 m s-1 ,
or 28 m s-1 when
adopting the CDMS rest frequencies (Molaro et al. 2009),
was determined by comparing the inversion
NH3 (1,1) and rotational N2H+
(1-0) transitions observed in the target L183; this correction
is justifable only when ![]()
![]() .
Reliable calibrations of the hyperfine transition frequencies of N2H+
can be performed only by a high precision laboratory measurement.
.
Reliable calibrations of the hyperfine transition frequencies of N2H+
can be performed only by a high precision laboratory measurement.
We note in passing that the estimate of the mean radial
velocity based on the simultaneous fitting of n hyperfine
transitions should be more precise than that based on
a single line. However, the improvement is not as high as
![]() because the relative positions of the individual hfs transitions are
correlated. If we consider n velocity
differences
because the relative positions of the individual hfs transitions are
correlated. If we consider n velocity
differences ![]() ,
v2 - v0,
,
v2 - v0,
![]() ,
,
![]() ,
where v0 is the reference
velocity, then it is easy to show that the correlation coefficient
,
where v0 is the reference
velocity, then it is easy to show that the correlation coefficient
![]() between two of them (
between two of them (![]() )
is given by
)
is given by
where
The covariance matrix
![]() contains n diagonal terms
contains n diagonal terms ![]() and n(n-1) non-diagonal terms
and n(n-1) non-diagonal terms
![]() ,
where
,
where ![]() represents the variance
in a single measurement. The error in the mean radial velocity caused
by the laboratory uncertainties (referred to as
represents the variance
in a single measurement. The error in the mean radial velocity caused
by the laboratory uncertainties (referred to as
![]() hereafter) can be calculated as described by, e.g., Stuart &
Ord (1994)
hereafter) can be calculated as described by, e.g., Stuart &
Ord (1994)
In cases of equal accuracy, the weight
Thus, the gain factor,
5 Results
We first consider the entire sample of sources listed in Table 1. By applying the
same computational procedure to all available spectra from the three
radio telescopes, we find that not all of the molecular profiles can be
described adequately
with a single-component Gaussian model. In total, we measured n
= 55 molecular pairs. The corresponding velocity offsets ![]() are shown in Fig. 10
by three types of symbols: filled squares and circles (NH3/HC3N
pairs), and open circles (NH3/N2H+
pairs) are, respectively, data points from the 32-m, 100-m, and 45-m
telescopes. Some molecular cores
(L183, L1495, TMC-1C) were partially mapped. The offset coordinates in
arcsec with respect to the source positions from Table 1 are shown in
parentheses. Two objects (L183 and TMC-1C) were observed at the 32-m
telescope with different spectrometers ARCOS and MSpec0, as indicated
in the figure. Five sources, TMC-1/HC3N (Medicina), TMC-2, L1521F, and
L1544 (Effelsberg), and
TMC-2 (Nobeyama) from Table 1
exhibit asymmetric profiles that are not consistent with a simple
Gaussian model (we do not show them in Fig. 10). A considerable
fraction of the molecular pairs from the total sample
exhibit non-thermal motion, i.e., the Doppler broadening parameter
b(NH3)
are shown in Fig. 10
by three types of symbols: filled squares and circles (NH3/HC3N
pairs), and open circles (NH3/N2H+
pairs) are, respectively, data points from the 32-m, 100-m, and 45-m
telescopes. Some molecular cores
(L183, L1495, TMC-1C) were partially mapped. The offset coordinates in
arcsec with respect to the source positions from Table 1 are shown in
parentheses. Two objects (L183 and TMC-1C) were observed at the 32-m
telescope with different spectrometers ARCOS and MSpec0, as indicated
in the figure. Five sources, TMC-1/HC3N (Medicina), TMC-2, L1521F, and
L1544 (Effelsberg), and
TMC-2 (Nobeyama) from Table 1
exhibit asymmetric profiles that are not consistent with a simple
Gaussian model (we do not show them in Fig. 10). A considerable
fraction of the molecular pairs from the total sample
exhibit non-thermal motion, i.e., the Doppler broadening parameter
b(NH3) ![]() (HC3N,
N2H+).
(HC3N,
N2H+).
Several sources were observed at different radio telescopes. Since these data points have different systematic errors, we treat them as ``independent'' measurements in the following statistical estimates.
The weighted mean (weights inversionally proportional to the
variances) of the ensemble of n=55 ![]() values is
values is
![]() m s-1 ,
the scale (standard deviation) is 32.6 m s-1 ,
and the median is 17 m s-1 .
We also used a robust redescending M-estimate for
the mean
and the normalized median absolute deviation (
m s-1 ,
the scale (standard deviation) is 32.6 m s-1 ,
and the median is 17 m s-1 .
We also used a robust redescending M-estimate for
the mean
and the normalized median absolute deviation (
![]() MAD) for the scale.
These statistics work well for inhomogeneous data sets
with outliers and deviations from normality
(corresponding formulae are given in Appendix).
The M-estimate infers that
MAD) for the scale.
These statistics work well for inhomogeneous data sets
with outliers and deviations from normality
(corresponding formulae are given in Appendix).
The M-estimate infers that
![]() m s-1
(scale 29.6 m s-1 ).
A poor concordance between three mean estimates (
m s-1
(scale 29.6 m s-1 ).
A poor concordance between three mean estimates (
![]() ,
,
![]() ,
and the median)
is caused by large systematic shifts and, as a result,
by ``heavy tails'' of the probability distribution function. The
scatter in the points reflects effects related to the gas kinematics
and the chemical segregation of one molecule with respect to
the other.
,
and the median)
is caused by large systematic shifts and, as a result,
by ``heavy tails'' of the probability distribution function. The
scatter in the points reflects effects related to the gas kinematics
and the chemical segregation of one molecule with respect to
the other.
An additional decrease in the noise component
![]() in Eq. (7)
is possible if we select from the sample of the observed
targets the systems with ``simple'' geometry and internal kinematics.
The ideal target would be a homogeneous spherical cloud where different
molecules are co-spatially distributed (no chemical segregation) and
where turbulence is suppressed (thermally
dominated motion). In this case, any deviations from the expected zero
mean value of the radial velocity difference between rotational and
inversion molecular transitions in Eq. (5) could be ascribed to
the non-zero
in Eq. (7)
is possible if we select from the sample of the observed
targets the systems with ``simple'' geometry and internal kinematics.
The ideal target would be a homogeneous spherical cloud where different
molecules are co-spatially distributed (no chemical segregation) and
where turbulence is suppressed (thermally
dominated motion). In this case, any deviations from the expected zero
mean value of the radial velocity difference between rotational and
inversion molecular transitions in Eq. (5) could be ascribed to
the non-zero ![]() value.
value.
In practice, molecular cores are not ideal spheres and when observed at higher angular resolutions they frequently exhibit complex substructures. The line profiles may be asymmetric because of non-thermal bulk motions. Taking this into account, the following criteria were formulated:
- 1.
- The line profiles are symmetric described well by a
single-component Gaussian model
(i.e., the minimum value of
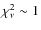 ).
This selection increases the accuracy of the line center measurement.
Multiple line components may shift the line barycenter and affect the
velocity
difference between molecular transitions because, e.g., the ratio NH3/HC3N
can vary from one component to another.
).
This selection increases the accuracy of the line center measurement.
Multiple line components may shift the line barycenter and affect the
velocity
difference between molecular transitions because, e.g., the ratio NH3/HC3N
can vary from one component to another.
- 2.
- The line widths do not greatly exceed the Doppler width
because of the thermal motion of material,
i.e., the non-thermal component (infall, outflow, tidal flow,
turbulence) does not dominate the line broadening. This ensures that
selected molecular lines correspond to the same kinetic temperature and
arise cospatially. For the molecules in question we require that the
ratio of the Doppler b-parameters,
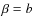 (NH3)/b(HC3N)
or
(NH3)/b(HC3N)
or 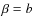 (NH3)/b(N2H+),
be
(NH3)/b(N2H+),
be 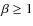 .
.
- 3.
- The spectral lines are sufficiently narrow (
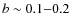 km s-1 )
for hyperfine structure components to be resolved. This allows us to
validate the measured radial velocity by means of different hfs lines
of the same molecular transition.
km s-1 )
for hyperfine structure components to be resolved. This allows us to
validate the measured radial velocity by means of different hfs lines
of the same molecular transition.
- 4.
- The spectral lines are not heavily saturated and their
profiles are not affected by optical depth effects.
The total optical depth of the NH3 hf
transitions is
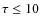 .
.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13007f1.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg141.png)
|
Figure 1: Sketch of the hyperfine transitions for the NH3 (1, 1), HC3N (2-1), and N2H+ (1-0) states. Line identification numbers are given in each panel (see Tables 2-4). |
| Open with DEXTER | |
Table 5 lists the values obtained from the analysis of the NH3 (1,1) and HC3N (2-1) transitions, whereas in Table 6 the NH3 (1,1) and N2H+ (1-0) measurements are presented. Where individual hfs transitions can be analyzed separately, the results of these analyse are also given. The data obtained for NH3 are divided formally into 4 groups, which are marked in Fig. 1 and Table 2 by the following numbers: ``outer'' - 1 and 5, ``inner'' -2 and 4, ``central'' - 3, and ``total'' combines all hfs lines (Cols. 2-5 of Table 5, respectively). For HC3N, the measurements are presented in 3 groups, which are marked in Fig. 1 and Table 3 as: ``low'' - 1, 5, and 6, ``high'' - 3 and 4, and ``total'' -1, 3, 4, 5, and 6 (Cols. 6-8 of Table 5, respectively). Line number 2 (F=1-2) is very weak and was never detected in our observations. For N2H+, we divided the hfs lines into 3 groups on the basis of their relative theoretical intensities. These groups are indicated in Fig. 1 and Table 4 as: ``low'' - 1, 2, 5, and 7, ``high'' - 3, 4, and 6, and `total' combines all hfs lines (Cols. 6-8 of Table 6, respectively).
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13007f2.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg142.png)
|
Figure 2: Spectra of NH3 (1, 1) and HC3N (2-1) toward the cores L1512 and L183 obtained at the Medicina 32-m radio telescope. The histogram shows the data, the solid curve shows the fit, and the residual is plotted below each profile. The horizontal thick bars mark spectral windows used in the fitting procedure. The data are the arithmetic means of all the observations. The size of the resolution element (pixel) is 62 m s-1 for NH3, and 80 m s-1 for HC3N. For each spectrum, the signal-to-noise ratio (S/N) per pixel at the maximum intensity peak is depicted. |
| Open with DEXTER | |
The analyzed molecular line profiles are shown in Figs. 2-9. The smooth curves
are synthetic spectra calculated in the simultaneous fit of all
hyperfine components to the observed profiles. Bold horizontal lines
mark the spectral ranges included in the ![]() -minimization procedure. The
quality of individual fittings can be characterized by the
normalized
-minimization procedure. The
quality of individual fittings can be characterized by the
normalized ![]() values given in Tables 5
and 6
for each group of measurements. The residuals ``observed data-model''
are depicted beneath each spectrum in Figs. 2-9.
The signal-to-noise ratio (S/N) per resolution element shown in these
figures
is calculated at the maximum intensity peak.
values given in Tables 5
and 6
for each group of measurements. The residuals ``observed data-model''
are depicted beneath each spectrum in Figs. 2-9.
The signal-to-noise ratio (S/N) per resolution element shown in these
figures
is calculated at the maximum intensity peak.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13007f3.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg143.png)
|
Figure 3: Spectra of NH3 (1,1) and HC3N (2-1) toward the cores L1498, L1495, and L1400K obtained at the Effelsberg 100-m radio telescope. The histogram shows the data, the solid curve shows the fit, and the residual is plotted below each profile. The horizontal thick bars mark spectral windows used in the fitting procedure. The data are the arithmetic means of all the observations. The size of the resolution element (pixel) is 15 m s-1 for NH3, and 20 m s-1 for HC3N. For each spectrum, the signal-to-noise ratio (S/N) per pixel at the maximum intensity peak is depicted. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13007f4.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg144.png)
|
Figure 4:
Same as Fig. 3
but for the cores CB22, TMC-1C (offset
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm]{13007f5.eps}
\vspace*{7mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg145.png)
|
Figure 5: Same as Fig. 3 but for the cores L1512, L183, and L260-NH3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13007f6.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg146.png)
|
Figure 6: Same as Fig. 3 but for the cores L234A, B335, and L1251C. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13007f7.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg147.png)
|
Figure 7: Spectra of NH3 (1,1) and N2H+ (1-0) toward the cores L1498, L1536, and CB23 obtained at the Nobeyama 45-m radio telescope. The histogram shows the data, the solid curve shows the fit, and the residual is plotted below each profile. The horizontal thick bars mark spectral windows used in the fitting procedure. The data are the arithmetic means of all the observations. The size of the resolution element (pixel) is 49 m s-1 for NH3, and 25 m s-1 for N2H+. For each spectrum, the signal-to-noise ratio (S/N) per pixel at the maximum intensity peak is depicted. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm]{13007f8.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg148.png)
|
Figure 8: Same as Fig. 7 but for the cores L1517B, L1512, and L183. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm]{13007f9.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg149.png)
|
Figure 9:
Same as Fig. 7
but for the cores L183 (offset
|
| Open with DEXTER | |
The velocity offsets, ![]() ,
and their statistical errors are listed in Col. 9 of
Tables 5
and 6.
When calculating
,
and their statistical errors are listed in Col. 9 of
Tables 5
and 6.
When calculating
![]() ,
we used the mean
,
we used the mean ![]() radial velocities based on the simultaneous fitting of all hyperfine
transitions. The
radial velocities based on the simultaneous fitting of all hyperfine
transitions. The ![]() values estimated in 23 measurements
are marked in Fig. 11
by the circles with 1
values estimated in 23 measurements
are marked in Fig. 11
by the circles with 1![]() error bars.
The filled circles indicate sources with thermally dominated motions.
We also show the ratios of the Doppler b-parameters:
error bars.
The filled circles indicate sources with thermally dominated motions.
We also show the ratios of the Doppler b-parameters:
![]() (NH3)/b(HC3N)
or
(NH3)/b(HC3N)
or ![]() (NH3)/b(N2H+),
in parentheses provide their
(NH3)/b(N2H+),
in parentheses provide their ![]() errors. For the 32-m and 100-m telescopes,
errors. For the 32-m and 100-m telescopes,
![]() (HC3N)
(HC3N)
![]() (NH3),
whereas for the 45-m telescope
(NH3),
whereas for the 45-m telescope
![]() (N2H+)
(N2H+)
![]() (NH3).
(NH3).
Among the selected clouds, we discover that only one (L260-NH3)
violates the selection rule No. 4. The total optical depth in
this case is ![]() .
We used this cloud since the spectrum of NH3 was
of high S/N and other selection criteria were fulfilled. We note,
however, that this cloud has the minimum
.
We used this cloud since the spectrum of NH3 was
of high S/N and other selection criteria were fulfilled. We note,
however, that this cloud has the minimum ![]() value consistent with a zero offset (see Table 5 and Fig. 11).
value consistent with a zero offset (see Table 5 and Fig. 11).
Both data sets exhibit an excess of positive velocity offsets.
The most accurate results are obtained for the L1498 and L1512
molecular cores observed with the 100-m Effelsberg
telescope, ![]() m s-1 .
In this case, the systematic error due to the rest frequency
uncertainties does not exceed 3 m s-1 .
The maximum spread between the individual hfs
m s-1 .
In this case, the systematic error due to the rest frequency
uncertainties does not exceed 3 m s-1 .
The maximum spread between the individual hfs
![]() velocities for NH3 is 5.5 m s-1
(L1498)
and 4.5 m s-1
(L1512), but it is only 1.0 m s-1
for the
HC3N hyperfine transitions
in both sources.
The molecular lines are narrow with b(NH3)
velocities for NH3 is 5.5 m s-1
(L1498)
and 4.5 m s-1
(L1512), but it is only 1.0 m s-1
for the
HC3N hyperfine transitions
in both sources.
The molecular lines are narrow with b(NH3)
![]() m s-1 ,
b(HC3N)
m s-1 ,
b(HC3N) ![]() m s-1
(L1498), and b(NH3)
m s-1
(L1498), and b(NH3) ![]() m s-1 ,
b(HC3N)
m s-1 ,
b(HC3N) ![]() m s-1
(L1512), which is in line with the assumption that in these
two clouds both molecules trace the same volume elements.
m s-1
(L1512), which is in line with the assumption that in these
two clouds both molecules trace the same volume elements.
The sources with thermally dominated motions (n
= 7) marked by the filled circles in Fig. 11
give the weighted mean of
![]() m s-1 ,
the scale 3.4 m s-1 ,
and the median 22 m s-1 .
The corresponding M-estimate is
m s-1 ,
the scale 3.4 m s-1 ,
and the median 22 m s-1 .
The corresponding M-estimate is
![]() m s-1
(scale 4.8 m s-1 ).
m s-1
(scale 4.8 m s-1 ).
For the ensemble of n=23 ![]() values, we found the weighted mean of
values, we found the weighted mean of
![]() m s-1 ,
the scale 14.4 m s-1 ,
and the median 22 m s-1 .
The robust M-estimate is
m s-1 ,
the scale 14.4 m s-1 ,
and the median 22 m s-1 .
The robust M-estimate is
![]() m s-1
(scale 13.4 m s-1 ).
Thus, in the reduced sample, we have good agreement between all three
estimates of the mean.
The scatter in the points (the Doppler noise) is
lower by a factor of two than that of the n=55 data
set.
m s-1
(scale 13.4 m s-1 ).
Thus, in the reduced sample, we have good agreement between all three
estimates of the mean.
The scatter in the points (the Doppler noise) is
lower by a factor of two than that of the n=55 data
set.
The individual data from the 100-m and 45-m telescopes provide
the following estimates. Effelsberg:
![]() m s-1
(n=12, scale 10.7 m s-1 ,
median 22 m s-1 ),
m s-1
(n=12, scale 10.7 m s-1 ,
median 22 m s-1 ),
![]() m s-1
(scale 13.3 m s-1 ).
Nobeyama:
m s-1
(scale 13.3 m s-1 ).
Nobeyama:
![]() m s-1
(n=9, scale 21.6 m s-1 ,
median 22 m s-1 ),
m s-1
(n=9, scale 21.6 m s-1 ,
median 22 m s-1 ),
![]() m s-1
(scale 12.7 m s-1 ).
m s-1
(scale 12.7 m s-1 ).
Although the robust M-estimates of the
mean for both the Effelsberg and Nobeyama observations are consistent,
the latter has a larger systematic error due to its lower accuracy at
the rest
frequencies of the N2H+
(1-0) transition. Taking into account that the rest
frequencies of the HC3N (2-1) are known with a
sufficiently high accuracy
(the uncertainties in the laboratory and observational frequencies are
comparable), we take the Effelsberg robust mean as a final value for
the velocity offset between the rotational and inversion transitions.
Being interpreted in terms of the electron-to-proton mass ratio
variation, this provides the value
![]() =
=
![]() ppb (1 ppb = 10-9).
ppb (1 ppb = 10-9).
5.1 Data reproducibility
Taking into account numerous perturbation effects discussed above
and variations in specific parameters such as spectral resolution and
signal-to-noise ratio, we question the consistency
of the measured ![]() values
obtained for independent telescope systems. This consistency was first
tested at the 32-m Medicina telescope, where
we observed two cores, L183 and TMC-1C, in lines of NH3
(1,1) and HC3N (2-1) with the ARCOS and MSpec0
digital spectrometers.
For L183, we found
values
obtained for independent telescope systems. This consistency was first
tested at the 32-m Medicina telescope, where
we observed two cores, L183 and TMC-1C, in lines of NH3
(1,1) and HC3N (2-1) with the ARCOS and MSpec0
digital spectrometers.
For L183, we found ![]() m s-1
(MSpec0) and
m s-1
(MSpec0) and ![]() m s-1
(ARCOS), whereas for TMC-1C, the corresponding quantities were measured
to be
m s-1
(ARCOS), whereas for TMC-1C, the corresponding quantities were measured
to be
![]() m s-1
and
m s-1
and ![]() m s-1 .
Both results are in good agreement to within the 1
m s-1 .
Both results are in good agreement to within the 1![]() uncertainty interval.
uncertainty interval.
We also tested the reliability of the velocity offsets by
obtaining observations of the same cores at different telescopes.
For instance, a quiescent low-mass molecular core L1512 in the Taurus
Cloud was observed in the NH3 (1,1) and HC3N
(2-1) lines at
the 32-m and 100-m telescopes. The corresponding velocity offsets are
![]() m s-1
and
m s-1
and ![]() m s-1 .
Other examples can be
found in Fig. 10,
where velocity offsets
m s-1 .
Other examples can be
found in Fig. 10,
where velocity offsets ![]() of
molecular pairs consistent with a singe-component Gaussian model are
depicted.
of
molecular pairs consistent with a singe-component Gaussian model are
depicted.
Some of our targets were partially mapped as indicated in
Fig. 10.
The six points of TMC-1C are scattered between
![]() m s-1
and
m s-1
and ![]() m s-1 ,
which is indicative of large systematic
shifts caused by bulk motions. Indeed, the line widths of NH3
and
HC3N demonstrate the dominant influence of the
non-thermal component.
The measured ratio
m s-1 ,
which is indicative of large systematic
shifts caused by bulk motions. Indeed, the line widths of NH3
and
HC3N demonstrate the dominant influence of the
non-thermal component.
The measured ratio ![]() (NH3)/b(HC3N)
at these points is equal to
1.0, 0.8, 1.2, 1.0, 1.2, and 1.0 at, respectively,
(NH3)/b(HC3N)
at these points is equal to
1.0, 0.8, 1.2, 1.0, 1.2, and 1.0 at, respectively,
![]() ,
and (60,-45) arcsec.
Similar velocity offsets are observed for L1495 and L183.
In general, the scatter for the whole sample covers the range
,
and (60,-45) arcsec.
Similar velocity offsets are observed for L1495 and L183.
In general, the scatter for the whole sample covers the range
![]() m s-1 .
However, the scatter for the subsample selected in accord
with the additional selection criteria from Sect. 5 decreases
considerably. The corresponding points shown in Fig. 11 are distributed
across the interval from -10to 43 m s-1 .
Thus, as expected, molecular cores with thermally dominated gas motions
are
the most suitable targets for precise measurements of
m s-1 .
However, the scatter for the subsample selected in accord
with the additional selection criteria from Sect. 5 decreases
considerably. The corresponding points shown in Fig. 11 are distributed
across the interval from -10to 43 m s-1 .
Thus, as expected, molecular cores with thermally dominated gas motions
are
the most suitable targets for precise measurements of
![]() .
.
It is essential that the observed spectral-line displacements are based on differential measurements of radial velocities recorded at the same telescope over short periods of time. It is also important that different receivers used in these observations enable the independent Doppler tracking of the observed molecular lines. Thus, there is no need for an accurate definition of the zero point, and only internal precisions of the measured line positions and the uncertainties in the rest-frame frequencies restrict the accuracy of the measured velocity offset.
5.2 Comparison with previously obtained results
In our preliminary analysis (LMK), we used high quality radio spectra of molecular cores in lines of NH3 (J,K) = (1,1) (23 GHz), CCS JN = 21-10 (22 GHz), HC3N J = 5-4 (45 GHz), and N2H+ J = 1-0 (93 GHz). The observations were carried out with the 100-m Green Bank Telescope (GBT) by Rosolowsky et al. (2008) for the Perseus molecular cloud, by Rathborne et al. (2008) for the Pipe Nebula, and with the Nobeyama 45-m telescope by Sakai et al. (2008) for infrared dark clouds (IRDCs).
The most accurate estimates were obtained from carefully
selected subsamples of the NH3/CCS pairs
observed with high spectral resolution (FWHM =
25 m s-1 ) in the
Perseus molecular cloud (n = 21) and the Pipe Nebula
(n = 8):
![]() m s-1
and
m s-1
and
![]() m s-1 ,
respectively.
The analysis of the n = 36 NH3/N2H+
pairs and
n = 27 NH3/HC3N
pairs observed at lower spectral resolution (
FWHM =
120-500 m s-1 ) in
the IRDCs inferred that
m s-1 ,
respectively.
The analysis of the n = 36 NH3/N2H+
pairs and
n = 27 NH3/HC3N
pairs observed at lower spectral resolution (
FWHM =
120-500 m s-1 ) in
the IRDCs inferred that
![]() m s-1
and
m s-1
and
![]() m s-1 ,
respectively.
At the same time, the rotational-rotational velocity differences for
the IRDCs did not show any significant offset:
m s-1 ,
respectively.
At the same time, the rotational-rotational velocity differences for
the IRDCs did not show any significant offset:
![]() (N2H+)
- V(HC3N) =
(N2H+)
- V(HC3N) =
![]() km s-1 .
km s-1 .
The physical properties of low-mass (
![]() )
molecular cores observed with the GBT are similar to those analyzed in
the present paper. However, the IRDCs are more massive
objects (
)
molecular cores observed with the GBT are similar to those analyzed in
the present paper. However, the IRDCs are more massive
objects (
![]() )
with high turbulent velocities (
)
with high turbulent velocities (![]() 1-3 km s-1 ).
The IRDCs are also more distant clouds, which are located towards the
Galactic center at distances
of 2-5 kpc. The spectral resolution used in observations of
the IRDCs does not
allow us to resolve the hyperfine structure of the HC3N
J=5-4 transition (Sakai et al. 2008).
The spectra of the HC3N lines were fitted to a
single
Gaussian function and the corresponding radial velocities
were calculated based on a single
hyperfine line J=5-4,
F=5-4 with the frequency 45490.3102(3) MHz
taken from the JPL catalog
1-3 km s-1 ).
The IRDCs are also more distant clouds, which are located towards the
Galactic center at distances
of 2-5 kpc. The spectral resolution used in observations of
the IRDCs does not
allow us to resolve the hyperfine structure of the HC3N
J=5-4 transition (Sakai et al. 2008).
The spectra of the HC3N lines were fitted to a
single
Gaussian function and the corresponding radial velocities
were calculated based on a single
hyperfine line J=5-4,
F=5-4 with the frequency 45490.3102(3) MHz
taken from the JPL catalog![]() .
As a result, a systematic shift related to unresolved hyperfine
components
was introduced. We also note that the JPL frequencies are
systematically shifted with respect to the CDMS catalogue (Müller
et al. 2005).
The CDMS frequency of the
J=5-4,
F=5-4 transition is, for example,
45490.3137(5) MHz. Thus, it seems plausible that the large
offset,
.
As a result, a systematic shift related to unresolved hyperfine
components
was introduced. We also note that the JPL frequencies are
systematically shifted with respect to the CDMS catalogue (Müller
et al. 2005).
The CDMS frequency of the
J=5-4,
F=5-4 transition is, for example,
45490.3137(5) MHz. Thus, it seems plausible that the large
offset,
![]() m s-1 ,
deduced from the IRDCs is caused by the superposition of unaccounted
systematic shifts.
m s-1 ,
deduced from the IRDCs is caused by the superposition of unaccounted
systematic shifts.
![\begin{figure}
\par\includegraphics[width=8.5cm]{13007f10.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg186.png)
|
Figure 10:
Doppler velocity differences, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13007f11.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg187.png)
|
Figure 11:
Doppler velocity differences, |
| Open with DEXTER | |
As for the low-mass cores in the Perseus molecular cloud and the Pipe
Nebula, the discrepancy between our present estimate,
![]() m s-1 ,
and the previously obtained value,
m s-1 ,
and the previously obtained value,
![]() m s-1 ,
is probably caused by uncertainties in the rest-frame frequency of the
CCS JN
= 21-10 transition. In
particular, the frequency 22344.033(1) MHz of this
transition
(used by both Rosolowsky et al. and Rathborne et al.)
was calculated by comparing with the HC3N J
= 5-4 line
observed towards a cold dark cloud L1498 assuming that (i)
CCS and HC3N
are co-spatially distributed and (ii) the rest-frame
frequency of HC3N J = 5-4, F
= 5-4 is 45490.316(1) MHz (Yamamoto et al. 1990). If the
HC3N frequency is 2 kHz lower as
indicated in the CDMS catalogue, then the laboratory frequency of CCS
decreases by 1 kHz, where 1 kHz at 22.3 GHz
corresponds to 13.4 m s-1 ,
i.e., the difference
V(CCS) - V(NH3)
becomes equal to
m s-1 ,
is probably caused by uncertainties in the rest-frame frequency of the
CCS JN
= 21-10 transition. In
particular, the frequency 22344.033(1) MHz of this
transition
(used by both Rosolowsky et al. and Rathborne et al.)
was calculated by comparing with the HC3N J
= 5-4 line
observed towards a cold dark cloud L1498 assuming that (i)
CCS and HC3N
are co-spatially distributed and (ii) the rest-frame
frequency of HC3N J = 5-4, F
= 5-4 is 45490.316(1) MHz (Yamamoto et al. 1990). If the
HC3N frequency is 2 kHz lower as
indicated in the CDMS catalogue, then the laboratory frequency of CCS
decreases by 1 kHz, where 1 kHz at 22.3 GHz
corresponds to 13.4 m s-1 ,
i.e., the difference
V(CCS) - V(NH3)
becomes equal to ![]() 46 m s-1 .
The only known laboratory measurement of the CCS frequency
infers, however, that 22344.029(4) MHz (Lovas et al. 1992). With this
value V(CCS) - V(NH3)
46 m s-1 .
The only known laboratory measurement of the CCS frequency
infers, however, that 22344.029(4) MHz (Lovas et al. 1992). With this
value V(CCS) - V(NH3)
![]() 6 m s-1 ,
but its error reaches 53 m s-1
(4 kHz at 22.3 GHz). The rest-frame frequency of CCS
reported in the CDMS is 22344.0308(10) MHz. With this
frequency, we obtain for the Perseus molecular cloud the offset
6 m s-1 ,
but its error reaches 53 m s-1
(4 kHz at 22.3 GHz). The rest-frame frequency of CCS
reported in the CDMS is 22344.0308(10) MHz. With this
frequency, we obtain for the Perseus molecular cloud the offset
![]() m s-1 ,
which is in full agreement with our present estimate,
m s-1 ,
which is in full agreement with our present estimate,
![]() m s-1 .
This consideration makes it quite obvious that
to increase the reliability of the results obtained, high precision
laboratory measurements of molecular transition frequencies are badly
needed.
m s-1 .
This consideration makes it quite obvious that
to increase the reliability of the results obtained, high precision
laboratory measurements of molecular transition frequencies are badly
needed.
6 Conclusions and future prospects
Using the 32-m Medicina, 100-m Effelsberg, and 45-m Nobeyama radio
telescopes, we have performed precise spectral measurements of the
relative radial velocity differences between the rotational transitions
in HC3N (J=2-1) and N2H+
(J=1-0) and the inversion
transition in NH3
(J,K)=(1,1).
We detect a velocity offset of
![]() m s-1
between the rotational and inversion
lines observed in cold molecular cores with dominating thermal motion.
We do not find any plausible systematic effects that
could mimic an offset of about 20 m s-1
between rotational and inversion transitions and would be regularly
reproduced in observations of different cold
molecular cores with different facilities. The measured positive offset
is qualitatively consistent with our preliminary result,
m s-1
between the rotational and inversion
lines observed in cold molecular cores with dominating thermal motion.
We do not find any plausible systematic effects that
could mimic an offset of about 20 m s-1
between rotational and inversion transitions and would be regularly
reproduced in observations of different cold
molecular cores with different facilities. The measured positive offset
is qualitatively consistent with our preliminary result,
![]() m s-1 ,
obtained on the basis of the GBT observations of Rosolowsky
et al. (2008)
and Rathborne et al. (2008) of the
NH3/CCS pairs in
molecular cores in the Perseus molecular cloud and the Pipe Nebula
(LMK). However, the rest-frame frequency of the CCS
JN
= 21-10 transition is not
well known, and before deciding whether the difference between the
current and preliminary results is statistically significant or not,
new high precision laboratory measurements of the CCS frequency should
be carried out.
m s-1 ,
obtained on the basis of the GBT observations of Rosolowsky
et al. (2008)
and Rathborne et al. (2008) of the
NH3/CCS pairs in
molecular cores in the Perseus molecular cloud and the Pipe Nebula
(LMK). However, the rest-frame frequency of the CCS
JN
= 21-10 transition is not
well known, and before deciding whether the difference between the
current and preliminary results is statistically significant or not,
new high precision laboratory measurements of the CCS frequency should
be carried out.
If we assume that the measured velocity offset is caused by
the electron-to-proton mass ratio variation, then
![]() =
=
![]() ppb.
To account for the conditions of the terrestrial laboratory
experiments, the non-zero
ppb.
To account for the conditions of the terrestrial laboratory
experiments, the non-zero ![]() would require chameleon-like scalar field models that predict a strong
dependence of mass and coupling constant on the ambient matter density.
would require chameleon-like scalar field models that predict a strong
dependence of mass and coupling constant on the ambient matter density.
In any case, our estimate defines a strongest conservative
upper limit to
![]() ,
which can be considered as a reference point at z =
0. We note that extragalactic molecular clouds have gas densities
similar to those in the interstellar clouds of the Milky Way. Thus, the
value of
,
which can be considered as a reference point at z =
0. We note that extragalactic molecular clouds have gas densities
similar to those in the interstellar clouds of the Milky Way. Thus, the
value of ![]() in high-z molecular systems is expected to be at the
same level as in the interstellar clouds, i.e.,
in high-z molecular systems is expected to be at the
same level as in the interstellar clouds, i.e.,
![]()
![]() ,
provided that no temporal dependence of the electron-to-proton mass
ratio is present.
,
provided that no temporal dependence of the electron-to-proton mass
ratio is present.
To be completely confident
that the derived velocity shift is not caused by kinematic effects in
the
clouds but reflects the density-modulated variation of
![]() ,
new high precision radio-astronomical
observations are needed for a wider range of objects. These
observations should also target different molecules (i.e., not NH3)
with tunneling transitions sensitive to the changes in
,
new high precision radio-astronomical
observations are needed for a wider range of objects. These
observations should also target different molecules (i.e., not NH3)
with tunneling transitions sensitive to the changes in ![]() and
molecules with
and
molecules with ![]() -doublet
lines that also exhibit enhanced
sensitivity to variations in
-doublet
lines that also exhibit enhanced
sensitivity to variations in ![]() and
and ![]() (Kozlov 2009).
(Kozlov 2009).
For the molecular transitions in question, it is very important to measure their rest-frame frequencies with an accuracy of about 1 m s-1 in laboratory experiments. In some cases the present uncertainties in the rest-frame frequencies are larger than the errors of radio-astronomical measurements, thus preventing unambiguous conclusions.
In addition, searches for variations in the fine-structure
constant ![]() within the Milky Way disk using mid- and
far-infrared fine-structure transitions in atoms and ions (Kozlov
et al. 2008),
or searches for variations in the combination of
within the Milky Way disk using mid- and
far-infrared fine-structure transitions in atoms and ions (Kozlov
et al. 2008),
or searches for variations in the combination of
![]() using
the [C
II]
using
the [C
II] ![]()
![]() m line and
CO rotational lines (Levshakov et al. 2008b), or
the [C I]
m line and
CO rotational lines (Levshakov et al. 2008b), or
the [C I]
![]()
![]() m line and
low-lying rotational lines of 13CO (Levshakov
et al. 2009)
would be of great importance for cross-checking these results.
m line and
low-lying rotational lines of 13CO (Levshakov
et al. 2009)
would be of great importance for cross-checking these results.
We are grateful to the staffs of the Medicina, Effelsberg, and Nobeyama radio observatories for excellent supports in our observations. The authors thank Dieter Engels for assistance in observations at the Medicina 32-m telescope. The project has been supported by DFG Sonderforschungsbereich SFB 676 Teilprojekt C4 and by the RFBR grant No. 09-02-12223. S.A.L. is supported by the RFBR grant No. 09-02-00352-a, and by the Federal Agency for Science and Innovations grant NSh 2600.2008.2. A.V.L. is supported by the RFBR grant No. 08-02-92001 and by the Program IV.12/2.5 of the Physical Department of the RAS.
Appendix A: Robust statistics
A comprehensive review of robust statistical procedures is given by Hampel et al. (1986) (see also Chap. 15.7 in Press et al. 1992).
Robust estimates are insensitive to departures of the
distribution shape from the assumed data
distribution. In particular, M-estimates
(maximum-likelihood)
are usually relevant for the estimate of parameters with continuous
distributions. The shift (mean), m, and the scale
(standard deviation),
s, of a sample of data points ![]() are estimated by
minimizing the sum
are estimated by
minimizing the sum
![]() .
Here
.
Here ![]() is a weighting function such that the weights given to
individual points first increase with deviations from m,
and then
decrease so that very outlying points (outliers) are not counted at all
(re-descending M-estimate). The following functions
are prescribed for
use as
is a weighting function such that the weights given to
individual points first increase with deviations from m,
and then
decrease so that very outlying points (outliers) are not counted at all
(re-descending M-estimate). The following functions
are prescribed for
use as ![]() :
:
Hampel's function
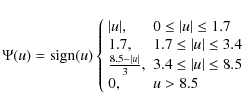
Andrew's sine

optimal value for c = 2.1, and
Tukey's biweight
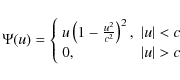
optimal value for c = 5-6.
The minimization occurs iteratively,
the initial guess for m being the median of the
data set,
and for the scale s the normalized median absolute
deviation (1.48![]() MAD).
All estimations presented in the paper were obtained with Tukey's
biweight.
Other
MAD).
All estimations presented in the paper were obtained with Tukey's
biweight.
Other ![]() -functions
provide similar results.
-functions
provide similar results.
References
- Benson, P. J., & Myers, P. C. 1983, ApJ, 270, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, P. J., & Myers, P. C. 1989, ApJS, 71, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Blatt, S., Ludlow, A. D., Campbell, G. K., et al. 2008, Phys. Rev. Lett., 100, 140801 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brax, P., van de Bruck, C., Davis, A.-C., Khoury, J., & Weltman, A. 2004, Phys. Rev. D, 70, 123518 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Burrage, C., Davis, A.-C., & Shaw, D. J. 2009, Phys. Rev. D, 79, 044028 [NASA ADS] [CrossRef] [Google Scholar]
- Caldwell, R. R., Dave, R., & Steinhardt, P. J. 1998, Phys. Rev. Lett., 80, 1582 [Google Scholar]
- Calmet, X., & Fritzsch, H. 2002, Eur. Phys. J. C, 24, 639 [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Meyers, P. S., & Thaddeus, P. 1995, ApJ, 455, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Benson, P. J., Meyers, P. S., et al. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Chand, H., Srianand, R., Petitjean, P., et al. 2004, A&A, 417, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Churchwell, E., Nash, A. G., & Walmsley, C. M. 1984, ApJ, 287, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Codella, C., Welser, R., Henkel, C., Benson, P. J., & Myers, P. C. 1997, A&A, 324, 203 [NASA ADS] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Daniel, F., Cernicharo, J., Roueff, E., Gerin, M., & Dubernet, M. L. 2007, ApJ, 667, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, A.-C., Schelpe, C. A. O., & Shaw, D. J. 2009, Phys. Rev. D, 80, 064016 [NASA ADS] [CrossRef] [Google Scholar]
- Di Francesco, J., Evans, N. J., II, Caselli, P., et al. 2007, in Protostars and Planets. V., ed. B. Reipurth, D. Jewitt, & K. Keil (Uni. Arizona Press, Tucson), 17 [Google Scholar]
- Dickman, R. L. 1975, ApJ, 202, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Dine, M., Nir, Y., Raz, G., et al. 2003, Phys. Rev. D, 67, 015009 [NASA ADS] [CrossRef] [Google Scholar]
- Flambaum, V. V., Leinweber, D. B., Thomas, A. W., et al. 2004, Phys. Rev. D, 69, 115006 [Google Scholar]
- Flambaum, V. V., & Kozlov, M. G. 2007, Phys. Rev. Lett., 98, 240801 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2006, A&A, 456, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuller, G. A., & Myers, P. C. 1993, ApJ, 418, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Griest, K., Whitmore, J. B., Wolfe, A. M., et al. 2010, ApJ, 708, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Hampel, F. R., Ronchetti, E. M., Rousseeuw, P. J., et al. 1986, Robust Statistics. The Approach Based on Influence Functions (N.Y.: John Wiley & Sons) [Google Scholar]
- Henkel, C., Menten, K. M., Murphy, M. T., et al. 2009, A&A, 500, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ho, P. T. P. 1977, Ph.D. Thesis, Massachusetts Institute of Technology [Google Scholar]
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Hotzel, S., Harju, J., & Walmsley, C. M. 2004, A&A, 415, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hougen, J. T. 1972, J. Chem. Phys., 57, 4207 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, D. A., Millar, T. J., Schilke, P., et al. 1994, MNRAS, 267, 59 [NASA ADS] [Google Scholar]
- Jijina, J., Hyers, P. C., & Adams, F. C. 1999, ApJS, 125, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Khoury, J., & Weltman, A. 2004, Phys. Rev. Lett., 93, 171104 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- King, J. A., Webb, J. K., Murphy, M. T., et al. 2008, Phys. Rev. Lett., 101, 251304 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kozlov, M. G., Porsev, S. G., Levshakov, S. A., Reimers, D., & Molaro, P. 2008, Phys. Rev. A, 77, 032119 [NASA ADS] [CrossRef] [Google Scholar]
- Kozlov, M. G. 2009, Phys. Rev. A, 80, 022118 [Google Scholar]
- Kukolich, S. G. 1967, Phys. Rev., 156, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Langacker, P., Segrè, G., & Strassler, M. J. 2002, Phys. Lett. B, 528, 121 [CrossRef] [Google Scholar]
- Lapinov, A. V. 2006, in 15th Symp. on High-Resolution Molecular Spectroscopy, ed. Y. N. Ponomarev, S. N. Mikhailenko, & L. N. Sinitsa, Proc. SPIE, 6580, 658001 [Google Scholar]
- Lee, H.-H., Herbst, E., Pineau des Forêts, G., Roueff, F., & Le Bourlot, J. 1996, A&A, 311, 690 [NASA ADS] [Google Scholar]
- Lee, C. W., Myers, P. C., & Tafalla, M. 1999, ApJ, 526, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S. H., Park, Y.-S., Sohn, J., Lee, C. W., & Lee, H. M. 2007, ApJ, 660, 1326 [NASA ADS] [CrossRef] [Google Scholar]
- Levshakov, S. A., Dessauges-Zavadsky, M., D'Odorico, S., et al. 2002, MNRAS, 333, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Levshakov, S. A., Centurión, M., Molaro, P., et al. 2005, A&A, 434, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levshakov, S. A., Molaro, P., Lopez, S., et al. 2007, A&A, 466, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levshakov, S. A., Molaro, P., & Kozlov, M. G. 2008a, unpublished, [arXiv:0808.0583] [LMK] [Google Scholar]
- Levshakov, S. A., Reimers, D., Kozlov, M. G., Porsev, S. G., & Molaro, P. 2008b, A&A, 479, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levshakov, S. A., Molaro, P., & Reimers, D. 2009, A&A, submitted [Google Scholar]
- Lovas, F. J., Suenram, R. D., Ogata, T., et al. 1992, ApJ, 399, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., Linke, R. A., & Benson, P. J. 1983, ApJ, 264, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, P., Reimers, D., Agafonova, I. I., et al. 2008, EPJST, 163, 173 [Google Scholar]
- Molaro, P., Levshakov, S. A., & Kozlov, M. G. 2009, Nucl. Phys. Proc. Suppl., 194, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Mota, D. F., & Barrow, J. D. 2004, MNRAS, 349, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Mota, D. F., & Shaw, D. J. 2007, Phys. Rev. D, 75, 063501 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., & André, P. 2001, A&A, 365, 440 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, M. T., Flambaum, V. V., Webb, J. K., et al. 2004, Lect. Notes Phys., 648, 131 [NASA ADS] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., et al. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, M. T., Webb, J. K., & Flambaum, V. V. 2008a, MNRAS, 384, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, M. T., Flambaum, V. V., Muller, S., & Henkel, C. 2008b, Science, 320, 1611 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nakajima, T., Sakai, T., Asayama, S., et al. 2008, PASJ, 60, 435 [NASA ADS] [Google Scholar]
- Olano, C. A., Walmsley, C. M., & Wilson, T. L. 1988, A&A, 196, 194 [NASA ADS] [Google Scholar]
- Olive, K. A., & Pospelov, M. 2008, Phys. Rev. D, 77, 043524 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Daniel, F., & Dubernet, M.-L. 2009, A&A, 494, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Park, Y.-S., Lee, C. W., & Myers, P. C. 2004, ApJS, 152, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E., & Rata, B. 2003, Rev. Mod. Phys., 75, 559 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., et al. 1992, Numerical Recipes in C (Cambridge: Cambridge Uni. Press) [Google Scholar]
- Quast, R., Reimers, D., & Levshakov, S. A. 2004, A&A, 415, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rathborne, J. M., Lada, C. J., Muench, A. A., Alves, J. F., & Lombardi, M. 2008, ApJS, 174, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Reinhold, E., Buning, R., Hollenstein, U., et al. 2006, Phys, Rev. Lett., 96, 151101 [Google Scholar]
- Rosenband, T., Hume, D. B., Schmidt, P. O., et al. 2008, Science, 319, 1808 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rosolowsky, E. W., Pineda, J. E., Foster, J. B., et al. 2008, ApJS, 175, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Rydbeck, O. E. H., Sume, A., Hjalmarson, A., et al. 1977, ApJ, 215, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, T., Sakai, N., Kamegai, K., et al. 2008, ApJ, 678, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Shelkovnikov, A., Butcher, R. J., Chardonnet, C., et al. 2008, Phys. Rev. Lett., 100, 150801 [Google Scholar]
- Srianand, R., Chand, H., Petitjean, P., et al. 2008, Phys. Rev. Lett., 100, 029902 [NASA ADS] [CrossRef] [Google Scholar]
- Stuart, A., & Ord, K. 1994, Kendall's Advanced Theory of Statistics, vol. I (Hodder Arnild: London) [Google Scholar]
- Suzuki, H., Yamamoto, S., Ohishi, M., et al. 1992, ApJ, 392, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., et al. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, R. I. 1975, Astrophys. Lett., 16, 3 [Google Scholar]
- Thompson, R. I., Bechtold, J., Black, J. H., et al. 2009, ApJ, 703, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- van Veldhoven, J., Küpper, J., Bethlem, H. L., et al. 2004, Eur. Phys. J. D, 31, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varshalovich, D. A., & Levshakov, S. A. 1993, J. Exp. Theor. Phys. Lett., 58, 237 [Google Scholar]
- Walmsley, C. M., & Ungerechts, H. 1983, A&A, 122, 164 [NASA ADS] [Google Scholar]
- Walsh, A. J., Myers, P. C., & Burton, M. C. 2004, ApJ, 614, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Wendt, M., & Reimers, D. 2008, EPJST, 163, 197 [Google Scholar]
- Yamamoto, S., Saito, S., Kawaguch, K., et al. 1990, ApJ, 361, 318 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... method
![[*]](/icons/foot_motif.png)
- Based on observations obtained with the Medicina 32-m telescope operated by INAF - Istituto di Radioastronomia, the 100-m telescope of the Max-Planck Institut für Radioastronomie at Effelsberg, and the Nobeyama Radio Observatory 45-m telescope of the National Astronomical Observatory of Japan.
- ... as
![[*]](/icons/foot_motif.png)
- The sign of the
sensitivity coefficient
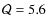 was misprinted in van Veldhoven et al. (2004), as noted by Flambaum & Kozlov (2007).
was misprinted in van Veldhoven et al. (2004), as noted by Flambaum & Kozlov (2007).
- ... telescope
![[*]](/icons/foot_motif.png)
- The 32-m VLBI antenna at Medicina is operated by the INAF-Istituto di Radioastronomia in Bologna.
- ...
package
![[*]](/icons/foot_motif.png)
- http://www.iram.fr/IRAMFR/GILDAS/
- ... Effelsberg
![[*]](/icons/foot_motif.png)
- The 100-m telescope at Effelsberg/Germany is operated by the Max-Planck-Institut für Radioastronomie on behalf of the Max-Planck-Gesellschaft (MPG).
- ... telescope
![[*]](/icons/foot_motif.png)
- The 45-m radio telescope is operated by Nobeyama Radio Observatory, a brach of the National Astronomical Observatory of Japan.
- ... catalog
![[*]](/icons/foot_motif.png)
- http://spec.jpl.nasa.gov
All Tables
Table 1: Target list.
Table 2: Hyperfine components of the NH3 (J,K) = (1,1) transition.
Table 3: Hyperfine components of the HC3N J = 2-1 transition.
Table 4: Hyperfine components of the N2H+ J = 1-0 transition.
Table 5:
Radial velocities, ![]() ,
Doppler parameters, b, and corresponding
,
Doppler parameters, b, and corresponding
![]() values normalized per degree
of freedom.
values normalized per degree
of freedom.
Table 6:
Radial velocities, ![]() ,
Doppler parameters, b, and corresponding
,
Doppler parameters, b, and corresponding
![]() values normalized per degree of freedom.
values normalized per degree of freedom.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13007f1.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg141.png)
|
Figure 1: Sketch of the hyperfine transitions for the NH3 (1, 1), HC3N (2-1), and N2H+ (1-0) states. Line identification numbers are given in each panel (see Tables 2-4). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13007f2.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg142.png)
|
Figure 2: Spectra of NH3 (1, 1) and HC3N (2-1) toward the cores L1512 and L183 obtained at the Medicina 32-m radio telescope. The histogram shows the data, the solid curve shows the fit, and the residual is plotted below each profile. The horizontal thick bars mark spectral windows used in the fitting procedure. The data are the arithmetic means of all the observations. The size of the resolution element (pixel) is 62 m s-1 for NH3, and 80 m s-1 for HC3N. For each spectrum, the signal-to-noise ratio (S/N) per pixel at the maximum intensity peak is depicted. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13007f3.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg143.png)
|
Figure 3: Spectra of NH3 (1,1) and HC3N (2-1) toward the cores L1498, L1495, and L1400K obtained at the Effelsberg 100-m radio telescope. The histogram shows the data, the solid curve shows the fit, and the residual is plotted below each profile. The horizontal thick bars mark spectral windows used in the fitting procedure. The data are the arithmetic means of all the observations. The size of the resolution element (pixel) is 15 m s-1 for NH3, and 20 m s-1 for HC3N. For each spectrum, the signal-to-noise ratio (S/N) per pixel at the maximum intensity peak is depicted. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13007f4.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg144.png)
|
Figure 4:
Same as Fig. 3
but for the cores CB22, TMC-1C (offset
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{13007f5.eps}
\vspace*{7mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg145.png)
|
Figure 5: Same as Fig. 3 but for the cores L1512, L183, and L260-NH3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13007f6.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg146.png)
|
Figure 6: Same as Fig. 3 but for the cores L234A, B335, and L1251C. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{13007f7.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg147.png)
|
Figure 7: Spectra of NH3 (1,1) and N2H+ (1-0) toward the cores L1498, L1536, and CB23 obtained at the Nobeyama 45-m radio telescope. The histogram shows the data, the solid curve shows the fit, and the residual is plotted below each profile. The horizontal thick bars mark spectral windows used in the fitting procedure. The data are the arithmetic means of all the observations. The size of the resolution element (pixel) is 49 m s-1 for NH3, and 25 m s-1 for N2H+. For each spectrum, the signal-to-noise ratio (S/N) per pixel at the maximum intensity peak is depicted. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{13007f8.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg148.png)
|
Figure 8: Same as Fig. 7 but for the cores L1517B, L1512, and L183. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{13007f9.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg149.png)
|
Figure 9:
Same as Fig. 7
but for the cores L183 (offset
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{13007f10.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg186.png)
|
Figure 10:
Doppler velocity differences, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13007f11.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa13007-09/Timg187.png)
|
Figure 11:
Doppler velocity differences, |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



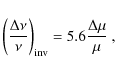
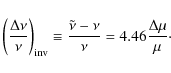
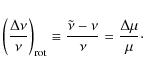
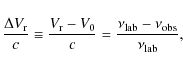
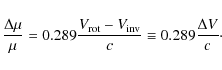
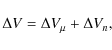
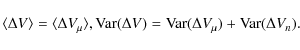
![\begin{displaymath}T(v) = A\cdot \left[ 1 - {\rm e}^{-t(v)} \right],
\end{displaymath}](/articles/aa/full_html/2010/04/aa13007-09/img95.png)
![\begin{displaymath}t(v) = \tau\cdot \sum^k_{i=1}~ a_i~ \exp\left[ -
\frac{(v - v_i - V_{\rm lsr})^2}{b^2} \right],
\end{displaymath}](/articles/aa/full_html/2010/04/aa13007-09/img96.png)
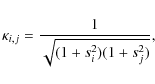
![\begin{displaymath}\varepsilon_{\rm sys} = \left[ \sum^n_{i=1}\sum^n_{j=1} \omega_i\omega_j
{\rm Cov}(v_i - v_0, v_j - v_0) \right]^{1/2}.
\end{displaymath}](/articles/aa/full_html/2010/04/aa13007-09/img127.png)