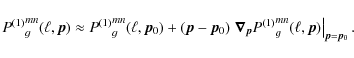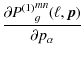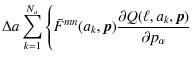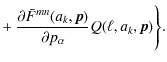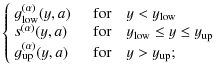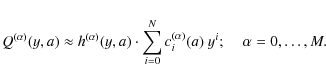| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 7 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201014829 | |
| Published online | 07 September 2010 | |
Fitting formulae of the reduced-shear power spectrum for weak lensing![[*]](/icons/foot_motif.png) (Research Note)
(Research Note)
M. Kilbinger1,2,3
1 -
Excellence Cluster Universe, Technische Universität München,
Boltzmannstr. 2, 85748 Garching, Germany
2 -
Universitäts-Sternwarte München, Scheinerstr. 1, 81679 München, Germany
3 -
Shanghai Key Lab for Astrophysics, Shanghai Normal University,
Shanghai 200234, PR China
Received 20 April 2010 / Accepted 9 June 2010
Abstract
Context. Weak gravitational lensing is a powerful probe of
large-scale structure and cosmology. Most commonly, second-order
correlations of observed galaxy ellipticities are expressed as a
projection of the matter power spectrum, corresponding to the
lowest-order approximation between the projected and the
three-dimensional power spectrum.
Aims. The dominant lensing-only contribution beyond the
zero-order approximation is the reduced shear, which takes into account
not only lensing-induced distortions but also the isotropic
magnification of galaxy images. This involves an integral over the
matter bispectrum. We provide a fast and general way to calculate this
correction term.
Methods. Using a model for the matter bispectrum, we fit
elementary functions to the reduced-shear contribution and its
derivatives with respect to cosmological parameters. The dependence on
cosmology is encompassed in a Taylor-expansion around a fiducial model.
Results. Within a region in parameter space comprising the WMAP7
68% error ellipsoid, the total reduced-shear power spectrum (shear plus
fitted reduced-shear correction) is accurate to 1% (2%) for ![]() (
(
![]() ).
This corresponds to a factor of four reduction in the bias compared to
the case where no correction is used. This precision is necessary to
match the accuracy of current non-linear power spectrum predictions
from numerical simulations.
).
This corresponds to a factor of four reduction in the bias compared to
the case where no correction is used. This precision is necessary to
match the accuracy of current non-linear power spectrum predictions
from numerical simulations.
Key words: gravitational lensing: weak - large-scale structure of Universe
1 Introduction
Cosmic shear surveys exploit the distortions of distant galaxy images
induced by the matter structures in the Universe on large scales. Weak
cosmological lensing has become an important tool to measure
cosmological parameters. The current precision in the measured shapes
of high-redshift galaxies is at the few percent level providing
important constraints on the matter density
![]() and the
power-spectrum normalisation
and the
power-spectrum normalisation ![]() .
Future surveys aim to achieve
sub-percent level accuracy in measuring dark-energy properties or
deviations from general relativity.
.
Future surveys aim to achieve
sub-percent level accuracy in measuring dark-energy properties or
deviations from general relativity.
To reach this precision for cosmological parameters, efforts not only on the observational but also on the theoretical side have to be made. To predict the shear power spectrum from theoretical models, several approximations are usually made to facilitate calculations. When comparing and fitting models to observations, these simplifications can significantly bias the resulting cosmological parameters. One of these approximations is to neglect the correction due to the so-called reduced shear.
The observed ellipticity of galaxies is an estimator of the
reduced shear
where
The effect of reduced shear was examined using N-body
simulations by White (2005) and compared with theoretical predictions
in Dodelson et al. (2006). Corrections to the lensing skewness
were discussed in Schneider et al. (1998) and
Dodelson & Zhang (2005).
An extensive study of
higher-order corrections to the weak-lensing power spectrum, including
reduced shear, was presented by Krause & Hirata (2009). Compared
with corrections due to light-path integration (relaxation of the Born
approximation) and lens-lens coupling
(e.g., Bernardeau et al. 1997; Seitz 1993), reduced-shear
corrections represent the dominant contribution to the weak-lensing
power spectrum. The lowest-order correction term, which is of order
![]() in the gravitational potential
in the gravitational potential ![]() ,
reaches 10%
of the total lensing spectrum. This is the term that we consider
in this work. The next-order correction at
,
reaches 10%
of the total lensing spectrum. This is the term that we consider
in this work. The next-order correction at
![]() is one
magnitude below the
is one
magnitude below the
![]() -term (Krause & Hirata 2009).
Ignoring reduced shear will cause a bias in cosmological parameters,
which is comparable to the statistical error from future surveys like
DES
-term (Krause & Hirata 2009).
Ignoring reduced shear will cause a bias in cosmological parameters,
which is comparable to the statistical error from future surveys like
DES![]() , LSST
, LSST![]() ,
or Euclid
,
or Euclid![]() (Shapiro 2009). For the weak-lensing results of
the COSMOS survey
(Shapiro 2009). For the weak-lensing results of
the COSMOS survey![]() , an estimate from
numerical simulations yielded a 1% underestimation of
, an estimate from
numerical simulations yielded a 1% underestimation of ![]() (Schrabback et al. 2010).
(Schrabback et al. 2010).
Another correction to weak lensing from a magnitude-limited galaxy sample is the so-called magnification bias. Hamana (2001) found its contribution to the lensing power spectrum to be small. The corresponding third-order correction terms were also calculated and compared to numerical simulations by Ménard et al. (2003). However, if not corrected for, future surveys will yield significantly biased cosmological parameter constraints (Schmidt et al. 2009a). The lowest-order correction term has the same functional form as the reduced-shear one, and therefore both can be dealt with simultaneously. Higher-order terms contribute by smaller than one percent to the lensing power spectrum (Krause & Hirata 2009).
There are additional important sources of contamination to the weak lensing observables, some of which may be larger than the reduced-shear corrections. These involve galaxy clustering, the intrinsic alignment of galaxies with each other or with the surrounding dark matter haloes, and the modelling of the non-linear dark-matter power spectrum and baryonic processes. The modelling of these effects requires detailed understanding of baryonic physics, galaxy formation, the interplay between galaxies and dark matter, and massive numerical simulations in the case of the non-linear power spectrum. In contrast, taking into account the reduced shear is straightforward and can be done with sufficient accuracy to render it a sub-dominant contamination.
In the next section, we review the expressions for the lowest-order reduced-shear term, and introduce a fitting scheme to efficiently model this term. In Sect. 3, we present our results, demonstrating the accuracy of the fits. We conclude this paper in Sect. 4.
2 Reduced shear
2.1 Lowest-order expansion
For small values of the convergence,
![]() ,
the reduced
shear (1) is expanded as
,
the reduced
shear (1) is expanded as
To calculate the power spectrum of the reduced shear g, we apply a Fourier transform to Eq. (2) to second order
| (3) |
In our notation, the convolution of
We assume that the reduced shear is measured in redshift bins. With Pgmn, we denote the reduced-shear (cross-)power spectrum for two redshift bins with indices m and n. In general, the shear field can be decomposed into an E-mode (gradient) and a B-mode (curl). However, as is the case for cosmic shear at lowest order, the reduced-shear correction of order
where gm denotes the reduced shear measured from galaxies in the mth redshift bin, the asterisk (*) denotes complex conjugation, and
The reduced-shear power spectrum is the sum of the convergence power spectrum (which equals the shear power spectrum) and a correction given by
Using the relation between shear and convergence,
With this, we derive the correction term
Without loss of generality, we have set
The convergence bispectrum can be expressed in terms of the three-dimensional matter
bispectrum ![]() using Limber's equation
(Limber 1953; Kaiser 1992) providing
using Limber's equation
(Limber 1953; Kaiser 1992) providing
The lower limit of the integral over the scale factor a corresponds to the limiting redshift,
![\begin{displaymath}G^m(a) = \frac 3 2 \left(\frac{H_0}c\right)^2 \frac{\Omega_{\...
...me) \frac{f_K[\chi(a^\prime) - \chi(a)]}{f_K[\chi(a^\prime)]},
\end{displaymath}](/articles/aa/full_html/2010/11/aa14829-10/img47.png)
|
(11) |
which includes an integral over the probability distribution pm of the number density of source galaxies in the mth bin.
2.2 Expansion around a fiducial model
In the expressions needed to calculate the first-order reduced-shear power spectrum
in Eqs. (9, 10), we can interchange the ![]() - and the
a-integration, and replace the latter by a finite sum. Then
- and the
a-integration, and replace the latter by a finite sum. Then
Evaluating the
Table 1:
Parameter limits for where the accuracy of the fitted
reduced-shear power spectrum is better than ![]() for
for ![]() ,
and better than
,
and better than ![]() for
for
![]() (see also
Fig. 3).
(see also
Fig. 3).
We perform a Taylor-expansion to first order
P(1)mng as a function of a cosmological
parameter vector
![]() around a fiducial cosmological model with
parameter
around a fiducial cosmological model with
parameter ![]()
Inserting Eq. (12), the derivatives with respect to cosmological parameters are given by
In Sect. 3, we consider the cosmological parameters
2.3 Magnification and size bias
A typical galaxy sample used in weak cosmological lensing is selected
by both magnitude and galaxy size. Magnification due to lensing
changes both quantities (e.g. Bartelmann & Schneider 2001), and therefore introduces
a correlation between number density and convergence. If the number
density of galaxies with fluxes higher than some flux S, and sizes
larger than some size R can be written as power laws,

|
(15) |
the observed number density differs from the unlensed one p0to first order, becoming
| (16) |
according to Schmidt et al. (2009b,a). This simple linear model assumes that the galaxy selection function depends on flux and size in a separable way. We refer to Wyithe et al. (2003) for a generalisation that takes into account correlations between the two quantities.
Magnification and size bias induces a lowest-order correction to the
lensing power spectrum which has the same form as for reduced
shear. Therefore, we can add the corresponding correction term
![]() to Eq. (6) with
to Eq. (6) with
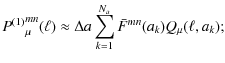
|
|||
| (17) |
where the function Q is given in Eq. (12).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14829Fg1}
\end{figure}](/articles/aa/full_html/2010/11/aa14829-10/Timg69.png)
|
Figure 1:
The function
|
| Open with DEXTER | |
|
Figure 2:
Fit coefficients as a function of scale factor.
Left: the polynomial fit coefficients c(0)i for
|
| Open with DEXTER | |
|
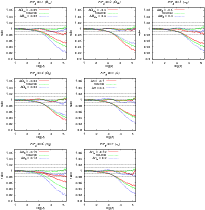
Figure 3:
The fitted reduced-shear power spectrum (thick lines) and
the uncorrected convergence power spectrum (thin lines). Both
quantities are plotted as ratios with respect to the reduced-shear
power spectrum (6), where the first-order correction
|
| Open with DEXTER | |
2.4 Fitting formulae
For simplicity, we define
Q(0) = Q and
![]() for
for
![]() .
These correspond to the
.
These correspond to the ![]() -dependent terms in
Eqs. (12) and (14), which behave as near-power laws for
both small and large
-dependent terms in
Eqs. (12) and (14), which behave as near-power laws for
both small and large ![]() .
With the abbreviation
.
With the abbreviation
![]() ,
we
perform two linear fits of
,
we
perform two linear fits of
![]() for
for
![]() and
and
![]() ,
respectively.
We smoothly piece together these two asymptotic functions with a cubic
spline
,
respectively.
We smoothly piece together these two asymptotic functions with a cubic
spline
![]() such that the composite function
such that the composite function
![]() and its first derivative are continuous
and its first derivative are continuous
for the linear functions
| (19) |
and the cubic spline
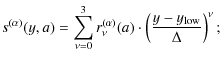
|
|||
| (20) |
The ratios
We note that we cannot fit the logarithm of the functions
The fit coefficients
![]() are expected to
smoothly vary with the scale factor a. We therefore perform another series
of fits by polynomials of order Nb and Nc, respectively
are expected to
smoothly vary with the scale factor a. We therefore perform another series
of fits by polynomials of order Nb and Nc, respectively
The two matrices
3 Results
We use a fiducial flat ![]() CDM cosmological model with WMAP7-like
parameters,
CDM cosmological model with WMAP7-like
parameters,
![]() and
and
![]() (Komatsu et al. 2010). The dark-matter bispectrum is calculated
according to Scoccimarro & Couchman (2001). Their fitting formula is
accurate to only 30-50% on small scales; this is however
sufficient for our purpose. We note also that the bispectrum is not
calibrated for any dark-energy model other than
(Komatsu et al. 2010). The dark-matter bispectrum is calculated
according to Scoccimarro & Couchman (2001). Their fitting formula is
accurate to only 30-50% on small scales; this is however
sufficient for our purpose. We note also that the bispectrum is not
calibrated for any dark-energy model other than ![]() CDM. For the
matter power spectrum, we use the ``halofit'' fitting formula of
Smith et al. (2003) and the transfer function ``shape fit''
from Eisenstein & Hu (1998). Following the icosmo.org code
(Refregier et al. 2008) for models with
CDM. For the
matter power spectrum, we use the ``halofit'' fitting formula of
Smith et al. (2003) and the transfer function ``shape fit''
from Eisenstein & Hu (1998). Following the icosmo.org code
(Refregier et al. 2008) for models with ![]() ,
we
modify ``halofit'' to interpolate between
,
we
modify ``halofit'' to interpolate between ![]() CDM and w=-1/3,
which behaves in a similar way to an OCDM model (for
more details, see Schrabback et al. 2010).
CDM and w=-1/3,
which behaves in a similar way to an OCDM model (for
more details, see Schrabback et al. 2010).
The function Q and the corresponding fit with the composite function
given in Eq. (21) are shown in Fig. 1. The polynomial that
is part of the composite function has order N=6. The fitting
coefficients b(0)i and ci(0) are plotted in
Fig. 2. Although the higher-order polynomial
coefficients have relatively low amplitudes (right panel), we found that a
polynomial of order 6 is necessary to provide a good fit to the
reduced-shear power spectrum, as discussed below. For the
polynomial fits of the coefficients as functions of a (22), we chose
Nb = Nc = 3. These
cubic polynomials provide sufficient accuracy, in particular
for
![]() ,
where the coefficients show the most
variation. This is important because the reduced-shear correction
spectrum in Eq. (12) obtains a large contribution from large a.
,
where the coefficients show the most
variation. This is important because the reduced-shear correction
spectrum in Eq. (12) obtains a large contribution from large a.
We perform the fits in the ![]() -range between 0.1 and
-range between 0.1 and
![]() .
The functions
.
The functions
![]() are not perfect power laws,
therefore the fit for large
are not perfect power laws,
therefore the fit for large ![]() is not excellent. We found an
improvement of our final results for the total power spectrum by
adding 0.05 to b2 after performing the fits.
is not excellent. We found an
improvement of our final results for the total power spectrum by
adding 0.05 to b2 after performing the fits.
The fitting functions for the reduced-shear power spectrum corrections
provide accurate results over a wide range in ![]() .
We illustrate
the case of a single redshift bin with distribution
.
We illustrate
the case of a single redshift bin with distribution
![]() and parameters
and parameters
![]() ,
and z0 = 0.5. The maximum considered redshift is
,
and z0 = 0.5. The maximum considered redshift is
![]() ,
which results in a mean redshift of 0.75.
At
,
which results in a mean redshift of 0.75.
At
![]() the reduced-shear correction to the
convergence power spectrum starts to become important. On smaller
scales, the latter underestimates the total power spectrum by more
than 1%. For
the reduced-shear correction to the
convergence power spectrum starts to become important. On smaller
scales, the latter underestimates the total power spectrum by more
than 1%. For
![]() ,
we fit
,
we fit
![]() (Eq. (7)) to better than 20%. This is sufficient to provide an
approximation of the total power spectrum at the percent-level.
(Eq. (7)) to better than 20%. This is sufficient to provide an
approximation of the total power spectrum at the percent-level.
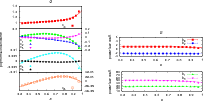
In Fig. 3, we the plot the ratio of the reduced-shear power
spectrum derived using our fitting functions to that obtained by numerical
integration of Eq. (12). This is compared to the case of no
correction for reduced-shear, corresponding to just the convergence
power spectrum. In this latter power spectrum, a downward bias is evident, since
the power is underestimated. This bias increases from 1% at
![]() to 6% at
to 6% at
![]() for the fiducial
cosmology. In models with more structure, this bias is larger,
e.g., 8% for
for the fiducial
cosmology. In models with more structure, this bias is larger,
e.g., 8% for
![]() .
In contrast, our fitted correction is
accurate to better than 1% for
.
In contrast, our fitted correction is
accurate to better than 1% for
![]() at the fiducial
point.
at the fiducial
point.
We test different redshift distributions by changing to z0 = 0.3 and z0 = 0.7, corresponding to mean redshifts of 0.45 and 1, respectively, and also a redshift bin of width 0.1 around z=0.75. In all cases, the fitting formula remains accurate to within 1% at the fidicual model.
In Table 1, we denote the parameter ranges for which our
fitting formulae are accurate to better than ![]() for
for ![]() ,
and better than
,
and better than ![]() for
for
![]() .
.
4 Conclusions
The lowest-order correction term for the reduced-shear power spectrum
is the dominant contribution from lensing-only effects
(Krause & Hirata 2009). This term is proportional to the third
power of the gravitational potential ![]() ,
and includes an integral
over the lensing bispectrum. In this paper, we have presented fitting
formulae for this integral and its derivative with respect to
cosmological parameters. This has permitted a more efficient
calculation of the reduced-shear correction power spectrum within a
parameter range comprising the 68% confidence region of
WMAP7. The fitting scheme reduces the computational effort from tens
of minutes for the full integration to a fraction of a second.
,
and includes an integral
over the lensing bispectrum. In this paper, we have presented fitting
formulae for this integral and its derivative with respect to
cosmological parameters. This has permitted a more efficient
calculation of the reduced-shear correction power spectrum within a
parameter range comprising the 68% confidence region of
WMAP7. The fitting scheme reduces the computational effort from tens
of minutes for the full integration to a fraction of a second.
For currently available weak-lensing data, the uncertainty in the non-linear power spectrum on small scales is still larger than the bias due to the reduced-shear. For example, the widely-used fitting prescription by Smith et al. (2003) strongly underestimates the power on small scales. More recent numerical simulations however provide fitting formulae that improve the accuracy by a factor 5 to 10 (Heitmann et al. 2009; Lawrence et al. 2010; Heitmann et al. 2008). Moreover, their emulation scheme can be applied to a wide range of cosmological parameters. This range is comprised in the hypercube for which our fits are valid. In combination, these results provide us with predictions for the weak lensing power spectrum that are accurate to the few percent level.
AcknowledgementsWe thank Peter Schneider for helpful comments on the manuscript, and the anonymous referee whose suggestions helped to improve the paper. This research was supported by the DFG cluster of excellence Origin and Structure of the Universe and the Chinese National Science Foundation Nos. 10878003 and 10778725, 973 Program No. 2007CB 815402, Shanghai Science Foundations and Leading Academic Discipline Project of Shanghai Normal University (DZL805).
References
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 297
- Bernardeau, F., Van Waerbeke, L., & Mellier, Y. 1997, A&A, 322, 1
- Dodelson, S., & Zhang, P. 2005, Phys. Rev. D, 72, 083001
- Dodelson, S., Shapiro, C., & White, M. 2006, Phys. Rev. D, 73, 023009
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605
- Hamana, T. 2001, MNRAS, 326, 326
- Heitmann, K., Higdon, D., White, M., et al. 2009, ApJ, 705, 156
- Heitmann, K., White, M., Wagner, C., Habib, S., & Higdon, D. 2008, ApJ, 715, 104
- Kaiser, N. 1992, ApJ, 388, 272
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2010, ApJS, submitted, [arXiv:1001.4538]
- Krause, E., & Hirata, C. M. 2009, A&A, accepted, [arXiv:0910.3786]
- Lawrence, E., Heitmann, K., White, M., et al. 2010, ApJ, 713, 1322
- Limber, D. N. 1953, ApJ, 117, 134
- Ménard, B., Hamana, T., Bartelmann, M., & Yoshida, N. 2003, A&A, 403, 817
- Refregier, A., Amara, A., Kitching, T., & Rassat, A. 2008, A&A, submitted, [arXiv:0810.1285]
- Schmidt, F., Rozo, E., Dodelson, S., Hui, L., & Sheldon, E. 2009a, ApJ, 702, 593
- Schmidt, F., Rozo, E., Dodelson, S., Hui, L., & Sheldon, E. 2009b, Phys. Rev. Lett., 103, 051301
- Schneider, P., Van Waerbeke, L., Jain, B., & Kruse, G. 1998, MNRAS, 296, 873
- Schneider, P., Van Waerbeke, L., & Mellier, Y. 2002, A&A, 389, 729
- Schrabback, T., Hartlap, J., Joachimi, B., et al. 2010, A&A, 516, A63
- Scoccimarro, R., & Couchman, H. M. P. 2001, MNRAS, 325, 1312
- Seitz, S. 1993, in Liege International Astrophysical Colloquia, ed. J. Surdej, D. Fraipont-Caro, E. Gosset, S. Refsdal, & M. Remy, 31, 579
- Shapiro, C. 2009, ApJ, 696, 775
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311
- White, M. 2005, Astropart. Phys., 23, 349
- Wyithe, J. S. B., Winn, J. N., & Rusin, D. 2003, ApJ, 583, 58
Online Material
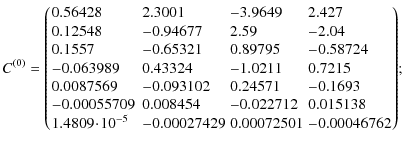
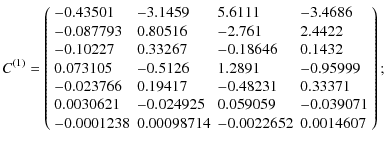
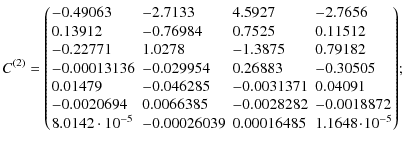
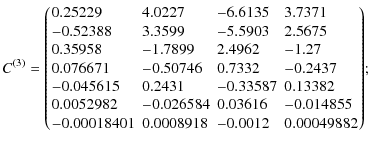
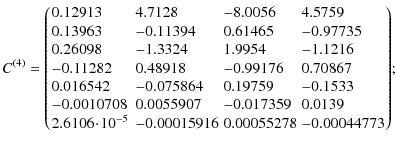
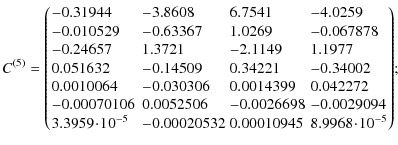
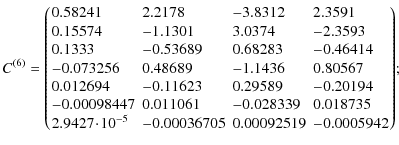
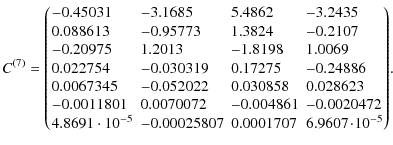
Appendix A: Fitting matrices
The matrices
![]() and
and
![]() (22),
(22),
![]() contain the coefficients of the reduced-power
spectrum fits given in Eq. (21). Here, we provide the numerical values from
our fits. The index
contain the coefficients of the reduced-power
spectrum fits given in Eq. (21). Here, we provide the numerical values from
our fits. The index ![]() corresponds to the function Q(12) in the fiducial cosmology, and
corresponds to the function Q(12) in the fiducial cosmology, and
![]() to its
derivatives with respect to cosmological parameters (see Table
1). The matrices are also available in electronic form
with an example code
to its
derivatives with respect to cosmological parameters (see Table
1). The matrices are also available in electronic form
with an example code![]() .
.

|

|

|

|
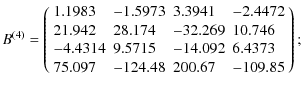
|
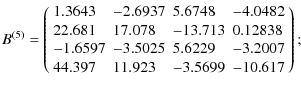
|

|

|
|
|
|
|
|
|
|
|
Footnotes
- ... lensing
![[*]](/icons/foot_motif.png)
- Appendix A is only available in electronic form at http://www.aanda.org
- ...
DES
![[*]](/icons/foot_motif.png)
- http://www.darkenergysurvey.org
- ... LSST
![[*]](/icons/foot_motif.png)
- http://www.lsst.org
- ... Euclid
![[*]](/icons/foot_motif.png)
- http://www.ias.u-psud.fr/imEuclid
- ... survey
![[*]](/icons/foot_motif.png)
- http://cosmos.astro.caltech.edu
- ... code
![[*]](/icons/foot_motif.png)
- http://www2.iap.fr/users/kilbinge/reduced
All Tables
Table 1:
Parameter limits for where the accuracy of the fitted
reduced-shear power spectrum is better than ![]() for
for ![]() ,
and better than
,
and better than ![]() for
for
![]() (see also
Fig. 3).
(see also
Fig. 3).
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{14829Fg1}
\end{figure}](/articles/aa/full_html/2010/11/aa14829-10/Timg69.png)
|
Figure 1:
The function
|
| Open with DEXTER | |
| In the text | |

|
Figure 2:
Fit coefficients as a function of scale factor.
Left: the polynomial fit coefficients c(0)i for
|
| Open with DEXTER | |
| In the text | |

|
Figure 3:
The fitted reduced-shear power spectrum (thick lines) and
the uncorrected convergence power spectrum (thin lines). Both
quantities are plotted as ratios with respect to the reduced-shear
power spectrum (6), where the first-order correction
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




![\begin{displaymath}g = \frac{\gamma}{1-\kappa} = \gamma [ 1 + \kappa
+ \kappa^2
+ \ldots ].
\end{displaymath}](/articles/aa/full_html/2010/11/aa14829-10/img22.png)
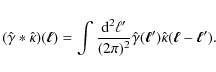
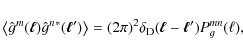
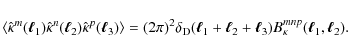
![\begin{displaymath}{P^{(1)}}^{mn}_{g}(\ell) = \int
\frac{{\rm d}^2\ell^{\prime}...
...) +
B^{nmm}_\kappa(\vec \ell_0, -\vec \ell^{\prime}) \right].
\end{displaymath}](/articles/aa/full_html/2010/11/aa14829-10/img37.png)
![$\displaystyle B_\kappa^{mnp}(\vec \ell_1, \vec \ell_2) = \int_{a_{\rm lim}}^1
{...
...{\vec \ell_1}{f_K[\chi(a)]},
\frac{\vec \ell_2}{f_K[\chi(a)]}; \chi(a)
\right);$](/articles/aa/full_html/2010/11/aa14829-10/img43.png)
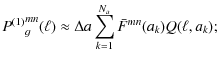
![$\displaystyle Q(\ell, a) = 2 \int \frac{{\rm d}^2 \ell^\prime}{(2\pi)^2} \cos (...
...ac{\vec\ell_0}{f_K[\chi(a)]},
\frac{-\vec\ell^\prime}{f_K[\chi(a)]}\right)\cdot$](/articles/aa/full_html/2010/11/aa14829-10/img51.png)