Table A.1
Iteration cycles for the equatorial wind from a rotating O5–V main-sequence star with Vrot = 300 km s-1 (see upper table) and Vrot = 500 km s-1 (see lower table) without distortion.
| Step | v ∞ | log Ṁ | v ∞, fit | β | γ fit | δ fit |
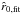
|
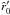
|
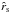
|
| no. | [km s-1] | [M⊙/yr] | [km s-1] | ||||||
|
|
|||||||||
| –1 | 2020 | –5.500 | – | 1.0000 | – | – | – | – | – |
| 0 | 5805 | –5.641 | 2365 | 0.8664 | 0.7329 | 0.4917 | 1.0008 | 1.0066 | 1.0175 |
| 1 | 4063 | –6.154 | 3633 | 0.7929 | 0.5859 | 0.7077 | 1.0026 | 1.0086 | 1.0102 |
| 2 | 3002 | –6.262 | 4077 | 0.7440 | 0.4879 | 0.7669 | 1.0039 | 1.0098 | 1.0112 |
| 3 | 2554 | –6.199 | 3818 | 0.7279 | 0.4557 | 0.7563 | 1.0020 | 1.0101 | 1.0114 |
| 4 | 2393 | –6.112 | 3436 | 0.7347 | 0.4693 | 0.7402 | 0.9985 | 1.0099 | 1.0114 |
| 5 | 2476 | –6.047 | 3175 | 0.7486 | 0.4972 | 0.7262 | 0.9967 | 1.0097 | 1.0113 |
| 6 | 2843 | –6.026 | 3143 | 0.7385 | 0.4769 | 0.6859 | 1.0012 | 1.0095 | 1.0113 |
| 7 | 2666 | –6.064 | 3287 | 0.7310 | 0.4619 | 0.6992 | 1.0006 | 1.0096 | 1.0109 |
| 8 | 2419 | –6.061 | 3215 | 0.7461 | 0.4923 | 0.7376 | 0.9965 | 1.0097 | 1.0110 |
| 9 | 2542 | –6.026 | 3032 | 0.7696 | 0.5393 | 0.7554 | 0.9953 | 1.0095 | 1.0113 |
| 10 | 2915 | –6.026 | 3086 | 0.7574 | 0.5149 | 0.7156 | 1.0005 | 1.0093 | 1.0114 |
| Step | v ∞ | log Ṁ | v ∞, fit | β | γ fit | δ fit |
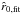
|
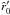
|
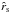
|
| no. | [km s-1] | [M⊙/yr] | [km s-1] | ||||||
|
|
|||||||||
| –1 | 2020 | –5.500 | – | 1.0000 | – | – | – | – | – |
| 0 | 4553 | –5.641 | 2365 | 0.8664 | 0.7329 | 0.4917 | 1.0008 | 1.0066 | 1.0175 |
| 1 | 2930 | –6.057 | 3148 | 0.8132 | 0.6265 | 0.7377 | 1.0005 | 1.0084 | 1.0105 |
| 2 | 2513 | –6.095 | 3303 | 0.7799 | 0.5598 | 0.7572 | 1.0022 | 1.0093 | 1.0117 |
| 3 | 2116 | –6.059 | 3146 | 0.7751 | 0.5501 | 0.7580 | 0.9984 | 1.0094 | 1.0117 |
| 4 | 2186 | –5.982 | 2860 | 0.7727 | 0.5454 | 0.7265 | 0.9987 | 1.0092 | 1.0119 |
| 5 | 2324 | –5.953 | 2822 | 0.7652 | 0.5304 | 0.6898 | 1.0000 | 1.0091 | 1.0117 |
| 6 | 1996 | –5.957 | 2787 | 0.7859 | 0.5717 | 0.7361 | 0.9932 | 1.0091 | 1.0114 |
| 7 | 2262 | –5.907 | 2608 | 0.7949 | 0.5898 | 0.7171 | 0.9962 | 1.0089 | 1.0121 |
| 8 | 2248 | –5.923 | 2658 | 0.8031 | 0.6063 | 0.7337 | 0.9950 | 1.0089 | 1.0117 |
| 9 | 2372 | –5.929 | 2706 | 0.7951 | 0.5903 | 0.7144 | 0.9975 | 1.0088 | 1.0119 |
| 10 | 2227 | –5.954 | 2767 | 0.7934 | 0.5868 | 0.7292 | 0.9960 | 1.0089 | 1.0116 |
| 11 | 2176 | –5.944 | 2707 | 0.8085 | 0.6170 | 0.7513 | 0.9936 | 1.0089 | 1.0118 |
| 12 | 2334 | –5.930 | 2652 | 0.8106 | 0.6213 | 0.7439 | 0.9959 | 1.0088 | 1.0121 |
| 13 | 2317 | –5.948 | 2728 | 0.8189 | 0.6378 | 0.7493 | 0.9943 | 1.0088 | 1.0119 |
| 14 | 2416 | –5.956 | 2763 | 0.8109 | 0.6217 | 0.7408 | 0.9969 | 1.0088 | 1.0121 |
| 15 | 2528 | –5.974 | 2887 | 0.7818 | 0.5637 | 0.7017 | 1.0006 | 1.0089 | 1.0119 |
| 16 | 2183 | –5.997 | 2928 | 0.7853 | 0.5706 | 0.7507 | 0.9973 | 1.0092 | 1.0114 |
| 17 | 2058 | –5.962 | 2744 | 0.8115 | 0.6230 | 0.7657 | 0.9914 | 1.0091 | 1.0119 |
| 18 | 2299 | –5.922 | 2606 | 0.8278 | 0.6557 | 0.7611 | 0.9934 | 1.0088 | 1.0124 |
| 19 | 2613 | –5.937 | 2720 | 0.8081 | 0.6163 | 0.7274 | 0.9993 | 1.0087 | 1.0123 |
Notes. The variable stellar and wind parameters at each iteration step until convergence. For the fixed stellar parameters L, Teff, R, M, and Γ, see upper part of Table 1 in Sect. 4. The line acceleration parameters γfit (or equivalently β), δfit and 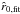 , and the terminal velocity v∞, fit, were determined by (a simplified version of) fitting formula Eq. (71), applied to the results from a numerical calculation of the line acceleration
, and the terminal velocity v∞, fit, were determined by (a simplified version of) fitting formula Eq. (71), applied to the results from a numerical calculation of the line acceleration 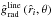 at the equator (θ = π/2). The parameter
at the equator (θ = π/2). The parameter 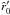 (in the β velocity law, Eq. (64)) and the sonic radius
(in the β velocity law, Eq. (64)) and the sonic radius 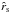 are output values from ISA-Wind, whereas log Ṁ is the improved estimated mass-loss rate numerically obtained (by MC-Wind and Eq. (74)). At each iteration step, the value of v∞ was calculated by (a simplified version of) Eq. (75) and used as the new input value for the terminal velocity in the next iteration step, together with the new estimates of Ṁ and β (cf. description of iteration process in Sect. 3.3). Convergence is achieved when the values of v∞, fit and v∞ have become equal or close to each other. In this case, the condition that the critical radius
are output values from ISA-Wind, whereas log Ṁ is the improved estimated mass-loss rate numerically obtained (by MC-Wind and Eq. (74)). At each iteration step, the value of v∞ was calculated by (a simplified version of) Eq. (75) and used as the new input value for the terminal velocity in the next iteration step, together with the new estimates of Ṁ and β (cf. description of iteration process in Sect. 3.3). Convergence is achieved when the values of v∞, fit and v∞ have become equal or close to each other. In this case, the condition that the critical radius 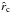 (determined by Eq. (42)) has to be equal to the sonic radius
(determined by Eq. (42)) has to be equal to the sonic radius 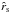 (determined by ISA-Wind) is fulfilled.
(determined by ISA-Wind) is fulfilled.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


