| Issue |
A&A
Volume 700, August 2025
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 7 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202555098 | |
| Published online | 07 August 2025 | |
Dielectronic recombination studies of ions relevant to kilonovae and nonlocal thermodynamic equilibrium plasma
Max-Planck-Institut für Kernphysik,
Saupfercheckweg 1,
69117
Heidelberg,
Germany
★ Corresponding author: suvamsingh18sep@gmail.com
Received:
9
April
2025
Accepted:
17
June
2025
This study presents calculations of rate coefficients, resonance strengths, and cross sections for the dielectronic recombination (DR) of Y+, Sr+, Te2+, and Ce2+ – low-charge ions relevant to kilonovae and nonlocal thermodynamic equilibrium (non-LTE) plasmas. Using relativistic atomic structure methods, we computed DR rate coefficients under conditions typical of these environments. These DR rate coefficients and cross sections were calculated using the Flexible Atomic Code. The DR resonance features were identified by comparing theoretical resonance energies, estimated as the difference between National Institute of Standards and Technology excitation energies and Dirac binding energies, with dominant autoionizing states confirmed through an analysis of autoionization rates. Our results highlight the critical role of low-lying DR resonances in shaping rate coefficients at kilonova temperatures (~104 K) and regulating charge-state distributions. Pronounced near-threshold DR resonances significantly influence the evolving ionization states and opacity of neutron star merger ejecta. Comparisons with previous studies emphasize the necessity of including high-n Rydberg states for accurate DR rate coefficients, especially for complex heavy ions with dense energy levels. Discrepancies with existing datasets underscore the need for refined computational techniques to minimize uncertainties. These results provide essential input for interpreting spectroscopic observations of neutron star mergers, including James Webb Space Telescope data. We also put forward suitable candidates for experimental studies, recognizing the challenges involved in such measurements. The data presented here have the potential to refine models of heavy-element nucleosynthesis, enhance plasma simulation accuracy, and improve non-LTE plasma modeling in astrophysical and laboratory settings.
Key words: atomic data / atomic processes / plasmas
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
Dielectronic recombination (DR) affects the ionization balance, radiative cooling, and energy distribution in plasmas, particularly under nonlocal thermodynamic equilibrium (non-LTE) conditions (Burgess 1964; Gau et al. 1980; Fano & Cooper 1968; Rosmej et al. 2020; Bautista & Badnell 2007; Fritzsche 2021; Badnell et al. 2003; Badnell 2006; Schmidt et al. 2008). In such non-LTE environments, where ionization states are not governed by local thermodynamic equilibrium, understanding the interplay between ionization and recombination processes such as DR is critical for determining plasma dynamics across both astrophysical and laboratory systems with diverse ionization states. An accurate treatment of DR is crucial for improving plasma models and interpreting observational data.
In laboratory plasmas, DR significantly influences energy loss mechanisms and increases plasma stability, particularly in fusion research. The sensitivity of high Rydberg states to weak electric fields increases DR rates at low plasma densities, making it relevant to environments such as the solar corona and magnetic confinement fusion devices (Rosmej et al. 2020). By emitting photons, DR helps regulate the plasma temperature, a key factor for both experimental investigations and theoretical models.
Furthermore, DR is essential to collisional-radiative models, which describe the interactions between charged particles and photons in non-LTE plasmas (Leontyev & Lisitsa 2016; Chung et al. 2013). These models predict plasma responses to varying conditions, including the external field effects on ionization potentials and recombination rates. Incorporating DR in these models provides insight into Auger electron heating, hot electron instabilities, and ionization potential depression, which are key to plasma diagnostics and nonequilibrium plasma theory (Galtier et al. 2011; Petitdemange & Rosmej 2013; Rosmej et al. 2021).
Dielectronic recombination studies on kilonova-relevant ions remain an area of active investigation. Astrophysical plasmas in kilonovae present extreme, non-LTE environments where ionization structure and radiative processes are strongly influenced. DR plays a dominant role in electron-ion recombination, significantly influencing spectral evolution. As it involves high Rydberg states, DR is highly sensitive to density effects, which govern redistributive collisions before radiative stabilization occurs. In kilonovae, which serve as key sites for rapid neutron-capture (r-process) nucleosynthesis at temperatures of approximately 104 K, DR often competes with or even surpasses radiative recombination (RR) in shaping the ionization structure of the ejecta. Under such extreme conditions, DR becomes the predominant recombination mechanism for many heavy ions, surpassing RR (Pognan et al. 2022). This underscores DR’s critical role in determining kilonova ejecta’s ionization structure, transient emission, and the synthesis of elements much heavier than Fe (Drake 2023; Dalgarno & Lepp 2006; Eichler et al. 1989).
As a kilonova evolves from the diffusion to the nebular phase, recombination alters ionization fractions, changing spectral line intensities and causing the emergence or suppression of features in the optical and near-infrared regions. DR rate coefficients in r-process elements exhibit a strong temperature dependence, particularly for singly to doubly ionized species at T ~ 104 K. Even slight variations in ejecta conditions can significantly affect the ionization balance and, consequently, kilonova spectra. In contrast, RR tends to dominate in lower-temperature environments, such as those in the nebular phase of supernovae. Thus, accurate temperature-dependent DR rates are essential for reliable spectral modeling and interpreting transient astrophysical events.
The importance of DR in kilonovae also stems from the complex electron shell structures of heavy elements, which have dense energy levels and numerous autoionizing states, increasing DR efficiency. The photon emission in DR during radiative stabilization serves as a crucial diagnostic tool for interpreting kilonova spectra and constraining plasma parameters such as temperature and electron density. As a result, DR-driven emission plays a vital role in X-ray spectroscopy and plasma diagnostics, offering valuable insights into the physical conditions of astrophysical plasmas (Rosmej et al. 2020; Song & Kato 2005).
Low-charged heavy ions such as Y+, Sr+, Te2+, Ce2+ (Watson et al. 2019; Levan et al. 2024; Domoto et al. 2022) are highly relevant to kilonovae. The James Webb Space Telescope has detected Te2+ in GRB 230307A, and Sr+ was detected in kilonova AT2017gfo, underscoring the need for accurate recombination data to understand low-charge ions in astrophysical plasmas (Levan et al. 2024; Watson et al. 2019). Heavy ions with low-lying excited states (e.g., Y+, Sr+, and Ce2+) exhibit complex DR behavior even at low densities, causing discrepancies in ionization balance calculations. Moreover, different elements affect kilonova opacity and spectra uniquely: Sr and Y produce strong optical and near-infrared transitions, making them observable, while Te and Ce, with their intricate electronic structures, significantly affect mid-infrared opacities. Their recombination rates determine the ionization fractions over time, shaping kilonova spectral evolution. Thus, precise recombination data are essential for improving kilonova models and interpreting spectral signatures accurately.
Accurate data on DR rates, oscillator strengths, and electronimpact cross sections are essential for quantitative analyses of astrophysical spectra, particularly in kilonova ejecta and non-LTE plasmas. However, the scarcity of DR data for key r-process elements such as Y, Sr, Te, and Ce introduces uncertainties in modeling ionization balances and spectral evolution. The dense energy level structures of heavy elements further complicate direct comparisons, as recombination rates can vary significantly across ions and even between transitions within the same species. Due to experimental challenges in measuring DR rates for low-charged heavy elements, models often rely on extrapolations from lighter elements (Pognan et al. 2023) or simplified approximations, leading to substantial inaccuracies. In particular, kilonova and non-LTE plasma models often depend on crude estimates for low-charged heavy ions, where discrepancies can reach an order of magnitude, directly impacting astrophysical predictions. Theoretical studies of these ions are also difficult: while highly charged heavy ions have been widely studied (Schuch et al. 2005; Schippers et al. 2025; Wang et al. 2024; Mahmood et al. 2012; Orban et al. 2006; Harman et al. 2019; Beilmann et al. 2011; González Martinez et al. 2005; Fritzsche et al. 2025), research on low-charge species remains limited. To address this gap, we used state-of-the-art atomic structure calculations to provide reliable DR rate coefficients for such ions. These theoretical benchmarks are essential for improving simulation accuracy, refining ionization balance calculations, and enhancing the interpretation of observational data from neutron star mergers and other transient astrophysical events.
To the best of our knowledge, this work presents one of the first computations for the current targets. No experimental measurements exist in the literature, and the only available theoretical data come from a recent study by Banerjee et al. (2025), which includes only a few of the ions considered here. Another key objective is to provide reference data for experimentalists to facilitate state-of-the-art research in this field. Recent experimental advancements have enabled the study of low-charge heavy ions at the cryogenic storage ring of the Max Planck Institute for Nuclear Physics in Heidelberg (Isberner 2025). Notably, successful DR measurements on Xe3+ represent the highest mass-to-charge ratio experiments conducted to date. However, these experiments face major challenges, including difficulties in ion source generation, high background noise, and weak DR signals that are often obscured (Isberner 2025). Given these experimental limitations, theoretical calculations such as those presented here are required. They provide critical insights and benchmarks not only for experimentalists striving to overcome these challenges but also for astrophysicists modeling and interpreting complex astrophysical phenomena with greater accuracy.
Section 2 of this article covers the theoretical specifics that are employed in the present work. The computational results are discussed and presented in Sect. 3, and Sect. 4 contains some concluding remarks.
2 Theoretical calculations
The four DR reactions studied in the present work are:
-
for Y II to Y I (for l ≤ 9 and n = 6,..., 35),
-
for Sr II to Sr I (for l ≤ 9 and n = 6, . . . , 35);
-
for Te III to Te II (for l ≤ 9 and n = 6,...,35);
-
and (iv) for Ce III to Ce II (for l < 9 and n = 6, . . . , 24),
Here, i denotes the ground state, d the intermediate states, and f the final states. The Rydberg electron is represented as nlj, where n is the principal quantum number of the captured electron and was determined based on convergence. Including more n values (e.g., hundreds) would have only a minor effect on the results. However, this contributes to some uncertainty in the calculation, which has been accounted for in the overall uncertainty estimations. The emitted decay photons are denoted by hv. For a given n, the angular momentum states l = 0,1,..., 9 and  are included. Radiative decay involves all electric dipole transitions to lower-lying states, which means there are a significant number of states to consider. Except for the 4d state of Sr+ and the 4f state of Ce2+, all transitions occur within the same shell (Δn = 0), while the 5s → 4d transition in Sr+ and the 4f → 5d transition in Ce2+ involve inter-shell excitation (Δ n = 1).
are included. Radiative decay involves all electric dipole transitions to lower-lying states, which means there are a significant number of states to consider. Except for the 4d state of Sr+ and the 4f state of Ce2+, all transitions occur within the same shell (Δn = 0), while the 5s → 4d transition in Sr+ and the 4f → 5d transition in Ce2+ involve inter-shell excitation (Δ n = 1).
For a DR channel, i.e., for the two-step transition i → d → f, the cross section is expressed as a function of the electron kinetic energy (E) in the independent resonances approximation (in atomic units) as (see, e.g., Haan & Jacobs 1989; Zimmerer et al. 1990; Zimmermann et al. 1997; Shabaev 1994; Harman et al. 2019)
The initial state of the DR process consists of the ground-state ion and a continuum electron with an asymptotic momentum (p) and a spin projection (ms). In addition, Γd is the total natural width of the intermediate autoionizing state, which is the sum of the radiative and autoionization widths:  (here in atomic units with ħ = 1). Ld(E) is the Lorentzian line shape function, expressed as
(here in atomic units with ħ = 1). Ld(E) is the Lorentzian line shape function, expressed as
and is normalized to unity on the energy scale where  is the modulus of the free-electron momentum associated with the kinetic energy (E).
is the modulus of the free-electron momentum associated with the kinetic energy (E).
The dielectronic capture rate is related to the rate of its time-reversed process, i.e., the Auger process, by the principle of detailed balance:
Here, Jd and Ji are the total angular momenta of the intermediate and the initial states of the recombination process, respectively. Neglecting the energy dependence of the electron momentum in the vicinity of the resonance, the dielectronic resonance strength, defined as the integrated cross section for a given resonance peak,
is given as
where  is implicitly defined in Eq. (7). The factor
is implicitly defined in Eq. (7). The factor  defines the phase space density, and the 1/2 stems from the spin degeneracy of the free electron.
defines the phase space density, and the 1/2 stems from the spin degeneracy of the free electron.
The total rate coefficients (αDR) for astrophysical and thermal plasmas are described by
derived by summing across all possible autoionization channels and averaging over the Maxwellian distribution of electron energies (Dubau & Volonte 1980). In this expression, k denotes the Boltzmann constant, h the Planck constant, which we write explicitly here, T the electron temperature, and E the resonance energy.
 |
Fig. 1 Total DR cross section for Y+ recombining into Y plotted against the relative electron energy. The Lorentzian line shapes are convoluted with a Gaussian function with a width of 100 meV. |
3 Results and discussion
In this study, the relativistic configuration interaction method with independent-particle basis wave functions was utilized to calculate the energy levels, radiative rates, autoionization rates, and DR cross sections and rates as implemented in the Flexible Atomic Code (FAC; Gu 2003, 2004; Singh & Harman 2025). The relativistic distorted-wave approximation was employed to describe the continuum states. For the calculation of wave functions and energy levels corresponding to the initial states, intermediate doubly excited states, and radiative final states, contributions from electron correlations, quantum electrodynamics effects, and Breit interactions were systematically accounted for, ensuring an accurate determination of energy levels and wave functions.
The DR resonance features were identified by comparing the theoretically calculated resonance energies with known excitation energies of the core ion, as listed in the National Institute of Standards and Technology (NIST) Atomic Spectra Database. The DR resonance energy, EDR, is approximately given by the difference between the excitation energy of the bound core electron, Eex, and the binding energy of the captured free electron, EB; that is, EDR = Eex - EB. Here, Eex values were taken from NIST, while EB was estimated using Dirac binding energies (Bernhardt et al. 2015). This provides an approximate position for the expected DR resonance features. To further verify these identifications, we analyzed the autoionization rates of the intermediate states. Since higher autoionization rates typically correspond to stronger DR resonance features, the dominant contributors identified through rate analysis were found to be consistent with the states inferred from energy comparisons.
Figure 1 illustrates the total DR cross sections for the recombination of Y+ into Y. The resolution width is set to 100 meV and is modeled as a Lorentzian profile convoluted with a Gaussian. The calculations include Rydberg states up to n = 6, . . . , 35. A strong DR resonance is observed near the threshold, accompanied by relatively weak resonance peaks at approximately 0.3 eV and 0.6 eV. These peaks are attributed to the 4d5s 3DJ states (where J = 1, 2, 3). Additionally, a small resonance around 2 eV is associated with the 5s5p 3P°J states (where J = 0, 1, 2).
The DR resonance strength for Y+ is approximately an order of magnitude higher than that of the ions previously studied by our group (Singh & Harman 2025; Isberner 2025). The presence of strong resonances at low energies suggests that DR is dominated by optically allowed core excitations, and it is a dominant recombination mechanism for Y+ under various plasma conditions, particularly in astrophysical environments. Given the exceptionally strong resonance near the threshold, Y+ is an excellent candidate for experimental validation, as background effects are expected to be minimal, increasing detection feasibility. However, experimental challenges remain, particularly in distinguishing the DR signal from RR, which is typically prominent at near-threshold energies. Effectively separating these contributions will be crucial for future measurements. The findings of this work could facilitate both observational and experimental studies of Y+ in the near future.
The total DR spectrum for Sr+ recombining into neutral Sr is presented in Fig. 2, with a resolution width set to 100 meV. The DR cross section exhibits characteristic resonance peaks, arising from the capture of free electrons into autoionizing Rydberg states via core excitations (5s → 5p, 4d). A strong DR resonance feature is observed near zero energy; however, its exact origin remains unidentified. There is a strong possibility that it results from a theoretical artifact associated with the Rydberg state n = 6, as observed in our calculations, since no such excited states have been reported in the literature at such low energies. Another prominent resonance appears at approximately 2.3 eV, primarily originating from the 4p64d 2D5/2 and 2D3/2 states, with the 2D5/2 state being the dominant contributor. Additionally, a strong DR resonance, attributed to the 4p65p 2Po1/2 and 2Po3/2 states, is observed around 2.7 eV. These states are also responsible for the knee-like resonances observed around 3 eV.
Of the ions studied in this work, the DR spectrum of Sr+ exhibits the weakest signal strength, which may present significant challenges for experimental observation with currently available setups. Its DR signal strength is approximately one to two orders of magnitude lower than that of the other ions studied in this work as well as in previous works (Singh & Harman 2025; Isberner 2025). To detect this spectrum experimentally, it would be necessary to significantly reduce background noise.
Figure 3 presents the total DR cross section for Te2+ recombining into Te+, calculated with a resolution width of 100 meV. In the DR spectrum, a small resonance is observed at low energies, below 0.5 eV, and is attributed to the 5s25p2 3PJ states (where J = 0, 1, 2). At approximately 14.5 eV, two prominent resonance structures appear, corresponding to the 5p5d 3DJo (where J = 1, 2, 3) and 3PoJ (where J = 0, 1, 2) states, with the 3Do1 and 3P1o states being the dominant contributors. Additionally, several significant resonance peaks, arising from the 5s5p3 states, are observed on both sides of this strong resonance feature. Given the presence of a well-defined resonance near the threshold and strong DR resonance features at higher energies, along with a relatively high DR signal strength, this ion is a promising candidate for further DR spectroscopy studies, both experimental and theoretical.
Figure 4 presents the total DR cross sections for the recombination of Ce2+ into Ce+, calculated with a resolution width of 100 meV. A strong DR resonance is observed near the threshold, primarily due to the convolution of the 4f2 and 4f 5d states. At energies close to 0 eV, the 4f2 3H5 state is the dominant contributor, whereas toward the tail end of the peak, the 4f5d1Go4 state becomes the most significant. As seen in Table 1, although the excitation energy of the 4f5d1 Go4 state appears to be lower than that of the 4f2 3H5 state in the FAC calculations, the inclusion of the Rydberg electron introduces additional configuration mixing. As a result, the resonance energy associated with the 4f5d1G°4 state becomes higher than that of the 4f2 3H5 state. The contribution of the 4f5d1G°4 state at the tail end of the resonance feature is further supported by the analysis of the autoionization rates. Although the spectrum appears to decline beyond 0.2 eV, the cross-section magnitude remains on the order of 107 barns, emphasizing the strength of this prominent resonance feature. This suggests that Ce2+ could serve as a strong candidate for experimental study near the threshold energy, similar to Y+. Furthermore, the exceptionally strong DR signal might indicate a considerable probability of its detection in a kilonova.
Table 1 presents a comparison of the energy levels calculated in this work using the FAC with the values available from the NIST Atomic Spectra Database (Kramida et al. 2024). As noted by Gu (2003), energy levels computed using FAC can exhibit uncertainties due to an incomplete treatment of correlations, limitations in the atomic model, or a lack of configuration mixing. From Table 1, it is evident that the calculated energy levels deviate from the NIST values by approximately 1-1.5 eV. Such differences are expected for near-neutral heavy ions, as the estimated uncertainty in energy levels calculated using FAC can be on the order of a few electronvolts. A recent study by Nahar (2024), which also investigates low-charged lanthanides relevant to kilonovae, reports similar discrepancies of a few electronvolts when comparing theoretical values with NIST data. This supports the observation that such deviations are typical when modeling complex atomic structures. In addition to energy uncertainties, there are inherent uncertainties in the computed rates and cross sections. According to the FAC manual authored by Gu (2016), in the case of near-neutral ions (as in the present case), the uncertainties associated with radiative decay rates and autoionization rates can reach 20% or, in certain instances, exceed this value. Additionally, limiting the number of states (n) introduces an uncertainty of approximately 10%. Therefore, the overall uncertainty in the present calculation of DR cross section and strengths is estimated to be around 30%. Given the substantial amount of data generated in this work, all data are made available as supplementary material.
Figure 5 illustrates the dependence of the total DR rate coefficients on electron temperature, calculated by incorporating Rydberg states with principal quantum numbers ranging from n = 6 to n = 35, except for Ce2+. While the high-temperature rates (T > 105 K) may not have significant practical relevance, they are included for completeness. At high temperatures (T), the DR rate coefficient decreases following a ~T-3/2 dependence, as the increasing kinetic energy of free electrons reduces the probability of recombination. In contrast, at low temperatures, the DR process is predominantly influenced by a number of resonances situated just above the threshold. These resonances contribute significantly to the recombination rate, ensuring that DR remains efficient even at lower temperatures. This occurs because the ~T-3/2 factor compensates for the lowness of the temperature. The calculated values have an estimated uncertainty of around 38%, as determined using the error propagation rule from Eq. (10). At low temperatures, DR is primarily governed by near-zero-energy resonances, where the energy of free electrons closely matches the energy levels of states within the ion, enabling highly efficient recombination processes. The dominance of these resonances increases the recombination probability, significantly influencing the ionization balance of the kilonova ejecta. Notably, the behavior of DR at these temperatures can resemble that of RR, highlighting the need for precise resonance data for accurate modeling. As the temperature increases, contributions from high-n Rydberg states become more prominent. These states, with their highly excited electrons near the ionization threshold, play a crucial role in recombination dynamics at higher temperatures. The interplay between the thermal energy of the electrons and the populations of these excited states alters the overall recombination efficiency, resulting in a shift in the effective ionization balance. This shift is particularly significant for ions with one or two electrons outside closed shells (e.g., Y+, Sr+, and Ce2+), as it impacts the interpretation of kilonova spectra and the modeling of non-LTE plasmas (Badnell et al. 2003).
It is worth noting that the uncertainty reported in the present work may appear large; however, we have included an additional 10% uncertainty to account for the contribution from higher Rydberg states that were not included in the present calculations. If experimental observations are carried out for the current set of ions, it is highly likely that these contributions would also be suppressed due to field ionization effects, which typically limit the population of high-n Rydberg states in experimental setups. Therefore, the additional 10% uncertainty we have included would have a relatively minor impact when comparing with experimental results. Nonetheless, we have included this 10% additional uncertainty to provide a more cautious upper bound on the theoretical uncertainty. Furthermore, several previous studies on both high- and low-charge ions (Kaur et al. 2018; Bleda et al. 2022; Nahar 2024) have reported similarly large uncertainties, in terms of both the energy scale and the rate coefficient, which is to be expected when dealing with complex, many-electron systems such as those considered in this work.
Table 2 presents the DR rate coefficients at temperatures of 103, 104, and 105 K. The complete set of DR rate coefficients as a function of temperature is provided in the supplementary material. Among the studied ions, Ce2+ exhibits relatively high DR rate coefficients at very low temperatures compared to the other ions. In the kilonova-relevant temperature range (~104 K), as shown in Table 2, the rate coefficients for Y+ and Ce2+ become comparable and significantly exceed those of Sr+ and Te2+. This indicates that Y+ and Ce2+ have a stronger tendency to populate lower ionization states over time, while Sr+ and Te2+ remain ionized for a longer duration in the expanding ejecta. These DR trends have critical implications for kilonova spectra. Higher DR rates, as seen for Y+ and Ce2+, are expected to promote efficient recombination to lower ionization states, contributing to optical and near-infrared spectral features. In contrast, the slower recombination associated with Sr+ and Te2+ can lead to the retention of higher ionization states, producing spectral features characterized by higher-energy transitions and shifts toward shorter wavelengths. The availability of these computed DR rates will be instrumental in refining spectral models, improving predictions of line emission, and enhancing our understanding of kilonova ejecta composition, as they provide crucial inputs for astrophysical modeling tools such as the SUMO spectral synthesis code used in kilonova simulations (Jerkstrand et al. 2011).
In Fig. 6, a comparison is made between the DR rate coefficients obtained in this work and those reported in the only existing study over the temperature range characteristic of the nebular phase of kilonovae. During this phase, the temperature is typically around 10 000 K (Metzger 2020; Tanaka et al. 2020). To account for the temperature evolution from the early weeks after the event to later stages, influenced by the evolving ejecta composition, the rate coefficients are presented across a broader temperature range, from 1000 K to 30 000 K.
In the case of Y+, the present values are approximately an order of magnitude larger than those reported by Banerjee et al. (2025). The same number of intermediate states was considered in the two studies; however, the difference in magnitude arises from the inclusion of a significantly larger number of Rydberg states in the present work. The inclusion of high-n Rydberg states increases the recombination probability (Nahar 1997). Additionally, differences in the number of orbital angular momentum states (l) considered in the two studies may further contribute to the observed discrepancy in the rate coefficients.
A different trend is observed for Sr+, for which our results show a good agreement with those of Banerjee et al. (2025). This consistency can be attributed to the inclusion of an additional 4p64f state in their study, which increases their rate coefficient. However, this is counterbalanced by their lower number of Rydberg states and l values, resulting in an overall accidental numerical agreement between the two datasets. The role of Rydberg states is particularly significant in singly charged ions such as Y+ and Sr+, where dense energy levels allow for extensive recombination pathways (Dunn 1992). Despite some variations in magnitude, the present DR rate coefficients remain within an order of magnitude of those determined in previous studies, or even closer. This level of consistency supports the reliability of the present work.
 |
Fig. 2 Total DR cross section for Sr+ recombining into Sr plotted against the relative electron energy. |
 |
Fig. 3 Total DR cross section for Te2+ recombining into Te+ plotted against the relative electron energy. |
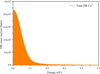 |
Fig. 4 Total DR cross section for Ce2+ recombining into Ce+ plotted against the relative electron energy. |
Comparison of energy levels (in eV) from present FAC calculations and NIST (Kramida et al. 2024) for selected ions.
 |
Fig. 5 Rate coefficient for Y+, Sr+, Te2+, and Ce2+ plotted against the electron temperature. |
DR rate coefficients (10-11 cm3/s) at temperatures 103, 104, and 105 K.
 |
Fig. 6 Comparison of rate coefficients for Y+ and Sr+ with available results from Banerjee et al. (2025). |
4 Conclusions
Given the importance of DR in kilonova spectra and non-LTE plasmas, systematic calculations of DR rates, strengths, and cross sections for low-charge heavy ions such as Y+, Sr+, Te2+, and Ce2+ are critical. These data are essential for interpreting transient emissions across multiple electromagnetic bands in kilonovae and improving plasma models for astrophysical and laboratory contexts. Studying DR processes in non-LTE plasmas enhances our understanding of plasma behavior across diverse environments, advancing theoretical and experimental plasma physics.
Strong near-threshold DR resonances for Y+ and Ce2+ highlight their role in modifying the ionization balance of kilonova ejecta. DR rate sensitivity to plasma conditions, such as temperature and density, underscores the need for precise data to refine ionization state modeling. These rate coefficients are crucial for interpreting observational data from instruments such as the James Webb Space Telescope, as seen in the detection of tellurium in specific kilonovae. Additionally, the methodology employed in this study can be extended to further DR investigations, improving simulations beyond the crude approximations currently employed.
Comparing our calculated DR rates with previous studies reveals the impact of including high-n Rydberg states, illustrating challenges in achieving accurate results for complex heavy ions. Discrepancies between our data and other studies highlight the need for continued advancements in computational techniques to reduce uncertainties in DR rate coefficients. This work identifies several candidates for experimental measurements, such as Y+ and Ce2+ for near-threshold DR studies due to their strong DR signal strengths. Te2+ also emerges as a promising candidate for DR spectrum studies and benchmarking DR analyses. These findings enhance interpretations of transient phenomena and provide a foundation for experimental validation.
Data availability
The supplementary dataset is available at Zenodo: https://doi.org/10.5281/zenodo.15683885
References
- Badnell, N. 2006, A&A, 447, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R., O’Mullane, M., Summers, H., et al. 2003, A&A, 406, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banerjee, S., Jerkstrand, A., Badnell, N., et al. 2025, arXiv e-prints [arXiv:2501.18345] [Google Scholar]
- Bautista, M., & Badnell, N. 2007, A&A, 466, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beilmann, C., Mokler, P., Bernitt, S., et al. 2011, Phys. Rev. Lett., 107, 143201 [Google Scholar]
- Bernhardt, D., Brandau, C., Harman, Z., et al. 2015, Phys. Rev. A, 91, 012710 [Google Scholar]
- Bleda, E., Altun, Z., & Badnell, N. 2022, A&A, 668, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgess, A. 1964, ApJ, 139, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, H.-K., Bowen, C., Fontes, C., Hansen, S., & Ralchenko, Y. 2013, HEDP, 9, 645 [Google Scholar]
- Dalgarno, A., & Lepp, S. 2006, Springer Handbook of Atomic, 1235 [Google Scholar]
- Domoto, N., Tanaka, M., Kato, D., et al. 2022, ApJ, 939, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, G. W. 2023, Springer Handbook of Atomic, Molecular, and Optical Physics (Springer Nature) [Google Scholar]
- Dubau, J., & Volonte, S. 1980, Rep. Prog. Phys., 43, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Dunn, G. H. 1992, in Recombination of Atomic Ions (Springer), 115 [Google Scholar]
- Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Fano, U., & Cooper, J. 1968, Rev. Mod. Phys., 40, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Fritzsche, S. 2021, A&A, 656, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fritzsche, S., Huang, H., Huang, Z.-K., et al. 2025, EPJD, 79, 22 [Google Scholar]
- Galtier, E., Rosmej, F., Dzelzainis, T., et al. 2011, Phys. Rev. Lett., 106, 164801 [Google Scholar]
- Gau, J., Hahn, Y., & Retter, J. 1980, JQSRT, 23, 131 [Google Scholar]
- González Martinez, A. J., López-Urrutia, J. R. C., Braun, J., et al. 2005, Phys. Rev. Lett., 94, 203201 [Google Scholar]
- Gu, M. 2003, ApJ, 590, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F. 2004, in AIP Conf. Proc., 730, 14th APS Topical Conference on Atomic Processes in Plasmas (New York: American Institute of Physics), 127 [Google Scholar]
- Gu, M. F. 2016, Github - Flexible Atomic Code, [Online]. Available: https://github.com/flexible-atomic-code/fac [Google Scholar]
- Haan, S. L., & Jacobs, V. L. 1989, Phys. Rev. A, 40, 80 [Google Scholar]
- Harman, Z., Shah, C., González Martínez, A. J., et al. 2019, Phys. Rev. A, 99, 012506 [Google Scholar]
- Isberner, L. 2025, PhD thesis, Ruprecht-Karls-Universität Heidelberg, Germany [Google Scholar]
- Jerkstrand, A., Fransson, C., & Kozma, C. 2011, A&A, 530, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaur, J., Gorczyca, T., & Badnell, N. 2018, A&A, 610, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramida, A., Ralchenko, Reader, J. Yu., & NIST ASD Team. 2024, NIST Atomic Spectra Database (ver. 5.12), [Online]. Available: https://physics.nist.gov/asd [2025, February 27] (Gaithersburg, MD: National Institute of Standards and Technology) [Google Scholar]
- Leontyev, D., & Lisitsa, V. 2016, Contrib. Plasma Phys., 56, 846 [Google Scholar]
- Levan, A. J., Gompertz, B. P., Salafia, O. S., et al. 2024, Nature, 626, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Mahmood, S., Ali, S., Orban, I., et al. 2012, ApJ, 754, 86 [Google Scholar]
- Metzger, B. D. 2020, Living Rev. Relativ., 23, 1 [Google Scholar]
- Nahar, S. N. 1997, Phys. Rev. A, 55, 1980 [NASA ADS] [CrossRef] [Google Scholar]
- Nahar, S. N. 2024, Atoms, 12, 24 [Google Scholar]
- Orban, I., Glans, P., Altun, Z., et al. 2006, A&A, 459, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petitdemange, F., & Rosmej, F. 2013, in New Trends in Atomic and Molecular Physics: Advanced Technological Applications (Springer), 91 [Google Scholar]
- Pognan, Q., Jerkstrand, A., & Grumer, J. 2022, MNRAS, 510, 3806 [NASA ADS] [CrossRef] [Google Scholar]
- Pognan, Q., Grumer, J., Jerkstrand, A., & Wanajo, S. 2023, MNRAS, 526, 5220 [NASA ADS] [CrossRef] [Google Scholar]
- Rosmej, F., Astapenko, V., Lisitsa, V., & Vainshtein, L. 2020, MRE, 5, 064201 [Google Scholar]
- Rosmej, F. B., Astapenko, V. A., & Lisitsa, V. S. 2021, Plasma Atomic Physics, 650 (Springer) [Google Scholar]
- Schmidt, E., Schippers, S., Bernhardt, D., et al. 2008, A&A, 492, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schippers, S., Brandau, C., Fuchs, S., et al. 2025, arXiv e-prints [arXiv:2502.15433] [Google Scholar]
- Schuch, R., Lindroth, E., Madzunkov, S., et al. 2005, Phys. Rev. Lett., 95, 183003 [Google Scholar]
- Shabaev, V. M. 1994, Phys. Rev. A, 50, 4521 [Google Scholar]
- Singh, S., & Harman, Z. 2025, Phys. Rev. A, 111, 042802 [Google Scholar]
- Song, M.-Y., & Kato, T. 2005, Dielectronic recombination of Xe10+ ions and satellite line of Xe9+ ions, Technical report (National Institute for Fusion Science) [Google Scholar]
- Tanaka, M., Kato, D., Gaigalas, G., & Kawaguchi, K. 2020, MNRAS, 496, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S.-X., Brandau, C., Fritzsche, S., et al. 2024, EPJD, 78, 122 [Google Scholar]
- Watson, D., Hansen, C. J., Selsing, J., et al. 2019, Nature, 574, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Zimmerer, P., Grün, N., & Scheid, W. 1990, Phys. Lett. A., 148, 457 [Google Scholar]
- Zimmermann, M., Grün, N., & Scheid, W. 1997, J. Phys. B, 30, 5259 [Google Scholar]
All Tables
Comparison of energy levels (in eV) from present FAC calculations and NIST (Kramida et al. 2024) for selected ions.
All Figures
 |
Fig. 1 Total DR cross section for Y+ recombining into Y plotted against the relative electron energy. The Lorentzian line shapes are convoluted with a Gaussian function with a width of 100 meV. |
| In the text | |
 |
Fig. 2 Total DR cross section for Sr+ recombining into Sr plotted against the relative electron energy. |
| In the text | |
 |
Fig. 3 Total DR cross section for Te2+ recombining into Te+ plotted against the relative electron energy. |
| In the text | |
 |
Fig. 4 Total DR cross section for Ce2+ recombining into Ce+ plotted against the relative electron energy. |
| In the text | |
 |
Fig. 5 Rate coefficient for Y+, Sr+, Te2+, and Ce2+ plotted against the electron temperature. |
| In the text | |
 |
Fig. 6 Comparison of rate coefficients for Y+ and Sr+ with available results from Banerjee et al. (2025). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{aligned} {\rm Y}^{+}[5s^2 (i)] + e^- &\to \left\{ \begin{array}{l} {\rm Y}^*[5s ~5p ~nl_j (d)] \\ {\rm Y}^*[5s ~4d ~nl_j (d)] \end{array} \right\} \to {\rm Y}(f) + h\nu\,; \end{aligned}](/articles/aa/full_html/2025/08/aa55098-25/aa55098-25-eq1.png)
![\begin{aligned} {\rm Sr}^{+}[5s (i)] + e^- &\to \left\{ \begin{array}{l} {\rm Sr}^*[5p ~nl_j (d)] \\ {\rm Sr}^*[4d ~nl_j (d)] \end{array} \right\} \to {\rm Sr}(f) + h\nu\,. \end{aligned}](/articles/aa/full_html/2025/08/aa55098-25/aa55098-25-eq2.png)
![\begin{aligned} {\rm Te}^{2+}[5s^2 ~5p^2 (i)] + e^- &\to \left\{ \begin{array}{l} {\rm Te}^{+*}[5s^2 ~5p ~5d ~nl_j (d)] \\ {\rm Te}^{+*}[5s ~5p^3 ~nl_j (d)] \end{array} \right\} \nonumber \\ &\to {\rm Te}^{+}(f) + h\nu, \end{aligned}](/articles/aa/full_html/2025/08/aa55098-25/aa55098-25-eq3.png)
![\begin{aligned} {\rm Ce}^{2+}[4f^2 (i)] + e^- &\to \left\{ \begin{array}{l} {\rm Ce}^{+^*}[4f~5d~nl_j (d)] \end{array} \right\} \nonumber \\ &\to {\rm Ce}^{+}(f) + h\nu . \end{aligned}](/articles/aa/full_html/2025/08/aa55098-25/aa55098-25-eq4.png)





