Calibration and performances of the integrated Mach—Zehnder wavefront sensor for extreme adaptive optics

Open Access

Table 1

Notations and main results for the iMZ model.

Symbol	Description
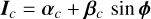$I_{c} = α_{c} + β_{c} \sin ϕ$ $\bm{I}_{c} = \bm{\alpha}_{c} + \bm{\beta}_{c}\,\sin\bm{\phi}$	Intensity in output channel 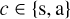$c \in {s, a}$ $c \in \{\Sym,\Asym\}$ of the iMZ.
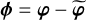$ϕ = φ - \tilde{φ}$ $\bm{\phi} = \bm{\varphi} - \filtered{\bm{\varphi}}$	Phase measured by the iMZ.
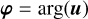$φ = \arg (u)$ $\bm{\varphi} = \arg(\bm{u})$	Phase in pupil plane.
u	Complex amplitude of the pupil plane re-imaged on the detector.
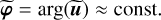$\tilde{φ} = \arg (\tilde{u}) \approx const.$ $\filtered{\bm{\varphi}} = \arg(\filtered{\bm{u}}) \approx \text{const.}$	Phase after filtering by the pinhole.
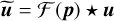$\tilde{u} = F p ⋆ u$ $\filtered{\bm{u}} = \FT{\bm{p}} \star \bm{u}$	Complex amplitude filtered by the pinhole, 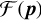$F p$ $\FT{\bm{p}}$ is the two-dimensional Fourier transform of p and ⋆ denotes the two-dimensional convolution.
p	Pinhole mask (0 where transparent, 1 where opaque).
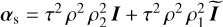$α_{s} = τ^{2} ρ^{2} ρ_{2}^{2} I + τ^{2} ρ^{2} ρ_{1}^{2} \tilde{I}$ $\bm{\alpha}_{\Sym} = \tau^{2}\,\rho^{2}\,\rho_{2}^{2}\,\bm{I} + \tau^{2}\,\rho^{2}\,\rho_{1}^{2}\,\filtered{\bm{I}}$	Baseline intensity in symmetric output channel.
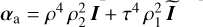$α_{a} = ρ^{4} ρ_{2}^{2} I + τ^{4} ρ_{1}^{2} \tilde{I}$ $\bm{\alpha}_{\Asym} = \rho^{4}\,\rho_{2}^{2}\,\bm{I} + \tau^{4}\,\rho_{1}^{2}\,\filtered{\bm{I}}$	Baseline intensity in asymmetric output channel.
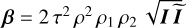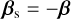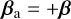$β = 2 τ^{2} ρ^{2} ρ_{1} ρ_{2} \sqrt{I \tilde{I}}$ $\bm{\beta} = 2\,\tau^{2}\,\rho^{2}\,\rho_{1}\,\rho_{2}\,\sqrt{\bm{I}\,\filtered{\bm{I}}}$	Intensity factor in the output channels: $β_{s} = - β$ $\bm{\beta}_\Sym = -\bm{\beta}$ and $β_{a} = + β$ $\bm{\beta}_\Asym = +\bm{\beta}$ .
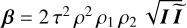$I = \| u \|^{2}$ $\bm{I} = \Abs*{\bm{u}}^{2}$	Intensity of the pupil plane re-imaged on the detector.
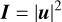$\tilde{I} = \| \tilde{u} \|^{2}$ $\filtered{\bm{I}} = \Abs*{\filtered{\bm{u}}}^{2}$	Pinhole filtered intensity of the pupil plane re-imaged on the detector.
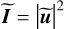$γ = \| \tilde{u} \| / \| u \|$ $\bm{\gamma} = \Abs{\filtered{\bm{u}}}/ \Abs{\bm{u}}$	Filtered relative amplitude.
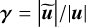$r = ρ e^{i φ_{R}}$ $r = \rho\,\mathe^{\mathi\,\varphi_{\text{R}}}$	Complex reflectance of the beam splitter.
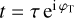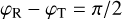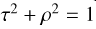$t = τ e^{i φ_{T}}$ $t = \tau\,\mathe^{\mathi\,\varphi_{\text{T}}}$	Complex transmittance of the beam splitter. A lossless symmetric beam splitter is assumed, hence $φ_{R} - φ_{T} = π / 2$ $\varphi_{\text{R}} - \varphi_{\text{T}} = \pi/2$ and $τ^{2} + ρ^{2} = 1$ $\tau^{2} + \rho^{2} = 1$ .
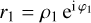$r_{1} = ρ_{1} e^{i φ_{1}}$ $r_{1} = \rho_{1}\,\mathe^{\mathi\,\varphi_{1}}$	Complex reflectance of the pinhole on Side 1 of the iMZ, with 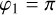$φ_{1} = π$ $\varphi_{1} = \pi$ .
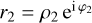$r_{2} = ρ_{2} e^{i φ_{2}}$ $r_{2} = \rho_{2}\,\mathe^{\mathi\,\varphi_{2}}$	Complex reflectance of the coating on Side 2 of the iMZ, with 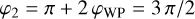$φ_{2} = π + 2 φ_{WP} = 3 π / 2$ $\varphi_{2} = \pi + 2\,\varphi_{\text{WP}} = 3\,\pi/2$ .
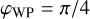$φ_{WP} = π / 4$ $\varphi_{\text{WP}} = \pi/4$	Phase shift by the λ/8 waveplate on Side 2 of the iMZ.
N	Mean number of photons available in the pupil per wavefront phase sample to be measured.
M	Number of successive images acquirred with a different perturbation to measure a phase.

Notes. Bold symbols denote quantities depending on the position in a transverse plane with respect to the propagation direction. Arithmetical operations and mathematical functions are applied element-wise.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.