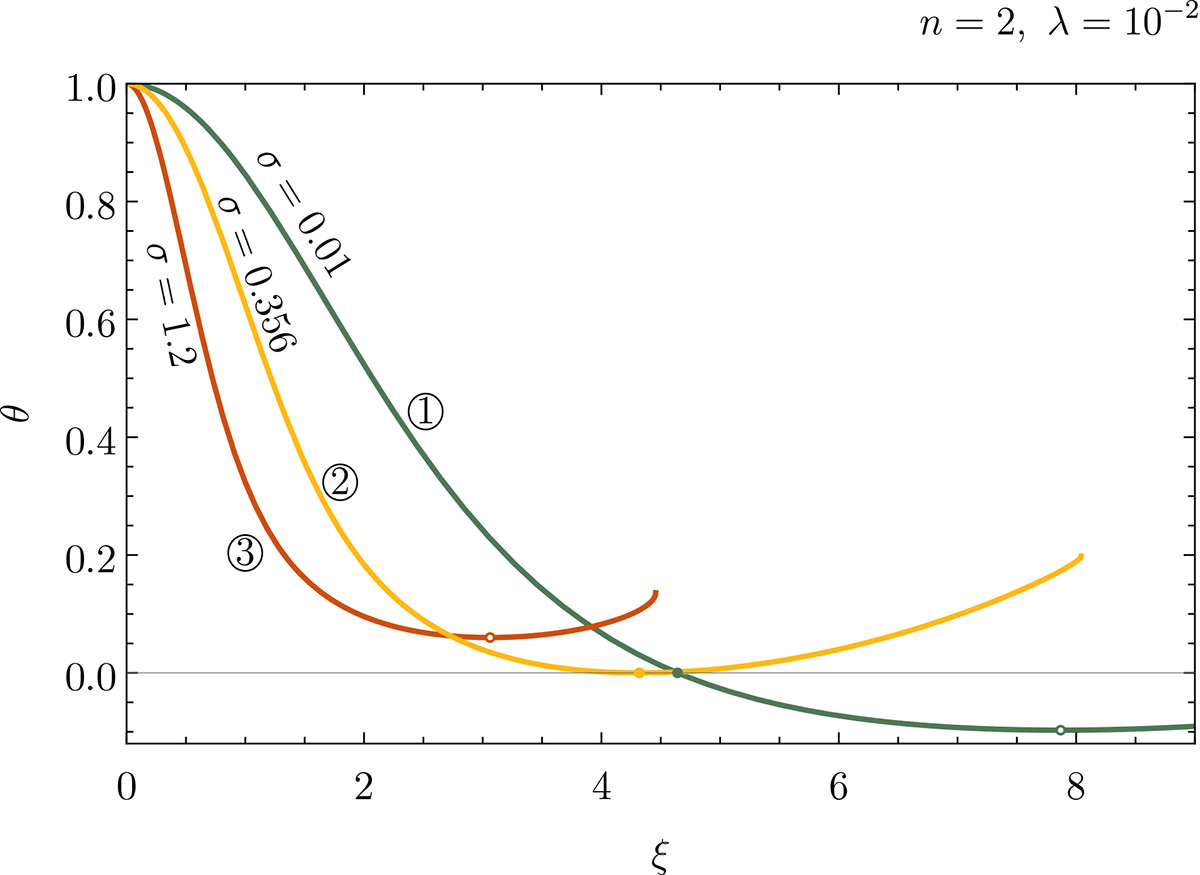
Dependence of the pressure, θ, to the dimensionless radial coordinate, ξ. The surface of the polytropic sphere is determined by the first zero of θ(ξ), if it exists. Such points are depicted on the plot by solid dots, see curves ① and ②. The expected θ-curve (corresponding to pressure) is a monotonically decreasing function. As a manifestation of the influence of the cosmological parameter λ, the θ function can start to increase even before the first zero is reached, see curve ③. Change of monotonicity occurs in local minimum dθ/dξ = 0 and if such a minimum occurs at ξ₁, where θ(ξ₁) = 0, such a point is identified as the “static radius of the external spacetime” of such a polytrope, ξ_s = 3ν(ξ₁)/2λ, see curve ②. If θ(ξ_min) > 0 at such a minimum localized at ξ_min, like on the curve ③, the ratio ${\xi }_{\min }/\left(\frac{3}{2}\frac{\nu ({\xi }_{\min })}{\lambda }\right)>1$. At the center of each configuration, the value of $\underset{\xi \to 0}{lim}\xi /\left(\frac{3}{2}\frac{\nu (\xi )}{\lambda }\right)={\left(2\lambda \right)}^{1/3}$ is smaller than 1 for λ < 1/2 (we take our attention only to the positive cosmological constant). Thus, for curves like ③, there exists a point in the interval 0 < ξ < ξ_min, where ξ = 3ν(ξ)/2λ. We do not consider such cases in the present paper, postponing them for a future study. (Notice that calculation to the negative values of θ is possible only for special values of n and the corresponding part of the curve ① is shown here for illustration only. Generally, such curves end on θ = 0. Depicted ends of the curves ② and ③ are due to the stiffness problem, which does not need to be overcome in normal situations as we stop calculation at ξ₁ or ξ_min.)