Solar flares versus solar energetic particle events: Probabilistic projections to extreme events

Open Access

Table B.1.

Metrics, χ² per degree of freedom (χ²/dof) and AIC, of the various CDF fits to the empirical CCP data (Figure 2).

CDF	Equation	f₃₀ > 0		f₁₀₀ > 0		f₈₀₀ > 3 ⋅ 10³ cm⁻²

		χ²/dof	AIC	χ²/dof	AIC	χ²/dof	AIC
Lognormal	$\frac{1}{2} [1 + \erf (\frac{ln x - μ}{σ \sqrt{2}})]$ $\frac{1}{2}\left[1 + {erf}\left(\frac{\ln x - \mu}{\sigma\sqrt{2}}\right)\right]$	0.28	-6.17	0.26	-6.57	0.33	-5.15
Exponential	1 − e^−λx	0.79	-0.49	0.27	-7.00	0.81	-0.39
Normal	$\frac{1}{2} [1 + \erf (\frac{x - μ}{σ \sqrt{2}})]$ $\frac{1}{2}\left[1 + {erf}\left(\frac{x - \mu}{\sigma\sqrt{2}}\right)\right]$	16.21	18.28	12.99	16.95	16.92	18.54
Weibull	1 − e^{−(x/μ)^σ}	0.69	-0.69	0.33	-5.11	1.00	1.58
Pareto	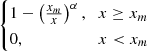${\begin{array}{l} 1 - {(\frac{x_{m}}{x})}^{α}, & x \geq x_{m} \\ 0, & x < x_{m} \end{array}$ $\begin{cases} 1 - \left(\frac{x_m}{x}\right)^\alpha, & x \ge x_m \\ 0, & x < x_m \end{cases}$	5.41	11.70	6.26	12.57	5.46	11.75
Gamma	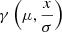$γ (μ, \frac{x}{σ})$ $\gamma\left(\mu, \frac{x}{\sigma}\right)$	0.74	-0.25	0.33	-5.04	0.99	1.52
Gumbel	exp(−e^{−(x − μ)/σ})	10.39	15.61	9.29	14.94	11.55	16.25
Generalized Logistic	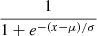$\frac{1}{1 + e^{- (x - μ) / σ}}$ $\frac{1}{1 + e^{-(x - \mu)/\sigma}}$	17.49	18.74	15.34	17.95	18.24	18.99
Log Exponential	1 − e^−λlnx	38.03	22.74	28.33	20.97	15.26	17.26
Log Pareto	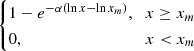${\begin{array}{l} 1 - e^{- α (\ln x - \ln x_{m})}, & x \geq x_{m} \\ 0, & x < x_{m} \end{array}$ $\begin{cases} 1 - e^{-\alpha(\ln x - \ln x_m)}, & x \ge x_m \\ 0, & x < x_m \end{cases}$	45.53	24.48	27.19	21.38	5.46	11.75
Log Gumbel	exp(−e^{−(lnx − μ)/σ})	0.83	0.48	1.16	2.48	0.82	0.40

Notes. SPEs with the fluences f₃₀ > 0, f₁₀₀ > 0, and f₈₀₀ > 3 ⋅ 10³ cm⁻² are demonstrated. Most CDFs have two fitting parameters, except for Exponential and Log Exponential, which use a single parameter.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.