Hydrodynamical models of the β Lyr A circumstellar disc

Open Access

Table 2

Overview of modified Shakura-Sunyaev models for β Lyr A disc.

Assumption	Designation	κ(ρ, T)	Consistency	T ∝ r^γ	Figs.
P_g ≫ P_r	Kramers	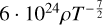$6 \cdot 10^{24} ρ T^{- \frac{7}{2}}$ $6 \cdot 10^{24} \rho T^{-\frac{7}{2}}$	Yes	−0.75	1,2a,2b,2c,2d
P_g ≫ P_r	“Ridge”	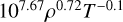$10^{7.67} ρ^{0.72} T^{- 0.1}$ $10^{7.67} \rho^{0.72} T^{-0.1}$	Yes, except for α ≤ 0.01	−1.08	D.1a, D.1b
P_g ≫ P_r	High temperatures	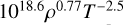$10^{18.6} ρ^{0.77} T^{- 2.5}$ $10^{18.6} \rho^{0.77} T^{-2.5}$	Yes	−0.79	D.2
P_g ≈ P_r	Kramers	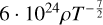$6 \cdot 10^{24} ρ T^{- \frac{7}{2}}$ $6 \cdot 10^{24} \rho T^{-\frac{7}{2}}$	No		1
P_g ≈ P_r	“Ridge”	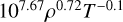$10^{7.67} ρ^{0.72} T^{- 0.1}$ $10^{7.67} \rho^{0.72} T^{-0.1}$	No		D.1a,D.3a, D.3b
P_g ≈ P_r	Inverse problem	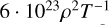$6 \cdot 10^{23} ρ^{2} T^{- 1}$ $6 \cdot 10^{23} \rho^{2} T^{-1}$	Only in the inner disc for α = 0. 1		D.4, D.5a, D.5b, D.5c, D.5d
P_g ≪ P_r	Kramers	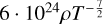$6 \cdot 10^{24} ρ T^{- \frac{7}{2}}$ $6 \cdot 10^{24} \rho T^{-\frac{7}{2}}$	No		1
P_g ≪ P_r	“Ridge”	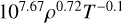$10^{7.67} ρ^{0.72} T^{- 0.1}$ $10^{7.67} \rho^{0.72} T^{-0.1}$	No		D.1a
P_g ≪ P_r	Extreme temperatures	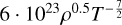$6 \cdot 10^{23} ρ^{0.5} T^{- \frac{7}{2}}$ $6 \cdot 10^{23} \rho^{0.5} T^{-\frac{7}{2}}$	Only close to α ≈ 1 .0		D.6, D.7a, D.7b, D.7c, D.7d

Notes. The assumption refers to the choice of pressure approximation, the designation to the choice of opacity approximation (i.e. a region of the opacity function Rogers & Iglesias 1992) and κ(ρ, T) is the specific form of the prescription. The consistency reports whether there are any contradictions between the computed profiles and assumptions used in the derivation. The power law is a qualitative description of the computed temperature profile that dominates in the outer part of the disc, where the ‘bending’ term (Eq. (5)) is negligible.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.