A great diversity of spectral shapes in the ionising spectra of z ∼ 0.6–1 galaxies revealed by HST/COS and possible detection of nebular LyC emission

Open Access

Table 6.

LyC escape fraction.

Name	λ₀^a	A(LyC)_MW^b	I_mod^c, d	I_obs^c, e	I_esc^c, f	f_esc^g	f_esc^h
	(Å)	(mag)				(%)	(%)
SDSS+COS
J0232+0025ⁱ	880-912	0.159	93.84 ± 1.92	31.29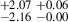 $_{- 2.16}^{+ 2.07}_{- 0.00}^{+ 0.06}$ $^{+2.07}_{-2.16} {\,}^{+0.06}_{-0.00}$	36.27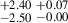 $_{- 2.50}^{+ 2.40}_{- 0.00}^{+ 0.07}$ $^{+2.40}_{-2.50} {\,}^{+0.07}_{-0.00}$	38.66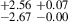 $_{- 2.67}^{+ 2.56}_{- 0.00}^{+ 0.07}$ $^{+2.56}_{-2.67} {\,}^{+0.07}_{-0.00}$	47.65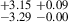 $_{- 3.29}^{+ 3.15}_{- 0.00}^{+ 0.09}$ $^{+3.15}_{-3.29} {\,}^{+0.09}_{-0.00}$
J0232+0025ⁱ	850-870	0.159	93.84 ± 1.92	8.56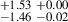 $_{- 1.46}^{+ 1.53}_{- 0.02}^{+ 0.00}$ $^{+1.53}_{-1.46} {\,}^{+0.00}_{-0.02}$	9.85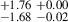 $_{- 1.68}^{+ 1.76}_{- 0.02}^{+ 0.00}$ $^{+1.76}_{-1.68} {\,}^{+0.00}_{-0.02}$	10.55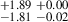 $_{- 1.81}^{+ 1.89}_{- 0.02}^{+ 0.00}$ $^{+1.89}_{-1.81} {\,}^{+0.00}_{-0.02}$	12.94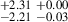 $_{- 2.21}^{+ 2.31}_{- 0.03}^{+ 0.00}$ $^{+2.31}_{-2.21} {\,}^{+0.00}_{-0.03}$
J0256+0122	850-890	0.510	39.53 ± 3.95	< 1.70^j	< 2.76	< 7.01	< 4.46
J0815+2942	850-890	0.214	57.49 ± 3.29	< 1.80^j	< 2.21	< 3.82	< 6.21
J0837+4512	870-890	0.162	60.28 ± 3.70	2.12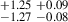 $_{- 1.27}^{+ 1.25}_{- 0.08}^{+ 0.09}$ $^{+1.25}_{-1.27} {\,}^{+0.09}_{-0.08}$	2.42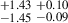 $_{- 1.45}^{+ 1.43}_{- 0.09}^{+ 0.10}$ $^{+1.43}_{-1.45} {\,}^{+0.10}_{-0.09}$	4.03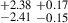 $_{- 2.41}^{+ 2.38}_{- 0.15}^{+ 0.17}$ $^{+2.38}_{-2.41} {\,}^{+0.17}_{-0.15}$	2.52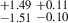 $_{- 1.51}^{+ 1.49}_{- 0.10}^{+ 0.11}$ $^{+1.49}_{-1.51} {\,}^{+0.11}_{-0.10}$
J0901+5111	870-890	0.137	43.73 ± 4.87	< 1.10^j	< 1.20	< 2.70	< 1.60
J0908+4626	850-890	0.103	55.46 ± 4.50	2.57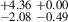 $_{- 2.08}^{+ 4.36}_{- 0.49}^{+ 0.00}$ $^{+4.36}_{-2.08} {\,}^{+0.00}_{-0.49}$	2.77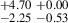 $_{- 2.25}^{+ 4.70}_{- 0.53}^{+ 0.00}$ $^{+4.70}_{-2.25} {\,}^{+0.00}_{-0.53}$	4.94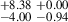 $_{- 4.00}^{+ 8.38}_{- 0.94}^{+ 0.00}$ $^{+8.38}_{-4.00} {\,}^{+0.00}_{-0.94}$	3.56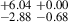 $_{- 2.88}^{+ 6.04}_{- 0.68}^{+ 0.00}$ $^{+6.04}_{-2.88} {\,}^{+0.00}_{-0.68}$
J0955+3935	850-890	0.074	58.22 ± 5.82	1.86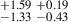 $_{- 1.33}^{+ 1.59}_{- 0.43}^{+ 0.19}$ $^{+1.59}_{-1.33} {\,}^{+0.19}_{-0.43}$	1.97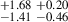 $_{- 1.41}^{+ 1.68}_{- 0.46}^{+ 0.20}$ $^{+1.68}_{-1.41} {\,}^{+0.20}_{-0.46}$	3.39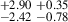 $_{- 2.42}^{+ 2.90}_{- 0.78}^{+ 0.35}$ $^{+2.90}_{-2.42} {\,}^{+0.35}_{-0.78}$	3.17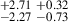 $_{- 2.27}^{+ 2.71}_{- 0.73}^{+ 0.32}$ $^{+2.71}_{-2.27} {\,}^{+0.32}_{-0.73}$
J1021+0436ⁱ	820-912	0.134	119.41 ± 3.41	41.18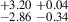 $_{- 2.86}^{+ 3.20}_{- 0.34}^{+ 0.04}$ $^{+3.20}_{-2.86} {\,}^{+0.04}_{-0.34}$	46.56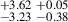 $_{- 3.23}^{+ 3.62}_{- 0.38}^{+ 0.05}$ $^{+3.62}_{-3.23} {\,}^{+0.05}_{-0.38}$	38.98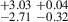 $_{- 2.71}^{+ 3.03}_{- 0.32}^{+ 0.04}$ $^{+3.03}_{-2.71} {\,}^{+0.04}_{-0.32}$	38.49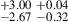 $_{- 2.67}^{+ 3.00}_{- 0.32}^{+ 0.04}$ $^{+3.00}_{-2.67} {\,}^{+0.04}_{-0.32}$
J1021+0436ⁱ	750-800	0.134	119.41 ± 3.41	< 0.14^j	< 0.16	< 0.13	< 0.13
J1252+5237	870-890	0.072	62.98 ± 5.30	4.06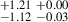 $_{- 1.12}^{+ 1.21}_{- 0.03}^{+ 0.00}$ $^{+1.21}_{-1.12} {\,}^{+0.00}_{-0.03}$	4.36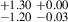 $_{- 1.20}^{+ 1.30}_{- 0.03}^{+ 0.00}$ $^{+1.30}_{-1.20} {\,}^{+0.00}_{-0.03}$	6.93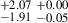 $_{- 1.91}^{+ 2.07}_{- 0.05}^{+ 0.00}$ $^{+2.07}_{-1.91} {\,}^{+0.00}_{-0.05}$	3.47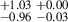 $_{- 0.96}^{+ 1.03}_{- 0.03}^{+ 0.00}$ $^{+1.03}_{-0.96} {\,}^{+0.00}_{-0.03}$
J1358+4611	870-890	0.067	108.99 ± 3.02	2.52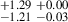 $_{- 1.21}^{+ 1.29}_{- 0.03}^{+ 0.00}$ $^{+1.29}_{-1.21} {\,}^{+0.00}_{-0.03}$	2.72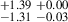 $_{- 1.31}^{+ 1.39}_{- 0.03}^{+ 0.00}$ $^{+1.39}_{-1.31} {\,}^{+0.00}_{-0.03}$	2.52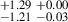 $_{- 1.21}^{+ 1.29}_{- 0.03}^{+ 0.00}$ $^{+1.29}_{-1.21} {\,}^{+0.00}_{-0.03}$	1.81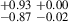 $_{- 0.87}^{+ 0.93}_{- 0.02}^{+ 0.00}$ $^{+0.93}_{-0.87} {\,}^{+0.00}_{-0.02}$
J1450+3913	870-890	0.067	87.29 ± 6.51	< 0.92^j	< 1.02	< 1.12	< 1.02
XShooter+COS
J0232+0025	880-912	0.159	56.01 ± 0.52	31.29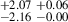 $_{- 2.16}^{+ 2.07}_{- 0.00}^{+ 0.06}$ $^{+2.07}_{-2.16} {\,}^{+0.06}_{-0.00}$	35.98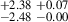 $_{- 2.48}^{+ 2.38}_{- 0.00}^{+ 0.07}$ $^{+2.38}_{-2.48} {\,}^{+0.07}_{-0.00}$	64.40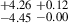 $_{- 4.45}^{+ 4.26}_{- 0.00}^{+ 0.12}$ $^{+4.26}_{-4.45} {\,}^{+0.12}_{-0.00}$	37.51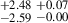 $_{- 2.59}^{+ 2.48}_{- 0.00}^{+ 0.07}$ $^{+2.48}_{-2.59} {\,}^{+0.07}_{-0.00}$
J0232+0025	850-870	0.159	56.01 ± 0.52	8.56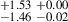 $_{- 1.46}^{+ 1.53}_{- 0.02}^{+ 0.00}$ $^{+1.53}_{-1.46} {\,}^{+0.00}_{-0.02}$	9.85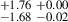 $_{- 1.68}^{+ 1.76}_{- 0.02}^{+ 0.00}$ $^{+1.76}_{-1.68} {\,}^{+0.00}_{-0.02}$	17.62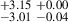 $_{- 3.01}^{+ 3.15}_{- 0.04}^{+ 0.00}$ $^{+3.15}_{-3.01} {\,}^{+0.00}_{-0.04}$	10.25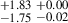 $_{- 1.75}^{+ 1.83}_{- 0.02}^{+ 0.00}$ $^{+1.83}_{-1.75} {\,}^{+0.00}_{-0.02}$

Notes. ^aRest-frame wavelength range in angstrom used to determine the LyC flux. ^bMilky Way extinction at the mean observed wavelengths of the range used to determine the LyC flux. The Cardelli et al. (1989) reddening law with R(V) = 3.1 is adopted here. ^cQuantities expressed in 10⁻¹⁸ erg s⁻¹ cm⁻² Å⁻¹. ^dIntrinsic LyC flux derived from the modelled SED. ^eObserved LyC flux derived from the spectrum with shadow exposure. ^fLyC flux corrected for the Milky Way extinction. ^gf_esc(LyC) = I_esc(total)/I_mod, with I_mod derived from the modelled SED (first method). ^hf_esc(LyC) = I_esc(total)/I_mod, with I_mod derived from Hβ flux (second method). ⁱTwo wavelength ranges considered for the determination of f_esc(LyC). The first corresponds to the LyC bump, and the second to the stellar LyC emission. ^j1σ confidence upper limit.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.