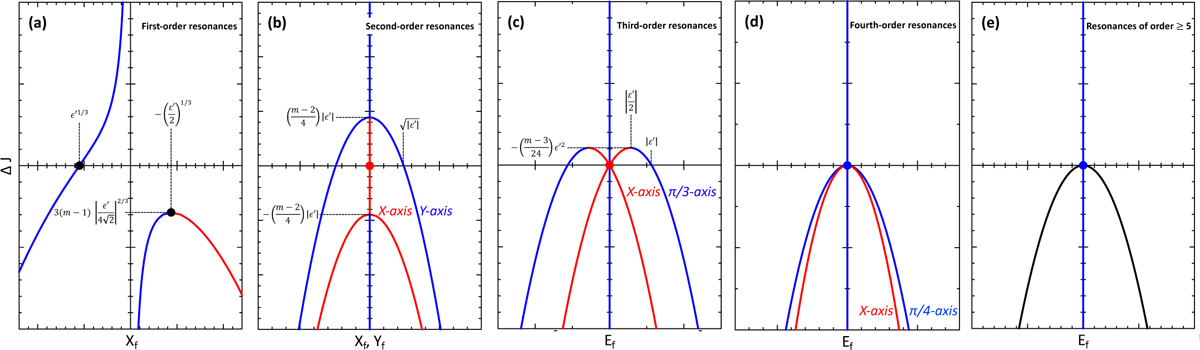
Fixed points given by Eq. (16) as a function of ΔJ for resonances of various orders. They are the solutions of Eqs. (18), (20), (22), (24), and (26). In all the plots, the values of ϵ′ are taken as negative, as is the case for outer resonances. The cubic root, ϵ′^1/3, is then understood as the real root, i.e., ignoring the complex roots. The blue (resp. red) branches corresponding to stable elliptic (resp. unstable hyperbolic) points. Similarly, blue (resp. red) dots at the origin indicate a stable (resp. unstable) point. The units of all the plots are arbitrary. Panel a: first-order resonances. The positions of two particular points are specified: the solution corresponding to ΔJ = 0 and the pitchfork bifurcation point at the lower right. Panel b: second-order resonances. The parabolic branches are the solutions of Eq. (20). The positions of three particular points are specified. Panel c: third-order resonances. The parabolic branches are the solutions of Eq. (22). The positions of three particular points are specified. The origin of the phase portrait (X_f = E_f =0) is stable everywhere, except for the value ΔJ = 0 (red dot), where it is hyperbolic. Panel d: fourth-order resonances. The parabolic branches are the solutions of Eq. (24). The origin of the phase portrait (X_f = E_f =0) is stable everywhere, except for large values of ϵ (see Eq. (14)). Panel e: resonances of orders j ≥ 5. In this case, X_f = E_f (Eq. (26)), so that the stability of the points corresponding to each branch cannot be indicated on the plot; hence, the black color used here. This plot is now indistinguishable from the unperturbed case (ϵ′ = 0).