TOI-7510: A solar-analog system of three transiting giant planets near a Laplace resonance chain

Home

All issues

Volume 704 (December 2025)

A&A, 704 (2025) L16

Full HTML

Open Access

Table D.3.

Inferred system parameters.

Parameter	Units	Prior	Median and 68.3% CI
Star
Stellar mass, M_★	(M_⊙)	N(1.053, 0.068)	1.063 ± 0.065
Stellar radius, R_★	( $R_{⊙}^{N}$ $\mathcal{R}^{\mathrm{N}}_{\odot}$ )	N(1.030, 0.046)	1.035 ± 0.026
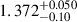Stellar mean density, ρ_★	(g cm⁻³)		$1 . 372_{- 0.10}^{+ 0.050}$ $1.372^{+0.050}_{-0.10}$
Surface gravity, log g	(cgs)		$4 . 439_{- 0.027}^{+ 0.014}$ $4.439^{+0.014}_{-0.027}$
Planets			Planet b	Planet c	Planet d
Semi-major axis, a	(au)		0.1019 ± 0.0020	0.1595 ± 0.0032	0.2672 ± 0.0053
Eccentricity, e			0.0572 ± 0.0033	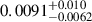$0 . 0091_{- 0.0062}^{+ 0.010}$ $0.0091^{+0.010}_{-0.0062}$	0.040 ± 0.022
Argument of periastron, ω	(°)		95.9 ± 5.6	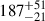$187_{- 21}^{+ 51}$ $187^{+51}_{-21}$	338 ± 37
Inclination, i	(°)	S(0, 180)_b, c, S(0, 90)_d	90.03 ± 0.72	90.11 ± 0.34	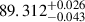$89 . 312_{- 0.043}^{+ 0.026}$ $89.312^{+0.026}_{-0.043}$
Longitude of the ascending node, Ω	(°)	U(90, 270)_b, d	180.0 ± 1.8	180 (fixed at t_ref)	179.63 ± 0.42
Mean anomaly, M₀	(°)		116.2 ± 5.0	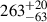$263_{- 63}^{+ 20}$ $263^{+20}_{-63}$	170 ± 39
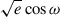$\sqrt{e} cos ω$ $\sqrt{e}\cos{\omega}$		U(−1, 1)	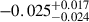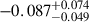$- 0 . 025_{- 0.024}^{+ 0.017}$ $-0.025^{+0.017}_{-0.024}$	$- 0 . 087_{- 0.049}^{+ 0.074}$ $-0.087^{+0.074}_{-0.049}$	0.155 ± 0.081
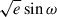$\sqrt{e} sin ω$ $\sqrt{e}\sin{\omega}$		U(−1, 1)	0.2372 ± 0.0052	−0.011 ± 0.040	−0.073 ± 0.098
Mass ratio, M_p/M_★		U(0, 1)	(5.12 ± 0.36)×10⁻⁵	(36.9 ± 2.3)×10⁻⁵	(53.5 ± 4.6)×10⁻⁵
Radius ratio, R_p/R_★		U(0, 1)	0.06480 ± 0.00098	0.09578 ± 0.00092	0.0933 ± 0.0011
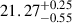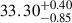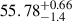Scaled semi-major axis, a/R_★			$21 . 27_{- 0.55}^{+ 0.25}$ $21.27^{+0.25}_{-0.55}$	$33 . 30_{- 0.85}^{+ 0.40}$ $33.30^{+0.40}_{-0.85}$	$55 . 78_{- 1.4}^{+ 0.66}$ $55.78^{+0.66}_{-1.4}$
Impact parameter, b			0.18 ± 0.13	0.14 ± 0.13	0.681 ± 0.026
T₀′-2450000	(BJD_TDB)	U(8386, 10386)	9382.5322 ± 0.0016	9386.4191 ± 0.0011	9377.8713 ± 0.0021
P′	(d)	U(0, 1000)	11.52195 ± 0.00090	22.5617 ± 0.0031	48.9176 ± 0.0047
K′	(m s⁻¹)		4.93 ± 0.36	28.4 ± 1.9	31.8 ± 2.8
Planet mass, M_p	(M_E)		18.1 ± 1.7	131 ± 11	190 ± 20
	(M_J)		0.0571 ± 0.0052	0.412 ± 0.036	0.597 ± 0.064
Planet radius, R_p	(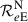 $R_{e E}^{N}$ $\mathcal{R}^{\mathrm{N}}_{e \mathrm{E}}$ )		7.31 ± 0.23	10.81 ± 0.32	10.52 ± 0.32
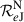	( $R_{e J}^{N}$ $\mathcal{R}^{\mathrm{N}}_{e \rm J}$ )		0.652 ± 0.020	0.964 ± 0.029	0.939 ± 0.029
Planet mean density, ρ_p	(g cm⁻³)		0.255 ± 0.026	0.573 ± 0.062	0.89 ± 0.11
Planet surface gravity, log g_p	(cgs)		2.521 ± 0.039	3.042 ± 0.043	3.224 ± 0.049
Equilibrium temperature, T_eq	(K)		878 ± 13	702 ± 10	542.4 ± 7.8
Mutual inclination, I_b, c	(°)		$1 . 37_{- 0.78}^{+ 1.4}$ $1.37^{+1.4}_{-0.78}$
Mutual inclination, I_c, d	(°)		0.97 ± 0.39
RV
Coralie jitter		U(0, 10)	0.79 ± 0.14
Coralie offset	[m s⁻¹]	U(−10⁵, 10⁵)	13675.5 ± 3.9
Linear ephemerides
Period	(d)		11.5308690	22.5687423	48.8644680
T₀-2450000	(BJD_TDB)		8656.213656	8664.157045	8693.788019

Notes. The table lists: Prior, posterior median, and 68.3% credible interval (CI) for the photodynamical analysis (Sect. C). The Jacobi orbital elements are given for the reference time t_ref = 2 459 386.419785 BJD_TDB. The planetary equilibrium temperature is computed for zero albedo and full day-night heat redistribution. P′ and T₀′ should not be confused with the linear ephemeris, and they were only used to reduce the correlations between jump parameters, replacing the semi-major axis and the mean anomaly at t_ref. The linear ephemerides are derived from the median posterior transit times spanning the years 2019 to 2026. 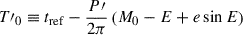$T'_{0} \equiv t_{ref} - \frac{P'}{2 π} (M_{0} - E + e sin E)$ $T\prime_0 \equiv t_{\mathrm{ref}} - \frac{P\prime}{2\pi}\left(M_0-E+e\sin{E}\right)$ with $E = 2 arctan {\sqrt{\frac{1 - e}{1 + e}} tan [\frac{1}{2} (\frac{π}{2} - ω)]}$ $E=2\arctan{\left\{\sqrt{\frac{1-e}{1+e}}\tan{\left[\frac{1}{2}\left(\frac{\pi}{2}-\omega\right)\right]}\right\}}$ , $P' \equiv \sqrt{\frac{4 π^{2} a^{3}}{G M_{★}}}$ $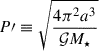P\prime \equiv \sqrt{\frac{4\pi^2a^{3}}{\mathcal{G}M_{\star}}}$ , $K' \equiv \frac{M_{p} sin i}{M_{★}^{2 / 3} \sqrt{1 - e^{2}}} {(\frac{2 π G}{P'})}^{1 / 3}$ $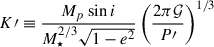K\prime \equiv \frac{M_p \sin{i}}{M_\star^{2/3}\sqrt{1-e^2}}\left(\frac{2 \pi \mathcal{G}}{P\prime}\right)^{1/3}$ . CODATA 2018: 𝒢 = 6.674 30 × 10⁻¹¹ m³ kg⁻¹ s⁻². IAU 2012: au = 149 597 870 700 m. 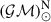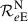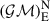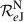IAU 2015: $R_{⊙}^{N}$ $\mathcal{R}^{\mathrm{N}}_{\odot}$ = 6.957 × 10⁸ m, ${(GM)}_{⊙}^{N}$ $(\mathcal{GM})^{\mathrm{N}}_{\odot}$ = 1.327 124 4 ×10²⁰ m³ s⁻², $R_{e E}^{N}$ $\mathcal{R}^{\mathrm{N}}_{e \mathrm{E}}$ = 6.378 1 ×10⁶ m, ${(GM)}_{E}^{N}$ $(\mathcal{GM})^{\mathrm{N}}_{\mathrm{E}}$ = 3.986 004 ×10¹⁴ m³ s⁻², $R_{e J}^{N}$ $\mathcal{R}^{\mathrm{N}}_{e \rm J}$ = 7.149 2 × 10⁷ m, 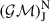${(GM)}_{J}^{N}$ $(\mathcal{GM})^{\mathrm{N}}_{\mathrm{J}}$ = 1.266 865 3 × 10¹⁷ m³ s⁻². 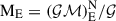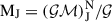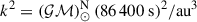$M_{⊙} = {(GM)}_{⊙}^{N} / G$ $M_{\odot} = (\mathcal{GM})^{\mathrm{N}}_{\odot}/\mathcal{G}$ , $M_{E} = {(GM)}_{E}^{N} / G$ $\mathrm{M_E} = (\mathcal{GM})^{\mathrm{N}}_{\mathrm{E}}/\mathcal{G}$ , $M_{J} = {(GM)}_{J}^{N} / G$ $\mathrm{M}_{\mathrm{J}} = (\mathcal{GM})^{\mathrm{N}}_{\mathrm{J}}/\mathcal{G}$ , $k^{2} = {(GM)}_{⊙}^{N} {(86 400 s)}^{2} / {au}^{3}$ $k^2 = (\mathcal{GM})^{\mathrm{N}}_{\odot}\,(86\,400\ \rm{s})^2/\rm{au}^3$ . N(μ, σ): Normal distribution with mean μ and standard deviation σ. U(a, b): A uniform distribution defined between a lower a and upper b limit. S(a, b): A sinusoidal distribution defined between a lower a and upper b limit.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.