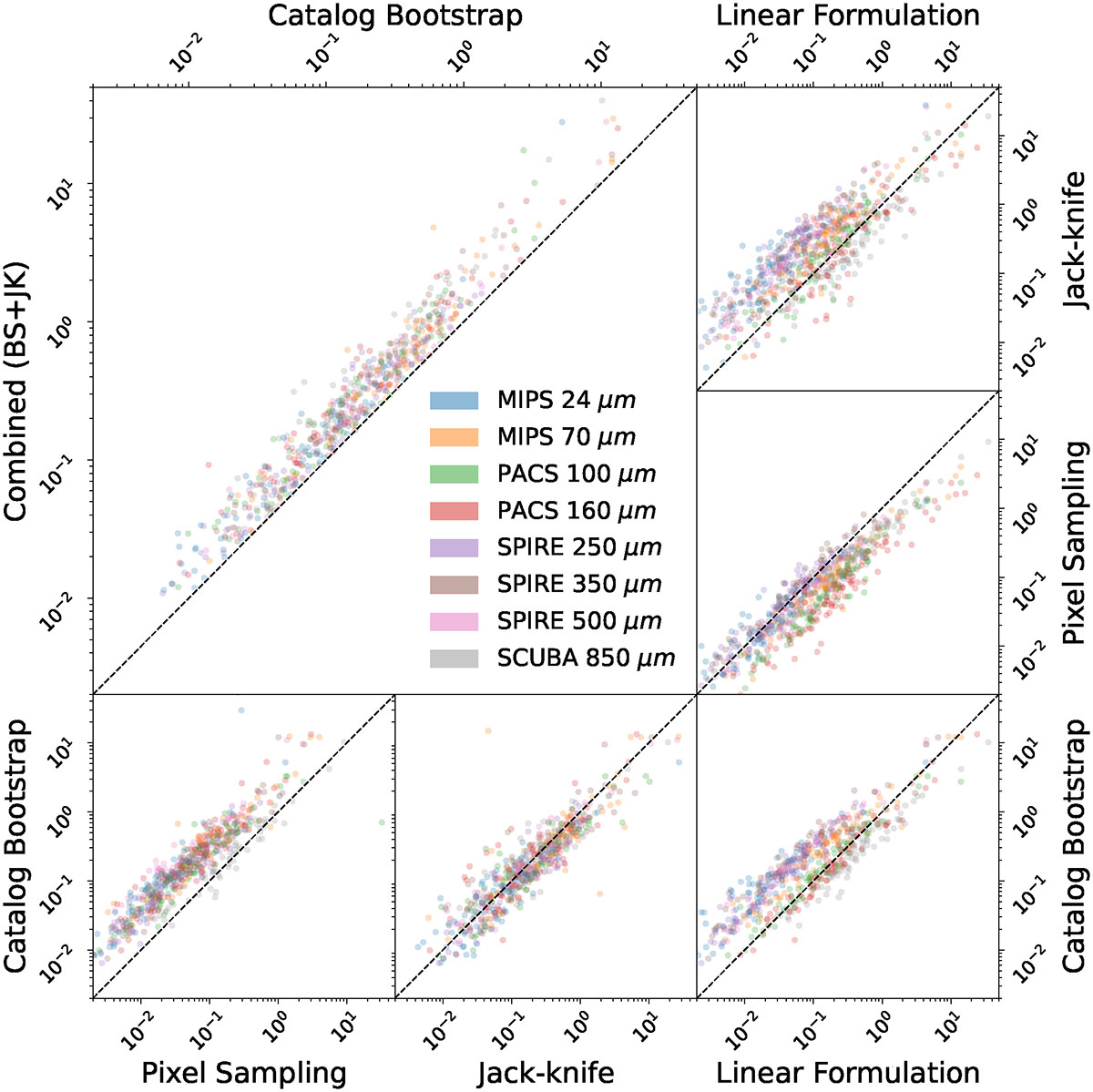
Errors in stacked mean intensities estimated via four methods (see Section 3.2). Fractional errors in the stacked fluxes, obtained as outputs of the LinSimStack are color-coded by band. The statistical lower bound is given by the closed-form error formulation, obtained by writing the stacking problem as a linear regression. Bootstrapping the catalog or the pixels captures the additional systematic errors, as it samples different realizations of pixel noise and emitter variance; empirically, the bootstrapping over the catalog (lower left subplot) typically yields the more conservative error estimates. Jack-knifing (JK) provides an estimate of the cosmic variance (CV) at the scale of the map. We conservatively add in, in quadrature, the JK estimate with the maximum of the other three estimates. This effectively lower-bounds our bootstrapping error estimate by the analytical linear formulation limit. Past analyses (Viero et al. 2022, 2013) have only used catalog bootstrapping as the error estimation method. The main subplot above (top-left) compares our final error estimates with those from catalog bootstrapping alone. Our estimates are more conservative by definition and additionally include a measure of CV.