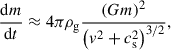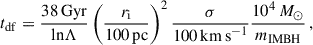| Issue |
A&A
Volume 705, January 2026
|
|
|---|---|---|
| Article Number | L15 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202557595 | |
| Published online | 14 January 2026 | |
Letter to the Editor
Intermediate-mass black hole incubators
Gas accretion onto stellar black hole clusters in galactic central molecular zones
1
Charles University, Faculty of Mathematics and Physics, Astronomical Institute V Holešovičkách 2 CZ-18000 Prague, Czech Republic
2
Helmholtz-Institut für Strahlen- und Kernphysik, University of Bonn Nussallee 14-16 D-53115 Bonn, Germany
3
University of Bonn Regina-Pacis-Weg 3 D-53113 Bonn, Germany
★ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
7
October
2025
Accepted:
15
December
2025
Context. The stellar dynamical evolution of massive star clusters formed during starburst periods leads to the segregation of ≳104 M⊙ stellar-mass black hole sub-clusters in their centres. In gas-rich environments, such as galactic central molecular zones, these black hole clusters are likely to accrete large amounts of the gas from their surroundings, which in turn affects their internal dynamics.
Aims. In this Letter we estimated the corresponding accretion rate onto the black hole cluster and its radiative feedback. We assessed whether such an accretion flow can lead to the collapse of the black hole cluster into an intermediate-mass black hole.
Methods. The estimates were obtained analytically, considering the astrophysical conditions and star formation history reported for the central molecular zone of our Galaxy.
Results. We find that a stellar black hole cluster with mass ≳104 M⊙ located in the twisted ring of molecular clouds with radius ≈100 pc that is observed in the central molecular zone of our Galaxy can accrete about the same mass in gas on a timescale of a few million years. We suggest that this is sufficient for its subsequent collapse into an intermediate-mass black hole. Based on an estimate of the dynamical friction inspiral time, we further argue that the locations of the intermediate-mass black hole candidates recently observed in the central molecular zone are compatible with their formation therein during the last starburst period reported to have occurred ≈1 Gyr ago.
Key words: accretion, accretion disks / stars: black holes / Galaxy: center
© The Authors 2026
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1. Introduction
Black holes were theoretically predicted more than a century ago. Their observational discovery in the Universe, however, had to wait many decades for the technological advances to catch up with theory. The existence of the stellar-mass black holes (≲102 M⊙) representing the remnants of stellar evolution has been gradually proven beyond any reasonable doubt (Webster & Murdin 1972; LIGO Scientific Collaboration and Virgo Collaboration 2016a,b; Sahu et al. 2022). The same holds for the supermassive black holes (SMBHs; ≳105 M⊙; Eckart & Genzel 1996; Ghez et al. 1998; GRAVITY Collaboration 2022; Event Horizon Telescope Collaboration 2019, 2022) that are widely accepted to reside in the centres of major galaxies.
The intermediate-mass black holes (IMBHs) with masses ≈102 − 5 M⊙, however, have been eluding discovery so far. In an intuitive agreement with their masses, the theoretically formulated stellar dynamical formation scenarios for IMBHs typically place them at the centres of massive globular clusters and dwarf galaxies (see Mezcua 2017; Greene et al. 2020, for reviews) or in regions near SMBHs embedded in dense galactic nuclear star clusters (see Rose et al. 2022, and references therein). A notable candidate was most recently reported in the centre of ω Centauri by Häberle et al. (2024).
Nevertheless, quite independently of any formation scenario, five IMBH candidates have also been reported (Maillard et al. 2004; Oka et al. 2016; Tsuboi et al. 2017; Takekawa et al. 2019a,b, 2020) in the central molecular zone (CMZ) of our Galaxy, a region rich in gas (Morris & Serabyn 1996; Battersby et al. 2020, 2025) that extends to about 250 pc in radius from the central SMBH Sgr A★ (GRAVITY Collaboration 2022). Observations of the candidates typically revealed gas (or stellar) motions that are best described by orbits around a massive and very compact source of gravitational potential.
In this Letter we present a new formation scenario for IMBHs in such environments that relies on agents naturally present there. In particular, the driving effect of the IMBH formation in the presented model is the accretion of the abundant gas onto massive stellar black hole clusters assumed to be the remnants of massive star clusters that form during starburst periods in gas-rich regions.
2. Collapse of the black hole cluster flooded by gas to an intermediate-mass black hole
An effective formation mechanism for SMBHs was revealed by Kroupa et al. (2020) that enables them to emerge soon enough after the Big Bang to explain the cosmological observations. In their model, the SMBHs form through a two-phase collapse of a hypermassive cluster of stellar-mass black holes at the centre of the forming galaxies. These stellar-mass black holes are considered to be the remnants of the primordial very massive stars born in the early metal-free Universe at the centres of collapsing pre-galactic gas clouds. In the first phase, the stellar black holes are pushed together by the gas inflowing from the farther parts of the forming galaxy owing to their friction on the gas and due to the deepening of the gravitational potential well caused by the accumulation of the gas within the cluster. Once the cluster becomes compact enough, the second phase of the collapse driven by the emission of gravitational waves starts, thus leading to a swift formation of the SMBH seed through mergers of the stellar black holes.
In the perspective of the formation of IMBHs proposed in this Letter, the inflow of gas into the stellar-mass black hole cluster is realized through the accretion of the surrounding medium onto such a cluster. With enough gas accreted, the black hole cluster starts to shrink, as in the model of Kroupa et al. (2020). The timescale on which the shrinking black hole cluster flooded by gas reaches the relativistic second phase of its collapse, trel, depends on its radius, R, and mass, MBH, and on the mass of the individual black holes, mBH, and the mass of the gas, Mg, within the cluster. For the purpose of the estimates given in this Letter, we assume these quantities are set to representative values R = 0.1 pc, MBH = 104 M⊙, mBH = 10 M⊙, and Mg = 104 M⊙. As we show in the following sections, black hole clusters of such properties are expected to have formed in the CMZ of our Galaxy during its last known starburst period (Nogueras-Lara et al. 2020).
Calculation of the shrinkage timescale for the representative cluster gives trel ≈ 1.9 Myr (see Appendix A for details and a discussion of wider parameter ranges). Hence, such a black hole cluster naturally collapses to an IMBH, which suggests a new formation scenario for IMBHs in the Galactic CMZ.
3. Massive clusters formed during starbursts
The star formation rate and the properties of the emerging star clusters depend on the astrophysical conditions in the subject region, such as the matter density or metallicity. It has been shown (e.g. Weidner et al. 2004) that in starbursting regions where these conditions are favourable, the newly born star clusters can be as massive as 105 − 7 M⊙. For the canonical initial stellar mass function (Kroupa 2001; Kroupa et al. 2026), dN/dm ∝ m−2.3, such clusters contain 2.5 × 102 − 4 stars initially more massive than 20 M⊙ that end their lives as black holes. However, combined theoretical and observational investigations suggest that the initial mass function in massive star clusters is rather top-heavy (Gjergo et al. 2025, Fig. 2 therein). If a top-heavy initial mass function with a power-law index equal to –1 is considered, the number of stars with initial mass higher than 20 M⊙ increases to 103 − 5. For the representative mass of each of the black holes, mBH = 10 M⊙, the corresponding mass of the black hole sub-cluster is thus MBH ≳ 104 M⊙. The radius of such a black hole sub-cluster can be estimated as R ≈ 0.1 pc according to Arca-Sedda (2016).
According to Nogueras-Lara et al. (2020), a starburst period occurred about 1 Gyr ago in the nuclear stellar disc, a dense stellar structure within the Galactic CMZ (Launhardt et al. 2002), possibly due to a close encounter of the Sagittarius dwarf galaxy with the Galactic centre. During this starburst event, stars with the total mass of about 4 × 107 M⊙ were formed within ≈100 Myr. Even though the properties of the resulting star clusters are not known, the above-mentioned empirical expectations of Weidner et al. (2004) as well as observations of various starburst galaxies (e.g. Levy et al. 2024) suggest that these clusters were likely massive enough to form stellar black hole sub-clusters with masses MBH ≳ 104 M⊙.
4. Accretion of gas onto the clusters
Star clusters that formed in vast regions rich in gas (such as the CMZ of our Galaxy) accrete gas for much of their lifetimes (Pflamm-Altenburg & Kroupa 2009). The accretion rate and its impact on the cluster evolution are determined by the astrophysical properties of the cluster momentary surroundings, such as the gas density, the stellar (remnant) content of the cluster, and by the relative motion of the cluster with respect to the gas reservoir. In full, this represents a very complex stellar and hydrodynamical problem that includes a plethora of astrophysical processes. Here, we point out the main relationships, and leave more detailed investigations for future work.
For the description of the accretion, we adopt the Bondi-Hoyle-Lyttleton model (Hoyle & Lyttleton 1939; Bondi 1952) in which the matter accretion rate, dm/dt, onto the central object of mass m can be written as
with ρg being the mass density of the gas in the reservoir far away from the accreting object, cs the speed of sound in the undisturbed gas, v the relative velocity of the object with respect to the gas reservoir, and G the gravitational constant.
Accretion of gas onto a cluster of stars or stellar remnants can be viewed from two perspectives. In the first, the cluster as a whole is considered to be the accreting body with the combined mass of its members. The second approach is to quantify the accretion rates for the individual cluster members independently and sum these together. It has been shown by Kaaz et al. (2019) that the correct description lies somewhere between these two approaches and depends on the internal structure of the cluster. In agreement with the intuitive understanding, denser clusters with more massive members act more as single-body accretors. Since we primarily focus on dense black hole sub-clusters from the cores of their parent star clusters stripped by the Galactic tidal forces, we here adopt the single-body accretor approach.
It is commonly accepted that the gas particle density, ng, within the CMZ of our Galaxy is about 104 cm−3 on average. The actual value of ng, however, strongly depends on the particular location as it reaches up to 107 cm−3 in the densest parts of the molecular clouds, while it falls to 102 cm−3 in regions poorer in gas (Mills et al. 2018, and references therein). The average value of ng implies ρg ≈ 250 M⊙ pc−3, which we take as a representative number for the estimate of the accretion rate (1) onto the black hole cluster.
Newly born star clusters inherit the motion patterns of their parent molecular clouds in the Galactic potential and keep these until the combined effect of subsequent encounters with other massive bodies and possible secular perturbations change them. The velocity dispersion, σcl, of the clusters is thus roughly equal to the velocity dispersion, σm, of the clouds for some period of time, σcl ≈ σm. The length of this period depends on the hostility of the cluster environment. For the CMZ and galactocentric distances of about 100 pc, it is reasonable to assume that the equality holds for at least a few orbital periods, i.e. a few dozen million years (see Appendix C for the dynamical friction inspiral time estimate). During this period of time, the most massive stars evolve into black holes and segregate in the cluster centre (Portegies Zwart et al. 2002). Simultaneously, the Galactic tidal stripping causes a loss of the less massive stars from the cluster outskirts, transforming the cluster into a dark star cluster (Banerjee & Kroupa 2011; Wu et al. 2024; Rostami-Shirazi et al. 2024) that consists of the central black hole sub-cluster orbited by a significantly reduced number of luminous stars with masses lower than a few M⊙. This is convenient as the absence of massive stars with potentially strong stellar winds facilitates the gas accretion onto the black hole cluster. The cluster feedback is driven only by the accretion of some amount of the infallen gas directly onto the individual black holes (see Appendix B).
The molecular clouds in the CMZ of our Galaxy are mostly located in a twisted ring with a radius of about 100 pc. The overall velocity dispersion of the gas, σg, at such galactocentric distances has recently been determined to be σg ≈ 30 km/s (Schultheis et al. 2021, Fig. 14 therein). The molecular clouds in the ring, however, appear to orbit the innermost parts of the Galaxy (including the SMBH Sgr A★) coherently. Their relative motions are thus considerably slower and so σm < σg. The particular value of σm depends on the details of the dynamics of the clouds in the ring. For the purpose of our estimate, we assume σm ≈ 10 km/s.
The temperature of the gas in the clouds is low. This suggests that the accretion of the gas onto the clusters is dominated by their motion through the clouds rather than the thermodynamics of the clouds, v ≫ cs.
For the representative cluster of black holes with mass MBH ≈ 104 M⊙, v ≈ σcl ≈ σm ≈ 10 km/s, and ρg ≈ 250 M⊙ pc−3, the accretion rate (1) equals 5.9 × 103 M⊙ Myr−1. At this rate, the black hole cluster accretes gas of the total mass, Mg, equal to its own mass Mg ≈ MBH ≈ 104 M⊙ in about 2 Myr. This is fast enough for the assumption of low relative velocity discussed above to hold through the whole accretion period.
5. Discussion
In this Letter we have formulated a novel IMBH formation scenario with two dynamically distinct phases. In the first, the cluster of stellar black holes is accreting gas from its surroundings and shrinking due to the gas drag and mass accumulation as a result. Within a few million years, the velocity dispersion of the black holes increases enough for the second phase driven by the emission of gravitational waves to bring the cluster to its final collapse to the IMBH on a timescale orders of magnitude shorter (see Kroupa et al. 2020).
So far, we have assumed that the black hole cluster parameters are set to their representative values (see Section 2). Variation of these values affects not only the resulting mass of the IMBH, mIMBH, but also the efficiency of the individual processes included in its formation.
The accretion rate (1) for the black hole cluster depends quadratically on its total mass, MBH. This indicates that clusters with MBH < 104 M⊙ are likely to accrete sufficient gas within their lifetimes only during encounters with the densest parts of the molecular clouds, which are rare. In contrast, clusters with MBH > 104 M⊙ accrete the gas very efficiently. Furthermore, massive black hole clusters originating from massive star clusters are more compact (Arca-Sedda 2016), and thus denser, which makes them better justified single-body accretors (see Section 4) in terms of the quantitative single-body accretion criterion of Kaaz et al. (2019). We note, however, that this criterion was derived under the assumption of uniform spatial distribution of the cluster members. In real astrophysical clusters, the member spatial density increases towards their centres.
The mass function of the black hole cluster also influences its accretion rate in a way such that a higher abundance of massive black holes facilitates the accretion, while the opposite is true for low-mass black holes (see Appendix B). In addition, larger accretion radii of the more massive black holes improve the conditions for the single-body accretor regime for the whole cluster, similarly to the above-mentioned higher cluster density. For these reasons, top-heavy initial mass functions of the parent star clusters are favourable for the gas accretion onto the black hole clusters formed from them.
The shrinkage of the black hole cluster under the assumptions of the model of Kroupa et al. (2020) is similarly efficient for all reasonable values of the cluster parameters (see Fig. A.2 in Appendix A). Investigating the efficiency of the subsequent relativistic collapse to the IMBH in the conditions of the still ongoing gas accretion is a complex problem that requires dedicated efforts that are beyond the scope of this Letter. However, it has been discussed by Kroupa et al. (2020) that the mass-loss due to the gravitational wave emission can be estimated as ≈5%. The impact of the kicks imparted during black hole mergers on IMBH formation is likely to be less significant for higher-mass clusters, due to their deeper gravitational potential well and stronger accretion gas inflow.
In general, we find that the IMBH formation scenario suggested in this Letter is more feasible for massive black hole clusters (≳104 M⊙) originating from massive star clusters (≳105 M⊙) with a top-heavy initial mass function, which ensures a larger number of high-mass black holes. Such clusters can form during starburst periods.
The overall star formation efficiency for such starburst periods is not known. Even if we assumed, however, that during the starburst in the CMZ of our Galaxy (Nogueras-Lara et al. 2020), much of the gas there had been transformed to stars, the Galactic bar would have likely been able to replenish the gas reservoir for the subsequent accretion onto the black hole clusters within a few dozen million years, given its currently estimated gas transport rate of 0.1–1 M⊙ yr−1 (Morris & Serabyn 1996).
5.1. Observed intermediate-mass black hole candidates
Intermediate-mass black holes are long-lived objects, and it can thus be expected that their orbits in the CMZ evolve on longer timescales due to two-body relaxation and related effects such as the dynamical friction. For an IMBH of the representative mass mIMBH = 104 M⊙ formed in the ≈100 pc ring of molecular clouds, the characteristic time of the inspiral, tdf, owing to the dynamical friction can be estimated as tdf ≈ 3.8 Gyr (see Appendix C).
Such a timescale suggests that IMBHs could have significantly migrated from the orbits on which they formed not only within the age of the Universe, but also since the last major starburst in the Galactic centre about 1 Gyr ago (Nogueras-Lara et al. 2020). This is consistent with the fact that all of the five currently observed IMBH candidates in the CMZ (Maillard et al. 2004; Oka et al. 2016; Tsuboi et al. 2017; Takekawa et al. 2019a,b, 2020) are located well within the ring of molecular clouds, making them compatible with the IMBH formation scenario suggested in this Letter. We caution, however, that in order to place the predictions of this scenario into the proper observational context, a more detailed follow-up modelling of its individual aspects is crucial.
The inspiral due to the dynamical friction can be further complemented by an increase in the eccentricity of the IMBH orbit thanks to its interaction with the population of significantly more massive objects, such as the giant molecular clouds (Perets et al. 2007). In such a way, the IMBHs can draw even closer to the central SMBH Sgr A★. This is of special relevance for one of the IMBH candidates that is found only about 0.14 pc in projection from Sgr A★, within the IRS 13E complex (Maillard et al. 2004; Tsuboi et al. 2017; Peißker et al. 2024).
5.2. Further considerations
On their orbits through the CMZ, the newly formed IMBHs continue to accrete gas from their momentary surroundings at rates similar to those of the stellar black hole clusters derived in Section 4. This accretion can lead to a direct increase in their mass, but also to the formation of accretion discs around them in which new generations of stars can form. Such a star formation channel is considered to account for the presence of the young stars observed in the innermost parsec of our Galaxy on orbits around Sgr A★ (e.g. Levin & Beloborodov 2003). The stellar black holes originating from these new stellar populations can eventually coalesce with the central IMBH in the way described in this Letter, thus causing its possibly significant sequential growth.
A similar recurrent accretion may also occur for initially less massive star clusters with MBH ≈ 102 − 4 M⊙ and may lead to a gradual growth of their black hole sub-clusters. At some point, these may become massive enough to form an IMBH. Such an evolution is possible for the Arches and Quintuplet clusters that are nowadays observed in the Galactic centre and whose masses are estimated to be ≳104 M⊙ (Figer et al. 1999).
6. Conclusions
In this Letter we have investigated the accretion of interstellar medium onto clusters of stellar black holes in order to assess the feasibility of their collapse into intermediate-mass black holes driven by the gas inflow (as described by Kroupa et al. 2020, for the case of supermassive black holes at the centres of forming galaxies). The black hole clusters are thought to represent the remnants of the stellar dynamical evolution of their parent star clusters (dark star clusters) formed in gas-rich regions such as galactic central molecular zones.
Using the Bondi-Hoyle-Lyttleton accretion model, we have estimated the accretion rate for a 104 M⊙ black hole cluster located in the central molecular zone of our Galaxy whose astrophysical properties are best known. Such massive black hole clusters are likely to have emerged during the last known starburst period in the Galactic centre reported to have occurred about ≈1 Gyr ago. We have found that, owing to the high gas densities in the Galactic central molecular zone and the coherent motions of the molecular clouds located in the twisted ring with the radius of ≈100 pc, the black hole cluster accretes gas of the same mass, 104 M⊙, in about 2 Myr or less. Based on the model of Kroupa et al. (2020), this creates favourable conditions for the cluster to directly collapse to an intermediate-mass black hole within additional ≈2 Myr. Even if the ring of molecular clouds is a generally convenient part of the Galactic centre for intermediate-mass black hole formation, a black hole cluster can undergo its collapse at any other location if it encounters a dense enough gas cloud at a low enough relative velocity.
We have further shown that the effect of dynamical friction leads to a migration of the newly formed intermediate-mass black holes towards the Galactic central supermassive black hole Sgr A★ on the timescale of a few billion years. This is compatible with the observed locations of the reported intermediate-mass black hole candidates found within the distance of a few tens of parsecs from Sgr A★. Such a conclusion holds even if their formation at the location of the current ring of molecular clouds during the starburst event ≈1 Gyr ago is assumed.
It is likely that the astrophysical conditions in the central molecular zone of our Galaxy are not exceptional among galaxies of similar type. This suggests that the intermediate-mass black hole formation mechanism described in this Letter is widely applicable.
Since the inherent collapse of a stellar black hole cluster into an intermediate-mass black hole is accompanied by an emission of gravitational waves, a theoretical investigation of their pattern together with an observational campaign to detect them present a direct way to test the hypothesis formulated here. Similarly, a more detailed investigation of the radiative signatures of the stellar black hole cluster collapse in the gaseous medium as well as the preceding accretion process could possibly provide a link to an already observed class of sources of high-energy radiation or establish a new class of such sources.
Acknowledgments
We thank the anonymous referee for their useful comments that helped to improve this manuscript. PK acknowledges support through the DAAD Eastern-European Bonn-Prague exchange programme.
References
- Arca-Sedda, M. 2016, MNRAS, 455, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S., & Kroupa, P. 2011, ApJ, 741, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Battersby, C., Keto, E., Walker, D., et al. 2020, ApJS, 249, 35 [Google Scholar]
- Battersby, C., Walker, D. L., Barnes, A., et al. 2025, ApJ, 984, 156 [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edn. (Princeton and Oxford, USA: Princeton University Press) [Google Scholar]
- Bondi, H. 1952, MNRAS, 112, 195 [Google Scholar]
- De Buizer, J. M., Lim, W., Radomski, J. T., & Karnath, N. 2025, ApJ, 983, 66 [Google Scholar]
- Eckart, A., & Genzel, R. 1996, Nature, 383, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019, ApJ, 875, L1 [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022, ApJ, 930, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Figer, D. F., Kim, S. S., Morris, M., et al. 1999, ApJ, 525, 750 [Google Scholar]
- Ghez, A. M., Klein, B. L., Morris, M., & Becklin, E. E. 1998, ApJ, 509, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Gjergo, E., Zhang, Z., Kroupa, P., et al. 2025, Res. Astron. Astrophys., 26, 025003 [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2022, A&A, 657, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Strader, J., & Ho, L. C. 2020, ARA&A, 58, 257 [Google Scholar]
- Häberle, M., Neumayer, N., Seth, A., et al. 2024, Nature, 631, 285 [CrossRef] [Google Scholar]
- Hoyle, F., & Lyttleton, R. A. 1939, PCPS, 35, 405 [Google Scholar]
- Johnson, J. L., & Upton Sanderbeck, P. R. 2022, ApJ, 934, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaz, N., Antoni, A., & Ramirez-Ruiz, E. 2019, ApJ, 876, 142 [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Subr, L., Jerabkova, T., & Wang, L. 2020, MNRAS, 498, 5652 [Google Scholar]
- Kroupa, P., Gjergo, E., Jerabkova, T., & Yan, Z. 2026, Encyclopedia Astrophys., 2 [Google Scholar]
- Launhardt, R., Zylka, R., & Mezger, P. G. 2002, A&A, 384, 112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levin, Y., & Beloborodov, A. M. 2003, ApJ, 590, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Levy, R. C., Bolatto, A. D., Mayya, D., et al. 2024, ApJ, 973, L55 [NASA ADS] [CrossRef] [Google Scholar]
- LIGO Scientific Collaboration and Virgo Collaboration (Abbott, B. P., et al.) 2016a, PhRvL, 116, 061102 [Google Scholar]
- LIGO Scientific Collaboration and Virgo Collaboration (Abbott, B. P., et al.) 2016b, PhRvL, 116, 241103 [Google Scholar]
- Maillard, J. P., Paumard, T., Stolovy, S. R., & Rigaut, F. 2004, A&A, 423, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mezcua, M. 2017, Int. J. Mod. Phys. D, 26, 1730021 [Google Scholar]
- Mills, E. A. C., Ginsburg, A., Immer, K., et al. 2018, ApJ, 868, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M., & Serabyn, E. 1996, ARA&A, 34, 645 [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Gallego-Calvente, A. T., et al. 2020, NatAs, 4, 377 [Google Scholar]
- Oka, T., Mizuno, R., Miura, K., & Takekawa, S. 2016, ApJ, 816, L7 [Google Scholar]
- Peißker, F., Zajaček, M., Labaj, M., et al. 2024, ApJ, 970, 74 [CrossRef] [Google Scholar]
- Perets, H. B., Hopman, C., & Alexander, T. 2007, ApJ, 656, 709 [CrossRef] [Google Scholar]
- Pflamm-Altenburg, J., & Kroupa, P. 2009, MNRAS, 397, 488 [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., Makino, J., McMillan, S. L. W., & Hut, P. 2002, ApJ, 565, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, S. C., Naoz, S., Sari, R., & Linial, I. 2022, ApJ, 929, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Rostami-Shirazi, A., Haghi, H., Zonoozi, A. H., Farhani, Asl A., & Kroupa, P. 2024, MNRAS, 531, 4166 [Google Scholar]
- Sahu, K. C., Anderson, J., Casertano, S., et al. 2022, ApJ, 933, 83 [Google Scholar]
- Schultheis, M., Fritz, T. K., Nandakumar, G., et al. 2021, A&A, 650, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takekawa, S., Oka, T., Iwata, Y., Tsujimoto, S., & Nomura, M. 2019a, ApJ, 871, L1 [Google Scholar]
- Takekawa, S., Oka, T., Tokuyama, S., et al. 2019b, PASJ, 71S, 21 [Google Scholar]
- Takekawa, S., Oka, T., Iwata, Y., Tsujimoto, S., & Nomura, M. 2020, ApJ, 890, 167 [Google Scholar]
- Tsuboi, M., Kitamura, Y., Tsutsumi, T., et al. 2017, ApJ, 850, L5 [Google Scholar]
- Webster, B. L., & Murdin, P. 1972, Nature, 235, 37 [Google Scholar]
- Weidner, C., Kroupa, P., & Larsen, S. S. 2004, MNRAS, 350, 1503 [CrossRef] [Google Scholar]
- Wu, W., Kroupa, P., & Pflamm-Altenburg, J. 2024, MNRAS, 530, 5155 [Google Scholar]
Appendix A: Black hole cluster shrinkage time
In this Letter we based our estimates on the stellar-mass black hole cluster with the following representative properties: MBH ≈ 104 M⊙, R = 0.1 pc, mBH = 10 M⊙, and Mg = ηgMBH = 104 M⊙, where ηg denotes the ratio of the masses of the gas Mg and the black hole cluster MBH. For such a setting, a numerical integration of Eq. (30) from Kroupa et al. (2020) that governs the cluster shrinkage leads to trel ≈ 1.9 Myr (see Fig. A.1) if dMg/dt = 0 and dmBH/dt = 0 is assumed for simplicity. Resulting values of trel for a wider set of initial settings are displayed in Fig. A.2.
 |
Fig. A.1. Temporal evolution of the black hole cluster radius, R, from its representative initial value R0 = 0.1 pc. The cluster consists of N = 1000 equal mass black holes with mBH = 10 M⊙. The total mass of the gas, Mg, within the cluster is set to Mg = ηgMBH = ηgNmBH = 104 M⊙, i.e. ηg = 1. The cluster reaches the relativistic phase of its collapse at time trel ≈ 1.9 Myr. |
 |
Fig. A.2. Time, trel, necessary for the cluster to reach the relativistic phase of its collapse for various values of its total mass, MBH (assumed to be constant and formally denoted by its ‘initial’ value, MBH, 0, for a more direct comparison with Fig. 8 in Kroupa et al. 2020), and initial radius, R0. The mass of the individual stellar black holes, mBH, and the ratio ηg = Mg/MBH, where Mg is the mass of the gas within the cluster, are given at the top of each panel. Values of the initial radius R0 cover the interval (0.05,0.5) pc. |
Appendix B: Black hole cluster feedback
A fraction of the accreted gas within the cluster inevitably accretes directly onto the individual black holes, which leads to the generation of high-energy radiation. The accretion rate, dmBH/dt, for each of the black holes is determined by the gas mass density, ρgcl, within the cluster and the velocity dispersion, σBH, of the black holes within the cluster rather than the motion of the cluster as a whole or the properties of the embedding environment.
The density of the gas within the black hole cluster, ρgcl, increases owing to the ongoing accretion. If we assume that the total gas mass equals the cluster mass, Mg ≈ MBH ≈ 104 M⊙, and that the characteristic radius, R, of the cluster is about 0.1 pc, we obtain ρgcl ≈ 2.4 × 106 M⊙ pc−3, which corresponds to a gas particle density, ngcl, within the cluster of ngcl ≈ 108 cm−3.
The velocity dispersion of the black holes, σBH, can be estimated by the circular velocity at the characteristic radius R ≈ 0.1 pc and so 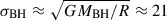 km/s. Hence, the accretion rate (1) for each of the black holes with mass mBH = 10 M⊙ roughly gives dmBH/dt ≈ 5.8 M⊙ Myr−1.
km/s. Hence, the accretion rate (1) for each of the black holes with mass mBH = 10 M⊙ roughly gives dmBH/dt ≈ 5.8 M⊙ Myr−1.
This is about a factor of 30 higher than the Eddington accretion rate, (dmBH/dt)Edd, for a 10 M⊙ black hole in pure hydrogen gas under the assumption that the radiation generation efficiency, ϵ, is set to the typically considered ϵ = 0.1. It was shown by Johnson & Upton Sanderbeck (2022) that for super-Eddington accretion rates that fulfil the condition dmBH/dt ≳ 2(dmBH/dt)Edd/ϵ ≈ 20(dmBH/dt)Edd, the generated radiation is trapped in the infalling gas, allowing the accretion to proceed unhindered until the gas reservoir is emptied.
The transition into the regime of super-Eddington accretion with trapped radiation is more likely for high-mass black holes, due to the fact that the Eddington accretion limit depends only linearly on the black hole mass, while the accretion rate (1) depends quadratically. Low-mass black holes, on the other hand, are less prone to such a transition. Which of these two black hole sub-sets in the cluster has a dominant impact on the gas accretion flow into the cluster depends on the particular shape of its mass function and on the details of the accretion process itself. In general, however, the super-Eddington accretion onto the individual black holes in the cluster with trapped radiation is established once the gas density within the cluster, ρgcl, is sufficiently increased. Before this occurs, the cluster may undergo phases of lower and higher accretion, depending on the pressure of the radiation generated by the the momentary accretion flows onto the black holes.
A significantly enhanced accretion takes place in the densest clumps of the giant molecular clouds where the gas particle density ng ≈ 106 − 7 cm−3. In such clumps, the cluster with parameters set to their representative values (see Section 2) accretes Mg ≈ MBH ≈ 104 M⊙ as fast as in 2 × 103 − 4 yr according to Eq. (1). With such an accretion rate, the criterion of Johnson & Upton Sanderbeck (2022) for the transition into the regime with trapped radiation is immediately fulfilled regardless of the black hole mass. Given the assumed v ≈ 10 km/s, the cluster covers a distance of about 0.02–0.2 pc within the cloud over the above period of time, which corresponds to the size of individual molecular cores (De Buizer et al. 2025, and references therein).
Appendix C: Dynamical friction time estimate for the intermediate-mass black holes
The characteristic time of inspiral owing to the dynamical friction, tdf, for an IMBH with mass mIMBH located initially on a circular orbit around Sgr A★ with radius ri can be estimated as (Binney & Tremaine 2008, Eq. 8.12 therein)
where σ is the velocity dispersion of the stars and ln Λ stands for the Coulomb logarithm that can be estimated by ln Λ ≈ 10 (Binney & Tremaine 2008, Eq. 8.1b therein) for the reference values from equation (C.1).
The typical velocity dispersion of the stars in the surroundings of the IMBH during its inspiral towards the centre of the Galaxy is higher than within the ring (≈100 pc in radius) of molecular clouds where it was formed, σ ≈ 100 km/s (Schultheis et al. 2021, Fig. 14 therein). Hence, for an IMBH with the representative mass mIMBH = 104 M⊙ initially on an orbit with radius ri ≈ 100 pc, the inspiral time (C.1) gives tdf ≈ 3.8 Gyr.
All Figures
 |
Fig. A.1. Temporal evolution of the black hole cluster radius, R, from its representative initial value R0 = 0.1 pc. The cluster consists of N = 1000 equal mass black holes with mBH = 10 M⊙. The total mass of the gas, Mg, within the cluster is set to Mg = ηgMBH = ηgNmBH = 104 M⊙, i.e. ηg = 1. The cluster reaches the relativistic phase of its collapse at time trel ≈ 1.9 Myr. |
| In the text | |
 |
Fig. A.2. Time, trel, necessary for the cluster to reach the relativistic phase of its collapse for various values of its total mass, MBH (assumed to be constant and formally denoted by its ‘initial’ value, MBH, 0, for a more direct comparison with Fig. 8 in Kroupa et al. 2020), and initial radius, R0. The mass of the individual stellar black holes, mBH, and the ratio ηg = Mg/MBH, where Mg is the mass of the gas within the cluster, are given at the top of each panel. Values of the initial radius R0 cover the interval (0.05,0.5) pc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.