A distance measurement for blazar TXS 0506+056 using its radio variability and very long baseline interferometry images

Open Access

Table A.1.

Intensities of elliptic cylindrical symmetric morphologies.

Morphology	Intensity I(p)
Disk	I₀H(1 − p)
Ellipsoid	$I_{0} \sqrt{1 - p^{2}} H (1 - p)$ $I_{0}\sqrt{1-p^{2}}H(1-p)$
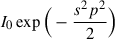Gaussian	$I_{0} exp (- \frac{s^{2} p^{2}}{2})$ $I_{0}\exp{\Big(-\frac{s^{2}p^{2}}{2}\Big)}$

Notes. H(x) is the Heaviside function, I₀ is the center intensity where p = 0, p is the normalized coordinate defined as Eq. (A.1), and s is the factor defining the Gaussian morphology as θ_R = sσ_I in Eq. (A.1), where σ_I is the standard deviation of the Gaussian intensity distribution.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.