Hillas meets Eddington: The case for blazars as ultra-high-energy neutrino sources

Open Access

Table 1.

Best-fit parametersand core assumptions of the extended jet model.

	Source		TXS 0506+056		PKS 0605-085	3HSP J1528+2004
	Associated neutrino event		IceCube-170922A		KM3-230213A	Abbasi et al. (2022b)
			Steady state	2017 flare
Properties	z		0.34		0.87	0.52
	M_BH/(10⁸ M_⊙)		6.31		7.41	2.51
	L_Edd/10⁴⁶ erg s⁻¹		7.95		9.34	3.16
	L_disc/10⁴⁴ erg s⁻¹		3.55		199.53	3.74
	log₁₀(ν_peak^syn/Hz)		14.3 ± 0.4		12.7 ± 0.2	16.9 ± 0.5

Model parameters	Energetics	L_j/L_Edd	0.45		0.55	0.90

	B-field	α_B	1.06		1.04	1.17

	Acceleration	η_max	0.29		0.08	0.33
		r_η, max/r_BLR	4.20		1.70	2.80
		α_η	0.7		1.6	1.5

	Particle density	α_n	1.95		1.90	1.89
		ξ_H	0.70		0.08	0.94
		f_NT	1.3 × 10⁻⁷	8.0 × 10⁻⁶	4.0 × 10⁻⁶	1.8 × 10⁻⁶
		f_e	13.0		12.5	1.0

	Geometry	f_θ	0.22		0.25	0.20
		θ_obs (°)	0.6		0.6	1.0
		r_flare / r_BLR		2.60

		χ_r²		3.51	2.29	6.36	2.81

Assumptions	The jet parameters vary only with distance r to the black hole.
	The jet has sub-Eddington power: L_j = L_B(r)+L_k(r) = const < L_Edd.
	The jet is magnetically launched at r_base = 3 r_S: L_B(3r_S) = L_j.
	The B-field strength decreases along the jet: B′(r) = B(10¹⁷ cm) r^−α_B, α_B ≳ 1.
	The jet is collimated, with opening radius R_j(r) = rtan[f_theta/Γ_j(r)], f_θ < 1.
	The external medium follows a power-law density profile: n(r)∝r^−α_n.
	The density profile n(r) is normalized to the hydrogen column density, N_H = 10²² ξ_H cm⁻².
	The jet picks up a constant fraction ξ_H of the medium particles: 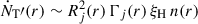${\dot{N}}_{T}' (r) \sim R_{j}^{2} (r) Γ_{j} (r) ξ_{H} n (r)$ $Mathematical equation: $ \dot{N}_{\text{T}}\prime(r)\sim R_j^2(r) \,\Gamma_j(r) \,\xi_{\mathrm{H}} \, n(r) $$ .
	A fraction f_NT ∼ 10⁻⁷-10⁻⁵ of thermal particles are accelerated to a nonthermal spectrum: 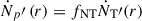${\dot{N}}_{p}' (r) = f_{NT} {\dot{N}}_{T}' (r)$ $Mathematical equation: $ \dot{N}_{p}\prime\,(r) = f_{\mathrm{NT}} \dot{N}_{\mathrm{T}}\prime(r) $$ .
	Pairs may contribute additional nonthermal electrons: 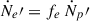${\dot{N}}_{e}' = f_{e} {\dot{N}}_{p}'$ $Mathematical equation: $ \dot{N}_e\prime = f_e\, \dot{N}_p\prime $$ , with f_e ≳ 1, assumed constant for simplicity.
	Nonthermal particles follow a power-law spectrum with index p_e, p = 1.8 (before cooling).
	The maximum particle energies γ_e, p^′max(r) are determined by the acceleration efficiency (Eq. (10)) following Eqs. (12) and (14).
	The minimum particle energies are fixed to γ_e^′min(r) = γ_p^′min(r) = 100. This choice affects only the best-fit value of f_NT.
	The diffusion coefficient scales as D_E′∝E′^δ. Jointly fitting optical, γ-ray, and neutrino data requires δ ≈ 0.3.
	The BLR and dusty torus radii scale with the disk luminosity (Ghisellini & Tavecchio 2009), as indicated in Figs. 2 and C.2.
	The covering factors of the BLR and dusty torus are fixed to 0.1 and 0.3, respectively.

Notes. The best-fit reduced chi-squared value (χ_r²) is calculated in logarithmic space, for 11 model parameters, and binning the data following the prescription described in Appendix C. The core assumptions of the model listed in the lower panel are detailed in Section 2 and further in Appendix C. The jet properties that emerge from these best-fit parameters are plotted in Figs. 2c–g.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.