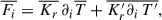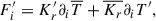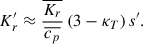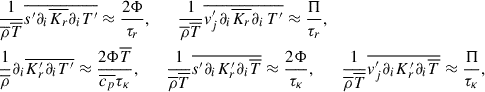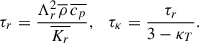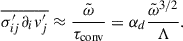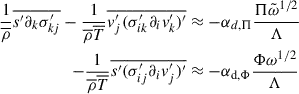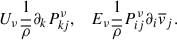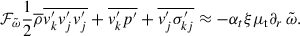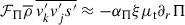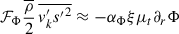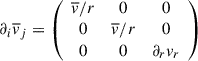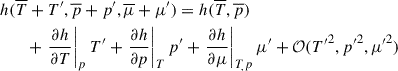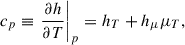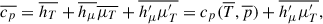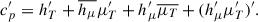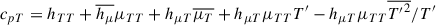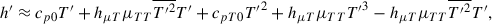| Issue |
A&A
Volume 706, February 2026
|
|
|---|---|---|
| Article Number | A267 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202557008 | |
| Published online | 17 February 2026 | |
Three-equation turbulent convection models in classical variables
1
ELTE Eötvös Loránd University, Gothard Astrophysical Observatory, Szombathely Szent Imre h. u. 112. H-9700, Hungary
2
HUN-REN Research Centre for Astronomy and Earth Sciences, Konkoly Observatory, MTA Centre of Excellence Konkoly Thege Miklós út 15-17. H-1121 Budapest, Hungary
3
Eötvös Loránd University, Institute of Physics and Astronomy Pázmány Péter sétány 1/a H-1117 Budapest, Hungary
4
MTA–HUN-REN CSFK Lendület “Momentum” Stellar Pulsation Research Group Konkoly Thege Miklós út 15-17. H-1121 Budapest, Hungary
★ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
27
August
2025
Accepted:
17
December
2025
Context. Turbulent convection models in nonlinear radial stellar pulsation models rely on an extra equation for turbulent kinetic energy and fail to adequately explain mode-selection problems. Since multidimensional calculations are computationally expensive, it is reasonable to search for generalizations of physically grounded 1D models that approximate multidimensional results with sufficient accuracy, at least in a given parameter range. A natural way of progressing from one-equation models is to use additional nonlocal equations. While these types of models also exist in the literature, they have not been adopted for this type of object.
Aims. We aim to adapt the three-equation turbulent convection model from Kuhfuss to radial stellar pulsation modeling.
Methods. We use a Reynolds-stress one-point closure approach to derive our extensions alongside the model, while using additional models from the literature to close the anisotropy and dissipation terms.
Results. We provide five extensions to the original model. These include an enhanced dissipation correction to the mixing length, a local anisotropy model replacing eddy viscosity, a second-order correction for turbulent ion transport in the atmosphere (alongside opacity effects), and turbulent damping of entropy fluctuations and convective flux.
Key words: convection / hydrodynamics / stars: oscillations
© The Authors 2026
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1. Introduction
Modeling turbulent convection inside stellar cores and envelopes is one of the most important problems in astrophysics. While most studies have focused on phenomenological improvements to the mixing-length theory of Böhm-Vitense (1958) (Kupka & Muthsam 2017), in the case of radial stellar pulsations, time-dependent convection models were necessary (Houdek & Dupret 2015) to describe the significant effects of the narrow convective zones in the envelope of these stars. In these objects, envelope convection is confined to partial ionization zones, which also drive radial pulsations via the κ–γ mechanism. Despite the envelope being mostly radiative, these zones provide major damping for the pulsations.
The most straightforward way of modeling stellar convection is to use 3D numerical hydrocodes. Geroux & Deupree (2011, 2013) developed the multidimensional stellar pulsation code SPHERLS, which was the first to successfully model RR Lyrae stars at maximum amplitudes in 2D (Geroux & Deupree 2013, 2014) and 3D (Geroux & Deupree 2015), although this was achieved using relatively simple numerical methods1. Mundprecht et al. (2013) extended the ANTARES (Muthsam et al. 2010) code to model radial stellar pulsations; they compared the 2D structure to 1D treatments for a Cepheid model (Mundprecht et al. 2015). Vasilyev et al.; Vasilyev et al. (2017; 2018, and references therein) used the COBOLD5 software to model a 2D Cepheid variable and then used it as input for spectral synthesis models. Recently, Stuck et al. (2025) performed a 2D model analysis of the convective region in Cepheid models using the MUSIC code, while Kovács et al. (2025) performed a similar study of RR Lyrae stars using the SPHERLS code. However, both studies investigated these stars in the static limit.
All of the aforementioned studies either focus on a special case or calculate only a few stellar models due to the extreme computational cost of these simulations. Multidimensional simulations of these stars remain challenging, because adaptive grids are required to keep the partial ionization regions (which drive the pulsation) resolved as the star undergoes rapid expansion and contraction. Meanwhile, to reach maximum amplitudes, one must simulate several (thousands) pulsation cycles. This makes improving 1D convection theories an important task (Kupka & Muthsam 2017; Kovács et al. 2023), as these models can be used in large model surveys (e.g., Smolec 2016) and also serve as inputs for multidimensional simulations.
Traditionally, asteroseismology has been studied primarily using linear approximations (Aerts et al. 2010), which have also provided important information on radial pulsators (Cox 1980). While linear theory can provide accurate pulsation frequencies, pulsation amplitudes enter the equations only as a normalization factor. Linear pulsation analysis can be performed in the adiabatic approximation, in which case the theory provides only frequencies. Linear nonadiabatic calculations also provide information about the growth rates of pulsation modes (i.e., whether a mode is pulsationally unstable) and result in somewhat different frequencies. Meanwhile, one can only approximately describe coupling between modes through amplitude equations. Nonlinear calculations, on the other hand, include every amplitude-dependent effect present in the system (and more accurate coupling with convection). This modifies the linear frequencies and provides additional results comparable to observations, such as light curves, amplitudes, and the actual nonlinearly selected pulsational modes. This is particularly important, because we often observe monomode pulsators where multiple modes are linearly excited. Therefore, mode selection studies investigate the nonlinear behavior of pulsation modes to determine which pulsation mode is excited, which survives if multiple modes are present, or whether they can coexist in double-mode pulsation. This, along with other nonlinear phenomena, has been central to radial pulsation modeling over the past two decades (see, e.g., Kolláth et al. 2002; Szabó et al. 2004; Smolec 2016). Nevertheless, both linear and nonlinear studies have shown that including turbulent convection is crucial for describing radial stellar pulsations (Baker 1987).
Building on the pioneering work of Gough (1965), Unno (1967), and Castor (1968), the nonlocal models2 of Stellingwerf (1982a), Kuhfuss (1986), and Gehmeyr & Winkler (1992) are used in current state-of-the-art nonlinear radial stellar pulsation hydrocodes developed in the 1990s and early 2000s (Bono & Stellingwerf 1994; Kolláth et al. 2002; Smolec & Moskalik 2008a; Paxton et al. 2019). For a detailed summary, see Kovács et al. (2023).
Meanwhile, these models have their own limitations: they have many free parameters; nonlinear phenomena such as mode selection and double-mode pulsations are model-dependent (Szabó et al. 2004; Smolec & Moskalik 2008b; Kovács et al. 2023, 2024); light and radial velocity curves show discrepancies with observations (Marconi 2017; Kovács et al. 2023) and the models produce unphysical stratification in the stellar envelope (Canuto & Dubovikov 1998; Kupka et al. 2022; Kovács et al. 2023).
Many of these problems stem from the so-called downgradient approximation of the convective flux and the resulting nonphysical stratification of turbulent kinetic energy (TKE) (Canuto & Dubovikov 1998; Kupka et al. 2022; Kovács et al. 2023). In the downgradient approximation, the convective flux is considered proportional to the super-adiabatic gradient. There is a further assumption that in stable regions (i.e., where the gradient is negative), the gradient is taken as zero (Stellingwerf 1982a). This approximation also affects the TKE profile, which in turn influences mode selection through the turbulent pressure and viscous stress terms. This effect determined whether simulations reproduce or fail to exhibit double-mode pulsation (Smolec & Moskalik 2008a,b; Kovács et al. 2023). Neglecting negative convective flux leads to insufficient turbulent damping, causing overshooting into the deep stellar interiors. This provides additional damping that can stabilize double-mode pulsations (Smolec & Moskalik 2008b; Kovács et al. 2023). Meanwhile, maintaining a negative flux prevents TKE leakage to deeper regions but leads to unstable double-mode pulsations, where one mode is eventually damped despite a “physically more correct” picture. This occurs because negative flux terms cause strong turbulent damping in the overshooting region, where convective elements behave as if colliding with a rigid wall (Kupka et al. 2022; Kovács et al. 2023). Both pictures are nonphysical, illustrating the limitations of one-equation models. While the aforementioned problems depend primarily on the coupling between convection and radial pulsation, other observed features – such as the Blazhko effect (Blažko 1907) and additional modes (the so-called fx modes; see, e.g., Szabó et al. 2015) – can be explained by resonances with non-radial modes (see, e.g., Van Hoolst et al. 1998; Dziembowski & Mizerski 2004; Dziembowski 2016). Although such resonances require multidimensional treatment, improving the 1D description cannot be ruled out as a means to explain these features.
The analysis of multidimensional models by Mundprecht et al. (2013, 2015) and Kovács et al. (2025) reveals that a natural progression is to incorporate nonlocal time-dependent differential equations describing the convective flux and temperature fluctuations. Developed by Xiong (1980, 2021), Xiong et al. (1998b) and Kuhfuß (1987), these so-called three-equation models were incorporated into stellar evolution codes (see Flaskamp 2002, 2003; Weiss & Schlattl 2008) and used in linear non-radial pulsation theory (Xiong et al. 1998a, 2000, 2016, 2018, and references therein). However, further adjustments to these models are necessary, since convection in classical pulsators substantially differ from standard astrophysical convection:
-
Highly dynamical regime. The convection timescale is comparable with the cycle of the pulsation, making a time-dependent description important, while the large structural changes during pulsation create more complex coupling between pulsation and convection.
-
Anisotropy effects. Convective eddies convert kinetic energy into TKE through shear. This eddy viscosity is crucial in damping convection (Gonczi 1981; Stellingwerf 1982a), and it arises from the anisotropy of convective motions (Gehmeyr & Winkler 1992). Consequently, modeling anisotropies is also important (Mundprecht et al. 2015).
-
Sharp ionization regions, especially in the case of RR Lyraes. Most of these stars exhibit a sharp HI ionization region. Small perturbations in ionization levels have a drastic effect on specific heat and opacity, which must be taken into account (Kovács et al. 2025).
We introduce an extended version of the Kuhfuss three-equation model in this paper (Kuhfuß 1987)3, which provides a basis for improving 1D nonlinear stellar pulsation codes.
2. Extended Kuhfuss three-equation model
We provide the basic equations of the extended Kuhfuß (1987) model below, while a derivation consistent with our notation is given in Appendix A. The equations are the following:
Here, dt = ∂t + v∂r denotes the Stokes derivative, and ∂r is the spatial derivative relative to the r, radius coordinate4. The thermodynamic quantities follow standard notation: p is pressure, ρ is the density, T is the temperature, e is specific internal energy, and cp is specific heat at constant pressure. The variable v describes the velocity of a given spherical shell, while g = Gm/r2 denotes the gravitational acceleration, where m is the mass inside a sphere of radius r within the star. Fr is the radiative energy flux in the diffusion approximation:
where κ(T, ρ) is the Rosseland-mean opacity and σB is the Stefan-Boltzman constant. The remaining quantities relate to turbulent convection and its coupling to the dynamics. The specific TKE is denoted by 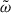 , the entropy fluctuation is denoted by Φ, and Π denotes the velocity entropy covariance.
, the entropy fluctuation is denoted by Φ, and Π denotes the velocity entropy covariance.
The convective flux, Fc, is represented by a second-order description:
where cpT = (∂lncp/∂lnT)p and αc is a dimensionless factor of order of unity.
The term 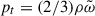 denotes turbulent pressure, while terms Eν and Uν denote the turbulent viscous energy and momentum transfer rates (Wuchterl & Feuchtinger 1998):
denotes turbulent pressure, while terms Eν and Uν denote the turbulent viscous energy and momentum transfer rates (Wuchterl & Feuchtinger 1998):
Here, ξ denotes the flow anisotropy (see Appendix A). In Eqs. (3)–(6), we refer to buoyancy-driven terms as source terms denoted by S, while shear-related terms are referred to as production terms (Pope 2000) denoted by 𝒫:
where ∂rs is the specific entropy.
The dissipation terms are modeled locally through the dissipation and radiative timescales. First, the dissipation of TKE (ε) is modeled using the convective timescale. This is constructed from a characteristic length (i.e., mixing length) and characteristic velocity (approximated as 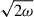 ). This yields
). This yields 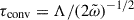 ,
, 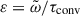 , and
, and
where the factor 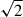 is incorporated into the dimensionless constant αd of order unity. The dissipation of the entropy fluctuations (ϵΦ) and velocity-entropy covariance (ϵΠ) has two components: a radiative (
is incorporated into the dimensionless constant αd of order unity. The dissipation of the entropy fluctuations (ϵΦ) and velocity-entropy covariance (ϵΠ) has two components: a radiative (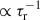 ) and a viscous part (∝Λ−1):
) and a viscous part (∝Λ−1):
The radiation timescale can be determined from the Péclet number, since 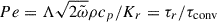 . Thus,
. Thus,
where αr = 3/16, is a dimensionless constant5.
The final timescale introduced is the opacity-induced dissipation-production timescale, which provides additional dissipation or production of entropy fluctuations. It is defined by τκ = τr/(3 − κT), where κT = (∂lnκ/∂lnT)p.
Finally, the third-order moments (TOMs) describe the turbulent flux of turbulent quantities and are approximated by the down-gradient approximation6 (Castor 1968; Xiong 1980):
where 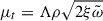 is the turbulent viscosity.
is the turbulent viscosity.
3. Modifications
3.1. Enhanced dissipation
The local model of viscous dissipation, ε, is known to be insufficient in the dynamically stable regions (Canuto 1993) when using the standard prescription for the mixing length Λ = Λ0 = αΛHp, where Hp = pr2/(ρGm) is the pressure scale height and αΛ is a dimensionless parameter. This problem arises because gravity waves provide extra damping in the stable regions. Kupka et al. (2022) derived a correction to the mixing length, which we adopt here using the formula introduced of Ahlborn et al. (2022):
where
is the ratio of the dissipative to buoyancy timescales in the stable regions, and αβ and ατ are dimensionless parameters. Here, ∇ − ∇ad = HpT−1∂rs is the dimensionless super-adiabatic gradient, with ∇ = (∂lnT/∂lnp) and ∇ad = (∂lnT/∂lnp)s.
3.2. Local anisotropy equation
We follow the traditional splitting of the Reynolds-tensor into isotropic turbulent pressure and anisotropic turbulent viscous stress tensor. The latter is usually modeled using the eddy-viscosity hypothesis (Pope 2000), which yields the anisotropy parameter
Kuhfuß (1987) applied the above formulation only to the turbulent viscous stress tensor, setting ξ = 1/3 elsewhere7. Recently Kovács et al. (2023, 2024) showed that the αν parameter correlates with αd and significantly affects mode selection (Kovács et al. 2024) and nonlinear behavior (Kolláth et al. 2011). Therefore, instead of Eq. (18), we propose a local prescription derived from the nonlocal model of Canuto (1998) using the method given in Kupka et al. (2022), but retaining the shear terms (see appendix B):
equivalent to Kupka et al.’s (2022) solution in the static case. Here, 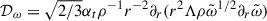 describes diffusion of ξ through isotropic TKE flux,
describes diffusion of ξ through isotropic TKE flux, ![$ \tau_\xi^{-1}=(2/3)\left[\alpha_1(v/r)+(2\alpha_1-1)\partial_r v\right] - 5\varepsilon/(2\tilde{\omega}) $](/articles/aa/full_html/2026/02/aa57008-25/aa57008-25-eq31.gif) , while α1 = 1.08 and β5 = 0.7 are constant parameters given by Canuto et al. (1994).
, while α1 = 1.08 and β5 = 0.7 are constant parameters given by Canuto et al. (1994).
3.3. Ionization energy transport
The second term in Eq. (7) provides a second-order correction representing the ionization energy flux carried by ions transported via convection. In fact, this reflects a change in chemical potential, even though ionization effects are usually absorbed into cp and κ (Kippenhahn & Weigert 1990). It becomes a significant component of the total enthalpy flux due to the sharp stratification present in RR Lyrae stars (Kovács et al. 2025). Since its primary effect is on specific heat, we parameterize it through temperature fluctuations (see Appendix C).
3.4. Opacity effects
Sharp stratification in the ionization zones also results in strong opacity bumps; therefore, opacity fluctuations cannot be neglected. Thus, we must track changes in radiative conductivity Kr, approximated by a first-order Taylor series of Kr(T, κ), and κ(T) (Xiong 1980). While the opacity bumps enhance radiative losses, they also generate further fluctuations analogous to the κ-mechanism. This is handled through the opacity-induced dissipation-production timescale, τκ.
3.5. Viscous dissipation
The sometimes short dynamical timescales alongside enhanced opacity (i.e., less efficient cooling) make the otherwise insignificant viscous damping of the entropy fluctuations and flux relevant. Assuming scale similarity with kinetic energy damping and the convective timescale 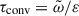 , the second terms in (13) follow.
, the second terms in (13) follow.
4. Discussion
The model proposed here reduces to the standard three-equation model of Kuhfuß (1987) when using (18) in Eν and Uν, setting ξ = 1/3 elsewhere, neglecting τκ terms, using Λ = αΛHp, and also setting the parameters αc,αd, Π,αd, Φ to zero. Some of our extensions can also be incorporated into one-equation models, such as the local anisotropy formulation.
Most of the free dimensionless parameters can be adopted from the existing literature. Assuming isotropy in the dissipation regime, we can adopt the dissipation parameter of Kuhfuß (1987) calibrated to the mixing-length theory: 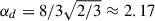 .
.
The diffusion parameters can be obtained from those of Kuhfuß (1987) by dividing them by 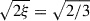 . Therefore, we obtain αΠ = 6 and αΦ = 4. In the case of αt, we can start from the local condition of the one-equation model
. Therefore, we obtain αΠ = 6 and αΦ = 4. In the case of αt, we can start from the local condition of the one-equation model 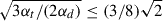 , which gives αt ≤ 4/8.
, which gives αt ≤ 4/8.
Regarding the remaining dissipation terms, Kuhfuss sets the viscous dissipation timescale of Π and Φ to ε/(cpT) and then neglects it in the local limit (Kuhfuß 1987). This is equivalent to scaling αd, Π ≈ αd, Φ parameters with αd such that 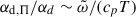 , which is between 10−1 and 10−2 in the ionization region. Thus, we adopt αd, Φαd, Π = 0.0217 ≈ αd/100.
, which is between 10−1 and 10−2 in the ionization region. Thus, we adopt αd, Φαd, Π = 0.0217 ≈ αd/100.
The mixing-length parameters, αΛ and αβ, can follow the standard values used in existing 1D codes (Kupka et al. 2022; Kovács et al. 2024): αΛ = 1.5 and αβ = 1. The value ατ = 0.2 is given by Kupka et al. (2022). The authors also give ατ = 5/(32αd). These two values match only when αd = 0.8, derived from Kolmogorov-scaling (Canuto & Dubovikov 1998).
We chose αr = 3/16, consistent with simple Péclet number dependence for the radiative timescale, rather than the mixing-length calibrated value of (Kuhfuß 1987) (equivalent to αr = 48 in our notation).
Lastly, αc = 1 effectively captures ionization energy transport effects (see Appendix C), whereas Montgomery & Kupka (2004) used αc = 0.5 from second-order Taylor series enthalpy fluctuations.
Although our modifications improve the original Kuhfuß (1987) model for nonlinear pulsation codes, we retain a mixing length approach and a local description of turbulent dissipation and anisotropy. A more complete model (e.g., Canuto 1998) is not recommended at this stage, because a gradual improvement in the treatment help identify the key phenomena governing nonlinear pulsation. Similar to its predecessor, our model is based on the assumption of local thermodynamic equilibrium and neglects radiative transfer in optically thin regions. As these are essential for accurately modeling light curves, the next step should implement them into the models8.
In conclusion, implementing this model into a new hydrocode should be done gradually. Successive modifications may likely have diminishing effects: the first two have the largest effect, followed by the convection correction and opacity effects. The effect of the additional dissipation terms is likely to have an effect only in mode selection and nonlinear phenomena. We also note that the chosen parameters given here also require observational calibration.
5. Conclusions
In this paper, we presented our extended version of the Kuhfuss three-equation turbulent convection model (Kuhfuß 1987), tailored for use in the field of nonlinear radial stellar pulsations. Our main modifications include:
-
the adoption of the enhanced turbulent dissipation from Kupka et al. (2022),
-
the derivation of a local non-static anisotropy model from Canuto (1998),
-
a second-order correction to the convective flux,
-
a first-order correction accounting for opacity fluctuations. This and the flux correction represent effects of sharp ionization regions and opacity sensitivity (Kovács et al. 2025).
-
the retention of turbulent dissipation for entropy fluctuations and flux, expected to have additional stabilizing effect on nonlinear behavior.
Numerical comparison with state-of-the-art one-equation hydrocodes (as analyzed in Kovács et al. 2023, 2024) and a detailed analysis of the model approximations, based on multidimensional results, will be presented in upcoming papers.
Acknowledgments
We are grateful to the anonymous referee for the careful and thorough reading of our manuscript, and whose suggestions improved the quality of this paper. The research was supported by the EKÖP-24 University Excellence Scholarship Program of the Ministry for Culture and Innovation from the source of the National Research, Development and Innovation Fund, through the EKÖP-24-4-I-ELTE-363 grant. This project has been supported by the ‘SeismoLab’ KKP-137523 Élvonal grant, Lendület program of the Hungarian Academy of Sciences project No. LP2025-14/2025, OTKA projects K-129249, SNN-147362, K-147131 and NN-129075, as well as the NKFIH excellence grant TKP2021-NKTA-64. This research was also supported by the International Space Science Institute (ISSI) in Bern/Beijing through ISSI/ISSI-BJ International Team project ID #24-603 - “EXPANDING Universe” (EXploiting Precision AstroNomical Distance INdicators in the Gaia Universe). On behalf of Project ’Hydrodynamical modeling of classical pulsating variables with SPHERLS’ we are grateful for the usage of HUN-REN Cloud (see Héder et al. 2022, https://science-cloud.hu/) which helped us achieve the results published in this paper.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology [Google Scholar]
- Ahlborn, F., Kupka, F., Weiss, A., & Flaskamp, M. 2022, A&A, 667, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baker, N. H. 1987, in Physical Processes in Comets, Stars and Active Galaxies, eds. W. Hillebrandt, E. Meyer-Hofmeister, H. C. Thomas, & R. Kippenhahn, 105 [Google Scholar]
- Blažko, S. 1907, Astron. Nachr., 175, 325 [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Bono, G., & Stellingwerf, R. F. 1994, ApJS, 93, 233 [Google Scholar]
- Canuto, V. M. 1992, ApJ, 392, 218 [Google Scholar]
- Canuto, V. M. 1993, ApJ, 416, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M. 1998, ApJ, 508, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M., & Dubovikov, M. 1998, ApJ, 493, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M., Minotti, F. O., & Schilling, O. 1994, ApJ, 425, 303 [Google Scholar]
- Castor, J. I. 1968, unpublished manuscript [Google Scholar]
- Cox, J. P. 1980, Theory of Stellar Pulsation (PSA-2), 2 [Google Scholar]
- Dorfi, E. A., & Feuchtinger, M. U. 1991, A&A, 249, 417 [NASA ADS] [Google Scholar]
- Dziembowski, W. A. 2016, Commmun. Konkoly Observatory Hungary, 105, 23 [NASA ADS] [Google Scholar]
- Dziembowski, W. A., & Mizerski, T. 2004, Acta Astron., 54, 363 [Google Scholar]
- Flaskamp, M. 2002, ASP Conf. Ser., 259, 456 [Google Scholar]
- Flaskamp, M. 2003, Ph.D. Thesis, Munich University of Technology, Germany [Google Scholar]
- Gehmeyr, M., & Winkler, K. H. A. 1992, A&A, 253, 92 [Google Scholar]
- Geroux, C. M., & Deupree, R. G. 2011, ApJ, 731, 18 [Google Scholar]
- Geroux, C. M., & Deupree, R. G. 2013, ApJ, 771, 113 [Google Scholar]
- Geroux, C. M., & Deupree, R. G. 2014, ApJ, 783, 107 [Google Scholar]
- Geroux, C. M., & Deupree, R. G. 2015, ApJ, 800, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Gonczi, G. 1981, A&A, 96, 138 [Google Scholar]
- Gough, D. O. 1965, in Summer Study Program in Geophysical Fluid Dynamics at the Woods Hole Oceanographic Institution, Vol. II., Notes on the 1965 Summer Study Program in Geophysical Fluid Dynamics at the Woods Hole Oceanographic Institution, eds. W. V. R. Malkus, & M. C. Thayer (Woods Hole Oceanographic Institution), 49 [Google Scholar]
- Gough, D. O. 1977, ApJ, 214, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Héder, M., Rigó, E., Medgyesi, D., et al. 2022, Információs Társadalom, 22, 128 [Google Scholar]
- Houdek, G., & Dupret, M.-A. 2015, Liv. Rev. Sol. Phys., 12, 8 [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution [Google Scholar]
- Kolláth, Z., Buchler, J. R., Szabó, R., & Csubry, Z. 2002, A&A, 385, 932 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolláth, Z., Molnár, L., & Szabó, R. 2011, MNRAS, 414, 1111 [CrossRef] [Google Scholar]
- Kovács, G. B., Nuspl, J., & Szabó, R. 2023, MNRAS, 521, 4878 [CrossRef] [Google Scholar]
- Kovács, G. B., Nuspl, J., & Szabó, R. 2024, MNRAS, 527, L1 [Google Scholar]
- Kovács, G. B., Nuspl, J., & Szabó, R. 2025, A&A, 700, A268 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuhfuss, R. 1986, A&A, 160, 116 [NASA ADS] [Google Scholar]
- Kuhfuß, R. 1987, Ph.D. Thesis, Max-Planck-Institut für Astrophysik, Technische Universität München [Google Scholar]
- Kupka, F., & Muthsam, H. J. 2017, Liv. Rev. Comput. Astrophys., 3, 1 [Google Scholar]
- Kupka, F., Ahlborn, F., & Weiss, A. 2022, A&A, 667, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marconi, M. 2017, Eur. Phys. J. Web Conf., 152, 06001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montgomery, M. H., & Kupka, F. 2004, MNRAS, 350, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Mundprecht, E., Muthsam, H. J., & Kupka, F. 2013, MNRAS, 435, 3191 [NASA ADS] [CrossRef] [Google Scholar]
- Mundprecht, E., Muthsam, H. J., & Kupka, F. 2015, MNRAS, 449, 2539 [NASA ADS] [CrossRef] [Google Scholar]
- Muthsam, H. J., Kupka, F., Löw-Baselli, B., et al. 2010, New Astron., 15, 460 [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Pope, S. B. 2000, Turbulent Flows (Cambridge University Press) [Google Scholar]
- Smolec, R. 2016, MNRAS, 456, 3475 [NASA ADS] [CrossRef] [Google Scholar]
- Smolec, R., & Moskalik, P. 2008a, ActAA, 58, 193 [Google Scholar]
- Smolec, R., & Moskalik, P. 2008b, Acta Astron., 58, 233 [NASA ADS] [Google Scholar]
- Stellingwerf, R. F. 1982a, ApJ, 262, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Stellingwerf, R. F. 1982b, ApJ, 262, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Stuck, M., Pratt, J., Baraffe, I., et al. 2025, A&A, 698, A304 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szabó, R., Kolláth, Z., & Buchler, J. R. 2004, A&A, 425, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szabó, R., Benkő, M. J., Paparó, M., et al. 2015, Eur. Phys. J. Web Conf., 101, 01003 [Google Scholar]
- Unno, W. 1967, PASJ, 19, 140 [NASA ADS] [Google Scholar]
- Van Hoolst, T., Dziembowski, W. A., & Kawaler, S. D. 1998, MNRAS, 297, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Vasilyev, V., Ludwig, H. G., Freytag, B., Lemasle, B., & Marconi, M. 2017, A&A, 606, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasilyev, V., Ludwig, H. G., Freytag, B., Lemasle, B., & Marconi, M. 2018, A&A, 611, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viallet, M., Meakin, C., Arnett, D., & Mocák, M. 2013, ApJ, 769, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., & Schlattl, H. 2008, Ap&SS, 316, 99 [CrossRef] [Google Scholar]
- Wuchterl, G., & Feuchtinger, M. U. 1998, A&A, 340, 419 [NASA ADS] [Google Scholar]
- Xiong, D.-R. 1980, Chin. Astron., 4, 234 [Google Scholar]
- Xiong, D.-R. 2021, Front. Astron. Space Sci., 7, 95 [NASA ADS] [Google Scholar]
- Xiong, D. R., Cheng, Q. L., & Deng, L. 1998a, ApJ, 500, 449 [Google Scholar]
- Xiong, D. R., Deng, L., & Cheng, Q. L. 1998b, ApJ, 499, 355 [Google Scholar]
- Xiong, D. R., Cheng, Q. L., & Deng, L. 2000, MNRAS, 319, 1079 [CrossRef] [Google Scholar]
- Xiong, D. R., Deng, L., Zhang, C., & Wang, K. 2016, MNRAS, 457, 3163 [Google Scholar]
- Xiong, D. R., Deng, L., & Zhang, C. 2018, MNRAS, 480, 2698 [Google Scholar]
For a recent overview and calibration of SPHERLS, see Kovács et al. (2025).
It is available through the Universitätsbibliothek Technische Universität München at https://mediatum.ub.tum.de/doc/1718437/1718437.pdf.
The system of equations can be converted onto a Lagrangian grid with mass coordinates using the mass coordinate defined as dm = 4πr2ρdr (Kippenhahn & Weigert 1990).
Local equations for the TOMs can also be derived by localizing the full nonlocal equations of Canuto (1992). However, this method introduces new variables that complicate numerical solutions. Meanwhile, to determine which terms have real effects on radial stellar pulsations, it is better to proceed one step at a time.
Using Eq. (18) recovers the original definitions of Uν and Eν from Wuchterl & Feuchtinger (1998).
For one-equation models, this procedure was performed by Gehmeyr & Winkler (1992) as well as Dorfi & Feuchtinger (1991).
We note that we do not use dimensionless derivatives in this derivation, in contrast with Sect. 2.
Appendix A: Deriving the model
We start from the Navier-Stokes equations, of the continuity, momentum, and energy conservation in index notation. As we focus on envelope convection in a pulsating envelope, we neglect any energy production from nucleosynthesis and rotation, while we keep all time derivatives. Thus, we have:
Here, ρ denotes the density, v denotes the velocity, p is the thermodynamic pressure, σ is the viscous stress tensor, g = −Gm/r2 is the gravitational acceleration, where m is the mass inside the spherical shell with radius r. F denotes radiative flux and e is the internal energy. The symbol 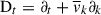 . Additionally, we define the heat sources as the radiative flux and viscous heat production, that is, the specific entropy (s) production is
. Additionally, we define the heat sources as the radiative flux and viscous heat production, that is, the specific entropy (s) production is
We define Reynolds-average as the horizontal average of a quantity, namely
This operation is commutative with (Eulerian) spatial and time derivatives. Using this operation, we split quantities into mean and fluctuation parts (denoted as ( ⋅ )′), for example:
The operator has the following identities:
We denote the Stokes derivative related to the average field as (Kuhfuss 1986)
Now we derive equations for the mean and fluctuating quantities. First, we neglect ρ′ except buoyancy, then write Eq. (A.1) as
Here, (A.7) is called anelastic approximation.
Taking the average of Eq. (A.2), we get the momentum equation of the pulsation (i.e., large-scale motion)
Here, the second term can be converted into a tensor divergence, using Eq. (A.7), one can show that 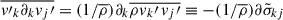 , where we define the Reynolds tensor as (Kuhfuss 1986)
, where we define the Reynolds tensor as (Kuhfuss 1986)
After rearranging, Eq. (A.8).
We derive the momentum equation of the fluctuating field by subtracting Eq. (A.8) from Eq. (A.2), thus
Here, the first term of the right-hand side can be expanded as
, where the second term is usually neglected in the small Mach-number approximation (Gough 1977). On the other hand, Canuto (1992) gives an explanation of the importance of pressure fluctuations, while Viallet et al. (2013) showed that pressure transport can be a significant contribution to envelope convection.
Next, we derive the mean total energy equation similarly to Kuhfuss (1986). Applying averaging, the left-hand side of Eq. (A.3) becomes (Kuhfuss 1986; Kuhfuß 1987):
Here, the Reynolds stress-related terms are derived by using Eq. (A.7) and the definition (A.9). The term 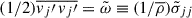 is the kinetic energy stored in the turbulence, and proved to be crucial in modeling radial stellar pulsations (Stellingwerf 1982b). Therefore, it’s necessary to close it through an exact equation. The third order moment (TOM)
is the kinetic energy stored in the turbulence, and proved to be crucial in modeling radial stellar pulsations (Stellingwerf 1982b). Therefore, it’s necessary to close it through an exact equation. The third order moment (TOM) 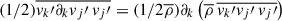 , where Eq. (A.7) was used, and it describes the turbulent flux of the TKE.
, where Eq. (A.7) was used, and it describes the turbulent flux of the TKE.
The RHS of the averaged (A.3) is
Multiplying (A.10) with 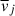 , one can eliminate the kinetic energy of the averaged field. The pressure fluctuation term can be put together on the right-hand side after rearranging the
, one can eliminate the kinetic energy of the averaged field. The pressure fluctuation term can be put together on the right-hand side after rearranging the 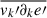 term using Eq. (A.7), because
term using Eq. (A.7), because 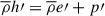 , where h is the specific enthalpy. Using this, the average of the total energy becomes
, where h is the specific enthalpy. Using this, the average of the total energy becomes
Neglecting viscocity transport, we need to determine 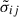 ,
, 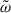 ,
, 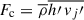 , and
, and 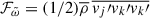 to close Eq. (A.10) and (A.12). Since
to close Eq. (A.10) and (A.12). Since 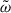 is half of the trace of
is half of the trace of 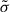 , we derive the overall equation, and then derive
, we derive the overall equation, and then derive 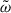 . First, we multiply (A.11) with vi′, then we take the some of this equation and the one with switched indices. Lastly, we take the average. The result after rearranging is:
. First, we multiply (A.11) with vi′, then we take the some of this equation and the one with switched indices. Lastly, we take the average. The result after rearranging is:
The first term of the right-hand side is the turbulent flux of the tensor component, the second term is the so-called shear production (Pope 2000), which converts kinetic energy into turbulence. The third term can be split into two parts as vi′∂jp′=∂j(vi′p′) − p′∂jvi′. The first term describes the pressure transport, and the second term is the pressure-velocity rate-of-strain tensor. The role of this latter is to restore the isotropy of the turbulence. The last two terms are the bouyancy source term, which converts internal energy into turbulent energy, and the viscous dissipation, which again is composed of a transport term and a sink term, which generates heat (vi′∂kσkj′=∂k(vi′σkj′) − σkj′∂kv′i). Let the tensor, pressure, and viscosity transport term be note by 𝒯, 𝒯p, 𝒯σ, the production term by 𝒫, the pressure-velocity rate-of-strain tensor by Πij, the source by 𝒮 and the dissipation by ε. Eq. (A.13) is then
Eq. (A.14) shows, that the eddy viscosity hipothesis, that 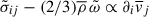 is a very crude approximation. Therefore, Canuto & Dubovikov (1998) developed a model that takes into account these terms, including rotation, and calibrated it to observational and simulation results.
is a very crude approximation. Therefore, Canuto & Dubovikov (1998) developed a model that takes into account these terms, including rotation, and calibrated it to observational and simulation results.
The half of the trace of Eq. (A.14) gives the equation for the specific TKE, 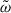 , which is
, which is
where Πjj ≈ 0 was used9.
To close our system of equations, we need to define the remaining primed quantities. First, we model the enthalpy flux. Using the Taylor series
and under the small Mach-number approximation (Kuhfuss 1986), we have 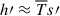 . One can use this argument to produce the source term of Eq. (A.15) as
. One can use this argument to produce the source term of Eq. (A.15) as 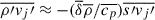 . In short, we reduce the two terms to a function of
. In short, we reduce the two terms to a function of 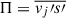 . To produce an equation for Π, one needs an equation for s′ as well. First, we divide Eq. (A.4) by T and take the average, thus:
. To produce an equation for Π, one needs an equation for s′ as well. First, we divide Eq. (A.4) by T and take the average, thus:
where the second term of the right-hand side provides the coupling with the entropy fluctuations. We get the equation of the fluctuating entropy by taking the difference of Eq. (A.4) and (A.17), thus
One produces the equation of Π by multiplying Eq. (A.11) by s′ and Eq. (A.18) by vj′, and take the average of the sum. This is
Here, Eq. (A.7) was used in the first term. Neglecting p′, the fourth term of the RHS reduces to 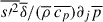 , hence we produce our last equation to
, hence we produce our last equation to 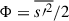 by multiplying Eq. (A.18) by s′ and take the average, that is
by multiplying Eq. (A.18) by s′ and take the average, that is
The remaining terms need to be closed algebraically because we want to produce a three-equation model.
Firstly, we consider the average and fluctuating radiative flux. The flux can be written as Fi = Kr(T, κ)∂iT, then its average and first-order fluctuation is:
where, introducing κT = (∂lnκ/∂lnT)p, we have
To describe the radiation dissipation effects, we have to model 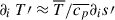 . To do this, following Kuhfuß (1987), we introduce the radiation dissipation length Λr, hence ∂is′≈s′/Λr. This means, that the radiation fluctuation terms are modeled as:
. To do this, following Kuhfuß (1987), we introduce the radiation dissipation length Λr, hence ∂is′≈s′/Λr. This means, that the radiation fluctuation terms are modeled as:
where
Here we note that although τκ has the dimension of time, it is not a simple dissipation timescale, as when κT < −3, it provides an additional source of entropy-fluctuation.
The next term we model is the dissipation of the TKE. We use the local 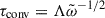 approximation leading to
approximation leading to
We consider the dynamic dissipation of Π and Φ to happen on similar scale then on 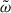 thus
thus
Now, we consider the property of averaging that only keeps radial terms of the vectors. This means that 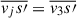 , and
, and 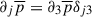 .
.
Furthermore, we define anisotropy as 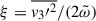 , and assume horizontal isotropy thus,
, and assume horizontal isotropy thus, 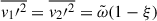 . Using this, we split the Reynolds tensor to the isotropic turbulent pressure, and anisotropic eddy viscous pressure (Gehmeyr & Winkler 1992):
. Using this, we split the Reynolds tensor to the isotropic turbulent pressure, and anisotropic eddy viscous pressure (Gehmeyr & Winkler 1992): 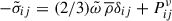 , so only Pijν is need to be modeled, which equivalent with
, so only Pijν is need to be modeled, which equivalent with 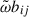 in Canuto & Dubovikov (1998) notation. Contributions of the eddy viscous pressure in Eq. (A.10) and Eq. (A.12) are called turbulent momentum transfer rate (Uν) and turbulent viscous energy transfer rate (Eν), respectively (Wuchterl & Feuchtinger 1998). Their definitions ar
in Canuto & Dubovikov (1998) notation. Contributions of the eddy viscous pressure in Eq. (A.10) and Eq. (A.12) are called turbulent momentum transfer rate (Uν) and turbulent viscous energy transfer rate (Eν), respectively (Wuchterl & Feuchtinger 1998). Their definitions ar
Lastly, we describe the TOMs. In Eq. (A.15) we absorb pressure, viscosity transport, and the TOM into a single diffusion flux term using the diffusion approximation, we introduce the turbulent dynamic viscosity as 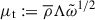 , thus
, thus
The remaining TOMs in eqs. (A.19)-(A.20) become
The model equations presented in Sect. 2. can be derived by using spherical symmetry and substituting all previously described terms into Eqs. (A.6), (A.10), (A.12), (A.15), (A.19), and (A.20).
Appendix B: Preliminaries for the anisotropy expression
From Canuto (1998) (25a) and (27a), one can derive the evolution equation of 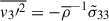 using the same steps as Kupka et al. (2022). To derive the shear terms, one has to use the definition of the mean velocity, that is
using the same steps as Kupka et al. (2022). To derive the shear terms, one has to use the definition of the mean velocity, that is 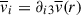 . Therefore
. Therefore
and the flux term is λihj = δi3δijS. Furthermore, we assume isotropy in the horizontal direction, thus 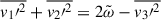 .
.
Appendix C: Derivation of the value of αc
The modeling of the convective flux is based on the Taylor expansion of the enthalpy as a function of temperature, which is equivalent to eq (A.16) with using: 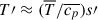 . On the other hand, the transport of ions means that the mean molecular weight also changes, that is,
. On the other hand, the transport of ions means that the mean molecular weight also changes, that is,
The absorption of ionization effects into cp = (∂h/∂T)p and (∂h/∂p)T is a usual process (Kippenhahn & Weigert 1990), but in this case the specific heat is
where hT = (∂h/∂T)p, μ, hμ = (∂h/∂μ)p, t, μT = (∂μ/∂T)p. If we use Reynolds-averaging, we get
Now, we assume that all fluctuations are due to temperature fluctuation in the first order. Thus cp′=cpTT′, hT′=hTTT′ 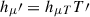 , where T in the subscript means derivative by T, for example, hTT = (∂2h/∂T2)p, and all second derivatives are considered to be functions of average values only10. Substituting these into (C.4) and dividing by T′ we get
, where T in the subscript means derivative by T, for example, hTT = (∂2h/∂T2)p, and all second derivatives are considered to be functions of average values only10. Substituting these into (C.4) and dividing by T′ we get
Let 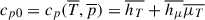 and
and 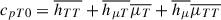 . These are the specific values that can be exactly determined from the mean values, and as we can see, cp ≠ cp0. Now substitute these back into the definition of h′, and we get
. These are the specific values that can be exactly determined from the mean values, and as we can see, cp ≠ cp0. Now substitute these back into the definition of h′, and we get
therefore setting αc = 1 is adequate to follow ionization changes in first-order.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



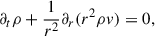
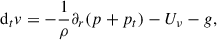
![$$ \begin{aligned} \mathrm{d}_t e + p\frac{1}{r^2}\partial _r (r^2v)&= -\frac{1}{\rho r^2}\partial _r\left[r^2\left(F_{\rm r}+F_{\rm c}\right)\right]-\frac{2T\mathrm \Phi }{c_p\tau _\kappa }-S+\varepsilon ,\end{aligned} $$](/articles/aa/full_html/2026/02/aa57008-25/aa57008-25-eq3.gif)
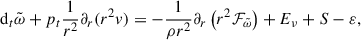
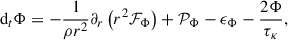
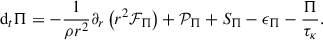
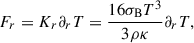
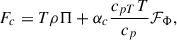
![$$ \begin{aligned} U_\nu&= \frac{1}{\rho }\partial _r\left[\left(\xi -\frac{1}{3}\right) 2\tilde{\omega }\rho \right] + \left(\xi -\frac{1}{3}\right)\frac{6\tilde{\omega }}{r}, \end{aligned} $$](/articles/aa/full_html/2026/02/aa57008-25/aa57008-25-eq11.gif)
![$$ \begin{aligned} E_\nu&= 2\tilde{\omega }\left[\left(\xi -\frac{1}{3}\right)\partial _rv+ 2\left(\frac{1}{3}-\xi \right)\frac{v}{r}\right]. \end{aligned} $$](/articles/aa/full_html/2026/02/aa57008-25/aa57008-25-eq12.gif)
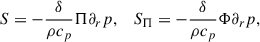
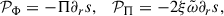
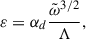
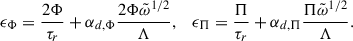
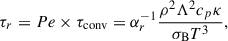
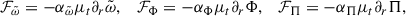
![$$ \begin{aligned} \Lambda (r) = \left\{ \begin{array}{cc} \displaystyle - \frac{r+\Lambda _0}{2\tau ^\star }+\sqrt{\left[\frac{r+\Lambda _0}{2\tau ^\star }\right]^2+ \frac{\Lambda _0 r}{\tau ^\star }} \quad&\text{ if} (\nabla -\nabla _{\rm ad}) <0,\\ \\ \displaystyle \frac{\alpha _\beta r}{\Lambda _0+\alpha _\beta r} \Lambda _0&\text{ if} (\nabla -\nabla _{\rm ad}) \ge 0, \end{array} \right. \end{aligned} $$](/articles/aa/full_html/2026/02/aa57008-25/aa57008-25-eq26.gif)
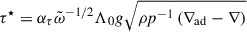
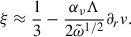
![$$ \begin{aligned} \xi = \frac{1}{3} + \frac{\tau _\xi }{3\tilde{\omega }}\left[\mathcal{D} _\omega -\left(2\beta _5+1\right)S+\varepsilon \right]- \frac{2\tau _\xi }{9}\left[\left(\alpha _1-\frac{1}{5}\right)\partial _rv-2\frac{v}{r}\right], \end{aligned} $$](/articles/aa/full_html/2026/02/aa57008-25/aa57008-25-eq29.gif)
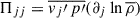
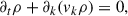
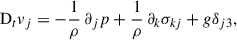
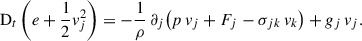
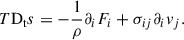
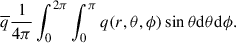
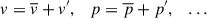
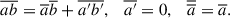
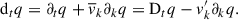
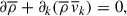
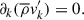
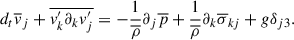
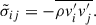
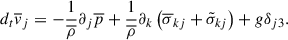
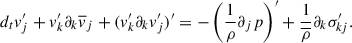
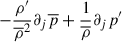
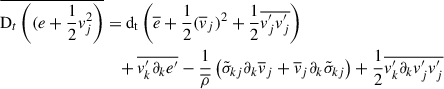
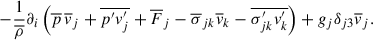
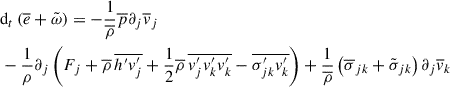
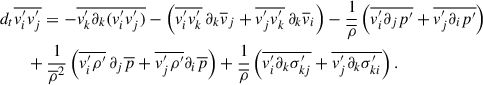
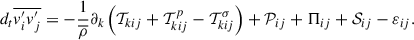
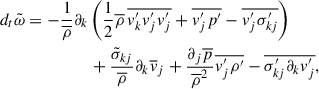
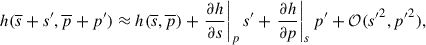
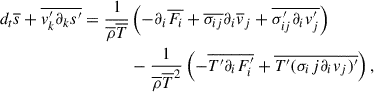
![$$ \begin{aligned} d_t s^{\prime } + v_k^{\prime }\partial _k\overline{s} + (v_k^{\prime }\partial _ks{^{\prime }})^{\prime } = -\frac{1}{\overline{\rho }\overline{T}}\left[\partial _iF_i^{\prime } - (\sigma _{ij}^{\prime }\partial _i v^{\prime }_j)^{\prime }\right] + \text{ higher} \text{ order} \text{ terms}. . \end{aligned} $$](/articles/aa/full_html/2026/02/aa57008-25/aa57008-25-eq80.gif)
![$$ \begin{aligned} \mathrm{d}_t \mathrm{\Pi }&= -\frac{1}{\overline{\rho }}\partial _k\left(\overline{\rho }\,\overline{v_k^{\prime } v_j^{\prime } s^{\prime }}\right) - \frac{1}{\overline{\rho }}\tilde{\sigma }_{jk}\partial _k\overline{s} - \overline{v_k^{\prime } s^{\prime }}\partial _k \overline{v}_j \nonumber \\&\quad - \overline{\left(\frac{1}{\rho }\partial _jp\right)^{\prime }s^{\prime }} + \frac{1}{\overline{\rho }}\overline{s^{\prime }\partial _k\sigma _{kj}^{\prime }}-\frac{1}{\overline{\rho }\overline{T}}\left[\overline{v_j^{\prime }\partial _iF^{\prime }_i}-\overline{v_j^{\prime }(\sigma _{ik}^{\prime }\partial _iv_k^{\prime })^{\prime }}\right]. \end{aligned} $$](/articles/aa/full_html/2026/02/aa57008-25/aa57008-25-eq81.gif)
![$$ \begin{aligned} \mathrm{d}_t \mathrm{\Phi } = - \frac{1}{2\overline{\rho }}\partial _k\left(\overline{\rho }\,\overline{v_k^{\prime }s{^{\prime }}^2}\right) - \overline{s^{\prime } v_k^{\prime }}\partial _k\overline{s}-\frac{1}{\overline{\rho }\,\overline{T}}\left[\overline{s^{\prime }\partial _iF_i^{\prime }} - \overline{s^{\prime }(\sigma _{ij}^{\prime }\partial _iv_j{^{\prime }})^{\prime }}\right]. \end{aligned} $$](/articles/aa/full_html/2026/02/aa57008-25/aa57008-25-eq84.gif)