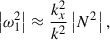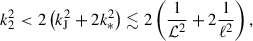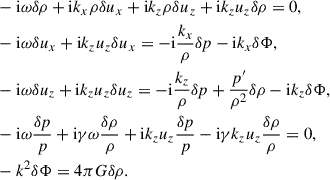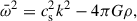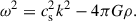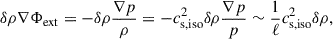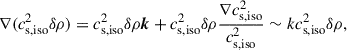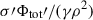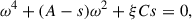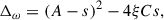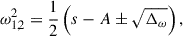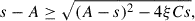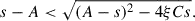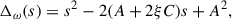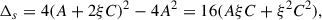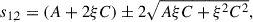| Issue |
A&A
Volume 706, February 2026
|
|
|---|---|---|
| Article Number | A238 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202557742 | |
| Published online | 12 February 2026 | |
The Jeans criterion for hydrostatic and infalling gas
Dipartimento di Fisica e Astronomia “Augusto Righi”, Alma Mater Studiorum – Università di Bologna Via Gobetti 93/2 40129 Bologna, Italy
★ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
17
October
2025
Accepted:
10
January
2026
Aims. We study the local gravitational instability of non-rotating astrophysical fluids allowing for the presence of an external gravitational potential in addition to the fluid self-gravity.
Methods. We present a self-consistent linear-perturbation analysis, taking into account pressure and density gradients in the background medium. We explore two different steady-state configurations for the unperturbed gas: hydrostatic equilibrium and infall into a gravitational potential well.
Results. We show that in both cases the instability criterion is the classical Jeans criterion, which, contrary to previous claims, is not modified by the presence of the external gravitational field. While in the case of hydrostatic equilibrium linear local perturbations are always gravitationally stable, the conditions for gravitational instability can be met in the case of infalling gas, also in the presence of additional non-gravitational forces such as those due to winds.
Conclusions. We conclude that the Jeans criterion can have a role in regulating the formation of clumps and star clusters in streams or shells of gas infalling into galactic gravitational potential wells, as well as, on smaller scales, the fragmentation of gas in collapsing molecular clouds.
Key words: instabilities / stars: formation / ISM: clouds / galaxies: kinematics and dynamics / galaxies: star formation
© The Authors 2026
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1. Introduction
The local gravitational instability of astrophysical gas is a fundamental mechanism, which is believed to have a role, for instance, in the formation of gas clumps and star clusters in galaxies (e.g. Sect. 8.3 of Cimatti et al. 2019), in the fragmentation of molecular clouds (Field et al. 2008; Vázquez-Semadeni et al. 2025), and in the formation of planets (Kratter & Lodato 2016). The conditions for local gravitational instability are more easily found in rotation-supported gaseous discs (Toomre 1964; Goldreich & Lynden-Bell 1965) than in pressure-supported gaseous systems, where local self-gravitating perturbations are stabilized by thermal or turbulent pressure (Binney & Tremaine 2008; Bertin 2014; see also Nipoti 2023).
Recent studies on the formation of gas clumps and stellar clusters in galaxies have pointed out that there are two channels in which gas can fragment via local gravitational instability: not only in rotating gaseous discs, but also in low-angular-momentum gas infalling in the galaxy gravitational potential either in filamentary streams (Freundlich et al. 2014; Mandelker et al. 2018; van Donkelaar et al. 2023) or in roughly spherical shells (Dekel et al. 2023). In this paper we focus on the case of infalling gas and present a linear-perturbation analysis of gas steadily inflowing in the presence of an external gravitational potential (generated, for instance, by the galaxy dark-matter halo and stellar components) in addition to the fluid self-gravity. We address the problem self-consistently, taking into account that the infalling gas can have density, pressure, and velocity gradients, as it is natural in the presence of a gravitational field. We also discuss the effect of additional non-gravitational forces such as those due to winds.
Before addressing the case of infalling gas, we find it appropriate to present a self-consistent local gravitational stability analysis of stratified gas in hydrostatic equilibrium in its own gravity plus an external gravitational potential. Our analysis of the hydrostatic case can be seen as a revisited Jeans (1902) gravitational-stability analysis, in which, by allowing for the presence of gradients in the background quantities, we do not resort to the so-called Jeans swindle (e.g. Binney & Tremaine 2008).
The paper is organized as follows. Sect. 2 introduces the relevant equations. Sects. 3 and 4 present the analyses of the hydrostatic and infalling gas, respectively. Our results are compared with previous work in Sect. 5. Sect. 6 concludes.
2. Reference equations
We want to study the conditions for local gravitational instability of gas either in hydrostatic equilibrium or infalling into a gravitational potential. For an adiabatic inviscid unmagnetized fluid, the relevant set of equations is
where the first three equations are the hydrodynamic mass, momentum, and entropy equations, and the last equation is the Poisson equation. Here, 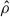 ,
, 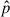 ,
, 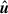 , and
, and 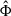 are the gas density, pressure, velocity, and gravitational potential, respectively. In addition, Φext is a fixed external gravitational potential and γ is the adiabatic exponent.
are the gas density, pressure, velocity, and gravitational potential, respectively. In addition, Φext is a fixed external gravitational potential and γ is the adiabatic exponent.
Without loss of generality, we worked in a two-dimensional Cartesian coordinate system (x, z), in which the z axis has the same direction as the unperturbed gravitational field, but opposite orientation (see Fig. 1). For instance, in the case of a spherical gravitational potential, z is the radial direction and x is a generic tangential direction. Given that we performed a local perturbation analysis, the curvature is negligible, so for our purposes Cartesian coordinates work as well as curvilinear coordinates. In our system of coordinates, the system of equations (1) becomes
 |
Fig. 1. Scheme of the local Cartesian x − z coordinate system adopted to describe a parcel of gas immersed in a gravitational potential. Here g is the gravitational field produced by the unperturbed total gravitational potential at the position of the parcel of gas. |
Let us consider a generic quantity 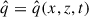 describing a property of the fluid (such as
describing a property of the fluid (such as 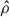 ,
, 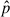 , and
, and 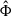 or any component of
or any component of 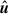 ): q can be written as
): q can be written as 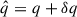 , where the (time-independent) quantity q describes the stationary unperturbed fluid and the (time-dependent) quantity δq describes the Eulerian perturbation. The external gravitational potential Φext is assumed to be independent of time and not affected by the perturbation.
, where the (time-independent) quantity q describes the stationary unperturbed fluid and the (time-dependent) quantity δq describes the Eulerian perturbation. The external gravitational potential Φext is assumed to be independent of time and not affected by the perturbation.
3. Hydrostatic gas
Though we are mainly interested in the case of gas infalling into a gravitational potential well (Sect. 4), it is instructive to first discuss the case in which the unperturbed gas is in hydrostatic equilibrium.
3.1. Unperturbed system
Under the assumption of hydrostatic equilibrium, the unperturbed configuration is a static solution of the system of equations (2), so all the time derivatives and all the components of u are null. We further assume that the quantities describing the unperturbed system can have non-null gradients only along the z direction, so ∂q/∂x = 0. In the following we use ‘′’ to indicate derivatives with respect to z, so q′≡dq/dz and q″ ≡ d2q/dz2 for any unperturbed quantity q = q(z).
Under these assumptions the unperturbed medium is in equilibrium in the total gravitational potential and thus satisfies 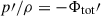 , where Φtot = Φ + Φext and Φ″ = 4πGρ. Given that u = 0, the stationary entropy equation does not put constraints on the entropy profile, so the unperturbed system can have σ′≠0 where σ ≡ ln(pρ−γ) is the normalized specific entropy.
, where Φtot = Φ + Φext and Φ″ = 4πGρ. Given that u = 0, the stationary entropy equation does not put constraints on the entropy profile, so the unperturbed system can have σ′≠0 where σ ≡ ln(pρ−γ) is the normalized specific entropy.
3.2. Perturbations and linearized equations
We consider small (|δq|≪|q|) plane-wave perturbations with wavevector k = (kx, kz) in the form δq ∝ exp[i(kxx + kzz − ωt)], where ω is the frequency. We further assume that the perturbations are local, so |kz|≫1/ℓ, where ℓ ≡ |q/q′| is the characteristic length over which any quantity q varies in the unperturbed configuration at the position of the disturbance. Under these assumptions, the linearized perturbed equations are
where k2 = kx2 + kz2. In the first equation of the above system, we omitted the term ρ′δuz, which is negligible compared with ikzρδuz for local perturbations. The system (3) is reduced to the biquadratic dispersion relation
where cs2 ≡ γp/ρ is the sound speed squared and N2 ≡ −σ′p′/(γρ), which can be null, negative, or positive, is the buoyancy frequency squared.
3.3. Wavenumbers of local perturbations
The dispersion relation (4) was derived assuming that the perturbations are local, so k must be larger not only than 1/ℓ, but also than 1/ℒ, where ℒ is the macroscopic length scale of the gaseous system (see Nipoti 2023). Before proceeding to the analysis of the dispersion relation, it is useful to compare the wavenumbers of such local perturbations with two characteristic wavenumbers associated with the physical properties of the unperturbed system. The first is the Jeans wavenumber
the second, defined only when N2 > 0, is
which is the wavenumber of a disturbance for which the sound-wave frequency is the same as the buoyancy frequency. We now show that, for the hydrostatic case considered here, local perturbations have k larger than both kJ and k*.
As it is well known (e.g. Binney & Tremaine 2008; Bertin 2014), for a self-gravitating cloud in hydrostatic equilibrium, kJ ∼ 1/ℒ. A similar result is obtained for gas in hydrostatic equilibrium in the presence of an external gravitational potential in addition to its own gravitational field. Let us assume that the total gravitational potential is generated by a mass fM, where M is the gas mass and f > 1 accounts for the mass generating the external potential. In this total potential, a hydrostatic gas with sound speed cs has a characteristic size of ℒ ≈ GfM/cs2. Using M ≈ 4πρℒ3/3, where ρ is the mean gas density, we get ℒ2 ≈ 3cs2/(4πfGρ)≈3/(fkJ2). So, for a gaseous system in equilibrium with its self-gravity and an external potential, kJ is of the order of or smaller than 1/ℒ. Thus, local perturbations have k larger than kJ.
From the definition of N2 (Sect. 3.2), assuming σ′> 0 in order to have N2 > 0 (given that p′< 0), we get
because |p′|/p ∼ 1/ℓ and σ′∼1/ℓ. Thus k* ∼ 1/ℓ and local perturbations have k > k*.
3.4. Stability criterion
In Appendix A we report the full formal analysis of the dispersion relation (4), considering all wavevectors. Combining the results of Appendix A with the physical restrictions on the perturbation wavenumber discussed in Sect. 3.3, we draw the following conclusions about the stability or instability of self-gravitating perturbations.
-
When N2 = 0, the condition for stability is k ≥ kJ, so all local perturbations are stable. We cannot draw conclusions about perturbations with k ≲ kJ, because these perturbations are not local.
-
When N2 < 0, all local perturbations are unstable, but the instability is essentially convective (e.g. Tassoul 1978), and thus not expected to lead to clump formation. Mathematically, the convective nature of the instability is apparent if one considers that the fastest-growing unstable mode has a growth rate of |ω12|1/2, with ω12 given by Eq. (A.3). In the relevant regime k > kJ the absolute value of ω12 can be rewritten as
When k/kJ is sufficiently large, we can replace k2 − kJ2 with k2 and then, using |N2|≪cs2k2 (see Eq. 7), we can Taylor-expand the square root and get
which is the convective-instability growth rate squared.
-
When N2 > 0, limiting ourselves to the relevant wavenumbers with k > kJ and k > k*, we never have monotonic instability. Perturbations with k > k2 (where k2 ≥ kJ is a critical wavenumber defined in Appendix A) are stable. In principle there is room for overstable disturbances with kJ < k < k2, but
so a k < k2 perturbation cannot be considered local. We conclude that all local perturbations are stable.
The bottom line is that the local gravitational instability never occurs in gas that is in hydrostatic equilibrium. This conclusion holds true also in the presence of an external gravitational potential.
4. Infalling gas
4.1. Unperturbed system
Also when the gas is infalling, the unperturbed configuration is assumed to be a stationary solution of the system of equations (2), so all time derivatives are null. Given that the fluid is inflowing, we have uz < 0, while ux = 0. We further assume that the quantities describing the unperturbed system can have non-null gradients only along the z direction, so ∂q/∂x = 0 for any unperturbed quantity q. Under these assumptions the unperturbed medium is a stationary Bondi-like solution (Bondi 1952) with ρuz = const, pρ−γ = const (thus σ′ = 0), 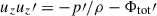 , and Φ″ = 4πGρ.
, and Φ″ = 4πGρ.
4.2. Perturbations and linearized equations
Applying the same kind of plane-wave perturbations as in Sect. 3.2 and linearizing the system of equations (2), in the case of infalling gas, we get
This linear system leads to the dispersion relation
where 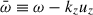 is the ‘Doppler-shifted’ frequency (Malagoli et al. 1987).
is the ‘Doppler-shifted’ frequency (Malagoli et al. 1987).
4.3. Stability criterion
Noting that the imaginary part of ω is equal to the imaginary part of 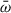 , the condition for instability is
, the condition for instability is 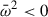 , i.e. cs2k2 < 4πGρ, which is just the Jeans criterion k < kJ. Thus, we can have unstable perturbations, provided that the Jeans length is small compared to the macroscopic scales of the system (i.e. kJ > |ρ′/ρ|,
, i.e. cs2k2 < 4πGρ, which is just the Jeans criterion k < kJ. Thus, we can have unstable perturbations, provided that the Jeans length is small compared to the macroscopic scales of the system (i.e. kJ > |ρ′/ρ|, 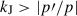 and kJ > |uz′/uz|). While local perturbations have k > kJ when the unperturbed medium is in hydrostatic equilibrium (Sect. 3.3), there can be local perturbations with k < kJ when the gas is infalling. This can be seen by considering, for instance, that kJ (Eq. (5)), at a given ρ, increases for decreasing cs, while the macroscopic scale of the system (e.g. |ρ/ρ′|) is not directly related to cs, because the gas is not in hydrostatic equilibrium.
and kJ > |uz′/uz|). While local perturbations have k > kJ when the unperturbed medium is in hydrostatic equilibrium (Sect. 3.3), there can be local perturbations with k < kJ when the gas is infalling. This can be seen by considering, for instance, that kJ (Eq. (5)), at a given ρ, increases for decreasing cs, while the macroscopic scale of the system (e.g. |ρ/ρ′|) is not directly related to cs, because the gas is not in hydrostatic equilibrium.
We conclude that the local gravitational stability or instability of gas infalling into a gravitational potential well is regulated by the Jeans criterion. If the Jeans length is smaller than the macroscopic scales of the system, perturbations with k < kJ are expected to be gravitationally unstable.
4.4. Additional non-gravitational external forces
The above results on infalling gas are essentially unaltered if we allow for the presence of another external force, in addition to the external gravitational field, such as that due to a wind directed along z and opposite to the gravitational field, in a configuration similar to the one envisaged by Dekel et al. (2023) in their shell scenario for star cluster formation. If the wind partially balances the gravitational field, the unperturbed gas undergoes infall, which can be stationary, as described by the equations reported in Sect. 4.1. In principle, if the wind, combined with possible pressure gradients, balances the gravitational force exactly, the unperturbed gas can also be static. In neither case do the restrictions to the perturbation wavenumber described in Sect. 3.3 apply, because the characteristic macroscopic scales are not determined by the equilibrium between gravity and pressure gradients. It follows that, also in the presence of non-gravitational external forces, such as those exerted by winds, the linear stability criterion is the classical Jeans criterion, and the conditions for instability can be met.
5. The role of the external gravitational potential
In some respect, the analysis presented in this paper is comparable with that of Jog (2013), who studied the Jeans instability of a static fluid in the presence of an external gravitational potential Φext, but (different from what is done here) assuming that the unperturbed medium is homogeneous and with no pressure gradients (see also Zavala-Molina et al. 2023).
Jog (2013) found the dispersion relation 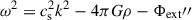 , which must be compared with our dispersion relation (4) that, for N2 = 0 (as is the case for a medium with no gradients), becomes the classical Jeans dispersion relation
, which must be compared with our dispersion relation (4) that, for N2 = 0 (as is the case for a medium with no gradients), becomes the classical Jeans dispersion relation
We note that Φext does not appear in our dispersion relation, because, apart from N2, all the terms containing 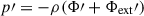 were self-consistently neglected during the analysis when compared with similar terms containing kzp instead of p′. As far as we can tell, the entire analysis of Jog (2013) was undermined by an ill-defined unperturbed solution, in which a static, homogeneous gas with no pressure gradients was assumed to be in a steady state in the presence of a non-vanishing external gravitational field. More specifically, using the notation of the present paper and defining the isothermal sound speed cs, iso = γ−1/2cs, in equation (8) of Jog (2013), the term δρ∇Φext is negligible compared to the term ∇(cs, iso2δρ), because
were self-consistently neglected during the analysis when compared with similar terms containing kzp instead of p′. As far as we can tell, the entire analysis of Jog (2013) was undermined by an ill-defined unperturbed solution, in which a static, homogeneous gas with no pressure gradients was assumed to be in a steady state in the presence of a non-vanishing external gravitational field. More specifically, using the notation of the present paper and defining the isothermal sound speed cs, iso = γ−1/2cs, in equation (8) of Jog (2013), the term δρ∇Φext is negligible compared to the term ∇(cs, iso2δρ), because
where ∇p would be the pressure gradient required to balance ∇Φext in the unperturbed configuration, while
where we have used k ≫ |∇cs, iso2|/cs, iso2 ∼ 1/ℓ.
Another paper presenting an analysis related to this work is Lee & Hennebelle (2018, see also Colman & Teyssier 2020; Dumond & Chabrier 2025), who studied the stability of non-linear density fluctuations in the presence of an external field. Lee & Hennebelle (2018) conclude that the tidal forces due to the external field can have a stabilizing effect. This result is not in tension with our findings, because, while we focussed on linear and local disturbances, the perturbations considered by Lee & Hennebelle (2018) are not only non-linear (with a typical density contrast ≳1), but also non-local (i.e. such that the external gravitational field has a non-negligible gradient across the size of the perturbation). Regardless of the behaviour of such non-linear and non-local disturbances, an underlying question is how such disturbances are produced in the first place. The results of the present work can help understand under which conditions they can originate from small local perturbations.
In conclusion, even in the presence of an external gravitational field, when the unperturbed medium is in hydrostatic equilibrium with no entropy gradients (σ′ = 0), the dispersion relation for linear, local self-gravitating perturbations is the classical Jeans dispersion relation (13). When σ′≠0, the dispersion relation takes the more general form of Eq. (4). In neither case is the stability criterion modified by the presence of the external field1.
For essentially the same reasons, the external field does not appear in the dispersion relation when the unperturbed gas is infalling (Eq. (12)). This implies, for instance, that the classical Jeans criterion can be applied to study the stability of infalling gaseous streams such as those studied by Mandelker et al. (2018).
6. Conclusions
We have revisited the problem of the local gravitational instability of non-rotating astrophysical gas, considering the cases of hydrostatic gas and of gas infalling into a gravitational potential well. We have shown that in both cases the linear gravitational stability criterion is the classical Jeans criterion, which is not modified by the presence of an external gravitational potential.
While all local perturbations turn out to be stable in the hydrostatic case, the conditions for local instability can be met in the case of infalling gas, even in the presence of additional non-gravitational forces, such as those produced by winds. Taken at face value, our results suggest that the classical Jeans criterion can regulate the formation of gas clumps and star clusters in gas infalling into galactic gravitational potentials, as well as, on smaller scales, the fragmentation of gas in collapsing molecular clouds. However, a more realistic description of these processes should also include other ingredients, such as magnetic fields, turbulence, radiative cooling, and a more complex geometry (e.g. Hosseinirad et al. 2017), which were neglected in our analysis and can play an important role.
Acknowledgments
I am grateful to Alessandro Romeo and to an anonymous referee for helpful comments. The research activities described in this paper have been co-funded by the European Union – NextGenerationEU within PRIN 2022 project n. 20229YBSAN – Globular clusters in cosmological simulations and in lensed fields: from their birth to the present epoch.
References
- Bertin, G. 2014, Dynamics of Galaxies (Cambridge: Cambridge University Press) [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton: Princeton University Press) [Google Scholar]
- Bondi, H. 1952, MNRAS, 112, 195 [Google Scholar]
- Cimatti, A., Fraternali, F., & Nipoti, C. 2019, Introduction to Galaxy Formation and Evolution: From Primordial Gas to Present-day Galaxies (Cambridge: Cambridge University Press) [Google Scholar]
- Colman, T., & Teyssier, R. 2020, MNRAS, 492, 4727 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Sarkar, K. C., Birnboim, Y., Mandelker, N., & Li, Z. 2023, MNRAS, 523, 3201 [NASA ADS] [CrossRef] [Google Scholar]
- Dumond, P., & Chabrier, G. 2025, A&A, 694, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Field, G. B., Blackman, E. G., & Keto, E. R. 2008, MNRAS, 385, 181 [Google Scholar]
- Freundlich, J., Jog, C. J., & Combes, F. 2014, A&A, 564, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Lynden-Bell, D. 1965, MNRAS, 130, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Hosseinirad, M., Naficy, K., Abbassi, S., & Roshan, M. 2017, MNRAS, 465, 1645 [Google Scholar]
- Jeans, J. H. 1902, Phil. Trans. Roy. Soc. London Ser. A, 199, 1 [CrossRef] [Google Scholar]
- Jog, C. J. 2013, MNRAS, 434, L56 [NASA ADS] [CrossRef] [Google Scholar]
- Kratter, K., & Lodato, G. 2016, ARA&A, 54, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y.-N., & Hennebelle, P. 2018, A&A, 611, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malagoli, A., Rosner, R., & Bodo, G. 1987, ApJ, 319, 632 [Google Scholar]
- Mandelker, N., van Dokkum, P. G., Brodie, J. P., van den Bosch, F. C., & Ceverino, D. 2018, ApJ, 861, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C. 2023, MNRAS, 518, 5154 [Google Scholar]
- Tassoul, J.-L. 1978, Theory of Rotating Stars (Princeton: Princeton University Press) [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- van Donkelaar, F., Mayer, L., Capelo, P. R., et al. 2023, MNRAS, 522, 1726 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., Palau, A., Gómez, G. C., et al. 2025, MNRAS, in press [arXiv:2408.10406] [Google Scholar]
- Zavala-Molina, R., Ballesteros-Paredes, J., Gazol, A., & Palau, A. 2023, MNRAS, 524, 4614 [CrossRef] [Google Scholar]
Appendix A: Analysis of the dispersion relation (4)
The dispersion relation (4) can be written in the form
where A ≡ 4πGρ > 0, s ≡ cs2k2 > 0, ξ ≡ kx2/k2, by definition such that 0 ≤ ξ ≤ 1, and C ≡ N2, which can be null, negative or positive. We now examine each of these three cases.
-
The case C = 0. When C = 0 the dispersion relation becomes ω2 = s − A, which implies stability for s ≥ A and instability for s < A.
-
The case C < 0. The discriminant of equation (A.1),
is always positive when C < 0, which implies that ω2 is real. The roots of equation (A.1) are
defined so that ω12 ≤ ω22. We have stability when ω12 ≥ 0, i.e.
and instability when ω12 < 0, i.e.
The latter condition, which is evidently satisfied when s < A, when s ≥ A becomes 4ξCs < 0, which is always the case when C < 0. We conclude that all perturbations are unstable when C < 0.
-
The case C > 0. Expanding Eq. (A.2) we get
which has discriminant
which is always positive when C > 0. The zeros of Δω(s) are
defined so that s1 ≤ s2. It is useful to note that 0 < s1 < A + 2C and s2 < 2A + 4C. When s1 < s < s2 we have Δω2 < 0 and thus overstability. When either s < s1 or s > s2, Δω2 > 0, so, using Eqs. (A.4) and (A.5), we infer that perturbations with s > A are stable, while perturbations with s < A are monotonically unstable. Given that s2 > A, we conclude that, when C ≥ 0, perturbations with s > s2 are stable and the only monotonically unstable perturbations are those with s < s1 and s < A.
In summary, recalling that k2 = s/cs2 and kJ2 = A/cs2, and defining k1 and k2 such that k12 = s1/cs2 and k22 = s2/cs2, we have the following criteria.
-
When N2 = 0 the condition for stability is k > kJ.
-
When N2 < 0 perturbations with any k are unstable.
-
When N2 > 0 we have overstability when k1 < k < k2, stability when kJ < k < k1 and when k > k2, and monotonic instability when k < kJ and k < k1.
All Figures
 |
Fig. 1. Scheme of the local Cartesian x − z coordinate system adopted to describe a parcel of gas immersed in a gravitational potential. Here g is the gravitational field produced by the unperturbed total gravitational potential at the position of the parcel of gas. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



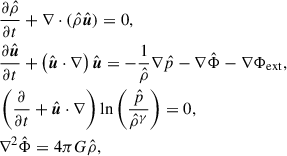
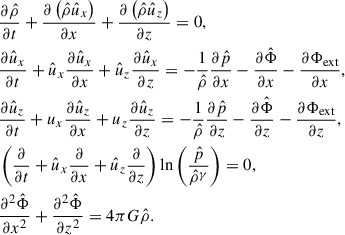
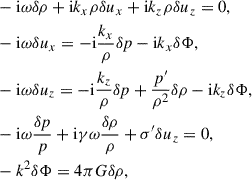
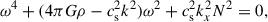
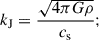
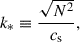
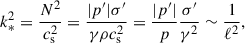
![$$ \begin{aligned} \left|\omega ^2_1\right|=\frac{c_{\rm s}^2}{\sqrt{2}}\left(k^2-k_{\rm J}^2\right)\left[\sqrt{1+\frac{4k_x^2|N^2|}{c_{\rm s}^2(k^2-k_{\rm J}^2)^2}}-1\right]. \end{aligned} $$](/articles/aa/full_html/2026/02/aa57742-25/aa57742-25-eq19.gif)