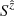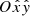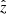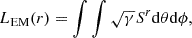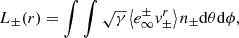| Issue |
A&A
Volume 700, August 2025
|
|
|---|---|---|
| Article Number | L19 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202555826 | |
| Published online | 20 August 2025 | |
Letter to the Editor
Effect of magnetic field inclination on black hole jet power and particle acceleration
1
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
2
Princeton Plasma Physics Laboratory, Princeton, NJ 08540, USA
⋆ Corresponding author: enzo.figueiredo@univ-grenoble-alpes.fr
Received:
5
June
2025
Accepted:
21
July
2025
Rotating black holes are known to launch relativistic jets and accelerate particles if they accrete a magnetized plasma. It remains unclear, however, how the global magnetic field orientation affects the jet powering efficiency. We propose the first kinetic study of a collisionless plasma around a Kerr black hole embedded in a magnetic field that is inclined with respect to the black hole spin axis. Using three-dimensional general relativistic particle-in-cell simulations, we show that while oblique magnetic field configurations significantly reduce the jet power, particle acceleration still remains highly efficient. This suggests that black holes producing a weak jet might still be bright sources of nonthermal radiation and cosmic rays.
Key words: acceleration of particles / black hole physics / plasmas / methods: numerical
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Black holes power relativistic jets from galactic scales with stellar-mass black holes in X-ray binaries (Mirabel & Rodríguez 1994, 1999; Fender 2006) to extragalactic scales with supermassive black holes in active galactic nuclei (Urry & Padovani 1995; Blandford et al. 2019). The most promising mechanism to explain how black holes launch jets was proposed by Blandford & Znajek (1977). In this model, the jet power depends on the black hole spin and on the amount of magnetic flux that crosses its horizon. This mechanism was first studied numerically with general relativistic magnetohydrodynamic (GRMHD) simulations (Komissarov 2001; Koide et al. 2002). In addition to the fluid-like behavior in MHD, the near-horizon environment of a black hole may produce nonthermal radiation. This suggests that particle acceleration occurs there (Event Horizon Telescope Collaboration 2022). This is corroborated by recent general relativistic particle-in-cell (GRPIC) simulations that showed that efficient particle acceleration takes place within the black hole magnetosphere via magnetic reconnection or polar-cap discharge (Parfrey et al. 2019; Crinquand et al. 2020, 2021; Bransgrove et al. 2021; Yuan et al. 2025).
Particle acceleration and the jet-powering mechanism have been studied in axisymmetric setups, where the direction of the black hole spin is aligned with the orientation of the surrounding magnetic field (Parfrey et al. 2019). Although this was motivated for the modeling and numerical simplicity, many systems may have a preferred direction for the magnetic field that may be inclined to the black hole spin. Wind-fed black holes may be such examples, as well as neutron star–black hole binaries, high-mass X-ray binaries, and the Gaia black holes (El-Badry et al. 2023). In the Galactic Center, Sagittarius A* (Sgr A*) may accrete stellar winds from the surrounding stars, although it is still unclear whether it produces a jet (Royster et al. 2019). Isolated black holes fed by the interstellar medium (Barkov et al. 2012; Kin et al. 2025) might be another favorable configuration for an inclined magnetic field. Inclined magnetospheres have been studied using GRMHD simulations (Palenzuela et al. 2010; Ressler et al. 2021, 2023; James et al. 2024). These studies clearly showed that the jet launching is weaker when the magnetic field and the black hole spin are inclined, but cannot capture nonideal plasma physics and particle acceleration self-consistently.
We present the first kinetic plasma study of a black hole that is embedded in an inclined magnetic field to understand how the jet forms and to understand its impact on the particle acceleration. We perform three-dimensional (3D) GRPIC simulations using the code GRZeltron (Cerutti et al. 2013; Parfrey et al. 2019). We assume a Kerr spacetime, using the Kerr-Schild spherical coordinates (t, r, θ, ϕ), and solve the particle and field equations in the 3+1 formalism (Komissarov 2004). We use geometrized units G = c = M = 1, M being the black hole mass, and the characteristic units of length and time are rg = GM/c2 and tg = rg/c respectively.
2. Methods
The computational domain covered r ∈ [0.98rh, 16rg], θ ∈ [0.013π, 0.987π], and ϕ ∈ [0, 2π], where 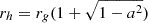 is the radius of the event horizon, and a is the black-hole spin parameter. The grid consisted of Nr × Nθ × Nϕ = 1024 × 512 × 768 cells, equally spaced in log r, θ and ϕ, such that the grid was finer near the horizon. We assumed axial symmetry as θ boundary conditions, and particles passing through the axis were absorbed. Waves and particles were absorbed in a layer at the outer radial boundary of the box in which the magnetic field lines matched the initial field. The initial electromagnetic configuration followed the solution by Bicak & Janis (1985). This is the electromagnetic configuration in vacuum for a rotating black hole that is embedded in an asymptotically uniform magnetic field B0 inclined at an angle χ. Similarly to the Wald solution (χ = 0o, Wald 1974), the electric field D in some regions has a component parallel to the magnetic field B, where D and B are measured by the local fiducial observers (FIDOs; Komissarov 2004).
is the radius of the event horizon, and a is the black-hole spin parameter. The grid consisted of Nr × Nθ × Nϕ = 1024 × 512 × 768 cells, equally spaced in log r, θ and ϕ, such that the grid was finer near the horizon. We assumed axial symmetry as θ boundary conditions, and particles passing through the axis were absorbed. Waves and particles were absorbed in a layer at the outer radial boundary of the box in which the magnetic field lines matched the initial field. The initial electromagnetic configuration followed the solution by Bicak & Janis (1985). This is the electromagnetic configuration in vacuum for a rotating black hole that is embedded in an asymptotically uniform magnetic field B0 inclined at an angle χ. Similarly to the Wald solution (χ = 0o, Wald 1974), the electric field D in some regions has a component parallel to the magnetic field B, where D and B are measured by the local fiducial observers (FIDOs; Komissarov 2004).
We studied a magnetosphere in a nearly ideal force-free regime, which implies that any electric field parallel to the magnetic field is screened and that the plasma is magnetically dominated. The FIDO-measured pair number density n should therefore exceed the same observer’s Goldreich-Julian number density n0 = ωhB0/4πe (Goldreich & Julian 1969) and the plasma magnetization σ = B2/4πnm ≫ 1, where m and e are the electron mass and charge, and ωh = a/2rh is the angular velocity of the event horizon. Plasma injection was accomplished by using an ad hoc prescription. The domain in which pairs can be injected covered r ∈ [1.2rh, 6rg]. In each cell, the magnetization σ was computed: When it was higher than a ceiling value σc, a pair was injected in that cell with a density δn = ℛn0B2/B02, where ℛ is the injection rate. The particles were injected with a velocity randomly drawn from a Maxwellian moving with the FIDO and having a temperature kT = 0.5m. Although plasma injection was not modeled self-consistently, it was sufficient to capture most of the features of a force-free magnetosphere (Parfrey et al. 2019). We were unable, however, to reproduce the spark-gap physics observed with realistic pair injection (Crinquand et al. 2020). This matter is left to a future study. We achieved a force-free-like regime in our simulations by setting the dimensionless magnetic field strength 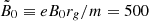 and the injection parameters σc = 580 and ℛ = 1. The resolution of the characteristic plasma skin depth d0 on the event horizon was
and the injection parameters σc = 580 and ℛ = 1. The resolution of the characteristic plasma skin depth d0 on the event horizon was 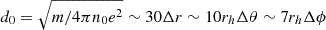 .
.
3. Results
We explored four inclinations, χ = 0° (aligned), 30°, 60°, and 85° and considered a high (a = 0.99) and a moderate (a = 0.7) spin value. An equivalent axisymmetric two-dimensional simulation was also performed for a = 0.99. After a transient regime, the simulations reached a quasi-steady state at physical time between 45 tg and 80 tg, depending on the inclination, from which point, the global features appear static. All the results and the figures shown in this Letter were processed after this steady state was reached. In the top panel of Fig. 1, we provide 3D visualizations of the magnetosphere with a spin a = 0.99 for different inclination values. The moderate spin simulations, with a = 0.7, show the same qualitative behavior, although it is less pronounced because the ergosphere is smaller. The aligned case qualitatively matches expectations from 2D (Parfrey et al. 2019): The magnetic field lines are dragged within the ergosphere, eventually enter the horizon and assume a helical shape. A magnetic discontinuity appears between the upper (θ < π/2) and the lower hemispheres (θ > π/2) that is supported by an equatorial current layer in the ergosphere. This current layer then fragments due to the onset of the tearing instability, which mediates fast magnetic reconnection. Inclined simulations also showed that the field lines threaded the horizon, but their geometry was altered because they asymptotically followed the magnetic field direction at infinity. The jet direction is fully determined from the launching regions to infinity by the orientation of the large-scale field. A current layer still forms within the ergosphere, is transverse to the asymptotic magnetic field orientation (i.e., no longer in the equatorial plane), and shows the development of magnetic reconnection. For high inclination values, the current sheet is also warped along the azimuthal direction close to the black hole equator.
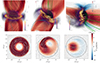 |
Fig. 1. Top: 3D visualizations of black hole magnetospheres with spin a = 0.99. We show magnetic field lines (a few are highlighted in green or blue) and volume renderings of the plasma number density over the whole domain and of the radial Poynting flux density (Sr) on half of the domain (ϕ ∈ [0, π]). The inclination angle values from left to right are χ = 0°, χ = 30°, and χ = 85°. Bottom: Outgoing Poynting flux density in a cross section of the jet ( |
To trace the regions of electromagnetic energy extraction within the magnetosphere, we represent the radial Poynting flux density (Sr) for an observer at infinity in the top panel of Fig. 1. The bottom panel displays several cross sections perpendicular to the jet axis for different magnetic field inclinations. For χ = 0°, the Poynting flux distribution is axisymmetric and concentrated in a sheath around the jet core. The jet section shows a single magnetic cell, inherited from the helical shape of the field, that supports an outgoing electric current in the jet core (not shown here). Although the jet still follows the magnetic field direction for inclined configurations, its internal structure is significantly altered. The jet cross sections show that the magnetic geometry loses the helical structure for a more complex shape, in which the two hemispheres of the magnetosphere actually contribute to the same side of the jet. This is clearly visible for χ = 85°: The two counter-rotating helices of the magnetic field follow from the connection of the field lines to both hemispheres, each sending a current with an opposite sign (see the dual magnetic cell structure in Fig. 1). The electromagnetic flux thus no longer appears to lie within a sheath, but becomes less symmetric for moderate inclinations (e.g., χ = 30°), shrinking one side of the sheath while expanding the other. For χ = 85°, the maximum power appears rather concentrated within the jet core, where the transverse magnetic field strength is highest. This simulation shows a negative Poynting flux contribution from polar regions of the magnetosphere that accounts for electromagnetic energy being instead absorbed by the black hole.
These simulations also allow us to understand the added value of 3D simulations even for an aligned magnetosphere. As opposed to 2D studies, the toroidal component of the magnetic field is not just an out-of-plane component here, but can also reconnect efficiently in the plasmoid-dominated regime. It even clearly dominates reconnection of the radial field component by a factor of 4–5. This explains the large difference in the amount of dissipation and particle acceleration in the top panel of Fig. 2. This figure shows the dependence of the electromagnetic and particle outgoing powers on the radial coordinate in the χ = 0° and a = 0.99 simulation; these quantities are defined as
 |
Fig. 2. Radial dependence of the outgoing energy flux as measured by an observer at infinity; a = 0.99 in all cases. The yellow lines represent the electromagnetic powers (LEM), and the blue and red lines indicate the kinetic power of electrons and positrons (L±), respectively. Top panel: comparison between the aligned 3D simulation (solid lines) and the 2D axisymmetric simulation (dotted lines). Bottom panel: Comparison between the χ = 0° simulation (solid lines) with the inclined χ = 85° run (dashed lines). All curves were averaged over 4 tg. |
where the + (−) index indicates the positron (electron) kinetic energy flux, γ is the determinant of the spatial three-metric, n± is the number density measured by the FIDO, v±r is the particle’s radial coordinate-basis three-velocity, and e∞± = −ut± is the particle energy as measured by an observer at infinity (uμ being the particle covariant four-velocity). The product of these latter two quantities was averaged over each cell. In 3D, a higher fraction of the total power is carried by the particles inside the ergosphere because of magnetic dissipation, which reduces the electromagnetic power with decreasing radius. The electromagnetic power appears to be slightly higher asymptotically (∼15%) than in the 2D case, which may be due to a slight difference in the geometry of the electromagnetic fields, caused by the more vigorous magnetic reconnection in the current layer. The asymmetry in the electron and positron powers within the ergosphere is explained by the global electric polarization of the magnetosphere induced by the black hole rotation. If the spin or the magnetic field direction were inverted, we would see the opposite trend for the two species. These results show that 3D models are necessary to capture the correct level of magnetic dissipation and particle energization in the magnetosphere.
Inclining the magnetic field with respect to the black hole spin axis also strongly affects the energy transport within the magnetosphere. In the bottom panel of Fig. 2, we present the same physical quantities as discussed above, but for inclinations χ = 85° and χ = 0° and with a spin a = 0.99. The Poynting flux decreases significantly when the magnetic field is inclined, mostly because the field lines are less twisted in the oblique magnetosphere. The drop in the electromagnetic power within the ergosphere with respect to its asymptotic value is also relatively larger for the χ = 85° case (i.e., a drop of nearly 80%, as opposed to ∼40% for χ = 0°) and can be explained by the contributing negative Poynting power observed around the polar region of the horizon in Fig. 1. In contrast, particle energization is nearly unaffected by inclination. Although its geometry changes with magnetic inclination, the properties of the current layer and of the upstream plasma remain mostly unchanged. This leads to a similar conversion of the Poynting flux to energetic particles. The positron kinetic energy fluxes are very similar for χ = 0° and χ = 85° for this reason. The inclination also appears to quench the polarization of the magnetosphere described in the last paragraph, analogously to pulsar magnetospheres (Philippov & Spitkovsky 2018). The same trend is therefore observed between the electron and positron power for χ = 85°.
The dependence of the magnetospheric energetics on the inclination is summarized in Fig. 3. The Poynting power at a radius r = 4 rg is represented for all inclinations and spin values we explored and is normalized to ωh2ΦBH2, with ΦBH = ∬dΩ|Br|/2 the magnetic flux through the event horizon (LEM/ωh2ΦBH2 reaches a steady-state value for all simulations). The magnetic flux of the horizon is weakly dependent on the spin and the inclination. It lies in the range ΦBH/2πrg2B0 ∼ 2.5 − 3 in all simulations. However, the two Poynting power curves show the same trend toward a significant decrease of the electromagnetic power with the inclination angle χ. The difference between the aligned and the χ = 85° cases reaches a factor ∼5 for a = 0.99 and ∼3 for a = 0.7. The significant drop in power means that the jet power in the χ= 85°, a = 0.99 simulation is comparable to that of the aligned a = 0.7 simulation. This creates a degeneracy in the jet power between a lower spin value and a highly inclined magnetic field. This is a larger effect than in force-free studies (Palenzuela et al. 2010), where the electromagnetic power decreased by a factor of ∼2 (at a = 0.7). The similarity of the trends for the two spin values shows the robustness of the dependence on ωh2ΦBH2 and χ, but we recall that ωh reaches a higher value for a higher spin. A high-spin black hole should therefore power a stronger jet than one with a lower spin, with χ fixed.
 |
Fig. 3. Energy flux dependence on the inclination angle χ for the electromagnetic power (LEM, blue) and the positron kinetic power (L+, red). The squares represent values for a spin a = 0.7, and the circles show a = 0.99. |
The positron power on the black hole horizon is also represented in Fig. 3. As previously shown, a reconnecting current sheet always appears within the ergosphere, and thus, particles should be energized in the same way. We do not observe a strong dependence on the positron power for different inclination angles for this reason. The clear higher absolute energies reached in the a = 0.99 case compared to the a = 0.7 case arise from the different sizes of the ergosphere: There is more room in the a = 0.99 case for accelerating particles before they reach the event horizon. These results demonstrate that although it is no efficient jet engine, an inclined magnetosphere is an efficient particle accelerator. The particle energy distributions (see Fig. A.1 in the appendix) featured nearly identical power-law tails for all inclinations, and the indices and cutoff energies were consistent with local studies of magnetic reconnection (Sironi & Spitkovsky 2014; Werner et al. 2016).
4. Conclusions
We understood several key aspects of black hole magnetospheres. Consistently with previous studies, we showed that an inclined magnetic configuration with respect to the black hole spin significantly decreases the jet power. Kinetic simulations are crucial for showing that this weakening of the jet is not associated with a decrease in particle energization within the magnetosphere, however. Instead, magnetic reconnection appears to be very robust in providing nonthermal particle acceleration. In this sense, black holes that do not power a jet because of a suboptimal magnetic configuration might still leave high-energy radiative signatures; this may be relevant to the case of Sgr A*. The different magnetic geometry induced within the jet is nontrivial and is expected to leave imprints on the polarimetric signature. A byproduct of our study is the demonstration that 3D simulations of black hole magnetospheres are essential for realistically modeling the dissipation within the ergosphere. Significantly more magnetic energy is released into particle acceleration in 3D, which has implications for the estimated radiative flux of the magnetosphere.
Our work was limited by the nonphysical pair creation we used, however. A complementary study would present more realistic pair creation using self-consistent Monte Carlo modeling of high-energy photons and inverse-Compton scattering (Crinquand et al. 2020; Yuan et al. 2025) and would allow us to understand the alteration in the spark-gap physics by this nonaxisymmetric setup. The shape of the current layer, which is the expected main source of high-energy radiation, would lead to different light curves or polarization signatures, which are expected to be valuable constraints on the environment of the black hole. A setup with a time-varying magnetic field direction would also be relevant to the case of a black hole that is embedded in a pulsar wind.
Acknowledgments
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 863412). Computing resources were provided by TGCC under the allocations SS010415385 and A0170407669 made by GENCI. KP acknowledges support from the Laboratory Directed Research and Development Program at Princeton Plasma Physics Laboratory, a national laboratory operated by Princeton University for the U.S. Department of Energy under Prime Contract No. DE-AC02-09CH11466. We are thankful to the referee for their comments that helped us clarifying some of our results.
References
- Barkov, M. V., Khangulyan, D. V., & Popov, S. B. 2012, MNRAS, 427, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Bicak, J., & Janis, V. 1985, MNRAS, 212, 899 [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., Meier, D., & Readhead, A. 2019, ARA&A, 57, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Bransgrove, A., Ripperda, B., & Philippov, A. 2021, Phys. Rev. Lett., 127, 055101 [NASA ADS] [CrossRef] [Google Scholar]
- Cerutti, B., Werner, G. R., Uzdensky, D. A., & Begelman, M. C. 2013, ApJ, 770, 147 [Google Scholar]
- Crinquand, B., Cerutti, B., Philippov, A., Parfrey, K., & Dubus, G. 2020, Phys. Rev. Lett., 124, 145101 [Google Scholar]
- Crinquand, B., Cerutti, B., Dubus, G., Parfrey, K., & Philippov, A. 2021, A&A, 650, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El-Badry, K., Rix, H.-W., Cendes, Y., et al. 2023, MNRAS, 521, 4323 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022, ApJ, 930, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R. 2006, in Compact stellar X-ray sources, eds. W. H. G. Lewin, & M. van der Klis, 39, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [Google Scholar]
- James, B., Janiuk, A., & Karas, V. 2024, A&A, 687, A185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kin, K., Kuze, R., & Kimura, S. S. 2025, ApJ, 985, 251 [Google Scholar]
- Koide, S., Shibata, K., Kudoh, T., & Meier, D. L. 2002, Science, 295, 1688 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S. 2001, MNRAS, 326, L41 [Google Scholar]
- Komissarov, S. S. 2004, MNRAS, 350, 427 [Google Scholar]
- Mirabel, I. F., & Rodríguez, L. F. 1994, Nature, 371, 46 [Google Scholar]
- Mirabel, I. F., & Rodríguez, L. F. 1999, ARA&A, 37, 409 [Google Scholar]
- Palenzuela, C., Garrett, T., Lehner, L., & Liebling, S. L. 2010, Phys. Rev. D, 82, 044045 [Google Scholar]
- Parfrey, K., Philippov, A., & Cerutti, B. 2019, Phys. Rev. Lett., 122, 035101 [Google Scholar]
- Philippov, A. A., & Spitkovsky, A. 2018, ApJ, 855, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., Quataert, E., White, C. J., & Blaes, O. 2021, MNRAS, 504, 6076 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., White, C. J., & Quataert, E. 2023, MNRAS, 521, 4277 [CrossRef] [Google Scholar]
- Royster, M. J., Yusef-Zadeh, F., Wardle, M., et al. 2019, ApJ, 872, 2 [Google Scholar]
- Sironi, L., & Spitkovsky, A. 2014, ApJ, 783, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Wald, R. M. 1974, Phys. Rev. D, 10, 1680 [Google Scholar]
- Werner, G. R., Uzdensky, D. A., Cerutti, B., Nalewajko, K., & Begelman, M. C. 2016, ApJ, 816, L8 [Google Scholar]
- Yuan, Y., Chen, A. Y., & Luepker, M. 2025, ApJ, 985, 159 [Google Scholar]
Appendix
Particles’ energy distribution
 |
Fig. A.1. Positrons’ energy distributions for different χ values with a = 0.99. Power law scaling dN/dγ ∝ γ−2 is shown in dashed lines. |
All Figures
 |
Fig. 1. Top: 3D visualizations of black hole magnetospheres with spin a = 0.99. We show magnetic field lines (a few are highlighted in green or blue) and volume renderings of the plasma number density over the whole domain and of the radial Poynting flux density (Sr) on half of the domain (ϕ ∈ [0, π]). The inclination angle values from left to right are χ = 0°, χ = 30°, and χ = 85°. Bottom: Outgoing Poynting flux density in a cross section of the jet ( |
| In the text | |
 |
Fig. 2. Radial dependence of the outgoing energy flux as measured by an observer at infinity; a = 0.99 in all cases. The yellow lines represent the electromagnetic powers (LEM), and the blue and red lines indicate the kinetic power of electrons and positrons (L±), respectively. Top panel: comparison between the aligned 3D simulation (solid lines) and the 2D axisymmetric simulation (dotted lines). Bottom panel: Comparison between the χ = 0° simulation (solid lines) with the inclined χ = 85° run (dashed lines). All curves were averaged over 4 tg. |
| In the text | |
 |
Fig. 3. Energy flux dependence on the inclination angle χ for the electromagnetic power (LEM, blue) and the positron kinetic power (L+, red). The squares represent values for a spin a = 0.7, and the circles show a = 0.99. |
| In the text | |
 |
Fig. A.1. Positrons’ energy distributions for different χ values with a = 0.99. Power law scaling dN/dγ ∝ γ−2 is shown in dashed lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.