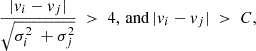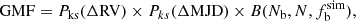EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 702 (October 2025) A&A, 702 (2025) A11 Full HTML
Open Access
Issue
A&A
Volume 702, October 2025
Article Number A11
Number of page(s) 8
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202555002
Published online 26 September 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Blue horizontal branch (BHB) stars are low-mass (< 1.0 M⊙) metal-poor Population II stars that are typically found in the Galactic halo; the majority are A-type stars (Arp et al. 1952; Behr 2003; Gray & Corbally 2009; Catelan 2009). These stars are horizontal branch (HB) stars positioned to the blue side of RR Lyrae variables, where they undergo core helium fusion while sustaining hydrogen shell burning in their outer layers (Searle & Rodgers 1966; Ruhland et al. 2011; Culpan et al. 2021). Similar to RR Lyrae stars, BHB stars are used as standard candles, due to their nearly constant luminosity across a wide range of effective temperatures (Dorman 1995; Layden et al. 1996; Culpan et al. 2024). Given that BHB stars are over ten times more abundant than RR Lyrae stars, they are more commonly used to investigate the Galactic halo and serve as the preferred tracer for estimating its mass distribution (Pier 1984; Beers et al. 1996; York et al. 2000; Xue et al. 2008; Catelan 2009; Xue et al. 2011).

Some studies have investigated the formation of BHB stars (Arp et al. 1952; Castellani & Renzini 1968; Iben & Rood 1970; Sweigart 1990; Maxted et al. 2001; Ruhland et al. 2011; Girardi 2016; Heber 2016). Hoyle & Schwarzschild (1955) were the first to accurately recognize that HB stars originate from low-mass red giant branch (RGB) stars undergoing core helium burning while sustaining hydrogen shell burning (Faulkner 1966; Moehler 2001). During the RGB phase, stars experience significant mass loss; blue HB stars lose more mass than red HB stars, which accounts for their color differences (Catelan 2009). High-metallicity star clusters typically have a predominantly red horizontal branch, while low-metallicity clusters generally exhibit a blue horizontal branch (Faulkner 1966). Additionally, several studies suggest that BHB stars may also have a binary-related origin (Liebert et al. 1994; Bailyn 1995; Rich et al. 1997; Hubrig et al. 2009; Li et al. 2024), although the specific mechanisms remain unclear due to limited research.

The binary fraction is very important for understanding the evolution of stellar populations and the formation of many objects (Raghavan et al. 2010; Duchêne & Kraus 2013; Moe & Di Stefano 2017; Chen et al. 2018; Liu 2019; Han et al. 2020; Chen et al. 2024). However, observed fractions can be affected by observational biases (Kobulnicky & Fryer 2007; Sana & Evans 2011; Sana et al. 2012). To correct for observational biases, Sana et al. (2013) proposed a method using Monte Carlo simulations, which has been widely adopted in many studies to obtain the intrinsic binary fraction by correcting the observed fraction for these biases (Sana et al. 2012; Dunstall et al. 2015; Banyard et al. 2022; Mahy et al. 2022; Guo et al. 2022a; Luo et al. 2021). A homogeneous sample with multiple observations and reliable radial velocity (RV) measurements would yield more reliable results (Luo et al. 2021; Guo et al. 2022b).

The current spectroscopic surveys, including the Sloan Digital Sky Survey (SDSS) (York et al. 2000) and the Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST) (Cui et al. 2012; Liu et al. 2020), offer valuable opportunities to study stellar statistical properties with huge homogeneous samples. Xue et al. (2011) selected 4985 BHB stars from SDSS DR8 using color cuts and criteria derived from Balmer-line profiles. Ju et al. (2024) cataloged 5355 BHB stars using low-resolution spectra from LAMOST. The sample of Ju et al. (2024) includes multiple observations and reliable radial velocity (RV) measurements after cross-matching with the RV catalog from LAMOST MRS (Zhang et al. 2021). Given the potential binary-related origin of BHB stars and the observed correlations between their metallicities, kinematics, and horizontal branch morphology, in this work we aim to investigate the relationship between the binary fractions of BHB stars, their metallicities and kinematics, and their positions on the Hertzsprung–Russell (HR) diagram, applying the method of Sana et al. (2013) based on the sample from Ju et al. (2024).

The structure of the paper is as follows. We introduce the LAMOST data in Section 2. In Section 3 we describe the sample grouping and criteria for the binary. A brief description of the Monte Carlo method to correct for observational biases is provided in Section 4. The results are presented in Sect. 5. Finally, we summarize the work and present our conclusions in Sect. 6.

2. Data

The Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST), located at the Xinglong Station of the National Astronomical Observatories in China, is a four-meter quasi-meridian reflecting Schmidt telescope. Its innovative design allows for a wide field of view, with a focal plane spanning 5 degrees and accommodating up to 4000 fibers simultaneously (Cui et al. 2012; Zhao et al. 2012; Deng et al. 2012). Since 2012, LAMOST has been conducting the Low-Resolution Spectroscopic survey (LRS), characterized by a resolving power of R ∼ 1800 and a wavelength range of 3690 ∼ 9100 Å (Deng et al. 2012). In October 2018, LAMOST initiated the Medium-Resolution Survey (MRS) with a resolution of R ∼ 7500 to collect multi-epoch observations. The MRS spectra obtained with the blue arm span a wavelength range from 495 to 535 nm, while the red arm covers a wavelength range from 630 to 680 nm (Liu et al. 2020).

By measuring the equivalent widths of multiple absorption line profiles and spectral features, Ju et al. (2024) identified 5355 BHB stars from LAMOST low-resolution spectra. In this work, we utilized the BHB stars and their atmospheric parameters identified by Ju et al. (2024) from LAMOST DR5 and cross-matched these stars with the updated RV catalog from LAMOST DR10 based on medium-resolution spectra (Zhang et al. 2021) to analyze their binarity.

3. Sample selection and binary criteria

3.1. Sample selection

Since we aim to investigate the binary properties of BHB stars, our sample selection requires each star to have at least two observations (see Sect. 3.3). Starting from an initial sample of 5355 BHB stars, we obtained a subset of 345 sources with more than twice reliable RV measurements (signal-to-noise ratio ≥ 20) and robust atmospheric parameters.

Blue horizontal branch stars are particularly susceptible to contamination from main-sequence (MS) stars. In Ju et al. (2024), the sample was filtered using equivalent width cuts on Hγ and G4300, along with Balmer-line profile cuts, to remove MS contaminants. However, because this method relies on automated selection across a large sample without visual inspection, some residual contamination may remain. Since MS contamination impacts the BHB samples differently depending on their characteristics, the detailed removal of MS contaminants is described in Sect. 3.2 after classification. After removal, we ultimately obtained a subset of 299 sources and the distribution of observation frequencies in our sample is shown in Figure 1. We find that 87% of the sources have more than three observations, while only a few stars have a higher number of epochs. We present the information for each star in Table 1.

thumbnail Fig. 1.

Distribution of the number of observational epochs for the 299 BHB stars in our sample. All stars with more than ten observations are grouped in the “> 10” bin.

Table 1.

Radial velocity catalogs.

According to Sana et al. (2013), Luo et al. (2021), Guo et al. (2022a), and Guo et al. (2022b), both sample size and observation frequency significantly influence the uncertainty of the binary fraction. Therefore, we need to ensure sufficient observation frequency while maintaining an adequate sample size for statistical reliability. To assess the impact of observation frequency, we tested the results for samples with more than two, three, four, five, and six observations. However, we found that for four, five, and six observations, the sample size became too small for reliable statistical analysis. Therefore, our further analysis and main conclusions are based on the results for stars with at least two and three observations.

3.2. Grouping of the sample

According to the age–metallicity relation, stars with higher metallicity generally tend to be younger, while those with lower metallicity are typically older (Twarog 1980; Carraro et al. 1998; Rocha-Pinto et al. 2000). Additionally, azimuthal velocity (Vϕ) provides insight into the Galactic component to which these stars belong: higher Vϕ values indicate significant rotational motion, characteristic of disk stars, and lower Vϕ values suggest weaker rotational support, consistent with halo stars (Tian et al. 2019; Belokurov et al. 2020; Tian et al. 2024). Figure 2 presents the relationship between azimuthal velocity (Vϕ) and metallicity ([Fe/H]) for our sample, where the data points are divided into two main groups using the magenta dashed line. Based on these two properties, we classify stars with higher metallicity and higher azimuthal velocity as disk-like BHB stars, while those with lower metallicity and lower azimuthal velocity are classified as halo-like BHB stars. This classification is motivated by the investigation of the correlation between metallicity, kinematics, and binary fraction. It is worth noting that the [Fe/H]–Vϕ classification is not absolute: some stars with [Fe/H] ∼ −1 and high Vϕ may still be genuine halo members, while those with [Fe/H] ∼ −1.5 and Vϕ ∼ 200 km/s could in fact belong to the thick disk. To further investigate the relationship between binary fraction and effective temperature, we divided our sample into two groups based on effective temperature using Teff = 9200 K as the boundary, which approximately corresponds to the midpoint of our sample’s temperature range. We note that under these two classifications, we have also ensured that the number of detectable binaries in each group is comparable (see the Nb column in Table 3) since too few detectable binaries may lead to increased random errors.

thumbnail Fig. 2.

Classification of BHB stars based on kinematics and metallicity. The magenta dashed line represents the boundary used to separate halo-like (gray) and disk-like (black) BHB stars in the plane of azimuthal velocity and metallicity.

After the classification, we subsequently excluded residual MS contaminants from each group, as motivated by the reasons detailed in Section 3.1. Since MS contamination affects only the disk sample (hot MS stars are young and not expected in halos), we further cleaned the disk-like BHB sample with the following step. Salgado et al. (2013) show that horizontal branch stars with Teff ≤ 10 500 K inhabit log g ∼ 3.0 − 4.0 dex, whereas MS stars at similar Teff lie at log g > 4.0. We therefore removed 26 redder disk-like (Teff ≤ 10 500 K) candidates with log g > 4.0 dex. Additionally, recognizing that some halo-like stars may be misclassified non-halo objects, we applied the same criterion to the halo-like BHB group and removed four additional stars. We derived the absolute V-band magnitude (MV) for each star by calculating the absolute Gaia G-band magnitude (MG) and applying the photometric transformation coefficients provided in the Gaia Data Release 3 documentation1. The distances and extinction values required in this process were obtained from Ju (in prep.), who constructed new BP-band absolute magnitude-(BP-RP) relations for BHB stars based on accurate Gaia distances estimated by Bailer-Jones et al. (2021). These values were then derived through repeated iterations. Because genuine red HB stars are typically brighter than MS stars, with MV ∼ 0.5 − 1.0, and the sample becomes increasingly dispersed above MV > 1.3, we excluded 16 disk-like BHB candidates with MV > 1.3 to minimize the MS contamination. Unfortunately, for the hotter disk-like BHBs, the difference in MV between genuine BHBs and MS stars becomes too small to separate cleanly. In addition, even after applying the spectral profile diagnostics described in Ju et al. (2024), we cannot effectively remove MS contaminants from the hotter BHB sample. Therefore, throughout Section 5, we highlight, for every relevant result, the limitations associated with hotter disk-like BHB stars that may be affected by MS contamination. As shown in Figure 3, a magenta vertical line at Teff = 9200 K separates the hotter bluer BHB stars from the cooler redder BHB stars. The halo-like BHB stars are depicted as gray dots, while the disk-like BHB stars are represented by black dots. Observed binaries (see Sect. 3.3) are distinguished by color; the red star markers are halo-like binaries and the cyan stars are disk-like binaries.

thumbnail Fig. 3.

Classification of BHB stars based on their positions on the Kiel diagram. The magenta dashed line marks the boundary distinguishing redder BHB stars and bluer BHB stars in the plane of effective temperature and surface gravity. The gray dots represent halo-like BHB stars, while the black dots denote disk-like BHB stars. Halo-like observed binaries (red stars) and disk-like observed binaries (cyan stars) are highlighted accordingly.

3.3. Criterion for the binary

To identify binary systems in our sample, we applied the criterion from Equation (4) in Sana et al. (2013), which has been widely used in previous studies (Sana et al. 2012; Dunstall et al. 2015; Luo et al. 2021; Mahy et al. 2022; Banyard et al. 2022; Guo et al. 2022a). This criterion classifies a star as a binary if its radial velocities (RVs) satisfy the following conditions:

| v i − v j | σ i 2 + σ j 2 > 4 , and | v i − v j | > C , $$ \begin{aligned} \frac{|v_{i} - v_{j}|}{\sqrt{\sigma _{i}^2 \ + \sigma _{j}^2}}\ > \ 4, \,\mathrm{and}\, {|v_{i} - v_{j}|}\ > \ C, \end{aligned} $$(1)

where vi(j) represents the RV measured from the spectrum at epoch i (j), and σi(j) is the corresponding uncertainty. To mitigate the significant RV variations caused by stars with pulsations, Sana et al. (2013) introduced threshold C here as a filter to remove pulsating stars. Based on the kinks observed in the RV distributions of their sample, Sana et al. (2013) adopted C = 20 km s−1 for O-type stars, while Dunstall et al. (2015) set C = 16 km s−1 for B-type stars. For our sample, the kink is weak, so it is more reasonable to adopt C based on the typical RV amplitudes of potential pulsators. Blue horizontal branch (BHB) stars are not located in the classical instability strip, and thus pulsating stars are rare among them (Aerts et al. 2010; Gaia Collaboration 2019; Gao et al. 2025). To date, only one such pulsator has been identified (Østensen et al. 2012), indicating that a significant number of pulsating stars are not expected in our sample, and thus the threshold is unnecessary. We therefore adopted C = 0 km s−1 for our subsequent analysis. In addition, we performed tests with C = 10 and 20 km/s to assess their impact on the intrinsic binary fractions, as discussed in Sect. 5.

4. Correction for observational biases

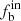Based on the observed binary fraction ( f b obs $ f_{\mathrm{b}}^{\mathrm{obs}} $), we applied several Monte Carlo (MC) simulations, similar to those of Sana et al. (2013), Dunstall et al. (2015), and Guo et al. (2022b) to assess the intrinsic binary fraction ( f b in $ f_{\mathrm{b}}^{\mathrm{in}} $). To conduct the simulations, we needed to generate two synthetic cumulative distribution functions (CDFs), one for the radial velocity variance (ΔRV), which represents the maximum RV variation across individual exposures, and another for the minimum time interval between exposures (ΔMJD). For the orbital period P and mass ratio q, we adopted a power-law distribution (Sana et al. 2013), expressed as f(P)∝Pπ and f(q)∝qκ, using log P instead of (log P)π because the linear form is more sensitive to short-period binaries (Guo et al. 2022a). Table 2 lists the variable ranges for the above parameters and the power index.

Table 2.

Range of different parameters and power indexes used in MC simulation.

Generally, a two-body kinetic system in Keplerian motion is characterized by several orbital parameters: the inclination (i), the semimajor axis (a), the argument of periastron (ω), the eccentricity (e), and the epoch of periastron (τ). The inclination is randomly selected between 0 and π/2 following a sin(i) probability distribution. The semimajor axis is related to the orbital period (P). Meanwhile, ω is uniformly distributed over the range 0–2π. The eccentricity is modeled by a distribution proportional to e raised to the power of eη. Given that the global merit function is insensitive to η (see Sana et al. 2013), we adopt −0.5 as in Sana et al. (2013), and τ is chosen at random, in units of days. Based on these assumptions, we can generate simulated radial velocity (RV) data, which then allows us to derive the cumulative distribution functions (CDFs) for both ΔRV and ΔMJD.

To evaluate the final results, we compare the constructed simulated CDFs with the observed ones using the Kolmogorov-Smirnov (KS) test, and the simulated fraction of detected binaries (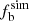 f b sim $ f_{\mathrm{b}}^{\mathrm{sim}} $) are analyzed through a binomial distribution (Sana et al. 2013). Finally, we employ the global merit function (GMF) from Sana et al. (2013) to determine the best-fitting results. The GMF consists of the KS probabilities of ΔRV and ΔMJD distributions and the binomial probability,

GMF = P ks ( Δ RV ) × P ks ( Δ MJD ) × B ( N b , N , f b sim ) , $$ \begin{aligned} \mathrm{GMF}= P_{\rm ks} (\Delta \mathrm{RV}) \times P_{ks}(\Delta \mathrm{MJD}) \times B(N_{\rm b},N,f_{\rm b}^\mathrm{sim}), \end{aligned} $$(2)

where Nb represents the number of binaries in the observations, and N denotes the sample size.

In our previous work by Guo et al. (2022a), we revisited the dataset of 360 O-type stars from Sana et al. (2013) and confirmed that its statistical properties align with those presented in Sana et al. (2013). Moreover, Luo et al. (2021), Guo et al. (2022a), and Guo et al. (2022b) have successfully applied this method to the LAMOST data, further demonstrating its applicability to our current study.

5. Results and discussions

According to the criterion (1), the observed binary factions of our BHB stars are 18%±2% for cases with n ≥ 2, and 21%±3% for cases with n ≥ 3, where n represents the number of observations for each sample. These results are summarized in Table 3. The error bars of 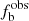f b obs $ f_{\mathrm{b}}^{\mathrm{obs}} $ were estimated through a bootstrap analysis (Raghavan et al. 2010; Guo et al. 2022a). Table 3 shows that none of the 55 detected binary were detected with only n = 2 epochs, so adding them to the n ≥ 3 sample leaves 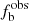f b obs $ f_{\mathrm{b}}^{\mathrm{obs}} $ essentially unchanged. To further quantify this, we ran Monte Carlo simulations assuming a 30% intrinsic binary fraction. For n = 2, the simulations show that only about 3 of 55 binaries are detected, demonstrating the very low detection efficiency with only two epochs.

Table 3.

Observed and intrinsic binary fractions for all BHB stars, and for halo-like, disk-like, redder, and bluer BHB subgroups, including sample size N and number of observed binaries Nb.

After the correction for observation bias (see Sect. 4), the 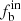f b in $ f_{\mathrm{b}}^{\mathrm{in}} $ of our BHB stars are 31%±3% for cases with n ≥ 2, and 32%±3% for cases with n ≥ 3, where the error bars are derived from the larger value between p84–p50 and p50–p16, corresponding to the 50th (p50), 16th (p16), and 84th (p84) percentiles of the intrinsic value distribution obtained from 50 synthetic datasets (Sana et al. 2013; Dunstall et al. 2015).

To assess the impact of C on the intrinsic binary fraction, we performed additional tests using C = 10 and 20 km/s. For our BHB sample, we obtained intrinsic binary fractions of 29% and 20% for C = 10 and 20 km/s, respectively. This difference arises because increasing C changes the sample composition, which alters the observational cumulative distribution functions of both ΔRV and ΔMJD, ultimately leading to variations in the final results. In addition, the effectiveness of the correction depends on the total number of detected binaries. As C increases, the number of detected binaries (Nbin) decreases significantly, from 55 at C = 0 km/s to 19 at C = 20 km/s. For smaller samples, the correction of f b in $ f_{\mathrm{b}}^{\mathrm{in}} $ is more susceptible to statistical uncertainties, thus exerting a greater influence on the final results.

The values of π and κ are consistent within the uncertainty range, with our study yielding π = −7.2 ± 0.8 and −7.5 ± 0.8, and κ = 1.1 ± 1.3 and 0.9 ± 1.3 for n ≥ 2 and n ≥ 3, respectively. Figure 4 illustrates the projections of the GMF for n ≥ 3 as an example, with the green cross (x) marking the position of the absolute maximum of 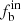f b in $ f_{\mathrm{b}}^{\mathrm{in}} $, π, and κ.

thumbnail Fig. 4.

Projections of the GMF onto planes defined by different pairs of π, κ, and f b in $ f_{\mathrm{b}}^{\mathrm{in}} $. The green cross (x) marks the position of the absolute maximum. The red, blue, green, and black contours indicate respectively regions of equal value corresponding to 60%, 80%, and 95% of the absolute maximum of the GMF.

5.1. Dependence on metallicities and kinematics

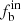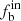The observed binary fraction is 15%±2% and 18%±3% for halo-like BHB stars and 30%±6% and 35%±7% for disk-like BHB stars for n ≥ 2 and n ≥ 3, respectively. Our results reveal a difference in the f b in $ f_{\mathrm{b}}^{\mathrm{in}} $ between halo-like and disk-like BHB stars. For cases with n ≥ 2, the f b in $ f_{\mathrm{b}}^{\mathrm{in}} $ is 28%±3% for halo-like BHB stars and 46%±11% for disk-like BHB stars; for n ≥ 3, the f b in $ f_{\mathrm{b}}^{\mathrm{in}} $ is 29%±3% for halo-like BHB stars and 51%±11%. These results are summarized in Table 3.

The low binary fraction of halo-like BHB stars may be explained as follows. Horizontal branch (HB) stars are generally formed from low-mass stars when they remove some envelope and ignite central helium in a degenerate core (He flashes; Sweigart 1990; Liebert et al. 1994; Dorman 1995). For halo-like BHB stars, the progenitors (before He flash) are older (and less massive) and have lower metallicity than that of disk-like BHB stars (Lee et al. 1990, 1994). For stars with low mass and low metallicity, helium ignition in single-star evolution results in relatively high temperatures, directly placing them near the BHB region, with many likely originating from disrupted globular clusters (Xue et al. 2011). The low binary fraction (28–29%) of halo-like BHB stars aligns with this scenario and indicates that binary interaction has little contribution to halo-like BHB stars. However, this fraction is not particularly low.

Moe et al. (2019) report that the intrinsic binary fraction of metal-poor giants branch is approximately 35%–55% across the metallicity range −3.5 < [Fe/H] < −1.0, while metal-rich giants with [Fe/H] > −1.0 exhibit lower binary fractions of about 20%–35%. Since BHB stars generally originate from red giant branch (RGB) stars, comparing the binary fractions of these progenitor populations with those of BHB stars provides key insights into the role of binarity in BHB formation (Hoyle & Schwarzschild 1955; Sweigart & Gross 1976; Dorman et al. 1993). If binary interaction plays a dominant role in the formation of BHB stars, one would expect the BHB binary fraction to be significantly higher than that of their RGB progenitors. Conversely, comparable binary fractions would suggest that binary interaction may not be a key factor. The comparable binary fractions of metal-poor RGB stars (35%–55%) and our halo-like BHBs (29%), together with the even higher binary fraction of metal-poor low-mass MS stars (54%; Moe et al. 2019) and intermediate-mass MS stars (∼50%; Gao et al. 2017), suggest that most binary systems may be preserved during the evolution from the main sequence through the RGB to the BHB stage or, alternatively, that BHB binaries may originate from different evolutionary channels.

Metal-rich stars evolving via single-star evolution typically evolve into red clump (RC) stars rather than BHB stars because the lower temperature during helium burning causes them to directly settle on the RC (Girardi 2016; Moehler 2025). Therefore, for metal-rich stars to appear on the BHB, they may have much thinner envelopes–potentially achieved either through enhanced mass loss via stellar winds or through binary interactions. The significantly higher binary fraction of disk-like BHBs (51%) compared to both metal-rich RGB stars (20%–35%) and metal-rich low-mass MS stars (17%) strongly supports a binary-related formation scenario for these stars. Although metal-rich intermediate-mass MS stars exhibit binary fractions of 30%–60% Gao et al. 2017; Moe et al. 2019; Guo et al. 2022b, comparable to our disk-like BHBs, suggesting that binarity may not play a significant role in this case. However, due to the IMF, their contribution is small and may have little effect on the disk-like BHB binary fraction. Several studies have proposed a possible binary-related origin for BHB stars (Liebert et al. 1994; Bailyn 1995; Rich et al. 1997; Heber 2009). Similar to the formation of extreme horizontal branch (EHB) stars, stable Roche-lobe overflow (RLOF), common envelope (CE) ejection, and merger channels are plausible pathways for removing the hydrogen envelope (Maxted et al. 2001; Han et al. 2002; Han 2008). Additionally, halo-like BHB stars are generally older than disk-like BHB stars and exhibit a lower binary fraction, which may be partly attributed to age differences. According to the simulations of Han (2008), as stellar populations age (i.e., transitioning from young disk-like systems to old halo-like systems), the dominant formation channel for EHB stars shifts from stable mass transfer to mergers, resulting in a lower binary fraction among older stars. This trend may also be relevant for BHB stars, suggesting that similar binary interaction processes influence the formation and binary properties of both EHB and BHB stars. While the dominant mechanism remains uncertain, the higher binary fraction in metal-rich BHB stars (45–48%) compared to halo-like BHBs supports the idea that binary interactions are a key factor in their formation. In addition, we find that the disk-like group contains more hotter stars, so the higher binary fraction may also result from this temperature distribution (see Fig. 5 and the discussion in Section. 5.1). Notably, because we cannot entirely rule out residual MS contamination in the disk-like sample, the reported binary fraction may be slightly overestimated.

thumbnail Fig. 5.

Histogram of the number of halo-like BHB (black dashed) and disk-like BHB (black solid) stars as a function of their Teff (in kK).

The values of π and κ are consistent within the uncertainty range. For halo-like BHB stars, our study yields π = −5.8 ± 1.4 and −5.4 ± 1.4, and κ = 0.7 ± 1.6 and 0.9 ± 1.6 for n ≥ 2 and n ≥ 3, respectively. Similarly, for disk-like BHB stars, we obtain π = −6.5 ± 0.6 and −6.0 ± 0.6, and κ = 1.1 ± 1.3 and 3.6 ± 1.3 for n ≥ 2 and n ≥ 3, respectively.

5.2. Dependence on Kiel diagram

The observed binary fraction is 23%±4% and 27%±4% for bluer BHB stars and 14%±3% and 16%±3% for redder BHB stars for n ≥ 2 and n ≥ 3, respectively. We then examined the 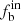f b in $ f_{\mathrm{b}}^{\mathrm{in}} $ at different positions on the Kiel diagram and found that the bluer BHB sample exhibits a significantly higher f b in $ f_{\mathrm{b}}^{\mathrm{in}} $ (42%±6% for n ≥ 2 and 45%±6% for n ≥ 3) than the redder BHB sample (24%±5% for n ≥ 2 and 23%±5% for n ≥ 3). These results are summarized in Table 3.

Extreme horizontal branch stars, which are core-helium burning stars exhibiting lower masses and higher temperatures than canonical BHB stars, are strongly linked to binary interactions (Maxted et al. 2001; Han et al. 2002, 2003; Heber 2009). The minimum binary fraction for EHB stars is inferred to be 60%±8% based on Maxted et al. (2001), while Han et al. (2003) report an intrinsic binary fraction ranging from 76% to 89%. Stable Roche-lobe overflow and common envelope evolution serve as the main channels for envelope stripping in red giant stars. These processes effectively remove the outer envelope, leaving behind a core-helium burning star with a lower mass and a higher effective temperature. Similarly, BHB stars are also formed through mass loss on the red giant branch. In this context, the formation mechanisms of BHB stars and sdOB stars may follow a common evolutionary channel, but the BHB stars experience a less extreme degree of envelope removal. High envelope removal efficiency may favor evolution into an EHB, whereas lower efficiency may result in the star remaining as a BHB object. The bluer a BHB star is (i.e., the closer it is to the EHB region), the more extensive the envelope stripping required. This may make the single-star channel increasingly unlikely, and suggests that binary interactions could play a significant role in achieving such stripping. This aligns with our finding that the bluer BHB sample exhibits a significantly higher intrinsic binary fraction (45%) compared to the redder BHB sample (23%) and the observed binary fraction. These observations suggest that the actual envelope ejection process in CE evolution may be less “clean” or efficient than idealized models predict, and this evidence can help constrain the physical parameters and efficiency of envelope stripping in CE evolution, potentially refining our understanding of binary evolution.

Figure 5 displays the number of halo-like BHB and disk-like BHB stars as a function of effective temperature. The histogram shows that halo-like stars are systematically cooler, while the disk-like sample contains a great number of hotter stars. This distinction may leads to higher overall binary fraction observed in the disk sample because hotter BHB stars have higher binary fractions. It is important to note that we cannot completely eliminate MS contamination from the hotter disk-like BHB sample. Any residual contaminants may still lead to a modest overestimation of the binary fraction.

In Figure 3, we find that the halo-like BHB stars are relatively evenly distributed across the diagram, and their observed binaries (red stars) also do not exhibit pronounced clustering. In contrast, the disk-like observed binaries (cyan stars) show a tendency to cluster toward the bluer region. Although this may hint at a higher fraction of detectable binaries in those specific areas, the pattern should be viewed cautiously as more data would be needed to confirm any definitive trend.

The trend of π and κ remains consistent within the uncertainty range across different subsets of BHB stars. For bluer BHB stars, our analysis yields π = −5.4 ± 1.9 and −6.2 ± 1.9, with corresponding κ values of 0.5 ± 1.4 and 0.4 ± 1.4 for n ≥ 2 and n ≥ 3, respectively. Likewise, for redder BHB stars, we derive π = −6.4 ± 1.1 and −6.1 ± 1.1, along with κ = 3.4 ± 1.2 and 3.5 ± 1.2 for n ≥ 2 and n ≥ 3.

6. Summary

Blue horizontal branch stars are valuable tracers of the Galactic halo, commonly used to study its structure and kinematics. Their nearly constant luminosity across a wide range of temperatures makes them reliable standard candles. Investigating their binary properties provides crucial insights into their formation pathways and the role of binary interactions in stellar evolution.

In this work, we first selected a sample of 299 BHB stars with multiple observations from the catalog of Ju et al. (2024). We then classified the sample into disk-like and halo-like groups based on their metallicities and kinematics, and separately into bluer and redder groups according to their effective temperature, in order to investigate their relationship with the binary fraction. Using the Markov chain Monte Carlo (MCMC) framework developed by Sana et al. (2013), we corrected the observed binary fraction for any observational biases.

The intrinsic binary fraction of all 299 BHB stars is 31%±3% for n ≥ 2 and 32%±3% for n ≥ 3. A difference was observed in the intrinsic binary fraction between halo-like and disk-like BHB stars. Halo-like BHB stars exhibited an 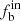f b in $ f_{\mathrm{b}}^{\mathrm{in}} $ of 28%±3% for n ≥ 2 and 29%±3% for n ≥ 3, whereas disk-like BHB stars had a much higher binary fraction of 46%±11% and 51%±11% for n ≥ 2 and n ≥ 3, respectively, indicating that binary interactions play a more significant role in disk-like BHB stars. We further examined the binary fraction at different positions on the Kiel diagram and found that the bluer BHB sample exhibited a significantly higher f b in $ f_{\mathrm{b}}^{\mathrm{in}} $ (42%±6% for n ≥ 2 and 45%±6% for n ≥ 3) compared to the redder BHB sample (24%±5% for n ≥ 2 and 23%±5% for n ≥ 3), suggesting a potential correlation between binarity and the effective temperature of BHB stars. These observations may help to better constrain the efficiency of envelope stripping during common envelope evolution, offering a modest refinement in our understanding of binary evolution. We find no significant correlation between π (κ) and metallicity or kinematics, nor with the position of BHB stars on the Kiel diagram.

Data availability

Table 1 is only available at the CDS via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/702/A11

Acknowledgments

This work is supported by the Natural Science Foundation of China (Nos. 12288102,12125303,12090040/3,12103064,12403039,12373036), the National Key R&D Program of China (grant Nos. 2021YFA1600403/1, 2021YFA1600400), and the Natural science Foundation of Yunnan Province (Nos. 202201BC070003, 202001AW070007), the International Centre of Supernovae, Yunnan Key Laboratory (No. 202302AN360001), the “Yunnan Revitalization Talent Support Program"-Science, Technology Champion Project (N0. 202305AB350003), and Yunnan Fundamental Research Projects (grant Nos. 202501CF070018).

References

  1. Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer Science+Business Media B.V.) [Google Scholar]
  2. Arp, H. C., Baum, W. A., & Sandage, A. R. 1952, AJ, 57, 4 [CrossRef] [Google Scholar]
  3. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
  4. Bailyn, C. D. 1995, ARA&A, 33, 133 [NASA ADS] [CrossRef] [Google Scholar]
  5. Banyard, G., Sana, H., Mahy, L., et al. 2022, A&A, 658, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Beers, T. C., Wilhelm, R., Doinidis, S. P., & Mattson, C. J. 1996, ApJS, 103, 433 [NASA ADS] [CrossRef] [Google Scholar]
  7. Behr, B. B. 2003, ApJS, 149, 67 [NASA ADS] [CrossRef] [Google Scholar]
  8. Belokurov, V., Sanders, J. L., Fattahi, A., et al. 2020, MNRAS, 494, 3880 [Google Scholar]
  9. Carraro, G., Ng, Y. K., & Portinari, L. 1998, MNRAS, 296, 1045 [NASA ADS] [CrossRef] [Google Scholar]
  10. Castellani, V., & Renzini, A. 1968, Ap&SS, 2, 310 [Google Scholar]
  11. Catelan, M. 2009, Ap&SS, 320, 261 [Google Scholar]
  12. Chen, X., Li, Y., & Han, Z. 2018, Sci. Sin. Phys. Mech. Astron., 48, 079803 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chen, X., Liu, Z., & Han, Z. 2024, Progr. Part. Nucl. Phys., 134, 104083 [Google Scholar]
  14. Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, Res. Astron. Astrophys., 12, 1197 [Google Scholar]
  15. Culpan, R., Pelisoli, I., & Geier, S. 2021, A&A, 654, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Culpan, R., Dorsch, M., Geier, S., et al. 2024, A&A, 685, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Deng, L.-C., Newberg, H. J., Liu, C., et al. 2012, Res. Astron. Astrophys., 12, 735 [Google Scholar]
  18. Dorman, B. 1995, Liege International Astrophysical Colloquia, 32, 291 [Google Scholar]
  19. Dorman, B., Rood, R. T., & O’Connell, R. W. 1993, ApJ, 419, 596 [NASA ADS] [CrossRef] [Google Scholar]
  20. Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
  21. Dunstall, P. R., Dufton, P. L., Sana, H., et al. 2015, A&A, 580, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Faulkner, J. 1966, ApJ, 144, 978 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gaia Collaboration (Eyer, L., et al.) 2019, A&A, 623, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Gao, S., Zhao, H., Yang, H., & Gao, R. 2017, MNRAS, 469, L68 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gao, X., Chen, X., Wang, S., & Liu, J. 2025, ApJS, 276, 57 [Google Scholar]
  26. Girardi, L. 2016, ARA&A, 54, 95 [Google Scholar]
  27. Gray, R. O., & Corbally, J. C. 2009, Stellar Spectral Classification (Princeton University Press) [Google Scholar]
  28. Guo, Y., Li, J., Xiong, J., et al. 2022a, Res. Astron. Astrophys., 22, 025009P [Google Scholar]
  29. Guo, Y., Liu, C., Wang, L., et al. 2022b, A&A, 667, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Han, Z. 2008, A&A, 484, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [Google Scholar]
  32. Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
  33. Han, Z.-W., Ge, H.-W., Chen, X.-F., & Chen, H.-L. 2020, Res. Astron. Astrophys., 20, 161 [CrossRef] [Google Scholar]
  34. Heber, U. 2009, ARA&A, 47, 211 [Google Scholar]
  35. Heber, U. 2016, PASP, 128, 082001 [Google Scholar]
  36. Hoyle, F., & Schwarzschild, M. 1955, ApJS, 2, 1 [NASA ADS] [CrossRef] [Google Scholar]
  37. Hubrig, S., Castelli, F., de Silva, G., et al. 2009, A&A, 499, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Iben, I., Jr, & Rood, R. T. 1970, ApJ, 161, 587 [Google Scholar]
  39. Ju, J., Cui, W., Huo, Z., et al. 2024, ApJS, 270, 11 [Google Scholar]
  40. Kobulnicky, H. A., & Fryer, C. L. 2007, ApJ, 670, 747 [NASA ADS] [CrossRef] [Google Scholar]
  41. Layden, A. C., Hanson, R. B., Hawley, S. L., Klemola, A. R., & Hanley, C. J. 1996, AJ, 112, 2110 [NASA ADS] [CrossRef] [Google Scholar]
  42. Lee, Y.-W., Demarque, P., & Zinn, R. 1990, ApJ, 350, 155 [Google Scholar]
  43. Lee, Y.-W., Demarque, P., & Zinn, R. 1994, ApJ, 423, 248 [NASA ADS] [CrossRef] [Google Scholar]
  44. Li, Z., Zhang, Y., Chen, H., et al. 2024, ApJ, 964, 22 [NASA ADS] [CrossRef] [Google Scholar]
  45. Liebert, J., Saffer, R. A., & Green, E. M. 1994, AJ, 107, 1408 [Google Scholar]
  46. Liu, C. 2019, MNRAS, 490, 550 [NASA ADS] [Google Scholar]
  47. Liu, C., Fu, J., Shi, J., et al. 2020, ArXiv e-prints [arXiv:2005.07210] [Google Scholar]
  48. Luo, F., Zhao, Y.-H., Li, J., Guo, Y.-J., & Liu, C. 2021, Res. Astron. Astrophys., 21, 272 [Google Scholar]
  49. Mahy, L., Lanthermann, C., Hutsemékers, D., et al. 2022, A&A, 657, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Maxted, P. F. L., Heber, U., Marsh, T. R., & North, R. C. 2001, MNRAS, 326, 1391 [CrossRef] [Google Scholar]
  51. Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
  52. Moe, M., Kratter, K. M., & Badenes, C. 2019, ApJ, 875, 61 [NASA ADS] [CrossRef] [Google Scholar]
  53. Moehler, S. 2001, PASP, 113, 1162 [NASA ADS] [CrossRef] [Google Scholar]
  54. Moehler, S. 2025, A&A, 693, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Østensen, R. H., Degroote, P., Telting, J. H., et al. 2012, ApJ, 753, L17 [CrossRef] [Google Scholar]
  56. Pier, J. R. 1984, ApJ, 281, 260 [Google Scholar]
  57. Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [Google Scholar]
  58. Rich, R. M., Sosin, C., Djorgovski, S. G., et al. 1997, ApJ, 484, L25 [NASA ADS] [CrossRef] [Google Scholar]
  59. Rocha-Pinto, H. J., Maciel, W. J., Scalo, J., & Flynn, C. 2000, A&A, 358, 850 [NASA ADS] [Google Scholar]
  60. Ruhland, C., Bell, E. F., Rix, H.-W., & Xue, X.-X. 2011, ApJ, 731, 119 [NASA ADS] [CrossRef] [Google Scholar]
  61. Salgado, C., Moni Bidin, C., Villanova, S., Geisler, D., & Catelan, M. 2013, A&A, 559, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
  63. Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Sana, H., & Evans, C. J. 2011, in Active OB Stars: Structure, Evolution, Mass Loss, and Critical Limits, eds. C. Neiner, G. Wade, G. Meynet, & G. Peters, IAU Symp., 272, 474 [Google Scholar]
  65. Searle, L., & Rodgers, A. W. 1966, ApJ, 143, 809 [Google Scholar]
  66. Sweigart, A. V. 1990, in Confrontation Between Stellar Pulsation and Evolution, eds. C. Cacciari, & G. Clementini, ASP Conf. Ser., 11, 1 [Google Scholar]
  67. Sweigart, A. V., & Gross, P. G. 1976, ApJS, 32, 367 [NASA ADS] [CrossRef] [Google Scholar]
  68. Tian, H., Liu, C., Xu, Y., & Xue, X. 2019, ApJ, 871, 184 [NASA ADS] [CrossRef] [Google Scholar]
  69. Tian, H., Liu, C., Li, J., & Zhang, B. 2024, MNRAS, 531, 1730 [Google Scholar]
  70. Twarog, B. A. 1980, ApJ, 242, 242 [NASA ADS] [CrossRef] [Google Scholar]
  71. Xue, X. X., Rix, H. W., Zhao, G., et al. 2008, ApJ, 684, 1143 [Google Scholar]
  72. Xue, X.-X., Rix, H.-W., Yanny, B., et al. 2011, ApJ, 738, 79 [NASA ADS] [CrossRef] [Google Scholar]
  73. York, D. G., Adelman, J., Anderson, J. E., Jr, et al. 2000, AJ, 120, 1579 [Google Scholar]
  74. Zhang, B., Li, J., Yang, F., et al. 2021, ApJS, 256, 14 [NASA ADS] [CrossRef] [Google Scholar]
  75. Zhao, G., Zhao, Y.-H., Chu, Y.-Q., Jing, Y.-P., & Deng, L.-C. 2012, Res. Astron. Astrophys., 12, 723 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Radial velocity catalogs.

In the text
Table 2.

Range of different parameters and power indexes used in MC simulation.

In the text
Table 3.

Observed and intrinsic binary fractions for all BHB stars, and for halo-like, disk-like, redder, and bluer BHB subgroups, including sample size N and number of observed binaries Nb.

In the text

All Figures

thumbnail Fig. 1.

Distribution of the number of observational epochs for the 299 BHB stars in our sample. All stars with more than ten observations are grouped in the “> 10” bin.
In the text
thumbnail Fig. 2.

Classification of BHB stars based on kinematics and metallicity. The magenta dashed line represents the boundary used to separate halo-like (gray) and disk-like (black) BHB stars in the plane of azimuthal velocity and metallicity.
In the text
thumbnail Fig. 3.

Classification of BHB stars based on their positions on the Kiel diagram. The magenta dashed line marks the boundary distinguishing redder BHB stars and bluer BHB stars in the plane of effective temperature and surface gravity. The gray dots represent halo-like BHB stars, while the black dots denote disk-like BHB stars. Halo-like observed binaries (red stars) and disk-like observed binaries (cyan stars) are highlighted accordingly.
In the text
thumbnail Fig. 4.

Projections of the GMF onto planes defined by different pairs of π, κ, and f b in $ f_{\mathrm{b}}^{\mathrm{in}} $. The green cross (x) marks the position of the absolute maximum. The red, blue, green, and black contours indicate respectively regions of equal value corresponding to 60%, 80%, and 95% of the absolute maximum of the GMF.
In the text
thumbnail Fig. 5.

Histogram of the number of halo-like BHB (black dashed) and disk-like BHB (black solid) stars as a function of their Teff (in kK).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.