EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 702 (October 2025) A&A, 702 (2025) A211 Full HTML
Open Access
Issue
A&A
Volume 702, October 2025
Article Number A211
Number of page(s) 22
Section Planets, planetary systems, and small bodies
DOI https://doi.org/10.1051/0004-6361/202555253
Published online 20 October 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Following the conclusion of the primary Kepler mission, NASA’s K2 mission expanded the search for transiting exoplanets by targeting stars along the ecliptic plane (Howell et al. 2014). Unlike Kepler, which focused on a fixed field, K2 covered a broader sky region, observed a more diverse stellar population, and prioritized brighter stars, making them ideal candidates for radial-velocity (RV) follow-up studies. These extensive long-term surveys led to the unexpected discovery of numerous sub-Neptune-sized planets (1.75 R⊕ ≲ Rp ≲ 3.5 R⊕, following Kopparapu et al. 2018) in compact, coplanar multi-planetary systems (e.g., Borucki et al. 2011; Latham et al. 2011; Weiss et al. 2018; Bean et al. 2021). The prevalence of such systems has made them key cornerstones of exoplanet research, offering crucial insights into planetary formation and evolution while bridging the gap between the Solar System and the wide diversity of known exoplanetary architectures (Bean et al. 2021). Among this population, sub-Neptunes on long-period orbits are exceptionally valuable. Situated at larger orbital distances, they are shielded from the intense stellar X-ray and ultraviolet (XUV) radiation that drives atmospheric escape via photoevaporation (Lopez & Fortney 2014; Owen & Wu 2017). Consequently, these planets are expected to retain their primordial atmospheres. Their present-day atmospheric properties, such as mass fraction and composition, therefore, offer a more direct probe of the conditions within the proto-planetary disk during their formation as well as their evolution. This makes them prime targets for constraining planet formation models through atmospheric characterization studies (Madhusudhan 2019; Bean et al. 2021). In this context, the multi-planet system around the bright (mV = 8.93) late F-type star HIP 41378 (K2-93) stands out as one of only five systems, alongside those around 55 Cnc (Butler et al. 1997), HD 219134 (Gillon et al. 2017), HD 110067 (Luque et al. 2023), HD 191939 (Badenas-Agusti et al. 2020), and Kepler-444 (Campante et al. 2015) that host more than four confirmed planets with both mass and radius constraints, while also hosting a star brighter than mV = 9 mag.

The system was first identified by Vanderburg et al. (2016) during Campaign 5 of the K2 mission (April–July 2015). After its discovery, the system was reobserved three years later during Campaign 18 (May–July 2018) (Berardo et al. 2019, hereafter B19; Becker et al. 2019). The K2 data revealed a system of five transiting planets (from b to f), with the two inner sub-Neptunes (HIP 41378 b and c) exhibiting well-constrained orbital periods of 15.6 and 31.7 days respectively, near a 2:1 period commensurability. However, for the three outer planets, an insufficient number of transits were recovered to determine their orbital periods, leaving only a set of possible period aliases. Based on the 75-day baseline of the K2 C5 campaign and the long transit durations of the planets, the highest-probability aliases derived suggested long-period orbits for the outer planets (P > 100 days). The first mass measurements of the planets in the system were obtained by Santerne et al. (2019, hereafter S19) using radial velocity (RV) observations from HARPS, HARPS-N, the Carnegie Planet Finder Spectrograph (PFS; Crane et al. 2006, 2008, 2010) and HIRES (High Resolution Echelle Spectrometer). The authors detected strong RV signals from planets b, c, and f, but were unable to retrieve any signal from planets d and e. Additionally, they identified a periodic signal at ~62 days, attributed to a possible non-transiting planet (hereafter HIP 41378 g) near a 2:1 period commensurability with planet c raising the possibility of strong dynamical interactions among the inner three planets in a near-resonant chain, which could result in observable transit timing variations (TTVs) (Agol et al. 2005; Holman & Murray 2005). Their analysis also constrained the orbital period of HIP 41378 f to Pf = 542 days, making it one of the longest-period planets discovered via transit photometry. A subsequent intensive ground-based follow-up by Bryant et al. (2021) confirmed this period and revealed significant TTVs, indicating strong dynamical interactions among the outer planets.

In this work, we present a global dynamical analysis of the sub-Neptunes HIP 41378 b and HIP 41378 c. This combines 15 single-visit observations from the CHaracterising ExOPlanets Satellite (CHEOPS; Benz et al. 2021), eight new sectors from the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015), archival photometry from Kepler (K2), Spitzer, and the Hubble Space Telescope (HST), and RV measurements from HARPS (Mayor et al. 2003). Using measurements from Spitzer, B19 reports hints of TTV for planet c, with variations exceeding one hour. Motivated by this detection, we analyzed the potential TTVs of HIP 41378 c and HIP 41378 b. Additionally, we examined the dynamical influence of the non-transiting candidate planet HIP 41378 g, assessing its role in shaping the observed TTVs and the overall dynamics of the system. The paper is organized as follows: In Section 2, we describe the spectroscopic and photometric observations. Section 3 presents the newly derived stellar parameters. Section 4 details the photometric and dynamical modeling, including transit timing extraction and orbital parameter retrieval. Our results are presented in Section 5. In Section 6, we discuss the system’s architecture, the implications of the inner planets’ “peas-in-a-pod” configuration, and potential planetary compositions. Lastly, Section 7 summarizes the key findings and outlines future observational priorities.

2 Observations extraction and reduction

This section presents the observations and data extraction of both proprietary CHEOPS light curves and publicly available spectroscopic and photometric data for HIP 41378 b & c (including K2, TESS, Spitzer, HST, and HARPS), spanning over ten years and comprising a total of 47 transit light curves (32 for -b and 15 for -c). For each TESS sector and K2 campaign, we isolated individual transits of both planets by selecting portions of the light curve that encompassed the transit duration plus three CHEOPS orbits (~98.77 minutes each). This allowed us to have a consistent out-of-transit baseline across all observations. The center of the transits, determined using a linear ephemeris, and the transit durations were based on the values reported by B19.

K2. The K2 mission observed the system during campaign 5 (2015 April 27–2015 July 10) and campaign 18 (2018 May 12–2018 July 02), under the identifier EPIC 211311380 (K2-93), with long- and short-cadence photometry (30 minutes and 1 minute, respectively). A total of ten transits of planets b & c were observed during the K2 mission (seven of b and three of c). From the Mikulski Archive for Space Telescopes (MAST1) we extracted the high-level science data products (HLSP) based on the photometric pipeline EVEREST (EPIC Variability Extraction and Removal for Exoplanet Science Targets, version 2.0; Luger et al. 2016, 2018).

Spitzer. We used photometric data of HIP 41378 collected with the Infrared Array Camera (IRAC) 4.5 μm channel of Spitzer telescope (Werner et al. 2004), taken as part of the observing programs 11026 and 13052 (PI: Werner), focused on K2 followups. The observations, presented by B19, cover a transit of planet b and one of planet c.

TESS. The TESS mission Ricker et al. (2015) observed the system (TOI-4304, TIC 366443426) from Cycles 1 to 7 in sectors: 7, 34, 44, 45, 46, 61, 72 and 88 with a cadence of 120 s. We downloaded the photometric time series processed by the Science Processing Operations Center (SPOC; Jenkins et al. 2016) from the MAST archive, and we corrected the simple aperture photometry (SAP) for systematic effects by following the procedure and using the Cotrending Basis Vectors described in Nardiello et al. (2021, 2025). As shown in Nardiello et al. (2022), Presearch Data Conditioned SAP (PDC-SAP) light curves can suffer from overcorrection problems, that can introduce new systematic errors in the light curves, change the shape of the stellar activity and planetary transits, and also mimic false transit signals. A total of nine transits of planet b and six of planet c were extracted from the light curves. The first transit of planet b during sector 72 fell in a data discontinuity gap; thus, only a partial transit light curve was retrieved.

HST. We used the publicly available HST/WFC3 (Marinelli & Green 2024) transit observations of HIP 41378 b from the MAST archive. These data, obtained using the G141 grism (1.088 to 1.680 μm), cover three transits of the planet (January 14, 2018, May 3, 2020, and May 20, 2020) and were taken as part of program GO-15333 (PI: Ian Crossfield). The data were first published by Edwards et al. (2023b), and later reanalyzed by Brande et al. (2024). The calibration of the raw WFC3 data, the reduction and the extraction of the white light curves were done using the IRACLIS dedicated pipeline (Tsiaras et al. 2016a,b, 2018), following the methodology of Edwards et al. (2023b). Our reduction also includes the frame-splitting method (see Edwards et al. 2023a, for a complete description) that takes into account the persistence effect dependent upon the brightness of the host star, the scanning rate, and the readout scheme employed.

CHEOPS. HIP 41378 was observed with CHEOPS within the frame of the guaranteed time observation (GTO) as part of two programs: M-R relation in planetary systems2, dedicated to the follow-up of TTVs in planetary systems to better constrain masses, orbital parameters, and planetary compositions (Nascimbeni et al. 2023, 2024), and architecture of resonant chains (ARC)3, centered on the follow-up of resonant chains (Leleu et al. 2021; Delrez et al. 2023; Leleu et al. 2024). We obtained 15 visits acquired between December 23, 2020, and March 11, 2025, of which 11 were centered on transits of planet b and four on those of planet c. For each observation we used the exposure cadence of 38 seconds, avoiding saturation. The complete log of the observations is reported in Table A.1. The CHEOPS raw data were automatically processed by the CHEOPS data reduction pipeline (DRP v13.1.0; Hoyer et al. 2020). The DRP corrects for instrumental (e.g., bias, flat and dark current) and environmental effects (e.g., cosmic rays, background) (Fortier et al. 2024). The pipeline performs aperture photometry extracting four different light curves. For our study we used the light curve corresponding to the DEFAULT photometric aperture of 25 pixels, which has the lowest rms. Following the extraction of the light curves we performed a clipping of the outliers with respect to the median flux value of the light curves plus five times the mean absolute deviation (MAD).

HARPS. We recovered the publicly available HARPS (Mayor et al. 2003) high-precision RV observations from the ESO Science Archive website4. We downloaded 370 spectra obtained under the observing programs 198.C-0169(A) and 0102.C-0171(A) (PI: Santerne) previously published by Santerne et al. (2019). The system was monitored between January 2017 and April 2019, with a typical integration time of 15 minutes. The observations yielded a median formal measurement uncertainty of 2 m s−1. The spectra were extracted using the HARPS online data reduction pipeline (DRS) (Cosentino et al. 2014, version 3.8). We rejected the points taken to monitor granulation and p-modes in the two consecutive nights: March 10, 2018, and March 11, 2018. We additionally discarded all the data points with an error greater than 5σ of the median value. These selections left us with 311 RV measurements.

3 Stellar parameters

The stellar spectroscopic parameters (Teff, log g, microturbulence vtur, and [Fe/H]) were derived using the ARES+MOOG methodology as described in Santos et al. (2013); Sousa (2014); Sousa et al. (2021). For this we used the latest version of ARES5 (Sousa et al. 2007, 2015) to consistently measure the equivalent widths (EW) of selected iron lines in the combined HARPS spectrum of HIP 41378. For this, we used the iron line list presented in Sousa et al. (2008). The best spectroscopic parameters are found by converging into ionization and excitation equilibrium. In this process, a grid of Kurucz model atmospheres (Kurucz 1993) and the radiative transfer code MOOG (Sneden 1973) are used. We also derived a more accurate trigonometric surface gravity using the Gaia DR3 data following the same procedure as described in Sousa et al. (2021). Stellar abundances of Si and Mg were then derived using the classical curve-of-growth analysis method assuming local thermodynamic equilibrium. The same codes and models were used for abundance determinations. For the derivation of chemical abundances of refractory elements, we closely followed the methods described in (e.g., Adibekyan et al. 2012, 2015). All of the [X/H] ratios were obtained by performing a differential analysis with respect to a high S/N solar (Vesta) spectrum from HARPS. We determined the HIP 41378 stellar radius using a Markov chain Monte Carlo (MCMC) modified infrared flux method (IRFM – Blackwell & Shallis 1977; Schanche et al. 2020). Within this MCMC framework, we produced synthetic photometry from a constructed spectral energy distribution (SED) based on stellar atmosphere models (Castelli & Kurucz 2003), using our spectroscopically derived stellar parameters as priors. To compute the stellar bolometric flux, we compared these simulated data to broadband fluxes in the following bandpasses: 2MASS J, H, and K, WISE W1 and W2, and Gaia G, GBP, and GRP (Skrutskie et al. 2006; Wright et al. 2010; Gaia Collaboration 2023). Lastly, this was converted into the effective temperature and angular diameter, from which we derived the stellar radius via combination with the offset-corrected Gaia parallax (Lindegren et al. 2021). Assuming Teff, [Fe/H], and R⋆ along with their uncertainties as input parameters, we derived the isochronal mass and age using two different stellar evolutionary models. The first set of mass and age estimates was computed using the isochrone placement routine (Bonfanti et al. 2015, 2016), which interpolates the input parameters within precomputed grids of PARSEC6 v1.2S (Marigo et al. 2017) isochrones and evolutionary tracks. The second set of mass and age values, instead, was estimated via the CLES (Code Liègeois d’Évolution Stellaire; Scuflaire et al. 2008) code, which builds up the best-fit evolutionary track following a Levenberg-Marquadt minimization scheme (see, e.g., Salmon et al. 2021). After checking the mutual consistency of the two respective pairs of outcomes via the χ2 criterion outlined in Bonfanti et al. (2021), we finally computed our final estimates for the mass and age that turned out to be M⋆ = 1.245−0.043+0.037$\[1.245_{-0.043}^{+0.037}\]$ M⊙ and t⋆ = 1.8−0.6+0.7$\[1.8_{-0.6}^{+0.7}\]$ Gyr; see Bonfanti et al. (2021) for further details about the statistical treatment. The stellar parameters are summarized in Table 1. Our derived stellar parameters were found to be consistent with asteroseismic values from Lund et al. (2019). Given the higher precision offered by asteroseismology, we adopted the asteroseismic constraints from Lund et al. (2019) as priors for all our subsequent analysis.

Table 1

Derived stellar parameters of HIP 41378.

4 Data analysis

4.1 CHEOPS-only analysis

Upon visually examining the CHEOPS data, each light curve presented significant systematics. We used the PYORBIT7 software (Malavolta et al. 2016, 2018) to simultaneously fit a transit model and detrend each individual CHEOPS light curve. All visits corresponding to the same planet were modeled using a common transit model. A set of 14 instrumental and environmental detrending vectors8 was applied globally across all light curves. These included: spacecraft roll-angle (ϕ) (df/d cos ϕ, df/d sin ϕ, df/d cos 2ϕ, df/d sin 2ϕ, df/d cos 3ϕ, df/d sin 3ϕ), background level (df/dbg), photometric contamination estimate (df/dcontam), smear estimate (df/dsmear), thermal variation ΔT of CHEOPS sensors, x centroid and y centroid (df/dx, d2f/dx2, df/dy, d2f/dy2). The detrended transit light curves, where then used for the global fitting.

4.2 Global transit light curve modeling

We homogeneously analyzed all the transit light curves to retrieve the individual planetary parameters from the photometric datasets (i.e., CHEOPS, TESS, K2, HST and Spitzer) using PYORBIT. The transits were modeled with the batman package (Kreidberg et al. 2015), and for the K2 transits we used a super-sampling factor of 30. We assumed circular orbits, by fixing the eccentricity value to zero, for the two planets. We fixed the orbital periods (P) to the values we inferred from the CHEOPS pre-modeling i.e., Pb = 15.571893 ± 0.000068, Pc = 31.70838 ± 0.00041 (see Sect. 4.1), in order to retrieve the transit timings of each individual event. We included a third-order polynomial temporal trend (4 free parameters) for each of the K2, Spitzer, and HST light curves. For all five instrument pass-bands, the stellar parameters (see Table 1) were used as Gaussian priors to compute the quadratic limb darkening (LD) coefficients with PYLDTK (Husser et al. 2013; Parviainen & Aigrain 2015). We used these computed values, with a conservative uncertainty of 0.05, as Gaussian priors in the global analysis, using the LD parameterization (q1, q2) introduced by Kipping (2013). Gaussian priors were imposed on the stellar radius and mass based on the stellar spectroscopic analysis conducted in Section 3. Uninformative uniform priors were imposed on all other free parameters (see Table A.2). The analysis had a total of 134 fitting parameters: 10 LD coefficients (two for CHEOPS, TESS, K2, Spitzer, and HST), four planetary parameters (b, Rp/R⋆ for −b and −c), 47 transit times (T0), stellar density (ρ⋆), 12 jitter parameters (one for each telescope, and one for each TESS sector), and 60 (15 × 4) polynomial trend coefficients. Global parameter optimization was carried out using the PYDE9 differential evolution algorithm (Storn & Price 1997; Parviainen et al. 2016), using 100 000 generations with a population of 10 × Npara, where Npara is the number of free parameters. The output parameters were used as the initial values for the Bayesian analysis, performed using the emcee package (Foreman-Mackey et al. 2013), which implements the affine invariant MCMC ensemble sampler (Goodman & Weare 2010). We performed an autocorrelation analysis on the chains and the chains were considered converged if they were longer than 100 times the estimated autocorrelation time and this estimate varied by less than 1%. We ran the sampler with 10 × ndim walkers (where ndim is the number of dimensions of the model) for 450 000 steps. We discarded the first 100 000 steps, assuring the convergence of the chains, and set a thinning factor of 100. All the fitted parameters and their corresponding priors as well as the derived posteriors are shown in Table A.2. All the inferred central times of transit (T0) are displayed in Tables 2 and 3. We show the phase-folded light curves with the best fit transit model in Figure. A.1.

4.3 Dynamical modeling with TRADES

When two neighboring planets are close to a mean motion resonance (MMR), their orbital periods approach a ratio of small integers (p/q). To quantify the proximity to resonance, we used the fractional deviation Δ, as introduced by Lithwick et al. (2012), defined as: Δ=Pout/Pinp/q−1,$\[\Delta=\frac{P_{out} / P_{in}}{p / q}-1,\]$(1)

where Pout and Pin are the orbital periods of the outer and inner planets, respectively. As discussed in Section 1, the periods of the two inner planets are near the 2:1 period commensurability (p = 2, q = 1), with Δ ≈ 0.018, which suggests we might observe large TTV signals due to strong mutual gravitational interactions (Agol et al. 2005; Lithwick et al. 2012; Steffen et al. 2012). We dynamically simulated the TTV signals and integrated the system parameters of HIP 41378 b & c simultaneously fitting the retrieved T0s, (see Section 4.2 and Tables 2–3), and RVs (see Section 2) using the N-body dynamical integrator TRADES10 (Borsato et al. 2014, 2019, 2021, 2022; Nascimbeni et al. 2023; Borsato et al. 2024; Nascimbeni et al. 2024). We selected as the start of the integration and reference time Tref,dyn = 2 457 137 (BJDTDB), with the integration time (Tint = 3620 days) chosen to cover the entire time span of all observations. Following the detection of an additional planetary RV signal by S19, with an estimated period of approximately 62 days, near the 2:1 period commensurability with planet c, we decided to investigate this possibility further by testing two models in our analysis.

4.3.1 Two-planet model

In the first configuration we tested a two-planet model formed by HIP 41378 b and HIP 41378 c. We used as fitting parameters the planetary-to-star mass ratio Mp/M⋆, the period P, the eccentricity e, and the mean longitude λ11. Rather than fitting eccentricity e and argument of periastron ω individually, we used the parametrization (ecos⁡ω,esin⁡ω$\[\sqrt{e} ~\cos~ \omega, \sqrt{e} ~\sin~ \omega\]$). The mass ratios are used as fitting parameters instead of absolute masses, since TTVs only provide constraints on the relative masses of the planets and the host star. We set the longitude of ascending node Ω = 180° for −b, and fit it for −c (following Winn 2010; Borsato et al. 2014). We fixed the planetary and stellar radii (Rp, R⋆), stellar mass (M⋆) and the inclination i, according to the values from Tables 1 and A.2. For the RV dataset we fit a jitter term (σj) in log2 and an offset (RVγ). We imposed half-Gaussian priors on the eccentricities following Van Eylen et al. (2019). To assess potential biases introduced by this choice, we performed an additional fit using uninformative-uniform priors on e. This alternative analysis yielded posteriors consistent within 1σ but resulted in a higher BIC12 value. When comparing models using the BIC, a lower value indicates a better fit to the data, accounting for the complexity of the model. Therefore, we chose to adopt the results from the model with the half-Gaussian prior as our reference solution. For each remaining parameter we imposed uniform-uninformative priors (see Table A.3).

Table 2

Transit times of HIP 41378 b from the global photometric analysis with PYORBIT.

Table 3

Transit times of HIP 41378 c from the global photometric analysis with PYORBIT.

4.3.2 Three-planet model

Building on the two-planet configuration, we performed a dynamical analysis by including an additional planet, HIP 41378 g. The setup for the three-planet model was identical to that of the two-planet model, with a few additional parameters introduced for the third planet. In contrast to the other planets, for planet g we additionally fit the inclination (i). The prior ranges for these parameters were chosen to allow for both transiting and non-transiting orbital configurations. Half-Gaussian priors were applied to the eccentricities, and uninformative priors were used for the remaining parameters (see Table A.3).

4.4 Analysis

For both two- and three-planet models, we first ran PYDE with a population size of 120 (i.e. the number of different initial parameter sets) for 70 000 steps. The best-fit outputs from PYDE were then used as initial conditions for the EMCEE package, which we ran for 600 000 steps using 120 walkers, corresponding to 9 and 6 times the dimensionality (number of free parameters) in the respective models. Following the methodology described in Nascimbeni et al. (2024), we employed a combination of the differential evolution proposal (80% of the walkers; Nelson et al. 2014) and the snooker differential evolution proposal (20% of the walkers; ter Braak & Vrugt 2008) as the sampler within EMCEE.

We used a thinning factor of 100 and discarded 450 000 steps as burn-in, long after the chains converged according to the Geweke (Geweke 1991), Gelman-Rubin (Gelman & Rubin 1992), autocorrelation function (Goodman & Weare 2010), and visual inspection criteria. The uncertainty associated with each parameter was computed as the highest density interval (HDI) at the 68.27% credibility level from the marginalized posterior distribution, representing the most probable region of the posterior. Best-fit values were defined as the maximum a posteriori (MAP) estimates, computed from the posterior distributions and constrained to lie within the HDIs of the fitting parameters.

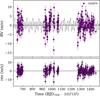thumbnail Fig. 1

Radial velocities of HIP 41378. Upper panel: RV plot minus the offset γ. TRADES MAP model is shown as a black line with the shaded gray areas indicating the 1σ, 2σ, and 3σ confidence intervals. HARPS observations are depicted as purple circles. Lower Panel: RV residuals after subtracting the model.

5 Results

Using the N-body dynamical integrator within TRADES, we performed joint modeling of the TTV and RV signals, and successfully retrieved the orbital configuration of HIP 41378 b, HIP 41378 c and HIP 41378 g (see Figures 1–2). The best-fit model was selected using both the BIC and the log Bayes factor, which provide complementary model comparison metrics. The comparison between the two-planet and three-planet models (BIC2p = 4170.08 and BIC3p = 1353.72) yields a difference of ΔBIC = 2816.36, strongly favoring the inclusion of the third planet, HIP 41378 g. To strengthen this conclusion, we also computed the logarithm of the Bayes factor (Kass & Raftery 1995) between the two models, by using the the approximation found on page seven of Shen & González (2021), obtaining log ℬ3p,2p = 1400, which provides decisive evidence in favor of the three-planet model. This confirms that the addition of HIP 41378 g significantly improves the fit and is statistically justified. Thereafter, we decided to adopt the posteriors of the three-planet model as reference hereafter in the paper. We were able to determine the planetary mass of HIP 41378 g with a ~6σ level of significance, enabled by the dynamical simultaneous modeling of both TTVs and RVs data. Our analysis places the orbital period of HIP 41378 g at approximately ~64 days, close to the 2:1 period commensurability with HIP 41378 c (Pg/Pc ~ 2.04), in agreement with the RV signal found by S19. The orbital solution shows a compact inner system comprising three sub-Neptunes, which are near a 1:2:4 period ratio. Our final posterior values along with the priors and the uncertainty intervals are presented in Table A.3. Plots of the Observed-minus-Calculated (O-C) diagrams of both planets and the RV plots are shown in Figs. 1–2.

As a complementary result of our dynamical analysis, TRADES evaluates the Hill stability of the system using the AMD-Hill criterion (Eq. (26) Petit et al. 2018), which is based on the angular momentum deficit (AMD; Laskar 1997; Laskar 2000; Laskar & Petit 2017). We find that the entire posterior distribution satisfies the AMD-Hill stability criterion, indicating the long-term dynamical stability of the posterior. However, to further assess the stability and chaotic behavior of the posterior solutions, considering effects of planet-planet interactions, mean-motion resonances and planetary ejections, we used the N-body integrator rebound (Rein & Liu 2012; Rein & Tamayo 2016). Specifically, we employed the Mean Exponential Growth factor of Nearby Orbits (MEGNO; or ⟨Y⟩) chaos indicator (Cincotta & Simó 2000; Cincotta et al. 2003). A planetary system is considered to be in a stable configuration if it satisfies the condition ⟨Y⟩ ≲ 2, while a planet is considered as ejected if its semi-major axis exceeded 100 times that of planet c. We computed the orbits for a total of 100 Kyr using the symplectic integrator WHFast, with a step size corresponding to 10% of the orbital period of planet b. We obtained ⟨Y⟩ ≲ 2 for the best-fit (MAP within HDI) solution indicating that the configuration is stable in the integrated time. We then checked a family of solutions randomly selected from our posterior distribution. After running the same integration for 200 solutions, we find that 87.5% of the simulations exhibited strong stable dynamics.

6 Discussion

Our discussion is divided into six parts. In Section 6.1, we contextualize the derived planetary parameters with literature values and the broader sub-Neptune population using the mass-radius diagram. The system’s potential architecture is discussed in Section 6.2. The interior composition of the planets is analyzed in Section 6.4.

6.1 Planets in context

When compared with the values reported by S19, we find some statistical discrepancies in the masses of planets b and c. S19 derived a mass for planet c of Mc = 4.4 ± 1.1 M⊕, suggesting a low bulk density (ρc = 1.19 ± 0.30 g cm−3), which placed it among the sub-Neptune puffy population. This made it the second lowest-density planet in the system, alongside the super-puff HIP 41378 f (ρf = 0.09 ± 0.02 g cm−3), whose unusually low density has been proposed to result from the presence of opaque, oblique planetary rings (Piro & Vissapragada 2020; Akinsanmi et al. 2020). In contrast, our updated mass for planet c (Mc = 6.53−0.42+1.33$\[6.53_{-0.42}^{+1.33}\]$ M⊕) places it within the typical range for sub-Neptunes (ρc = 1.854−0.031+0.572$\[1.854_{-0.031}^{+0.572}\]$ g cm−3), ruling out the puffy scenario (see Figure 3). This reassessment of planet c highlights the potential for a similar reevaluation for HIP 41378 f as additional RV and photometry data become available, potentially refining its mass and density estimates.

Although S19 identified the RV signal of HIP 41378 g and provided a minimum mass estimate, they were unable to detect any transits in their available photometry. This is consistent with the duration of the K2 C5 campaign, which lasted 75 days, slightly longer than our inferred period of ~64 days. In our dynamical analysis (see Sect. 4.3), we explored both transiting and non-transiting configurations for the planet. The resulting inclination of 95−10+1$\[95_{-10}^{+1}\]$ deg suggests a non-transiting orbit. From our line of sight, any planet farther out than planet c (i.e., with a semimajor axis exceeding ac = 34.60 R⋆) will not transit its host star unless its orbital inclination lies within a narrow range, 88.32° < ig < 91.68°, as derived from arccos(±b/34.60), with b = (R⋆ + Rg)/R⋆13. Supporting the results of the dynamical analysis, we detected no transits of HIP 41378 g in the newly available TESS and CHEOPS photometric data. These results differ from statistical studies on Kepler multi-planet systems, which have been shown to be largely coplanar with a typical scatter of ±3° (Fang & Margot 2012; Weiss et al. 2023).

To compare the planets with the current sub-Neptune population and to provide an initial constraint on their possible bulk compositions, we placed the two planets in the mass-radius diagram (see Figure 3). Since HIP 41378 g does not transit its radius remains undetermined; hence, we did not include it in the diagram. By placing the planets in the mass-radius diagram, we can see that they are consistent with the current sub-Neptune population. However the position of the planets does not allow us to uniquely determine their composition. We displayed the mass-radius models from Zeng et al. (2019) and Lopez & Fortney (2014), which account for a 50% water-world composition and an Earth-like core with different envelope compositions. The planets fall at the intersections of multiple composition tracks, making it challenging to break the degeneracy between H/He envelope and water-world compositions, based on mass and radius alone. For a more detailed analysis of their internal composition, see Section 6.4.

thumbnail Fig. 2

O-C diagrams of HIP 41378 b (left) and c (right). Each dataset is plotted with a different marker and color. Top: best-fit two-planet TRADES model (black line with gray-shaded 1σ, 2σ, and 3σ confidence intervals). Bottom: best-fit three-planet TRADES model. Lower panels in each plot show the residuals with respect to the corresponding model.
thumbnail Fig. 3

Mass–radius diagram including all confirmed planets with radii below 4 R⊕ with masses and radii measured to better than 30% precision (Gray points). Planet parameters are taken from the NASA Exoplanet Archive’s confirmed planets table, as queried on January 20, 2025. The purple pentagon represents the position of HIP 41378 b, while the green diamond represents the postion of HIP 41378 c. The color-coded lines show different theoretical mass–radius relations corresponding to the planet compositions taken from Zeng et al. (2019) (solid lines) and Lopez & Fortney (2014) (dashed lines; 1 Gyr, solar metallicity and incident flux of 10 S⊕). Also shown are Earth, Uranus and Neptune, for reference.

6.2 On the architecture of the planetary system

The HIP 41378 system hosts six planets, five of which transit the star along our line of sight. As of now, the periods of two outer planets, HIP 41378 d and HIP 41378 e, remain unresolved. A single transit of HIP 41378 e was observed during K2 Campaign 5, preventing an estimation of its orbital period. On the other hand, HIP 41378 d was observed to transit during both K2 campaigns (5 and 18), enabling the identification of a set of 23 orbital period aliases. The new TESS sector observations, combined with the findings of Sulis et al. (2024), effectively ruled out the shortest orbital periods for HIP 41378 d, narrowing the set of aliases to three values: ~278, ~371, and ~1113 days. Each of these periods places the planet near a first-order period commensurability with HIP 41378 f (i.e. 2:1, 3:2 and 1:2), which could explain the strong TTVs (>4 hours) observed for the planet (Bryant et al. 2021; Alam et al. 2022). This could suggest the potential existence of a second quasi-resonance chain involving the three outer planets.

Based on the possible orbital periods of the two unresolved outer planets, and the confirmed planetary signal of planet g, we suggest two dynamical configurations for the system: (i) a system-wide quasi-resonant chain or (ii) hierarchical multi-planet architecture. In the first scenario, the planets follow a continuous quasi-resonant chain, with period ratios that closely align with small integer values. This would suggest a dynamically structured system, where all the planets may have experienced convergent migration and undergone resonant capture (Wong & Lee 2024). This would imply the potential presence of additional, yet-undetected planets between the inner and outer regions, completing the resonance chain. In the second configuration, the system possesses a middle-gap, separating the three inner sub-Neptunes from the three outer Neptunes. As a result, the system is assumed to be hierarchical, meaning that it can be divided into two independently stable subsystems (Laskar & Petit 2017). In this scenario, the outer planets would be dynamically decoupled from the inner trio, suggesting that they should not significantly influence the observed TTV signals of the inner planets. Additionally, the three outer planets could be close to a resonant chain, potentially near a low-order period commensurability. This would suggest that, while the system remains hierarchical, the outer planets could still be dynamically linked through resonant interactions. Similar architectures have been observed in systems such as Kepler-90 (Cabrera et al. 2013), which hosts both 2:3:4 and 5:4 quasi-resonant chains, and HD 191939 (Orell-Miquel et al. 2023), exhibiting coupled 1:3:4 and 3:1 configurations. Further observations of the outer planets will be necessary to precisely constrain their orbital periods and determine the system’s unique dynamical configuration. The outer-system architecture will be further explored in Grouffal et al. (in prep.). To investigate the two hypotheses and put further constraints on the known outer planets (HIP 41378 d, HIP 41378 e, and HIP 41378 f), we conducted a four- and six-planet dynamical analysis with TRADES. This included testing for a hypothetical planet “h” situated between planets g and d. The setup mirrored the one used for HIP 41378 g, employing broad priors to explore a wide parameter space for radius, mass, and period, based on the findings of S19 and B19. However, we were unable to constrain the masses and orbital periods of the additional planets, resulting in poor fits for all planets, with BIC3p ≪ BIC6p, BIC4p.

For now, the planetary architecture for HIP 41378 remains an unresolved puzzle. However, the dynamical evidence of HIP 41378 g enables us to further investigate this peculiar multi-planet configuration. Given the limited constraints on the orbital architecture of the outer planets, we focused on the configuration of the inner planets. Following the classification scheme proposed by Howe et al. (2025), the inner planets display a closely spaced “peas-in-a-pod” configuration, indicating a high degree of uniformity in their orbital and physical properties. To measure the degree of this similarity, we applied the approach of Otegi et al. (2022). Specifically, we evaluated the distances in logarithmic space for the mass (DM), radius (DR), and their combined global distance (D). In this metric, lower values correspond to greater similarity. According to our calculated values of DR = 0.007, DM = 0.08, and D = 0.08, the three planets exhibit strong similarity. These results classify the inner system of HIP 41378 as the fifth14 most uniform in the sample of 48 systems analyzed by Otegi et al. (2022). This reinforces the “closed-spaced peas-in-a-pod” scenario (Weiss et al. 2018; Howe et al. 2025) and potentially hints at a common formation pathway. Furthermore, consistent with the trend reported by Otegi et al. (2022), the inner planetary system shows greater similarity in radius than in mass. As pointed out by the authors, this could be attributed to the similarity in planetary density within a system. Given that the density is three times more sensitive to radius variations than to mass variations, it is expected to have a stronger uniformity in radius than in mass.

6.3 Investigation on the mean-motion resonant state

The inferred orbital period of HIP 41378 g, near a 2:1 period commensurability with planet c, positions the inner HIP 41378 system close to a three-body 1:2:4 resonant chain. Dynamical configurations in or near MMRs are expected to arise during the early stages of planetary system formation, within the gas-rich protoplanetary disk. For low-mass planets these configurations are thought to result from Type-I convergent migration in gas-rich disks, during which the forming planets are captured in resonance (e.g., Malhotra 1993; Kley & Nelson 2012; Delisle 2017; Izidoro et al. 2017; MacDonald & Dawson 2018). To investigate whether the three-body chain is in a true mean-motion resonance, we studied the evolution of the three-body angle Ψ123. This angle is defined by the difference between two critical resonant angles: ϕ12=2λc−λb−ϖc,ϕ23=2λg−λc+ϖc,Ψ123=ϕ12−ϕ23=3λc−λb−2λg.$\[\begin{aligned}\phi_{12} & =2 \lambda_c-\lambda_b-\varpi_c, \\\phi_{23} & =2 \lambda_g-\lambda_c+\varpi_c, \\\Psi_{123} & =\phi_{12}-\phi_{23}=3 \lambda_c-\lambda_b-2 \lambda_g.\end{aligned}\]$(2)

For a (2:1, 2:1) resonant configuration, Siegel & Fabrycky (2021) predict that the three-body angle should librate (oscillate around a fixed value) around 180°. We integrated the MAPHDI solutions using the N-body code rebound (Rein & Liu 2012) and the symplectic integrator WHFast (Rein & Tamayo 2016), for a total duration of 10 000 years. Our results, depicted in Figure 4, indicate that the three planets are out of resonance, with the three-body angle circulating from 0 to 360°.

thumbnail Fig. 4

Three-body Laplace resonant angles evolution for HIP 41378 b, c and g, for the MAPHDI solutions. The top two panels show the evolution of the critical angles ϕ12 and ϕ23. The bottom panel shows the three-body angle, which is a linear combination of the mean longitudes of the planets.

6.4 Interior bulk composition

Based on the derived planetary parameters, we used the internal structure modeling framework plaNETic15 (Egger et al. 2024) to infer the interior compositions of HIP 41378 b and HIP 41378 c. planETic uses a neural network as a surrogate model for the planetary structure forward model BICEPS (Haldemann et al. 2024) to speed up the inference process, which allows for a fast, but still reliable analysis. The modeled planets are assumed to consist of an envelope of uniformly mixed H/He and water, a mantle layer composed of silicon, magnesium, and iron oxides, and an inner iron core, diluted with up to 19% sulfur as a placeholder for any lighter elements. Both observed planets are modeled simultaneously.

Since this remains a highly degenerate problem with many possible interior structures compatible with the observed planetary bulk properties, the outcome of the inference process depends to a certain extent on the chosen priors. We therefore ran six models assuming different combinations of priors, compatible with different assumptions on the system’s formation and evolution history. First, we consider two distinct priors for the planet’s water content: one based on a formation scenario beyond the ice-line (Case A, water-rich) and another corresponding to formation within the ice-line (Case B, water-poor). For each of these water priors, we consider three different assumptions for the planetary Si/Mg/Fe ratios. In the first case, we assume the planet’s composition directly reflects the stellar Si/Mg/Fe ratios (Thiabaud et al. 2015). In the second case, we account for iron enrichment relative to the host star using the empirical fit from (Adibekyan et al. 2021). In the third case, we model the planet’s composition independently of the stellar ratios, sampling the Si, Mg, and Fe molar fractions uniformly from the simplex where their sum is 1, with an upper limit of 0.75 for Fe. A detailed description of these priors can be found in (Egger et al. 2024).

The resulting posterior distributions for the most important internal structure parameters are visualized in Figures A.6 and A.7, with the results for the full list of internal structure parameters summarized in Tables A.4 and A.5. We do not constrain the core and mantle layer mass fractions for either planet; the inferred posteriors mostly match the priors. In the water-rich case, we infer envelope mass fractions between 38% and 42% for planet b and of 31% for planet c, with envelope water mass fractions of almost 100% for planet b and around 90% for planet c. In the water-poor case, on the other hand, we constrain the envelope mass fractions quite well with values of the order on 0.3–0.6% for planet b and 0.8–1.2% for planet c. A future JWST transmission spectrum of HIP 41378 b and HIP 41378 c could help resolve this degeneracy by directly probing the atmospheric composition of their upper envelope layers.

7 Summary and conclusions

Using CHEOPS observations, TESS sectors, and archival data, we conducted a dynamical analysis of the two inner sub-Neptune planets transiting the bright star HIP 41378 (mV = 8.9 mag). We report the detection of large TTVs in the multi-planet HIP 41378 system, with amplitudes of 30 minutes and ≳3 hours for planets b and c, respectively (see Figure 2). Combining these TTVs with RV data, we significantly refined the planetary parameters (see Tables A.2–A.3) and dynamically confirmed the additional non-transiting planet, HIP 41378 g, which lies close to the 2:1 period commensurability with planet c (Pg/Pc ~ 2.04), suggesting a near 1:2:4 resonant chain for the inner planets. This detection raises further questions regarding the overall architecture which remains only partially resolved, with the orbital properties of two long-period planets (HIP 41378 d and e) yet to be constrained.

Our interior structure analysis revealed significant degeneracy in the interior structures of HIP 41378 b and c, with solutions heavily dependent on formation assumptions, highlighting the compositional degeneracy inherent to sub-Neptunes (Figures A.6–A.7). Water-rich scenarios suggest ~31–42% water-dominated envelopes, while water-poor cases yield compact H/He envelopes (~0.3–1%). These ambiguities highlight the need for JWST atmospheric spectroscopy to distinguish between competing models. For sub-Neptunes such as HIP 41378 b and HIP 41378 c, mass measurements paired with atmospheric studies will help resolve the compositional degeneracy between gas dwarfs (rocky planets with H/He envelopes; Lopez & Fortney 2014; Rogers et al. 2023) and water worlds (rocky planets with water-rich compositions; Léger et al. 2004; Dorn & Lichtenberg 2021; Aguichine et al. 2021; Luque & Pallé 2022).

Finally, HIP 41378 will not be reobserved by TESS in year 8. This calls for new observations that could shed light on the possible quasi-resonant chain of the outer system, by exploring the possible period alias of the transiting HIP 41378 d or even detecting another transit of HIP 41378 e.

Acknowledgements

This publication was produced while attending the PhD program in Space Science and Technology at the University of Trento, Cycle XXXVIII, with the support of a scholarship cofinanced by the Ministerial Decree no. 351 of 9th April 2022, based on the NRRP – funded by the European Union – NextGenerationEU – Mission 4 “Education and Research”, Component 2 “From Research to Business”, Investment 3.3 – CUP E63C22001340001. CHEOPS is an ESA mission in partnership with Switzerland with important contributions to the payload and the ground segment from Austria, Belgium, France, Germany, Hungary, Italy, Portugal, Spain, Sweden, and the United Kingdom. The CHEOPS Consortium would like to gratefully acknowledge the support received by all the agencies, offices, universities, and industries involved. Their flexibility and willingness to explore new approaches were essential to the success of this mission. CHEOPS data analyzed in this article will be made available in the CHEOPS mission archive (https://cheops.unige.ch/archive_browser/). We thank Elena Gol for her artistic advice. LBo, VNa, GPi, TZi, IPa, RRa, and GSc acknowledge support from CHEOPS ASI-INAF agreement no. 2019-29-HH.0. LBo acknowledges financial support from the Bando Ricerca Fondamentale INAF 2023, Mini-Grant: “Decoding the dynamical properties of planetary systems observed by TESS and CHEOPS through TTV analysis with parallel computing”. LPa acknowledge support from a scholarship cofinanced by the Ministerial Decree no. 118 of 2nd March 2023, based on the NRRP – funded by the European Union – NextGenerationEU – Mission 4 Component 1 – CUP C96E23000340001. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. D.K. was supported by a Schrödinger Fellowship supported by the Austrian Science Fund (FWF) project number J4792 (FEPLowS). TWi acknowledges support from the UKSA and the University of Warwick. ABr was supported by the SNSA. MNG is the ESA CHEOPS Project Scientist and Mission Representative. BMM is the ESA CHEOPS Project Scientist. KGI was the ESA CHEOPS Project Scientist until the end of December 2022 and Mission Representative until the end of January 2023. All of them are/were responsible for the Guest Observers (GO) Programme. None of them relay/relayed proprietary information between the GO and Guaranteed Time Observation (GTO) Programmes, nor do/did they decide on the definition and target selection of the GTO Programme. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. AL acknowledges support of the Swiss National Science Foundation under grant number TMSGI2_211697. YAl acknowledges support from the Swiss National Science Foundation (SNSF) under grant 200020_192038. RAl, DBa, EPa, IRi, and EVi acknowledge financial support from the Agencia Estatal de Investigación of the Ministerio de Ciencia e Innovación MCIN/AEI/10.13039/501100011033 and the ERDF “A way of making Europe” through projects PID2021-125627OB-C31, PID2021-125627OB-C32, PID2021-127289NB-I00, PID2023-150468NB-I00 and PID2023-149439NB-C41. SCCB acknowledges the support from Fundação para a Ciência e Tecnologia (FCT) in the form of work contract through the Scientific Employment Incentive program with reference 2023.06687.CEECIND. CBr and ASi acknowledge support from the Swiss Space Office through the ESA PRODEX program. ACC acknowledges support from STFC consolidated grant number ST/V000861/1, and UKSA grant number ST/X002217/1. ACMC acknowledges support from the FCT, Portugal, through the CFisUC projects UIDB/04564/2020 and UIDP/04564/2020, with DOI identifiers 10.54499/UIDB/04564/2020 and 10.54499/UIDP/04564/2020, respectively. A.C., A.D., B.E., K.G., and J.K. acknowledge their role as ESA-appointed CHEOPS Science Team Members. P.E.C. is funded by the Austrian Science Fund (FWF) Erwin Schroedinger Fellowship, program J4595-N. This project was supported by the CNES. A.De. This work was supported by FCT – Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 through the research grants UIDB/04434/2020, UIDP/04434/2020, 2022.06962.PTDC. O.D.S.D. is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by national funds through FCT. B.-O.D. acknowledges support from the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract number MB22.00046. ADe, BEd, KGa, and JKo acknowledge their role as ESA-appointed CHEOPS Science Team Members. This project has received funding from the Swiss National Science Foundation for project 200021_200726. It has also been carried out within the framework of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation under grant 51NF40_205606. The authors acknowledge the financial support of the SNSF. MF and CMP gratefully acknowledge the support of the Swedish National Space Agency (DNR 65/19, 174/18). DG gratefully acknowledges financial support from the CRT foundation under Grant No. 2018.2323 “Gaseousor rocky? Unveiling the nature of small worlds”. M.G. is an F.R.S.-FNRS Senior Research Associate. CHe acknowledges financial support from the Österreichische Akademie 1158 der Wissenschaften and from the European Union H2020-MSCA-ITN-2019 1159 under Grant Agreement no. 860470 (CHAMELEON). Calculations were performed using supercomputer resources provided by the Vienna Scientific Cluster (VSC). K.W.F.L. was supported by Deutsche Forschungsgemeinschaft grants RA714/14-1 within the DFG Schwerpunkt SPP 1992, Exploring the Diversity of Extrasolar Planets. This work was granted access to the HPC resources of MesoPSL financed by the Region Ile de France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. ML acknowledges support of the Swiss National Science Foundation under grant number PCEFP2_194576. PM acknowledges support from STFC research grant number ST/R000638/1. This work was also partially supported by a grant from the Simons Foundation (PI Queloz, grant number 327127). NCSa acknowledges funding by the European Union (ERC, FIERCE, 101052347). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. S.G.S. acknowledge support from FCT through FCT contract nr. CEECIND/00826/2018 and POPH/FSE (EC). The Portuguese team thanks the Portuguese Space Agency for the provision of financial support in the framework of the PRODEX Programme of the European Space Agency (ESA) under contract number 4000142255. GyMSz acknowledges the support of the Hungarian National Research, Development and Innovation Office (NKFIH) grant K-125015, a a PRODEX Experiment Agreement No. 4000137122, the Lendület LP2018-7/2021 grant of the Hungarian Academy of Science and the support of the city of Szombathely. V.V.G. is an F.R.S-FNRS Research Associate. JV acknowledges support from the Swiss National Science Foundation (SNSF) under grant PZ00P2_208945. NAW acknowledges UKSA grant ST/R004838/1. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. AL and JKo acknowledge support of the Swiss National Science Foundation under grant number TMSGI2_211697.

Appendix A Additional tables and plots

A.1 CHEOPS observations log

Table A.1

Log of CHEOPS observations.

A.2 Global transit light curve analysis

Table A.2

Posteriors and derived orbital parameters for HIP 41378 b & c from the global photometric analysis with PYORBIT, presented in Section 4.2

thumbnail Fig. A.1

Phase-folded light curves of HIP 41378 b & c, combining observations from K2, Spitzer, HST, CHEOPS, and TESS. The oversampled best-fit transit models are overlaid on the light curves.
thumbnail Fig. A.2

Individual TESS phase-folded transit light curves of HIP 41378 b. The binned points are showed in red. The oversampled best-fit transit models are overlaid on the light curves.
thumbnail Fig. A.3

Individual TESS phase-folded transit light curves of HIP 41378 c. The binned points are showed in red. The oversampled best-fit transit models are overlaid on the light curves.
thumbnail Fig. A.4

Individual CHEOPS phase-folded transit light curves of HIP 41378 b. The binned points are showed in red. The oversampled best-fit transit models are overlaid on the light curves.
thumbnail Fig. A.5

Individual CHEOPS phase-folded transit light-curves of HIP 41378 c. The binned points are showed in red. The oversampled best-fit transit models are overlaid on the light curves.

A.3 Dynamical analysis

Table A.3

Posteriors and derived orbital parameters (MAP and HDI) for HIP 41378 b, c, and g obtained from the dynamical analysis with TRADES.

A.4 Internal structure

thumbnail Fig. A.6

Posteriors for the main internal structure parameters of HIP 41378 b, namely the mass fractions of the planet’s inner core (far left), mantle (middle left), and envelope layers (middle right), as well as the mass fraction of water in the envelope layer (far right). We show models assuming the planet’s Si/Mg/Fe ratios match those of the host star exactly (purple), are Fe-enriched compared to the host star (pink), and are independent of the host star metallicity (blue). For all three options, we also use two water priors, favoring a water-rich (top row) and water-poor composition (bottom row), respectively. The vertical dashed lines show the medians of the inferred distributions and the dotted lines the chosen priors.
thumbnail Fig. A.7

Same as Figure A.6 but for HIP 41378 c.
Table A.4

Results of the internal structure modeling for HIP 41378 b.

Table A.5

Results of the internal structure modeling for HIP 41378 c.

References

  1. Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Adibekyan, V., Figueira, P., Santos, N. C., et al. 2015, A&A, 583, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Adibekyan, V., Dorn, C., Sousa, S. G., et al. 2021, Science, 374, 330 [NASA ADS] [CrossRef] [Google Scholar]
  4. Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [Google Scholar]
  5. Aguichine, A., Mousis, O., Deleuil, M., & Marcq, E. 2021, ApJ, 914, 84 [NASA ADS] [CrossRef] [Google Scholar]
  6. Akinsanmi, B., Santos, N. C., Faria, J. P., et al. 2020, A&A, 635, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Alam, M. K., Kirk, J., Dressing, C. D., et al. 2022, ApJ, 927, L5 [NASA ADS] [CrossRef] [Google Scholar]
  8. Badenas-Agusti, M., Günther, M. N., Daylan, T., et al. 2020, AJ, 160, 113 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bean, J. L., Raymond, S. N., & Owen, J. E. 2021, J. Geophys. Res. (Planets), 126, e06639 [NASA ADS] [Google Scholar]
  10. Becker, J. C., Vanderburg, A., Rodriguez, J. E., et al. 2019, AJ, 157, 19 [Google Scholar]
  11. Benz, W., Broeg, C., Fortier, A., et al. 2021, Exp. Astron., 51, 109 [Google Scholar]
  12. Berardo, D., Crossfield, I. J. M., Werner, M., et al. 2019, AJ, 157, 185 [NASA ADS] [CrossRef] [Google Scholar]
  13. Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bonfanti, A., Ortolani, S., Piotto, G., & Nascimbeni, V. 2015, A&A, 575, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bonfanti, A., Ortolani, S., & Nascimbeni, V. 2016, A&A, 585, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bonfanti, A., Delrez, L., Hooton, M. J., et al. 2021, A&A, 646, A157 [EDP Sciences] [Google Scholar]
  17. Borsato, L., Marzari, F., Nascimbeni, V., et al. 2014, A&A, 571, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Borsato, L., Malavolta, L., Piotto, G., et al. 2019, MNRAS, 484, 3233 [NASA ADS] [CrossRef] [Google Scholar]
  19. Borsato, L., Piotto, G., Gandolfi, D., et al. 2021, MNRAS, 506, 3810 [NASA ADS] [CrossRef] [Google Scholar]
  20. Borsato, L., Nascimbeni, V., Piotto, G., & Szabó, G. 2022, Exp. Astron., 53, 635 [NASA ADS] [CrossRef] [Google Scholar]
  21. Borsato, L., Degen, D., Leleu, A., et al. 2024, A&A, 689, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Borucki, W. J., Koch, D. G., Basri, G., et al. 2011, ApJ, 736, 19 [Google Scholar]
  23. Brande, J., Crossfield, I. J. M., Kreidberg, L., et al. 2024, ApJ, 961, L23 [NASA ADS] [CrossRef] [Google Scholar]
  24. Bryant, E. M., Bayliss, D., Santerne, A., et al. 2021, MNRAS, 504, L45 [NASA ADS] [CrossRef] [Google Scholar]
  25. Butler, R. P., Marcy, G. W., Williams, E., Hauser, H., & Shirts, P. 1997, ApJ, 474, L115 [Google Scholar]
  26. Cabrera, J., Csizmadia, S., Lehmann, H., et al. 2013, ApJ, 781, 18 [NASA ADS] [CrossRef] [Google Scholar]
  27. Campante, T. L., Barclay, T., Swift, J. J., et al. 2015, ApJ, 799, 170 [Google Scholar]
  28. Castelli, F., & Kurucz, R. L. 2003, in IAU Symposium, 210, Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, A20 [Google Scholar]
  29. Cincotta, P. M., & Simó, C. 2000, A&AS, 147, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Cincotta, P. M., Giordano, C. M., & Simó, C. 2003, Physica D Nonlinear Phenomena, 182, 151 [NASA ADS] [CrossRef] [Google Scholar]
  31. Cosentino, R., Lovis, C., Pepe, F., et al. 2014, SPIE Conf. Ser., 9147, 91478C [Google Scholar]
  32. Crane, J. D., Shectman, S. A., & Butler, R. P. 2006, SPIE Conf. Ser., 6269, 626931 [NASA ADS] [Google Scholar]
  33. Crane, J. D., Shectman, S. A., Butler, R. P., Thompson, I. B., & Burley, G. S. 2008, SPIE Conf. Ser., 7014, 701479 [NASA ADS] [Google Scholar]
  34. Crane, J. D., Shectman, S. A., Butler, R. P., et al. 2010, SPIE Conf. Ser., 7735, 773553 [NASA ADS] [Google Scholar]
  35. Delisle, J. B. 2017, A&A, 605, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Delrez, L., Leleu, A., Brandeker, A., et al. 2023, A&A, 678, A200 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Dorn, C., & Lichtenberg, T. 2021, ApJ, 922, L4 [NASA ADS] [CrossRef] [Google Scholar]
  38. Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [Google Scholar]
  39. Edwards, B., Changeat, Q., Tsiaras, A., et al. 2023a, AJ, 166, 158 [NASA ADS] [CrossRef] [Google Scholar]
  40. Edwards, B., Changeat, Q., Tsiaras, A., et al. 2023b, ApJS, 269, 31 [NASA ADS] [CrossRef] [Google Scholar]
  41. Egger, J. A., Osborn, H. P., Kubyshkina, D., et al. 2024, A&A, 688, A223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Fang, J., & Margot, J.-L. 2012, ApJ, 761, 92 [Google Scholar]
  43. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  44. Fortier, A., Simon, A. E., Broeg, C., et al. 2024, A&A, 687, A302 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Gelman, A., & Rubin, D. B. 1992, Statist. Sci., 7, 457 [NASA ADS] [Google Scholar]
  47. Geweke, J. F. 1991, Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments, Staff Report 148, Federal Reserve Bank of Minneapolis [Google Scholar]
  48. Gillon, M., Demory, B.-O., Van Grootel, V., et al. 2017, Nat. Astron., 1, 0056 [Google Scholar]
  49. Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Computat. Sci., 5, 65 [Google Scholar]
  50. Haldemann, J., Dorn, C., Venturini, J., Alibert, Y., & Benz, W. 2024, A&A, 681, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [Google Scholar]
  52. Howe, A. R., Becker, J. C., Stark, C. C., & Adams, F. C. 2025, AJ, 169, 149 [Google Scholar]
  53. Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [Google Scholar]
  54. Hoyer, S., Guterman, P., Demangeon, O., et al. 2020, A&A, 635, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Izidoro, A., Ogihara, M., Raymond, S. N., et al. 2017, MNRAS, 470, 1750 [Google Scholar]
  57. Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, SPIE Conf. Ser., 9913, 99133E [Google Scholar]
  58. Kass, R. E., & Raftery, A. E. 1995, J. Am. Statist. Assoc., 90, 773 [CrossRef] [Google Scholar]
  59. Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
  60. Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [Google Scholar]
  61. Kopparapu, R. K., Hébrard, E., Belikov, R., et al. 2018, ApJ, 856, 122 [NASA ADS] [CrossRef] [Google Scholar]
  62. Kreidberg, L., Line, M. R., Bean, J. L., et al. 2015, ApJ, 814, 66 [NASA ADS] [CrossRef] [Google Scholar]
  63. Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data (Smithsonian Astrophysical Observatory) [Google Scholar]
  64. Laskar, J. 1997, A&A, 317, L75 [NASA ADS] [Google Scholar]
  65. Laskar, J. 2000, Phys. Rev. Lett., 84, 3240 [Google Scholar]
  66. Laskar, J., & Petit, A. C. 2017, A&A, 605, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Latham, D. W., Rowe, J. F., Quinn, S. N., et al. 2011, ApJ, 732, L24 [NASA ADS] [CrossRef] [Google Scholar]
  68. Leleu, A., Alibert, Y., Hara, N. C., et al. 2021, A&A, 649, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Leleu, A., Delisle, J. B., Delrez, L., et al. 2024, A&A, 688, A211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
  71. Lithwick, Y., Xie, J., & Wu, Y. 2012, ApJ, 761, 122 [Google Scholar]
  72. Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [Google Scholar]
  73. Luger, R., Agol, E., Kruse, E., et al. 2016, AJ, 152, 100 [Google Scholar]
  74. Luger, R., Kruse, E., Foreman-Mackey, D., Agol, E., & Saunders, N. 2018, AJ, 156, 99 [Google Scholar]
  75. Lund, M. N., Knudstrup, E., Aguirre, V. S., et al. 2019, AJ, 158, 248 [CrossRef] [Google Scholar]
  76. Luque, R., & Pallé, E. 2022, Science, 377, 1211 [NASA ADS] [CrossRef] [Google Scholar]
  77. Luque, R., Osborn, H. P., Leleu, A., et al. 2023, Nature, 623, 932 [NASA ADS] [CrossRef] [Google Scholar]
  78. Léger, A., Selsis, F., Sotin, C., et al. 2004, Icarus, 169, 499 [Google Scholar]
  79. MacDonald, M. G., & Dawson, R. I. 2018, AJ, 156, 228 [Google Scholar]
  80. Madhusudhan, N. 2019, ARA&A, 57, 617 [NASA ADS] [CrossRef] [Google Scholar]
  81. Malavolta, L., Nascimbeni, V., Piotto, G., et al. 2016, A&A, 588, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Malavolta, L., Mayo, A. W., Louden, T., et al. 2018, AJ, 155, 107 [NASA ADS] [CrossRef] [Google Scholar]
  83. Malhotra, R. 1993, Nature, 365, 819 [CrossRef] [Google Scholar]
  84. Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [Google Scholar]
  85. Marinelli, M., & Green, J. 2024, in WFC3 Instrument Handbook for Cycle 33, 17 [Google Scholar]
  86. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  87. Nardiello, D., Deleuil, M., Mantovan, G., et al. 2021, MNRAS, 505, 3767 [NASA ADS] [CrossRef] [Google Scholar]
  88. Nardiello, D., Malavolta, L., Desidera, S., et al. 2022, A&A, 664, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Nardiello, D., Akana Murphy, J. M., Spinelli, R., et al. 2025, A&A, 693, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Nascimbeni, V., Borsato, L., Zingales, T., et al. 2023, A&A, 673, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Nascimbeni, V., Borsato, L., Leonardi, P., et al. 2024, A&A, 690, A349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Nelson, B., Ford, E. B., & Payne, M. J. 2014, ApJS, 210, 11 [Google Scholar]
  93. Orell-Miquel, J., Nowak, G., Murgas, F., et al. 2023, A&A, 669, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Otegi, J. F., Helled, R., & Bouchy, F. 2022, A&A, 658, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Owen, J. E., & Wu, Y. 2017, ApJ, 847, 29 [Google Scholar]
  96. Parviainen, H., & Aigrain, S. 2015, MNRAS, 453, 3821 [Google Scholar]
  97. Parviainen, H., Pallé, E., Nortmann, L., et al. 2016, A&A, 585, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Parviainen, H., Luque, R., & Palle, E. 2023, MNRAS, 527, 5693 [NASA ADS] [CrossRef] [Google Scholar]
  99. Petit, A. C., Laskar, J., & Boué, G. 2018, A&A, 617, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Piro, A. L., & Vissapragada, S. 2020, AJ, 159, 131 [CrossRef] [Google Scholar]
  101. Rein, H., & Liu, S. F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Rein, H., & Tamayo, D. 2016, MNRAS, 459, 2275 [Google Scholar]
  103. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
  104. Rogers, J. G., Schlichting, H. E., & Owen, J. E. 2023, ApJ, 947, L19 [NASA ADS] [CrossRef] [Google Scholar]
  105. Salmon, S. J. A. J., Van Grootel, V., Buldgen, G., Dupret, M. A., & Eggenberger, P. 2021, A&A, 646, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Santerne, A., Malavolta, L., Kosiarek, M. R., et al. 2019, arXiv e-prints [arXiv:1911.07355] [Google Scholar]
  107. Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A&A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Schanche, N., Hébrard, G., Collier Cameron, A., et al. 2020, MNRAS, 499, 428 [NASA ADS] [CrossRef] [Google Scholar]
  109. Schwarz, G. 1978, Ann. Statist., 6, 461 [Google Scholar]
  110. Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap&SS, 316, 83 [Google Scholar]
  111. Shen, N., & González, B. 2021, arXiv e-prints [arXiv:2104.14725] [Google Scholar]
  112. Siegel, J. C., & Fabrycky, D. 2021, AJ, 161, 290 [NASA ADS] [CrossRef] [Google Scholar]
  113. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  114. Sneden, C. A. 1973, PhD thesis, University of Texas, Austin [Google Scholar]
  115. Sousa, S. G. 2014, in Determination of Atmospheric Parameters of B (Springer), 297 [Google Scholar]
  116. Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015, A&A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Sousa, S. G., Adibekyan, V., Delgado-Mena, E., et al. 2021, A&A, 656, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. Steffen, J. H., Ford, E. B., Rowe, J. F., et al. 2012, ApJ, 756, 186 [Google Scholar]
  121. Storn, R., & Price, K. V. 1997, J. Glob. Optim., 11, 341 [CrossRef] [Google Scholar]
  122. Sulis, S., Borsato, L., Grouffal, S., et al. 2024, A&A, 686, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  123. ter Braak, C. J. F., & Vrugt, J. A. 2008, Statist. Comput., 18, 435 [NASA ADS] [CrossRef] [Google Scholar]
  124. Thiabaud, A., Marboeuf, U., Alibert, Y., Leya, I., & Mezger, K. 2015, A&A, 574, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  125. Tsiaras, A., Rocchetto, M., Waldmann, I. P., et al. 2016a, ApJ, 820, 99 [NASA ADS] [CrossRef] [Google Scholar]
  126. Tsiaras, A., Waldmann, I. P., Rocchetto, M., et al. 2016b, ApJ, 832, 202 [NASA ADS] [CrossRef] [Google Scholar]
  127. Tsiaras, A., Waldmann, I. P., Zingales, T., et al. 2018, AJ, 155, 156 [NASA ADS] [CrossRef] [Google Scholar]
  128. Van Eylen, V., Albrecht, S., Huang, X., et al. 2019, AJ, 157, 61 [Google Scholar]
  129. Vanderburg, A., Becker, J. C., Kristiansen, M. H., et al. 2016, ApJ, 827, L10 [Google Scholar]
  130. Weiss, L. M., Isaacson, H. T., Marcy, G. W., et al. 2018, AJ, 156, 254 [Google Scholar]
  131. Weiss, L. M., Millholland, S. C., Petigura, E. A., et al. 2023, in Astronomical Society of the Pacific Conference Series, 534, Protostars and Planets VII, eds. S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, & M. Tamura, 863 [Google Scholar]
  132. Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [NASA ADS] [CrossRef] [Google Scholar]
  133. Winn, J. N. 2010, in Exoplanets, ed. S. Seager, 55 [Google Scholar]
  134. Wong, K. H., & Lee, M. H. 2024, AJ, 167, 112 [NASA ADS] [CrossRef] [Google Scholar]
  135. Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
  136. Zeng, L., Jacobsen, S. B., Sasselov, D. D., et al. 2019, PNAS, 116, 9723 [Google Scholar]
2

CH_PR100025, V. Nascimbeni.

3

CH_PR140080, A. Leleu.

5

The latest version, ARES v2, can be downloaded at https://github.com/sousasag/ARES

6

PAdova and TRieste Stellar Evolutionary Code: https://stev.oapd.inaf.it/cgi-bin/cmd

8

Here, f refers to the measured flux.

11

λ = ℳ + ω + Ω, where ℳ is the mean anomaly, ω is the argument of periastron (or pericenter), and Ω is the longitude of the ascending node.

12

Bayesian information criterion (BIC; Schwarz 1978).

13

The radius of planet g was estimated using the Bayesian radius–density–mass relation for small planets implemented in spright (Parviainen et al. 2023), obtaining a value of 2.42−0.5+0.5$\[2.42_{-0.5}^{+0.5}\]$ R⊕.

14

The four above are: Kepler-60, Kepler-29, TOI 763 and L 98-59.

All Tables

Table 1

Derived stellar parameters of HIP 41378.

In the text
Table 2

Transit times of HIP 41378 b from the global photometric analysis with PYORBIT.

In the text
Table 3

Transit times of HIP 41378 c from the global photometric analysis with PYORBIT.

In the text
Table A.1

Log of CHEOPS observations.

In the text
Table A.2

Posteriors and derived orbital parameters for HIP 41378 b & c from the global photometric analysis with PYORBIT, presented in Section 4.2

In the text
Table A.3

Posteriors and derived orbital parameters (MAP and HDI) for HIP 41378 b, c, and g obtained from the dynamical analysis with TRADES.

In the text
Table A.4

Results of the internal structure modeling for HIP 41378 b.

In the text
Table A.5

Results of the internal structure modeling for HIP 41378 c.

In the text

All Figures

thumbnail Fig. 1

Radial velocities of HIP 41378. Upper panel: RV plot minus the offset γ. TRADES MAP model is shown as a black line with the shaded gray areas indicating the 1σ, 2σ, and 3σ confidence intervals. HARPS observations are depicted as purple circles. Lower Panel: RV residuals after subtracting the model.
In the text
thumbnail Fig. 2

O-C diagrams of HIP 41378 b (left) and c (right). Each dataset is plotted with a different marker and color. Top: best-fit two-planet TRADES model (black line with gray-shaded 1σ, 2σ, and 3σ confidence intervals). Bottom: best-fit three-planet TRADES model. Lower panels in each plot show the residuals with respect to the corresponding model.
In the text
thumbnail Fig. 3

Mass–radius diagram including all confirmed planets with radii below 4 R⊕ with masses and radii measured to better than 30% precision (Gray points). Planet parameters are taken from the NASA Exoplanet Archive’s confirmed planets table, as queried on January 20, 2025. The purple pentagon represents the position of HIP 41378 b, while the green diamond represents the postion of HIP 41378 c. The color-coded lines show different theoretical mass–radius relations corresponding to the planet compositions taken from Zeng et al. (2019) (solid lines) and Lopez & Fortney (2014) (dashed lines; 1 Gyr, solar metallicity and incident flux of 10 S⊕). Also shown are Earth, Uranus and Neptune, for reference.
In the text
thumbnail Fig. 4

Three-body Laplace resonant angles evolution for HIP 41378 b, c and g, for the MAPHDI solutions. The top two panels show the evolution of the critical angles ϕ12 and ϕ23. The bottom panel shows the three-body angle, which is a linear combination of the mean longitudes of the planets.
In the text
thumbnail Fig. A.1

Phase-folded light curves of HIP 41378 b & c, combining observations from K2, Spitzer, HST, CHEOPS, and TESS. The oversampled best-fit transit models are overlaid on the light curves.
In the text
thumbnail Fig. A.2

Individual TESS phase-folded transit light curves of HIP 41378 b. The binned points are showed in red. The oversampled best-fit transit models are overlaid on the light curves.
In the text
thumbnail Fig. A.3

Individual TESS phase-folded transit light curves of HIP 41378 c. The binned points are showed in red. The oversampled best-fit transit models are overlaid on the light curves.
In the text
thumbnail Fig. A.4

Individual CHEOPS phase-folded transit light curves of HIP 41378 b. The binned points are showed in red. The oversampled best-fit transit models are overlaid on the light curves.
In the text
thumbnail Fig. A.5

Individual CHEOPS phase-folded transit light-curves of HIP 41378 c. The binned points are showed in red. The oversampled best-fit transit models are overlaid on the light curves.
In the text
thumbnail Fig. A.6

Posteriors for the main internal structure parameters of HIP 41378 b, namely the mass fractions of the planet’s inner core (far left), mantle (middle left), and envelope layers (middle right), as well as the mass fraction of water in the envelope layer (far right). We show models assuming the planet’s Si/Mg/Fe ratios match those of the host star exactly (purple), are Fe-enriched compared to the host star (pink), and are independent of the host star metallicity (blue). For all three options, we also use two water priors, favoring a water-rich (top row) and water-poor composition (bottom row), respectively. The vertical dashed lines show the medians of the inferred distributions and the dotted lines the chosen priors.
In the text
thumbnail Fig. A.7

Same as Figure A.6 but for HIP 41378 c.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.