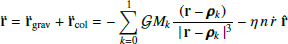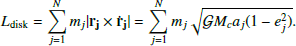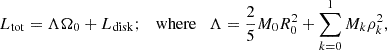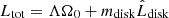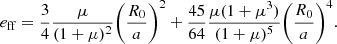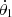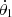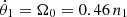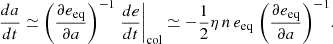| Issue |
A&A
Volume 702, October 2025
|
|
|---|---|---|
| Article Number | L15 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202556383 | |
| Published online | 21 October 2025 | |
Letter to the Editor
A formation mechanism for narrow rings around minor bodies
1
Observatorio Astronómico, Universidad Nacional de Córdoba, Laprida 854, (X5000BGR) Córdoba, Argentina
2
Instituto de Astronomía Teórica y Experimental (IATE), UNC-CONICET, Laprida 854, (X5000BGR) Córdoba, Argentina
⋆ Corresponding author: cbeauge@unc.edu.ar
Received:
12
July
2025
Accepted:
23
September
2025
Context. The recent discovery of narrow rings around minor bodies has raised many questions regarding their origin and current dynamics. Sharp ring boundaries seem indicative of shepherding moonlets, but none have been found. All rings lie close to spin-orbit resonances (SORs) with the central body, particularly the 1/3, even though it is not clear how these may be related. Furthermore, in at least one case the location of the ring is exterior to the Roche radius, adding to the striking differences with respect to giant planets.
Aims. We study the dynamical evolution of a particle disk around a minor body, perturbed by the non-spherical component of the gravity field, particle collisions, and spin changes of the central mass linked to angular momentum conservation. By varying key parameters, we search for cases where the combined effects may lead to resonance capture and orbital configurations similar to those that have been observed.
Methods. We performed N-body simulations of massless particles orbiting a central spherical body with a co-rotating mass anomaly. Collisions were modeled by adopting a simple radial damping force. Angular momentum conservation links the body’s spin to the disk’s orbital evolution. Since the gravitational effect of the test particles is neglected, this back-reaction is introduced externally assuming ad hoc spin-down rates and disk mass.
Results. Interaction between non-sphericity and collisions leads to the formation of a narrow ring that slowly recedes from the central mass. Spin-down of the minor planet shifts the SORs outward, enabling resonant capture. For suitable parameters, a portion – or all – of the initial disk can become trapped in the 1/3 SOR with the mass anomaly, in dynamically stable low-eccentricity orbits. Although the required disk mass is high (≳1% of the central body), long-term collisional erosion could reduce it to values that are consistent with observed ringlets.
Key words: methods: numerical / celestial mechanics / minor planets / asteroids: general / planets and satellites: rings
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
As of the writing of this paper, dense and narrow rings have been detected around three minor bodies: the centaur object Chariklo (Braga-Ribas et al. 2014) and two dwarf planets, Haumea (Ortiz et al. 2017) and Quaoar (Morgado et al. 2023). Although these objects exhibit significant diversity in size (roughly between 127 and 712 km) and rotational period (between 4 and 17 hours), the rings show surprising similarities. All are located very close to spin-orbit resonances (SORs) with the central mass, mainly the 1/3, and they show no evidence of any shepherding companions to explain the lack of radial diffusion1. Even more baffling, the location of the main ring around Quaoar lies outside the Roche radius, raising the question as to why such a dense population of bodies did not accrete into a single satellite. The existence of a small outer moon (Weywot) close to a 6/1 mean-motion resonance (MMR) with the ring may increase the eccentricities and inhibit accretion; however, there is little concrete evidence of such a scenario.
The proximity to resonances is particularly challenging and contrasts with the dynamical characteristics of ring systems around giant planets. To date no plausible mechanism has been presented to explain how SORs could have shaped the structure of rings around minor bodies or how orbital evolution could have led to such configurations. Resonance capture requires convergent migration, while the outward spiraling of ring particles due to collisions and/or diffusive effects gives rise to a divergent migration. These difficulties have resulted in a certain consensus that perhaps there is no causal relation between the observed population and SORs.
In this Letter we explore the possibility that resonance capture in SORs could have occurred as a result of the combination of three effects: (i) gravitational perturbations from the non-spherical component of the central mass, (ii) collisions in the proto-ring, and (iii) secular changes in the rotational period of the minor body due to angular momentum conservation of the full (body plus ring) dynamical system. While the roles of the first two interactions have been analyzed in the past, the back-reaction onto the central mass due to the orbital evolution of the proto-ring has not been considered and will prove crucial. For adequate values of system parameters, we will show how these interactions, particularly the spin-down of the central mass, can lead to resonance capture in a 1/3 SOR of a significant part of an initial particle disk and the formation of a stable narrow ring similar to those observed. Our analysis, however, is more oriented toward presenting a proof of concept of this mechanism and is not aimed at reproducing any particular detail of the known ring systems around Centaurs, trans-neptunian objects (TNOs), or dwarf planets.
2. Numerical simulations
2.1. Physical scenario and dynamical interactions
Following previous studies (Sicardy et al. 2019; Madeira et al. 2022; Giuliatti Winter et al. 2023), we approximated the gravitational field of the irregularly shaped central body of total mass Mc by a spherical component of mass M0, physical radius R0, and spin frequency Ω0, plus a point-mass anomaly M1, fixed on its surface2. We note that Mc = M0 + M1. Given the oblateness parameters estimated for Chariklo (ϵ ∼ 0.2), Haumea (ϵ ∼ 0.61), and Quaoar (ϵ ≳ 0.1), we expected the ratio μ = M1/M0 to be considerable, even if quantitative values are beyond our possibilities. The barycentric positions of each mass component, Mk, (with k = 0, 1) is denoted by ρk, with modulus 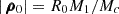 and
and 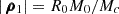 , both with angular frequency Ω0.
, both with angular frequency Ω0.
We assumed a particle disk orbited the central mass and was the precursor of the observed ring structure. Its formation and origin lies beyond the scope of this work, but we presume it resulted from a partially disruptive collision of the central mass with an external body or from the fragmentation of a primordial satellite (see, e.g., Melita et al. 2017). We assumed the disk to be coplanar with the equator of the massive body and to be radially bounded between rmin and rmax. Additionally, we supposed a certain surface density profile Σdisk(r), and a total mass mdisk. Any initial eccentricity distribution proved immaterial, rapidly reaching equilibrium values (denoted as eeq, see next sub-section) in a few orbital periods. The size distribution of the particles is relevant only when modeling their collisional evolution.
The equations of motion of each disk particle may be written, in a barycentric reference frame, as:
where  is the gravitational constant. The dynamical system is thus described by a circular restricted three-body problem,
is the gravitational constant. The dynamical system is thus described by a circular restricted three-body problem, 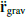 , with non-Keplerian motion of the primaries, plus an external radial friction term,
, with non-Keplerian motion of the primaries, plus an external radial friction term, 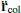 . We disregarded mutual gravitational interactions between elements of the disk, treating them as massless particles. The external force
. We disregarded mutual gravitational interactions between elements of the disk, treating them as massless particles. The external force 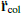 is a simple analytical prescription that mimics the dynamical effects of mutual collisions between ring elements (Sicardy et al. 2019). In this expression, n is the mean motion of the particle, and η is a dimensionless coefficient related (among other things) to the particle size and density profile at the location. We explored values between 10−4 and 10−2.
is a simple analytical prescription that mimics the dynamical effects of mutual collisions between ring elements (Sicardy et al. 2019). In this expression, n is the mean motion of the particle, and η is a dimensionless coefficient related (among other things) to the particle size and density profile at the location. We explored values between 10−4 and 10−2.
Since the external force is radial, it will preserve the angular momentum of each particle and thus of the disk as a whole. While this simplistic collisional model cannot compete with fully interacting N-body simulations, it does appear to reproduce many of its general features (Salo et al. 2021).
2.2. Equilibrium eccentricity and radial confinement
Conservation of angular momentum by 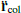 implies that a(1 − e2) = const, and the orbits suffer a damping (proportional to η) while exhibiting almost no change in the semimajor axis. Were it not for the mass anomaly, an eccentric initial disk would end as a circular structure analogous to the Saturn rings. However, the non-spherical component of the central mass introduces an equilibrium eccentricity, eeq, around which the particles oscillate (see Appendix A). Under the effects of an exterior non-conservative force such as our radial term, this stable solution morphs into an attractor, and any initial eccentricity distribution tends toward these values, hence the name “equilibrium eccentricity”.
implies that a(1 − e2) = const, and the orbits suffer a damping (proportional to η) while exhibiting almost no change in the semimajor axis. Were it not for the mass anomaly, an eccentric initial disk would end as a circular structure analogous to the Saturn rings. However, the non-spherical component of the central mass introduces an equilibrium eccentricity, eeq, around which the particles oscillate (see Appendix A). Under the effects of an exterior non-conservative force such as our radial term, this stable solution morphs into an attractor, and any initial eccentricity distribution tends toward these values, hence the name “equilibrium eccentricity”.
The top frame of Fig. 1 shows the orbital evolution of two elements of an extended disk. The initial conditions are shown with large filled circles, while arrows indicate the flow. Regardless of the initial orbit chosen above (green) or below (gray) eeq, the non-conservative force will rapidly lead the eccentricity to oscillate around the equilibrium eccentricity highlighted in orange. Once this occurs, the disk continues to evolve outward (see Appendix A), albeit at a much slower rate.
 |
Fig. 1. Orbital evolution of two disk particles under the effects of gravitational perturbations and collisional drag (η = 10−3). The central body was defined by μ = 0.05, R0 = 115 km and Ω0/n1 = 0.46. Top: Eccentricity versus semimajor axis. Initial conditions are indicated in filled circles, while arrows show the direction of flow. The equilibrium eccentricity eeq, is highlighted in orange. Bottom: Semimajor axes as a function of time. Notice that the semimajor axes of the particles converge over time. |
Perhaps the most interesting result of this section is shown in the bottom frame of Fig. 1, where we compare the semimajor axes of the two disk particles over time. As a grows, eeq is strongly reduced. Even though the eccentricity gradient also decreases, it is insufficient to counteract the previous trend, and the rate of change of the semimajor axis decreases. The resulting effect is an accumulation of the disk particles into an increasingly narrow ring. The time necessary for this radial confinement depends on several factors, including (i) the initial width and location of the disk; (ii) the collision coefficient, η; (iii) the mass ratio, μ; and (iv) the spin rate of the central body, Ω0. All other things being equal, this mechanism indicates that slow rotators are more efficient at converting disks into rings (Appendix A).
2.3. Rotational spin-down and resonance capture
Provided the confinement mechanism described above is more effective than any radial diffusion, the end product will be a stable narrow ring without the need of any shepherding satellite. As shown in the bottom frame of Fig. 1, the ring will continue to recede from the central body, albeit at an increasingly slowler rate. The eccentricity of the ring particles oscillate around eeq, taking values of the order of e ∼ 10−4 − 10−2, depending on the system parameters. The dynamics, however, are completely secular, and so far there is no reference to an SOR. The fact that all observed rings around minor planets favor SORs, particularly the 1/3, indicates that other dynamical phenomena must be at play.
For resonance capture to occur, orbital migration must be convergent (e.g., Beaugé & Cerioni 2022). In the case of exterior spin-orbit resonances, this implies that the frequency ratio n/Ω0 must increase over time. Since the orbital dynamics described in the previous section leads to an increase of the semimajor axis of the disk particles and consequently a reduction in the orbital frequency n, convergent migration can only occur if the spin rate, Ω0, were to also decrease at an even faster rate.
Although a secular variation in the body’s spin seems unlikely, it is nonetheless expected when assuming the conservation of the total angular momentum of the system. More importantly, its magnitude may be estimated from the back-reaction of the disk migration acting on the rotation of Mc.
Even if self-gravity was not considered in our numerical simulations, the disk is expected to have a certain mass mdisk, following a surface density profile, Σdisk(r). By representing this population by a set of N particles, each of mass mj, semimajor axis aj, and eccentricity ej, the orbital angular momentum of the disk may then be expressed as:
Assuming that the disk retains radial symmetry throughout its orbital evolution, the center of mass of the complete system will coincide with that of the central mass, Mc. Consequently, the total angular momentum may be written in barycentric coordinates as:
with Λ = Λ(M0, M1, R0), a function of the physical characteristics of the central body and independent of its rotation. The first term stems from the rotational motion of M0, while the second is the contribution from the translational motion of the central dipole. Invariance of Ltot implies that any increase in the disk angular momentum due to outward migration will lead to a decrease in the rotational frequency of the central body.
Lacking an explicit expression for eeq(a), our analytical insights could not go any further. However, we could perform numerical simulations introducing ad hoc spin-down rates 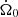 , and study its effect on the disk dynamics. Fig. 2 presents three examples plotting the semimajor axes of disk particles as a function of time. We chose a Chariklo-like body for a central mass, with Mc = 6.3 × 1018 kg, a reference radius of R0 = 115 km, and a rotational period Prot ≡ 2π/Ω0 = 7.004 hs (Leiva et al. 2017; Sicardy et al. 2019). The non-sphericity was modeled by a single mass anomaly with μ = 0.05. The initial disks were assumed to be circular with radial symmetry, between rmin = 2.5R0 (slightly above the co-rotation radius) and rmax = 3.8R0.
, and study its effect on the disk dynamics. Fig. 2 presents three examples plotting the semimajor axes of disk particles as a function of time. We chose a Chariklo-like body for a central mass, with Mc = 6.3 × 1018 kg, a reference radius of R0 = 115 km, and a rotational period Prot ≡ 2π/Ω0 = 7.004 hs (Leiva et al. 2017; Sicardy et al. 2019). The non-sphericity was modeled by a single mass anomaly with μ = 0.05. The initial disks were assumed to be circular with radial symmetry, between rmin = 2.5R0 (slightly above the co-rotation radius) and rmax = 3.8R0.
 |
Fig. 2. Three sets of simulations of the dynamical evolution of particle disks considering different values for the collisional coefficient, η. In all cases, the mass anomaly was taken to be equal to μ = M1/M0 = 0.05, while a spin-down rate with e-folding time τs = 105 years was adopted for the rotational frequency. The blue curves show the semimajor axes associated with the 1/3 and 1/2 SORs. The vertical lines indicate the times at which the spin-down reached values of Ω0 equal to 90% and 80% of the initial rotation frequency. |
Each disk, consisting of 35 massless particles under the effects of gravitational perturbations and radial drag, was integrated for 105 years. We also included an ad hoc spin-down of the central mass with a characteristic timescale of 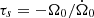 . The simulations shown in Fig. 2 used τs = 105 years. Since the equilibrium eccentricity is inversely proportional to (Ω0 − n), the spin-down helped fuel the outward migration of the disk and greatly reduced the evolution timescale. More importantly, variations in Ω0 moved the position of the SORs outward.
. The simulations shown in Fig. 2 used τs = 105 years. Since the equilibrium eccentricity is inversely proportional to (Ω0 − n), the spin-down helped fuel the outward migration of the disk and greatly reduced the evolution timescale. More importantly, variations in Ω0 moved the position of the SORs outward.
Each frame shows results for a different value of η. The inner initial disk, corresponding to orbits with a semimajor axis of a ≲ 3.0R0, has large values of equilibrium eccentricities eeq, and thus suffers a very fast radial migration, reaching separations of the order of 3R0 in a few decades. After this first stage, evolution continues more slowly. For η = 10−2 (top panel), the initial disk converges to a narrow ring in timescales on the order of T ∼ 103 years. However, the outward evolution of the ring proved faster than that of the SORs, leading to divergent migration and no resonance capture.
For η = 10−3 (center panel of Fig. 2) the outcome is very different. Even if the radial confinement takes longer (T ∼ 104 years), resonance capture is observed early in the process for initial conditions above and below the location of the 1/3 SOR. The resonant dynamics is preserved throughout the evolution of the narrow ring, with eccentricities displaying short-period variations between 10−3 and 10−2. The width of the ring continues to decrease as it recedes from the central body and M0 spins down, reaching values analogous to those currently observed.
Finally, in the case of η = 10−4 (bottom panel of Fig. 2) we observed the formation of two rings. The first ring is narrow, captured again in the 1/3 SOR. It formed a bit earlier than in the previous example and consists of particles initially exterior to the resonance location. A second broader ring is formed closer to the central body and is ultimately trapped in the 1/2 SOR. However, this requires a spin-down of more than 50% of the initial value, and may thus be considered an unlikely result.
These simulations are illustrative and have been chosen to highlight the different possible outcomes. While the mechanism leading to radial confinement is extremely robust and was found in all simulations, resonance capture is more sensitive. The SORs require a minimum width for trapping to take place, which depends on the value of μ. We found no resonant ring for μ < 10−3, although the limit is a function of η. Similarly, convergent migration requires minimum values for the spin-down rates, and such a condition was not met for τs ≳ 106 years. Within these ranges, outcomes analogous to the bottom frame of Fig. 2 were more frequent than that depicted in the center panel. However, our exploration of the parameter space is far from thorough.
Since our simulations are not self-consistent, we had to estimate the disk mass necessary to generate the assumed spin-down rate used for Fig. 2. Once again, we invoked the conservation of total angular momentum. Considering disk elements of equal mass, we rewrote expression (3) as:
where 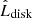 is the disk angular momentum per unit mass, a value that can be calculated from the numerical simulations at any given time. By calculating this quantity at two different times, say at t = 0 and when the spin was reduced by 20%, we could calculate the values of mdisk that preserves Ltot.
is the disk angular momentum per unit mass, a value that can be calculated from the numerical simulations at any given time. By calculating this quantity at two different times, say at t = 0 and when the spin was reduced by 20%, we could calculate the values of mdisk that preserves Ltot.
The results from Fig. 2 yield values for the total disk mass in the range of mdisk ∼ 8 × 10−3M0, showing only a weak dependence with η. No significant changes were observed when varying the time at which the disk angular momentum is evaluated, indicating a fairly robust estimation. Although these values are much larger than the current estimations (Pan & Wu 2016), collisional grinding within the dense ring could have pulverized a large portion of the original mass later ejected by radiation pressure (Morgado et al. 2023). This process could also aid in reducing the spin-down and lead to a steady-state configuration.
3. Conclusions
In this work, we have proposed a dynamical model for the origin and evolution of dense narrow rings around minor bodies, starting from an extended debris disk and evolving toward dynamical structures similar to those observed in several Centaurs and TNOs. Based on first principles, the observed radial confinement is the natural outcome of the gravitational interactions with the central body and a radial external force. Although we assumed a radial Stokes-like acceleration, analogous results should be obtained for any non-conservative force resulting in strong eccentricity damping.
The back-reaction on the central body’s spin is also a crucial ingredient, leading to convergent migration and (at least for some disk particles) resonance capture. Coincidental with observed systems, the 1/3 SOR appears as the most preferable commensurability. The radial confinement is maintained by resonant dynamics and the eccentricity gradient, without the need of shepherding satellite companions. The eccentricities remain low (∼10−3 − 10−2) but are large enough to inhibit accretional collisions (e.g., Brilliantov et al. 2015), and thus perhaps explain the existence of rings beyond the Roche radius, as observed around Quaoar. Since no apsidal alignment was detected, the rings would be observed as circular.
These promising results require debris disks that are more massive than estimated for the observed rings. While we cannot rule out the limitations of our numerical method and models for particle interactions (collisions and self-gravity), this discrepancy could be partially solved by collisional grinding over long timescales, which are particularly active once the localized surface density increases as a consequence of radial confinement.
A second ring around Quaoar discovered by Pereira et al. (2023) seems to lie close to the 5/7 SOR.
Acknowledgments
Simulations were carried out with the computing facilities hosted at IATE as well as in the High Performance Computing Center of the Universidad Nacional de Córdoba (CCAD-UNC). This research was funded by CONICET and Secyt/UNC.
References
- Beaugé, C., & Cerioni, M. 2022, Celest. Mech. Dyn. Astron., 134, 57 [CrossRef] [Google Scholar]
- Braga-Ribas, F., Sicardy, B., Ortiz, J. L., et al. 2014, Nature, 508, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Brilliantov, N., Krapivsky, P. L., Bodrova, A., et al. 2015, Proc. Natl. Acad. Sci., 112, 9536 [Google Scholar]
- Giuliatti Winter, S. M., Madeira, G., Ribeiro, T., et al. 2023, A&A, 679, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leiva, R., Sicardy, B., Camargo, J. I. B., et al. 2017, AJ, 154, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Madeira, G., Giuliatti Winter, S. M., Ribeiro, T., & Winter, O. C. 2022, MNRAS, 510, 1450 [Google Scholar]
- Melita, M. D., Duffard, R., Ortiz, J. L., & Campo-Bagatin, A. 2017, A&A, 602, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morgado, B. E., Sicardy, B., Braga-Ribas, F., et al. 2023, Nature, 614, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, J. L., Santos-Sanz, P., Sicardy, B., et al. 2017, Nature, 550, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Leinhardt, Z. M., Thébault, P., & Baruteau, C. 2012, ApJ, 754, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, M., & Wu, Y. 2016, ApJ, 821, 18 [CrossRef] [Google Scholar]
- Pereira, C. L., Sicardy, B., Morgado, B. E., et al. 2023, A&A, 673, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salo, H., Sicardy, B., Mondino-Llermanos, A., et al. 2021, in European Planetary Science Congress, EPSC2021–338 [Google Scholar]
- Sicardy, B., Leiva, R., Renner, S., et al. 2019, Nat. Astron., 3, 146 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The semi-secular and equilibrium eccentricities
In addition to the system parameters defined in 2.1, let θ1 denote the azimuthal angle of the position of M1 in a given inertial reference frame. In the two-body problem, where the motion of the perturber M1 with respect to the center of mass is keplerian, i.e. 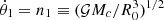 , the equilibrium eccentricity eeq lies close to the semi-secular forced eccentricity eff, associated to stable fixed points in the restricted three-body problem, averaged over the orbital period of the perturber. For initial conditions exterior to the binary M0 + M1, an octupole-level expansion of the disturbing functions yields:
, the equilibrium eccentricity eeq lies close to the semi-secular forced eccentricity eff, associated to stable fixed points in the restricted three-body problem, averaged over the orbital period of the perturber. For initial conditions exterior to the binary M0 + M1, an octupole-level expansion of the disturbing functions yields:
A simplified version, limited to the quadrupole level, was found by Paardekooper et al. (2012). However, given the proximity of the future ring to Mc, an extension to octupole terms proves necessary. It is important to note that eff is equivalent to the classical secular forced eccentricity for exterior orbits (a > R0) in the case where the perturber lies in a circular orbit.
The dashed black line in Fig. A.1 plots eff as function of a/R0, assuming a mass ratio μ = 0.05. The exact values of the equilibrium eccentricity, in the case of M1 in keplerian orbit, are shown in red, and were obtained from N-body simulations whose outputs were averaged over timescales much larger than orbital period. As expected, eeq ≃ eff, and the discrepancy tends to zero for increasing semimajor axis. Although the difference could be due to higher order terms in the Legendre expansion of the disturbing function, its origin lies elsewhere and is much more interesting.
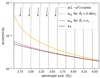 |
Fig. A.1. Schematic view of the different interactions acting on the initial particle disk. Curves of constant angular momentum (per unit mass) are shown in gray, with arrows indicating evolutionary routes due to a radial drag term. Red and orange curves highlight the equilibrium eccentricities of initial conditions undergoing both collisions and gravitational perturbations (assuming μ = 0.05 and R0 = 115 km). Both differ in the assumed angular frequency |
We return to our minor body Mc = M0 + M1, where M1 co-rotates with M0. In such a case, the motion of the perturber with respect to the center of mass is sub-keplerian, with a corresponding angular ("orbital") frequency equal to Ω0 < n1. The orange curve in Fig. A.1 shows the equilibrium eccentricity in this case, considering Ω0 = 0.46n1, a value similar to the current spin of Chariklo. The values of this new equilibrium eccentricity are significantly higher than those obtained for  and the semi-secular limit eff.
and the semi-secular limit eff.
Numerical simulations, backed by perturbation theory, indicate that the change in eeq is related to the magnitude of short-period variations, which, by construction, are not considered in the secular or semi-secular disturbing functions. While a detailed model for the sub-keplerian equilibrium eccentricity is outside the scope of this Letter, its main features may be described by an expression of the type: eeq2 − eff2 ∝ n/(k1Ω0 − k2n)2, with k1 and k2 integers. Thus, slow-rotating central bodies generate larger equilibrium eccentricities than fast rotators. As the orbital frequency of M1 increases, the difference with eff decreases, as observed comparing the red and dashed black curves.
For low eccentricities (say ≲10−2), the curves of constant angular momentum are practically vertical en in (a, e) plane and the dominant effect is focused on the eccentricity. Thus, when the disk particle reaches the equilibrium eccentricity, the non-conservative term has a non-zero component along the gradient of eeq(a). This eccentricity gradient then generates a secular change in the semimajor axis toward larger values. The rate of change in a may be written as:
Since the equilibrium eccentricity gradient is always negative, all disk particles recede from the central body over time.
All Figures
 |
Fig. 1. Orbital evolution of two disk particles under the effects of gravitational perturbations and collisional drag (η = 10−3). The central body was defined by μ = 0.05, R0 = 115 km and Ω0/n1 = 0.46. Top: Eccentricity versus semimajor axis. Initial conditions are indicated in filled circles, while arrows show the direction of flow. The equilibrium eccentricity eeq, is highlighted in orange. Bottom: Semimajor axes as a function of time. Notice that the semimajor axes of the particles converge over time. |
| In the text | |
 |
Fig. 2. Three sets of simulations of the dynamical evolution of particle disks considering different values for the collisional coefficient, η. In all cases, the mass anomaly was taken to be equal to μ = M1/M0 = 0.05, while a spin-down rate with e-folding time τs = 105 years was adopted for the rotational frequency. The blue curves show the semimajor axes associated with the 1/3 and 1/2 SORs. The vertical lines indicate the times at which the spin-down reached values of Ω0 equal to 90% and 80% of the initial rotation frequency. |
| In the text | |
 |
Fig. A.1. Schematic view of the different interactions acting on the initial particle disk. Curves of constant angular momentum (per unit mass) are shown in gray, with arrows indicating evolutionary routes due to a radial drag term. Red and orange curves highlight the equilibrium eccentricities of initial conditions undergoing both collisions and gravitational perturbations (assuming μ = 0.05 and R0 = 115 km). Both differ in the assumed angular frequency |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.