Table 2
Retrieved atmospheric (log) abundances as volume mixing ratios.
| Retrieval | Instrument | H2O | CH4 | CO | CO2 | NH3 |
|---|---|---|---|---|---|---|
| Z19-freea | WFC3 | 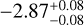 |
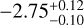 |
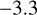 |
 |
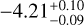 |
| Z19-constr.b | WFC3 | 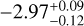 |
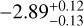 |
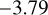 |
 |
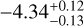 |
| This workc | WFC3 + GNIRS + MIRI | 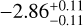 |
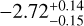 |
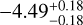 |
 |
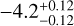 |
Notes. Log abundances are expressed units of volume mixing ratios. (a)Called the “free” model with 31 parameters. This incorporates a 80 MJup mass prior upper limit. The 3σ upper limits are from Table 4 of Zalesky et al. (2019). (b)Called the “constrained” model, also with 31 parameters. Here the previously used upper mass limit is removed and restraints are applied on the priors of radius and log g, as 0.7 < R/RJup < 2.0 and 3.5 < log(g) < 5.5, respectively. The 3σ upper limits are computed from the marginal posteriors obtained by Zalesky et al. (2019). (c)3σ upper limits computed from the marginal posteriors obtained in our work. The volume mixing ratios in this work were calculated by converting the mass fractions from the cloud-free retrieval.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


