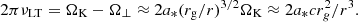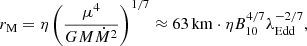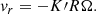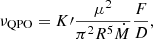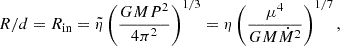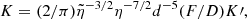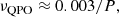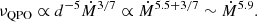| Issue |
A&A
Volume 703, November 2025
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202555210 | |
| Published online | 03 November 2025 | |
Magnetic precession as a model for quasi-periodic oscillations in pulsating ultraluminous X-ray sources and in flat-top noise sources
1
Nicolaus Copernicus Superior School, College of Astronomy and Natural Sciences, Gregorkiewicza 3, 87-100 Toruń, Poland
2
Nicolaus Copernicus Astronomical Center of the Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
3
Research Centre for Computational Physics and Data Processing, Institute of Physics, Silesian University in Opava, Bezručovo nám. 13, CZ-746 01 Opava, Czech Republic
4
Academia Sinica, Institute of Astronomy and Astrophysics, PO Box 23-141 Taipei 106, Taiwan
⋆ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
18
April
2025
Accepted:
27
August
2025
Context. Several instances of low-frequency quasi-periodic oscillations (QPOs) have been reported for ultraluminous X-ray sources (ULXs), including three observed for pulsating ULXs (PULXs) to date. The nature of various ULXs and the detailed properties of accretion in PULXs remain unclear.
Aims. We seek to determine if there exists a QPO model that fits the data and we investigate whether mHz QPOs can be used to constrain the magnetic field and accretion rate of the neutron stars in PULXs. Furthermore, we consider whether all the low-frequency QPOs in ULXs can be interpreted as a manifestation of the same phenomenon.
Methods. The available data indicates that the mHz QPO frequency is inversely proportional to the neutron star rotational period in PULXs. We examined two different physical models that could potentially explain this frequency-period dependence: 1) a precession of the inner accretion disk and torus in the strong gravity of a spinning neutron star and 2) inner disk precession forced by the neutron star magnetic field. In the latter case, we applied a magnetic precession model to the PULX data, with the magnetic threading of the accretion disk constrained by recent simulations.
Results. Based on the magnetic precession model and on recent progress in the study of the inner structure of accretion disks, we predict an inverse scaling of QPO frequency with the neutron star period in PULXs. The theoretical curve is largely independent of the stellar magnetic field or mass accretion rate and agrees with the data for the known QPOs in PULXs. Alternatively, precession of strong-gravity origin would imply a restrictive upper limit on the stellar magnetic dipole. The flat-top noise QPOs detected in (non-pulsating) ULXs display observational properties that appear to be very different from the QPOs detected in PULXs, indicating they might have different origins.
Key words: accretion, accretion disks / stars: neutron / X-rays: binaries
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1. Introduction
Ultraluminous X-ray sources (ULXs) are extragalactic off-nuclear, point-like sources with extremely high X-ray luminosities, typically in the range LX ≈ 1039 − 1041 erg s−1 (Fabbiano 1989; Read & Pietsch 1999; Roberts & Warwick 2000). The observed emission from these sources generally exceeds the Eddington limit of stellar-mass objects (Makishima et al. 2000; King et al. 2001). Recently, Tranin et al. (2024) reported 1901 such objects using Chandra, XMM-Newton, and Swift data. As a result of the super-Eddington luminosities, they were initially classified as intermediate-mass black holes (IMBH) (Kaaret et al. 2006; Kong et al. 2007). However, stellar evolution theories generally do not predict the formation of such objects and the observed abundance is difficult to produce even in dense star clusters (King 2004; Madhusudhan et al. 2006). A significant breakthrough in discovering the true nature of ULXs occurred when Bachetti et al. (2014) discovered a coherent pulsation with an average period of ≈1.37 s from the source ULX M82 X-2. This strongly suggested that the compact accretor was a neutron star. Since then, several ULXs have been observed with a coherent pulsation (see e.g. Fürst et al. 2016; Israel et al. 2017a; Carpano et al. 2018; Rodríguez Castillo et al. 2020; Pintore et al. 2025). The IMBH scenario has been largely ruled out for these sources.
The challenge to explain the extreme super-Eddington luminosities for stellar-mass compact objects was met by King et al. (2001), who proposed that beamed emission could boost the observed flux of accreting objects to very high values. As an extension of this idea, King et al. (2017) proposed a mechanism (the KLK model) that accounts for the extremely high spin-up rates and the high apparent luminosity of these pulsars within the standard Shakura-Sunyaev framework (Shakura & Sunyaev 1973). In the KLK model, an analysis of spin-up torques yields moderate magnetic fields of B ∼ 1011 G. Alternatively, a strong magnetic field (B > 1013 G) has been proposed to reduce the opacity, which would allow the true luminosity to be several times the Eddington limit (Paczynski 1992; Mushtukov et al. 2015).
Although they are rarely observed in ULXs overall, quasi-periodic oscillations (QPOs) from these sources provide us with another distinct timescale alongside pulsations that helps probe deeper into the accretion process. Several examples of these oscillations have been reported in the ULX sources over the past few years (see e.g. Feng et al. 2010; Avdan et al. 2014; Agrawal & Nandi 2015; Urquhart et al. 2022; Imbrogno et al. 2024). Among these, only a few sources have reported measurements for both the pulsation period and QPO frequency; currently, these are M82 X-2 (Feng et al. 2010), ULX-7 M51 (Imbrogno et al. 2024), and NGC 7793 P13 (Imbrogno 2024).
In this work, we try to identify QPO models which could be compatible with the observed PULX QPOs. In Section 3, we show that general-relativistic precession models are unlikely to apply to the mHz QPOs in PULXs. However, there are alternatives that do not invoke strong gravity. In particular, we revisited the precession model for tilted accretion disks, which was initially proposed by Lai (1999) and verified numerically in Pfeiffer & Lai (2004). An interest in the model was revived when Veresvarska et al. (2024) identified quasi-periodic oscillations in accreting white dwarfs, which could be interpreted within the framework of this precession model. Here, we chose to apply general scaling laws to restrict the model. Refining the precession frequency equation, we proposed an inverse relationship between the QPO frequency and the neutron star rotation period (Section 4). A discussion of the relevance of this suggestion to the known QPOs in PULXs (described in Section 2) is carried out in Section 5 and their properties are contrasted with those of flat-top noise QPOs in ULXs in Section 6.
2. mHz QPOs in PULXs
We are aware of only three PULXs for which mHz QPOs have been reported: M51 ULX7, M82 X-2, and NGC7793 P13; their spin periods and approximate QPO frequencies are listed in Table 1. Remarkably, the QPO frequencies are inversely correlated with the neutron star spin periods (Fig. 1). Below, we start with a brief summary of what is known about the three sources.
PULX mHz QPOs
 |
Fig. 1. mHz QPO frequency versus the neutron star period in PULXs. A νQPO = const ⋅ 1/P line (in solid black) is plotted to guide the eye. The data points are plotted with error bars as per Table 1. |
2.1. M82 X-2
The X-ray source X42.3+59 was identified as an ultraluminous X-ray source (ULX) using Chandra X-ray observations (Kaaret et al. 2006; Kong et al. 2007) and it was subsequently named M82 X-2. Kaaret et al. (2006) found significant timing noise at 1 mHz from this source; subsequently, QPOs in the range in the range 2.77–3.98 mHz were reported by Feng et al. (2010). Later, Bachetti et al. (2014) discovered a pulsation from this source with an average period of 1.37 s and a sinusoidal modulation of around 2.5 days; the nearly circular orbit with eccentricity < 0.003 and the high luminosity (1.8 × 1040 erg s−1) suggested accretion through Roche lobe overflow. During the interval MJD 56696 to 56701 the spin-up rate was Ṗ ≈ − 2 × 10−10 ss−1. Bachetti et al. (2022) found spin-down during the period 2016–2020 and stated that the spin history suggests that the source is near spin equilibrium. Liu (2024) followed the evolution from the last 20 years to find a gradual spin down, with occasional spin-up events in between. Bachetti et al. (2022) suggested a B > 1013 G magnetic field to explain the high luminosity of about 200 times the Eddington limit. In the KLK model, B ≈ 1011 G is found from the spin torques and a beaming factor of b ≈ 0.06 is required to explain the luminosity (King et al. 2017).
2.2. M51 ULX-7
First discovered as an X-ray source by Roberts & Warwick (2000) in the ROSAT survey, it was observed to have a 2.1 h periodicity (Liu et al. 2002) in a Chandra ACIS observation. Earnshaw et al. (2016) found a strong variability (> 10%) in this source, even in the hard state (photon index Γ ≈ 1.5), which is uncommon in ULXs. The pulsar nature of the compact object was demonstrated when Rodríguez Castillo et al. (2020) detected a pulsation at ≈2.8 s using data from the XMM-Newton Large Program UNSEeN. They suggested this source to be a High Mass X-ray Binary (HMXB) with luminosity varying from LX < 3 × 1038 erg s−1 to LX ≈ 1040 erg s−1, accreting at ≈20 times the Eddington rate. They also measured a spin-up rate of Ṗ ≈ − 1.5 × 10−10s ss−1 during the two months 2018 May and June. Later, Brightman et al. (2022) followed up the spin evolution in the period 2018–19 to report an average spin-up rate of Ṗ ≈ − 3 × 10−10s ss−1. However, a long-term (2005–2018) secular spin-up rate of Ṗsec ≈ −10−9s ss−1 was also reported by Rodríguez Castillo et al. (2020) in the same study. Recently, quasi-periodic oscillations in the frequency range 0.449 − 0.565 mHz were discovered by Imbrogno et al. (2024). This made ULX-7 the second object from which QPOs have been detected from a PULX accreting at a super-Eddington luminosity. While Vasilopoulos et al. (2020) estimated the surface magnetic field to be close to 2 − 7 × 1013 G based on accretion torques, Rodríguez Castillo et al. (2020) inferred a wider range of B ≈ 8 × 1011 − 1013 G considering both the effects of spin-up torques and column accretion (Mushtukov et al. 2015); in the same study, the beaming factor was estimated to lie between 1/12 < b < 1/4. Applying the KLK model, King & Lasota (2020) obtain b = 0.09 and B between 6.9 × 109 G and 1.9 × 1011 G, depending on the spin-up rate.
2.3. NGC 7793 P13
This object was first observed as a highly luminous (LX ≈ 1039 erg s−1) variable X-ray source by Read & Pietsch (1999) in a ROSAT survey. Motch et al. (2014) detected this to be a binary system with a compact accretor and a B9Ia donor star, with an orbital period of ≈64 days. Fürst et al. (2016) discovered a nearly sinusoidal pulsation at ≈0.42 s, confirming the accretor to be a neutron star. The luminosity they obtained was close to 50LEdd; however, the beaming factor necessary to explain this observation (b ≈ 1/50) was thought to be incompatible with the smooth sinusoidal pulsations. During the 2013–2016 period, they detected a spin-up at a rate of Ṗ ≈ − 3.486 × 10−11s ss−1 from this source. Fürst et al. (2021) followed the spin evolution to find a continuous spin-up up to 2020, after which it went into a low state. A similar phase also occurred previously in the period 2011–2013. Fürst et al. (2024) followed up the source to discover that it reemerged from the low state in 2022, with the spin-up rate accelerated to −1 = −6.28 × 10−11 ss−1. A QPO at ≈10 mHz was recently discovered in this object (Imbrogno 2024). We note that the frequency range, attributed to Imbrogno (in prep.), was reported by Veresvarska et al. (2025) to be 11 − 15 mHz. Fürst et al. (2016) estimated the surface magnetic field of this source to be around B ≈ 5 × 1012 G, based on the standard disk accretion model from Ghosh & Lamb (1979). In the framework of the KLK model (King et al. 2017), a surface magnetic field of B ≈ 1010 G could be sufficient to describe the observed luminosity, with a beaming factor of b ≈ 0.18. This is the only known PULX with an optical counterpart to date (Motch et al. 2014). It has the shortest period among the known PULX sources (Israel et al. 2017b).
3. Strong-gravity models
Assuming that the correlation we have found in the still limited data set between the neutron star spin rate (ν* = 1/P) and the mHz QPO frequency (νQPO) is a real effect, any model of the PULX QPOs would have to explain the correlation νQPO ∝ ν*.
In fact, the proportionality of certain fluid-body mode frequencies to the spin rate of a central gravitating body is a very natural outcome of strong gravity in general relativity. It is widely known that to the lowest order in the dimensionless spin parameter, a*, in the Kerr metric, the difference between the test-particle orbital and vertical epicyclic frequency is proportional to the spin,
The frequency, νLT, is known as the Lense-Thirring frequency and it has been used in a discussion of the ∼100 Hz QPOs in LMXBs by Stella & Vietri (1998). Here, rg = GM/c2 is the gravitational radius and M is the mass of the central compact object. The formula applies equally well to slowly rotating neutron stars, as the Hartle-Thorne metric coincides with the Kerr metric to first order in a* = (c/G)J/M2, with J = 2πν*I the angular momentum of the star, and I = I45 ⋅ 1045 g cm2 its moment of inertia.
Crucially, the eigenfrequencies of exact modes of certain fluid bodies are given by epicyclic frequencies or the Lense-Thirring frequency, evaluated at a certain radial position inside the fluid body. Resonance between the m = 0 vertical epicyclic mode and the radial epicyclic mode has been invoked to explain the 3:2 ratio of the highest frequency QPOs observed in microquasars, accreting stellar-mass black holes (Bursa et al. 2004). The m = −1 vertical epicyclic mode (Blaes et al. 2006) has been invoked to explain the C-type QPOs in the same sources (Fragile et al. 2007; Ingram & Done 2011; Morales Teixeira et al. 2014). In the latter mode, the torus is tilted with respect to the equatorial plane and precesses at the Lense-Thirring rate, with its eigenfrequency given by Eq. (1).
Among the modes of thin black hole accretion disks, the trapped c-mode oscillations also occur at νLT (Silbergleit et al. 2001). For the calculations of this mode (as carried out for black holes) to be relevant to neutron stars, two conditions must be met. First the neutron star has to be within its marginally stable orbit (the ISCO), as allowed by some equations of state of ultra-dense matter (Kluzniak & Wagoner 1985; Kluzniak et al. 1990). Second, the disk must not be truncated by the magnetic field. The latter condition is necessary also for the precession of a torus (in the m = −1 mode mentioned above).
The known PULXs rotate so slowly that we are compelled to wonder whether the Lense-Thirring effect would not be dwarfed by other phenomena. For instance, accretion torques may be larger than the Lense-Thirring torque. However, Bollimpalli et al. (2025) pointed out that accretion torques do not affect the precession frequency (they change the direction of the precession axis, instead). For trapped c-modes of the thin disk, there is a restriction ruling out the slowest rotators. For the natural ‘free boundary’ condition, δvr = 0, the c-mode only exists for a* ≥ 1.4 ⋅ 10−4 (Silbergleit et al. 2001). This seems to be comfortably compatible with only two of our three sources (Table 2). With a zero-gradient inner boundary condition on the radial velocity, the restriction is relaxed by two orders of magnitude. At any rate, for the Lense-Thirring precession to be relevant to the PULX QPOs, the radius r in Eq. (1) must be sufficiently small for νLT to match the observed mHz QPOs in very slowly rotating neutron stars. For the modes discussed here, the precessing fluid body must necessarily extend on both sides of a radius of r = rLT.
Table 2 summarises the restrictions on the (fiducial) radius of precession. The parameter a* corresponds to the PULX periods from Table 1, assuming I45 = 1 and M = 1.4 M⊙. These values are then used to derive r = rLT that would give νLT from Eq. (1) matching the QPO frequencies in Table 1. Both the non-beamed models, which give larger magnetic field values, and the beaming KLK model values are presented. For the non-beamed models, the ULX luminosity, L = Lobs, is taken from observations. For the beamed model, L = bLobs.
The magnetospheric radius, where the equatorial accretion flow is terminated, can be estimated for our typical neutron star from the Elsner & Lamb (1977) formula
where B = B10 ⋅ (1010G) is the model (dipole) magnetic field strength from the literature, as reviewed in Section 2, and the mass accretion rate was estimated from 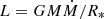 , with L = λEddLEdd, for our fiducial M = 1.4 M⊙ star with a radius of R* = 10 km, and LEdd = 1.4 × 1.3 ⋅ 1038 erg/s. The value of η in Elsner & Lamb (1977) is 1.8, while in the subsequent literature, we see η ≈ 1, varying by about a factor of 2, depending on the model assumptions (Kluźniak & Rappaport 2007, and references therein). In Table 2, we use a conservatively low value, namely, η = 0.5; larger values (such as η = 0.88 used in Section 4) would be even more restrictive for the Lense-Thirring model.
, with L = λEddLEdd, for our fiducial M = 1.4 M⊙ star with a radius of R* = 10 km, and LEdd = 1.4 × 1.3 ⋅ 1038 erg/s. The value of η in Elsner & Lamb (1977) is 1.8, while in the subsequent literature, we see η ≈ 1, varying by about a factor of 2, depending on the model assumptions (Kluźniak & Rappaport 2007, and references therein). In Table 2, we use a conservatively low value, namely, η = 0.5; larger values (such as η = 0.88 used in Section 4) would be even more restrictive for the Lense-Thirring model.
A necessary condition for the general-relativistic precession to be relevant to the PULX QPOs is that rLT > rM. As can be seen from Table 2, this is marginally satisfied for the KLK beamed model fields in NGC 7793 P13, and only for the lowest limit of the allowed range of the magnetic field in the same model for ULX-7 M51. For M82 X-2, the magnetic field value would have to be reduced by at least one order of magnitude. The same precession is completely incompatible with the non-beamed model of PULXs, for which rLT ≪ rM in all cases. In short, based on the published magnetic field values, we reject the Lense-Thirring precession as a model for the PULX mHz QPOs. If this precession were the correct explanation, the magnetic field value estimates would have to be revised severely downwards.
4. Dong Lai’s magnetic precession model and QPOs
We start with the formula for the precession frequency of a ring in a tilted accretion disk (Lai 1999), as summarised in Pfeiffer & Lai (2004) in their numerical work demonstrating the warping, tilting, and the rigid-like precession of an accretion disk subjected to the magnetic forces exerted by an inclined stellar magnetic dipole. The precession frequency is given by
Here, F(θ) = 2fcos2(θ)−sin2(θ) is a function of the (fixed) angle between the stellar spin axis and the axis of the (centred) magnetic dipole of magnitude, μ, while f is a factor describing the degree to which the accretion disk is threaded by the magnetic field of the dipole.
We take f = 1, corresponding to no threading of the disk, in agreement with the analytic calculations of Čemeljić et al. (2023). This was also confirmed by their numerical resistive MHD simulations, which showed that the magnetic field inside the disk is strongly suppressed with respect to the value above and below the disk. This is also consistent with radiative GRMHD simulations of ULX beaming by Abarca et al. (2021), Kayanikhoo et al. (2025). Hence, we take F(θ) = 2 cos2(θ)−sin2(θ), which varies between the value of 2 for θ = 0, and 5/4 for θ = 30°. Thus, we expect the value of F to vary by a factor of up to about 2 from source to source in beamed ULXs.
In a recent work, Veresvarska et al. (2025) analysed the opposite limit of f = 0. We expect that with this choice the inclination of the magnetic dipole to the spin axis would have a crucial influence on the observed QPO frequencies (because of the sin2θ dependence). If the disk is indeed threaded, with f = 0, then a larger sample of (as yet undiscovered) QPOs in PULXs would be unlikely to show the 1/P dependence we point out in this paper.
We assume the accretion disk is geometrically thick for ULX accretion rates, in agreement with the simulations of Abarca et al. (2021), Inoue et al. (2023), Inoue et al. (2024) and Kayanikhoo et al. (2025). The quantity D(r) in Eq. (3) is a geometrical factor that close to the inner edge of the disk then becomes 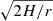 , with H the half-thickness of the disk. Without further ado, we take D(r) = const ≈ 1. Thus, for any given source, we can take F(θ)/D(r) = const ≈ 1.
, with H the half-thickness of the disk. Without further ado, we take D(r) = const ≈ 1. Thus, for any given source, we can take F(θ)/D(r) = const ≈ 1.
We identified the QPO frequency in PULXs with the frequency ν(R) of Eq. (3), where R is a characteristic radius (discussed below) of the inner precessing ring. The surface density of the disk, Σ, is unobservable, but it can be replaced with the mass accretion rate, Ṁ, through the mass conservation equation, Ṁ ≈ −2πrvrΣ, where vr is the radial velocity. Our crucial step is to assume that vr(R) scales as the azimuthal velocity, RΩ(R), in the inner disk,
This scaling is fairly general, being valid for both geometrically thick and thin accretion flows. It arises in analytic works on self-similar ADAF flows (Narayan & Yi 1994) and can be seen in radiative simulation of high-accretion-rate disks (Lančová et al. 2019). The scaling has been pointed out for thin disk models (Lipunov 1982; Kluzniak & Kita 2000), under which the constant is approximately equal to the alpha viscosity parameter, K′≈α. We can change this approximate equality into an exact one by introducing a new parameter, namely, a ≈ 1, so that K′=aα. The QPO frequency becomes
with F/D ≈ 1.
As our final assumption, we take the characteristic radius, R, to be somewhat larger than the radius of the inner edge of the disk, taken to be magnetically truncated below the corotation radius. The influence of the dipole on the disk is expected to drop as the square of its strength, in agreement with Eq. (3). Here, we take the standard picture, illustrated, for example, in Figure 5 of Veresvarska et al. (2024) or Figure 1 in Bollimpalli et al. (2025). We can see that the inner part of the disk precesses as a rigid body1, specifically: a ring starting at the inner edge of the disk, Rin, out to some outer radius, Rout, with the characteristic radius, R = d × Rin, between the two: Rin < R < Rout.
Thus, from
we have 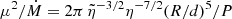 , where P is the neutron star rotation period, and the parameters satisfy d > 1,
, where P is the neutron star rotation period, and the parameters satisfy d > 1, 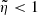 , while the constant η ≈ 1 takes into account the theoretical uncertainty of up to about a factor of 2 (Kluźniak & Rappaport 2007) in the value of the magnetic truncation radius (see the last term in Eq. (5)). Finally, based on our assumptions, we obtained a simple inverse proportionality between the QPO frequency and the stellar spin period, P,
, while the constant η ≈ 1 takes into account the theoretical uncertainty of up to about a factor of 2 (Kluźniak & Rappaport 2007) in the value of the magnetic truncation radius (see the last term in Eq. (5)). Finally, based on our assumptions, we obtained a simple inverse proportionality between the QPO frequency and the stellar spin period, P,
where the proportionality constant is
with the K′ of Eq. (4) given by K′=aα, as already noted. Taking as fiducial values (2/π)η−7/2 = 1 (i.e. η ≈ 0.88), a = 1, (F/D) = 1, we obtain 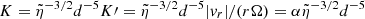 .
.
As |vr| < < rΩ, we necessarily have νQPO/P < < 1. In fact, since α ∼ 0.01 according to magneto-rotational instability (MRI, Balbus & Hawley 1991) simulations, we would expect the QPO frequency to be about two orders of magnitude smaller than the spin period when corotation (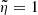 ) holds, νQPO ∼ 0.01/P. This seems to be roughly the case (Table 1). Assuming the center of the precessing torus to be at a radius some 30% larger than the truncation radius, Rin, we would take d = 1.3, along with a value giving QPO frequencies,
) holds, νQPO ∼ 0.01/P. This seems to be roughly the case (Table 1). Assuming the center of the precessing torus to be at a radius some 30% larger than the truncation radius, Rin, we would take d = 1.3, along with a value giving QPO frequencies,
which reproduces the observed trend reasonably well in the still very limited data, as seen in Fig. 1.
5. The QPO model for PULXs
In Fig. 1, we show the data points for the three PULX QPOs. We also show the theoretical curve of Eq. (6). Since the actual value of the α parameter is uncertain, we can fix the K constant at a reasonable value of K = 0.003. An interpretation of this value of K is offered in the discussion of Eq. (8). We note that the data are within a factor of 2 of the curve.
We applied Dong Lai’s magnetic precession model (Lai 1999) to ULXs, identifying the precession frequency with that of the observed QPOs. Pfeiffer & Lai (2004) have shown numerically that the inclined dipole will warp the disk and force it to move in a steady, rigid-body like precession of the inner region, with the frequency given by Eq. (3). The model assumes the accreting star to be endowed with a dipole moment of strength μ that is inclined (at an angle θ) to the rotation axis of the star. The disk is assumed to be truncated by the magnetosphere at a radius, Rin, so we necessarily assume that the radius of the star is smaller, namely, R* < Rin.
As it turns out, neither the radius, R*, nor the mass, M, of the neutron star enters into the final formula for the QPO frequency. However their values matter overall: they control the luminosity in the inner region, given by 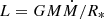 for a given accretion rate, Ṁ, through the inner regions of the accretion disk of an essentially non-rotating star, thus indirectly shaping the unperturbed shape of the inner disk. Assuming that the accretion disk is fairly thick (H ∼ r), we were able to transform Eq. (3) into the simple form of Eq. (6). In doing so, we introduced a number of parameters, each of value close to unity, which describe the unknown details of the system geometry, the physics of disk truncation, and the formation of the precessing torus. Together with the physical parameters describing the system (μ, θ, P, Ṁ), and the accretion physics (α), they come in three categories:
for a given accretion rate, Ṁ, through the inner regions of the accretion disk of an essentially non-rotating star, thus indirectly shaping the unperturbed shape of the inner disk. Assuming that the accretion disk is fairly thick (H ∼ r), we were able to transform Eq. (3) into the simple form of Eq. (6). In doing so, we introduced a number of parameters, each of value close to unity, which describe the unknown details of the system geometry, the physics of disk truncation, and the formation of the precessing torus. Together with the physical parameters describing the system (μ, θ, P, Ṁ), and the accretion physics (α), they come in three categories:
-
Parameters that are fixed once and for all.
-
Parameters that have fixed values for a given source.
-
Parameters that may vary with time.
The first category includes the η parameter of Eq. (5). It determines the exact value of the truncation radius as a function of the physical parameters of the system and is assumed to be the same for all disks to which we need to apply the last formula of Eq. (5). Its value in the literature varies from about 0.4 to about 1 (as reviewed in Kluźniak & Rappaport 2007). The other parameter in this category is a which, multiplied by the α viscosity, defines the ratio of radial to azimuthal velocities in the disk vr/(rΩ). The proportionality constant K in the final formula, Eq. (6), depends linearly on aα. Here, we used the value aα = 0.01 and took it to be fixed for all the discussed sources, assuming the disk to be in the same state (it is conceivable that a or α may change in a disk state transition). Finally, while the factor D depends on the exact shape of the inner disk, we took it to be the same for all sources, again assuming their accretion disks to be in the same state.
The second category is comprised of the two parameters defining the strength of the stellar magnetic dipole, μ, and its inclination, θ. Their influence on the constant K is very weak. As discussed in Section 4, θ might affect the QPO frequency by a factor of about 2, from source to source. The weak dependence of K on μ is discussed below.
The most important parameter that changes from source to source and (possibly) with the accretion rate is the factor d in Eq. (5). It is a measure of the radial extent of the precessing warped region of the inner disk. It must be related to the strength of the QPO in the light curve and it cannot be too close to unity if the QPO is to be observable with the current instruments. For the purposes of this paper, we take d = 1.3, but it could be 1.1 or 1.5 as well. At present, there is no theory of what would determine the size of the precessing region. The constant K in Eq. (5) depends rather sensitively on the value of d, being inversely proportional to its fifth power. Taking this into consideration, it is remarkable that a single curve fits the data so closely (Fig. 1).
The last category includes the physical parameter Ṁ and the 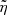 parameter in our formulae. The former enters the latter through the
parameter in our formulae. The former enters the latter through the 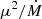 combination, with
combination, with 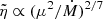 . We note the weak dependence (inverse two sevenths power) on the mass accretion rate. The
. We note the weak dependence (inverse two sevenths power) on the mass accretion rate. The 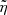 parameter defines how far from spin equilibrium the source is (at any given moment); thus, in principle, it can be determined from the spin history with no knowledge of the magnetic moment or of the mass accretion rate. In this sense, the observed QPO frequencies do not (further) constrain μ or Ṁ in this model, although the
parameter defines how far from spin equilibrium the source is (at any given moment); thus, in principle, it can be determined from the spin history with no knowledge of the magnetic moment or of the mass accretion rate. In this sense, the observed QPO frequencies do not (further) constrain μ or Ṁ in this model, although the 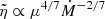 relation may provide a consistency check of the model. The further away from spin equilibrium the neutron star is, the further away the inner edge of the disk from corotation with the star must be, and hence, by Eqs. (6) and (7), the larger the QPO frequency. For a given neutron star, the model gives
relation may provide a consistency check of the model. The further away from spin equilibrium the neutron star is, the further away the inner edge of the disk from corotation with the star must be, and hence, by Eqs. (6) and (7), the larger the QPO frequency. For a given neutron star, the model gives 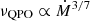 for a fixed value of the d parameter.
for a fixed value of the d parameter.
6. Flat-top noise ULXs
Next, we turn to another class of QPOs, namely, the sub-Hz QPOs in ULXs displaying a flat-top low-frequency noise and no coherent pulsations. Atapin et al. (2019) reported on the properties of flat-topped noise and 0.01 Hz to 1 Hz QPOs in several ULXs, none of which are known to exhibit coherent pulsations. A striking feature of those QPOs is that their frequency in individual sources typically varies by a factor of up to 4 or more, often in strong correlation with the count rate. In three of the six sources reported the QPO frequency exhibits a very strong dependence on the count rate in individual sources, following a power law dependence with index between 5 and 7 (c.f. Figure 4 of Atapin et al. 2019). This variability, strongly correlated with the luminosity in individual sources has not been explained as yet in any QPO models. To deepen the mystery, as we go from source to source, the data on five sources (out of a total of six) are strongly suggestive of a comparably steep anticorrelation of the QPO frequency with the count rate (ibid.). For the QPOs in PULXs, however, as we go from PULX source to source there is no correlation between the luminosity and the spin period; hence no correlation can be found between the luminosity and the QPO frequency (Tables 2 and 1); nor is there a strong variation in the QPO frequency in any given PULX source. These properties would make the QPOs in flat-top noise ULXs very different from the ones observed in PULXs.
PULX Properties
As no coherent pulsation has been detected in these flat-top noise ULXs, we do not know whether they are neutron stars or black holes and we know nothing about their angular momentum. In principle, the mHz QPOs in these sources could be a manifestation of strong-gravity precession. If so, it would follow from the discussion in Section 3 that these flat-top QPOs would be very different from the QPOs in PULXs.
We must consider whether strong-gravity precession could be expected to significantly vary in frequency in any given source. The c-modes of thin disks are good clocks, if the angular momentum of the gravitating source is constant over time (Silbergleit et al. 2001). The observed temporal variation in the flat-top noise QPOs (if they are c-modes) would imply that the spin rate of the compact object varies by as much at the same time. Strongly magnetised neutron stars, such as those in the X-ray pulsars, can spin up and spin down, depending on the torque exerted by the accretion disk, with its inner edge providing a large lever arm. Black holes are less likely to exhibit a significant spin variation in different observations. A c-mode varying with the spin of the compact object would then only work as an explanation for neutron star ULXs. A difficulty would remain in that the neutron star spin (and hence the c-mode frequency) reflects the history of the ups and downs of accretion; that is, related to a time integral of the accretion rate and not the instantaneous accretion rate.
For the m = −1 mode of a torus (Lense-Thirring precession model), the constraints are not as tight. The frequency of precession depends on the size and placement of the torus (Fragile et al. 2007; Ingram & Done 2011; Morales Teixeira et al. 2014), so that the model can be made consistent both for neutron stars and black holes with the observed variation seen for the QPO.
However, the correlation with the count rate would still need to be explained. The QPO frequency increasing as roughly the sixth power of the count rate would be difficult, but perhaps not impossible, to understand in terms of the magnetic precession model. As remarked earlier, in slowly rotating neutron stars the luminosity (and presumably the reported count-rate) is given by 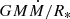 , so it depends on Ṁ alone. However, as we explain in the previous subsection, the magnetic precession model applied to PULXs yields
, so it depends on Ṁ alone. However, as we explain in the previous subsection, the magnetic precession model applied to PULXs yields 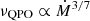 . To obtain approximately
. To obtain approximately 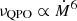 instead, we would have to assume that in any given source the size of the precessing torus and, hence, its characteristic radius (in units of the inner radius of the ring), d = R/Rin, depends on the mass accretion rate as approximately, Ṁ−1.1, so that
instead, we would have to assume that in any given source the size of the precessing torus and, hence, its characteristic radius (in units of the inner radius of the ring), d = R/Rin, depends on the mass accretion rate as approximately, Ṁ−1.1, so that
Without entering a discussion of whether or not it would be reasonable to assume the size of the inner precessing ring to be roughly inversely proportional to the mass accretion rate, we note that if it were universal, such a dependence would probably destroy the 1/P correlation of Eq. (8) and Fig. 1, if the mass accretion rate were to vary substantially in individual PULX sources.
On the other hand, we could try to apply the m = −1 vertical epicyclic mode of a torus (Blaes et al. 2006). The suggestion of proponents of the model (Stella & Vietri 1998; Fragile et al. 2007; Ingram & Done 2011; Morales Teixeira et al. 2014) is that the accretion flow changes at some radius from a thin disk to a thick and hot inner torus. This inner torus surrounded by a thinner accretion disk (Bollimpalli et al. 2024) is supposed to be inclined to the equatorial plane of a Kerr black hole and to precess. Taking the 1–10 keV count rate as a proxy for the X-ray luminosity of a thin multicolor disk truncated (as is often assumed) at some r = r0, within which a hot torus resides, we would expect the X-ray luminosity to be 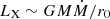 . In X-ray binaries, the value of r0 is derived from observations via spectral fits (e.g. Tomsick et al. 2009; Xu et al. 2020; Zdziarski et al. 2021). We can assume that the precessing hot torus has a characteristic radius, R < r0, and the QPO frequency is given by Eq. (1), with r = R. We would then expect the frequency to be proportional to R−3, giving LX6 ∝ νQPO ∝ 1/R3. With
. In X-ray binaries, the value of r0 is derived from observations via spectral fits (e.g. Tomsick et al. 2009; Xu et al. 2020; Zdziarski et al. 2021). We can assume that the precessing hot torus has a characteristic radius, R < r0, and the QPO frequency is given by Eq. (1), with r = R. We would then expect the frequency to be proportional to R−3, giving LX6 ∝ νQPO ∝ 1/R3. With 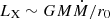 , this gives
, this gives 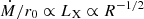 , or
, or 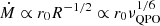 . The mass accretion through the inner disk/torus Ṁ is most likely related to the bolometric luminosity, through
. The mass accretion through the inner disk/torus Ṁ is most likely related to the bolometric luminosity, through 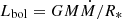 in neutron stars, with M and R* fixed for a given source, or through
in neutron stars, with M and R* fixed for a given source, or through 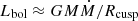 in black holes, with Rcusp the radius of the inner cusp (Abramowicz et al. 1978) of the accreting torus, known to be close to the fixed ISCO radius (Rcusp ≈ RISCO). Given that r0 is often measured directly in spectroscopic fits, and Lbol tracks Ṁ in individual sources, the model makes a potentially testable prediction: the truncation radius of the thin disk, within which a hot, thick torus resides, would be proportional to the bolometric luminosity and to the inverse one-sixth power of the QPO frequency,
in black holes, with Rcusp the radius of the inner cusp (Abramowicz et al. 1978) of the accreting torus, known to be close to the fixed ISCO radius (Rcusp ≈ RISCO). Given that r0 is often measured directly in spectroscopic fits, and Lbol tracks Ṁ in individual sources, the model makes a potentially testable prediction: the truncation radius of the thin disk, within which a hot, thick torus resides, would be proportional to the bolometric luminosity and to the inverse one-sixth power of the QPO frequency, 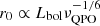 . Be that as it may, we note that flat-top QPOs detected in ULXs (known to be highly variable in frequency) seem to exhibit very different properties from the mHz QPOs detected in PULXs.
. Be that as it may, we note that flat-top QPOs detected in ULXs (known to be highly variable in frequency) seem to exhibit very different properties from the mHz QPOs detected in PULXs.
7. Conclusions
We found that the observed mHz QPO frequencies in PULXs are inversely proportional to the neutron star periods. While this behaviour is expected in the general-relativistic precession models of fluid bodies (c-mode of thin disks, or m = −1 vertical epicyclic mode of orbiting tori), the actual observed frequencies could only be accounted for if the precessing accretion structures were very close to the neutron star. This is excluded given the magnetic truncation of the disk, even in the weakest field models of ULXs (B > 1010 G). For this Lense-Thirring precession model to be viable, the precession must occur at a distance much larger than the magnetospheric radius. The possible span of the ratio of the characteristic radius at which strong-gravity precession occurs to the magnetospheric radius has been estimated in Table 2 for both the beaming and non-beamed models. In almost all cases, the value of rLT/rM lies below 1. Hence, we conclude that Lense-Thirring precession is unlikely to be the source of QPOs from these three sources.
Alternatively, the estimates of the neutron star magnetic field in these sources would have to be revised downwards if we were to allow general-relativistic precession at the observed QPO frequencies. Regardless of the model, the influence of the stellar magnetic field on the precession frequency is expected to be quite general in neutron star sources, since disk warping is strongest in the inner disk region (e.g. Fragile et al. 2007; Romanova et al. 2021; Liska et al. 2023).
Surprisingly, Dong Lai’s magnetic model also allows for the observed QPO frequency correlation with the neutron star spin rate. It could be interesting to check if the correlation is true also in individual sources as they spin up (or spin down). Based on our analysis of the magnetic precession model (Lai 1999; Pfeiffer & Lai 2004), as applied to PULXs, we arrive at the following conclusions.
-
The pulsation period (P) and the QPO frequency (νQPO) in PULXs should be inversely related to each other (for the same fractional size of the precessing part of the disk). We show that the expected QPO frequency is around two orders of magnitude lower than the pulsation frequency, νQPO = a few × (10−3/P). The model prediction seems to be indeed supported by the observations of the three known PULX sources with QPOs: M82 X-2, M51 ULX-7, and NGC 7793 P13.
-
Neither the magnetic dipole of the neutron star, nor its mass accretion rate, can be constrained directly by comparing the mHz QPO frequency with the predictions of the model. Remarkably, neither μ, nor Ṁ, appear explicitly in Eq. (6).
-
While the reported mHz QPO frequencies in the PULXs vary in time by no more than 20% and, thus, they might agree with the predicted dependence of Eq. (6) for roughly constant values of the parameters, the QPOs in the flat-top ULXs vary by a factor of at least 2–4. Displaying a very different behavior, notably a strong dependence of their frequency with the X-ray luminosity, the QPOs associated with flat-top noise may have a different origin and might not even be related to neutron stars.
We eagerly await reports of QPO measurements in other PULX sources. If they are also found to be in agreement with our interpretation of the magnetic precession model, it might prove possible to determine the size of the precessing part of the inner disk and to ultimately constrain the geometry of ULX accretion.
Rigid-body oscillations of a part of the disk are seen in some simulations (e.g. Fragile et al. 2007; Liska et al. 2018; Mishra et al. 2020).
Acknowledgments
This project was funded in part by the Polish NCN grant No. 2019/35/O/ST9/03965. MČ also acknowledges the Czech Science Foundation (GAČR) grant No. 21-06825X and the support by the International Space Science Institute (ISSI) in Bern, which hosted the International Team project #495 (Feeding the spinning top) with its inspiring discussions.
References
- Abarca, D., Parfrey, K., & Kluźniak, W. 2021, ApJ, 917, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M., Jaroszynski, M., & Sikora, M. 1978, A&A, 63, 221 [NASA ADS] [Google Scholar]
- Agrawal, V. K., & Nandi, A. 2015, MNRAS, 446, 3926 [NASA ADS] [CrossRef] [Google Scholar]
- Atapin, K., Fabrika, S., & Caballero-García, M. D. 2019, MNRAS, 486, 2766 [NASA ADS] [CrossRef] [Google Scholar]
- Avdan, H., Kayaci Avdan, S., Akyuz, A., & Balman, S. 2014, Ap&SS, 352, 123 [Google Scholar]
- Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Bachetti, M., Heida, M., Maccarone, T., et al. 2022, ApJ, 937, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [Google Scholar]
- Blaes, O. M., Arras, P., & Fragile, P. C. 2006, MNRAS, 369, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Bollimpalli, D. A., Fragile, P. C., Dewberry, J. W., & Kluźniak, W. 2024, MNRAS, 528, 1142 [Google Scholar]
- Bollimpalli, D. A., Horák, J., Kluźniak, W., & Fragile, P. C. 2025, ArXiv e-prints [arXiv:2503.20577] [Google Scholar]
- Brightman, M., Bachetti, M., Earnshaw, H., et al. 2022, ApJ, 925, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Bursa, M., Abramowicz, M. A., Karas, V., & Kluźniak, W. 2004, ApJ, 617, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Carpano, S., Haberl, F., Maitra, C., & Vasilopoulos, G. 2018, MNRAS, 476, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Čemeljić, M., Kluźniak, W., & Parthasarathy, V. 2023, A&A, 678, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Earnshaw, H. M., Roberts, T. P., Heil, L. M., et al. 2016, MNRAS, 456, 3840 [NASA ADS] [CrossRef] [Google Scholar]
- Elsner, R. F., & Lamb, F. K. 1977, ApJ, 215, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Fabbiano, G. 1989, ARA&A, 27, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, H., Rao, F., & Kaaret, P. 2010, ApJ, 710, L137 [CrossRef] [Google Scholar]
- Fragile, P. C., Blaes, O. M., Anninos, P., & Salmonson, J. D. 2007, ApJ, 668, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Fürst, F., Walton, D. J., Harrison, F. A., et al. 2016, ApJ, 831, L14 [Google Scholar]
- Fürst, F., Walton, D. J., Heida, M., et al. 2021, A&A, 651, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fürst, F., Walton, D., Bachetti, M., Earnshaw, H., & Brightman, M. 2024, Astron. Nachr., 346 [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 232, 259 [Google Scholar]
- Imbrogno, M. 2024, The QPOs awaken in the quest for pulsating ULXs, https://xmm-tools.cosmos.esa.int/external/xmm_science/workshop/2024_science/presentations/MImbrogno.pdf, workshop talk, XMM-NEWTON WORKSHOP [Google Scholar]
- Imbrogno, M., Motta, S. E., Amato, R., et al. 2024, A&A, 689, A284 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ingram, A., & Done, C. 2011, MNRAS, 415, 2323 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A., Ohsuga, K., Takahashi, H. R., & Asahina, Y. 2023, ApJ, 952, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A., Ohsuga, K., Takahashi, H. R., Asahina, Y., & Middleton, M. J. 2024, ApJ, 977, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Belfiore, A., Stella, L., et al. 2017a, Science, 355, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Papitto, A., Esposito, P., et al. 2017b, MNRAS, 466, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Simet, M. G., & Lang, C. C. 2006, ApJ, 646, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Kayanikhoo, F., Kluźniak, W., & Čemeljić, M. 2025, ApJ, 982, 95 [Google Scholar]
- King, A., & Lasota, J.-P. 2020, MNRAS, 494, 3611 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., Lasota, J.-P., & Kluźniak, W. 2017, MNRAS, 468, L59 [Google Scholar]
- King, A. R. 2004, MNRAS, 347, L18 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Davies, M. B., Ward, M. J., Fabbiano, G., & Elvis, M. 2001, ApJ, 552, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kluzniak, W., & Kita, D. 2000, ArXiv e-prints [arXiv:astro-ph/0006266] [Google Scholar]
- Kluzniak, W., & Wagoner, R. V. 1985, ApJ, 297, 548 [Google Scholar]
- Kluźniak, W., & Rappaport, S. 2007, ApJ, 671, 1990 [CrossRef] [Google Scholar]
- Kluzniak, W., Michelson, P., & Wagoner, R. V. 1990, ApJ, 358, 538 [Google Scholar]
- Kong, A. K. H., Yang, Y. J., Hsieh, P. Y., Mak, D. S. Y., & Pun, C. S. J. 2007, ApJ, 671, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D. 1999, ApJ, 524, 1030 [Google Scholar]
- Lančová, D., Abarca, D., Kluźniak, W., et al. 2019, ApJ, 884, L37 [CrossRef] [Google Scholar]
- Lipunov, V. M. 1982, Sov. Astron., 26, 174 [Google Scholar]
- Liska, M., Hesp, C., Tchekhovskoy, A., et al. 2018, MNRAS, 474, L81 [Google Scholar]
- Liska, M., Hesp, C., Tchekhovskoy, A., et al. 2023, Nat. Astron., 101, 102012 [Google Scholar]
- Liu, J. 2024, ApJ, 961, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J.-F., Bregman, J. N., Irwin, J., & Seitzer, P. 2002, ApJ, 581, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., Justham, S., Nelson, L., et al. 2006, ApJ, 640, 918 [NASA ADS] [CrossRef] [Google Scholar]
- Makishima, K., Kubota, A., Mizuno, T., et al. 2000, ApJ, 535, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Mishra, B., Kluźniak, W., & Fragile, P. C. 2020, MNRAS, 497, 1066 [NASA ADS] [CrossRef] [Google Scholar]
- Morales Teixeira, D., Fragile, P. C., Zhuravlev, V. V., & Ivanov, P. B. 2014, ApJ, 796, 103 [Google Scholar]
- Motch, C., Pakull, M. W., Soria, R., Grisé, F., & Pietrzyński, G. 2014, Nature, 514, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., & Poutanen, J. 2015, MNRAS, 454, 2539 [Google Scholar]
- Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [Google Scholar]
- Paczynski, B. 1992, Acta Astron., 42, 145 [NASA ADS] [Google Scholar]
- Pfeiffer, H. P., & Lai, D. 2004, ApJ, 604, 766 [Google Scholar]
- Pintore, F., Pinto, C., Rodriguez-Castillo, G., et al. 2025, A&A, 695, A238 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Read, A. M., & Pietsch, W. 1999, A&A, 341, 8 [Google Scholar]
- Roberts, T. P., & Warwick, R. S. 2000, MNRAS, 315, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez Castillo, G. A., Israel, G. L., Belfiore, A., et al. 2020, ApJ, 895, 60 [Google Scholar]
- Romanova, M. M., Koldoba, A. V., Ustyugova, G. V., et al. 2021, MNRAS, 506, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Silbergleit, A. S., Wagoner, R. V., & Ortega-Rodríguez, M. 2001, ApJ, 548, 335 [Google Scholar]
- Stella, L., & Vietri, M. 1998, ApJ, 492, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Tomsick, J. A., Yamaoka, K., Corbel, S., et al. 2009, ApJ, 707, L87 [Google Scholar]
- Tranin, H., Webb, N., Godet, O., & Quintin, E. 2024, A&A, 681, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urquhart, R. T., Soria, R., Di Stefano, R., et al. 2022, MNRAS, 511, 4528 [CrossRef] [Google Scholar]
- Vasilopoulos, G., Lander, S. K., Koliopanos, F., & Bailyn, C. D. 2020, MNRAS, 491, 4949 [Google Scholar]
- Veresvarska, M., Scaringi, S., Knigge, C., et al. 2024, MNRAS, 534, 3087 [Google Scholar]
- Veresvarska, M., Imbrogno, M., Amato, R., et al. 2025, MNRAS, 541, 3627 [Google Scholar]
- Xu, Y., Harrison, F. A., Tomsick, J. A., et al. 2020, ApJ, 893, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Dziełak, M. A., De Marco, B., Szanecki, M., & Niedźwiecki, A. 2021, ApJ, 909, L9 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. mHz QPO frequency versus the neutron star period in PULXs. A νQPO = const ⋅ 1/P line (in solid black) is plotted to guide the eye. The data points are plotted with error bars as per Table 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.