Numerical solutions of the complete two-body system in QUMOND

Open Access

Table 1

QUMOND transition functions used in this work.

Name	Function
Simple	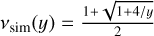$ν_{s i m} (y) = \frac{1 + \sqrt{1 + 4 / y}}{2}$ $\nu_\mathrm{sim}(y) = \frac{1+\sqrt{1+4/y}}{2}$
Standard	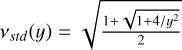$ν_{s t d} (y) = \sqrt{\frac{1 + \sqrt{1 + 4 / y^{2}}}{2}}$ $\nu_{std}(y) = \sqrt{\frac{1+\sqrt{1+4/y^2}}{2}}$
McG08	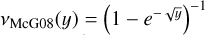$ν_{M c G 08} (y) = {(1 - e^{- \sqrt{y}})}^{- 1}$ $\nu_\mathrm{McG08}(y) = \left(1-e^{-\sqrt{y}}\right)^{-1}$
Maximum	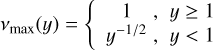$ν_{m a x} (y) = {\begin{array}{cc} 1 & y \geq 1 \\ y^{- 1 / 2} & y < 1 \end{array}$ $\nu_\mathrm{max}(y) = \left\{\begin{array}{c@{,}c} 1 \;\;&\;\;y \ge1\\ y^{-1/2} \;\;&\;\;y < 1\\ \end{array}\right.$

Notes. The simple transition function was introduced by Famaey & Binney (2005) in its corresponding AQUAL form and used in the wide-binary analysis in Banik et al. (2024). The standard interpolation function was introduced by Kent (1987) in its corresponding AQUAL form. The McG08 transition function was introduced by McGaugh (2008). The maximum transition function is introduced here for debugging purposes and as a convenient indicator whether a region is Newtonian or MONDian.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.