| Issue |
A&A
Volume 705, January 2026
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 14 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202555962 | |
| Published online | 09 January 2026 | |
Lunar reference systems and their realisations using INPOP ephemerides
1
Sorbonne Université, Observatoire Paris, Université PSL, CNRS, Laboratoire Temps Espace, LTE,
75014
Paris,
France
2
Observatoire de la Côte d’Azur, Université Côte d’Azur, CNRS, Géoazur, IRD,
250 avenue A. Einstein
06560
Valbonne,
France
3
Tor Vergata University of Rome, Department of Physics,
Via della Ricerca Scientifica 1,
00133
Rome,
Italy
4
Institute of Geodesy and Geoinformatics, Wrocław University of Environmental and Life Sciences,
Norwida 25,
Wrocław,
50-375,
Poland
5
Northumbria University,
Newcastle-upon-Tyne,
UK
★ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
16
June
2025
Accepted:
16
September
2025
Context. The definition of a reference system plays a crucial role in quantifying geodetic effects and in surface body cartography. Today, the development and specification of the lunar reference system is stimulated by future space missions, some of which will be manned, and by the needs of lunar space navigation.
Aims. This paper aims to describe the lunar reference system in use and determine the accuracy of its realisation in space and time. At present, two lunar reference systems are defined: the Principal Axis system (PA system), based on the Moon’s principal axes of inertia, and the Mean Earth/Polar Axis (ME system), defined by the Earth’s mean position on the Moon surface. A first step towards a relativistic definition of the lunar time scale is also introduced in agreement with that proposed by the International Astronomical Union (IAU) and other recent realisations.
Methods. We based the realisation of a PA lunar reference system on the choice of an ephemeris, which relied on the coordinates of the laser retro-reflectors on the Moon surface. We related the ME system and frame to the PA system and frame through a rotation transformation. This study provides a new method to determine the transformation procedure between the two systems, based on a series decomposition of librations and pole motion.
Results. We used the comparisons of the position of the lunar laser retro-reflectors obtained with different ephemerides to estimate the internal and external uncertainties of the different realisations of the PA and ME systems. It also includes comparisons between Euler angles and the propagation of their uncertainties.
Conclusions. This work provides the full expression of the transformation and a new series of libration and polar motion for the lunar motion. We also introduce possible realisations of lunar timescales, applicable depending on their use. The proposed procedure, with opportunities for future improvements, can help set new standards for lunar reference systems and their realisations.
Key words: celestial mechanics / ephemerides / reference systems / Moon
© The Authors 2026
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1 Introduction
The definition of a lunar body-fixed coordinate system is essential for lunar dynamics, global navigation systems, and establishing accurate cartography to locate points on its surface. These objectives are particularly crucial in the context of the Artemis programme (NASA) and for global navigation systems (Iess et al. 2025; Fienga et al. 2024), such as Moonlight (ESA) and Lunanet (NASA).
At present, two slightly different reference systems attached to the Moon are commonly used to define the lunar body-fixed coordinate system: the Mean Earth/Polar Axis (ME) reference system and the Principal Axis (PA) reference system (Archinal et al. 2018; Williams & Boggs 2008a). The ME axes are not aligned with the PA system because the Moon’s gravity field includes terms beyond degree two of the spherical harmonics representation and is subject to tidal deformation. Consequently, a small shift exists between the two systems. The PA system corresponds to the physical concept in which the orientation is such that the lunar tensor of inertia is diagonal. It is the preferred reference system for modelling and integrating the equations of motion.
In 2008, the Lunar Reconnaissance Orbiter (LRO) project and the Lunar Geodesy and Cartography Working Group (LCGWG) recommended using the ME system computed from the ephemerides DE421, the ME DE421 system, for future scientific data archiving, operations, and communication for LRO and the next NASA missions (LRO Project and Lunar Geodesy and Cartography Working Group 2008). The working group attached the ME system to a specific ephemeris because the transformation between the two reference systems, PA and ME, is classically realised using three static libration angles, which depend on the lunar gravity field coefficients, dissipative models, and the ephemeris.
Today, owing to the high accuracy of lunar laser ranging observations and the large volume of data (e.g. reviews in Murphy 2013; Müller et al. 2019; Chabé et al. 2020), it is necessary to accurately model a variety of dynamical and geo-physical effects to determine a lunar ephemeris accurate to a few centimetres. Several ephemerides have been developed (Park et al. 2021; Pitjeva et al. 2022; Fienga et al. 2021) that include Moon dynamics or focus exclusively on the Moon (Hofmann et al. 2018), with accuracies below 2 cm and 1 mas. New ephemerides are being developed, for example, Tian (2023). These models are based on a joint numerical integration of the orbits of the Moon, Earth, planets, small bodies, and lunar rotation. The dynamical partial derivatives of orbits and lunar Euler angles with respect to parameters such as moment of inertia, gravity field, tides, dissipation, core fluid interactions, and initial conditions are computed. Here, we use the Integration Numérique de l’Observatoire de Paris (INPOP) model, which has been in development since 2003 (Fienga et al. 2009; Manche 2011; Fienga et al. 2011, 2019; Viswanathan et al. 2018a; Fienga et al. 2021), and has been used in several space missions, such as Gaia, Bepi-Colombo, and JUpiter ICy moons Explorer (JUICE).
Moon-centred inertial reference systems are necessary for determining the orbits of spacecraft around the Moon. Current definitions of inertial systems are based on the recommendations of the International Astronomical Union, IAU B3 (Soffel et al. 2003; Petit & Luzum 2010) and the relativistic descriptions of the Barycentric Celestial Reference System (BCRS) and the Geocentric Celestial Reference System (GCRS) as described by Damour et al. (1991). The BCRS metric is kinematically fixed relative to distant quasistellar objects (QSO), as defined by Soffel et al. (2003) and following harmonic gauge conditions. A Moon-centred reference frame was recently specified by the IAU in August 2024 (IAU XXXII 2024). A kinematically non-rotating reference system centred on the Earth’s centre of mass was defined within the same framework, leading to the definition of the Geocentric Celestial Reference System (GCRS). Timescales derived from the BCRS and the GCRS metric are also provided by Soffel et al. (2003). For the Moon, Turyshev et al. (2013) proposed adopting the GCRS definition to the Moon in the context of the Gravity Recovery and Interior Laboratory, GRAIL, mission (Zuber et al. 2013). Recent propositions have been made in order to update these definitions (Kopeikin & Kaplan 2024; Turyshev et al. 2025; Fienga et al. 2024), with this study following the third proposition.
The paper is divided into four sections. Section 2 describes the current definitions of the PA and ME systems and introduces a new transformation matrix between these reference systems. In Sect. 3, we present a new description of the libration and polar motion series of the Moon from INPOP19a ephemeris, with particular emphasis on the determination of the constant angles. Section 4.1 provides a description of a Moon-centred inertial system, including a definition of the Moon-centred metric (Sect. 4.1.1) and timescale (Sect. 4.1.2). In Sect. 4.1.4, we assess the accuracy of two possible LCRS realisations by comparing the results obtained with DE421 (Folkner et al. 2014a) and INPOP19a (Fienga et al. 2019). Section 4.2 describes the lunar reference systems, followed by a discussion of the results and conclusions.
Construction steps of lunar reference systems and frames.
2 Definitions of lunar reference systems
2.1 Conventions
In our study, we follow the seminal works of Kovalevsky & Mueller (1981) and Kovalevsky et al. (1989), which describe the distinction between reference systems and reference frames used in celestial mechanics and Earth and planetary science. A reference system is defined by physical or dynamical properties, such as an inertial system in which the fundamental principles of dynamics are applied without pseudo-forces (also called inertial forces), whereas reference frames represent the materialisation of the reference system. For example, observations of extra-galactic objects such as quasars are used to realise (or materialise) the inertial system (Charlot et al. 2020) to International Celestial Reference Frame, ICRF3. In this study, the realisation of the reference system is based on the coordinates of the lunar retro-reflectors.
We focus on the construction of reference systems and frames attached to the Moon. Table 1 summarises the definitions and construction of reference systems for the Moon, following the method described in Kovalevsky & Mueller (1981) and Kovalevsky et al. (1989) The first step is to determine the ideal reference system, which is based on a conceptual definition. For the Moon, the two commonly used ideal reference systems are the PA and ME systems, as described in the Introduction. These systems correspond to the diagonal inertia matrix and the direction of the Earth, respectively. The second step is to choose the physical structure that characterises the ideal reference system. In the case of the PA system, the Moon is considered undistorted (Folkner et al. 2014b), whereas the ME system depends on the lunar gravity field and dissipation. This step defines the reference system. The third step concerns the values introduced into the models. The PA system is based on GRAIL measurements (since 2012), with Lunar Prospector data used previously. The ME system is defined dynamically and also depends on the ephemeris. The fourth stage concerns the realisation of the system, i.e. a reference point. Currently, this materialisation is based on measurements from the lunar laser ranging (LLR). Thus, the realisation is based on the position of the retro-reflectors in the chosen reference frame.
At present, owing to the Moon’s low flattening, the lunar body-fixed coordinate system is a planetocentric coordinate system. The planetocentric latitude of a surface point is defined as the angle between the radial vector at that point and the equatorial plane in the ME or PA system. The latitude is positive from the equator to the North Pole (0–90°) and negative towards the South Pole. The longitude is the angle between the meridian of the point and a prime meridian, and it is measured up to 360° in a direct sense, i.e. positively towards the east of the body (direct or retrograde rotation). These definitions follow the recommendations of the IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements (WGCCRE; (Archinal et al. 2018)). Both systems are centred at the Moon’s centre of mass. The Moon’s reference sphere radius can be taken as 1737.4 km following the WGCCRE of Solar System bodies (Archinal et al. 2018). The LRO paper of Smith et al. (2017) reports a radius of 1737.1513 ± 0.0005 km, corresponding to an uncertainty of 50 cm. This working group provides regular updates (see Archinal et al. 2018).
2.2 The PA lunar reference system
The PA system is centred on the Moon’s centre of mass and its realisation is derived from the temporal values of the Moon’s orientation provided by the ephemeris. This orientation is described through the rotation angles defined as follows:
- (a)
ψ, the precession angle, is the angle along the ICRF equator, from the ICRF x-axis to the descending node of the lunar equator;
- (b)
θ, the nutation angle, is the inclination of the lunar equator relative to the ICRF equator;
- (c)
φ, the proper rotation, is the angle along the lunar equator from the ascending node to the lunar prime meridian.
The transformation from the ICRF to the PA frame is expressed as (i.e. Folkner et al. 2014a)
![$\[X_{\mathcal{P}}=R_z(\varphi) R_x(\theta) R_z(\psi) X_\mathcal{I},\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq1.png) (1)
(1)
where Xℐ and X𝒫 represent the same vector expressed in the ICRF and PA systems, respectively. The matrices Rz and Rx are the elementary rotational matrices defined in the Appendix A.
2.3 The ME lunar reference system
The second lunar-fixed reference system commonly used in the literature is the ME system. This system is defined by the orientation of its z-axis along the mean rotational pole and its x-axis along the mean Earth direction, the prime meridian.
The intersection of the lunar equator and prime meridian occurs at the Moon mean sub-Earth point. The ME reference system differs from the averaged PA reference system due to high-degree lunar gravity terms and dissipation coefficients, causing a slight constant departure in the sub-Earth direction and mean pole orientation relative to a synchronously rotating triaxial ellipsoid (Williams & Boggs 2008b). The cosine director of the Earth seen from the lunar PA reference system is defined as u = r/|r|. As shown by Murphy (2013) and Williams (2018), the Earth’s direction in (u3, u2) coordinates traces loops describing the geometrical libration of the Moon, at one and six years. The average position of these loops is offset from zero (and is not visible on the scale of the figures in cited papers) and there is a constant offset between the mean position of the Earth and the u1 direction.
The ME reference system is currently defined from the numerical ephemeris of the PA system through the following transformation matrix relationship (e.g. Newhall & Williams 1996; Rambaux & Williams 2011; Folkner et al. 2014a):
![$\[X_{\mathcal{M}}=R_x\left(-\bar{p_2}\right) R_y\left(\bar{p_1}\right) R_z(-\bar{\tau}) X_{\mathcal{P}},\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq2.png) (2)
(2)
where the vector Xℳ is expressed in the ME system, and τ, p1, and p2 represent the libration in longitude and the coordinates of the ecliptic pole defined from the mean ecliptic of date and describing the lunar orientation according to Cassini’s laws (e.g. Newhall & Williams 1996; Rambaux & Williams 2011). The bar represents the constant part of these elements. Recently, Park et al. (2021) proposed using the combination ![$\[\left(-\bar{\tau}+I^{2} \frac{\bar{\sigma}}{2}\right)\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq3.png) in Rz to obtain the following relation:
in Rz to obtain the following relation:
![$\[X_{\mathcal{M}}=R_x\left(-\bar{p_2}\right) R_y\left(\bar{p_1}\right) R_z\left(-\bar{\tau}+I^2 \frac{\bar{\sigma}}{2}\right) X_{\mathcal{P}}=M X_{\mathcal{P}},\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq4.png) (3)
(3)
where ![$\[\bar{\sigma}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq5.png) is the libration constant term in precession, I is the mean lunar spin inclination and M represents the product of the three matrices.
is the libration constant term in precession, I is the mean lunar spin inclination and M represents the product of the three matrices.
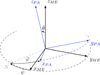 |
Fig. 1 Geometric transformation between the ME and PA systems. |
2.4 Complete rotation matrix for ME transformation
The full transformation from the PA system to the ME system can be derived from the Cassini laws (see, e.g. Eq. (1) in Rambaux & Williams (2011) and references therein). If the Cassini laws were exact, the Moon would, on average, point towards Earth and the PA and ME systems would coincide. However, as previously described, the two systems are slightly shifted due to high-degree lunar gravity terms and dissipation coefficients, and the librations angles describe the PA system. Figure 1 shows the transformation angles between the two systems. The transformation from the PA system to the ME system, R, can be expressed as the inverse of the following matrix:
![$\[R^{-1}=\left[\begin{array}{ccc}\cos~ \bar{\tau}+\frac{\bar{p_1}\left(\bar{p_2} ~\sin~ \bar{\tau}-\bar{p_1} ~\cos~ \bar{\tau}\right)}{1+\bar{p_3}} & ~\sin~ \bar{\tau}-\frac{\bar{p_1}\left(\bar{p_2} ~\cos~ \bar{\tau}+\bar{p_1} ~\sin~ \bar{\tau}\right)}{1+\bar{p_3}} & \bar{p_1} \\-~\sin~ \bar{\tau}+\frac{\bar{p_2}\left(\bar{p_2} ~\sin~ \bar{\tau}-\bar{p_1} ~\cos~ \bar{\tau}\right)}{1+\bar{p_3}} & ~\cos~ \bar{\tau}-\frac{\bar{p_2}\left(\bar{p_2} ~\cos~ \bar{\tau}+\bar{p_1} ~\sin~ \bar{\tau}\right)}{1+\bar{p_3}} & \bar{p_2} \\\bar{p_2} ~\sin~ \bar{\tau}-\bar{p_1} ~\cos~ \bar{\tau} & -\bar{p_2} ~\cos~ \bar{\tau}-\bar{p_1} ~\sin~ \bar{\tau} & \bar{p_3}\end{array}\right].\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq6.png) (4)
(4)
We introduced ![$\[\bar{p_{3}}=\sqrt{1-\bar{p_{1}}{ }^{2}-\bar{p_{2}}}{ }^{2}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq7.png) with
with ![$\[\bar{p_{1}}=~\sin~ \bar{\theta} ~\sin~ \bar{\varphi}, \quad \bar{p_{2}}= ~\sin~ \bar{\theta} ~\cos~ \bar{\varphi}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq8.png) , and
, and ![$\[\bar{\tau}=\bar{\psi}+\bar{\varphi}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq9.png) , where (
, where (![$\[\bar{\psi}, \bar{\theta}, \bar{\varphi}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq10.png) ) are constant Euler angles between the PA and ME systems. The first-order development of the rotation matrix R in (
) are constant Euler angles between the PA and ME systems. The first-order development of the rotation matrix R in (![$\[\bar{p_{1}}, \bar{p_{2}}, \bar{\tau}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq11.png) ) provides the following rotation matrix:
) provides the following rotation matrix:
![$\[R_1=\left[\begin{array}{ccc}1 & -\bar{\tau} & -\bar{p_1} \\\bar{\tau} & 1 & -\bar{p_2} \\\bar{p_1} & \bar{p_2} & 1\end{array}\right],\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq12.png) (5)
(5)
which corresponds to the relation given in Eq. (2). The second-order approximation is
![$\[R_2=\left[\begin{array}{ccc}1-\frac{\bar{p}_1~^2}{2}-\frac{\bar{\tau}^2}{2} & -\bar{\tau}-\frac{\bar{p}_1 \bar{p_2}}{2} & \bar{p_2} \bar{\tau}-\bar{p_1} \\\bar{\tau}-\frac{\bar{p}_1 \bar{p_2}}{2} & 1-\frac{\bar{p}_2~^2}{2}-\frac{\bar{\tau}^2}{2} & -\bar{p_1} \bar{\tau}-\bar{p_2} \\\bar{p_1} & \bar{p_2} & 1-\frac{\bar{p}_1~^2}{2}-\frac{\bar{p}_2~^2}{2}\end{array}\right].\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq13.png) (6)
(6)
This second-order expansion can be compared with the first-order expression of M,
![$\[M=\left[\begin{array}{ccc}1 & -\bar{\tau}+\frac{I^2 \bar{\sigma}}{2} & -\bar{p}_1 \\\bar{\tau}-\frac{I^2 \bar{\sigma}}{2} & 1 & -\bar{p_2} \\\bar{p_1} & \bar{p_2} & 1\end{array}\right].\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq14.png) (7)
(7)
We recall that ![$\[\bar{p_{1}}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq15.png) and
and ![$\[\bar{p_{2}}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq16.png) depend on I and
depend on I and ![$\[\bar{\sigma}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq17.png) (see Rambaux & Williams 2011). We note that the signs of the additional term in R2[1, 2] and M[1, 2] are opposite. To compare the two expressions, we computed the numerical values using those listed in Table 3,
(see Rambaux & Williams 2011). We note that the signs of the additional term in R2[1, 2] and M[1, 2] are opposite. To compare the two expressions, we computed the numerical values using those listed in Table 3,
![$\[R=\left[\begin{array}{ccc}0.999999874 & -0.000327680 & 0.000381040 \\0.000327681 & 0.999999947 & -1.281 \times 10^{-6} \\-0.000381039 & 1.406 \times 10^{-6} & 0.999999928\end{array}\right]\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq18.png) (8)
(8)
leading to a maximum difference between the matrix coefficients of 1.25 × 10−7. Using the position of the Apollo 15 retroreflector as an example, the difference between R and M matrices corresponds to an offset of (−0.19, 0.06, −0.05) metres on the lunar surface, assuming a mean radius of 1738 km. Similar computations for other retro-reflectors yield offsets of approximately 20 cm.
3 INPOP-related reference systems
3.1 INPOP librational series
The INPOP ephemeris provides the lunar orientation defined by the PA in terms of the temporal Euler angles (ψ, θ, φ) relative to the ICRF. The libration angles (Iσ, ρ, τ) and polar coordinates (p1, p2) were extracted from the Euler angles following the approach described in Newhall & Williams (1996) and updated by Rambaux & Williams (2011). Figure 2 illustrates the temporal evolution of these five variables over 1000 years. The libration angles at latitude (Iσ, ρ) exhibit a peak-to-peak amplitude of 200 arcseconds with short-period oscillations. The libration angle in longitude τ ranges from 0 to 200 arcseconds, with an offset (determined below) and a long-period modulation of 273 years. The coordinates (p1, p2) display amplitudes of roughly 5500 arcseconds with oscillations at short periods.
Next, we applied the procedure of Rambaux & Williams (2011) to decompose the libration angles and polar coordinates into polynomials and Fourier and Poisson series. However, in this study, we automated the search for argument combinations by comparing them with the orbital decomposition of Chapront et al. (2002) and using the series constructed for DE421 in Rambaux & Williams (2011) as a starting point. This systematic search allowed us to identify additional terms arising from lunar theory and to concurrently increase the accuracy of the reconstructed series. With the current approach, the tables of series in the Appendix demonstrate that most of the newly introduced terms correspond to orbital combinations. This means that the number of unrecognised terms remains nearly constant, serving as an initial indication of the method’s robustness.
Furthermore, we compared the amplitudes determined via least-squares fitting with the formal errors provided during inversion. In Figure 3, the amplitudes of cosine or sine coefficients for the series terms corresponding to the libration angles and pole coordinates are shown in blue. The order of the terms in the figure and the Appendix tables is identical, and they are arranged approximately in descending order. In each panel, the red curve illustrates the formal uncertainty of the cosine coefficient, since the formal uncertainty of the sine term is identical. Below the red curve, the amplitude values are no longer significant in the least-squares sense. This intersection occurs around an amplitude of 1 mas across the variables Iσ, ρ, τ, p1, and p2. Consequently, we truncated the full series at 1 mas. We further calculated the total root mean square (rms) of the residuals for each series. Table 2 lists the rms values, which are of the order of milliarcseconds for each variable, consistent with the formal uncertainties. In these figures, the different peaks in uncertainties are associated with Poisson terms with periods close to 18.6 years. We also provide the values of the polynomial coefficients in Table 3.
Table 4 presents the values of the constant terms for different ephemerides and for INPOP19a. The constant term for Iσ is −0.24706 ± 0.00182, i.e. a relative error of 0.7%.
The axes of the two systems differ by approximately 1 km at the lunar surface, depending on the accuracy in the representation. The rotations between these two frames depend on the Moon’s gravity field and tidal dissipation.
 |
Fig. 2 Temporal behaviour of three libration angles (Iσ, ρ, τ) and polar coordinates (p1, p2) over 1000 years from INPOP19a. |
3.2 Expressing solutions in ME DE421
Cartography preferably employs the DE421 ME frame, as recommended by LRO Project and Lunar Geodesy and Cartography Working Group in 2008. Here, we express the rotation angles from the INPOP19a PA frame to the DE421 ME frame, determined from the positions of the lunar laser retro-reflectors estimated in both frames. The problem involves minimising a function, f, defined as
![$\[f=X_{M E, D E 421}-R_1\left(\theta_1\right) R_2\left(\theta_2\right) R_3\left(\theta_3\right) X_{P A, I N P O P 19 a} \text {, }\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq20.png) (10)
(10)
which is a function of the rotation angles θ1, θ2, and θ3. In our case, the angles are equal to (−0.2769, −78.6358, and −67.7316) as, in good agreement with the rotation angles between the DE440 PA frame and the DE421 ME frame (Park et al. 2021).
The residuals of |f| are of the order of 0.13 m, reflecting that the transformation between these two frames is not a pure rotation. We also note that in this computation we used four lunar laser retro-reflectors, since the position of Lunokhod 2 was unknown at the time of DE421.
 |
Fig. 3 Amplitude (blue) and error (red) of the series for each variable. The points represent the cosine term amplitudes and the crosses represent the sine term amplitudes. |
Statistical values of the series of libration angles and polar coordinates for the INPOP19a ephemeris.
4 Description of the lunar reference systems, LCRS and LRS
4.1 The lunar celestial reference system (LCRS)
In this section, we describe the Moon-centred inertial reference system, called the lunar celestial reference system (LCRS), which is based on the geocentric celestial reference system (GCRS) conventional definition established by the IAU (2000).
Polynomial coefficients for the libration angles and polar coordinates from the INPOP19a ephemeris.
Rotation angles for the PA to ME reference frames.
4.1.1 Definition of the metric
The selenocentric metric tensor, Sab, of the LCRS is defined with selenocentric coordinates (T, X), where T is the lunar coordinate time (TCL), defined in the next section, and X is the coordinate vector of a spacecraft orbiting the Moon. The selenocentric tensor takes the general form given by (Soffel et al. 2003; Fienga et al. 2024):
![$\[\begin{aligned}& S_{00}=-1+\frac{2 L}{c^2}-\frac{2 L^2}{c^4}+\mathcal{O}\left(c^{-5}\right), \\& S_{0 a}=-\frac{4}{c^3} L^a+\mathcal{O}\left(c^{-5}\right), \\& S_{\mathrm{ab}}=\delta_{\mathrm{ab}}\left(1+\frac{2 L}{c^2}\right)+\mathcal{O}\left(c^{-4}\right),\end{aligned}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq28.png) (11)
(11)
where L(T, X) and La(T, X) are the Moon-centred scalar and vector potentials, δab is the Kronecker symbol, and c is the constant speed of light in vacuum.
The two potentials can be split into two parts: one arising from the gravitational action of the Moon (![$\[L_{M}, L_{M}^{a}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq29.png) ) and the second due to the external contributions related to tidal and inertial effects
) and the second due to the external contributions related to tidal and inertial effects ![$\[L_{\text {ext }}, L_{\text {ext }}^{a}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq30.png) . The main expressions for these potentials are (Turyshev et al. 2013; Fienga et al. 2024)
. The main expressions for these potentials are (Turyshev et al. 2013; Fienga et al. 2024)
![$\[L(T, \boldsymbol{X})=L_M(\boldsymbol{X})+L_{\mathrm{ext}}(T, \mathbf{X})+\mathcal{{O}}\left(c^{-4}\right),\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq31.png) (12)
(12)
![$\[L_{\mathrm{ext}}^a=-\frac{G}{2 X^3}\left[\mathbf{X} \times \mathbf{A}_{\mathrm{M}}\right]^a+\mathcal{O}\left(c^{-2}\right),\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq32.png) (13)
(13)
where G is the gravitational constant and AM is the angular momentum of the Moon. The quantity LM is the Newtonian multipole moment of the Moon. The dominant potential is the tidal contribution produced by all the Solar System bodies (excluding the Moon), estimated at the centre of mass of the Moon, which is the origin of the LCRS Soffel et al. (i.e. 2003).
The transformation between the barycentre celestial reference system (BCRS) and the LCRS is given using T=TCL, t = TCB (the time coordinate in the BCRS), and rM = x − xM, representing the differences between the vectors of the BCRS barycentric position of the lunar spacecraft, x. The expression of the LCRS coordinate vector X with respect to the BCRS x coordinate vector is given by
![$\[\begin{aligned}X=~ & \mathbf{r}_{\mathbf{M}}+\frac{1}{c^2}[\frac{1}{2} \mathbf{v}_{\mathbf{M}}.(\mathbf{v}_{\mathbf{M}}. \mathbf{r}_{\mathbf{M}})+\ell_{\mathrm{ext}}(\mathbf{x}_{\mathbf{M}}). \mathbf{r}_{\mathbf{M}} \\&+\mathbf{r}_{\mathbf{M}}.(\mathbf{a}_{\mathbf{M}}. \mathbf{r}_{\mathbf{M}})-\frac{1}{2} \mathbf{a}_{\mathbf{M}}. r_M~^2]+\mathcal{O}(c^{-4}),\end{aligned}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq33.png) (14)
(14)
where vM and aM are the velocity and acceleration of the Moon in BCRS and ![$\[\ell_{\text {ext}}(\mathbf{x}_{\mathbf{M}})=\sum{_{A ~\neq M}} \frac{G M_{A}}{r_{\mathrm{M}}^{A}}+\mathcal{{O}}(c^{-2})\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq34.png) where
where ![$\[\mathbf{r}_{\mathbf{M}}^{\mathbf{A}}=\mathbf{x}_{\mathbf{A}}- \mathbf{x}_{\mathbf{M}}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq35.png) , the moon-centred vector of the body, A, in BCRS.
, the moon-centred vector of the body, A, in BCRS.
The time transformation between BCRS time, t, and LCRS time, T, is
![$\[T=t-\frac{1}{c^2}\left[A(t)+v_M^i r_M^i\right]+\mathcal{O}\left(c^{-4}\right),\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq36.png) (15)
(15)
where ![$\[v_{M}^{i}, r_{M}^{i}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq37.png) , and
, and ![$\[a_{M}^{i}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq38.png) are the coordinates of the vectors vM, rM, and aM, respectively, and
are the coordinates of the vectors vM, rM, and aM, respectively, and
![$\[\frac{\mathrm{d} \mathrm{~A}~(t)}{\mathrm{dt}}=\frac{1}{2} v_M^2+L_{\mathrm{ext}}~(\mathbf{~X}).\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq39.png) (16)
(16)
The 𝒪(c−5) order expression is provided in Fienga et al. (2024).
4.1.2 Definition of the lunar timescale
The coordinated universal time (UTC) timescale is used for recording observations from the Earth surface. For defining selenodetic frames, or when Earth-based observations are used to study the dynamics of the Moon, the UTC timescale is transformed into barycentric dynamical time (TDB) (Fienga et al. 2009).
The GPS time (GPST) scale can be used as an intermediate timescale between lunar orbiters and ground-based stations, as proposed for receivers of Earth’s global navigation satellite system (GNSS) signals in lunar orbit.
For lunar surface timing or lunar constellations, we define the lunar (selenocentric) coordinate time (TCL), the relativistic time scale at the Moon’s centre of mass, similarly to the Geocentric Coordinate Time (TCG), the relativistic timescale at the geocentre (Soffel et al. 2003; Petit & Luzum 2010). Based on the previous equations, we can define TCL relative to TCB, in the same way that TCG is related to TCB, following Damour et al. (1991):
![$\[\frac{\mathrm{d} ~\mathrm{TCL}}{\mathrm{~d} ~\mathrm{TCB}}=1+\frac{1}{c^2} \alpha_M+\mathcal{O}\left(c^{-4}\right),\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq40.png) (17)
(17)
The numerical value of αM is approximately 1.4810−8 (Turyshev et al. 2013; Nelson & Ely 2006).
In the same way that TCL can be defined relative to TCB in Eq. (17), it is also possible to describe TCL relative to TCG in the GCRS. In this case, we have
![$\[\frac{\mathrm{d} ~\mathrm{TCL}}{\mathrm{~d} ~\mathrm{TCG}}=1+\frac{1}{c^2} \alpha_{M / C}+\mathcal{O}\left(c^{-4}\right),\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq42.png) (19)
(19)
where αM/C has the same definition as in Eq. (18), but with geocentric positions and velocities. In addition, the terrestrial time (TT) is defined relative to TCG as (Petit & Luzum 2010)
![$\[\frac{\mathrm{d~TT}}{\mathrm{d~TCG}}=1-L_G,\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq43.png) (20)
(20)
where LG = 6.969290134 × 10−10. Using TCL − TT = (TCL − TCG) + (TCG − TT) and Eq. (17) with the current definition of TT, (Eq. (20), we obtain
![$\[\frac{\mathrm{d} \text { TCL-TT }}{\mathrm{d} \text { TT }}=\frac{1}{1-L_G} \times\left[L_G+\frac{1}{c^2} \alpha_{M / C}\right]+\mathcal{O}\left(c^{-4}\right).\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq44.png) (21)
(21)
The results of integrating Eq. (21) in the frame of the INPOP planetary ephemeris are presented in Section 4.2.4. The full expressions at order 𝒪(c−5) are given in Fienga et al. (2024).
4.1.3 Transformation between LCRS and BCRS
From Eqs. (14) and (15) and the explicit expressions of non-rotating potentials L and La, the transformation between the local lunar-centred reference frame coordinates of an object in the vicinity of the Moon, X(TCL), hereafter X, and the coordinates of the same object in the BCRS relative to the Moon, rM(TDB), hereafterrM as in Eq. (14), is given by (Soffel et al. 2003; Turyshev et al. 2013)
![$\[\begin{aligned}\mathbf{r}_{\mathbf{M}}= & \mathbf{X}+\frac{1}{c^2}\left[-\frac{1}{2} \mathbf{v}_{\mathbf{M}}\left(\mathbf{v}_{\mathbf{M}}. \mathbf{X}\right)-\mathbf{X}. \mathbf{L}_{\mathbf{e x t}}\right. \\& \left.+\left(\mathbf{w}_{\mathbf{p}} \times \mathbf{X}\right)+\frac{1}{2} \mathbf{a}_{\mathbf{M}}.X^2-\mathbf{X}\left(\mathbf{X}. \mathbf{a}_{\mathbf{M}}\right)\right]+\mathcal{O}\left(c^{-4}\right).\end{aligned}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq45.png) (22)
(22)
Here, wp is the vector associated with the relativistic precession (see, e.g., Turyshev et al. 2013), and vM and aM are, respectively, the barycentric velocity and acceleration vectors of the Moon estimated at TDB (using the same notation as in Sect. 4.1.1). For present-day applications in space dynamics, Eq. (22) can be simplified as(Turyshev et al. 2013)
![$\[\mathbf{r}_{\mathbf{M}}=\mathbf{X}\left[1-\frac{1}{c^2} \sum_{b \neq M} L_b\left(\left.\mathbf{r}_{\mathbf{M}}^{\mathbf{b}}\right)\right)\right]-\frac{1}{2 c^2}\left(\mathbf{v}_{\mathbf{M}}. \mathbf{X}\right) \mathbf{v}_{\mathbf{M}},\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq46.png) (23)
(23)
where ![$\[\sum{_{b \neq M}} ~L_{b}(\mathbf{r}_{\mathbf{M}}^{\mathbf{b}})\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq47.png) is the gravitational potential due to the Solar System bodies excluding the Moon, at the Moon’s centre of mass in the BCRS. For the velocity, denoting v as the barycentric velocity of the orbiter in the BCRS at TDB and V as its velocity in the LCRS at TCL, the velocity transformation from the LCRS to the BCRS is given by (Turyshev et al. 2013)
is the gravitational potential due to the Solar System bodies excluding the Moon, at the Moon’s centre of mass in the BCRS. For the velocity, denoting v as the barycentric velocity of the orbiter in the BCRS at TDB and V as its velocity in the LCRS at TCL, the velocity transformation from the LCRS to the BCRS is given by (Turyshev et al. 2013)
![$\[\mathbf{v}-\mathbf{v}_{\mathbf{M}}=\left[\mathbf{V}\left(1-\frac{1}{c^2} \sum_{b \neq M} L_b\right)-\frac{1}{2 c^2}\left(\mathbf{v}_{\mathbf{M}}. \mathbf{V}\right) \mathbf{v}_{\mathbf{M}}\right] \times \frac{d T C L}{d T D B},\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq48.png) (24)
(24)
where ![$\[\frac{d~T C L}{d~T D B}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq49.png) is deduced from Eq. (17).
is deduced from Eq. (17).
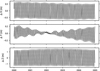 |
Fig. 4 Differences in the Moon’s centre positions relative to the Earth, in metres, estimated using DE421 and INPOP19a in the ICRS. |
4.1.4 Accuracy assessments of the realisation
This section discusses the realisation of the LCRS based on lunar ephemerides. At present, several ephemerides are available, and a crude approach to estimate their accuracy is to compare the position of the Moon’s origin relative to the Earth using different ephemerides. We considered the DE421 (Folkner et al. 2014a) ephemeris, which is the current standard for the definition of the lunar ME frame (see Sect. 2.3) and INPOP19a (Fienga et al. 2019). These two ephemerides differ due to additional normal points over 11 years, as well as in the modelling of the shape of the fluid core in core-mantle interactions and asteroid belts. Figure 4 illustrates the variations of the Moon’s centre relative to Earth over five years for these two ephemerides. Short-period oscillations are present, with the main difference occurring in the Z-coordinate, with an amplitude of 1.5 m amplitude. In terms of parameters, the ratio between the gravitational mass of the Earth-Moon barycentre in DE421 and INPOP19a is slightly greater than unity, with a value of (1.2 ± 10−11) × 10−8.
4.2 The lunar body-fixed reference system, LRS
A reference system attached to the Moon, the lunar reference system (LRS), can be defined in a manner analogous to the International Terrestrial Reference System, ITRS, used for the Earth. This system is constructed according to the properties of the PA system described in Section 2.2. Its realisation is initially materialised by the positions of the retro-reflectors on the lunar surface and therefore depends on a specific lunar and planetary ephemeris. The following sections provide different assessments of the accuracy of LRS realisations. First, we consider the differences between the Euler orientations from various lunar and planetary ephemerides, to estimate the sensitivity to additional data and improved modelling (Sect. 4.2.1). Next, we focus on INPOP19a ephemerides, whose accuracy is determined through the propagation of the timely covariance matrices of Euler orientation (Sect. 4.2.2). At present, the determination and accuracy of the LRS are determined using only one geodetic method, namely LLR. In 4.2.3, we discuss the link accuracy with other techniques, such as altimetry and images obtained with the LRO. Finally, we examine derived timescales that may be more appropriate than the TCL, depending on user positioning or spacecraft navigation, based on the definition proposed in Sect. 4.1.2.
 |
Fig. 5 Comparisons of the three lunar libration angles obtained using different ephemerides. The plotted differences are expressed as displacements on the Moon surface (left y-axis) assuming a mean radius of 1738 km. |
4.2.1 Comparisons between ephemerides
The LRS realisations based on the PA system, which depend on lunar and planetary ephemerides, have their precision and accuracy limited by data accumulation, physical modelling, and the reduction model. To analyse each effect, Figure 5 shows the differences in the rotational angles for various INPOP solutions, showing the resulting surface displacement due to differences in the ephemerides. We tested three cases. Case I, INPOP17a-INPOP13c, represents improvements in core-mantle interaction and accumulation of four years of LLR observations. Case II, INPOP19a-INPOP17a, involved modelling variations related to core-mantle oblateness and two years of observations. Finally, Case III, INPOP19a-INPOP21a, includes an additional two years of observations, without modifications to the rotation modelling. Improvements in physical modelling (Cases I and II) result in differences on the order of three metres (with 110 metres offset for ψ) and 50 centimetres, respectively, indicating that further refinement of the solution at the 50 cm level is still possible. Several avenues remain to improve the modelling, including solid core coupling, tidal deformation of the surface, viscoelastic contribution in deformation coefficients, and the impact of Earth orientation parameters. The accumulation of data (Case III) improves the solution by 10 cm over two years. The principal impact of extended LLR long observations would be to remove estimated range biases introduced in the reduction analysis, while adding new reflectors on the Moon surface would better disentangle the various contributions of libration mis-modelling and to facilitate a better study of physical unknowns described previously (Fienga et al. 2024)
In conclusion, with the most up-to-date modelling, differences in the rotation angles should not exceed 30 to 50 cm over a five-year period. The comparison between INPOP solutions and the maximum difference in rotation angles between INPOP19a and DE421 over a 30-year period is summarised in Table 5.
4.2.2 Propagation of the covariance matrix
The stability of the accuracy of the LRS realisation was assessed by propagating the covariance matrix of the rotation angles over time, following the method proposed by Tapley et al. (2004). Let H(t0) be the covariance matrix of the lunar rotation angles (ψ, θ, φ) at the reference time of the ephemeris t0 (for INPOP, t0 is J2000). The evolution of the uncertainties, H(t), for these angles at any date, t, was estimated by considering the Jacobian matrix, J(t), such that H(t) = J(t) H(t0) Jt(t). For this analysis, we used the covariance matrix and the partial derivatives of INPOP21a.
The initial uncertainties in (ψ, θ, φ) were approximately (6.0, 0.1, and 0.3) milliarcseconds (mas), respectively. The results of the covariance propagation are shown in Figure 6. The largest uncertainty was obtained for φ, reaching 35 cm over 25 years, followed by 30 cm for the ψ angle. Non-Gaussian errors may have arisen directly from the LLR data or from the modelling of tides and core-mantle coupling. However, the propagation of the covariance matrix remained stable and consistent with comparisons of the recent INPOP versions, INPOP17a, INPOP19a, and INPOP21a.
4.2.3 Connection between the LRS and the LRO digital terrain model
Currently, the accuracy and stability of the LRS reference system are determined using LLR geodetic techniques (see Sects. 4.2.1 and 4.2.2). Here, we discuss the accuracy of the reference system with respect to other geodetic techniques, notably images and altimetric data from space missions such as the LRO. These space missions determined allow us to determine the digital terrain model (DTM); the first link between LRO DTM and ME DE421 was obtained by (Oberst et al. 2019) in 2018. An additional, independent tie was established using the LRO Narrow Angle Camera (NAC; (Löcher et al. 2017)). Comparisons between the positions of the lunar laser retro-reflectors observed by the LRO NAC cameras and the Lunar Orbiter Laser Altimetry (LOLA) data and the positions deduced from JPL DE421 provide maximum differences of about ten metres, comparable to the RMS of LRO orbit overlaps (Mazarico et al. 2012). This value is ten times larger than the inferred LLRR position variations derived from different lunar ephemerides, which are approximately one metre (see Table 6). We can therefore infer that the current accuracy of the link to the LRO DTM is limited by the LRO orbit overlap accuracy of about ten metres.
4.2.4 LRS timescales
The timescales associated with the LRS could be realisations of TCL, as defined in Sect. 4.1.2, although other timescales can be proposed depending on the requested timing location (at the Moon centre, on the surface, or on board the orbiter). Equation (21) can be integrated independently of the planetary and lunar ephemeris chosen for the LCRS and LRS realisation, using either a simple integrator or directly with the planetary ephemerides. In this work, the solution was integrated directly with INPOP planetary ephemerides using a Adams-Cowell integrator of order 12 (see Fienga et al. (2006) and Fienga et al. (2008) for details). After a simultaneous integration with planetary orbits, we show TCL-TT shown in Figure 7. The TCL-TT time difference can be decomposed into two components: a secular drift of approximately 58.7μs per day and a periodic term with an amplitude of about 0.5 μs and a period of 27.56 days. These two terms are consistent with the expected trend obtained by adding LG to the term accounting for the Earth’s gravitational potential on the Moon, approximated as ![$\[\frac{3}{2 c^{2}} \frac{G M_{E}}{a_{M}}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq50.png) , where aM is the semi-major axis of the geocentric Moon orbit and GME is the gravitational mass of the Earth. The periodic term corresponds to the effect of the Moon’s eccentric orbit and is approximated by
, where aM is the semi-major axis of the geocentric Moon orbit and GME is the gravitational mass of the Earth. The periodic term corresponds to the effect of the Moon’s eccentric orbit and is approximated by ![$\[\frac{2}{c^{2}} \sqrt{G M_{E} a_{M}} e_{M} ~\sin~ E_{M}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq51.png) , where eM and EM are the eccentricity and eccentric anomaly of the Moon orbit. The differences between the full integration and these approximations (
, where eM and EM are the eccentricity and eccentric anomaly of the Moon orbit. The differences between the full integration and these approximations (![$\[L_{G}- \frac{3}{2 c^{2}} \frac{G M_{E}}{a_{M}}-\frac{2}{c^{2}} \sqrt{G M_{E} a_{M}} e_{M} ~\sin~ E_{M}\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq52.png) ) are approximately 0.2 μs. These approximations are also discussed in Nelson & Ely (2006).
) are approximately 0.2 μs. These approximations are also discussed in Nelson & Ely (2006).
Figure 7a and Table 7 show additional low-frequency components. These harmonics arise from the non-Keplerian motion of the Moon relative to Earth. The orbit of the Moon around Earth, derived from INPOP ephemerides that include the full model of perturbations. Thus, other harmonics are present even when considering only Earth’s potential on the Moon (perturbed in the full formalism) for the computation of TCL. We compared our results with the approach of Kopeikin & Kaplan (2024) who integrate the full-time transformation in closed form, also neglecting 2-PN contributions, which are practically unnoticeable. Their expression relating TCL and TCG provides a straightforward method of transforming from geocentric to lunarcentric time. In addition to integrating ten years of data using the DE440 ephemerides with 0.1 day steps, this approach allowed the authors to perform an analytical analysis of the equation. In contrast, our implementation starts from a standard differential rate form, expressed using the αM (1-PN) coefficient, and is then integrated using the INPOP21 ephemerides with a 0.002-day time step. We generated similar time series – consistent with the observed secular drift – and similar spectra (see Fig. 8), with only minor differences for major frequency terms (see Table 7). Based on the analytical decomposition proposed by Kopeikin & Kaplan (2024), the results given in Table 7 differ by only one period, which is not detected in our frequency analysis. This corresponds to the 2D − M + M′ term, which has a very low amplitude. The residuals between the time series of Kopeikin & Kaplan (2024) from 2020 to 2022 (Fig. 3 in Kopeikin & Kaplan 2024) and our evaluation over the same date range have a maximum amplitude of approximately 0.05 μs. The frequencies present in the residuals are also shown in Fig. 8. This corresponds to an agreement at the few-nanosecond level between the two computations.
Maximum differences in libration angles (converted to metres on the lunar surface) between different generations of ephemerides over 25 years.
 |
Fig. 6 Propagation of the INPOP21a covariance matrix for the three libration angles (ψ, θ, φ). The results are presented as displacement on the lunar surface (left y-axis) and as milliseconds of arcs (right y-axis). |
Maximum differences in LLRR positions between various ephemerides.
 |
Fig. 7 Left: difference (TCL-TT) as a function of time in TT (days). Right: same quantity after removing a drift of approximately 58.7 μs per day. Results in both plots are given in seconds. |
Major period terms in TT-TCL.
 |
Fig. 8 Power spectrum of periodicities of (TCL-TT) based on the integration of INPOP21a over 2019–2023, compared with the results of Kopeikin & Kaplan (2024) and with the spectrum of the residuals between the two-year TCL-TCG time series. |
5 Summary and conclusions
This study provides a detailed and precise framework for lunar reference systems, which are essential for lunar science, accurate lunar navigation, surface mapping, and mission planning-particularly relevant for programmes such as NASA’s Artemis and ESA’s Moonlight. The analysis focuses on two primary lunar reference systems: PA and ME. The PA system is based on the internal structure of the Moon, specifically its inertia tensor, making it suitable for modelling and integrating lunar dynamics. The ME system, in contrast, is geometrically defined by the Moon’s average orientation toward Earth and has been widely used in mission operations. A key contribution of this work is the derivation of a complete rotation matrix and a refined transformation between the PA and ME systems, based on new data from the INPOP19a lunar ephemeris. We extracted updated models of lunar libration and polar motion using the INPOP19a data set. These models are more accurate than previous versions and include hundreds of frequency terms, many of which are derived from orbital dynamics. The accuracy of the resulting series is within a few milliarcseconds, corresponding to errors of a few centimetres on the Moon surface. The transformation between the INPOP19a PA system and the ME system of DE421 results in a residual positional difference of approximately 13 cm. This highlights that the transformation cannot be approximated as a pure rotation and reflects the complex dynamical effects involved. We also propose a Moon-centred inertial reference frame analogous to the Earth-centred GCRS. This new lunar celestial reference system, or LCRS, uses a relativistic framework to describe spacecraft motion and reference timing around the Moon. The system introduces a new time standard called lunar coordinate time (TCL), which accounts for relativistic effects such as lunar gravity and tidal forces. We analysed differences between ephemerides, particularly INPOP19a and DE421, to estimate the realisation accuracy of the LCRS. These differences can reach up to 1.5 metres in the vertical component of the Moon centre position over a five-year period. The lunar reference system (LRS) is a Moon-fixed coordinate system tied to the PA frame. Its realisation depends primarily on position data from lunar retro-reflectors. Our comparison of multiple generations of INPOP ephemerides reveals that improvements in physical modelling—such as a better understanding of the Moon’s core-mantle interaction—can lead to differences in predicted surface positions of up to three metres. The effects of adding more data, without changing models, are smaller, improving accuracy by approximately 10 cm over two years. A propagation of covariance from the rotation model indicates that errors remain under 35 cm over a 25-year period, confirming the stability of the current frame. Beyond spatial reference systems, this study explores how timekeeping should be handled in lunar environments.
Data availability
The full series of librational and polar coordinates is available at the CDS via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/705/A88. The Appendix B lists the tables containing only the 20 main terms.
Acknowledgements
We thank the LLR stations at McDonald Observatory, Texas; Observatoire de la Côte d’Azur, France; Haleakala Observatory, Hawaii; Apache Point Observatory, New Mexico; Matera, Italy; and Wettzell, Germany, which provided the data sets that make LLR analyses possible. This study has been realised under ESA contract AO/1-10712/21/NL/CRS. Y.S. work has been co-funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or granting authority European Education and Culture Executive Agency (EACEA). Neither the European Union nor the granting authority can be held responsible for them. NR thanks language editor for valuable suggestions.
References
- Archinal, B. A., Acton, C. H., A’Hearn, M. F., et al. 2018, Celest. Mech. Dyn. Astron., 130, 22 [Google Scholar]
- Bretagnon, P. 1982, A&A, 114, 278 [NASA ADS] [Google Scholar]
- Chabé, J., Courde, C., Torre, J.-M., et al. 2020, Earth Space Sci., 7, e00785 [Google Scholar]
- Chapront, J., Chapront-Touzé, M., & Francou, G. 2002, A&A, 387, 700 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charlot, P., Jacobs, C. S., Gordon, D., et al. 2020, A&A, 644, A159 [EDP Sciences] [Google Scholar]
- Damour, T., Soffel, M., & Xu, C. 1991, Phys. Rev. D, 43, 3273 [Google Scholar]
- Dehant, V., Oberst, J., Nadalini, R., Schreiber, U., & Rambaux, N. 2012, Planet. Space Sci., 68, 94 [Google Scholar]
- Fienga, A., Manche, H., Laskar, J., & Gastineau, M. 2006, in IAU Joint Discussion, 26, IAU Joint Discussion, 15 [Google Scholar]
- Fienga, A., Manche, H., Laskar, J., & Gastineau, M. 2008, A&A, 477, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fienga, A., Laskar, J., Morley, T., et al. 2009, A&A, 507, 1675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fienga, A., Laskar, J., Manche, H., et al. 2011, Celest. Mech. Dyn. Astron., 111, 363 [Google Scholar]
- Fienga, A., Laskar, J., Manche, H., Gastineau, M. and Verma, A., 2014, New INPOP release: INPOP13c, https://www.imcce.fr/recherche/equipes/asd/inpop/download13c [Google Scholar]
- Fienga, A., Deram, P., Viswanathan, V., et al. 2019, Notes Scientifiques et Techniques de l’Institut de Mécanique Celeste, 109 [Google Scholar]
- Fienga, A., Deram, P., Di Ruscio, A., et al. 2021, Notes Scientifiques et Techniques de l’Institut de Mecanique Celeste, 110 [Google Scholar]
- Fienga, A., Rambaux, N., Sosnica, K., & Kaitiri, A. 2024, arXiv e-prints [arXiv:2409.10043] [Google Scholar]
- Folkner, W. M., Williams, J. G., Boggs, D. H., Park, R. S., & Kuchynka, P. 2014a, Interplanet. Netw. Prog. Rep., 196, 1 [Google Scholar]
- Folkner, W. M., Williams, J. G., Boggs, D. H., Park, R. S., & Kuchynka, P. 2014b, Interplanet. Netw. Prog. Rep., 196, 1 [Google Scholar]
- Hofmann, F., Biskupek, L., & Müller, J. 2018, J. Geodesy, 92, 975 [NASA ADS] [CrossRef] [Google Scholar]
- IAU XXXII. 2024, in General Assembly, resolution II [Google Scholar]
- Iess, L., Di Benedetto, M., Boscagli, G., et al. 2025, Navigation [Google Scholar]
- Kopeikin, S. M., & Kaplan, G. H. 2024, Phys. Rev. D, 110, 084047 [Google Scholar]
- Kovalevsky, J., & Mueller, I. I. 1981, in Astrophysics and Space Science Library, 86, IAU Colloq. 56: Reference Coordinate Systems for Earth Dynamics, eds. E. M. Gaposchkin & B. Kolaczek, 375 [Google Scholar]
- Kovalevsky, J., Mueller, I. I., & Kolaczek, B. 1989, in Reference Frames in Astronomy and Geophysics, eds. J. Kovalevsky, I. I. Mueller, & B. Kolaczek [Google Scholar]
- Löcher, A., Hofmann, F., Gläser, P., et al. 2017, in REFAG 2014, ed. T. van Dam (Cham: Springer International Publishing), 201 [Google Scholar]
- LRO Project and Lunar Geodesy and Cartography Working Group.. 2008, A Standardized Lunar Coordinate System for the Lunar Reconnaissance Orbiter and Lunar Datasets: LRO Project and LGCWG White Paper, Tech. rep., NASA [Google Scholar]
- Manche, H. 2011, PhD thesis, Observatoire de Paris [Google Scholar]
- Mazarico, E., Rowlands, D. D., Neumann, G. A., et al. 2012, J. Geodesy, 86, 193 [Google Scholar]
- Müller, J., Murphy, T. W., Schreiber, U., et al. 2019, J. Geodesy, 93, 2195 [CrossRef] [Google Scholar]
- Murphy, T. W. 2013, Rep. Prog. Phys., 76, 076901 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R., & Ely, T. 2006, in 38th Annual Precise Time and Time Interval Systems and Applications, 305 [Google Scholar]
- Newhall, X. X., & Williams, J. G. 1996, Celest. Mech. Dyn. Astron., 66, 21 [Google Scholar]
- Oberst, J., Haase, I., & Glaser, P. 2019, Verbesserung und Verdichtung des LOLA Mondkrontrollpunkt-netzes durch LROC/LOLA-Blochausgleiche und Landstellenanalysen anhand von DGM und Karten, Tech. rep., TUB, TUB Forderkennzeichen 50 OW1702 [Google Scholar]
- Park, R. S., Folkner, W. M., Williams, J. G., & Boggs, D. H. 2021, AJ, 161, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlov, D. 2020, J. Geodesy, 94, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, G., & Luzum, B. 2010, IERS Tech. Note, 36, 1 [NASA ADS] [Google Scholar]
- Pitjeva, E., Pavlov, D., Aksim, D., & Kan, M. 2022, in IAU Symposium, 364, Multi-Scale (Time and Mass) Dynamics of Space Objects, eds. A. Celletti, C. Galeş, C. Beaugé, & A. Lemaître, 220 [Google Scholar]
- Rambaux, N., & Williams, J. G. 2011, Celest. Mech. Dyn. Astron., 109, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. E., Zuber, M. T., Neumann, G. A., et al. 2017, Icarus, 283, 70 [Google Scholar]
- Soffel, M., Klioner, S. A., Petit, G., et al. 2003, Astron. J., 126, 2686 [Google Scholar]
- Tapley, B., Schutz, B., & Born, G. 2004, Statistical Orbit Determination (Elsevier) [Google Scholar]
- Tian, W. 2023, Celest. Mech. Dyn. Astron., 135, 38 [Google Scholar]
- Turyshev, S. G., Toth, V. T., & Sazhin, M. V. 2013, Phys. Rev. D, 87, 024020 [Google Scholar]
- Turyshev, S. G., Williams, J. G., Boggs, D. H., & Park, R. S. 2025, ApJ, 985, 140 [Google Scholar]
- Viswanathan, V., Fienga, A., Minazzoli, O., et al. 2018a, MNRAS, 476, 1877 [Google Scholar]
- Viswanathan, V., Fienga, A., Minazzoli, O., et al. 2018b, MNRAS [arXiv:1710.09167] [Google Scholar]
- Williams, J. G. 2018, Celest. Mech. Dyn. Astron., 130, 63 [Google Scholar]
- Williams, J. G., & Boggs, D. H. 2008a, DE421 lunar orbit, physical librations, and surface coordinates, Tech. rep., JPL, jPL Interoffice Memorandum IOM 335-JW [Google Scholar]
- Williams, J. G., & Boggs, D. H. 2008b, DE421 lunar orbit, physical librations, and surface coordinates, Tech. rep., JPL, jPL Interoffice Memorandum IOM 335-JW [Google Scholar]
- Zuber, M. T., Smith, D. E., Watkins, M. M., et al. 2013, Science, 339, 668 [Google Scholar]
Appendix A Expression of the elementary rotation matrices
In this paper, we use the passive or frame rotation convention for the rotation matrices. The expression of the elementary matrices are then:
![$\[R_x(\alpha)=\left[\begin{array}{ccc}1 & 0 & 0 \\0 & ~\cos~ \alpha & ~\sin~ \alpha \\0 & -~\sin~ \alpha & ~\cos~ \alpha\end{array}\right],\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq53.png) (A.1)
(A.1)
![$\[R_y(\alpha)=\left[\begin{array}{ccc}\cos~ \alpha & 0 & -~\sin~ \alpha \\0 & 1 & 0 \\\sin~ \alpha & 0 & ~\cos~ \alpha\end{array}\right],\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq54.png) (A.2)
(A.2)
![$\[R_z(\alpha)=\left[\begin{array}{ccc}\cos~ \alpha & ~\sin~ \alpha & 0 \\-~\sin~ \alpha & ~\cos~ \alpha & 0 \\0 & 0 & 1\end{array}\right].\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq55.png) (A.3)
(A.3)
Appendix B Librational and polar coordinates Tables
The following Tables present the 20 main terms that appear in the evolution of angles Iσ, ρ, τ, and polar coordinates p1, p2 as in Rambaux & Williams (2011). The argument is a combination of the Delaunay arguments D, l′, l, F that describe the orbital motion of the Moon around the Earth in the three body problem (Sun, Earth, and Moon). Ω is the ascending node of the orbit of the Moon, the argument L presents in p1 and p2 is Ω + F, and the first two letters of the planets represent the mean longitudes of the planets (Me=Mercury, Ve=Venus, etc.). The angles U, V, W correspond to the free librations in longitude, latitude, and wobble. Finally, Un denotes a libration term with frequency unidentified with a known argument. The Delaunay arguments are polynomial functions of time at order 4 and the coefficients of the polynomials are derived from Chapront et al. (2002). For the planetary arguments we used Bretagnon (1982). The Tables are given in cosine and sine form where the arguments contain the phases of the Delaunay, planetary or free terms. The Tables are sorted by the amplitude and then written to the milliarcseconds level.
Physical libration for Iσ.
Physical libration for ρ.
Physical libration for τ.
Physical libration for p1.
Physical libration for p2.
All Tables
Statistical values of the series of libration angles and polar coordinates for the INPOP19a ephemeris.
Polynomial coefficients for the libration angles and polar coordinates from the INPOP19a ephemeris.
Maximum differences in libration angles (converted to metres on the lunar surface) between different generations of ephemerides over 25 years.
All Figures
 |
Fig. 1 Geometric transformation between the ME and PA systems. |
| In the text | |
 |
Fig. 2 Temporal behaviour of three libration angles (Iσ, ρ, τ) and polar coordinates (p1, p2) over 1000 years from INPOP19a. |
| In the text | |
 |
Fig. 3 Amplitude (blue) and error (red) of the series for each variable. The points represent the cosine term amplitudes and the crosses represent the sine term amplitudes. |
| In the text | |
 |
Fig. 4 Differences in the Moon’s centre positions relative to the Earth, in metres, estimated using DE421 and INPOP19a in the ICRS. |
| In the text | |
 |
Fig. 5 Comparisons of the three lunar libration angles obtained using different ephemerides. The plotted differences are expressed as displacements on the Moon surface (left y-axis) assuming a mean radius of 1738 km. |
| In the text | |
 |
Fig. 6 Propagation of the INPOP21a covariance matrix for the three libration angles (ψ, θ, φ). The results are presented as displacement on the lunar surface (left y-axis) and as milliseconds of arcs (right y-axis). |
| In the text | |
 |
Fig. 7 Left: difference (TCL-TT) as a function of time in TT (days). Right: same quantity after removing a drift of approximately 58.7 μs per day. Results in both plots are given in seconds. |
| In the text | |
 |
Fig. 8 Power spectrum of periodicities of (TCL-TT) based on the integration of INPOP21a over 2019–2023, compared with the results of Kopeikin & Kaplan (2024) and with the spectrum of the residuals between the two-year TCL-TCG time series. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\[M=\left[\begin{array}{ccc}1.0 & -0.000327698 & 0.000381039 \\0.000327698 & 1.0 & -1.406 \times 10^{-6} \\-0.000381039 & 1.406 \times 10^{-6} & 1.0\end{array}\right],\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq19.png)
![$\[\alpha_M=-\frac{1}{2} v_M^2-\sum_{A ~\neq M} \frac{G M_A}{r_{\mathrm{M}}^A}.\]$](/articles/aa/full_html/2026/01/aa55962-25/aa55962-25-eq41.png)