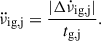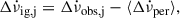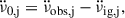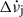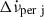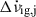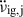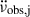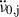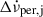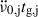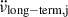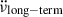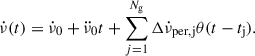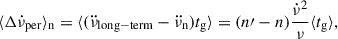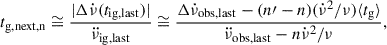| Issue |
A&A
Volume 706, February 2026
|
|
|---|---|---|
| Article Number | A216 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202556157 | |
| Published online | 10 February 2026 | |
Braking index of the frequently glitching PSR J0537−6910★
1
School of Arts and Sciences, Qingdao Binhai University Huangdao District 266555 Qingdao, People’s Republic of China
2
National Astronomical Observatories, Chinese Academy of Sciences 20A Datun Road Chaoyang District Beijing 100101, China
3
Bahçeşehir College, Çiçekliköy Bornova 35040 Izmir, Türkiye
4
Faculty of Engineering and Natural Sciences, Sabancı University, Orhanlı Tuzla 34956 Istanbul, Türkiye
5
Jodrell Bank Centre for Astrophysics, Department of Physics and Astronomy, The University of Manchester Manchester, UK
6
Departamento de Física, Universidad de Santiago de Chile (USACH), Estación Central, Chile
7
Center for Interdisciplinary Research in Astrophysics and Space Sciences (CIRAS), USACH Estación Central, Chile
8
Department of Astronomy and Space Sciences, Istanbul University Beyazıt 34119 Istanbul, Türkiye
★★ Corresponding authors: This email address is being protected from spambots. You need JavaScript enabled to view it.
; This email address is being protected from spambots. You need JavaScript enabled to view it.
; This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
28
June
2025
Accepted:
28
November
2025
Context. The pulsar J0537−6910 undergoes spin-up glitches more frequently than any other known pulsar, at a rate of roughly thrice per year. Its glitches are typically large and accompanied by abrupt changes in the spin-down rate (ν˙) that partially recover with a nearly constant positive frequency second derivative (ν¨) for the entire post-glitch interval until the next glitch. The effective long-term value of ν¨, however, is negative because ν˙ has decreased over the years of observations.
Aims. We wished to determine if ‘permanent shifts’ (non-relaxing parts of the glitch change, ν˙, in the spin-down rate, like those observed in the Crab pulsar) can explain the long-term enhancement of the spin-down rate, which results in an effective negative braking index. We demonstrate, as a proof of concept, that the actual braking index (n) associated with the pulsar’s braking torque can be ∼3 if the internal superfluid torque and permanent shifts are considered.
Methods. We used published RXTE and NICER data to calculate the average permanent shift per glitch needed to bring an underlying braking index (n) in line with the effective long-term value n′≅ − 1.2 inferred from the data. We then used this average value as the actual permanent shift in each glitch and extracted the contributions of the internal and external torques to the observed ν¨ for each inter-glitch interval, under the assumption that the next glitch occurs when all glitch-induced offsets to internal torques are fully restored.
Results. We find that if the braking index of the magnetospheric torque is close to ∼3, moderate permanent changes in the spin-down rate are required, of magnitudes similar to the persistent shifts inferred for the Crab pulsar. The natural candidate mechanism to produce such permanent changes is crust-quakes. Crustal failure associated with PSR J0537−6910 glitches can have interesting – and potentially observable – consequences, such as transient changes in the X-ray emission, the activation of radio emission, or the emission of gravitational waves.
Key words: stars: neutron / pulsars: general / pulsars: individual: PSR J0537−6910
© The Authors 2026
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1. Introduction
The X-ray pulsar PSR J0537−6910 in the Large Magellanic Cloud is exceptional in terms of its rotational properties. Its spin evolution is interrupted by large glitches, i.e. abrupt changes in the rotation and spin-down rates, followed by post-glitch relaxation (see reviews on pulsar glitches: Haskell & Melatos 2015; Zhou et al. 2022; Antonopoulou et al. 2022; Antonelli et al. 2022). This is the most frequently glitching known pulsar, with a quite regular rate of ≳3.2 glitches per year and glitch rotational frequency steps (Δν) among the largest observed in young pulsars (Middleditch et al. 2006; Antonopoulou et al. 2018; Ferdman et al. 2018; Abbott et al. 2021a; Ho et al. 2020, 2022).
The significant glitch activity makes the measurement of the braking index, 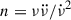 (where ν,
(where ν, 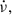 and
and  are the pulse frequency and its first and second time derivatives, respectively), quite ambiguous. A pulsar slowing down purely under magnetic dipole braking would have n = 3. Middleditch et al. (2006), Antonopoulou et al. (2018), and Ho et al. (2022) have determined an effective negative braking index from the overall increase in the spin-down rate (a more negative
are the pulse frequency and its first and second time derivatives, respectively), quite ambiguous. A pulsar slowing down purely under magnetic dipole braking would have n = 3. Middleditch et al. (2006), Antonopoulou et al. (2018), and Ho et al. (2022) have determined an effective negative braking index from the overall increase in the spin-down rate (a more negative  ) in the long run, while Antonopoulou et al. (2018) and Ferdman et al. (2018) have measured high inter-glitch braking indices (n), typically over ∼7 and up to ∼100, from data between successive glitches. These anomalously high values are dominated by the internal torques that couple the crust to the neutron star superfluid interior; separating their effects in the timing data allows one to find the underlying braking index due to the external braking torque.
) in the long run, while Antonopoulou et al. (2018) and Ferdman et al. (2018) have measured high inter-glitch braking indices (n), typically over ∼7 and up to ∼100, from data between successive glitches. These anomalously high values are dominated by the internal torques that couple the crust to the neutron star superfluid interior; separating their effects in the timing data allows one to find the underlying braking index due to the external braking torque.
In Sect. 2 we overview the timing data and rotation of PSR J0537−6910. In Sect. 3 we discuss the post-glitch spin-down evolution of multi-component neutron stars with references to the vortex creep model. In Sect. 4 we present the relationships between the observable quantities and the hidden underlying braking index, with the results for the model parameters detailed in Sect. 5. Section 6 discusses a method for estimating the time to the subsequent glitch, which could be used to schedule an observation campaign covering the next glitch in PSR J0537−6910. We discuss our results and their implications in Sect. 7.
2. Timing behaviour of PSR J0537−6910
PSR J0537−6910, discovered with the Rossi X-ray Timing Explorer (RXTE; Marshall et al. 1998), is located inside the 1 to 5 kyr old supernova remnant N157B (Chen et al. 2006) in the Large Magellanic Cloud, 49.6 kpc away from Earth (Pietrzyński et al. 2019). It is the fastest rotating young pulsar, with a spin frequency ν = 62 Hz, and has a very high spin-down rate (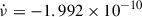 Hz s−1), resulting in the largest known spin-down luminosity Ė = 4.9 × 1038 erg s−1. The characteristic age
Hz s−1), resulting in the largest known spin-down luminosity Ė = 4.9 × 1038 erg s−1. The characteristic age 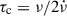 is about 4.9 kyr and the surface dipole magnetic field Bs is inferred to be ≅9.25 × 1011 G. The source is observed primarily in the X-ray band, with some weak radio emission detected recently (Crawford 2024).
is about 4.9 kyr and the surface dipole magnetic field Bs is inferred to be ≅9.25 × 1011 G. The source is observed primarily in the X-ray band, with some weak radio emission detected recently (Crawford 2024).
Glitches in PSR J0537−6910 were initially reported by Marshall et al. (1998, 2004). Later, all available RXTE observations were analysed by Antonopoulou et al. (2018), who reported a total of 45 glitches in the nearly 13-year period of data. Their findings were in agreement with Ferdman et al. (2018), who also reports no evidence of pulse flux and profile changes associated with the glitches. After the decommissioning of RXTE in 2012, PSR J0537−6910 was observed with the Neutron Star Interior Composition Explorer (NICER) that discovered 15 glitches (Ho et al. 2020; Abbott et al. 2021b; Ho et al. 2022). Five further glitches in the Jodrell Bank Glitch Catalogue1 are not included in our analysis as the timing data are not yet published for these recent glitches.
All PSR J0537−6910 glitches have similar glitch steps in the rotation frequency (Δν) and the spin-down rate (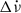 ), and similar relaxation properties. The glitch activity parameter, calculated as
), and similar relaxation properties. The glitch activity parameter, calculated as 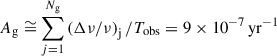 where Tobs is the total time span containing Ng observed glitches, each with fractional spin increases (Δν/ν)j. This is the second highest glitch activity parameter after PSR J1023–5746, which has Ag = 14.5 × 10−7 yr−1 (Gügercinoğlu et al. 2022).
where Tobs is the total time span containing Ng observed glitches, each with fractional spin increases (Δν/ν)j. This is the second highest glitch activity parameter after PSR J1023–5746, which has Ag = 14.5 × 10−7 yr−1 (Gügercinoğlu et al. 2022).
The magnitude of the spin-down rate, 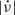 , usually increases at glitches such that
, usually increases at glitches such that 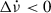 . This step partially recovers with a nearly constant positive spin frequency second derivative
. This step partially recovers with a nearly constant positive spin frequency second derivative  until the time of the next glitch. This is typical inter-glitch timing behaviour in pulsars with large glitches. For PSR J0537−6910, the inter-glitch spin-down rate evolves with
until the time of the next glitch. This is typical inter-glitch timing behaviour in pulsars with large glitches. For PSR J0537−6910, the inter-glitch spin-down rate evolves with 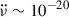 Hz s−2 on average, which implies an anomalously large average inter-glitch braking index nig ≅ 20. This value can be up to 5 times larger for some glitches. Exponentially relaxing components are not as prominent in PSR J0537−6910 glitches as for other pulsars, for example Vela. However, after the first glitch in the RXTE data, Antonopoulou et al. (2018) identified an exponentially decaying component with a timescale τd = 21 ± 4 days followed by a linear spin-down regime with an inter-glitch braking index 7.6 ± 0.1. Exponential recoveries have recently been detected for 11 additional glitches, most of which are followed by regimes with inter-glitch braking indices between 6 and 9 (Zubieta et al. 2026). Ferdman et al. (2018) applied Markov Chain Monte Carlo techniques to simultaneously fit all RXTE inter-glitch
Hz s−2 on average, which implies an anomalously large average inter-glitch braking index nig ≅ 20. This value can be up to 5 times larger for some glitches. Exponentially relaxing components are not as prominent in PSR J0537−6910 glitches as for other pulsars, for example Vela. However, after the first glitch in the RXTE data, Antonopoulou et al. (2018) identified an exponentially decaying component with a timescale τd = 21 ± 4 days followed by a linear spin-down regime with an inter-glitch braking index 7.6 ± 0.1. Exponential recoveries have recently been detected for 11 additional glitches, most of which are followed by regimes with inter-glitch braking indices between 6 and 9 (Zubieta et al. 2026). Ferdman et al. (2018) applied Markov Chain Monte Carlo techniques to simultaneously fit all RXTE inter-glitch  data by aligning them at the glitch epoch. They measured a decay timescale
data by aligning them at the glitch epoch. They measured a decay timescale 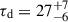 d and an inter-glitch braking index ∼7.4. Using likewise superposed inter-glitch data in terms of
d and an inter-glitch braking index ∼7.4. Using likewise superposed inter-glitch data in terms of 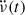 (Andersson et al. 2018) or in terms of the short-term braking index (Ho et al. 2020) yields timescales τd = 19 − 44 d for the post-glitch exponential relaxations. These exponential recovery timescales are consistent with the vortex creep response of the outer core of the neutron star (Gügercinoğlu 2017).
(Andersson et al. 2018) or in terms of the short-term braking index (Ho et al. 2020) yields timescales τd = 19 − 44 d for the post-glitch exponential relaxations. These exponential recovery timescales are consistent with the vortex creep response of the outer core of the neutron star (Gügercinoğlu 2017).
The high glitch activity of this source makes its braking index measurements ambiguous. In the long term, the evolution of the spin-down, 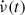 , has the characteristic sawtooth shape seen in pulsars with regular large glitches; however, the overall slope is negative. This translates into a long-term negative apparent braking index
, has the characteristic sawtooth shape seen in pulsars with regular large glitches; however, the overall slope is negative. This translates into a long-term negative apparent braking index 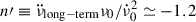 (Antonopoulou et al. 2018; Ho et al. 2022), where ν0 and
(Antonopoulou et al. 2018; Ho et al. 2022), where ν0 and 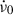 are the rotation frequency and spin-down rate, respectively, at some reference epoch and the long-term frequency second derivative
are the rotation frequency and spin-down rate, respectively, at some reference epoch and the long-term frequency second derivative 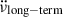 is measured for the entire data span, over many glitches. The long-term behaviour is likely the artefact of high glitch activity, as discussed in Antonopoulou et al. (2018), Ferdman et al. (2018), and Ho et al. (2022).
is measured for the entire data span, over many glitches. The long-term behaviour is likely the artefact of high glitch activity, as discussed in Antonopoulou et al. (2018), Ferdman et al. (2018), and Ho et al. (2022).
3. Spin-down of the multi-component neutron star with internal couplings
In steady-state, the crust and all interior components of the neutron star spin down at the same rate, dictated by the external (pulsar) braking torque and maintained by lags ω ≡ Ωs − Ωc > 0 between the rotation rates (Ωs) of the various interior (superfluid) components and the rotation rate (Ωc) of the outer crust (neutron star surface) and interior components co-rotating with the outer crust. In response to offsets from the steady-state lag introduced at each glitch (which decreases ω), the observed spin-down rate of the crust experiences step increases at each glitch. Subsequently, the lag will evolve back to the steady-state value under the effect of the external (pulsar) torque, resulting in relaxation of the observed crust spin-down rate (Alpar et al. 1984; Alpar 1989; Gügercinoğlu & Alpar 2020). This is the typical inter-glitch timing behaviour of pulsars with large glitches, of which the Vela pulsar is the prototype (Akbal et al. 2017; Gügercinoğlu et al. 2022). Internal contributions to the glitch-induced change in the spin-down rate will eventually fully relax back to the pre-glitch steady-state. Such features are common to multi-component systems driven by external torques or forces. In addition, as a result of possible structural changes that affect the coupling of the superfluid to normal components, there can be permanent, non-relaxing changes associated with glitches, similarly to what is seen as ‘persistent shifts’ in the spin-down rate of the Crab pulsar (Demianski & Proszynski 1983; Lyne et al. 1992, 2015).
If the coupling between some internal superfluid component and the crust is linear in the lag ω, then post-glitch relaxation will proceed exponentially. The return to steady-state on the timescale τd of the exponential decay can be discerned in the post-glitch timing data of many pulsars (e.g. Yu et al. 2013; Lower et al. 2021; Gügercinoğlu et al. 2022; Zubieta et al. 2023; Liu et al. 2024; Grover et al. 2025; Zubieta et al. 2026). On the other hand, if the coupling is non-linear, then the relaxation takes the form of either a power law, which has no scale, or some more complicated response function, which can involve ‘waiting times’ correlated with the offset introduced by the glitch, i.e. with the parameters of the glitch. Exponentials, power laws, and – occasionally – more complicated features are common in the inter-glitch behaviour of pulsars, indicating the presence of both linearly and non-linearly coupled regions. The most common manifestation of non-linear coupling is a roughly constant second derivative ( ), called ‘anomalous’ because its value is too large to be associated with n ∼ 3 dipole radiation torque, as the contribution of the internal torque is larger, and in many cases much larger than that of the external pulsar torque (Alpar & Baykal 2006). Such signatures are common in glitching pulsars (Yu et al. 2013; Lower et al. 2021; Gügercinoğlu et al. 2022; Zubieta et al. 2024; Liu et al. 2024), and are studied most extensively in the Vela pulsar (Alpar et al. 1984; Akbal et al. 2017; Gügercinoğlu et al. 2022; Grover et al. 2025).
), called ‘anomalous’ because its value is too large to be associated with n ∼ 3 dipole radiation torque, as the contribution of the internal torque is larger, and in many cases much larger than that of the external pulsar torque (Alpar & Baykal 2006). Such signatures are common in glitching pulsars (Yu et al. 2013; Lower et al. 2021; Gügercinoğlu et al. 2022; Zubieta et al. 2024; Liu et al. 2024), and are studied most extensively in the Vela pulsar (Alpar et al. 1984; Akbal et al. 2017; Gügercinoğlu et al. 2022; Grover et al. 2025).
The scale-free power laws arising from the internal torque can dominate the spin-down rate for an entire inter-glitch interval, and must be accounted for in order to find the contribution of the external torque and the actual braking index. A dataset containing many glitches, as in the case of PSR J0537−6910, makes it possible to calculate inter-glitch fits that extend all the way until the next glitch (Antonopoulou et al. 2018; Ferdman et al. 2018; Ho et al. 2020, 2022; Abbott et al. 2021b). Ignoring for a moment the effect of the external torque and any permanent changes, the measured  from such fits, together with the total increase in the spin-down rate observed at each glitch, gives a recovery timescale of
from such fits, together with the total increase in the spin-down rate observed at each glitch, gives a recovery timescale of 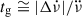 . This timescale can be interpreted as the waiting time for return to steady-state inside the neutron star, when conditions will be suitable for another glitch to occur (Alpar et al. 1984).
. This timescale can be interpreted as the waiting time for return to steady-state inside the neutron star, when conditions will be suitable for another glitch to occur (Alpar et al. 1984).
The vortex creep model (Alpar et al. 1984) explains the inter-glitch constant second derivative term quite naturally: In the presence of local pinning sites that hinder the free motion of vortices, the radially outward motion of vortex lines required to spin the superfluid down in response to the pulsar torque is achieved by thermal activation of vortices over pinning barriers. The process is highly non-linear because of Boltzmann factors that depend exponentially on the lag ω = Ωs − Ωc between the superfluid rotation rate (Ωs) and the crust rotation rate (Ωc). In the steady state, vortex creep sustains a radially outward current of vortices and thereby a continuous internal torque, i.e. angular momentum transfer, from superfluid to crust.
A glitch occurs when the difference between the local superfluid velocities and the rotation rate of the crustal normal matter becomes too large to be sustained by pinning forces. Unpinned vortices will move in the radially outward direction from the rotation axis. This results in a sudden transfer of angular momentum to the crust normal matter, observed as the glitch. The sudden decrease δΩ in the superfluid rotation rate and increase in the crust rotation rate reduces the lag, temporarily stopping the creep process. There is thus a sudden decrease in the internal torque (which is mediated by the creep process) on the crust, while the pulsar torque continues to spin the crust down. This results in an increase in the observed spin-down rate of the crust. The glitch-associated decrease (δΩ) in the superfluid rotation rate is proportional to the total number of unpinned vortices and relates to the size of the observed spin-up Δν. The total angular momentum transferred from the superfluid to the crust in a glitch is proportional to both δΩ and the moment of inertia of the distinct superfluid regions, including creep regions and vortex-depleted regions, through which the unpinned vortices have moved.
The vortex creep model also has a linear regime, prevailing in some superfluid regions whose response explains the prompt exponential relaxation and holds information on the temperature and pinning parameters. In PSR J0537−6910, in addition to the nearly constant  behaviour and the exponentials seen in 12 glitches, ten inter-glitch intervals show more complicated features. These are not addressed in the present paper, but can provide additional insights about the non-linear creep process and further estimates of the pinning parameters and local temperature. These detailed applications of the vortex creep model to PSR J0537−6910 are deferred to a separate paper (Gügercinoğlu & Alpar, in prep.).
behaviour and the exponentials seen in 12 glitches, ten inter-glitch intervals show more complicated features. These are not addressed in the present paper, but can provide additional insights about the non-linear creep process and further estimates of the pinning parameters and local temperature. These detailed applications of the vortex creep model to PSR J0537−6910 are deferred to a separate paper (Gügercinoğlu & Alpar, in prep.).
In addition to the recovering response of interior components to glitch-induced offsets, there can be permanent spin-down shifts. Persisting (but not necessarily permanent) shifts in the spin-down rate are seen for several pulsars. Using some of the Crab pulsar’s largest glitches, permanent changes with an average magnitude 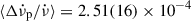 (Lyne et al. 2015), have been identified2. It has already been noted by Antonopoulou et al. (2018) that the cumulative effect of persistent shifts associated with glitches could explain the low (under 3 in general) inferred long-term braking indices for several glitching pulsars (Espinoza et al. 2017), including the negative effective braking index of PSR J0537−6910 (Antonopoulou et al. 2018). In this work, we considered the existence of true permanent shifts, which remain once the part of the initial glitch step
(Lyne et al. 2015), have been identified2. It has already been noted by Antonopoulou et al. (2018) that the cumulative effect of persistent shifts associated with glitches could explain the low (under 3 in general) inferred long-term braking indices for several glitching pulsars (Espinoza et al. 2017), including the negative effective braking index of PSR J0537−6910 (Antonopoulou et al. 2018). In this work, we considered the existence of true permanent shifts, which remain once the part of the initial glitch step 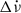 in spin-down rate has fully recovered due to both linear and non-linear internal torques (which lead to exponential and power-law-like recoveries, respectively). Note these permanent shifts differ from the measured persisting changes (
in spin-down rate has fully recovered due to both linear and non-linear internal torques (which lead to exponential and power-law-like recoveries, respectively). Note these permanent shifts differ from the measured persisting changes (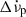 ) often given in the literature, which typically refer to all components of
) often given in the literature, which typically refer to all components of 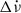 that do not recover exponentially. In most pulsars, measured
that do not recover exponentially. In most pulsars, measured 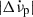 will thus contain a part that recovers under the rather stable
will thus contain a part that recovers under the rather stable  due to the non-linear internal torques, and will be larger than any true permanent shift. To make the distinction we shall use the notation
due to the non-linear internal torques, and will be larger than any true permanent shift. To make the distinction we shall use the notation 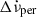 to denote true permanent shifts, with
to denote true permanent shifts, with 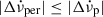 .
.
The Crab pulsar’s glitch behaviour, extensively discussed by Lyne et al. (2015) is unique. Post-glitch recoveries show exponential components but do not display the high  inter-glitch behaviour observed in PSR J0537−6910, the Vela and other pulsars. Long-term growing exponentials (in
inter-glitch behaviour observed in PSR J0537−6910, the Vela and other pulsars. Long-term growing exponentials (in 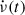 ), with τ = 320 days and initial amplitude
), with τ = 320 days and initial amplitude 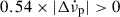 , settling to a permanent shift
, settling to a permanent shift 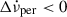 were seen following the 1975, 1989, and 2011 glitches, as described by Lyne et al. (2015, (in their Eq. (6), and displayed in their Fig. 3). They infer persistent shifts for ten Crab glitches in their Table 3 (there is a mistake in Eq. (6), which should contain the term
were seen following the 1975, 1989, and 2011 glitches, as described by Lyne et al. (2015, (in their Eq. (6), and displayed in their Fig. 3). They infer persistent shifts for ten Crab glitches in their Table 3 (there is a mistake in Eq. (6), which should contain the term 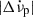 rather than
rather than 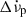 to reflect the behaviour shown in Fig. 3). Persistent shifts were already noted in the 1975 glitch (Demianski & Proszynski 1983) and in the 1989 glitch by Lyne et al. (1992) who also found the ‘wrong sign’ long-term exponential. As the next glitch often arrives long after the longest exponential component with τ ≅ 320 days has settled to its asymptotic value, the return to steady-state seems to be achieved before the arrival of the next glitch. Thus, the
to reflect the behaviour shown in Fig. 3). Persistent shifts were already noted in the 1975 glitch (Demianski & Proszynski 1983) and in the 1989 glitch by Lyne et al. (1992) who also found the ‘wrong sign’ long-term exponential. As the next glitch often arrives long after the longest exponential component with τ ≅ 320 days has settled to its asymptotic value, the return to steady-state seems to be achieved before the arrival of the next glitch. Thus, the 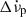 in the Crab appear to be permanent. In terms of the vortex creep model, the non-linear response of the internal torque in the Crab pulsar has a more complicated signature than the constant
in the Crab appear to be permanent. In terms of the vortex creep model, the non-linear response of the internal torque in the Crab pulsar has a more complicated signature than the constant  response because of the high internal temperature ACCP96. The observed behaviour led to the idea that permanent shifts occur simultaneously with Crab glitches, possibly associated with crust breaking and motion of crustal plates, leading to formation of new vortex traps or vortex depleted regions; in this scenario the ‘wrong sign’ exponential is explained qualitatively by plate motion towards the rotation axis, inducing inward vortex motion (Alpar et al. 1994, 1996; Gügercinoğlu & Alpar 2019).
response because of the high internal temperature ACCP96. The observed behaviour led to the idea that permanent shifts occur simultaneously with Crab glitches, possibly associated with crust breaking and motion of crustal plates, leading to formation of new vortex traps or vortex depleted regions; in this scenario the ‘wrong sign’ exponential is explained qualitatively by plate motion towards the rotation axis, inducing inward vortex motion (Alpar et al. 1994, 1996; Gügercinoğlu & Alpar 2019).
Since PSR J0537−6910 is a young pulsar with similarly high spin and spin-down rate as the Crab, the temperature profile inside these neutron stars and the crustal and superfluid pinning stresses could also be similar for the two pulsars. It is, therefore, plausible that PSR J0537−6910 glitches can also result in permanent shifts like those observed from the Crab pulsar, likely to be due to sustained structural changes inside the neutron star that permanently affect the rotational dynamics of some superfluid components. This could be common if the vortex unpinning events take place in conjunction with crust breaking and formation of pinned vortex traps in crustal superfluid components, and such models have been employed for PSR J1119−6127 (Akbal et al. 2015), PSR J1048−5832 (Liu et al. 2025) and the Crab pulsar (Gügercinoğlu & Alpar 2019). For both the Crab and Vela pulsars, model-dependent estimates of the time to the next glitch improve significantly when permanent shifts of magnitude 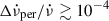 are assumed (Akbal et al. 2017; Gügercinoğlu & Alpar 2020). Note that whilst the inferred
are assumed (Akbal et al. 2017; Gügercinoğlu & Alpar 2020). Note that whilst the inferred 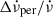 is an order of magnitude larger for the Vela pulsar than the corresponding fraction in the Crab pulsar, the permanent
is an order of magnitude larger for the Vela pulsar than the corresponding fraction in the Crab pulsar, the permanent 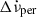 shifts are similar since the Crab slows down about 25 times faster than Vela.
shifts are similar since the Crab slows down about 25 times faster than Vela.
4. Model
Glitches in PSR J0537−6910 have typical magnitudes Δν/ν = a few × 10−7 and 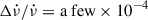 and happen approximately every ∼100 days. To obtain the contribution to the inter-glitch
and happen approximately every ∼100 days. To obtain the contribution to the inter-glitch  of the external braking torque from the pulsar’s magnetosphere (hereafter
of the external braking torque from the pulsar’s magnetosphere (hereafter 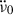 ) and the equivalent braking index, the glitch contributions (in the form of both recovering and permanent components) should be assessed and removed. Our approach involves two ingredients:
) and the equivalent braking index, the glitch contributions (in the form of both recovering and permanent components) should be assessed and removed. Our approach involves two ingredients:
(i) Most inter-glitch intervals display a roughly constant 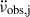 (the subscript j indicates this is for the inter-glitch interval after glitch j), which can be measured from observations. This trend can be decomposed in two components, corresponding to the external and internal torque contributions, as
(the subscript j indicates this is for the inter-glitch interval after glitch j), which can be measured from observations. This trend can be decomposed in two components, corresponding to the external and internal torque contributions, as 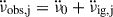 , in which
, in which 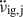 reflects the superfluid response.
reflects the superfluid response.
(ii) The total spin-down rate change 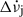 contains a part that recovers during the inter-glitch interval after glitch j, denoted
contains a part that recovers during the inter-glitch interval after glitch j, denoted 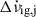 , and a persisting part that has not recovered when the next glitch occurs and might be permanent:
, and a persisting part that has not recovered when the next glitch occurs and might be permanent: 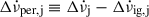 . The cumulative effect of frequent shifts that persist at the time of the next glitch could cause the effective negative braking index of PSR J0537−6910, as noted by Antonopoulou et al. (2018) and Ferdman et al. (2018).
. The cumulative effect of frequent shifts that persist at the time of the next glitch could cause the effective negative braking index of PSR J0537−6910, as noted by Antonopoulou et al. (2018) and Ferdman et al. (2018).
The glitches and persistent changes do not appear associated with changes in the electromagnetic signature of the pulsar, such as profile shape or intensity changes (Ferdman et al. 2018). Therefore, any permanent shifts likely reflect structural changes in the interior of the neutron star, namely in the solid crust. The natural physical model for such sudden and permanent structural changes is the star-quake model (Baym & Pines 1971). However, the overall glitch activity cannot be understood in terms of crust-quakes alone (see e.g. Antonopoulou et al. 2022 and Zhou et al. 2022) and requires the involvement of the internal superfluid (see e.g. the explanation in terms of vortex unpinning in Alpar et al. 1993 and Alpar 1995). Crust breaking associated with permanent shifts in the spin-down rate at the time of a glitch may be what triggers the sudden vortex unpinning, which in turn results in the angular momentum transfer to the outer crust observed as the glitch.
In this work we made the assumption (discussed further in the following) that a glitch takes place when the relaxation from the previous glitch due to the internal torques is complete, i.e. the recovery under 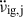 stops at the epoch of glitch j + 1 and any remaining shifts in
stops at the epoch of glitch j + 1 and any remaining shifts in  are truly permanent. Making use of the θ (or Heaviside) function, θ(t) = 0 for t < 0, and θ(t) = 1 for t ≥ 0, we can then express the spin-down rate evolution over a time span including a total of Ng glitches, with recovering and permanent components, occurring at times tj:
are truly permanent. Making use of the θ (or Heaviside) function, θ(t) = 0 for t < 0, and θ(t) = 1 for t ≥ 0, we can then express the spin-down rate evolution over a time span including a total of Ng glitches, with recovering and permanent components, occurring at times tj:
where 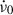 is a fiducial value and
is a fiducial value and 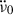 its (not directly observable) associated derivative based on the external dipole braking model. The first two terms then describe the evolution due to the external torque, whilst the rest are the glitch-associated changes. The third term, with
its (not directly observable) associated derivative based on the external dipole braking model. The first two terms then describe the evolution due to the external torque, whilst the rest are the glitch-associated changes. The third term, with 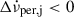 , represents the permanent shifts, whilst the two last terms are the recovering components due to the internal superfluid torques:
, represents the permanent shifts, whilst the two last terms are the recovering components due to the internal superfluid torques: 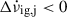 are the changes that recover with rate
are the changes that recover with rate 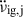 during the interval tg, j ≡ tj + 1 − tj until the next glitch j + 1, and
during the interval tg, j ≡ tj + 1 − tj until the next glitch j + 1, and 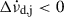 represent the exponentially recovering components.
represent the exponentially recovering components.
The total step increase in the spin-down rate observed at glitch j is the sum of the persistent component and the recovering components:
where the epoch tj+ is immediately after the glitch at time tj. The exponentially recovering components are not considered in this work, as they are not apparent in all glitches and, when measured, carry large uncertainties. Nonetheless, the inferred decay timescales (τ) are under 40 d, so the later inter-glitch evolution will be dominated by the constant  terms. The approach can be generalised to include exponentials in cases where it might prove necessary.
terms. The approach can be generalised to include exponentials in cases where it might prove necessary.
It is reasonable to expect that the time of completion of the inter-glitch recovery is close to the time of occurrence of the next glitch on average. This is because – even though the actual glitch trigger can have a stochastic component – physical conditions in the neutron star should be similar at the start of each glitch, given the regularity and similarity of their signatures in this pulsar. Moreover, it was observed for a sample of several pulsars that their average glitch waiting times scale with (and are in fact, very close to) their average 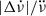 , further supporting this idea (Lower et al. 2021; Liu et al. 2024), and Ho et al. (2020, 2022) reported a similar correlation between
, further supporting this idea (Lower et al. 2021; Liu et al. 2024), and Ho et al. (2020, 2022) reported a similar correlation between 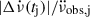 and the time tg, j from glitch j to the next glitch, j + 1 for PSR J0537−6910 specifically. We therefore made the aforementioned simplifying assumption, that the inter-glitch recovery is completed exactly at the time when the next glitch arrives. The full recovery of
and the time tg, j from glitch j to the next glitch, j + 1 for PSR J0537−6910 specifically. We therefore made the aforementioned simplifying assumption, that the inter-glitch recovery is completed exactly at the time when the next glitch arrives. The full recovery of 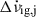 in the time interval tg, j ≡ tj + 1 − tj until the next glitch means that the contribution to
in the time interval tg, j ≡ tj + 1 − tj until the next glitch means that the contribution to  of the internal torque is
of the internal torque is
Unfortunately, the recovering and permanent parts 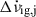 and
and 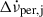 of the glitch step in the spin-down rate cannot be separately inferred from the data, even under the assumption that
of the glitch step in the spin-down rate cannot be separately inferred from the data, even under the assumption that 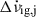 fully recovers exactly before the next glitch, because of the unknown external torque contribution. If, however, we assume a constant value of the permanent shift for all glitches, then we can estimate the relaxing part
fully recovers exactly before the next glitch, because of the unknown external torque contribution. If, however, we assume a constant value of the permanent shift for all glitches, then we can estimate the relaxing part 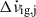 of the glitch step
of the glitch step 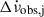 in glitch j as
in glitch j as
and use it in Eq. (3) to approximate 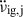 . Subtracting this internally driven
. Subtracting this internally driven 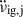 from the total observed
from the total observed 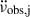 , gives
, gives 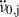 due to the external pulsar torque:
due to the external pulsar torque:
from which the braking index can be found. Equivalently, assuming a value for the braking index, the necessary permanent changes can be calculated. The effects of the external and internal torques and glitch-induced step changes in 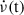 are sketched in Fig. 1.
are sketched in Fig. 1.
 |
Fig. 1. Upper panel: Model for the inter-glitch evolution of |
After many glitches, over the entire time span of the observations, Eq. (1) reduces to
The second sum in Eq. (1), which describes the recovering part of the glitch-induced steps in the spin-down rate, is zero based on our assumption of complete recoveries. Thus, it is the sum of the permanent shifts 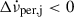 over all glitches that results in the negative long-term slope of
over all glitches that results in the negative long-term slope of 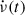 , despite a positive
, despite a positive 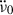 arising from the external (pulsar) torque.
arising from the external (pulsar) torque.
5. Results
In the following we use a sample of 32 glitches for which 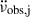 and
and 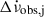 are relatively accurately measured. We chose to exclude glitches with uncertainties larger than 50% in either of these quantities. This criterion leaves 23 RXTE and 9 NICER glitches, whose properties are given in the first 3 columns of Table 1. The average inter-glitch interval for this sample is ⟨tg⟩≅ 122 days, with an rms deviation of 12 days. For a nominal value of the underlying braking index, taken as n = 3 in this instance, we used the observed parameters and Eqs. (3), (4), and 5) of the model to calculate the values of the permanent shifts
are relatively accurately measured. We chose to exclude glitches with uncertainties larger than 50% in either of these quantities. This criterion leaves 23 RXTE and 9 NICER glitches, whose properties are given in the first 3 columns of Table 1. The average inter-glitch interval for this sample is ⟨tg⟩≅ 122 days, with an rms deviation of 12 days. For a nominal value of the underlying braking index, taken as n = 3 in this instance, we used the observed parameters and Eqs. (3), (4), and 5) of the model to calculate the values of the permanent shifts 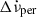 and
and 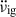 for these glitches, which are also presented in Table 1.
for these glitches, which are also presented in Table 1.
Glitch observables 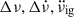 , and tg along with the values for persistent shift (
, and tg along with the values for persistent shift (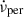 ) corresponding to a braking index (n) of 3.
) corresponding to a braking index (n) of 3.
If the long-term apparent braking index n′ is due to permanent shifts, we can calculate how big – on average – they must be, to bring an actual braking index of n due to the external torque down to the observed negative n′ value. The difference in  yields – from Eqs. (4), (3) and (5) and a given n – the average permanent shift needed:
yields – from Eqs. (4), (3) and (5) and a given n – the average permanent shift needed:
where 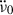 is the expected value for a spin-down law with a constant braking index (n).
is the expected value for a spin-down law with a constant braking index (n).
For the long-term n′, we used the value n′= − 1.234(9), corresponding to 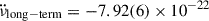 Hz s−2, measured by Ho et al. (2022) from a linear fit to the combined RXTE and NICER data. We, moreover, took the reference value n = 3, an average inter-glitch interval of ⟨tg⟩≅ 122 days, and a typical
Hz s−2, measured by Ho et al. (2022) from a linear fit to the combined RXTE and NICER data. We, moreover, took the reference value n = 3, an average inter-glitch interval of ⟨tg⟩≅ 122 days, and a typical 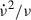 , and find that the average permanent shifts must be about
, and find that the average permanent shifts must be about 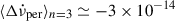 Hz s−1. This result is not very sensitive to the chosen value of the braking index n; for a range of 1 ≤ n ≤ 7 the corresponding required average permanent shifts vary from −1.5 to −5.5 ×10−14 Hz s−1. In general, the required average
Hz s−1. This result is not very sensitive to the chosen value of the braking index n; for a range of 1 ≤ n ≤ 7 the corresponding required average permanent shifts vary from −1.5 to −5.5 ×10−14 Hz s−1. In general, the required average 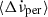 for the theoretically predicted range of magnetosphere-driven braking models (see e.g. Melatos 1997; Ruderman et al. 1998; Yan et al. 2012; Arzamasskiy et al. 2015; Ekşi et al. 2016; Zhang et al. 2022) are typically a modest fraction of the total change
for the theoretically predicted range of magnetosphere-driven braking models (see e.g. Melatos 1997; Ruderman et al. 1998; Yan et al. 2012; Arzamasskiy et al. 2015; Ekşi et al. 2016; Zhang et al. 2022) are typically a modest fraction of the total change 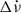 (quoted in Table 1). An upper limit for the permanent shifts can be obtained from the persistent steps: after the first glitch, for which the exponential decay can be accounted for, the persisting change is found to be
(quoted in Table 1). An upper limit for the permanent shifts can be obtained from the persistent steps: after the first glitch, for which the exponential decay can be accounted for, the persisting change is found to be 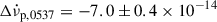 Hz s−1 (Antonopoulou et al. 2018). In the limiting case where the average permanent shifts are as large as the observed persisting one, the underlying braking index would be 9.
Hz s−1 (Antonopoulou et al. 2018). In the limiting case where the average permanent shifts are as large as the observed persisting one, the underlying braking index would be 9.
For comparison with possible permanent shifts in other pulsars, the ratio 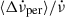 may be the relevant quantity, as it gives an effective fractional moment of inertia of the component responsible. In the Crab pulsar, the average of the persistent steps reported by Lyne et al. (2015) for ten glitches is
may be the relevant quantity, as it gives an effective fractional moment of inertia of the component responsible. In the Crab pulsar, the average of the persistent steps reported by Lyne et al. (2015) for ten glitches is 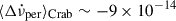 Hz s−1, which gives a fractional change of
Hz s−1, which gives a fractional change of 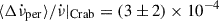 . This value is rather close to the value we infer for PSR J0537−6910 under an assumed n = 3:
. This value is rather close to the value we infer for PSR J0537−6910 under an assumed n = 3: 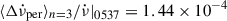 . For the Vela pulsar, Akbal et al. (2017) calculated the required permanent shifts in a model-dependent way, by assuming the same glitch signature as in Eq. (1) and calculating the average
. For the Vela pulsar, Akbal et al. (2017) calculated the required permanent shifts in a model-dependent way, by assuming the same glitch signature as in Eq. (1) and calculating the average 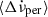 that minimises the difference between observed and predicted (assuming full recovery) glitch epochs. They obtained
that minimises the difference between observed and predicted (assuming full recovery) glitch epochs. They obtained 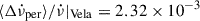 , which is an order of magnitude larger than the Crab and PSR J0537−6910 results3. However, their inferred
, which is an order of magnitude larger than the Crab and PSR J0537−6910 results3. However, their inferred 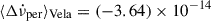 Hz s−1 is very similar to the ones we find for PSR J0537−6910. Similarly to the upper bound we obtain on
Hz s−1 is very similar to the ones we find for PSR J0537−6910. Similarly to the upper bound we obtain on 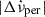 from observations of the first PSR J0537−6910 glitch, a limit for the permanent changes in Vela can be found from the observed persisting shifts (once exponentials have been removed). Using the persisting changes measured by Yu et al. (2013) for four Vela glitches, we find the limit
from observations of the first PSR J0537−6910 glitch, a limit for the permanent changes in Vela can be found from the observed persisting shifts (once exponentials have been removed). Using the persisting changes measured by Yu et al. (2013) for four Vela glitches, we find the limit 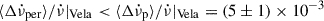 . It is thus conceivable that permanent changes such as the ones we assumed here occur in young glitching pulsars.
. It is thus conceivable that permanent changes such as the ones we assumed here occur in young glitching pulsars.
These considerations provide proof of concept that the irregular rotational evolution of PSR J0537−6910 can be explained by a regular underlying braking index, for instance n ∼ 1 − 7, and the effects of its glitches alone. The high inter-glitch braking indices are a result of the internal superfluid torque that dominates until the next glitch, whilst the anomalous long-term negative n′ is the cumulative result of glitch-related, abrupt permanent shifts with physically plausible magnitudes that can be accommodated by the timing data.
6. When is the next glitch due?
Within our model, given a chosen 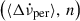 set of values obeying Eq. (7), one can deduct the contribution of the internal torque
set of values obeying Eq. (7), one can deduct the contribution of the internal torque 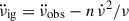 . If the last glitch of the pulsar has a measured
. If the last glitch of the pulsar has a measured 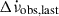 and we assume it involved a permanent shift of order
and we assume it involved a permanent shift of order 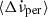 , then the recovering part is estimated as
, then the recovering part is estimated as 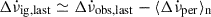 . From these we can estimate the time it takes for a full recovery:
. From these we can estimate the time it takes for a full recovery:
in which we substituted 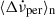 from Eq. (7). This timescale approximates the waiting time until the next glitch.
from Eq. (7). This timescale approximates the waiting time until the next glitch.
Another estimate of the time to the next glitch can be found using the vortex creep model. The sudden motion of unpinned vortices in the glitch transfers angular momentum from the superfluid to the crust. Equating the angular momentum transfer from the superfluid to the angular momentum change of the crust (manifested as the observed glitch), and relating the moments of inertia of the vortex creep and vortex-depleted superfluid regions with the step in the spin-down rate gives (Alpar et al. 1984)
where δνj is the decrease in the superfluid rotation frequency resulting from the sudden vortex motion driving the spin-up Δνj. In the vortex creep model 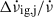 is interpreted as the fractional moment of inertia, denoted IA/I, of the vortex creep regions where vortices ‘creep’ against background of pinning sites, and βj is a model parameter representing the ratio of the moments of inertia of the vortex-depleted superfluid regions (whose fractional moment of inertia is denoted by IB/I in the vortex creep literature) to those regions that contain creeping vortices (Cheng et al. 1988; Alpar & Baykal 2006).
is interpreted as the fractional moment of inertia, denoted IA/I, of the vortex creep regions where vortices ‘creep’ against background of pinning sites, and βj is a model parameter representing the ratio of the moments of inertia of the vortex-depleted superfluid regions (whose fractional moment of inertia is denoted by IB/I in the vortex creep literature) to those regions that contain creeping vortices (Cheng et al. 1988; Alpar & Baykal 2006).
The next glitch is expected to occur roughly when the offset lag between the superfluid and the crust-normal matter rotation rates is recovered by the spin-down of the crust-normal matter. This leads to the estimation 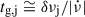 and to the second, approximate, equality in Eq. (9). Using Eqs. (3), (5), and (7) and assuming that the parameter βj = β, a constant representative value for all glitches, we obtain
and to the second, approximate, equality in Eq. (9). Using Eqs. (3), (5), and (7) and assuming that the parameter βj = β, a constant representative value for all glitches, we obtain
In the case of PSR J0537−6910, assuming n = 3 and the glitches in Table 1, a fit of Eq. (10) returns β = 18.4. This is much larger than inferred β parameters for other pulsars, which was found to vary from as low as ≲0.5 for the Crab and two more pulsars (Gügercinoğlu & Alpar 2019; Gügercinoğlu et al. 2022) up to ≅5 for other sources (Liu et al. 2024, 2025). The difference in inferred β for this pulsar poses some question for the interpretation within the creep model, but in principle β could be used in Eq. (10) together with Δνlast and 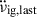 following the last glitch, to approximate tg, next.
following the last glitch, to approximate tg, next.
Even though none of the current observed (Ho et al. 2020; Lower et al. 2021; Liu et al. 2024) or theoretical correlations provides a very tight estimate of the time of a future glitch, the predictability of glitches in this pulsar can be used for targeted observations. The strong correlation between Δνobs, j and tg, j that is well established for this pulsar (Middleditch et al. 2006; Antonopoulou et al. 2018) gives a typical uncertainty window around 10–20 d for the time of the next glitch, assuming good coverage to accurately measure the Δν of the previous glitch (Ho et al. 2020, 2022).
7. Discussion and conclusions
We have studied the timing behaviour of the source PSR J0537−6910, which is unique in terms of its many glitches, using published timing fits (Antonopoulou et al. 2018; Ho et al. 2020, 2022; Abbott et al. 2021a) that measure a high, relatively constant, inter-glitch frequency second derivative 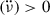 and an effective
and an effective 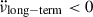 inferred from the decrease in
inferred from the decrease in  in the long term. We propose that the apparent long-term negative
in the long term. We propose that the apparent long-term negative 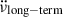 of PSR J0537−6910 arises from permanent, non-relaxing steps in the spin-down rate associated with each glitch, like the persistent shifts observed in the Crab pulsar (Lyne et al. 2015) and inferred for the Vela pulsar (Akbal et al. 2017) and for PSRs J1119-6127 (Akbal et al. 2015) and J1048–5832 (Liu et al. 2025). The separate effects of the external torque, the internal torque, and that of permanent
of PSR J0537−6910 arises from permanent, non-relaxing steps in the spin-down rate associated with each glitch, like the persistent shifts observed in the Crab pulsar (Lyne et al. 2015) and inferred for the Vela pulsar (Akbal et al. 2017) and for PSRs J1119-6127 (Akbal et al. 2015) and J1048–5832 (Liu et al. 2025). The separate effects of the external torque, the internal torque, and that of permanent  changes cannot be extracted from the timing evolution. Making a justified approximation, however, that a glitch occurs when the recovery (both exponential and power-law-like) from the previous glitch is completed, we find a relationship between the braking index (n) of the external torque and the averaged required permanent changes that will produce the effective
changes cannot be extracted from the timing evolution. Making a justified approximation, however, that a glitch occurs when the recovery (both exponential and power-law-like) from the previous glitch is completed, we find a relationship between the braking index (n) of the external torque and the averaged required permanent changes that will produce the effective 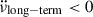 over the years. Adopting an underlying pulsar torque of braking index n ∼ 3 yields the permanent shift values
over the years. Adopting an underlying pulsar torque of braking index n ∼ 3 yields the permanent shift values 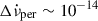 Hz s−1 listed in Table 1, with an average value
Hz s−1 listed in Table 1, with an average value 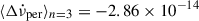 Hz s−1, of a similar order of magnitude as those inferred for the Crab and Vela pulsars. The fractional permanent changes inferred for the Vela pulsar are an order of magnitude larger, which is interpreted as indicating a larger connected network of vortex traps in the Vela pulsar (Akbal et al. 2017).
Hz s−1, of a similar order of magnitude as those inferred for the Crab and Vela pulsars. The fractional permanent changes inferred for the Vela pulsar are an order of magnitude larger, which is interpreted as indicating a larger connected network of vortex traps in the Vela pulsar (Akbal et al. 2017).
Thus, we have shown that internal torques combined with permanent shifts and external pulsar torques with braking indices not far from the canonical value of 3 suffice to explain the timing behaviour of PSR J0537−6910. We have based our discussion of the time between glitches on the expectation that the next glitch occurs at about the time when internal torques have recovered to pre-glitch equilibrium conditions. However, the requirement of permanent shifts in the spin-down rate suggests a possible rearrangement of the crust geometry in relation to the glitches. Crust breaking could be initiating local vortex unpinning, which then evolves into a large vortex avalanche and observed glitch, when the internal conditions are appropriate. Middleditch et al. (2006) discuss possible crust-quakes in PSR J0537−6910 in connection to its glitches, and crust failure is often suggested as a possible glitch trigger to explain the scale-invariant glitch size distributions seen in some pulsars like the Crab. Conversely, additional stresses to the crust by the pinned vortices could initiate both a crust-quake (Ruderman 1991) and (subsequent) large-scale unpinning when the superfluid lag grows large. The breaking and moving of a plate has also been invoked to explain some glitch signatures (and associated emission changes) in the highly magnetised pulsar PSR J1119−6127 akbal15; (Akbal & Alpar 2018). Such local breaking requires a non-axisymmetric treatment of elastic deformations, along the lines of recent work by Gangwar & Jones (2024) on mountains on neutron stars. A detailed discussion of the stresses induced by vortex pinning, the building of a vortex avalanche starting with vortices unpinned from a specific broken crustal plate, the motion of unpinned vortices under dissipative interactions with electrons, and their encounters with vortex traps (clusters) to unpin more vortices will be the subject of a separate paper (Gügercinoğlu & Alpar, in prep.). Here we just note in passing that the size of a broken plate, like the maximum height of a mountain above the neutron star surface, determines a local, non-axisymmetric deformation, which can source gravitational wave emission (Chamel & Haensel 2008; Gangwar & Jones 2024).
The large inter-glitch braking indices seen for PSR J0537−6910 (Antonopoulou et al. 2018; Ferdman et al. 2018) have also evoked the idea of possible emission of gravitational waves arising from internal fluid motions from r-modes (Andersson et al. 2018) or crustal deformations (Cutler 2002), which give predicted braking indices (n) of 7 and 5, respectively. Such contributions to the spin-down evolution are not ruled out by the current analysis. The expected gravitational wave strain amplitude from r-modes was estimated as h ∼ 2 − 3 × 10−26 (Andersson et al. 2018). Initial searches with the third LIGO (Laser Interferometer Gravitational-Wave Observatory)/Virgo survey have failed to detect gravitational radiation associated with PSR J0537−6910 (Fesik & Papa 2020; Abbott et al. 2021a,b, 2022). The most recent fourth LIGO-Virgo-KAGRA (Kamioka Gravitational Wave Detector) observing run (Abac et al. 2025), which covered the time span containing recent glitches of PSR J0537−6910 reported by Ho et al. (2020), place a constraining upper limit of h ≲ 10−26 for the gravitational wave strain amplitude. It remains imperative to discover if gravitational wave emission contributes to the braking of PSR J0537−6910, which – together with continuous monitoring in the X-rays – can significantly alter inferences for the internal and magnetospheric torques of this pulsar.
Frequent monitoring of PSR J0537−6910 is also vital to better characterising its glitches for use as input in theoretical calculations. Model-dependent analyses and simulations can help resolve the ambiguity in separating any permanent shifts in spin-down rate and the ongoing power-law recovery due to internal torques. In the framework of the vortex creep model, this can lead to estimates of the time to the next glitch; a complete analysis of the superfluid recovery contributing to the constant  behaviour, as well as the prompt exponential post-glitch relaxations, can yield information on the moments of inertia of the interior components involved, on the temperature, and on superfluid vortex pinning. Likewise, the reported correlations between glitch size and the time interval to the next glitch (Antonopoulou et al. 2018; Ferdman et al. 2018; Ho et al. 2020; Liu et al. 2024) is used to estimate superfluid moments of inertia and the angular momentum exchange at glitches (Gügercinoğlu & Alpar, in prep.).
behaviour, as well as the prompt exponential post-glitch relaxations, can yield information on the moments of inertia of the interior components involved, on the temperature, and on superfluid vortex pinning. Likewise, the reported correlations between glitch size and the time interval to the next glitch (Antonopoulou et al. 2018; Ferdman et al. 2018; Ho et al. 2020; Liu et al. 2024) is used to estimate superfluid moments of inertia and the angular momentum exchange at glitches (Gügercinoğlu & Alpar, in prep.).
As a final remark we would like to call attention to possible glitch-induced variations in pulse profile or emission properties. A handful of pulsars exhibited pulse profile changes associated with glitches (see e.g. Table 1 in Zhou et al. 2023). In particular, the best glitch resolved to date, the 2016 Vela glitch, displayed clear polarisation level variations and a nulling pulse around the spin-up (Palfreyman et al. 2018). These ephemeral changes might also point to a glitch-accompanying crust-quake, which can move the footpoints of the magnetic field lines close to the polar cap (Akbal et al. 2015) and release seismic energy into the magnetosphere (Bransgrove et al. 2020). While these short-lived and ephemeral changes observed at radio wavelengths are expected to arise from perturbations in the emission regions just above the polar cap, the origin of the X-rays likely lies in the outer gaps at much higher altitudes in the magnetosphere (Philippov & Kramer 2022). Because PSR J0537−6910 is only seen in X-rays, detecting a glitch-associated pulse profile variation could be more difficult; however, the predictability of a forthcoming glitch in PSR J0537−6910 can be used to plan future targeted observations.
Acknowledgments
We acknowledge the Scientific and Technological Research Council of Turkey (TÜBİTAK) for support under the grant 117F330. EG is supported by the Doctor Foundation of Qingdao Binhai University (No. BJZA2025025) and National Natural Science Foundation of China (NSFC) programme 11988101 under the Foreign Talents Grant QN2023061004L. D.A. acknowledges support from an EPSRC/STFC fellowship (EP/T017325/1). We thank the anonymous referee for many constructive comments and suggestions, that helped to improve the clarity of this article.
References
- Abac, A. G., Abbott, R., Abouelfettouh, I., et al. 2025, ApJ, 983, 99 [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2021a, ApJ, 913, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2021b, ApJ, 922, 71 [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2022, ApJ, 935, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Akbal, O., & Alpar, M. A. 2018, MNRAS, 473, 621 [Google Scholar]
- Akbal, O., Gügercinoğlu, E., Şaşmaz, Muş S., & Alpar, M. A. 2015, MNRAS, 449, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Akbal, O., Alpar, M. A., Buchner, S., & Pines, D. 2017, MNRAS, 469, 4183 [Google Scholar]
- Alpar, M. A. 1989, NATO Advanced Study Institute (ASI) Series C Proceedings, Timing Neutron Stars, 431 [Google Scholar]
- Alpar, M. A. 1995, NATO Advanced Study Institute (ASI) Series C Proceedings, Lives of the Neutron Stars, 185 [Google Scholar]
- Alpar, M. A., & Baykal, A. 2006, MNRAS, 372, 489 [Google Scholar]
- Alpar, M. A., Anderson, P. W., Pines, D., & Shaham, J. 1984, ApJ, 276, 325 [Google Scholar]
- Alpar, M. A., Chau, H. F., Cheng, K. S., & Pines, D. 1993, ApJ, 409, 345 [Google Scholar]
- Alpar, M. A., Chau, H. F., Cheng, K. S., & Pines, D. 1994, ApJ, 427, L29 [Google Scholar]
- Alpar, M. A., Chau, H. F., Cheng, K. S., & Pines, D. 1996, ApJ, 459, 706 [Google Scholar]
- Andersson, N., Antonopoulou, D., Espinoza, C. M., Haskell, B., & Ho, W. C. G. 2018, ApJ, 864, 137 [Google Scholar]
- Antonelli, M., Montoli, A., & Pizzochero, P. M. 2022, in Astrophysics in the XXI Century with Compact Stars, ed. C. A. Z. Vasconcellos (Singapore: World Scientific), 219 [Google Scholar]
- Antonopoulou, D., Espinoza, C. M., Kuiper, L., & Andersson, N. 2018, MNRAS, 473, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Antonopoulou, D., Haskell, B., & Espinoza, C. M. 2022, RPPh, 85, 126901 [Google Scholar]
- Arzamasskiy, L., Philippov, A., & Tchekhovskoy, A. 2015, MNRAS, 453, 3540 [Google Scholar]
- Baym, G., & Pines, D. 1971, AnPhy, 66, 816 [Google Scholar]
- Bransgrove, A., Beloborodov, A. M., & Levin, Y. 2020, ApJ, 897, 173 [Google Scholar]
- Chamel, N., & Haensel, P. 2008, LRR, 11 [Google Scholar]
- Chen, Y., Wang, Q. D., Gotthelf, E. V., et al. 2006, ApJ, 651, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Alpar, M. A., Pines, D., & Shaham, J. 1988, ApJ, 330, 835 [Google Scholar]
- Crawford, F. 2024, ApJ, 968, 99 [Google Scholar]
- Cutler, C. 2002, Phys. Rev. D, 66, 084025 [NASA ADS] [CrossRef] [Google Scholar]
- Demianski, M., & Proszynski, M. 1983, MNRAS, 202, 437 [Google Scholar]
- Ekşi, K. Y., Andaç, I. C., Çıkıntoğlu, S., et al. 2016, ApJ, 823, 34 [Google Scholar]
- Espinoza, C. M., Lyne, A. G., & Stappers, B. W. 2017, MNRAS, 466, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Ferdman, R. D., Archibald, R. F., Gourgouliatos, K. N., & Kaspi, V. M. 2018, ApJ, 852, 123 [Google Scholar]
- Fesik, L., & Papa, M. A. 2020, ApJ, 895, 11 [Google Scholar]
- Gangwar, Y., & Jones, D. I. 2024, MNRAS, 532, 2763 [Google Scholar]
- Grover, H., Gügercinoğlu, E., Joshi, B. C., et al. 2025, arXiv e-prints [arXiv:2506.02100] [Google Scholar]
- Gügercinoğlu, E. 2017, MNRAS, 469, 2313 [Google Scholar]
- Gügercinoğlu, E., & Alpar, M. A. 2019, MNRAS, 488, 2275 [CrossRef] [Google Scholar]
- Gügercinoğlu, E., & Alpar, M. A. 2020, MNRAS, 496, 2506 [CrossRef] [Google Scholar]
- Gügercinoğlu, E., Ge, M. Y., Yuan, J. P., & Zhou, S. Q. 2022, MNRAS, 511, 425 [CrossRef] [Google Scholar]
- Haskell, B., & Melatos, A. 2015, Int. J. Mod. Phys. D, 24, 1530008 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, W. C. G., Espinoza, C. M., Arzoumanian, Z., et al. 2020, MNRAS, 498, 4605 [Google Scholar]
- Ho, W. C. G., Kuiper, L., Espinoza, C. M., et al. 2022, ApJ, 939, 7 [Google Scholar]
- Liu, P., Yuan, J.-P., Ge, M.-Y., et al. 2024, MNRAS, 533, 4274 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Keith, M. J., Antonopoulou, D., et al. 2024, MNRAS, 532, 859 [Google Scholar]
- Liu, P., Yuan, J.-P., Ge, M.-Y., et al. 2025, MNRAS, 537, 1720 [Google Scholar]
- Lower, M. E., Johnston, S., Dunn, L., et al. 2021, MNRAS, 508, 3251 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Graham, Smith F., & Pritchard, R. S. 1992, Nature, 359, 706 [Google Scholar]
- Lyne, A. G., Jordan, C. A., Graham-Smith, F., et al. 2015, MNRAS, 446, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, F. E., Gotthelf, E. V., Zhang, W., Middleditch, J., & Wang, Q. D. 1998, ApJ, 499, L179 [Google Scholar]
- Marshall, F. E., Gotthelf, E. V., Middleditch, J., Wang, Q. D., & Zhang, W. 2004, ApJ, 603, 682 [Google Scholar]
- Melatos, A. 1997, MNRAS, 288, 1049 [Google Scholar]
- Middleditch, J., Marshall, F. E., Wang, Q. D., Gotthelf, E. V., & Zhang, W. 2006, ApJ, 652, 1531 [Google Scholar]
- Palfreyman, J., Dickey, J. M., Hotan, A., Ellingsen, S., & van Straten, W. 2018, Nature, 556, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Philippov, A., & Kramer, M. 2022, ARA&A, 60, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200 [Google Scholar]
- Ruderman, M. 1991, ApJ, 492, 267 [Google Scholar]
- Ruderman, M., Zhu, T., & Chen, K. 1998, ApJ, 492, 267 [Google Scholar]
- Yan, T., Perna, R., & Soria, R. 2012, MNRAS, 423, 2451 [Google Scholar]
- Yu, M., Manchester, R. N., Hobbs, G., et al. 2013, MNRAS, 429, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, C.-M., Cui, X.-H., Li, D., et al. 2022, Universe, 8, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, S., Gügercinoğlu, E., Yuan, J., Ge, M., & Yu, C. 2022, Universe, 8, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, S. Q., Gügercinoğlu, E., Yuan, J. P., et al. 2023, MNRAS, 519, 74 [Google Scholar]
- Zubieta, E., Missel, R., Sosa, Fiscella V., et al. 2023, MNRAS, 521, 4504 [Google Scholar]
- Zubieta, E., García, F., del Palacio, S., et al. 2024, A&A, 689, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zubieta, E., Espinoza, C. M., Antonopoulou, D., et al. 2026, A&A, 706, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Derived from Lyne et al. (2015), their Eq. (6) and Table 3, where a truly persistent term must be delineated from an exponentially decaying term.
The difference could be because the older Vela pulsar has accumulated a larger network of vortex trap sites that trigger glitches (Cheng et al. 1988; Alpar et al. 1993).
All Tables
Glitch observables 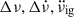 , and tg along with the values for persistent shift (
, and tg along with the values for persistent shift (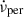 ) corresponding to a braking index (n) of 3.
) corresponding to a braking index (n) of 3.
All Figures
 |
Fig. 1. Upper panel: Model for the inter-glitch evolution of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \dot{\nu }(t)&=\dot{\nu }_{0}+\ddot{\nu }_{0}t + \sum _{j = 1}^{N_{\rm g}}\Delta \dot{\nu }_{\rm {per,j}}\theta (t-t_{j}) \nonumber \\&+\sum _{j = 1}^{N_{\rm g}} \left(\Delta \dot{\nu }_{\rm {ig, j}}+\ddot{\nu }_{\rm {ig,j}}(t-t_{\rm j}) \right)\;\theta (t-t_{\rm j})\theta (t_{\rm j+1}-t)\nonumber \\&+\sum _{j = 1}^{N_{\rm g}} [\Delta \dot{\nu }_{\rm {d,j}} \exp (- (t-t_{\rm j})/\tau _{\rm {d,j}})]\;\theta (t-t_{\rm j}), \end{aligned} $$](/articles/aa/full_html/2026/02/aa56157-25/aa56157-25-eq60.gif)
![$$ \begin{aligned} \Delta \dot{\nu }_{\rm {obs,j}} \equiv \dot{\nu }(t_{\rm {j+}}) - \dot{\nu }(t_{\rm j}) = \Delta \dot{\nu }_{\rm {per,j}} + \Delta \dot{\nu }_{\rm {ig,j}} + [\Delta \dot{\nu }_{\rm {d,j}}], \end{aligned} $$](/articles/aa/full_html/2026/02/aa56157-25/aa56157-25-eq67.gif)