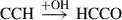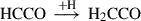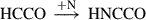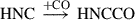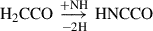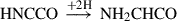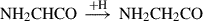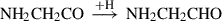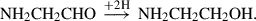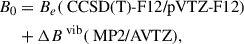| Issue |
A&A
Volume 706, February 2026
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 16 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202557179 | |
| Published online | 03 February 2026 | |
Formation pathways and detectability of interstellar C2HNO-bearing molecules
1
Universidad Autónoma de Chile, Facultad de Ingeniería, Instituto de Ciencias Aplicadas, Núcleo de Astroquímica & Astrofísica Av. Pedro de Valdivia 425 Providencia Santiago, Chile
2
Universidad de Chile, Facultad de Ciencias, departamento de química Av. Las Palmeras 3425 Ñuñoa Santiago, Chile
3
Universidad de Chile, Facultad de Ciencias Físicas y Matemáticas, Departamento de Astronomía Camino el Observatorio 1515 Las Condes Santiago, Chile
★ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
; This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
9
September
2025
Accepted:
22
October
2025
Aims. We explored N-bearing molecules of the general formula C2HNO. We provide their spectroscopic constants, structural properties relevant for detection, and reaction pathways to constrain their formation in the interstellar medium.
Methods. We investigated the molecular structures, spectroscopic constants, and the formation pathways for the isomers, and we report them here from ab initio calculations.
Results. Their formation pathways are mainly dominated by the components HCN + CO and HNC + CO → HNCCO for the second and third species, respectively. We identified five distinct families among the 15 isomers we investigated for C2HNO, in which global stability favors HCOCN (f1), while HNCCO (f6) has a smaller singlet–triplet gap than all the isomers. We also found additional formation pathways for HNCCO (f6) that have not been proposed before. Furthermore, we identified a connection between HCOCN (f1), HCONC (f2), HCNCO (f5), and HNCCO (f6) via proton transfer isomerization. HNCCO (f6) has also been proposed as a precursor to ethanolamine (NH2CH2CH2OH).
Conclusions. This suggests that HNCCO and other isomers we investigated might contribute to the formation of interstellar complex organic molecules and their observed abundances. In particular, we propose that HCONC (f2), c-HCNCO (f4), and HNCCO (f6 conformer) might be observable based on their dipole moments of 2.49, 3.58, and 1.25 Debye, respectively, which are comparable to the dipole moment of the already detected and most stable isomer HCOCN (2.50 Debye).
Key words: astrobiology / astrochemistry / molecular processes / ISM: abundances / ISM: molecules
© The Authors 2026
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1. Introduction
Complex organic molecules (COMs) are thought to be formed in icy dust grain mantles typically following nonenergetic (atom-addition) or energetic (UV-photon absorption) triggers, where they remain frozen in the prestellar stages of star formation. Subsequent effects from interstellar radiation fields and cosmic rays, or shocks and high-energy radiation from protostellar processes, sublimate the ice mantles of the dust grains and drive a rich interstellar chemistry in the gas phase Scibelli & Shirley (2020), Watanabe & Kouchi (2002), Chuang et al. (2017)). Nitrogen-bearing molecules such as ethanolamine (NH2CH2CH2OH) and HNCCO are thought to play a substantial role in astrophysical environments as likely precursors to biomolecules such as amino acids (Ramachandran et al. 2024). Ethanolamine (NH2CH2CH2OH) was recently detected in the G+0.693 region of the giant molecular cloud Sagittarius B2 (SgrB2; Rivilla et al. 2021). This discovery sparked significant interest in its formation pathways and adds to a growing inventory of interstellar COMs.
Rivilla et al. (2021) recently proposed plausible reaction pathways that might lead to the formation of NH2CH2CH2OH, as illustrated in Eqs. (1)–(9). It is of considerable interest to the astrochemistry community to understand the formation pathways by which these species are formed to better constrain the abundance and origin of N-bearing COMs,
Already detected species are highlighted in red, and species in black have not yet been detected in the interstellar medium (ISM). Equation (1) indicates the gas-phase reaction, and all other reactions connote surface chemistry reactions. The reaction pathways were proposed by Rivilla et al. (2021).
One of the intermediates to form along the formation route is HNCCO, but it remains unidentified to date. The scarcity of investigations regarding this species might be the cause. To confirm these pathways, the electronic structure, spectroscopy, and in extension, the existence of the molecular precursors involved at each step in the formation of NH2CH2CH2OH need to be validated.
In addition, the second molecule along the formation pathway of NH2CH2CH2OH, namely NH2CHCO, has been investigated by Alberton et al. (2024a,b). Although NH2CHCO remains undetected in the ISM, the study provided important structural and spectroscopic data that might complement experimental work and facilitate its future detection. The authors examined 14 isomers and conformers of NH2CHCO and showed that the previously proposed global minimum is not the actual lowest-energy structure. They instead identified two other minima that might represent more stable and potentially observable isomers. This investigation underscored the value of thoroughly evaluating potential energy surfaces and spectroscopic parameters when studying known and obscure interstellar molecules. Consequently, iminoethenone (HNCCO) remains poorly characterized. High-resolution spectroscopic data are largely unavailable, and its formation pathways in the interstellar medium is still uncertain.
In an early investigation via tandem mass spectrometry and ab initio studies of iminoethenone radical cations  , the iminoethenone isomer (HNCCO) was first encountered (Flammang et al. 1994). Flammang et al. (1994) and the group also predicted a linear HCN⋯CO molecular complex and an isomerization into [HNC⋯CO]. It was later highlighted that a weak interaction exists between HCN and CO in their ground state (Kameneva et al. 2017). According to Kameneva et al. (2017), upon irradiation with UV radiation, the complex HCN⋯CN undergoes interconversion to HNC⋯CO. The authors also noted that the reaction is catalyzed only in the presence of CO.
, the iminoethenone isomer (HNCCO) was first encountered (Flammang et al. 1994). Flammang et al. (1994) and the group also predicted a linear HCN⋯CO molecular complex and an isomerization into [HNC⋯CO]. It was later highlighted that a weak interaction exists between HCN and CO in their ground state (Kameneva et al. 2017). According to Kameneva et al. (2017), upon irradiation with UV radiation, the complex HCN⋯CN undergoes interconversion to HNC⋯CO. The authors also noted that the reaction is catalyzed only in the presence of CO.
In another investigation, Gronowski et al. (2017) carried out an in-depth analysis of the energetics of the C2HNO molecular formula using a hybrid exchange-correlation functional under density functional theory (DFT), the Becke, 3-parameter, Lee-Yang-Parr (B3LYP) (Becke 1993) with the Dunning correlation-consistent (cc) basis set, augmented with diffuse functions (aug)(aug-cc-pVTZ) (Woon & Dunning 1994) and an approach referred to as the high accuracy extrapolated ab initio thermochemistry (HEAT; Tajti et al. 2004; Gronowski & Kolos 2015; Gronowski et al. 2017) for the calculation of the energies of the five most stable isomers of C2HNO, implemented in the coupled-cluster techniques for computational chemistry program (CFOUR) (Matthews et al. 2020). Vibrational frequencies were calculated using coupled cluster quantum chemistry method that includes single and double electron excitations and a perturbative correction for triple excitations (CCSD(T)) (Watts et al. 1993) with the with the correlation-consistent Polarized Valence Triple Zeta basis set (cc-pVTZ) (Martin 1994), which is the standard in computational thermochemistry. Using the HEAT approach, they found that Etotal, HFcc-pv6Z and Ecorr, CCSD(T)cc-pvQZ exert the highest effect on the relative energies of the isomers, and part of their conclusion was that formyl isocyanide is sufficiently stable to potentially persist in a dense molecular cloud.
One of the reported isomers of the C2HNO group is the popularly known formylcyanide (HCOCN) that is present in interstellar environments such as the Sgr B2 molecular cloud (Remijan et al. 2008) and forms via formaldehyde and cyanide radical addition (Remijan et al. 2008). Its isomers (e.g., HCONC) are expected to be found in similar environments, but a literature search revealed a dearth of information regarding these species.
Identifying and characterizing the isomers of C2HNO requires a good ab initio structural analysis of the possible species, spectroscopic study of parameters such as its vibrational frequency, rotational constants, centrifugal distortion constants, and also the reaction pathways will help us to unravel the species. This calls for a thorough investigation via a more accurate approach that takes the effects of electronic correlation into account.
The challenges, as described above, are intended to be addressed in the current investigation by carrying out a comprehensive ab initio electronic structural study of the C2HNO isomers with a focus on the first three low-lying energies as potential observable gas-phase molecular species at a very high level of theory that takes the effect of higher-order correlation effects into account. This is followed by an accurate spectroscopic characterization aimed at providing highly accurate data to support an identification in the astrochemical laboratory and carry out a mechanistic study of the formation and destruction of these species. This paper begins with a comprehensive introduction, followed by the computational methods. The results and discussions are presented combined and are followed by the concluding remarks.
2. Computational details
Geometry optimizations, relative energy, rotational constants, vibrational frequencies, and dipole moments for the most stable isomers of interest were initially conducted using high-level ab initio theory using explicitly correlated coupled cluster singles, doubles, and perturbative triples with core-correlation (CCSD(T)-F12/cc-pCVTZ-F12) and without core-correlation (CCSD(T)-F12/cc-pVTZ F12) Raghavachari et al. (1989), Crawford & Schaefer (2000), Sylvetsky et al. (2014)) in the basis sets at the singlet (X1A′) and triplet states (X3A″). The geometries and vibrational frequencies were computed using multiple levels of theory to assess the correlation and basis set effects. High-level CCSD(T)-F12 calculations with cc-pCVTZ-F12 and cc-pVTZ-F12 basis sets provide an almost complete basis accuracy for equilibrium structures and anharmonic frequencies. Müller–Plesset perturbation theory of second order of perturbation (MP2) with cc-pVTZ-F12 basis set offer an intermediate-cost reference calculation, while B3LYP/6-31G(d,p) and B3LYP/aug-cc-pVTZ were used to generate initial geometries and to evaluate the dependence of the method on the vibrational properties. This choice was made to achieve highly accurate calculations for all-electron properties with the aim of convergence to the complete basis set (CBS) limit, especially when core-valence effects are significant (Hill et al. 2010), and to take advantage of the balance between accuracy and computational cost (Kruse et al. 2020). All calculations were performed via the code MOLPRO (Werner et al. 2010). All the vibrational frequencies were analyzed and ordered based on their point group symmetry, where the first seven values correspond to the A′ symmetry, and the last two correspond to the A″ symmetry. In addition, geometry optimizations together with harmonic and anharmonic vibrational frequency calculations were performed at MP2/aug-cc-pVTZ level of theory (Müller 1934) to benchmark our results and to provide anharmonic vibrational corrections to the CCSD(T)-F12 energies. We chose the aug-cc-pVTZ (Dunning 1989) basis set at the MP2 level because it includes diffuse functions, which enhance the description of electronic polarizability and facilitate a more accurate treatment of any multireference character present in the system Park & Shiozaki (2020). This combination ensures more reliable anharmonic corrections while maintaining computational efficiency.
The intrinsic reaction coordinate (IRC) approach is designed to follow the bond rearrangements from the transition states (TS) to the minima (reactants and products) (Fukui 1981). We used this to verify the connection between stationary points. We employed the B3LYP method (Becke 1993) with split-valence gaussian basis set with polarization functions (6-31G(d,p) (Krishnan et al. 1980) to search for the transition states that connect each reaction pathway. This procedure was followed by single-point energy calculations at the CCSD(T)/aug-cc-pVTZ level of theory for each minimum along the pathway. This approach ensures an improved accuracy of the energies obtained at the lower level of theory and is a common computational chemistry workflow (Alharzali et al. 2024). The activation energies presented along the IRC correspond to the electronic energy derived from single-point calculations for each reaction, bearing in mind that including the zeropoint vibrational correction might shift the relative energies slightly. A vibrational analysis was carried out for each reaction, and it indicated that the Hessian matrices of each transition state (TS) only have one imaginary eigenvalue. The displacement vectors corresponding to the imaginary vibration mode clearly establish a connection between the reactant and product in each case, which enabled us to confirm that the path was reasonable enough. Except for the barrierless reaction, all the other reactions were investigated on the singlet-state (X1A′) surface. These methods were chosen to balance the computational cost with the accuracy required for IRC calculations. The B3LYP/6-31G(d,p) was also employed to validate the point group of each isomer and conformer. These calculations were performed using the Gaussian 09 software package (Frisch et al. 2016). Finally, vertical excitation energies were calculated in the Cs symmetry group using the configuration interaction singles (CIS; Turro et al. 2010) method under an adiabatic approach to understand and compare the fundamental spectroscopic and photochemical properties.
3. Results and discussion
We present new results on the energetics, spectroscopic properties, and formation and destruction pathways of a comprehensive set of 15 C2HNO species, which we organize into five structural families. These families, labeled FI–FV and shown in Fig. 1, are defined according to the geometrical resemblance among the different isomeric forms, allowing a clearer interpretation of their chemical relationships and interconversion routes. Figure 2 shows the relative energy level diagram of the C2HNO isomers with respect to the global minimum (f1), computed at the CCSD(T)-F12/cc-pVTZ-F12 level of theory. All quantum-chemical calculations were performed using the high-accuracy, explicitly correlated coupled-cluster method CCSD(T)-F12 in combination with the cc-pVTZ-F12 basis set, ensuring reliable predictions of relative stabilities and vibrational and rotational spectroscopic properties. For clarity and ease of reference throughout this work, each isomer has been assigned a unique identifier, from f1 to f15, which we consistently use when discussing their structural features, thermochemistry, reaction mechanisms, and astrochemical relevance.
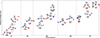 |
Fig. 1. Comparative analysis of the potential energies of the isomers and conformers of C2HNO with energy variations. The relative energies are computed at the CCSD(T)-F12/cc-pVTZ-F12 level of theory. f3 corresponds to the transition state (TS). |
 |
Fig. 2. Relative energy level diagram of the C2HNO isomers with respect to the global minimum (f1) computed at the CCSD(T)-F12/cc-pVTZ-F12 level of theory. |
3.1. Energetics and structural characterization of the C2HNO group
The first family FI includes (f1) HCOCN=formylcyanide, which is the global minimum assigned with 0.0 eV, (f2) HCONC=formylisocyanide, and (f3) HCOCN or formylcyanide-conformer. The relation between them is as follows: f1 and f2 are isomers, and f3 is a transition state connecting the two. We found that the global minima of the C2HNO is formylcyanide (f1). This agrees with the results of Gronowski et al. (2017), who used the CCSD(T)/cc-pVTZ level of theory.
The transformation of f1 to f2 via the transition state f3 involves key geometric and electronic rearrangements that facilitate bond-breaking and -forming. The transition state f3 plays a critical role in enabling two competing pathways: 1. Outward elongation (stretching of the NCC angle) leads to the formation of HCOCN through this pathway. The geometry allows the bond angle to increase, which weakens the bond between the atoms and facilitates a rearrangement that preserves the CN group while shifting the electron density toward oxygen and carbon. 2. Bond-formation C-C bond-breaking: The nitrogen atom of the cyano (CN) group can form a new bond with the second carbon atom, initiating cleavage of the C–C single bond. This produces HCONC and represents a rearrangement in which the connectivity of atoms changes significantly as a result of bond-formation and bond-breaking. The ≈70° NCC geometry is critical because it places the orbitals in a favorable alignment for either angle stretching or internal nucleophilic attack by nitrogen. This stabilizes the transition state and facilitates either outcome.
The isomer f2, isoformylcyanide, has a relative energy of 0.55 eV with respect to f1, which makes it the second most stable isomer for the whole family. f3 connects the two isomers by a 2.23 eV barrier, which corresponds to an isomerization process from the cyano-group to the isocyano-group HCOCN → f3 → HCONC at the theoretical level CCSD(T)-F12/cc-pVTZ-F12. These results are shown in Fig. 4.
 |
Fig. 3. Comparison of the isomer and conformer energies of the general formula C2HNO for f1 (formyl cyanide) observed in Sgr B2 (Remijan et al. 2008), computed using MP2/aug-cc-pVTZ, CCSD(T)-F12/cc-pVTZ-F12, and CCSD(T)-F12/cc-pCVTZ-F12. |
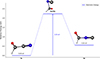 |
Fig. 4. Reaction energy profile for the conversion of f1 to f2 via the transition state f3. The energies were computed at the CCSD(T)-F12/cc-pVTZ-F12 level of theory. |
The second family (FII) has (f4) c-HCNCO or 2H-azirin-2-one and (f5) HCNCO. FII consists of two conformers, f4 and f5, with the molecular formula of HCNCO and relative energies of 1.29 and 2.20 eV relative to f1. f4 is cyclic, whereas f5 is quasi-linear. The cyclic conformer f4 is the most stable of all the cyclic systems we studied. The third family (FIII) includes iminoethenone (f6), linear iminoethenone (f7), cyclic iminoethenone (f8), and square-iminoethene (f9). The relative energies lie between 1.56, 3.05, 3.21, and 7.09 eV with respect to f1 and indicate that the f6 conformer is the most stable conformer in the FIII family. Of all the different conformations, f6 is the most stable structure of HNCCO and lies at 1.56 eV above the detected global minima (f1).
The fourth family (FIV) includes (f10) or azaethylenol, with relative energies of 1.98 eV with respect to the global minimum, and it includes iso-azaethynol (f11), which lies at 2.53 over the most stable isomer (f1). The fifth family (FV) includes f12 c-HOCNC at 2.62 eV, f13 HCCNO at 3.67 eV, f14 HCCNO, and f15 c-HONCC or hydroxy-aziryne at 5.60 and 5.72 eV above f1. We discuss the main findings of this research below.
In Fig. 3 we compare the energy at CCSD(T)-F12/cc-pVTZ-F12, CCSD(T)-F12/cc-pCVTZ-F12, and MP2/aug-cc-pVTZ. The figure shows that they follow the same behavior, with an increasing trend in energy from the isomer index f1 to f15. No significant deviation from the trend is observed. The plot highlights the most stable isomer, f1 (HCOCN), followed by f2 (HCONC), formylisocyanide f4 (HCNCO), and F6 (HNCCO). Formylcyanide has been observed in the Taurus molecular cloud 1 (TMC-1; Tonolo et al. 2020) and Sgr B2 (Rivilla et al. 2021). These observations suggest that the other low-lying isomers such as f2, f4, and f6 might also be relevant for astrophysics or might be found in similar environments. In general, the agreement between the methods appears to be good, except that MP2/aug-cc-pVTZ overestimates the absolute energies slightly. This is well known because higher-order correlation effects (triple excitations) are significant for our molecule, and the system appears to a have strong dynamic correlation, which is usually better captured by CCSD(T). The CCSD(T)-F12 therefore explicitly incorporates the electron correlation with a higher accuracy (Dallas et al. 2021). The core-correlation method CCSD(T)/cc-pCVTZ-F12 yielded lower energies than all the other ab initio methods and agreed better with the explicitly correlated CCSD(T)-F12/cc-pVTZ-F12 method, which does not consider core-correlation.
Table 1 shows the structural parameters (bond lengths and bond angles) of the first four isomers of C2HNO from families FI, FII, and FIII, as grouped in Fig. 1, and the other isomers are presented in Table A.1.
Structural parameters, relative energy (kJmol−1), equilibrium rotational constant (GHz), and frequencies (cm−1) of the C2HNO isomers at the CCSD(T)-F12/cc-pVTZ-F12 level of theory.
A comparative analysis revealed very little variation in the r(C1-H4) bond length across all the isomers (around 1.09 Å). This suggest that the hydrogen-carbon (C-H) bond is relatively unaffected by structural differences of the isomers. In contrast, the r(C1-O2) bond lengths vary more strongly (around 1.22 Å in f1, 1.19 Å in f2 and f3, and 1.17 Å in f6). This might be affected by the electronic environment or by the bonding character. r(C-N5) varies strongest, in particular, for the f4 isomer, where the bond length is 1.325, and it varies less when it is a C≡N bond (see the R3 bond length in f1). This shows differences in the delocalization or electron density distribution.
Additionally, we computed the triplet states. In particular, we observed that the singlet states are lower in energy for all isomers we studied.
Our findings show that (X1A′) f1 is the most stable isomer overall, with a wide singlet-triplet energy gap of 4.12 eV at the CCSD(T)-F12/cc-pVTZ-F12 level of theory (3.75 eV at MP2/aug-cc-pVTZ). These values are significantly higher than 2.69 eV (260 kJmol−1) from other previous theoretical work computed at B3LYP/aug-cc-pVTZ (Gronowski et al. 2017).
On the other hand, f6 exhibits a (X1A′)-(3A″) gap of 1.74 eV at CCSD(T)-F12/cc-pVTZ-F12 (0.79 eV at MP2/aug-cc-pVTZ). In addition, f6 3A″ has a lower energy than the triplet state 3A″ of f1. The absolute stabilities were compared by considering the most stable isomers in each state, as shown in Fig. 5.
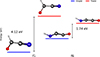 |
Fig. 5. Singlet–triplet electronic energy gaps for the f1 and f6 C2HNO isomers, calculated at the CCSD(T)-F12/cc-pVTZ-F12 level of theory. |
3.2. Excitations energies
To gain insight into the interaction of the C2HNO isomers with electromagnetic radiation under interstellar conditions, we computed vertical excitation energies, oscillator strengths, and transition dipole moments for the fourth most stable isomers. Accordingly, we obtained the excitation energies using the CIS method at the ground-state geometry, without structural relaxation in the excited state. Although CIS generally only provides a first-order approximation, these values are useful for identifying the spectral region (UV/Vis) in which the molecule is expected to absorb and for characterizing the nature of the lowest-lying electronic states. The vertical excitation energy corresponds to the electronic energy difference between the ground and an excited state, evaluated at the optimized ground-state equilibrium geometry. In accordance with the Franck–Condon principle, the excitation is described as ‘vertical’ because the electronic transition occurs on a timescale that is much faster than nuclear motion, such that the nuclei are effectively frozen during the process. The computed vertical excitation energies and associated properties are summarized in Table 2 and are illustrated in Fig. 6. The results reveal clear differences between the f1 and f6 C2HNO isomers. For the (X1A″) f1 isomer, the first three singlet excitations are located at S1 = 4.49 eV, S2 = 5.92 eV, and S3 = 6.66 eV. In contrast, the (X1A′) f6 (HNCCO) isomer exhibits significantly lower energies for the first excited state (S1 = 1.84 eV) and moderately lower energies for the second state (S2 = 5.17 eV), while the third excitation lies slightly higher than that for f1 ( S3 = 6.81 eV). Notably, f6 exhibits a much lower S1 energy, suggesting an earlier absorption onset, while higher excitations (S2, S3) occur in a comparable energy window for both isomers.
 |
Fig. 6. Vertical excitation energy of HCOCN (f1), f2, and f4 vs. that of HNCCO (f6). |
Vertical excitation energy, transition dipole moment (μ), and oscillator strength of the first three lowest electronic excited states of four isomers of C2HNO computed at CIS.
These results indicate that the first electronic excitation (S1) favors f6 over all other isomers with a lower excitation energy of 1.8380 eV, while f1, f2, and f4 have higher excitation energies within a range of 4–5 eV, which implies that a higher energy is required to cause electronic excitation in them. This suggests an earlier absorption in the UV–Vis spectrum and potentially enhanced photoreactivity in f6 than all other isomers.
Notably, while the triplet states may be important for stability and pathways, the calculated oscillator strengths for all triplet states are zero. This indicates that these transitions are spin-forbidden under the electric dipole approximation. Consequently, a direct photon absorption cannot populate the triplet states from the ground state, but nonradiative processes such as intersystem crossing (ISC) facilitated by spin–orbit or vibronic coupling could make them accessible experimentally.
Ultraviolet photons from young massive stars, such as O- and B-type stars, or from hot pre-main-sequence stars, can easily excite HNCCO from its ground to an excited electronic state. This might lead to photochemistry in molecular clouds or circumstellar environments.
3.3. Rotational constants and dipole moment
Table 1 also lists the rotational constants and dipole moments of the four low-lying energy isomeric species (f1, f2, f4, and f6) from the families FI, FII, and FIII of the group C2HNO calculated using the explicitly correlated coupled cluster method (CCSD(T)-F12/cc-pVTZ-F12). Starting with formylcyanide (FI-f1), we computed the rotational constants of f1 to compare them with its experimental values, which we intend to use as a benchmark for validation of all other isomers lacking experimental data. We present the calculated equilibrium and ground-state (G.S.) rotational constants and the experimentally measured values. The ground-state rotational constant at the CCSD(T)-F12/cc-pVTZ-F12 was obtained by introducing the corrections from the MP2/aug-cc-pVTZ calculations as shown below,
where ΔBvib is the vibrational contribution derived from the anharmonic MP2/AVTZ calculations (Toumi et al. 2022).
The equilibrium rotational constants are presented in Table 1. To facilitate the comparison with the ground-state experimental data, we present Table 3, which was derived using Eq. (10). The comparison between the calculated and experimental rotational constants for the f1 isomer (Table 3) shows a better correspondence, particularly for the B and C rotational constants. Specifically, the calculated and experimental values are B0 = 4973.5855 MHz and B0 = 5010.18856(34) MHz, and C0 = 4625.2315 MHz and C0 = 4656.60175(29) MHz. This means that the rotational constants A0, B0, and C0 of f1 in our results agree with the experimental values within approximately 1.6%, 0.4%, and 0.3%, respectively. This demonstrates that the approach predicts the B and C ground-state rotational constants from equilibrium states better and in comparison with experiments. For f2, the deviations from other theoretical works (Gronowski et al. 2017) are below approximately 1.1%. The deviations remain modest for f4, which reflects differences in the vibrational corrections, particularly in how the methods treat large-amplitude motions. Generally, our CCSD(T)-F12/cc-pVTZ-F12 approximation 10 slightly underestimates the rotational constants A0, B0, and C0.
Comparison of some spectroscopic parameters with those of known data.
This shows the accuracy of the method we chose to compute the rotational constants for these isomers, and an extension to other isomers lacking experimental data would imply a very reasonable approximation. As a result, the calculated rotational constants for the other isomers f2, f4, and f6 at this higher level of theory are also given in Table 1.
The experimental Ray asymmetry parameter (κ) for the f1 isomer, which corresponds to a prolate asymmetric top, is −0.9887. Our calculations yield a value of −0.9886, which agrees very well with the experimental result. The asymmetric parameter κ for isomers f2, f4, and f6 is −0.9879, −0.9099, and −0.9989, which satisfies the condition of the κ value (−1 < κ < +1) and means that they are also molecular species with a nearly prolate asymmetric top. We evaluated the centrifugal distortion corrections for each isomer. Because of their κ values, we adopted the symmetrically reduced Hamiltonian of Watson (Watson & Durig 1977). The S-reduced quartic and sextic centrifugal distortion constants are reported in Table 4, and the corresponding data for the other isomers are provided in Tables B.1 and B.2.
Rotational constants (MHz) and centrifugal distortion constants (quartic and sextic) of f1, f2, f4, and f6, calculated at the MP2/aug-cc-pVTZ level of theory.
Among the four lowest-lying isomers (f1, f2, f4, and f6), the rotational spectrum of f4 is predicted to exhibit the strongest transitions, which is consistent with its relatively high dipole moment of 3.58 D. This agrees with Gronowski et al. (2017). The next strongest transitions are expected for f2, which carries a dipole moment of 2.49 D.
3.4. Vibrational frequencies (harmonic and anharmonic)
Tables 1 and 5 contain the results of the vibrational analysis of the first four low-energy isomers of the C2HNO group, which includes f1, f2, f4, and f6. They were computed at the MP2/aug-cc-pVTZ (5) and at the more sophisticated CCSD(T)-F12/cc-pVTZ-F12 (1) level of theory. The analysis of all other isomers is presented in Tables A.1 and B.3 at the two levels of theory, respectively.
Fundamental vibrational frequencies (experimental vs. theoretical) of f1 and the three most stable isomers (f2, f4, and f6) of C2HNO, calculated at the MP2/aug-cc-pVTZ level of theory.
In Table 5, ω1 − ω9 and υ1 − υ9 depict specific vibrational modes where ω and ν represent harmonic and anharmonic vibrational modes, respectively. The vibrational frequencies of f1 obtained using MP2/aug-cc-pVTZ agree very well with the experimental observations (Judge et al. 1986), for instance, the calculated frequency for mode (ω7) for f1 is 216.1 (cm−1), corrected for anharmonicity to 216.8 (cm−1), while the experimental value observed for this mode is 217 (cm−1) (Judge et al. 1986). Considering this mode, the absolute error from the MP2/aug-cc-pVTZ calculation is 0.2 cm−1 in comparison with experimental values, which has a percentage error of 0.092%. The highest difference was observed at ω6 with a difference of 192.1 cm−1. The accuracy level of all the other modes is good in comparison with experimental values. Frequencies obtained using CCSD(T)-F12/cc-pVTZ are also generally very good with the lowest error recorded for ω7, whereas its highest difference was also recorded at the ω6 mode (194.7 and 204.2 cm−1 at MP2/aug-cc-pVTZ and CCSD(T)-F12/cc-pVTZ-F12, respectively), following the same trend in both methods. This indicates that the values obtained for this mode are reasonable predictions.
The analysis of the vibrational modes revealed that -CO and -NC bending and torsion produce lower frequencies (e.g., 287.5 cm−1 for f1 and 163.59 for f2 at CCSD(T)-F12/cc-pVTZ-F12, respectively), but -CN and -CO stretching produce higher vibrational frequencies (e.g., 2181.9 cm−1 for f1 and 2130.7 cm−1 for f6), while -CH and -NH stretch produces higher vibrational frequencies (e.g., 3044.8 cm−1 for f1, 3193.9 for f4, and 3406.6 for the NH stretch of f6). All four species belong to the Cs point group, with seven vibrational modes of the A′ symmetry and two modes of the A″ symmetry for each of them. The vibrational analysis indicates that the linear conformer of iminoethenone (f7) exhibits two imaginary frequencies, which confirms that it is not a true minimum on the potential energy surface, but rather a saddle point. This finding was consistent across calculations at MP2/aug-cc-pVTZ and CCSD(T)-F12/cc-pVTZ-F12, and therefore, f7 was omitted from the tables. Similarly, f3, which is a transition state and not a stable conformer, was not included in the tables that summarize stable structures.
3.5. The formation and destruction pathways
In Table 6 we present the investigated reactions pathways leading to the formation and destruction of the three low-lying isomers of C2HNO, accounting for HNCCO (f6, f8, and f9), HCNCO (f4 and f5), and HCONC (f2). These pathways illustrate different transformations. Generally, the reactions involving C2HNO are primarily characterized by radiative association reactions and isomerization reactions with a few other distinct reactant species. Figure 7 shows the formation pathways of HNCCO. Chemical species depicted in blue boxes have been identified in the interstellar medium, while those shown in pink have not yet been detected.
 |
Fig. 7. Formation pathways of HNCCO. The chemical species depicted in the square blue box were identified in the ISM, and those in pink are not yet identified. |
Formation and destruction pathways of HCONC (f2), HCNCO (f5), and HNCCO (f6) with their activation energies (energy barriers) and the thermodynamic nature of the reactions (enthalpy) at two different levels of theory.
Reactions R1 and R2 both involve an intramolecular hydrogen shift. R1 with an activation energy of 80.5 kcal⋅mol−1 enables the conversion of species f2 into the HOCNC isomer (f11) with energy absorption. The reaction R2 converts f5 into f2, with an activation energy of 16.45 kcal.mol−1 (0.7 eV) with an energy release (exothermic process).
Reaction R3 describes the bimolecular interaction of HCONC with molecular hydrogen to yield hydrogen isocyanide (HNC) and formaldehyde (CH2O). The process that occurs in X1A′ with an energy surplus also has a high activation energy of 61.55 kcal mol−1). In this IRC approach, the forward direction, molecular hydrogen interacts with the CN radical center of HCONC, leading to H–H homolytic bond cleavage. The dissociation generates two hydrogen atoms (radicals): One atom couples with the CN fragment to form hydrogen isocyanide (HNC), and the other atom adds to the HCO moiety, yielding formaldehyde (CH2O). Conversely, in the reverse direction, the hydrogen atoms recombine to regenerate molecular hydrogen, allowing the CN and HCO fragments to recombine and reform the HCONC precursor.
Reaction R4 represents another dissociation process of f2 that this time is induced by the addition of methane. The interaction of CH4 and HCONC, all in the X 1A′ state, begins with a hydrogen abstraction from methane by the nitrogen atom of the HCONC precursor, leading to a transient transition state in which the reacting species are well aligned. This transition state subsequently dissociates to yield the intermediates CN, HCO, and CH4. Following this, the CN radical abstracts a hydrogen atom from the liberated methane, while the HCO radical adds to the methyl fragment, ultimately forming HNC + CH3CHO as the final products. This process exhibits a barrier of 63.61 kcal. mol−1.
Reaction R5 corresponds to an exothermic conversion of f1 when it interacts with H2O to yield HCONCHOH. The associated activation energy for this interaction is (46.65 kcal.mol−1). Water ice exist in the cold outer regions of protoplanetary disks, where it can form ice mantles on dust grains that act as catalysts, facilitating or promoting reactions that would otherwise require a higher activation energy (Hebels 2024; Potapov et al. 2018).
In reaction R6, the hydrogen atom exists in a doublet ground state (2S), while the OCNC radical is also a doublet species (2Π). Upon interaction, the two unpaired electrons can couple (antiparallel), yielding an overall singlet spin state ((1X)). This is consistent with the formation of HCONC (a closed-shell (X 1A′).
Reactions R7 and R2 are mechanistically connected through the species HCNCO (f5). In R7, HCNCO (f5) is formed from its detected precursors, HCN and CO, which are both abundant in the interstellar medium. In R2, HCNCO (f5) undergoes an intramolecular hydrogen shift that leads to the formation of HCONC (f2). The hydrogen-shift process in HCNCO proceeds via the approach of its two carbon atoms. This geometry facilitates new bond-formation and properly aligns the migrating hydrogen atom. As a result, the hydrogen can transfer to the carbonyl carbon, yielding the isomer HCONC (f2).
The second group of reactions (R7–R12) focuses on the formation pathways of f4. Among these, R7 (HCN + CO → HCNCO) is particularly noteworthy because both HCN and CO are abundant and well-characterized species in a wide variety of interstellar environments, including cold molecular clouds, star-forming regions, and protoplanetary disks Boger & Sternberg (2005), Li et al. (2013), Huang et al. (2017)). This makes them highly accessible precursors for potential astrochemical pathways. Our calculations revealed that the reaction proceeds with an electronic activation energy of 63.00 kcal.mol−1, an endothermic process. Although this barrier might prevent the reaction under the extremely cold conditions of dark molecular clouds, it becomes feasible in warmer environments, such as protoplanetary disks or shock regions, where sufficient thermal or nonthermal energy is available. In this context, R7 represents a potentially important pathway for the astrochemical formation of HCNCO, as it directly links two highly abundant species (HCN and CO) to a more complex nitrogen–oxygen compound. Compared to alternative formation routes involving less abundant radicals or ions, the HCN + CO channel is significant because it can operate wherever these two stable and widespread molecules coexist under conditions energetic enough to overcome the barrier. Reaction R7 shows that HCN + CO forms f5 (HCNCO, labeled in Fig. 1). f5 (HCNCO) undergoes isomerization and converts into f2 (HCONC), while as expected, HNC + CO forms f6 (HNCCO).
Reaction R8 describes an isomerization process within HCNCO that converts the quasi-linear conformer (f5) into the cyclic conformer (f4) via an activation energy of 17.96 kcal mol−1. This occurs through the formation of a new bond between the two carbon atoms that generates the cyclic structure. The relatively low barrier indicates that this interconversion is energetically feasible under typical astrochemical conditions, such as in warm regions of molecular clouds or protoplanetary disks.
Reaction R9, on the other hand, involves the interaction of HCN and CO to form f4. The components are highly abundant in the ISM. Reaction R10 is a reversible association–dissociation process. Initially, hydrogen cyanide (HCN) interacts with carbon monoxide (CO) to form the transient adduct HCNCO. This intermediate is not strongly stabilized, however, and readily dissociates back into the original reactants. The overall process therefore suggests a weakly bound complex or van der Waals-type interaction. As a result, it might be found in regions in which CO and HCN are dominant. It shows a possible attractive force between CO and HCN that leads to HCNCO as a species or intermediate.
An additional isomerization process is represented by R11, which involves an intramolecular hydrogen shift leading to the conversion of HNCCO (f6) into HCNCO (f5). This pathway is particularly relevant because it illustrates how the two isomers are connected through a direct hydrogen-migration mechanism on the potential energy surface. Since f5 (HCNCO) is thermodynamically more stable than f6, the hydrogen shift drives the system toward a lower-energy minimum, making f5 the favored isomer under many astrochemical conditions. Although intramolecular hydrogen-transfer reactions of this type have been shown to possess relatively high activation barriers and may require catalytic assistance or quantum tunneling (Krasnokutski et al. 2024), the large barrier calculated for this system (51.38 kcal mol−1) makes the reaction unlikely to proceed in the low temperatures (10–100 K) typical of most interstellar environments. However, because CO is one of the dominant species in interstellar ices (Allamandola et al. 1999), it can diffuse and react with HCN, with the grain surface providing stabilization of intermediates. This suggests that a surface-mediated mechanism could facilitate the isomerization, either by allowing excess energy to dissipate into the ice matrix or by trapping reactive species and preventing their desorption (Garrod et al. 2007; Fresneau et al. 2014).
Reaction R12 shows that f5 can form efficiently without an energy barrier and that iminoethenone (f6) might serve as an important precursor to complex molecules such as ethanolamine, which links simple interstellar species to prebiotic chemistry.
In the case of R13 and R14, both reactions show how HNCCO (f6) is formed by the direct combination of HNC and CO, two molecules that are more or less abundant and are well characterized in the interstellar medium (ISM). HNCCO (f6) acts as a bridge between simple precursors and more stable or detectable molecules. This affects the observed abundances in astrochemical models.
The primary formation pathway of HNCCO is chiefly dominated by reaction R13, that is, the neutral-neutral association HNC + CO (X1A′), which yields f6, which is spin allowed. The reaction with reactants HNC and CO appears twice in Table 6 because the reactants follow two different transition-state paths. In reaction R13, HNC and CO undergo a carbon-carbon addition that breaks the triple bonds in them to form a double bond across the two carbons. The transition state here is just the structure with an overly longer double bond.
Reaction 14 in comparison with R13 has the lowest activation energy of 31.13 kcal.mol−1, whereas in reaction 13, the same process occurred. It passed through a different transition state, however, whose structure is very similar to the higher sq-conformer (f9) through which f6 (w-HNCCO) is formed. Reaction 13 has high activation energy of 157.4 kcal.mol−1, however, which indicates that the squared conformer can be found in a high-energy environment. When it is in a low-energy environment, it isomerizes to the quasi-linear conformer. HNC, a metastable isomer of HCN, serves as a principal precursor in the formation of both f4 (c-HCNCO) and f6 (HNCCO). HCN and HNC are known to be ubiquitous in the ISM (Hacar et al. 2020). They can be described as the chemical traces of the interstellar medium because they are present in diverse environments such as diffuse clouds, cold dark clouds, star-forming regions, circumstellar envelopes around evolved stars, external galaxies, and even objects with a high redshift (Daniel et al. 2012; Hacar et al. 2020; Herbst 2021). They might therefore also serve as tracers of f2, f4, f6, and other isomers of C2HNO.
Reaction R15 involves the dissociation of cyclic HNCCO (f6) back into its reactant components. This process is endothermic, meaning that it requires energy input, with an activation energy of 62.4 kcal.mol−1. The dissociation occurs through the simultaneous cleavage of the C–C and C–O bonds in the cyclic conformer. This bond-breaking step explains why a relatively high activation energy is needed: The reaction must overcome the energy that stabilizes the cyclic structure. Reaction R16 represents an alternative pathway for the formation of HNCCO (f6) via the isomerization of formylcyanide (HCOCN or f1) into iminoethenone (HNCCO or f6). This process occurs via a hydrogen transposition from carbon C1 to nitrogen N4, which leads to the formation of the transition state. During the process, the pi-bond between C3 and N4 was broken and a new pi-bond formed between the two carbons (C1 and C3). This stabilized the minima geometry. This migration is caused by hydrogen bonding (a special type of dipole-dipole interaction that occurs between lone pair of a highly electronegative atom (e.g., N, O, or F) and a hydrogen atom in an N-H, O-H, or F-H bond), giving the system a molecular polar covalent bond. N is more highly electronegative (electronegativity = 3.0) than carbon (electronegativity = 2.55), and this paves the way for this interaction. This process has a high activation energy of 109.02 kcal.mol−1, however. While these barriers are generally prohibitive under the cold ISM condition, possible environments that might provide the energy to overcome these barriers include a hot core, hot corinos, shock regions, and outflows (Inostroza-Pino et al. 2025; Zeng et al. 2023). Reactions R17 and R18 lead to the formation of isomers of the same molecular formula (NH3C2O). Both reactions occur without an energy barrier, making them highly probable in cold interstellar medium (ISM) conditions, where reactions with barriers are unlikely. This pathway was recently also suggested by Inostroza-Pino et al. (2025) as a product that was proposed as a pathway for the formation of ethanolamine NH2CH2CH2OH (Rivilla et al. 2021). In these reactions (R17 and R18), two hydrogen additions proceed without a barrier and lead to the formation of another intermediate (NHCHCHO and NH3CCO; all isomers of NH2CHCO). When the two H atoms in the reaction approach HNCCO with antiparallel spins (para-H2), the overall electronic configuration corresponds to a singlet state (1Σg+ for H2). Upon interaction, the system can couple into the singlet ground state of HNCCO-X1A′. Thus, the reaction proceeds on a singlet PES (1X) and can be characterized as spin-allowed. This enhances its feasibility under interstellar or astrophysical conditions. Moreover, at low temperatures (e.g., the ISM), para-hydrogen dominates because it is energetically favored over ortho-hydrogen (parallel spins; Breuer et al. 1998; Tsuge & Kouchi 2021). The reaction can therefore be characterized as spin-allowed following the Wigner rules, which makes it possible under astrophysical conditions. This pathway was proposed for the formation of NH2CH2CH2OH (Rivilla et al. 2021).
Other barrierless processes include R19 and R20, which lead to the formation of HNCCO (f6). Reactants involved in reaction R19 are HCCO (X2A″) and N (X4S3/2), which combine to form HNCCO (f6), preferably in its triplet state (X3A″). The combination leads to HNCCO, which can exist in singlet (X1A′) or triplet states (X3A″). The triplet state is generally more favored for barrierless radical-radical reactions because the total spin is conserved when a doublet (HCCO) and a quartet (N) species are combined. The resulting triplet is not allowed in the closed-shell singlet state, except in the triplet (X3A″) state, which is close to the singlet for f6 (HNCCO).
The reactant species involved in reaction R20 are CCO (the ketenyl radical), typically in its ground electronic state X2Σ+, and NH (the imidogen radical) in its ground state X2Π. When these two species interact, they can couple to form either singlet X1A′-HNCCO (f6) or triplet X3A″-HNCCO. Both electronic states of HNCCO have been detected and characterized as gas-phase chemical species in dark clouds (e.g., TMC-1, L483; Meyer & Roth 1991; Ohishi et al. 1991).
3.6. Astrophysical implications
It is important to note that while barrierless pathways are thermodynamically accessible, radiative associations and three-body reactions are often inefficient in the gas phase, particularly at low densities. They should therefore be interpreted with caution. In these cases, grain-surface and ice-mediated chemistry might become decisive, especially for reactions with significant barriers, where protonated intermediates are known to play an essential role in ion–molecule networks of interstellar chemistry (Boulet et al. 1999). Cold dense interstellar clouds, such as those found in star-forming regions, molecular clouds, and photodissociation regions (PDRs), represent likely environments in which these processes operate efficiently (Caselli 2012; Watanabe & Kouchi 2008).
HNCCO (f6), c-HCNCO (f4), and HCONC (f2) emerge as chemically interconnected species that might serve as precursors to larger interstellar complex organic molecules (COMs). Their relevance is underscored by the fact that they can participate in pathways leading to the formation of ethanolamine (NH2CH2CH2OH), a species recently detected in the ISM and proposed as a potential intermediate in prebiotic chemistry (Rivilla et al. 2021). The chemical network of reactions involving R2, R7, and R11 highlights that relatively simple species can evolve into more complex structures.
HCN and CO are known species in the ISM that participate in key reactions, and they are abundant species in the ISM. Reactions R7, R9, R13, and R14 buttress this observation, where these species formed more complex species. High-temperature chemistry can occur involving reactions R1 or R4 due to their high activation energy (80.57 and 63.61 kcal.mol−1, respectively), which means that they might easily occur in high-temperature environments (Inostroza-Pino et al. 2024) such as lightening strikes in planetary atmospheres, molecular clouds in the Galactic center, combustions systems, or degradation of N-bearing compounds.
Reaction R2 involves a curved quasi-linear conformer of HCNCO (f5), with hydrogen arranged in such a way as to enable migrations from the first to the second carbon during the transformation process that forms HCONC (f2). The reaction, which is exothermic in nature, has an activation energy of 16.45 kcal.mol−1. This barrier is high enough to prevent this transformation in the cold condition of the ISM. These reactions might be feasible via nonthermal processes, however, such as cosmic rays, UV irradiation, and quantum tunneling, and in warmer regions such as hot cores, shock regions, and grain surfaces (Inostroza-Pino et al. 2024). Dust grains might act as a catalyst for the reaction, and accretion of gas-phase molecules and in situ photochemical processing might also play a significant role. In reaction R7, HCN reacts with CO to form HCNCO (f5). The relatively high activation energy of 63.00 kcal.mol−1 makes it thermally unfeasible in the standard ISM. To overcome the high activation energy, high temperatures are essential, such as stellar atmospheres or protostellar outflows. Shock fronts in the ISM, combustion flames, and volcanic or lightning-induced reactions on planets might provide this energy (Draine & McKee 1993; Tielens 2005). Reactions R3, R4, R9, R10, R15, and R16 are considered potential gas-grain interactions because they likely involve species that can adsorb onto interstellar dust grains. In these processes, neutral molecules in the gas phase collide with and stick onto dust-grain surfaces with a very high efficiency. This initial attachment is typically physisorption, meaning that the molecules are held on the grain surface via weak van der Waals forces (Semenov et al. 2010) and do not form chemical bonds. When they are adsorbed, the molecules can undergo surface-mediated reactions, which are often critical in cold interstellar environments, in which gas-phase reactions are otherwise inefficient because the temperatures are low. Closer to the midplane of a protoplanetary disks lies the warm molecular layer (a partly X-ray and FUV shielded region). This mildly ionized, dense, and warm layer harbors a complex chemistry, in which gas-grain interactions and endothermic reactions are particularly active. The reactions might be favorable in these regions (Goicoechea et al. 2025; Semenov et al. 2010).
4. Conclusions
As proposed by Rivilla et al. (2021), the HNCCO species must be a key component in the pathway of ethanolamine NH2CH2CH2OH formation. We presented HNCCO species throughout family III, which is composed of f6, f7, f8, and f9. We determined that f6 is the most stable isomer in this family. All the families can be part of the pathway for the formation of ethanolamine (NH2CH2CH2OH), however. Some of them can be detected in environments similar to those in which formylcyanide is found or might contribute to the abundance of formylcyanides through isomerization, as we showed.
The relative intensities of the rotational spectra of the four lowest-lying C2HNO isomers (f1, f2, f4, and f6) can be rationalized based on their permanent dipole moments. Molecules with higher dipole moments are expected to show stronger transitions. In this regard, isomer f4, with the highest dipole moment of 3.58 D, is predicted to yield the strongest rotational signatures, in agreement with the findings of Gronowski et al. (2017) and collaborators. The next most intense transitions are expected for isomer f2, which possesses a dipole moment of 2.49 D. By contrast, the lower dipole moments of f1 and f6 imply that their rotational spectra are weaker, rendering their astronomical detection more challenging unless it is compensated by significantly higher abundances.
In addition, singlet-based photochemistry is likely to dorminate f1 (HCOCN) because of its significant singlet-triplet energy gap (4.12 eV), which is larger than the gap reported in previous works. On the other hand, although the singlet state (X1A′) for f6 (HNCCO) is more stable than the triplet (X3A′), f6 corresponds to the lowest-energy triplet state (X3A′) of the triplets of all isomers we studied. The intramolecular proton shift in the species we studied has a relatively high barrier, as shown in reactions R1, R2, R11, R16. As a result, low-temperature chemistry might proceed via a catalyst assist, such as dust-grain surfaces (surface-mediated), which provide a catalytic role in lowering the activation barriers. This enables energy dissipation and traps reactants for the reactions to occur, which might also be done via tunneling. Since formylcyanide has been observed, this makes the other isomers promising candidates for future detections. The provided activation energies are relevant for simulating the molecular abundances of these species and their concentration over time (Vincenzo & Floriano 2020). Bases on our results, we showed that the computational predictions would improve even better to a realistic threshold for spectroscopic applications, especially if vibrational corrections were included, especially for the B and C constants, for preliminary spectral assignments. Owing to the extremely low temperatures and densities of the ISM, reactions with little or no activation energy are crucial in shaping its chemical inventory. As summarized in Table 6, barrierless processes such as R6, R12, R19, and R20 provide efficient formation routes for HCONC (f2), c-HCNCO (f4), and HNCCO (f6). These reactions proceed without an energetic barrier, which makes them viable even under the harsh conditions of dark interstellar clouds (Simoncic et al. 2020). Importantly, the confirmed detections of the reactant species involved in R20 (the imidogen (NH) radical and the ketenyl radical (CCO)) in diffuse clouds toward ζPersei and HD27778 (Meyer & Roth 1991; Ohishi et al. 1991) provide strong observational evidence supporting the possible formation of HNCCO (f6) in these regions. Taken together, these considerations suggest that HCONC (f2), c-HCNCO (f4), and HNCCO (f6) can be efficiently synthesized in molecular clouds. This makes them promising targets for future astronomical searches. Reaction R8 provides a feasible pathway for a structural rearrangement, allowing HCNCO to access both linear and cyclic forms. This flexibility is crucial for understanding astrochemical stability, spectral signatures, and reaction pathways in environments such as molecular clouds and protoplanetary disks. Reactions R17 and R18 show that barrierless spin-allowed hydrogen additions to HNCCO can form different NH2CHCO isomers. These intermediates provide an important astrochemical route toward complex molecules such as ethanolamine, and they demonstrate that simple interstellar species can lead to prebiotic chemistry under ISM conditions.
These theoretical predictions can then guide experimentalists in localizing and identifying the rotational and vibrational transitions of these systems in either the solid (ice-mantle) phase or in the ice-gas interface under ISM conditions or extraterrestrial environments while acknowledging that these types of predictions are best supported by complementary observational or laboratory data, such as high-resolution rotational spectroscopy, because the interplay between the two plays an invaluable role in the studies of biomolecules (Barone et al. 2023) to assess their potential existence.
Acknowledgments
We acknowledge the PhD scholarship support by the DCA, Universidad Autónoma de Chile. NI acknowledges FONDECYT grant N°1241193 and VRIP.
References
- Alberton, D., Inostroza-Pino, N., Fortenberry, R. C., et al. 2024a, A&A, 691, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alberton, D., Inostroza-Pino, N., Fortenberry, R. C., et al. 2024b, A&A, 683, A198 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alharzali, N., Cernušák, I., Al Rawas, H. K., et al. 2024, J. Phys. Chem. A, 128, 10328 [Google Scholar]
- Allamandola, L. J., Bernstein, M. P., Sandford, S. A., & Walker, R. L. 1999, Evolution of Interstellar Ices (Netherlands: Springer), 219 [Google Scholar]
- Barone, V., Di Grande, S., & Puzzarini, C. 2023, Molecules, 28, 913 [Google Scholar]
- Becke, A. D. 1993, J. Chem. Phys., 98, 1372 [Google Scholar]
- Becke, A. D. 1993, J. Chem. Phys., 98, 5648 [Google Scholar]
- Boger, G. I., & Sternberg, A. 2005, ApJ, 632, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Bogey, M., Demuynck, C., Destombes, J., & Vallee, Y. 1995, J. Mol. Spectrosc., 172, 344 [Google Scholar]
- Boulet, P., Gilardoni, F., Weber, J., Chermette, H., & Ellinger, Y. 1999, Chem. Phys., 244, 163 [Google Scholar]
- Breuer, M., Agliozzo, S., Bassan, M., et al. 1998, Nucl. Instrum. Meth. Phys. Res. A., 415, 156 [Google Scholar]
- Caselli, P. 2012, A&AR, 20, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Chuang, K. J., Fedoseev, G., Qasim, D., et al. 2017, MNRAS, 467, 2552 [NASA ADS] [Google Scholar]
- Clouthier, J. D., & Moule, D. C. 1987, J. Am. Chem. Soc., 109, 6259 [Google Scholar]
- Crawford, T. D., & Schaefer, H. F. 2000, An Introduction to Coupled Cluster Theory for Computational Chemists (Wiley) [Google Scholar]
- Dallas, J. D., Westbrook, B. R., & Fortenberry, R. C. 2021, Front. Astron. Space Sci., 7 [Google Scholar]
- Daniel, F., Agúndez, M., Cernicharo, J., et al. 2012, A&A, 542, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., & McKee, C. F. 1993, ARA&A, 31, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Dunning, T. H. 1989, J. Chem. Phys., 90, 1007 [Google Scholar]
- Flammang, R., Van Haverbeke, Y., Laurent, S., et al. 1994, J. Phys. Chem., 98, 5801 [CrossRef] [Google Scholar]
- Fresneau, A., Danger, G., Rimola, A., et al. 2014, MNRAS, 443, 2991 [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 09, Revision A.02 [Google Scholar]
- Fukui, K. 1981, Acc. Chem. Res., 14, 363 [CrossRef] [Google Scholar]
- Garrod, R. T., Garrod, R. T., Valentine, W., & Eric, H. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Roncero, O., Roueff, E., et al. 2025, A&A, 703, A189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gronowski, M., & Kolos, R. 2015, J. Mol. Struct., 1090, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Gronowski, M., Eluszkiewicz, P., & Custer, T. 2017, J. Phys. Chem. A, A., 121, 3263 [Google Scholar]
- Hacar, A., Bosman, A. D., & van Dishoeck, E. F. 2020, A&A, 635, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hebels, T. 2024, Bachelor’s Thesis, University of Groningen, accessed: 2025-09-01 [Google Scholar]
- Herbst, E. 2021, Front Astron. Space Sci., 8, 207 [Google Scholar]
- Hill, J. G., Mazumder, S., & Peterson, K. A. 2010, J. Chem. Phys., 132, 054108 [Google Scholar]
- Huang, J., Oberg, K. I., Qi, C., et al. 2017, arXiv e-prints [arXiv:1701.01735] [Google Scholar]
- Inostroza-Pino, N., Emmanuel Godwin, O., Mardones, D., & Ge, J. 2024, A&A, 688, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inostroza-Pino, N., McKissick, M., Lattanzi, V., Caselli, P., & Fortenberry, R. C. 2025, Chemistry, 7, 140 [Google Scholar]
- Judge, R., Moule, D., Biernacki, A., et al. 1986, J. Mol. Spectrosc., 116, 364 [Google Scholar]
- Kameneva, S. V., Tyurin, D. A., & Feldman, V. I. 2017, PCCP, 19, 24348 [Google Scholar]
- Krasnokutski, S. A., Jäger, C., Henning, T., et al. 2024, Sci. Adv., 10, 16 [Google Scholar]
- Krishnan, R., Binkley, J. S., Seeger, R., & Pople, J. A. 1980, J. Chem. Phys., 72, 650 [CrossRef] [Google Scholar]
- Kruse, H., Szabla, R., & Šponer, J. 2020, J. Chem. Phys, 152, 214104 [Google Scholar]
- Lewis-Bevan, W., Gaston, R. D., Tyrrell, J., Stork, W. D., & Salmon, G. L. 1992, J. Am. Chem. Soc., 114, 1933 [Google Scholar]
- Li, J., Wu, Y., & Zhang, H. 2013, ApJ, 775, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, J. M. L. 1994, J. Chem. Phys., 100, 8186 [Google Scholar]
- Matthews, D. A., Cheng, L., Harding, M. E., et al. 2020, J. Chem. Phys., 152, 214108 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, D. M., & Roth, K. C. 1991, ApJ, 376, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, K. 1934, Z. Phys. Chem., 165, 123 [Google Scholar]
- Ohishi, M., Ishikawa, S., Yamada, C., et al. 1991, ApJ, 380, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Park, J. W., & Shiozaki, T. 2020, Chem. Rev., 120, 4757 [Google Scholar]
- Potapov, A., Linnartz, H., Kaiser, R. I., Bertin, M., & Fillion, J.-H. 2018, ApJ, 860, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [Google Scholar]
- Ramachandran, R., Sil, M., Gorai, P., et al. 2024, ApJ, 975, 181 [Google Scholar]
- Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2008, APJ, 675, L85 [Google Scholar]
- Rivilla, M. V., Jiménez-Serra, I., Martín-Pintado, J., et al. 2021, PNAS, 118, e2101314118 [NASA ADS] [CrossRef] [Google Scholar]
- Scibelli, S., & Shirley, Y. 2020, ApJ, 891, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simoncic, M., Semenov, D., Krasnokutski, S., Henning, T., & Jäger, C. 2020, A&A, 637, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sylvetsky, N., Kesharwani, M. K., Martin, J. M. L., & Tschumper, G. S. 2014, J. Chem. Theory Comput., 10, 4304 [Google Scholar]
- Tajti, A., Szalay, P. G., Császár, A. G., et al. 2004, JCP, 121, 11599 [Google Scholar]
- Tielens, A. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge: Cambridge University Press) [Google Scholar]
- Tonolo, F., Lupi, J., Puzzarini, C., & Barone, V. 2020, ApJ, 900, 85 [Google Scholar]
- Toumi, I., Dalbouha, S., Al-Mogren, M. M., et al. 2022, J. Phys. Chem. A, 126, 7230 [Google Scholar]
- Tsuge, M., Kouchi, A., & Watanabe, N. 2021, arXiv e-prints [arXiv:2109.12734] [Google Scholar]
- Turro, N. J., Ramamurthy, V., & Scaiano, J. C. 2010, Modern Molecular Photochemistry of Organic Molecules (University Science Books) [Google Scholar]
- Vincenzo, A. D., & Floriano, M. A. 2020, J. Chem. Educ., 97, 3630 [Google Scholar]
- Watanabe, N., & Kouchi, A. 2002, ApJ, 571, L173 [Google Scholar]
- Watanabe, N., & Kouchi, A. 2008, Prog. Surf. Sci., 83, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, J. K. G., & Durig, J. R. 1977, Vibrational Spectra and Structure (Amsterdam: Elsevier), 6, 1 [NASA ADS] [Google Scholar]
- Watts, J. D., Gauss, J., & Bartlett, R. J. 1993, J. Chem. Phys., 98, 8718 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H. J., Knowles, P. J., Knizia, G., et al. 2010, MOLPRO, version 2010.1, a package of ab initio programs, https://www.molpro.net [Google Scholar]
- Woon, D. E., & Dunning, Thom H., Jr 1994, J. Chem. Phys., 100, 2975 [Google Scholar]
- Zeng, S., Rivilla, V. M., Jiménez-Serra, I., et al. 2023, MNRAS, 523, 1448 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Energetics, geometry, and spectroscopic characterization of the isomers
This appendix provides an overview of the computed energetics, geometries, and spectroscopic parameters of the other C2HNO isomers. Table A.1 lists the relative energies (Er), zero-point corrected energies (ErZPVE), structural parameters, rotational constants, vibrational frequencies (ω), and dipole moments (μ).
Energetics, geometry and spectroscopic parameters of C2HNO isomers computed at the CCSD(T)-F12/cc-pVTZ-F12 level of theory.
Appendix B: Spectroscopic parameters of the isomers
This appendix summarizes the detailed spectroscopic parameters of the other C2HNO isomers and their level of theory. Table B.1 lists the rotational constants and centrifugal distortion constants (quartic and sextic) for isomers f5, f11, and f12, computed at the MP2/aug-cc-pVTZ level of theory. Additional rotational data for f11 and related isomers are provided in Table B.2, while vibrational frequency data are collected in Table B.3.
Rotational and centrifugal distortion constants (quartic and sextic) of isomers f5, f11, and f12 calculated at the MP2/aug-cc-pVTZ level of theory.
Rotational constants and centrifugal distortion constants (quartic and sextic) of f9, f10, f13, and f15 calculated at MP2/aug-cc-pVTZ level of theory.
Fundamental frequencies and anharmonic frequencies (cm−1) for the various isomers of C2HNO computed at MP2/aug-cc-pVTZ level of theory.
All Tables
Structural parameters, relative energy (kJmol−1), equilibrium rotational constant (GHz), and frequencies (cm−1) of the C2HNO isomers at the CCSD(T)-F12/cc-pVTZ-F12 level of theory.
Vertical excitation energy, transition dipole moment (μ), and oscillator strength of the first three lowest electronic excited states of four isomers of C2HNO computed at CIS.
Rotational constants (MHz) and centrifugal distortion constants (quartic and sextic) of f1, f2, f4, and f6, calculated at the MP2/aug-cc-pVTZ level of theory.
Fundamental vibrational frequencies (experimental vs. theoretical) of f1 and the three most stable isomers (f2, f4, and f6) of C2HNO, calculated at the MP2/aug-cc-pVTZ level of theory.
Formation and destruction pathways of HCONC (f2), HCNCO (f5), and HNCCO (f6) with their activation energies (energy barriers) and the thermodynamic nature of the reactions (enthalpy) at two different levels of theory.
Energetics, geometry and spectroscopic parameters of C2HNO isomers computed at the CCSD(T)-F12/cc-pVTZ-F12 level of theory.
Rotational and centrifugal distortion constants (quartic and sextic) of isomers f5, f11, and f12 calculated at the MP2/aug-cc-pVTZ level of theory.
Rotational constants and centrifugal distortion constants (quartic and sextic) of f9, f10, f13, and f15 calculated at MP2/aug-cc-pVTZ level of theory.
Fundamental frequencies and anharmonic frequencies (cm−1) for the various isomers of C2HNO computed at MP2/aug-cc-pVTZ level of theory.
All Figures
 |
Fig. 1. Comparative analysis of the potential energies of the isomers and conformers of C2HNO with energy variations. The relative energies are computed at the CCSD(T)-F12/cc-pVTZ-F12 level of theory. f3 corresponds to the transition state (TS). |
| In the text | |
 |
Fig. 2. Relative energy level diagram of the C2HNO isomers with respect to the global minimum (f1) computed at the CCSD(T)-F12/cc-pVTZ-F12 level of theory. |
| In the text | |
 |
Fig. 3. Comparison of the isomer and conformer energies of the general formula C2HNO for f1 (formyl cyanide) observed in Sgr B2 (Remijan et al. 2008), computed using MP2/aug-cc-pVTZ, CCSD(T)-F12/cc-pVTZ-F12, and CCSD(T)-F12/cc-pCVTZ-F12. |
| In the text | |
 |
Fig. 4. Reaction energy profile for the conversion of f1 to f2 via the transition state f3. The energies were computed at the CCSD(T)-F12/cc-pVTZ-F12 level of theory. |
| In the text | |
 |
Fig. 5. Singlet–triplet electronic energy gaps for the f1 and f6 C2HNO isomers, calculated at the CCSD(T)-F12/cc-pVTZ-F12 level of theory. |
| In the text | |
 |
Fig. 6. Vertical excitation energy of HCOCN (f1), f2, and f4 vs. that of HNCCO (f6). |
| In the text | |
 |
Fig. 7. Formation pathways of HNCCO. The chemical species depicted in the square blue box were identified in the ISM, and those in pink are not yet identified. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.