| Issue |
A&A
Volume 702, October 2025
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202556334 | |
| Published online | 30 September 2025 | |
Letter to the Editor
Scale-invariant vacuum guided resolution of the 7Li BBN problem
1
Institute for Advanced Physical Studies, Sofia, Bulgaria
2
National Coalition of Independent Scholars, Battleboro, VT, USA
3
Ronin Institute for Independent Scholarship 2.0, Sacramento, CA, USA
⋆ Corresponding author.
Received:
9
July
2025
Accepted:
10
September
2025
A possible resolution of the 7Li problem within the scenario of the standard model big bang nucleosynthesis (BNN) is presented. The key idea originates from the application of the scale-invariant vacuum (SIV) paradigm to the BBN. However, here we arrive at the conclusion that reparametrization-invariant symmetry scaling (RISS) is the more appropriate framework for the epoch of the BBN and use the SIV only as a guidance framework. The outcome is a χ2 < 0.04 fit to the observed primordial abundances of 4He, D/H, 3He/D, and a fit of χ2 ≈ 1 when including 7Li/H observations. The results are obtained and compared to the known standard BBN values by utilizing the publicly available PRIMAT code. The resolution of the 7Li problem requires a SIV-guided deviation from the local thermal equilibrium during BBN, such that the thermal energy of matter and radiation scale differently with respect to the SIV-conformal factor λ during the BBN epoch. This may be viewed as conformal symmetry breaking due to cooling of plasma and the properties of matter, which means that the framework may be of relevance to the problem of nuclear fusion as well. The deduced baryon matter content is Ωb ≈ 12% for unbroken SIV and Ωb ≈ 38% for partially broken SIV, but with λ < 1 in both cases, which signals preference for RISS over the conventional SIV viewpoint. Applying the RISS paradigm results in λ > 1 and Ωb ≈ 10% with a clear departure of nT from the naive SIV suggested value. In all the cases where the 7Li problem is resolved, the baryon content is significantly higher than the usually accepted value of Ωb ≈ 4.9% within the Lambda cold dark matter (ΛCDM) model.
Key words: nuclear reactions, nucleosynthesis, abundances / cosmology: theory / dark matter / early Universe / primordial nucleosynthesis
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Big Bang nucleosynthesis (BBN), first proposed by Gamow (1946) and later studied in detail by Coc & Vangioni (2017) and Iliadis & Coc (2020), predicts the primordial abundances of light elements, such as deuterium and helium-4 (Wagoner et al. 1967; Steigman 2007; Coc & Vangioni 2017; Iliadis & Coc 2020), in close agreement with astrophysical observations. This match is a cornerstone of the standard cosmological model Coc & Vangioni (2017). A major exception is lithium-7: the standard BBN overestimates its primordial abundance by a factor of three to four compared to observations of metal-poor halo stars (Cyburt et al. 2003; Coc et al. 2004; Cuoco et al. 2004; Asplund et al. 2006; Sbordone et al. 2010; Hou et al. 2017; Iliadis & Coc 2020). This discrepancy, known as the cosmological lithium problem (CLP) (Boesgaard & Steigman 1985; Steigman 2007; Hou et al. 2017), has persisted despite decades of attempts involving astrophysical, nuclear, and particle-physics solutions (Fields 2011; Cyburt et al. 2016; Coc & Vangioni 2017; Iliadis & Coc 2020). Its persistence shows the limits of our knowledge of stellar astrophysics and nuclear processes, and may even suggest new physics beyond the standard model (Hou et al. 2017; Coc & Vangioni 2017). Solving this problem is crucial in order to test the strength of BBN and to probe for new fundamental physics.
The scale-invariant vacuum (SIV) paradigm provides analytic expressions that allow an initial study of BBN (Maeder 2019; Gueorguiev & Maeder 2025a). This capability makes the SIV framework promising for BBN studies with computational tools such as the PRIMAT Mathematica code (Pitrou et al. 2018). The SIV paradigm has explained several astrophysical phenomena, including galactic rotation curves and density fluctuations, without dark matter (Maeder & Gueorguiev 2020; Gueorguiev & Maeder 2024). Despite its Lagrangian formulation Maeder & Gueorguiev (2023), the framework lacks a dynamical basis for λ. Instead, it relies on heuristic arguments, such as scale invariance of empty space and large-scale homogeneity, which may not hold at all scales or in matter-dominated regions. To address this, a new framework–reparametrization-invariant symmetry scaling (RISS) (Gueorguiev 2024, 2025) – has been proposed. Here, the gauge factor arises from time reparametrization invariance of physical laws rather than from vacuum symmetry assumptions Gueorguiev & Maeder (2025b). The RISS paradigm, while rooted in scale invariance, treats the conformal scale transformation differently and explores its implications for physical laws (Gueorguiev & Maeder 2021a). This leads to distinct predictions for processes such as primordial nucleosynthesis, the focus of this work. We extend the SIV approach to BBN beyond the analytic results of (Maeder 2019) and (Gueorguiev & Maeder 2025b), by using the PRIMAT code (Pitrou et al. 2018).
Early Universe cosmology, essential for BBN, rests on fundamental constants. These include H0, ρc0, G, T0, the blackbody constant aBB, and Boltzmann’s constant kB. In computational tools such as PRIMAT Pitrou et al. (2018), natural units are used (c = 1, kB = 1, ℏ = 1) with cosmological parameters Ωm = 0.31 and Ωb = 0.05. Modeling BBN requires solving thermonuclear reactions that govern nuclear abundances, expressed as Yi = ni/nb. Reaction rates are Γij → kl = nbγij → kl, in units of s−1. Forward and reverse rates satisfy 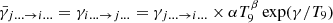 , with T9 in GK, assuming local thermodynamic equilibrium. Time evolution follows the Friedmann-Lemaître-Robertson-Walker (FLRW) equation,
, with T9 in GK, assuming local thermodynamic equilibrium. Time evolution follows the Friedmann-Lemaître-Robertson-Walker (FLRW) equation, 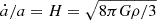 , which integrates to the cosmic time variable τ. The total energy density ρ includes radiation, matter, and corrections from neutrino decoupling. The latter introduces a distortion factor 𝒮(T) into the temperature–scale factor relation, Ta(T)𝒮1/3(T) = T0a0, relevant to near electron-positron annihilation. The 𝒮(T) affects the baryon-to-photon ratio η, linking constants, energy densities, time evolution, and the thermal history of the Universe Gueorguiev & Maeder (2025a).
, which integrates to the cosmic time variable τ. The total energy density ρ includes radiation, matter, and corrections from neutrino decoupling. The latter introduces a distortion factor 𝒮(T) into the temperature–scale factor relation, Ta(T)𝒮1/3(T) = T0a0, relevant to near electron-positron annihilation. The 𝒮(T) affects the baryon-to-photon ratio η, linking constants, energy densities, time evolution, and the thermal history of the Universe Gueorguiev & Maeder (2025a).
2. SIV guided method
The SIV framework for BBN introduces a near-constant scaling parameter λ, evolving from 1/tin in the early Universe to unity today. A key distinction is the use of different scaling exponents for rest-mass energy (nm = +1) and thermal energy (nT = −1/2), i.e., m → mλnm and T → TλnT. This follows from the conservation laws for matter (w = 0) and radiation (w = 1/3), governed by the SIV relation ρwa3(1 + w)λ1 + 3w = ρ0 (Maeder 2017, 2019). Despite their differences, energy conservation holds Gueorguiev & Maeder (2025a) since the λ-scaling of radiation energy matches rest-mass energy scaling in finite systems during photon absorption or emission. This imposes the constraint nm − 3 = 4nT, consistent with the SIV values.
These scalings require changes to thermonuclear reaction rates in tools such as PRIMAT. Forward rates are modified by a temperature factor λnT, while reverse rates include combined mass and temperature scalings, λnm + nT and λnm − nT, for terms such as γ/T9. The time parametrization in the SIV frame, dτ′=λdτ, means the Einstein general relativity (EGR) frame rates must also be rescaled by λ. This agrees with the λ-scaling of Gρ from the FLRW equation and ensures consistency across epochs. Radiation and matter energy densities are modified by λ4nT and λnm − 3, respectively, maintaining ρ scaling and time evolution. The PRIMAT scale factor a(T) and functions such as δρ(T) are corrected by rescaling their temperature arguments by λnT, giving a self-consistent SIV integration into BBN computations. The fit quality parameter χ2 is then used to compare theory with observations, scanning parameter space for Ωb and λ while fixing Ωd = 0, since dark matter has a negligible impact on the radiation-dominated BBN epoch.
This gives the first modifications for the forward and reverse reaction terms: γj…→i…(T)→γj…→i…(λnTT),αT9βexp(γ/T9) → α(λnm + nTT9)βexp(λnm − nTγ/T9). The scaling factors used throughout the text are Ť = λnT – overall temperature rescaling for forward reactions; mŤ = λnm + nT – combined scaling for mass and temperature; Q/Ť = λnm − nT – scaling for energy-to-temperature ratios such as γ/T9 in reverse rates. Auxiliary functions such as δρ(T) and 𝒮(T) also require modification. These are obtained by pulling back the corresponding EGR functions. For example, the SIV version of 𝒮′(T′) is 𝒮(T) = 𝒮′(T′(T)) = 𝒮′(TλnT), and similar transformations apply to dimensionless functions such as δρ(T).
3. Results
The results are summarized in Table 1, and show the abundances of key elements produced during BBN. The second column lists the observed values, and the third shows the results from the PRIMAT code. For this work, PRIMAT was run with a reduced network of 13 reactions, neutrinos were treated as decoupled, and quantum electrodynamics (QED) dipole corrections were omitted. These corrections have only a minor effect and are negligible for this study.
Light element abundances from standard and SIV-guided BBN under various scaling assumptions.
Baseline PRIMAT predictions: Using PRIMAT with standard cosmological parameters, Ωb = 4.9% for baryons and Ωm = 31% for total matter, gives abundances consistent with observations. Setting Ωd = 0 (so Ωm = Ωb) leaves the results unchanged. This reflects the radiation-dominated epoch, where nucleosynthesis depends on radiation density and baryon-photon interactions, not dark matter.
Marginal impact of neutrino and QED effects: Partially decoupled neutrinos or QED dipole corrections cause only small shifts and do not affect the main conclusions. Standard model neutrino decoupling and finite-temperature–QED effects produce shifts of order 10−3–10−4 in BBN yields, leaving the overall pattern unchanged (Froustey & Pitrou 2020; Pitrou et al. 2018; Pitrou & Pospelov 2020). This confirms that the simplified model is sufficient to capture the main SIV features.
Dark matter irrelevance in the BBN context: As expected, dark matter plays no role during the radiation-dominated epoch. Nucleosynthesis processes are unaffected by its presence or absence, showing that radiation sets the elemental abundances.
A parameter-space search reveals minimal χ values for λ > 0.5 with Ωd = 0. The scaling exponents nT and nm were varied to test their impact on abundances. Earlier SIV-guided methods Gueorguiev & Maeder (2025a) could not fully probe regions near λ = 1, where the lowest χ often occurs for nT = nm. To address this, a direct search was used, avoiding constraints on initial conditions and extending the analysis into unexplored regimes. Fits were performed over Ωb, λ, and the exponents nT and nm were treated as real numbers.
Table 1 highlights the robustness of the BBN formalism without dark matter. The results show not just numerical consistency but also theoretical coherence within SIV, even where it departs from standard approaches. The agreement with observed abundances, combined with the novel λ-based scalings, points to the promise of SIV as a cosmological framework.
The fourth to seventh columns show the best-fit results for a two-parameter fit over Ωb and λ > 0.5, for specific choices of nT and nm. The first case (column four, SIV0) follows the values motivated by earlier studies of BBN in the SIV framework Gueorguiev & Maeder (2025a). Here nT = −1/2 and nm = 0, reflecting the expectation that in the radiation epoch nT = −1/2, and that the pull-back of relevant functions may also allow nm = 0, as discussed in Gueorguiev & Maeder (2025a).
In the following cases, radiation and matter are in local thermal equilibrium, so both scale the same way (nT = nm). Specific values can then be assigned. The fifth column, labeled ℏ, reflects the assumption that ℏ acts as a conversion constant. Since thermal energy E = kBT is linked to the Planck relation E = ℏω, the SIV rescaling of time intervals dτ′=λdτ implies kBT′=kBTλ−1; thus, ℏ behaves as an in-scalar in this case. The next columns further explore the condition nT = nm for SIV-motivated epochs. Table 1 shows that these cases resemble the standard PRIMAT results, but with slightly different Ωb values. Imposing nT = nm tends to drive λ toward 1, in sharp contrast with the SIV expectation that λ should be greater than 1. The values of λ < 1 become prominent in the next set of columns. The eighth column (fit0) represents a three-parameter fit over −1 < nT < 1, together with Ωb and λ, but with nT = nm.
For all these cases the goodness of fit indicator χ is very small (almost zero or less than 0.1) when considering only 4He and deuterium data. When 3He is added, χ is between 0.15 and 0.25 indicating that the 7Li is the hardest data point to be described with such model parameters. The situation changes in the subsequent cases where nT ≠ nm, which brings the overall χ below 6 due to improvement in the 7Li. In these cases χ for 4He and deuterium is still often less than 0.1, but when 3He is added then χ could be above 1 showing that 3He is becoming a challenging data point as well.
The SIV-guided deviation from local thermal equilibrium begins with the two-parameter fit over Ωb and λ, shown in column SIV1. Column fit1 is a three-parameter fit over −1 < nT < 1, Ωb, and λ > 0.5, similar to fit0, but with the constraint nm = 3 + 4nT. The first column with λ = 1 is not a fit; it illustrates the effect of reverting to the standard time determination, while keeping the rescaling factors Ť, mŤ, and Q/Ť from the fit1 case. The next column shows a three-parameter fit over Ωb with temperature and mass scalings restricted to within 20% of the fit1 values. These results highlight the importance of distinct temperature and mass scalings for addressing the 7Li problem. While fit2 is a minimalistic fit, and loosely resembles Tsallis non-extensive statistics (Hou et al. 2017), it is difficult to justify in a simple way, as discussed in the next section.
The last three columns adopt the RISS perspective, where ℏ is fixed and nm = −1. The first choice keeps the SIV expectation nT = −1/2, which does not solve the 7Li problem. This may reflect a violation of the conserved quantity ρwa3(1 + w)λ1 + 3w = ρ0 and departures from nT = −1/2 and nρ = −2, as suggested by the role of the distortion term 𝒮(T). Such non-conservation also alters the scaling of ρ. One must then consider Gλ3 − nm − 2nT + nρρ(TλnT), which reduces to Gρ(T)λ4nT when nm = −1, nρ = −2, and nT = 1. There may be a factor λnρ, as explained in the caption of Table 1. Notably, for w = 1/3, nT is not −1/2, but closer to 0.9.
 |
Fig. 1. Element abundance for the case corresponding to fit* in Table 1. We note the similarity with the figures in the Appendix of Gueorguiev & Maeder (2025a) for the standard BBN and SIV case discussed there. |
4. Interpretation and conclusions
The SIV paradigm introduces specific modifications to reaction rates and their temperature dependence, necessary to maintain consistency between the EGR and Weyl integrable geometry (WIG) frames. As Table 1 shows, some cases produce Lambda cold dark matter (ΛCDM)-compatible baryon densities around Ωb ≈ 4%, but most do not solve the 7Li problem. Three cases yield χ ≈ 1, which usually indicates agreement between theory and observations within uncertainties. These cases offer a potential solution to the 7Li problem, which could improve further if astrophysical processes reduce the 7Li abundances (Navas et al. 2024). Pure astrophysical effects cannot reduce 7Li by a factor of 3–4, but along with possible 3He adjustments, it may help bring the overall χ value below 1 using the current approach.
The results suggest that resolving the 7Li problem may involve a deviation from local thermal equilibrium. An increased effective temperature (Ť > 1) is required in all cases with χ < 6. Within conventional physics, this could reflect local inhomogeneous matter moving with specific velocity, experiencing a higher surrounding radiation temperature. Even though this aligns with the idea that high-energy particles approach a massless state, the reduced mass-energy scale (mŤ < 1, Q/Ť < 1) is difficult to justify without a specific model. Tsallis non-extensive statistics (Hou et al. 2017) also provides no physical explanation for such deviations.
The λ-independent fit (fit2) with χ ≈ 1 yields Ť, mŤ, and Q/Ť values similar to fit1, the SIV-motivated relational choice; fit1 indicates partial breaking of scale-invariant symmetry, as nT deviates from the SIV value −1/2. Although Ť, mŤ, and Q/Ť are similar for fit1 and fit2, differences in Ωb arise from different constructions of the time parameter.
Applying SIV rules requires different scaling for matter and radiation. The best fit with nT = nm (fit0) cannot reach χ ≈ 1, while the SIV-motivated choice nT = −1/2 with nm = 3 + 4nT approaches χ ≈ 1 at nT = −0.55 (fit1). This indicates broken scale invariance due to the presence of matter. The distortion term 𝒮(T), arising from annihilation processes, modifies the relationships between a, ρ, T, and λ, implying deviations from conservation of the SIV quantity ρwa3(1 + w)λ1 + 3w, and thus a departure from the SIV-predicted nm and nT. This departure can be accommodated within the RISS framework.
SIV and RISS both use a time-dependent conformal factor λ(t), with conformal transformations keeping c fixed. SIV begins with a general λ(x) and restricts to time dependence due to large-scale homogeneity and isotropy. Neglecting ℏ and keeping G constant is reasonable for cosmological units, but may fail on smaller scales where homogeneity breaks down. RISS, on the other hand, starts with λ(t) derived from the fundamental symmetry of time reparametrization invariance for the description of process, applicable at all scales. Thus, keeping ℏ constant is relevant for BBN within RISS.
SIV breaking is also evident when λ < 1, which conflicts with the expected SIV gauge form λ = t0/t, where 0 ≤ tin < t ≤ t0 implies λ > 1 before the present time t0, often set to 1. The λ < 1 issue suggests that reparametrization invariance may provide a more general view than enforcing the SIV gauge. While SIV and RISS lead to similar equations (Gueorguiev & Maeder 2021b), RISS does not fix the functional form of λ(t). Then, the specific value of λ can be interpreted as a correction to the overall scale of the distortion factor 𝒮(T) defining a(T). This scale correction could reflect the effects of reheating and recombination that establish the observed CMB temperature T0. From the PRIMAT expression T a(T) = a0T0/𝒮1/3(T), taking a → a0 = 1 gives T0, but this is after BBN and does not include reheating and recombination. Thus, the SIV λ-correction to a(T) restores the correct post-BBN temperature, expected to differ from the standard CMB value: 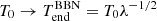 . In our experience, this correction to 𝒮(T) or T0 alone can resolve the minor discrepancy between theory and observation in deuterium abundance. Potential primordial deuteron tension was indicated by Pitrou et al. (2021), but this arose from differing rate evaluations. Comparisons of BBN codes (PRIMAT/PRyMordial/PArthENoPE) show small differences once networks and rates are harmonized Giovanetti et al. (2024). This also suggests future potential test and validations of the current results by using alternative BBN codes and reaction rates. Since SIV and RISS rely on time-dependent conformal transformations, obtaining a nearly constant λ(t) to fit light-element abundances indicates conformal symmetry breaking due to matter production and plasma temperature reduction.
. In our experience, this correction to 𝒮(T) or T0 alone can resolve the minor discrepancy between theory and observation in deuterium abundance. Potential primordial deuteron tension was indicated by Pitrou et al. (2021), but this arose from differing rate evaluations. Comparisons of BBN codes (PRIMAT/PRyMordial/PArthENoPE) show small differences once networks and rates are harmonized Giovanetti et al. (2024). This also suggests future potential test and validations of the current results by using alternative BBN codes and reaction rates. Since SIV and RISS rely on time-dependent conformal transformations, obtaining a nearly constant λ(t) to fit light-element abundances indicates conformal symmetry breaking due to matter production and plasma temperature reduction.
The interpretation of λ remains unclear within SIV. In RISS, however, it can be viewed as a gravitational effect on the unit of time. In the early Universe, when matter was denser, the gravitational influence on atomic clocks could shorten the effective time unit, which can be represented by λ. If λ is constant, this is equivalent to a change in units that does not alter the physics. If λ(t) varies with time, equations must remain reparametrization-invariant to avoid artificial effects in physical conclusions (Gueorguiev 2024, 2025).
It has been shown that assuming λ ≈ const. during BBN allows one to use 𝒮(T) within the SIV framework, or treat SIV as a background effect within standard BBN. This produces results compatible with standard BBN (see Table 1). To fit the observational data, one must depart from the standard SIV expression λ = 1/tin ≈ 1/Ωm1/3 ≥ 1, which is linked to the analytical solution a(t) as a function of Ωm (Jesus 2017). This departure allows a reduction of χ, as seen in columns SIV1 and fit1 in Table 1.
A pure SIV calculation with nT = −1/2 and nm = 1 gives Ωb ≈ 12%, while a partially broken SIV yields nT = −0.55, nm = 0.79, and Ωm ≈ 38%. The higher baryon content also increases the photon-to-baryon ratio to η10 ≈ 15, about 2.5 times the standard value of 6.09. In this study, η is treated as in-scalar (baryon-to-photon number ratios), but the expression may be reevaluated if temperature is used as a proxy for photon density.
The differences in the specific Ωm values should be viewed as artifacts of model assumptions. Determining the appropriate model parameters and achieving the same level of concordance as standard BBN with ΛCDM remains a long-term task. This exploration may also shed light on the Hubble tension. The discrepancy between the CMB-inferred and locally measured Hubble constants could potentially be addressed within the SIV gauge, since the relevant cosmic evolution is mostly in the matter-dominated epoch. However, for the early Universe, the RISS paradigm may be more appropriate. Its ultimate test would involve using the inverse temperature as the time parameter for BBN, t = T0/T, which would also require extending the FLRW equations to a fully reparametrization-invariant form.
The main conclusion is that the SIV paradigm offers useful guidance for constructing a BBN model compatible with the observed abundances of 4He, D/H, T/H, and 7Li/H, as achieved in standard BBN. While SIV faces the same 7Li problem as standard BBN, it also suggests a potential SIV-guided departure from local thermal equilibrium, as interpreted within RISS, which could help resolve the 7Li problem. This departure may also be relevant for nuclear fusion processes.
References
- Asplund, M., Lambert, D. L., Nissen, P. E., Primas, F., & Smith, V. V. 2006, ApJ, 644, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Boesgaard, A. M., & Steigman, G. 1985, ARA&A, 23, 319 [Google Scholar]
- Coc, A., & Vangioni, E. 2017, Int. J. Mod. Phys. E, 26, 1741002 [CrossRef] [Google Scholar]
- Coc, A., Vangioni-Flam, E., Descouvemont, P., Adahchour, A., & Angulo, C. 2004, ApJ, 600, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Cuoco, A., Iocco, F., Mangano, G., et al. 2004, Int. J. Mod. Phys. A, 19, 4431 [Google Scholar]
- Cyburt, R. H., Fields, B. D., & Olive, K. A. 2003, Phys. Lett. B, 567, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Fields, B. D., Olive, K. A., & Yeh, T.-H. 2016, Rev. Mod. Phys., 88, 015004 [NASA ADS] [CrossRef] [Google Scholar]
- Fields, B. D. 2011, Annu. Rev. Nucl. Part. Sci., 61, 47 [CrossRef] [Google Scholar]
- Froustey, J., & Pitrou, C. 2020, Phys. Rev. D, 101, 043524 [Google Scholar]
- Gamow, G. 1946, Phys. Rev., 70, 572 [CrossRef] [Google Scholar]
- Giovanetti, C., Lisanti, M., Liu, H., Mishra-Sharma, S., & Ruderman, J. T. 2024, arXiv e-prints [arXiv:2408.14538] [Google Scholar]
- Gueorguiev, V. G. 2024, J. Phys. Conf. Ser., 2910, 012014 [Google Scholar]
- Gueorguiev, V. G. 2025, J. Phys. Conf. Ser., 3002, 012003 [Google Scholar]
- Gueorguiev, V. G., & Maeder, A. 2021a, Symmetry, 13, 522 [Google Scholar]
- Gueorguiev, V. G., & Maeder, A. 2021b, Symmetry, 13, 379 [Google Scholar]
- Gueorguiev, V. G., & Maeder, A. 2024, Symmetry, 16, 657 [Google Scholar]
- Gueorguiev, V. G., & Maeder, A. 2025a, MNRAS, 539, 2926 [Google Scholar]
- Gueorguiev, V. G., & Maeder, A. 2025b, Universe, 11, 48 [Google Scholar]
- Hou, S. Q., He, J. J., Parikh, A., et al. 2017, ApJ, 834, 165 [Google Scholar]
- Iliadis, C., & Coc, A. 2020, ApJ, 901, 127 [Google Scholar]
- Jesus, J. F. 2017, arXiv e-prints [arXiv:1712.00697] [Google Scholar]
- Maeder, A. 2017, ApJ, 834, 194 [Google Scholar]
- Maeder, A. 2019, arXiv e-prints [arXiv:1902.10115] [Google Scholar]
- Maeder, A., & Gueorguiev, V. G. 2020, Universe, 6, 46 [Google Scholar]
- Maeder, A., & Gueorguiev, V. G. 2023, Symmetry, 15, 1966 [Google Scholar]
- Navas, S., Amsler, C., Gutsche, T., et al. 2024, Phys. Rev. D, 110, 030001 [CrossRef] [Google Scholar]
- Pitrou, C., & Pospelov, M. 2020, Phys. Rev. C, 102, 015803 [Google Scholar]
- Pitrou, C., Coc, A., Uzan, J.-P., & Vangioni, E. 2018, Phys. Rep., 754, 1 [Google Scholar]
- Pitrou, C., Coc, A., Uzan, J.-P., & Vangioni, E. 2021, MNRAS, 502, 2474 [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A&A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steigman, G. 2007, Annu. Rev. Nucl. Part. Sci., 57, 463 [CrossRef] [Google Scholar]
- Wagoner, R. V., Fowler, W. A., & Hoyle, F. 1967, ApJ, 148, 3 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Light element abundances from standard and SIV-guided BBN under various scaling assumptions.
All Figures
 |
Fig. 1. Element abundance for the case corresponding to fit* in Table 1. We note the similarity with the figures in the Appendix of Gueorguiev & Maeder (2025a) for the standard BBN and SIV case discussed there. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


