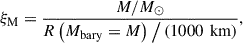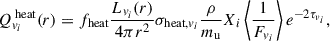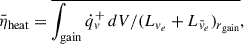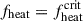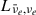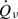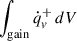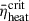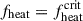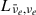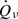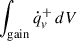EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 704 (December 2025) A&A, 704 (2025) A46 Full HTML
Open Access
Issue
A&A
Volume 704, December 2025
Article Number A46
Number of page(s) 13
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202555081
Published online 27 November 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

At the conclusion of massive star evolution, when the electron degeneracy pressure is no longer sufficient to counteract gravitational forces, the iron core undergoes collapse. Upon reaching nuclear saturation compactness, neutron degeneracy pressure renders the core rigid and incompressible. The infalling material generates a shock wave as it impacts the core (Janka 2017). The shock wave can weaken and stall as a result of two primary processes: the dissociation of heavy nuclei preceding the shock front (Colgate & White 1966), and the subsequent loss of neutrinos, which leads to the formation of an accretion shock wave (Janka 2017). If the shock wave successfully revives and breaks out of all envelopes, the supernova will successfully explode (Horiuchi et al. 2011; Li et al. 2011), leaving a neutron star, or forming a black hole (BH) via fallback accretion (Kuroda et al. 2018; Chan et al. 2018; Burrows et al. 2023; Heger et al. 2023). If the shock wave revives but fails to break out of the outer envelope, or if the shock wave fails to revive at all, the star will undergo failed supernova (FSN), forming a black hole (Fischer et al. 2009; O’Connor & Ott 2011; Heger et al. 2023; Boccioli et al. 2025). It is very important to understand the mechanics of core-collapse supernovae (CCSNe) and predict which progenitors will undergo explosion (Gogilashvili et al. 2023; Diehl et al. 2021; Fischer et al. 2009; Smartt 2015; Heger et al. 2023).

The prevailing shock-revival theory is the neutrino delayed-heating mechanism proposed by Bethe & Wilson (1985), which has been broadly supported by multidimensional simulations Janka (2025). This theory posits that hundreds of milliseconds after the initial rebound, electron-type neutrinos and antineutrinos transfer thermal energy from the protoneutron star (PNS) to the material located behind the shock wave. When the post-shock material attains sufficient energy, the shock wave is revitalized and continues to propagate outward (Janka 2017; Bethe & Wilson 1985). Notably, in the vast majority of one-dimensional (1D) supernova simulations, the neutrino heating mechanism proves inadequate for triggering a supernova explosion (Horowitz 2002; Burrows et al. 2006; Fischer et al. 2017) unless the neutrino heating efficiency is significantly enhanced (Gogilashvili et al. 2023; Liebendörfer et al. 2005; Buras et al. 2006a; Müller et al. 2017; Radice et al. 2017). With the enhancement of computational capabilities, it has become possible to conduct 2D (Miller et al. 1993; Herant et al. 1994) and 3D (Janka & Mueller 1996; Fryer & Warren 2002) CCSNe simulations. Multidimensional simulations can enable successful CCSNe explosions (Lentz et al. 2015; Müller 2015; Bruenn et al. 2016; Müller et al. 2019; Burrows et al. 2020; Vartanyan & Burrows 2023). The advancement of multidimensional simulations has brought to light additional explosion mechanisms, such as neutrino-driven turbulence and convection, which are increasingly recognized for their critical roles in supernova dynamics (Murphy & Burrows 2008; Mabanta & Murphy 2018). Consequently, assessing the potential for a supernova to explode necessitates multidimensional simulations.

Multidimensional simulations are extremely time-consuming and computationally intensive, however (Boccioli et al. 2021; Gogilashvili et al. 2023). In contrast, 1D simulations are significantly faster. O’Connor et al. (2018) conducted a comprehensive comparison of several simulation codes designed to study the CCSNe mechanism and found that the results from most codes were similar. This ensures the reliability of the code and provides a foundation for studying the effects of different parameters on supernova explodability.

Through 1D parametric simulations, certain physical parameters of pre-supernova stars are correlated with their explosive outcomes (Boccioli et al. 2021). These parameters allow us to rapidly assess the potential for pre-supernova stars to explode. To do this, O’Connor & Ott (2011) proposed the compactness parameter ξ2.5, Pejcha & Thompson (2015) employed the critical neutrino luminosity, Ertl et al. (2016) also introduced a method using two parameters, and Müller et al. (2016) used five physically motivated parameters to determine the outcomes. More recently, Maltsev et al. (2025) formulated a multiparameter criterion based on a large set of stellar models and achieved an accuracy of > 99% in predicting the outcomes of a semi-analytic supernova model.

Of all the models mentioned above, the compactness parameter ξ2.5 proposed by O’Connor & Ott (2011) to predict the explodability of pre-supernova stars is the simplest and most widely applied Heger et al. (2023). Some multidimensional simulations have cast doubt on the use of compactness for predicting pre-supernova explodability, however. Examples are the 2D simulations of 100 stars by Vartanyan & Burrows (2023) and Wang et al. (2022), along with the 3D simulations by Burrows et al. (2019, 2020, 2024). The criterion ξ2.5 is based on the 1D supernova collapse simulation code GR1D (O’Connor & Ott 2010; O’Connor 2015). Significant difficulties arise in one-dimensional simulations from the absence of neutrino-driven turbulence and convective motion for evaluating explodability. In the simulations, O’Connor & Ott (2011) therefore artificially increased the neutrino heating rate in the post-shock matter until explosions were triggered and then statistically determined the critical time-averaged heating efficiency required (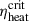 η heat crit $ \eta_{\mathrm{heat}}^{\mathrm{crit}} $) for a pre-supernova star explosion. They found that a pre-supernova with high compactness (ξ2.5) demanded extremely high 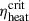η heat crit $ \eta_{\mathrm{heat}}^{\mathrm{crit}} $. Within the neutrino-driven paradigm, these high efficiencies were deemed unlikely, which led to the conclusion that these progenitors would not explode. Ultimately, the authors established a predictive criterion for CCSN explodability based on the pre-supernova star compactness parameter ξ2.5. This criterion was primarily established based on nonrotating pre-supernova star models, however. Recent studies (Takiwaki et al. 2016; Summa et al. 2018; Obergaulinger & Aloy 2020; Aguilera-Dena et al. 2020) suggested that centrifugal forces in a rapidly rotating massive pre-supernova star may significantly facilitate neutrino-driven explosions. Consequently, the original compactness-based criterion applied to predict the explodability of rapidly rotating massive pre-supernova stars might lead to erroneous conclusions.

Additionally, the evolution during the main-sequence phase can significantly affect the structure of pre-supernova stars and thereby affect the explosion outcome (Li et al. 2023, 2025). Extensive numerical simulations showed that the final iron core mass of stars does not monotonically increase with initial mass (Timmes et al. 1996; Sukhbold & Woosley 2014; Limongi & Chieffi 2018; Schneider et al. 2021; Temaj et al. 2024; Laplace et al. 2025). Changes in internal mixing, metallicity, and rotation all affect the relation between the initial and final mass of stars (Farrell et al. 2020) and thereby affect the explodability. Rotation can induce various instabilities during the evolutionary process (Heger & Langer 2000) that facilitate chemical mixing and angular momentum transfer Heger et al. (2023). Stellar rotation transports hydrogen from the outer layers to the core-burning region, which accelerates the growth of the helium core and increases its mass. On the other hand, rotational mixing stirs more helium into the envelope, which increases the mean atomic weight of the envelope and reduces its opacity (Sukhbold et al. 2016; Janka et al. 2016; Yoshida et al. 2021). A more massive helium core significantly enhances the stellar luminosity, while the increased helium abundance in the envelope promotes a blue solution (Saio et al. 1988; Langer 1992). Metallicity affects the mass-loss rate, which in turn affects the stellar mass during the evolution. In particular, a low metallicity combined with rapid rotation might lead to a chemically homogeneous evolution (CHE) (Maeder & Meynet 1987; Langer 1992; Brott et al. 2011), which enables the pre-supernova star to retain a higher mass and rotational velocity.

Current multiwavelength observations and theoretical studies collectively indicate that the vast majority of massive stars does not exist in isolation, but rather resides in close binaries or more complex multiple stellar systems (Kobulnicky & Fryer 2007; Sana et al. 2012, 2013, 2014). Massive stars in multiple star systems exchange mass through stable Roche-lobe overflow or merger events during their evolution (Stegmann et al. 2022; Henneco et al. 2024). This implies that the majority of supernovae originates from these mass-exchange objects Moe & Di Stefano (2017), Schneider et al. (2024). From pure helium star models that approximate stripped stars in binaries (Aguilera-Dena et al. 2022, 2023) to binary evolution simulations that incorporate stripped stars, accretors, and mergers (Laplace et al. 2021; Schneider et al. 2021, 2023, 2024), studies collectively demonstrated that binary interactions profoundly shape the pre-collapse core structures of stars. These structural changes directly impact the feasibility of neutrino-driven supernova explosions (Müller et al. 2019; Vartanyan et al. 2021; Woosley et al. 2020; Antoniadis et al. 2022). The complexity of binary and multiple stellar evolution, however, poses unique challenges that extend beyond the scope of this work. We focus on studying the impact of rotation and metallicity on the explodability of massive single stars during their evolution.

We simulated the entire evolution of stars from the main sequence to an explosion to obtain different explodability criteria for ξ2.5 in various model groups, and we investigated the effects of rotation and metallicity on the explodability of massive stars. In Section 2 we present the model parameter settings and research methods. In Section 3 we show the results of the study. A brief summary is provided in Section 4.

2. Model

In this section, we present the model parameter settings for the code called modules for experiments in stellar astrophysics (MESA) in version 10398 (Paxton et al. 2011, 2013, 2015, 2018, 2019) and GR1D. We also present the implementation of the (O’Connor & Ott 2011) explosion model and contextualize it against other explosion models.

2.1. Pre-collapse stellar models

We used the open-source 1D stellar evolution simulation code MESA to model the evolution from zero-age main sequence (ZAMS) to core collapse at 1000 km s−1. In the simulations, we configured initial rotational velocities (Vini: 0, 300 and 600 km s−1) and metallicities (Z⊙,  1/10 Z⊙,  1/50 Z⊙) with stellar initial masses at ZAMS spanning 10–80 M⊙.

Our MESA parameter settings agree with those of Li et al. (2023), with the exception of the solar metallicity, which we set to 0.014 (Asplund et al. 2009). The mixing-length parameter was αMLT = 1.5 (Böhm-Vitense 1958), with hydrogen-burning stage overshooting αov = 0.335 and the semiconvection mixing efficiency αSC = 0.01. The rotation can trigger the Goldreich–Schubert–Fricke instability, Eddington–Sweet circulation, dynamical instability, and secular instability, which produce the mixing (Heger et al. 2000). The ratio of turbulent viscosity to the diffusion coefficient was 1/30 (Heger et al. 2000). Stellar winds were modeled according to Yoon et al. (2006), Marchant et al. (2016): For hydrogen-rich stars (Xs > 0.7), we applied the prescription by Vink et al. (2001); for hydrogen-poor stars (Xs < 0.4), we adopted the formulas from Hamann et al. (1995); for intermediate compositions (0.4 ≤ Xs ≤ 0.7), we employed a linear interpolation. Rotational enhancement of mass loss was included following Bjorkman & Cassinelli (1993). Rotation was limited to Ω/Ωcrit < 0.98 to avoid the critical velocity (Langer 1998; Aguilera-Dena et al. 2020). The models were computed with the MESA approx21 nuclear network. The parameter mesh_delta_coeff was set to 0.5, and varcontrol_target was set to 3 × 10−4.

Following O’Connor & Ott (2011), we still adopted the compactness parameter ξ2.5 of pre-supernova stars to quantify their core compactness. The parameter ξM is defined as

ξ M = M / M ⊙ R ( M bary = M ) / ( 1000 km ) , $$ \begin{aligned} \xi _{\mathrm{M} } = \dfrac{M/M_{\odot }}{R\left(M_{\mathrm{bary} } = M\right) \big / \left(1000 \, \text{ km}\right)}, \end{aligned} $$(1)

where M typically represents 2.5 M⊙, and R(M) refers to the radius of a closed region with a baryonic mass of M, which is usually calculated at the core bounce or at a collapse velocity of 1000 km s−1. O’Connor & Ott (2011) provided the criterion for the explodability: when ξ2.5 < 0.45, a CCSN can successfully explode; otherwise, FSN may occur.

2.2. Core-collapse model

We simulated the CCSNe using GR1D (O’Connor & Ott 2010; O’Connor 2015), an open-source spherically symmetric general-relativistic neutrino-radiation hydrodynamics code. The six input parameters (enclosed mass, temperature, density, radial velocity, electron fraction, and angular velocity) required for each grid point of the progenitor supernova model in GR1D were provided by MESA when the iron core-collapse velocity reached 1000 km s−1. GR1D employs the M1 scheme (O’Connor 2015) for neutrino transport. The M1 transport is a sophisticated neutrino transport method that employs a two-moment scheme to solve the Boltzmann equation governing neutrino propagation (Shibata et al. 2011; Cardall et al. 2013). This transport is more complex than the neutrino transport approach adopted by O’Connor & Ott (2011).

We employed a computational grid comprising 600 radial zones. Within a radius of 20 km, the radial spacing was set to 300 m. Beyond 20 km, the grid extended logarithmically to an outer boundary where the density reaches 2000 g cm−3 (higher-resolution simulations are presented in Appendix A). Our simulations included the intrinsic rotation of the progenitor and incorporated an additional parametric neutrino-heating term, whose magnitude was controlled by an adjustable heating coefficient. The equation of state (EOS) we adopted was LS220 (Lattimer & Swesty 1991), featuring a nuclear incompressibility of 220 MeV. Similarly, the neutrino opacity table was generated using NuLib. For LS220, we used the same NuLib table as O’Connor (2015), both using three neutrino flavors and 18 energy groups. The simulations were evolved for a maximum physical time of 2 s. The remaining simulation parameters were set to the recommended values of the GR1D code (broadly consistent with O’Connor 2015). This setting prevented GR1D from terminating prematurely due to constraints in the parameter configuration.

2.3. Neutrino heating

The accretion history of the proto-neutron star (PNS) prior to shock revival determines the outcome: When the PNS accretes enough material to surpass its maximum supported mass (Tolman-Oppenheimer-Volkoff limit), it evolves into a black hole via an FSN; otherwise, a successful CCSN explosion occurs. This approach reflects the fact that in progenitor models where neutrino heating exceeds a critical threshold, sufficient energy deposition can trigger shock revival. To achieve explosion initiation in fully self-consistent 1D spherically symmetric simulations, artificial enhancement of neutrino energy deposition in the post-shock region is typically required. The GR1D code implements neutrino heating through the parameterization of Janka (2001), where the heating rate at radius r is

Q v i heat ( r ) = f heat L v i ( r ) 4 π r 2 σ heat , v i ρ m u X i 〈 1 F v i 〉 e − 2 τ v i , $$ \begin{aligned} Q^{\text{ heat}}_{v_i}(r) = f_{\text{heat}} \frac{L_{v_i}(r)}{4\pi r^2} \sigma _{\text{heat},v_i} \frac{\rho }{m_{\mathrm{u} }} X_i \left\langle \frac{1}{F_{v_i}} \right\rangle e^{-2\tau _{v_i}}, \end{aligned} $$(2)

where fheat is a scaling parameter introduced to parametrically amplify the heating rate, Lνi(r) is the neutrino luminosity interior to a radius r, and i refers to the neutrino flavors. τvi is the optical depth determined by the leakage scheme. σheat, vi denotes the energy-averaged absorption cross section, and Xi is the corresponding mass fraction for the neutrino interactions. The term ⟨1/Fvi⟩ represents the average inverse flux factor, which is analytically approximated as a function of the optical depth τ by comparison with the angle-dependent radiative transport calculations of Ott et al. (2008).

By increasing the fheat value, we enhanced the neutrino heating, thereby triggering CCSN explosion in 1D simulations. We adopted the same method as O’Connor & Ott (2011) and iteratively adjusted fheat to determine its critical value for explosion, 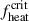f heat crit $ f_{\mathrm{heat}}^{\mathrm{crit}} $, within a relative precision of 1%. Figure 1 shows the shock radius evolution with time tbounce for different fheat values. For models with varying fheat, the shock emergence times remained identical. At low fheat, no explosions occurred in any of the models. As fheat increased, the shock stagnation phase became prolonged. With further increases in fheat, the shock propagated outward to the stellar surface and ultimately produced a CCSN. We note that shock waves in both models in the top panel (15 M⊙ ZAMS mass) oscillate with increasing fheat (Buras et al. 2006b), which is absent in the bottom panel (60 M⊙). The top panel requires fheat ≥ 2.58 (left) and 2.43 (right) for a successful shock revival, and the bottom panel demands fheat ≥ 2.05 (left) and 2.93 (right), respectively.

thumbnail Fig. 1.

Shock wave radius evolution vs. explosion time tbounce for different fheat values. The simulations started with an iron core-collapse velocity of 1000 km s−1, where t = 0 corresponds to the shock wave formation. The top and bottom panels show 15 M⊙ and 60 M⊙ ZAMS masses, respectively, with initial velocities Vini = 0 (left panels) and 300 km s−1 (right panels). All models have a metallicity of 1/10 Z⊙.

While we achieved CCSN explosion in 1D simulations through artificially enhanced neutrino heating in the previous section, it remains unclear whether these models can explode under self-consistent multidimensional natural scenarios with turbulence. Therefore, O’Connor & Ott (2011) used the time-averaged heating efficiency of the critical model (fheat = 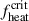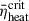f heat crit $ f_{\mathrm{heat}}^{\mathrm{crit}} $), η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $. Here, 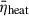η ¯ heat $ \bar{\eta}_{\mathrm{heat}} $ is defined as (O’Connor & Ott 2011)

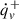η ¯ heat = ∫ gain q ˙ v + d V / ( L v e + L v ¯ e ) r gain ¯ , $$ \begin{aligned} \bar{\eta }_{\text{heat}} = \overline{\int _{\text{gain}} \dot{q}^{+}_{v} \, dV/(L_{v_{e}} + L_{\bar{v}_{e}})_{r_{\rm gain}}} , \end{aligned} $$(3)

where q ˙ v + $ \dot{q}^{+}_{v} $ denotes the net energy deposition rate within the gain region, and 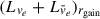( L v e + L v ¯ e ) r gain $ (L_{v_{e}} + L_{\bar{v}_{e}}) _{r_{\mathrm{gain}}} $ represents the luminosity of electron neutrinos and anti-electron neutrinos at the gain radius. We calculated the average value between the shock formation time and the explosion time. The explosion time is defined as the moment when the region behind the shock attains a positive velocity and accretion onto the PNS ceases (in GR1D simulations, outward shock propagation does not necessarily imply outward motion of the material behind the shock; when this point failed to occur, we increased fheat to continue the simulation). 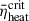η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $ characterizes how much of the available neutrino energy must be redeposited on average to explode a given progenitor, regardless of the transport scheme or numerical code (O’Connor & Ott 2011), therefore remains equally valid for the M1 neutrino transport model. By performing 1D simulations of the confirmed eruptive pre-supernova star models, we estimated the required range of η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $ values in 1D models that correspond to successful explosions. This approach allowed us to assess via 1D simulations whether a specific progenitor-EOS combination was more likely to result in explosion or BH formation.

Woosley & Weaver (1995) derived 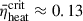η ¯ heat crit ≈ 0.13 $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} \approx 0.13 $ from simulations of a 15 M⊙ ZAMS progenitor with solar metallicity. Buras et al. (2006a) artificially exploded this progenitor in 1D and found 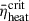η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $ ranging from 0.1 to 0.15. O’Connor & Ott (2011) found that their simulated data (EOS was LS180 and LS220) could be clearly divided into two categories: low-compactness models with 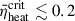η ¯ heat crit ≲ 0.2 $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} \lesssim 0.2 $ (the simulations exhibited some noise, with the average value being approximately 0.16, which is close to the value of 0.15 reported by Buras et al. 2006a), and high-compactness models with 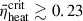η ¯ heat crit ≳ 0.23 $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} \gtrsim 0.23 $–0.27. Assuming that multidimensional simulations can achieve a fixed heating efficiency regardless of compactness, they proposed that the former category can produce successful explosions while the latter could not. The limitation of this method lies in the fact that this assumption cannot be guaranteed; multidimensional simulations by Boccioli et al. (2025) showed that neutrino heating varies with the compactness. We employed the 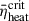η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $ as the explodability criterion from O’Connor & Ott (2011) and assumed it to be valid for rotating pre-supernova star models.

In Figure 2 we show the temporal evolution of the electron neutrino and antineutrino luminosities 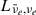L ν ¯ e , ν e $ L_{\bar{\nu}_e,\nu_e} $ (solid curves) at the gain radius and the net neutrino energy deposition rate 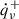q ˙ ν + $ \dot{q}^+_\nu $ (dashed curves) in the gain layer for the four models in Figure 1 with 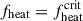f heat = f heat crit $ f_{\mathrm{heat}} = f_{\mathrm{heat}}^{\mathrm{crit}} $. Using Equation (2), we calculated the critical heating efficiency parameters 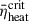η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $, with the upper panel (left to right) corresponding to 0.112 and 0.139, and the lower panel (left to right) to 0.242 and 0.257. Based on the explodability criterion ( 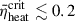η ¯ heat crit ≲ 0.2 $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} \lesssim 0.2 $) in O’Connor & Ott (2011), we determined that the first two models (15 M⊙) would explode, while the latter two (60 M⊙) would form FSN.

thumbnail Fig. 2.

For f heat = f heat crit $ f_{\mathrm{heat}} = f_{\mathrm{heat}}^{\mathrm{crit}} $, we show the evolution of the electron neutrino and antineutrino luminosities L ν ¯ e , ν e $ L_{\bar{\nu}_e,\nu_e} $ (solid lines) at the gain radius and the net neutrino energy deposition rate in the gain layer Q ˙ ν $ \dot{Q}_{\nu} $ ( ∫ gain q ˙ v + d V $ \int_{\text{gain}} \dot{q}^{+}_{v} \, dV $, dashed lines) vs. time tbounce. The simulations started with an iron core-collapse velocity of 1000 km s−1, where t = 0 corresponds to the shock wave formation. The top and bottom panels show 15 M⊙ and 60 M⊙ ZAMS masses, respectively, with initial velocities Vini = 0 (left panels) and 300 km s−1 (right panels). All models have a metallicity of 1/10 Z⊙.

For the two pre-supernova star models shown in the lower panels of Figure 1, evolutionary simulations for the critical model cannot be extended further due to limitations in the EOS and neutrino opacity tables. Although shock breakout occurred, they might lead to an FSN if the simulation can be continued, but this continuation cannot always be achieved. We demonstrate that these delayed failed supernova events affect our conclusions very little. First, critical models typically exhibit shock radii approaching or exceeding 1000 km, indicating penetration through most of the stellar envelope. Second, the derived 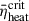η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $ values deviate by only ∼3% on average in the numerical resolutions.

2.4. Other explosion models

STIR model. Convection and turbulence are inherently three-dimensional phenomena. The model proposed by Couch et al. (2020) approximates turbulent effects in Newtonian simulations by parameterizing 3D neutrino-driven convection. Boccioli et al. (2021) extended this to a general-relativistic treatment and implemented it in the GR1D+ code. The code is computationally efficient and capable of capturing multi-D neutrino effects. Notably, at the time of writing, the current implementation does not support a simultaneous inclusion of STIR and rotation.

Ertl model. The 1D explosion model of Ertl et al. (2016) and Sukhbold et al. (2016) was based on the prescription by Ugliano et al. (2012). Within their explosion model, the inner 1.1 M⊙ core is removed after bounce and replaced by a moving inner boundary that sets the neutrino energy and luminosity Ugliano et al. (2012). Neutrino transport follows the gray treatment of Scheck et al. (2006). The calibration of the explosion model required the selection of different progenitor models representing SN 1987A and the calibration of the free parameters associated with the core-boundary prescription against the observables of SN 1987A (Ertl et al. 2016; Boccioli et al. 2025). However, Boccioli et al. (2025) identified a key theoretical limitation. The model selects a mild contraction for the 1.1 M⊙ shell, which mildly increases the average neutrino energies over time.

Muller model. The model by Müller et al. (2016) was built upon the theoretical frameworks developed by Janka (2001), Janka (2012), and Müller (2015), among other studies, and expanded upon and refined these frameworks. It does not require complex hydrodynamic simulations, but instead predicts the properties of neutrino-driven explosions based on the pre-collapse stellar structure. The Muller model incorporates the effects of neutrino-driven convection by substituting them with the shock radius multiplied by a scaling factor αturb. This causes convection in the explosion model to exert roughly the same influence on all progenitors. Multi-D simulations revealed, however, that the convection strength is strongly correlated with compactness (Boccioli et al. 2025).

These 1D explosion models each have inherent limitations. We chose the explosion model from O’Connor & Ott (2011) because the compactness parameter ξ2.5 is a widely adopted and the simplest parameter for predicting the explodability of pre-supernovae star, and GR1D is an open-source software.

3. Results

We computed the critical heating efficiency parameter 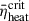η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $ for each model to assess whether these models can undergo supernova explosions under natural conditions where the nuclear EOS is similar to LS220. The explosion outcomes were then correlated with the compactness parameter ξ2.5. Therefore, according to 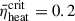η ¯ heat crit = 0.2 $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}}=0.2 $, we established the explodability criteria of ξ2.5 (they can be calculated directly by MESA) for the models with different metallicities and rotational velocities. By analyzing the effect of rapid rotation and metallicity on the explodability of massive stars, we linked their explosion outcomes with their initial ZAMS masses.

3.1. Explodability criteria of ξ2.5

Our computational resources were limited, and we therefore only selected a subset of stars from each group for GR1D simulations. We preferentially chose stars with ξ2.5 values closest to the threshold.

Figure 3 shows the central angular velocity versus MZAMS in pre-supernova star models with Vini = 300 km s−1 (left) and 600 km s−1 (right), where different colors indicate distinct metallicities. CHE occurs in all pre-supernova star models with Vini = 600 km s−1 at both 1/10 Z⊙ and 1/50 Z⊙ metallicities. For the Vini = 300 km s−1 and 1/50 Z⊙ subset, CHE is exclusively achieved by stars with initial masses MZAMS ≥ 33 M⊙. These CHE progenitors exhibit systematically higher central angular velocities (ωcore), predominantly in the 0.3–0.7 rad s−1 range. In contrast, non-CHE progenitors exhibit significantly lower central angular velocities (ωcore < 0.2 rad s−1), which may affect the compactness required for the formation of FSN.

thumbnail Fig. 3.

Central angular velocity (ωc) at a pre-supernova star for different ZAMS mass models vs. various Vini and metallicities. The left and right panels represent Vini = 300 km s−1 and Vini = 600 km s−1, respectively. Metallicities of Z⊙, 1/10 Z⊙, and 1/50 Z⊙, are shown in red, green, and black, respectively. The squares mark the occurrence of CHE.

Figure 4 shows the ξ2.5 values versus their corresponding 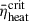η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $ for all stellar models, with the complete dataset tabulated in Table 1. 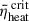η ¯ heat crit $ \bar{\eta}_{\text{heat}}^{\text{ crit}} $ increases with the augmentation of ξ2.5. All our models are clearly divided into two parts by 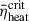η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $: the lower left zone with 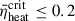η ¯ heat crit ≤ 0.2 $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}}\leq 0.2 $, and the upper right zone with 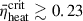η ¯ heat crit ≳ 0.23 $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} \gtrsim 0.23 $. Based on the explodability criterion of O’Connor & Ott (2011), the former would successfully undergo CCSN, while the latter would evolve into FSN.

thumbnail Fig. 4.

Compactness parameter ξ2.5 vs. the critical model time-averaged heating efficiency η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $. The left, center, and right panels correspond to initial velocities Vini = 0, 300 km s−1, and 600 km s−1, respectively. The data points in red, green, and black denote metallicities Z⊙, 1/10 Z⊙, and 1/50 Z⊙. The squares mark the occurrence of CHE. The hollow inverted triangles were calculated by O’Connor & Ott (2011), and the combinations of EOS and models LS220-sWH07, LS180-sWH07, and LS220-uWHW02 are represented in red, green, and black, respectively.

Table 1.

Summary of the core-collapse simulation parameters and explosion outcomes for all stellar models.

The left panel represents models with a ZAMS rotation of zero. The hollow inverted triangular data points are from O’Connor & Ott (2011), which include both LS180 and LS220 EOS with metallicities of Z⊙ and 10−4 Z⊙. A unified criterion of ξ2.5 = 0.45 is established for all nonrotating models across three metallicities in our work, consistent with the results of O’Connor & Ott (2011). The two models (lower right corner in the left panel) from O’Connor & Ott (2011) exhibit high compactness (ξ2.5 > 0.45), but still explode with 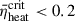η ¯ heat crit < 0.2 $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} < 0.2 $ because these models feature compositional interfaces where the density drops by 50%; when the shock reaches this interface, it rapidly breaks out, leading to a CCSN explosion (O’Connor & Ott 2011).

For the middle panel with Vini = 300 km s−1, the majority of pre-supernova star did not undergo CHE, retaining low rotation rates (ωc ≤ 0.2; Fig. 3 (left panel)). Stars with 1/50 Z⊙ and MZAMS ≥ 33 M⊙ undergo CHE, but none of our selected models exploded because of their exceptionally high compactness. We still attempted to construct a unified explodability criterion for the metallicities and derived ξ2.5 = 0.48.

In the right panel, with Vini = 600 km s−1, Z⊙ models exhibit lower pre-supernova star rotational velocities because their mass-loss rates are higher (Fig. 3 (right panel)), while the 1/10 Z⊙ and 1/50 Z⊙ models maintain higher rotation before collapse as a result of CHE. The ξ2.5 ranges for CCSN explosions between these two groups are significantly different. No unified criterion can be established: We obtained ξ2.5 = 0.47 for non-CHE models and ξ2.5 = 0.59 for CHE models. Using the pre-supernova star models simulated by Aguilera-Dena et al. (2020) (Vini = 600 km s−1, Z = 1/50 Z⊙), Halevi et al. (2023) calculated the compactness parameter ξ2.5 for rapidly rotating massive stars, and they derived ξ2.5 ∼ 0.6 for the explodability criterion, which is consistent with our results. The 12 M⊙ star with 1/10 Z⊙ cannot successfully explode although ξ2.5 < 0.59 as 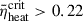η ¯ heat crit > 0.22 $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} > 0.22 $. This is primarily due to the low central rotation speed of its progenitor (weak centrifugal support) combined with excessive compactness.

For different model groups, we obtained distinct critical compactness criteria for explodability. By comparing them with the angular velocity ωc at the pre-supernova star center in Figure 3, we attribute this difference primarily to rotation. Higher pre-supernova star rotational velocities generate stronger centrifugal forces, which facilitate the explosion (Takiwaki et al. 2016; Summa et al. 2018; Aguilera-Dena et al. 2020; Obergaulinger & Aloy 2020) and thereby increase the upper limit of the critical compactness required for explosion.

Single parameters cannot always reliably predict the progenitor explosibility. Furthermore, the evolution of stars on the main sequence is inherently complex: Even for ZAMS stars with identical rotation and metallicity, the density profiles and rotational properties of their pre-supernova stars can be significantly different. These factors collectively mean that it is challenging to establish a unified explodability criterion for model groups with identical ZAMS conditions but varying masses. Our results reflect an overarching trend for all parameters.

3.2. Explodability of massive stars based on the ZAMS and CO-core masses

As discussed in Section 3.1, the explodability of massive stars is determined by their metallicity, rotation, and specific ZAMS masses. In this section, we present the relation between explodability criteria and ZAMS masses in our models.

Figure 5 shows the pre-supernova star compactness parameter ξ2.5 versus initial mass. Our results exhibit a trend similar to that of Li et al. (2023) and Aguilera-Dena et al. (2020). The ξ2.5 of our current model shows no significant positive correlation with MZAMS, which is consistent with the simulated results reported in other studies (Timmes et al. 1996; Schneider et al. 2021; Temaj et al. 2024). The final compactness, central entropy, iron-core mass, and binding energy as functions of initial mass follow similar patterns (Sukhbold & Woosley 2014; Takahashi et al. 2023; Schneider et al. 2021, 2024; Temaj et al. 2024). Laplace et al. (2025) investigated the underlying cause of this distinctive distribution. Taking the left panel of Fig. 5 as an example, Laplace et al. (2025) attributed the increasing compactness at ∼10–20 M⊙ and ∼25–30 M⊙ to the following reason: When the neutrino energy loss exceeds the energy released by carbon/neon burning, the core contracts, driving the burning front outward. As the MZAMS increases, a larger carbon/neon-free core forms at the center, ultimately yielding a more massive and denser iron core with higher compactness. In contrast, the compactness of stars with masses of ∼20–25 M⊙ and ∼30–35 M⊙ decreases. Laplace et al. (2025) argued that this drop is due to the earlier ignition of subsequent burning episodes, which slows down the progression of the carbon and oxygen burning fronts, caused by two factors: (1) the shortening of the main burning phase caused by fuel depletion and rising temperatures, and (2) the acceleration of core contraction when the fuel-depleted core exceeds the effective Chandrasekhar mass, leading to destabilization of electron degeneracy and accelerated collapse. These processes slow the core contraction down and lead to a reduced compactness. By examining the distribution of ξ2.5 with respect to MZAMS, we find that all model groups exhibit similar profiles. In the left and middle panels, the relation between MZAMS and ξ2.5 is similar. In the right panel, the profile shifts toward lower-mass regions with decreasing metallicity. This shift arises because CHE occurs in the 1/10 Z⊙ and 1/50 Z⊙ model groups. A lower metallicity promotes more efficient CHE, which produces larger He cores and CO cores for the same MZAMS compared to higher-metallicity models.

thumbnail Fig. 5.

ξ2.5 vs. initial mass for models with varying initial rotational velocities Vini and metallicities. The left, middle, and right panels correspond to models with Vini = 0, 300 km s−1, and 600 km s−1, respectively. Metallicities of Z⊙, 1/10 Z⊙, and 1/50 Z⊙are represented in red, green and black, respectively. The squares mark the occurrence of CHE. The left and middle blue triangles indicate model calculations from Li et al. (2023) (Z = 0.0017), and the right blue triangle denotes the rapidly rotating model from Aguilera-Dena et al. (2020) (1/50 Z⊙). The dashed lines mark explosion criteria for ξ2.5: the black line shows O’Connor & Ott (2011), and others from our results.

thumbnail Fig. 6.

ξ2.5 vs. CO-core mass for models with varying initial rotational velocities Vini and metallicities. The left, middle, and right panels correspond to models with Vini = 0, 300 km s−1, and 600 km s−1, respectively. Metallicities of Z⊙, 1/10 Z⊙, and 1/50 Z⊙ are shon in red, green, and black, respectively. The squares mark the occurrence of CHE.

Following Figure 5, we used our explodability criterion to determine the initial mass range for FSN. The left panel (Vini = 0) shows the explodability criterion of ξ2.5 = 0.45, and stars with initial masses between approximately 21 and 23 M⊙, between 30 and 41 M⊙, and above approximately 50 M⊙ cannot undergo supernova explosions. These results are consistent with previous studies by Sukhbold et al. (2018), Ugliano et al. (2012), and Ivanov & Fernández (2021). For the middle panel (Vini = 300 km s−1), based on ξ2.5 = 0.48, FSN forms in the initial mass ranges of approximately 20–22 M⊙, 27–35 M⊙, and above 40 M⊙. For the right panel (Vini = 600 km s−1), the results depend on the metallicity: At solar metallicity (Z = Z⊙), the FSN initial mass range is ∼14 M⊙, 23–40 M⊙, and above 50 M⊙; for 1/10 Z⊙, stars with MZAMS in the ranges of approximately ∼11 M⊙, 21–26 M⊙ and above 40 M⊙ fail to undergo CCSN explosions; for 1/50 Z⊙, stars with MZAMS in the ranges of approximately ∼11 M⊙, 17–20 M⊙ and above 32 M⊙ fail to undergo CCSN explosions.

For models without CHE, the initial mass range for the occurrence of FSN differs slightly from the results obtained using the traditional criterion (ξ2.5 = 0.45). In contrast, pre-supernova stars that have undergone CHE exhibit a reduced MZAMS range for forming FSN when the ξ2.5 = 0.59 criterion is applied. Their cores maintain higher pre-supernova star angular velocities (see Fig. 3), and these systems (even when they fail to produce successful CCSN explosions) are therefore more likely to generate long gamma-ray bursts (lGRBs) (Woosley 1993; Yoon et al. 2006). This results in luminous transients that might not conform to the observational definition of FSN (Yoon et al. 2006). lGRBs are produced when the specific angular (jco) momentum at any location within the CO core exceeds that of the last stable orbit (jKerr, LSO) (Bardeen et al. 1972). CHE progenitors undergoing core collapse leave bare CO cores and retain sufficient specific angular momentum during the black hole formation to facilitate lGRB production (Aguilera-Dena et al. 2018, 2020; Li et al. 2023).

Figure 6 shows the evolution of ξ2.5 as a function of CO core mass at core collapse for different model groups. The trends in all model groups are comparable: Distinct compact regions of high ξ2.5 appear at CO core masses of approximately 6–7 M⊙, ∼14 M⊙, and ≳21 M⊙. These high-ξ2.5 regions generally correspond to the domains that are favorable for failed supernova formation. Rotation and metallicity have very little effect on the overall distribution of ξ2.5 with CO core mass. Models with CHE significantly narrow the CO core mass interval, however, which leads to failed supernovae (reducing the width of the peaks). It is noteworthy that the locations of the first two compact peaks observed in this study (at ∼7 M⊙ and ∼14 M⊙) are comparable to those reported by Temaj et al. (2024). These authors indicated that the location of the peak in the ξ2.5 distribution versus CO core mass is affected by the convective-core overshooting value.

4. Conclusions

Using the MESA stellar evolution code, we simulated stars with initial rotational velocities of Vini = 0, 300 km s−1, and 600 km s−1 at three metallicities (Z⊙, 1/10 Z⊙, and 1/50 Z⊙). We tracked their evolution from the ZAMS until iron-core collapse at 1000 km s−1. Using the MESA models of iron-core collapse at 1000 km s−1, we extracted key parameters (enclosed mass, temperature, density, radial velocity, electron fraction, and angular velocity) as input parameters for GR1D, and we subsequently simulated the CCSN phase with GR1D. We iteratively determined the critical value of fheat such that it lay within 1% of the threshold required for a successful explosion. The corresponding time-averaged heating efficiency at this critical fheat, denoted as 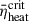η ¯ heat crit $ \bar{\eta }_{\mathrm{heat} }^{\mathrm{crit} } $, was then used to evaluate whether the progenitor can explode in multidimensional simulations. Finally, we established a correlation between the explosion outcomes and ξ2.5, and we derived the critical compactness parameters ξ2.5 for pre-supernova star explodability as follows: 0.45 for models with Vini = 0; 0.48 for the Vini = 300 km s−1 group; 0.47 for Vini = 600 km s−1 at Z = Z⊙ ; and 0.59 for low metallicity (Z = 1/10 and 1/50 Z⊙). These criteria enable a rapid assessment of pre-supernova stars explodability for EOS configurations resembling LS220. The upper limit of the pre-supernova star compactness for producing CCSNe is significantly higher in models where massive stars have undergone CHE compared to those without CHE. This discrepancy primarily arises because the centrifugal force generated by rotational motion in pre-supernova star more effectively facilitates explosions compared to nonrotating scenarios. Traditional criteria (ξ2.5 = 0.45) might not be suitable to evaluate the CHE progenitor explodability.

We established correlations between the explodability of stars in different model groups and their ZAMS masses. We determined the initial ZAMS mass ranges for an explosion formation in these groups. For models without CHE, the ZAMS mass ranges that lead to FSN vary less than the ranges obtained using the ξ2.5 < 0.45 explodability criterion. In contrast, model groups that underwent CHE showed a significantly increased initial ZAMS mass range for the occurrence of an explosion. They are more likely to produce lGRBs, which leads to a significantly reduced likelihood of FSN. Through our analysis of the compactness parameter ξ2.5 distribution as a function of CO core mass, we found that for model groups with otherwise identical initial parameters, rotation and metallicity affect the distribution of compactness with CO-core mass only little.

Acknowledgments

We thank Evan O’Connor for helpful discussions and advice about using GR1D. This work received the support of the National Natural Science Foundation of China under grants 12373038, 12163005, U2031204 and 12288102; the Natural Science Foundation of Xinjiang No.2022TSYCLJ0006 and 2022D01D85.

References

  1. Aguilera-Dena, D. R., Langer, N., Moriya, T. J., & Schootemeijer, A. 2018, ApJ, 858, 115 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aguilera-Dena, D. R., Langer, N., Antoniadis, J., & Müller, B. 2020, ApJ, 901, 114 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aguilera-Dena, D. R., Langer, N., Antoniadis, J., et al. 2022, A&A, 661, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Aguilera-Dena, D. R., Müller, B., Antoniadis, J., et al. 2023, A&A, 671, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Antoniadis, J., Aguilera-Dena, D. R., Vigna-Gómez, A., et al. 2022, A&A, 657, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [Google Scholar]
  8. Bethe, H. A., & Wilson, J. R. 1985, ApJ, 295, 14 [CrossRef] [Google Scholar]
  9. Bjorkman, J. E., & Cassinelli, J. P. 1993, ApJ, 409, 429 [NASA ADS] [CrossRef] [Google Scholar]
  10. Boccioli, L., Mathews, G. J., & O’Connor, E. P. 2021, ApJ, 912, 29 [CrossRef] [Google Scholar]
  11. Boccioli, L., Vartanyan, D., O’Connor, E. P., & Kasen, D. 2025, MNRAS, 540, 3885 [Google Scholar]
  12. Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
  13. Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bruenn, S. W., Lentz, E. J., Hix, W. R., et al. 2016, ApJ, 818, 123 [Google Scholar]
  15. Buras, R., Janka, H. T., Rampp, M., & Kifonidis, K. 2006a, A&A, 457, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Buras, R., Rampp, M., Janka, H. T., & Kifonidis, K. 2006b, A&A, 447, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Burrows, A., Reddy, S., & Thompson, T. A. 2006, Nucl. Phys. A, 777, 356 [Google Scholar]
  18. Burrows, A., Radice, D., & Vartanyan, D. 2019, MNRAS, 485, 3153 [NASA ADS] [CrossRef] [Google Scholar]
  19. Burrows, A., Radice, D., Vartanyan, D., et al. 2020, MNRAS, 491, 2715 [NASA ADS] [CrossRef] [Google Scholar]
  20. Burrows, A., Vartanyan, D., & Wang, T. 2023, ApJ, 957, 68 [NASA ADS] [CrossRef] [Google Scholar]
  21. Burrows, A., Wang, T., & Vartanyan, D. 2024, ApJ, 964, L16 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cardall, C. Y., Endeve, E., & Mezzacappa, A. 2013, Phys. Rev. D, 87, 103004 [NASA ADS] [CrossRef] [Google Scholar]
  23. Chan, C., Müller, B., Heger, A., Pakmor, R., & Springel, V. 2018, ApJ, 852, L19 [NASA ADS] [CrossRef] [Google Scholar]
  24. Colgate, S. A., & White, R. H. 1966, ApJ, 143, 626 [NASA ADS] [CrossRef] [Google Scholar]
  25. Couch, S. M., Warren, M. L., & O’Connor, E. P. 2020, ApJ, 890, 127 [NASA ADS] [CrossRef] [Google Scholar]
  26. Diehl, R., Lugaro, M., Heger, A., et al. 2021, PASA, 38, e062 [NASA ADS] [CrossRef] [Google Scholar]
  27. Ertl, T., Janka, H. T., Woosley, S. E., Sukhbold, T., & Ugliano, M. 2016, ApJ, 818, 124 [NASA ADS] [CrossRef] [Google Scholar]
  28. Farrell, E. J., Groh, J. H., Meynet, G., & Eldridge, J. J. 2020, MNRAS, 494, L53 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fischer, T., Whitehouse, S. C., Mezzacappa, A., Thielemann, F. K., & Liebendörfer, M. 2009, A&A, 499, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Fischer, T., Bastian, N.-U., Blaschke, D., et al. 2017, PASA, 34, e067 [NASA ADS] [CrossRef] [Google Scholar]
  31. Fryer, C. L., & Warren, M. S. 2002, ApJ, 574, L65 [Google Scholar]
  32. Gogilashvili, M., Murphy, J. W., & O’Connor, E. P. 2023, MNRAS, 524, 4109 [NASA ADS] [CrossRef] [Google Scholar]
  33. Halevi, G., Wu, B., Mösta, P., et al. 2023, ApJ, 944, L38 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hamann, W. R., Koesterke, L., & Wessolowski, U. 1995, A&A, 299, 151 [Google Scholar]
  35. Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [CrossRef] [Google Scholar]
  36. Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
  37. Heger, A., Müller, B., & Mandel, I. 2023, ArXiv e-prints [arXiv:2304.09350] [Google Scholar]
  38. Henneco, J., Schneider, F. R. N., & Laplace, E. 2024, A&A, 682, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Herant, M., Benz, W., Hix, W. R., Fryer, C. L., & Colgate, S. A. 1994, ApJ, 435, 339 [NASA ADS] [CrossRef] [Google Scholar]
  40. Horiuchi, S., Beacom, J. F., Kochanek, C. S., et al. 2011, ApJ, 738, 154 [NASA ADS] [CrossRef] [Google Scholar]
  41. Horowitz, C. J. 2002, Phys. Rev. D, 65, 043001 [NASA ADS] [CrossRef] [Google Scholar]
  42. Ivanov, M., & Fernández, R. 2021, ApJ, 911, 6 [CrossRef] [Google Scholar]
  43. Janka, H. T. 2001, A&A, 368, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Janka, H.-T. 2012, Annu. Rev. Nucl. Part. Sci., 62, 407 [NASA ADS] [CrossRef] [Google Scholar]
  45. Janka, H.-T. 2017, in Handbook of Supernovae, eds. A. W. Alsabti, & P. Murdin, 1095 [Google Scholar]
  46. Janka, H. T. 2025, ArXiv e-prints [arXiv:2502.14836] [Google Scholar]
  47. Janka, H. T., & Mueller, E. 1996, A&A, 306, 167 [NASA ADS] [Google Scholar]
  48. Janka, H.-T., Melson, T., & Summa, A. 2016, Annu. Rev. Nucl. Part. Sci., 66, 341 [Google Scholar]
  49. Kobulnicky, H. A., & Fryer, C. L. 2007, ApJ, 670, 747 [NASA ADS] [CrossRef] [Google Scholar]
  50. Kuroda, T., Kotake, K., Takiwaki, T., & Thielemann, F.-K. 2018, MNRAS, 477, L80 [NASA ADS] [CrossRef] [Google Scholar]
  51. Langer, N. 1992, A&A, 265, L17 [NASA ADS] [Google Scholar]
  52. Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
  53. Laplace, E., Justham, S., Renzo, M., et al. 2021, A&A, 656, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Laplace, E., Schneider, F. R. N., & Podsiadlowski, P. 2025, A&A, 695, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Lattimer, J. M., & Swesty, D. F. 1991, Nucl. Phys. A, 535, 331 [CrossRef] [Google Scholar]
  56. Lentz, E. J., Bruenn, S. W., Hix, W. R., et al. 2015, ApJ, 807, L31 [NASA ADS] [CrossRef] [Google Scholar]
  57. Li, W., Leaman, J., Chornock, R., et al. 2011, MNRAS, 412, 1441 [NASA ADS] [CrossRef] [Google Scholar]
  58. Li, L., Zhu, C., Guo, S., Liu, H., & Lü, G. 2023, ApJ, 952, 79 [Google Scholar]
  59. Li, Z., Lu, X., Lü, G., et al. 2025, ApJ, 979, L37 [Google Scholar]
  60. Liebendörfer, M., Rampp, M., Janka, H. T., & Mezzacappa, A. 2005, ApJ, 620, 840 [CrossRef] [Google Scholar]
  61. Limongi, M., & Chieffi, A. 2018, ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
  62. Mabanta, Q. A., & Murphy, J. W. 2018, ApJ, 856, 22 [CrossRef] [Google Scholar]
  63. Maeder, A., & Meynet, G. 1987, A&A, 182, 243 [NASA ADS] [Google Scholar]
  64. Maltsev, K., Schneider, F. R. N., Mandel, I., et al. 2025, A&A, 700, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Miller, D. S., Wilson, J. R., & Mayle, R. W. 1993, ApJ, 415, 278 [Google Scholar]
  67. Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
  68. Müller, B. 2015, MNRAS, 453, 287 [CrossRef] [Google Scholar]
  69. Müller, B., Heger, A., Liptai, D., & Cameron, J. B. 2016, MNRAS, 460, 742 [Google Scholar]
  70. Müller, B., Melson, T., Heger, A., & Janka, H.-T. 2017, MNRAS, 472, 491 [Google Scholar]
  71. Müller, B., Tauris, T. M., Heger, A., et al. 2019, MNRAS, 484, 3307 [Google Scholar]
  72. Murphy, J. W., & Burrows, A. 2008, ApJ, 688, 1159 [Google Scholar]
  73. Obergaulinger, M., & Aloy, M. Á. 2020, MNRAS, 492, 4613 [Google Scholar]
  74. O’Connor, E. 2015, ApJS, 219, 24 [CrossRef] [Google Scholar]
  75. O’Connor, E., & Ott, C. D. 2010, CQG, 27, 114103 [Google Scholar]
  76. O’Connor, E., & Ott, C. D. 2011, ApJ, 730, 70 [Google Scholar]
  77. O’Connor, E., Bollig, R., Burrows, A., et al. 2018, J. Phys. G Nucl. Phys., 45, 104001 [CrossRef] [Google Scholar]
  78. Ott, C. D., Burrows, A., Dessart, L., & Livne, E. 2008, ApJ, 685, 1069 [NASA ADS] [CrossRef] [Google Scholar]
  79. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  80. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  81. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  82. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  83. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  84. Pejcha, O., & Thompson, T. A. 2015, ApJ, 801, 90 [NASA ADS] [CrossRef] [Google Scholar]
  85. Radice, D., Burrows, A., Vartanyan, D., Skinner, M. A., & Dolence, J. C. 2017, ApJ, 850, 43 [NASA ADS] [CrossRef] [Google Scholar]
  86. Saio, H., Nomoto, K., & Kato, M. 1988, Nature, 334, 508 [Google Scholar]
  87. Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
  88. Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Sana, H., Le Bouquin, J. B., Lacour, S., et al. 2014, ApJS, 215, 15 [Google Scholar]
  90. Scheck, L., Kifonidis, K., Janka, H. T., & Müller, E. 2006, A&A, 457, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Schneider, F. R. N., Podsiadlowski, P., & Müller, B. 2021, A&A, 645, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Schneider, F. R. N., Podsiadlowski, P., & Laplace, E. 2023, ApJ, 950, L9 [NASA ADS] [CrossRef] [Google Scholar]
  93. Schneider, F. R. N., Podsiadlowski, P., & Laplace, E. 2024, A&A, 686, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Shibata, M., Kiuchi, K., Sekiguchi, Y., & Suwa, Y. 2011, Prog. Theor. Phys., 125, 1255 [CrossRef] [Google Scholar]
  95. Smartt, S. J. 2015, PASA, 32, e016 [NASA ADS] [CrossRef] [Google Scholar]
  96. Stegmann, J., Antonini, F., & Moe, M. 2022, MNRAS, 516, 1406 [NASA ADS] [CrossRef] [Google Scholar]
  97. Sukhbold, T., & Woosley, S. E. 2014, ApJ, 783, 10 [NASA ADS] [CrossRef] [Google Scholar]
  98. Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H. T. 2016, ApJ, 821, 38 [NASA ADS] [CrossRef] [Google Scholar]
  99. Sukhbold, T., Woosley, S. E., & Heger, A. 2018, ApJ, 860, 93 [NASA ADS] [CrossRef] [Google Scholar]
  100. Summa, A., Janka, H.-T., Melson, T., & Marek, A. 2018, ApJ, 852, 28 [Google Scholar]
  101. Takahashi, K., Takiwaki, T., & Yoshida, T. 2023, ApJ, 945, 19 [NASA ADS] [CrossRef] [Google Scholar]
  102. Takiwaki, T., Kotake, K., & Suwa, Y. 2016, MNRAS, 461, L112 [NASA ADS] [CrossRef] [Google Scholar]
  103. Temaj, D., Schneider, F. R. N., Laplace, E., Wei, D., & Podsiadlowski, P. 2024, A&A, 682, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1996, ApJ, 457, 834 [NASA ADS] [CrossRef] [Google Scholar]
  105. Ugliano, M., Janka, H.-T., Marek, A., & Arcones, A. 2012, ApJ, 757, 69 [NASA ADS] [CrossRef] [Google Scholar]
  106. Vartanyan, D., & Burrows, A. 2023, MNRAS, 526, 5900 [Google Scholar]
  107. Vartanyan, D., Laplace, E., Renzo, M., et al. 2021, ApJ, 916, L5 [NASA ADS] [CrossRef] [Google Scholar]
  108. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Wang, T., Vartanyan, D., Burrows, A., & Coleman, M. S. B. 2022, MNRAS, 517, 543 [NASA ADS] [CrossRef] [Google Scholar]
  110. Woosley, S. E. 1993, ApJ, 405, 273 [Google Scholar]
  111. Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [Google Scholar]
  112. Woosley, S. E., Sukhbold, T., & Janka, H. T. 2020, ApJ, 896, 56 [NASA ADS] [CrossRef] [Google Scholar]
  113. Yoon, S. C., Langer, N., & Norman, C. 2006, A&A, 460, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Yoshida, T., Takiwaki, T., Aguilera-Dena, D. R., et al. 2021, MNRAS, 506, L20 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Grid simulations at higher resolution

We set a high-resolution grid comprising 1200 radial zones. Within the inner 20 km, 200 radial zones are configured at a fine spacing of 100 m. Beyond 20 km, the grid extends logarithmically to an outer boundary where the density reaches 2000 g cm−3.

Figure A.1 shows the shock radius evolution with time tbounce for different fheat values. (The four pre-supernova star models simulated in here are identical to those presented in Figures 2 and 3 of the main text). Comparisons of simulations at different grid resolutions indicate that at low fheat values, results from both grid resolutions are nearly identical. As fheat increases, simulations remain consistent until the early shock stagnation phase; beyond this point, however, the finer grid demonstrates a higher likelihood of shock revival and explosion. Simulations of the identical initial setup performed at varying grid resolutions yield deviations in 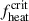f heat crit $ f_{\text{heat}}^{\text{crit}} $ that average less than 3%.

Figure A.2 depicts the temporal evolution of 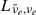L ν ¯ e , ν e $ L_{\bar{\nu}_e,\nu_e} $ at the gain radius and 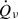Q ˙ ν $ \dot{Q}_{\nu} $ in the critical model across different grid resolutions. We calculate the critical heating efficiency parameters 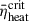η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $ for the 1200 grid configuration, with the upper panel (left to right) corresponding to 0.109 and 0.129, and the lower panel (left to right) to 0.246 and 0.253.

The results indicate a mean relative deviation of ∼3% in 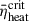η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $ between grid configurations. Given that simulations with high-resolution grids require over five times the computational resources of their low-resolution counterparts, we employed the low-resolution setup (600 total cells) for all models.

thumbnail Fig. A.1.

Shock wave radius evolution vs. explosion time tbounce for different fheat values. The simulations started with an iron core-collapse velocity of 1000 km s−1, where t = 0 corresponds to shock wave formation. Dashed curves depict simulations employing coarse numerical grids, while solid lines correspond to higher-resolution implementations. The top and bottom panels show 15 M⊙ and 60 M⊙ ZAMS masses respectively, with initial velocities Vini = 0 (left panels) and 300 km s−1 (right panels). All models have a metallicity of 1/10 Z⊙.

thumbnail Fig. A.2.

For f heat = f heat crit $ f_{\mathrm{heat}} = f_{\mathrm{heat}}^{\mathrm{crit}} $, we show the evolution of the electron neutrino and antineutrino luminosities L ν ¯ e , ν e $ L_{\bar{\nu}_e,\nu_e} $ (solid lines) at the gain radius and net neutrino energy deposition rate in the gain layer Q ˙ ν $ \dot{Q}_{\nu} $ ( ∫ gain q ˙ v + d V $ \int_{\text{gain}} \dot{q}^{+}_{v} \, dV $, dashed lines) vs. time tbounce. The simulations started with an iron core-collapse velocity of 1000 km s−1, where t = 0 corresponds to the shock wave formation. The red lines depict simulations employing coarse numerical grids, while black curves correspond to higher-resolution implementations. The top and bottom panels show 15 M⊙ and 60 M⊙ ZAMS masses respectively, with initial velocities Vini = 0 (left panels) and 300 km s−1 (right panels). All models have a metallicity of 1/10 Z⊙.

All Tables

Table 1.

Summary of the core-collapse simulation parameters and explosion outcomes for all stellar models.

In the text

All Figures

thumbnail Fig. 1.

Shock wave radius evolution vs. explosion time tbounce for different fheat values. The simulations started with an iron core-collapse velocity of 1000 km s−1, where t = 0 corresponds to the shock wave formation. The top and bottom panels show 15 M⊙ and 60 M⊙ ZAMS masses, respectively, with initial velocities Vini = 0 (left panels) and 300 km s−1 (right panels). All models have a metallicity of 1/10 Z⊙.
In the text
thumbnail Fig. 2.

For f heat = f heat crit $ f_{\mathrm{heat}} = f_{\mathrm{heat}}^{\mathrm{crit}} $, we show the evolution of the electron neutrino and antineutrino luminosities L ν ¯ e , ν e $ L_{\bar{\nu}_e,\nu_e} $ (solid lines) at the gain radius and the net neutrino energy deposition rate in the gain layer Q ˙ ν $ \dot{Q}_{\nu} $ ( ∫ gain q ˙ v + d V $ \int_{\text{gain}} \dot{q}^{+}_{v} \, dV $, dashed lines) vs. time tbounce. The simulations started with an iron core-collapse velocity of 1000 km s−1, where t = 0 corresponds to the shock wave formation. The top and bottom panels show 15 M⊙ and 60 M⊙ ZAMS masses, respectively, with initial velocities Vini = 0 (left panels) and 300 km s−1 (right panels). All models have a metallicity of 1/10 Z⊙.
In the text
thumbnail Fig. 3.

Central angular velocity (ωc) at a pre-supernova star for different ZAMS mass models vs. various Vini and metallicities. The left and right panels represent Vini = 300 km s−1 and Vini = 600 km s−1, respectively. Metallicities of Z⊙, 1/10 Z⊙, and 1/50 Z⊙, are shown in red, green, and black, respectively. The squares mark the occurrence of CHE.
In the text
thumbnail Fig. 4.

Compactness parameter ξ2.5 vs. the critical model time-averaged heating efficiency η ¯ heat crit $ \bar{\eta}_{\mathrm{heat}}^{\mathrm{crit}} $. The left, center, and right panels correspond to initial velocities Vini = 0, 300 km s−1, and 600 km s−1, respectively. The data points in red, green, and black denote metallicities Z⊙, 1/10 Z⊙, and 1/50 Z⊙. The squares mark the occurrence of CHE. The hollow inverted triangles were calculated by O’Connor & Ott (2011), and the combinations of EOS and models LS220-sWH07, LS180-sWH07, and LS220-uWHW02 are represented in red, green, and black, respectively.
In the text
thumbnail Fig. 5.

ξ2.5 vs. initial mass for models with varying initial rotational velocities Vini and metallicities. The left, middle, and right panels correspond to models with Vini = 0, 300 km s−1, and 600 km s−1, respectively. Metallicities of Z⊙, 1/10 Z⊙, and 1/50 Z⊙are represented in red, green and black, respectively. The squares mark the occurrence of CHE. The left and middle blue triangles indicate model calculations from Li et al. (2023) (Z = 0.0017), and the right blue triangle denotes the rapidly rotating model from Aguilera-Dena et al. (2020) (1/50 Z⊙). The dashed lines mark explosion criteria for ξ2.5: the black line shows O’Connor & Ott (2011), and others from our results.
In the text
thumbnail Fig. 6.

ξ2.5 vs. CO-core mass for models with varying initial rotational velocities Vini and metallicities. The left, middle, and right panels correspond to models with Vini = 0, 300 km s−1, and 600 km s−1, respectively. Metallicities of Z⊙, 1/10 Z⊙, and 1/50 Z⊙ are shon in red, green, and black, respectively. The squares mark the occurrence of CHE.
In the text
thumbnail Fig. A.1.

Shock wave radius evolution vs. explosion time tbounce for different fheat values. The simulations started with an iron core-collapse velocity of 1000 km s−1, where t = 0 corresponds to shock wave formation. Dashed curves depict simulations employing coarse numerical grids, while solid lines correspond to higher-resolution implementations. The top and bottom panels show 15 M⊙ and 60 M⊙ ZAMS masses respectively, with initial velocities Vini = 0 (left panels) and 300 km s−1 (right panels). All models have a metallicity of 1/10 Z⊙.
In the text
thumbnail Fig. A.2.

For f heat = f heat crit $ f_{\mathrm{heat}} = f_{\mathrm{heat}}^{\mathrm{crit}} $, we show the evolution of the electron neutrino and antineutrino luminosities L ν ¯ e , ν e $ L_{\bar{\nu}_e,\nu_e} $ (solid lines) at the gain radius and net neutrino energy deposition rate in the gain layer Q ˙ ν $ \dot{Q}_{\nu} $ ( ∫ gain q ˙ v + d V $ \int_{\text{gain}} \dot{q}^{+}_{v} \, dV $, dashed lines) vs. time tbounce. The simulations started with an iron core-collapse velocity of 1000 km s−1, where t = 0 corresponds to the shock wave formation. The red lines depict simulations employing coarse numerical grids, while black curves correspond to higher-resolution implementations. The top and bottom panels show 15 M⊙ and 60 M⊙ ZAMS masses respectively, with initial velocities Vini = 0 (left panels) and 300 km s−1 (right panels). All models have a metallicity of 1/10 Z⊙.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.