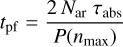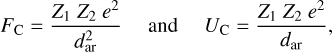| Issue |
A&A
Volume 704, December 2025
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202555203 | |
| Published online | 09 December 2025 | |
The essential elements of dust evolution: a-C(:H) nanoparticle sub-structures and photo-fragmentation
1
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale,
91405
Orsay,
France
2
IRAP, Université de Toulouse,
CNRS, UPS, 9Av. du Colonel Roche, BP 44346,
31028
Toulouse,
cedex 4,
France
★ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
18
April
2025
Accepted:
8
November
2025
Context. Hydrogenated amorphous carbon materials, a-C(:H), are heterogeneous structures consisting of carbon atoms in different hybridisation states and bonding configurations and are thought to constitute a significant and observationally important fraction of the interstellar dust material. The stability of interstellar a-C(:H) nanoparticles against photo-thermo-dissociation and Coulomb fragmentation needs to take their intrinsic heterogeneity into account.
Aims. This work aims to characterise semi-conducting a-C(:H) nanoparticle structures and, in particular, their property-characterising aromatic domain size distribution and so predict how they will behave in intense UV radiation fields that can fragment them through dissociative and charge effects as a result of carbon-carbon bond-breaking.
Methods. Using a statistical approach, we determined the typical sizes of the aromatic domains, their size distribution, how they are network-bonded, and where they are to be found within the structure. We consider the effects of thermal excitation, photo-dissociation and charging of a-C(:H) nanoparticles, and the products of their fragmentation.
Results. The derived UV photon-induced fragmentation lifetimes for nanometre-sized a-C(:H) nanoparticles, with radii ∼0.4-0.5 nm radius and containing ∼40-60 carbon atoms, are of the order of 106-107 yr in the diffuse interstellar medium and likely 102-104 times shorter in photodissociation regions, depending on the local radiation field intensity. Grains larger than this are stable against photodissociation. In HII regions only a-C(:H) nanoparticles with radii greater than 0.7 nm (≳150 carbon atoms) are likely to survive.
Conclusions. The photon-driven fragmentation of sub-nanometre a-C(:H) particles was determined to be important in the diffuse interstellar medium and also in high excitation regions, such as photodissociation and H II regions. However, in these same regions Coulomb fragmentation is unlikely to be an important dust destruction process.
Key words: solid state: refractory / ISM: abundances / dust, extinction / ISM: lines and bands / ISM: molecules / photon-dominated region (PDR)
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1 Introduction
It has recently been shown that the carbonaceous nanoparticle abundance in photo-dissociation regions (PDRs) is sensitive to the local physical conditions, especially to the hardness and intensity of the interstellar radiation field and that this has important consequences for the gas (Schirmer et al. 2020, 2021, 2022). However, the details of the effects working upon the nanoparticles in these regions have yet to be fully understood. For example it is not yet clear whether the observed nanoparticle depletion in PDRs (e.g. Arab et al. 2012; Compiègne et al. 2008; Schirmer et al. 2022) is due to thermal, photo-dissociative or charge effects, or a combination of these. The recent analysis and interpretation of James Webb Space Telescope (JWST) Orion Bar NIRCAM and MRS spectroscopic and photometric data (Elyajouri et al. 2024) reveals that, in this rather extreme PDR (G0 ~ 104), the dust is significantly processed. This work indicates that the shape of the nanoparticle size distribution, in the rather extreme case of Orion, appears to be similar to that of the diffuse interstellar medium (ISM) but that the mass associated with the carbonaceous nanoparticles is reduced by a factor of 15 with respect to the diffuse ISM. In their detailed analysis of the NIRSpec and MRS spectroscopic observations Elyajouri et al. (2024) elucidated variations in the degree of hydrogenation of the carbonaceous nanoparticles, with the least hydrogenated closest to the illuminating stars, suggesting significant UV photo-processing, and the most hydrogenated associated with the colder and denser molecular regions generally populated by larger grains.
Ultraviolet (UV) photons play a pivotal role in the processing of grains in the ISM and in circumstellar regions (e.g. Dartois et al. 2004, 2005; Alata et al. 2014, 2015; Jones & Habart 2015; Jones 2016b,c; Boutéraon et al. 2019; Habart et al. 2021), in that UV irradiation can act directly by dissociating CH and CC bonds or collectively through the thermal excitation of the entire particle, which may then undergo dissociative or sublimation losses. In either case chemical bond breaking is involved and leads to mass loss from the particle, and perhaps to its eventual destruction. Grain charging arises from UV photon absorption leading to electron ejection, and from ion (principally proton) and electron collision and sticking (e.g. Weingartner & Draine 2001; Weingartner et al. 2006; Kimura 2016). If a sufficiently high charge state results, fragmentation due to strong Coulomb repulsion can occur, that is, to a so-called Coulomb explosion. All of these processes place limits on the lifetime of small grains in PDRs and in the diffuse ISM in general. It is these same processes that also regulate the heating and ionisation state of the interstellar gas through the emission of energetic photo-electrons following UV photon absorption.
Previous work on the Coulomb explosion of grains as a result of catastrophic charging assumed that the grains were homogeneous and that only under special circumstances can this destructive process be important. (e.g. Weingartner et al. 2006). If we relax this assumption and allow that most carbonaceous grains in the ISM are amorphous, semi-conducting nanoparticles, and therefore heterogeneous (e.g., Jones 1990, 2012c, 2016a; Jones et al. 2013), then Coulomb effects may perhaps have been underestimated. This can arise because the inherent grain constituent binding energies may be less than in homogeneous bulk materials. However, in this case we should probably speak more in terms of Coulomb induced fragmentation rather than Coulomb explosion because the process is most likely to be incremental rather than catastrophic.
A wealth of earlier work indicates that interstellar carbonaceous nanograins may be an unstable dust population (Jochims et al. 1994; Allain et al. 1995, 1996a,b; Jochims et al. 1999; Micelotta et al. 2010b,a, 2011; Jones & Nuth 2011; Jones 2012c; Jones et al. 2013, 2014; Bocchio et al. 2014; Jones & Habart 2015; Jones 2016a,b; Jones et al. 2016, 2017; Jones & Ysard 2019; Schirmer et al. 2020, 2021, 2022; Elyajouri et al. 2024). In their study of the destruction of polycyclic aromatic hydrocarbons (PAHs) in supernova (SN) shock waves in the Milky Way Micelotta et al. (2010b) derived lifetimes of the order of a few ×108 yr for PAHs with 50-200 carbon atoms. Re-evaluations of the carbonaceous dust destruction by Jones & Nuth (2011) found lifetimes of ~2.6 ± 2.4 × 108 yr and, in their more detailed study, Bocchio et al. (2014) derived lifetimes of ~0.62 ± 0.56 × 108 yr. Clearly on galactic scales the uncertainties are large (e.g. see Jones & Nuth 2011). Early studies specifically concerning carbon dust survival in the diffuse ISM (Jochims et al. 1994; Allain et al. 1995, 1996a,b) showed that PAHs with less than 30-40 carbon atoms are readily dissociated in the diffuse ISM but for those with more than 50 carbon atoms the photo-destruction timescale is more than 109 yr. Thus, interstellar sub-nanometre carbonaceous particles would appear to be in a state of constant flux due to the competing processes of destruction, primarily driven by UV photons and including charge induced processes, and re-formation by the collisional fragmentation of larger carbonaceous grains, as proposed by Schirmer et al. (2022). This implies that, as in the case of PDRs, the net destruction and/or lack of reformation of the product carbonaceous nanograins dominates (Compiègne et al. 2008; Arab et al. 2012; Schirmer et al. 2020, 2021, 2022; Elyajouri et al. 2024). Thus, there must be environments where these processes are so rapid that they completely deplete the stock of large carbonaceous grains and therefore, ultimately, of all carbonaceous dust. Such regions would obviously show no carbonaceous dust emission bands in the infrared (IR), which may be the case in the interstellar clouds local to the Solar System (Slavin 2009) and also in some early type and dwarf galaxies (e.g. Galliano et al. 2008, 2018).
This work adopts the THEMIS (The Heterogeneous dust Evolution Model for Interstellar Solids)1 view of interstellar dust (see Jones et al. 2013; Köhler et al. 2014; Ysard et al. 2015; Jones et al. 2017; Ysard et al. 2024). Here we are most interested in the aromatic rich THEMIS hydrogenated amorphous carbon, a-C(:H), nanoparticles with radii ≲5 nm and comprising ~20% of the total dust mass, which also contain a significant fraction of aliphatic and olefinic carbon and a residual hydrogen atom fraction of the order of 5%. The form and structure of these particles was illustrated by Micelotta et al. (2012) in their proposal for fullerene formation around planetary nebulæ and also shown schematically by Jones & Habart (2015).
A key and critical component in our consideration of a-C(:H) nanoparticle stability in the ISM is knowledge of the aromatic domain size distribution in bulk a-C(:H) materials and within a-C(:H) nanoparticles. However, these size distributions are almost certainly not the same because of the structural constraints imposed by finite particle sizes, which are much less restrictive in the case of bulk materials. For bulk carbonaceous materials the aromatic domain size distribution was extensively discussed by Robertson (1986), Robertson & O’Reilly (1987) and Robertson (1988). We therefore begin with a discussion and a statistical description of the critical structures within a-C(:H) bulk materials and nanoparticles. This is followed by an exploration of the consequences of the molecular structure of nanoparticles within the context of their evolution in a range of interstellar media.
This paper studies two key aspects of a-C(:H) nanoparticle evolution in the ISM. Firstly, for those wishing to understand the chemical and structural makeup of these materials, Section 2 gives an overview of the a-C(:H) structural properties and Section 3 describes the chemical bonding of the aromatic domain sub-component within a-C(:H) networks. Secondly, Section 4 presents a UV photon-driven fragmentation model and determines a-C(:H) nanoparticlke lifetimes in the ISM and Section 5 considers the role of Coulomb fragmentation. Finally, Section 6 concludes and summarises this work.
2 Hydrogenated amorphous carbon, a-C(:H)
Amorphous carbons solids, from richly to poorly hydrogenated, a-C:H to a-C, respectively, encompass a wide compositional and structural range, generically indicated by the a-C(:H) descriptor. These materials are semiconducting, spanning the H-rich (60 ≳ at.% H ≳ 15), aliphatic-rich and wide band gap (2.7 eV ≳ Eg ≳ 1 eV) a-C:H solids at one end to the H-poor (15 ≳ at.% H ≳ 2), aromatic-rich and narrow band gap (1 eV ≳ Eg ≳ -0.1 eV) a-C at the other extreme (e.g. Robertson 1986, 1988; Robertson & O’Reilly 1987; Robertson 2001, 2002; Ferrari & Robertson 2000, 2004). Their structures consist of contiguous 3D networks of chemically bonded carbon and hydrogen atoms with the carbon atoms principally in sp3 and sp2 hybridisations, in aliphatic, olefinic, and aromatic configurations. Carbon atoms in sp hybridisation states are also possible but seemingly somewhat rare and are in any event rather unstable (Ferrari & Robertson 2004). Quite naturally bi-atomic a-C(:H) materials can include heteroatoms of an element X, which are indicated by the descriptors a-C(:H):X or a-C(:H)[:X], where the square brackets indicate minor concentrations of element X (e.g. ≪ 10 at.%). The most common heteroatoms within a-C(:H)[:X] materials are O and N atoms (e.g. Jones 2013, 2016a,b,c).
In this work we are most interested in the aromatic domains within a-C(:H) semiconducting solids because they are the principal determinants of their optical properties (e.g. Robertson 1986; Robertson & O’Reilly 1987). They are also the centres for activated conduction and therefore the most likely chargecarrying sites within such materials. Further, it is the π - π* transitions (Ehν < 5 eV) of these aromatic domains within a-C(:H) nanoparticles that absorb lower energy photons, while aliphatic and olefinic substructures absorb at somewhat higher energies. Here we explore the nature and size distribution of the aromatic domains within a-C(:H) as a function of the particle size.
The aromatic clusters or domains2 can be characterised by the number of their constituent carbon atoms, nC, number of aromatic six-fold rings, NR, and their mean carbon atom coordination number, mC (e.g. Jones 1990, 2012a,b,c, and references therein). The latter quantity is the mean number of carbon atoms directly bonded to a given carbon atom within the 3D network. In bulk a-C(:H) materials NR is a function of the bulk material band gap, Eg (Robertson & O’Reilly 1987), that is,
The atomic fraction of hydrogen, XH = NH/(NC + NH), within the structure is a characterising parameter that is also directly relatable to Eg via Eg ≃ (4.3 XH) eV (e.g. Robertson 1986). Another measure of the dimensions of the aromatic domains is the aromatic coherence length, La, which is related to the band gap by Eg[eV] ≃ 0.77/La[nm] (e.g. Robertson 1986, 1991). Combining these equations we have
For compact polycyclic aromatic structures nC (see Jones 2012a, Appendix A, Table A.1) and the radius of the most compact aromatic domain, aR (see Jones 2012b, Eq. (4)), can be expressed as functions of NR,
The agreement between Eqs. (2) and (4) is within a factor of ≃1.25 for large NR and within a factor of ≃2 for NR = 2, with aR always larger than La. This difference arises because aR is defined on a geometrical basis whereas La is determined optically.
The above expressions indicate a clear link between the bulk material band gap and the size of the intrinsic aromatic sub-structures within a-C(:H) materials. The properties of such materials can be described using a random covalent network model (RCN). A RCN uses an average nearest-neighbour atomic bonding environment to constrain macroscopic 3D networks of carbon and hydrogen atoms. Within such an atomic network the formation of covalent bonds generally increases stability. However, when that network is not a regular lattice the randomly-directed bonds lead to strain energy resulting from distortions in the bond lengths and angles. The optimal network is one that just balances the effect of bond-induced stability against structural strain. The full details of RCNs have been described elsewhere (e.g. Phillips 1979; Döhler et al. 1980; Robertson 1986; Jones 1990) and in its extended form (eRCN, Jones 2012a).
3 Aromatic domain network connections in a-C(:H)
How well a given aromatic domain connects within an a-C(:H) network structure is determined by the number of its edge sites that link to other parts of the contiguous network. In the eRCN model (Jones 2012a) not all edge sites can link because this leads to a highly-strained system that would tend to stabilise by de-linking to form dangling bonds. Such non-linking, dangling edge sites are not allowed in the eRCN model and are therefore assumed to be singly hydrogenated. It is this structure versus strain offset that the RCN and eRCN models take into account in what is, essentially, a statistical description of the nanoscopic structure and short range order within a-C(:H) solids. The aromatic domain connectivity within the RCN can be determined using the average cluster coordination number mcluster = (3.5√NR + 2.5), with lower and upper limits of (NR + 6) and (2NR + 4), respectively (see Jones 2012a, Appendix A, Table A.1).
Particularly important in the case of hydrogen-poor eRCNs is the need to consider the hydrogen content of the aromatic-linking, mixed bonding aliphatic (sp3) and olefinic (sp2) network substructures in addition to that of the sp2 aromatic domains. The aromatic cluster coordination number per carbon atom, mar, is given by the cluster coordination number, mcluster, divided by the number of constituent carbon atoms, nC,
where it was assumed that the aromatic domains are compact. From Jones (2012a) the atomic fraction of carbon in sp2 aromatic form bonded to a hydrogen atom, 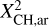 , (i.e. in aromatic CH bonds) is given by
, (i.e. in aromatic CH bonds) is given by
where f is the fraction of sp2 carbon atoms in aromatic domains3, Xsp2 is the atomic fraction of sp2 C atoms, which can be approximated4 by
and η = [H]/[C] = XH/(1 - XH) is the hydrogen to carbon atom ratio for bulk a-C(:H) materials, which was assumed to be the same for both sp2 and sp3 carbon atoms. Adopting the same hydrogen to carbon atom concentration ratio for olefinic and aliphatic carbon the fraction of hydrogenated aromatic domain edge sites, ζ, is given by
(1 - ζ) is then the fraction of aromatic domain edge sites that link to the network and (1 - ζ) mcluster the number of network links for a given NR. For nanoparticles consisting of a-C(:H) materials in the diffuse ISM, and particularly in PDRs and H II regions, the grains are likely to be predominantly H-poor and therefore of a-C composition with properties equivalent to those of bulk materials with Eg ≃ 0.1 eV (Jones et al. 2013) or even as low as 0.03 eV in the Orion Bar PDR (Elyajouri et al. 2024). Fig. 2 of Jones (2012c) shows that a-C(:H) nanoparticles, with radii from 0.4nm to 1nm, equivalent to the ~3 - 13 μm band emitters modelled by Elyajouri et al. (2024), have actual band gaps ranging from ~2.5 eV to ~0.8 eV, respectively. For nanoparticles in the diffuse ISM with an effective bulk band gap Eg ≃ 0.1 eV, XH ≃ 0.02 and Xsp2 = 0.88, we find ζ ≃ 0.01 to 0.02, for aromatic domains with NR = 1-10, nC = 6-32 and mcluster = 6-145. The derived values of ζ are therefore practically independent of size for the most abundant aromatic domains in a-C nanoparticles (i.e. NR = 1-5, Jones 2012c).
The overriding conclusion of this section is that, because of the paucity of H atoms in a-C nanoparticles, most of the peripheral aromatic domain carbon atoms must be linked into the 3D network at low values of XH in bulk a-C(:H) materials via aliphatic and/or olefinic bonds.
3.1 Size-dependent cluster network connections
Within the framework of THEMIS a major fraction of the carbon atoms in the a-C(:H) nanoparticles are found to be in aromatic domains, held together by aliphatic-olefinic bridges. Such network structures are consistent with their inferred stability and survival in the diffuse ISM.
As deduced above for bulk materials, the aromatic domain connectivity was determined by the number of edge sites that link within the network. In this section we reconsider this deduction within the framework of finite-sized particles where particle surfaces (and, in particular, their hydrogenation) and short-range structural order play a critical role.
For finite sized particles the number of carbon atoms per particle is given in Appendix A of Jones (2012c) as
where a, is the particle radius, the material density ρa-C:H = 1.3 + 0.4 exp(-(Eg + 0.2)) [g cm−3] (Jones 2012c), and for radii <0.5 nm, where the particles are shell-like we can calculate the number of carbon atoms based on the surface area, where
where ratom is the average radius of the constituent carbon atoms (see below). The hydrogen to carbon atom concentration ratio, η, for these particles is
where X′H, the H atom fraction6 that takes into account surface passivation by hydrogen atoms (Jones 2012c)7, is
where FS is the fraction of carbon atoms at the surface
and ratom is the average radius of a carbon atom, defined as
with Nj/NC (j = ar, ol, al) the C atom fraction of aromatic, olefinic, and aliphatic C atoms, and LCC (j) the CC bond lengths were taken to be 0.140, 0.134, and 0.154 nm, respectively8. In the eRCN model the mean coordination number of the carbon atoms, mC, can be expressed as
where Z is the number of constraints per carbon atom for the cluster, that is Z = Ncon,NR/nC where Ncon,NR = (2.5 mcoord - 3) (Jones 2012a), and
here 〈NR〉 is the average number of six-fold rings per aromatic domain for the nanoparticle composition under consideration. As above, the fraction of hydrogenated aromatic domain edge sites is ζ and (1 - ζ) mcluster the number of aromatic domain edge sites that link to the network for a given NR.
The small (nanoparticle) a-C(:H) grains in the diffuse ISM, PDRs, and H II regions, as mentioned at the end of the preceding section, are assumed to have Eg ≃ 0.1 eV9, f = 0.6, and Xsp2 = 0.88, which yields η = [H]/[C] ≃ 1.4 to 0.8 for nanoparticles with radii from 0.4 to 1.2nm, respectively.
Within the eRCN framework a given aromatic domain can only be counted as a sub-component of the contiguous a-C(:H) network if, firstly, nC(NR) is less than the total number of carbon atoms in the nanoparticle and, secondly, that it is connected to the network by at least two peripheral, linking single bonds10. The aromatic domain coordination number, mcluster, and the number of network linking aliphatic CC bonds, nlink, are shown by the red and black lines, respectively, in Fig. 1, and given in Table 1, as a function of the number of aromatic rings per domain, NR. The values of nlink are size dependent and shown for nanoparticle radii of 0.4, 0.6, 0.8, 1.0, and 1.2 nm, where the line thickness increases with increasing radius. For each radius the particle size-dependent hydrogen to carbon atomic ratios, [H]∕[C]×10, are indicated by the ordinates of the blue crosses. Fig. 1 shows that single rings are not favoured (i.e. NR ⩾ 2), which is because of the higher values of [H]/[C] (= 1 for benzene)11 that they would impose. Equivalently, the weak increase in the cluster coordination number with increasing NR (see Table 1) significantly reduces the network linking per carbon atom. With increasing radius increasingly smaller aromatic domains can be accommodated and for a ≳ 1.3 nm this encompasses single aromatic rings. Thus, for larger grains and bulk materials benzene-type aromatic rings can occur within the structures. Naïvely, it would seem that the smallest particles ought to be able to encompass single, benzene-like aromatic domains. However, and perhaps paradoxically, Fig. 1 shows that sub-nanometre radius particles, with ~40-80 carbon atoms (a ~ 0.4-0.8 nm), actually tend to favour larger aromatic domains (NR ~ 4-8) comprising ~20-30 carbon atoms. This apparent paradox arises because the RCN model balances the nearest neighbour covalent bonding constraints against strain energy introduced by bond angle and bond length distortions. In conclusion, a significant fraction of the carbon atoms in a-C(:H) nanoparticles must be in aromatic domains, which is consistent with their inferred composition and stability in the diffuse ISM (Jones et al. 2013).
A comparison of the mcluster and nlink behaviour in Fig. 1 indicates that only about half of the peripheral carbon atoms in the aromatic domains are linked to the network via single CC bonds in nanometre-sized particles. The degree of linking increases with increasing radius but is only weakly dependent on NR. Thus, the weakest bound domains, with the fewest network links, are the smallest, which has interesting consequences for a-C nanoparticle photo-dissociation in the ISM (see Section 4.2).
Support for small aromatic domains in a-C(:H) nanoparticles comes from steric considerations, which imply that the aromatic clusters should principally consist of isolated two- and three-ring systems containing about three quarters of the carbon atoms, see Jones (2012c) and Figs. 1 to 4 in Micelotta et al. (2012). The sub-nanometre, aromatic-aliphatic structures shown in Micelotta et al. (2012) were energetically minimised to ensure the structural integrity of the cluster by balancing the constraints imposed by bond angle and bond length distortions. The nonaromatic carbon atoms must be in aliphatic-olefinic bridging structures, mostly in the form of short chains with typically 26 carbon atoms: the only possible four carbon atom bridging structures are -CH2-CH2-CH2-CH2-, -CH2-CH=CH-CH2-, or -CH=CH-CH=CH- (Jones & Habart 2015). Note that the terminating bonds in these bridges must be single in order to preserve the aromaticity of the adjacent aromatic domains. Further, the flexibility of the aliphatic-olefinic bridges plays a key role in balancing the energies associated with the strain effects due to bond angle and bond length distortions within sub-nanometre a-C(:H) clusters. The aromatic rings are themselves somewhat strained in these structures and lose some of their planarity (e.g. see Figs. 1 to 4 of Micelotta et al. 2012). The spectra of subnanometre, H-poor a-C(:H) particles (with Eg = 0.1-0.5 eV) show predominantly aromatic CH and aliphatic CHn bands, which is compatible with the hypothesis of cluster structures consisting of aromatic domains with aliphatic-olefinic bridges (Micelotta et al. 2012; Jones 2012c) and is also consistent with experimental data (Carpentier et al. 2012).
 |
Fig. 1 Aromatic clusters coordination numbers, mcluster (red lines, upper and lower limits shown dashed), and number of network linking bonds, nlink, in a-C(:H) nanoparticles as a function of NR and radius (0.4, 0.6, 0.8, 1.0, 1.2 nm, thin to thick black and grey lines, respectively). For each particle radius (same line thickness) the blue cross ordinate indicates the size-dependent hydrogen to carbon atomic ratios, [H]/[C], multiplied by 10. |
Number aromatic rings, NR, cluster coordination number, mcluster, and number of network linking bonds, nlink.
3.2 Aromatic domain size distribution
In any given a-C(:H) material, the maximum aromatic domain size, NR(max), is given by that for a bulk material (e.g. Eq. (1) and Fig. 23 from Robertson 1986). For finite-sized particles, such as interstellar grains, NR (max) is further constrained by the particle size, NR(a), because the aromatic domains cannot be larger than the largest particle dimension. In fact they need to be smaller than this in order that the particle hangs together, that is, it is contiguous. NR(a) can then be obtained by solving for NR in Eq. (4). For a-C(:H) particles with radii a < 1 nm (NC < 300), NR(max) ≲ 60, and for the smallest a-C(:H) nanoparticles in the THEMIS diffuse ISM dust model a = 0.4 nm (NC ≲ 40) we have NR(max) ≲ 8 (see Fig. 1 and Jones 2012c). In THEMIS it is these a-C(:H) nanoparticles that are predicted to be responsible for the IR emission bands and the UV extinction bump in the diffuse ISM (Jones et al. 2013, 2017).
The largest possible aromatic domain, calculated above, is untenable because it is diametric and would isolate the atoms on either side of it from each other and therefore from forming a part of a contiguous, chemically-bonded, random covalent network structure. Hence, a more appropriate value of NR (max) would be equivalent to that of an aromatic domain with a radius of about half of that of the particle radius, that is an aromatic domain diameter equal to the particle radius. With this limitation, a-C(:H) particles with radii a < 1 nm (0.4 nm) would have NR (max) ≲ 13 (2). This is in reasonable agreement with the findings of the previous section, that to fulfil the network linking constraints within a-C(:H) nanoparticles requires NR(max) ~4-8.
The optical properties of the aromatic domains in bulk a-C(:H) materials manifest at UV and optical wavelengths through their σ - σ* and π-π* bands, respectively. They are also evident at longer wavelengths through the low energy wing of the π-π* band, which was modelled with a power-law NR distribution biased towards the smaller sizes (see Jones 2012c, Eq. (B.5)),
where n(NR) is the relative abundance of aromatic ring systems with NR rings. The power law exponent in this distribution, p, varies from 2.5 to 3.55 for the highest to lowest band gap materials, respectively12, and nc(NR) is the number of carbon atoms in an aromatic cluster with NR rings given by Eq. (3). Note that the cluster abundance is normalised by ΣnC,arom., the total number of carbon atoms in aromatic clusters per unit volume. However well this might work for bulk materials (e.g. see Jones 2012c, Appendix B), this same kind of power-law distribution cannot apply to nanoparticles because the relatively small number of carbon atoms per particle implies, as predicted by the steepness of the power-law, that the aromatic domain size distribution will be dominated by the smallest domains, each with only a few rings, that is NR = 1 to 5. This is clearly in contradiction with the above network linking results and is also in conflict with the requirement that the band gap of such particles is dominated by the presence of aromatic domains that are as large as possible for the given particle radius. Thus, for nanoparticles with less than -103 carbon atoms a different approach is needed, which begins with the inclusion of the largest possible aromatic domain for the given band gap and particle size (Jones 2012c). In this case, it is easy to imagine a particle in which the aromatic domains are effectively populated top-down starting with the largest possible domain and adding, depending on the residual carbon atoms, sequentially-smaller domains until the requisite number of aromatic carbon atoms is satisfied. This would be equivalent to a rather flat aromatic domain number distribution with some domain sizes unoccupied. Thus, a power-law type of aromatic domain distribution is almost certainly not appropriate for a-C(:H) nanoparticles because their cluster-like structures are finite and dominated by critical size-related effects, which do not apply in bulk materials. We therefore did not consider power law size distributions for the aromatic domains in nanoparticles but assumed the top-down approach described above.
3.3 Aromatic cluster spatial separation
Of particular interest in the nanophysics of a-C(:H) particle processing and (photo)fragmentation is the geometrical arrangement of and distance between the aromatic domains in these semi-conducting materials. This is important because the aromatic domains within a-C(:H) nanoparticles are the localised charge-carrying sites responsible for their electrical conductivity. These sites are isolated and therefore charge mobility, or electrical conduction, in a-C(:H) is necessarily excitation-driven.
a-C(:H) nanoparticles are richer in hydrogen than their bulk counterparts because of the need for surface passivation, in the absence of dangling bonds, and are also of lower effective density, with respect to bulk matter (see Jones 2012c, Appendix A). As shown by Micelotta et al. (2012) a-C(:H) nanoparticles with radii ≃0.7 nm containing about 100 carbon atoms (see their Figs. 3 and 4) likely exhibit very open cluster or shell-like structures. Closed cage-like structure can probably be maintained down to particles with NC ≃ 50-70 C atoms, that would be generically fullerene-like and hydrogenated. However, smaller particles will likely be progressively more open, bowl, tube, or ribbon-like, and planar or quasi-linear structures at the smallest particles size scales. This general hypothesis is supported by the laboratory observations and theoretical work of Ferrari & Robertson (2004) who pointed out that the larger sp2 clusters in a-C(:H) are rather three-dimensional, cage-like structures while smaller clusters are probably more chain-like. In view of this the aromatic domains in a typical a-C(:H) nanoparticle structure will be separated by, at most, a distance equivalent to the diameter of the particle, which is of the order of ≈ 1 nm in the above, NC ≈ 100, example taken from Micelotta et al. (2012). In larger particles the structure will tend to take on multiple conjoined or interlocking cage-like forms with each characteristic cluster structure having a diameter typically of the order of 0.35-0.5 nm (Wang et al. 2001; Micelotta et al. 2012). In the case of a conducting doubly-charged or di-cation particle a cage-like structure can be used to estimate a minimum condition for charge-induced fragmentation because the charged domains would be, at their most distant, in diametrically-opposed positions on the cage surface. However, a-C(:H) materials are semiconductors in which the charges are localised within aromatic domains (i.e. conduction is excitation-driven) and it is therefore possible, in a di-cationic or higher charged state, that the charged sub-domains may be located closer than the diameter of the particle.
The number of C atoms per a-C(:H) nanoparticle was given above in Eqs. (9) and (10) (Jones 2012c). For the a-C(:H) nanoparticles in the THEMIS model, with Eg = 0.1 eV (XH = 0.02), these parameters yield ρa-C:H = 1.5 g cm−3 and we have
where the radius is raised to the power of 0.8 to account for the more open structures of sub-nanometre radius a-C(:H) nanoparticles (see Jones 2012c, Appendix A). The fraction of carbon atoms in aromatic domains is given by fXsp2/(1 - XH) = (0.6 × 0.88)∕(1 - 0.02) = 0.54. From the earlier discussion in Section 3.1, if we attribute aromatic domains starting with the lowest allowed values of NR and summing the number of associated carbon atoms (10, 14, 16, 19, 22, 24, 27, 30, 32, for NR = 2,3,4,... 10)13 until a fraction of ~0.54 has been used, then we find that the number of aromatic domains per nanoparticle is ≈(a[nm]/0.38)2. The number of aromatic domains per a-C(:H) nanoparticles is given by
with NR = 3 to 5, we find that for radii of 0.4, 0.6, 0.8 and 1 nm, this equation predicts 1, 3-4, 6-8 and 9-13 aromatic domains, respectively. Assuming a quasi-spherical, single-shell, cage-like nanoparticle structure, the distance along the surface and between the centres of quasi-circular aromatic domains is
where the factor 0.91 is the area packing efficiency for circular domains. The chordal distance between the aromatic domains is
where a is the radius in nanometres, giving chordal distances ≃0.75 - 0.87 nm between the aromatic domains. However, if the radius of the a-C(:H) particle is larger than some characteristic size then the structure is most likely organised into multiple cage-like sub-domains (Ferrari & Robertson 2004), with typical cage radii of the order of 0.35 nm (e.g. Wang et al. 2001; Micelotta et al. 2012). Thus, if we simplistically assume spherical cages, with a 60% packing efficiency14, assuming a quasi-spherical particle, the number of cages per nanoparticle is
and 0.4, 0.6, 0.8, and 1nm radius a-C(:H) nanoparticles encompass ≃1,3,7, and 14 sub-structure cages, respectively.
4 Photon-driven fragmentation
There are currently no experimental data15 or theoretical models to aide us in predicting the fragmentation pathways of the contiguous amorphous structures that are typical of a-C(:H) nanoparticles, as illustrated in Figs. 3 and 4 of Micelotta et al. (2012). We therefore based our modelling of the photon-driven fragmentation of these nanograins on the methods applied to PAHs (Leger et al. 1989; Micelotta et al. 2010a) and adapted them and other theoretical modelling to the case of 3D arophat-ics, structures of mixed aromatic, olefinic, and aliphatic bonding (e.g. Micelotta et al. 2012).
In order to calculate the EUV photon-driven fragmentation of a-C(:H) nanoparticles we adopted the THEMIS size-, composition-, and wavelength-dependent absorption efficiency factors, Qabs(a, Eg, λ), to determine the fraction of incident photons absorbed by a given grain. The absorbed energy, Ehν, leads to the internal excitation (electronic and vibrational) of the grain, which then relaxes by dissociation and/or thermal IR emission. The dissociation can be by the loss of small radical fragments, such as C2 in the case of PAHs (Micelotta et al. 2010b), or by the loss of larger aliphatic/olefinic bridging structures (e.g. CnHk, where n ≃ 2-6 and k ≳ n) and the smaller, more weakly bound aromatic domains (NR ~ 1-3, Jones & Habart 2015).
Here, we are dealing with the destructive process acting on particles that result in the ejection of aromatic domains and the aliphatic-olefinic carbon bridges that link them. The particles that are considered here are small enough that they can be considered in terms of shell-like clusters with aromatic domains held together by bridges (carbon chains) of type -C-C-C-C-, -C-C=C-C-, -C=C-C-C- or -C=C-C=C- (e.g. see Fig. 2, where the positions of the CH bonds are indicated by the dangling bonds). Critical clusters probably contain 50-100 atoms (a ≃ 0.4-0.6 nm). The breaking of several linking bridges and/or the ejection of an aromatic domain from a cluster will most likely lead to the disruption (opening up) of the shell structure into a less stable or more easily dissociable form that will be even more susceptible to photon-driven fragmentation, that is it will have an even shorter lifetime. Thus, and as a reasonable approximation, we assumed that the removal of a single linking bridge (i.e. the breaking of two bonds on the same linear bridge) is the rate-determining step in the disruption of a-C(:H) nanoparticles.
The interesting paper by Quan-De Wang (2017) studied the thermal decomposition of n-hexane and n-hexene isomers, which are almost exact replicas of the mixed aliphatic-olefinic aromatic domain-linking bridges16 that we hypothesised exist within a-C(:H) nanoparticles. Based upon the findings of Quan-De Wang (2017), and in particular Fig. 1 of that paper, we can draw some key and perhaps surprising conclusions regarding the mechanism of a-C(:H) nanoparticle disruption. The bond energies in Table 2 (taken from Quan-De Wang 2017) indicate that the allyl-adjacent C-C bonds17 are the weakest and therefore the most likely to be broken by thermal- or photo-dissociative disruption, requiring an energy of the order of 2 × 3.2 = 6.4 eV to liberate a mixed aliphatic/olefinic linking bridge.
Further support for this kind of behaviour comes from the well-known fragmentation pathways for cycloalkene molecular ions in mass spectrometry. For cyclohexene, C6H10 (a six-fold ring with one C=C bond, -CH2-CH2-CH=CH-CH2-CH2-), this occurs via a retro-Diels-Alder18 reaction, which occurs through the simultaneous breaking of the two C-C bonds symmetrically opposite the C=C bond and a structural re-arrangement to yield, [H2C=CH-HC=CH2]+∙, a dienyl radical cation and ethene, H2C=CH2. The fragmentation pathway of cycloalkanes is similar, leading to ethene and an alkyl resultant radical cation.
Interestingly, pure aliphatic (CH2)4-5 bridges are more resistant than dehydrogenated mixed aliphatic-olefinic bridges. Thus, UV photon-driven dehydrogenation rather than tending toward increasing stability through olefinisation followed by aromatisation will actually, and on the way to increased aromaticity, lead to a weakening of the structure before it becomes more resistant.
A close look at Fig. 2 indicates that the possible fragments resulting from the breaking of two C-C bonds along a single bridging structure would liberate aliphatic and mixed aliphatic-olefinic chains such as (CH2)n(=1-4), CH2-CH=CH-CH2 (C4H6), and CH2-CH=CH-CH2-CH2 (C5H8). If three CC bonds, in the case of branched bridges, are broken during thermal decomposition then branched species resembling CH2-CH=C(CH2)-CH2 (C5H7), and CH2-CH=C(CH2)-CH2-CH2 (C6H9) are also possible dissociation products. In general all of these break-down fragments can be characterised by the following formula
where n is the number of C atoms in the longest chain in the fragment (excluding branchings), m is the number of double bonds in the longest chain and, in this case, p is the number of CH2 branchings. With the restrictions that m ≤ (n — 1)/2 [for odd n], m ≤ n/2 [for even n], and p ≤ (n - 2). This formula can be adapted for branchings other than by CH2 groups simply by replacing (CH) by the relevant pendant group (less one H atom). However, it is obvious that the energy required to release a fragment increases with the number of branchings, that is, with increasing p, and the probability of their being released must therefore be much lower than for simple linear bridging species.
Clearly the dissociation products described above may subfragment upon ejection or will themselves be subject to photodissociation into smaller and simpler secondary dissociation species (e.g. see section 3.3 in Jones & Habart 2015). As Fig. 2 shows, for an idealised a-C(:H) nanoparticle, the maximum fragments size is in the range C4H6 to C5H7 but most are expected to be somewhat smaller than this.
It appears that the above UV photon driven a-C(:H) nanoparticle decomposition mechanism could explain the origin of the C2H, C3H, l-C3H+, c-C3H2, l-C3H2, and C4H observed in the Horsehead Nebula PDR by Pety et al. (2012, 2005) and Guzmán et al. (2015). Within the proposed scenario, these species arise from the UV photo-fragmentation of the bridging aliphatic and olefinic (sub-)structures that link the aromatic domains in a-C(:H) nano-particles (Jones & Habart 2015).
Typical hydrocarbon bond-breaking energies. In the polyatomics, the energies are for the single C-C bonds indicated by -≀-.
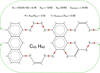 |
Fig. 2 Schematic structure of an idealised, simplified, and unfolded, shell-like a-C nanoparticle, C43H40, which could also be a substructure within a larger a-C(:H) nanoparticle network. The dashed green arrows indicate the common linking bonds that close the shell structure. The red dots indicate the equally probable (i.e. lowest energy) bond cleavage sites. The unadorned, dangling bonds mark the positions of H atoms. |
4.1 Photo-thermo-dissocation
The effects of photon-driven nanoparticle destruction were considered using the photo-thermo-dissocation (PTD) mechanism of Leger et al. (1989). After photon absorption the excited particle cools and after each cooling step the vibrational energy is redistributed and the particle may partially dissociate through the loss of atoms if the residual internal energy is high enough. These authors considered PAH molecule destruction for both hydrogenated and de-hydrogenated molecules, assuming that in the low density ISM they could be dehydrogenated to PAs. In contrast, the THEMIS a-C(:H) nanoparticles are clearly different from PAHs in that they contain an integral and essential aliphatic carbon component of lower C-C bond energy (~3.8 eV) than a typical CH bond (~4.3 eV) or aromatic and olefinic CC bonds (~5.4 and 6.3 eV, respectively). Table 2 gives a more complete listing of some typical hydrocarbon bond energies. Thus, the aliphatic CC bonds in a-C(:H) nanoparticles in the diffuse ISM could be photo-fragmented even while remaining hydrogenated. However, as discussed above for allyl configurations, C-C bonds two bonds distant from C=C bonds are even weaker (~3.2 eV) and will therefore be the first to break. Hence, the PTD approach needed to be modified for THEMIS nanoparticles in order to account for these hydrogens and the weaker aliphatic, allyl adjacent C-C bonds.
The Leger et al. (1989) PTD rate constant for the dissociation of PAH molecules, kd,CC, followed the Arrhenius equation
where the parameters ACC and BCC were those associated with the requisite C-C bond breaking that precedes particle fragmentation. For the dominant case of C3 loss from graphite Leger et al. (1989) adopted ACC = 1.5 × 1018 s−1 and an associated bond energy BCC = 7.97 eV. These numbers yielded a dissociation rate constant kd,CC = 0.710 s−1 and a lifetime of about one hundredth of a second for a nanoparticle with NC = 50 at 1000 K (the temperature attained upon absorption of a 13.6 eV photon), assuming that one C-C bond per C atom needs to be broken for complete destruction. This result indicated that such PAHs ought to be unstable in diffuse ISM given that they absorb of the order of one hard UV photon per year. Clearly the lifetime increases steeply with size and is sensitive to the exact bond breaking energies involved. Hence, and in the absence of dedicated laboratory data, it is not evident how applicable the PTD formalism is to particles with the kinds structures exhibited by the THEMIS a-C(:H) nanoparticles. Nevertheless, in the following we adapt this kind of methodology to the THEMIS nanograins.
4.2 Photon-induced thermal excitation fragmentation
In order to determine the loss rate of the absorbed photon energy via the dissociative loss of CnHk fragments (n ~ 2-4, k ≲ 2n) and via IR photon emission we followed and adapted the method of Micelotta et al. (2010a) that was developed for PAHs and described in their Section 4.1. We also made use of the PAH photo-processing study by Montillaud et al. (2013). Here we derived a photon-induced thermal excitation fragmentation process applicable to heterogeneous a-C(:H) nanoparticles, which is similar to that applied to PAHs. The fundamental mechanisms are the same, that is, UV photon absorption leads to thermal excitation and particle dissociation by partial fragmentation but do differ in the molecular-level details. The salient points of the methods are reproduced here as adapted to the THEMIS a-C(:H) nanoparticles, which are aromatic-rich but also contain significant aliphatic and olefinic components.
The Micelotta et al. (2010a) approach adopted a micro-canonical description for PAH molecules. Here we used the THEMIS a-C(:H) heat capacities (Jones et al. 2013) to determine the internal temperatures immediately following UV photon absorption and subsequent energy loss via thermal IR photon emission and/or fragmentation. The particle temperature, T, can be derived by solving the following equation for T
where T0 is the initial temperature (assumed to be 0K,), a is the grain radius and CV(T) its heat capacity. The energy E is initially the absorbed photon energy Ehν or the internal energy Eint following some degree of thermal emission and/or dissociative fragment loss. We assumed that the dissociation loss channel involves C4Hk bridging fragments, rather than C2 loss as in the Micelotta et al. (2010a) scheme, and that the energy required to remove these fragments is 6.4 eV as reasoned in Section 4. Thus, an a-C(:H) nanoparticle can shed excitation energy via bridging link fragment loss (Eloss = 6.4 eV) and/or incremental IR photon emission (e.g. Leger et al. 1989; Micelotta et al. 2010a; Montillaud et al. 2013).
The dissociative fragmentation rate constant, kdiss, can be defined by the Arrhenius form of a unimolecular rate (e.g. Micelotta et al. 2010a), that is
with Eloss = 6.4 eV the binding energy of the dissociated C4Hk fragment, kB the Boltzmann constant, and T the particle internal temperature calculated from Eq. (25).
The rate constant for IR photon emission, kIR, was taken to be fixed at 100 photons s−1 by Micelotta et al. (2010a). The later work by Montillaud et al. (2013) showed that, for the highly symmetric and rigid PAHs coronene C24H12 and circumcoronene C66H20, kIR is ≃10 and ~1-10 photons s−1, respectively, for internal energies in the range 7-15 eV. The lower internal energy cut-off is used here because only absorbed photon energies in excess of ~7 eV will lead to internal energies that exceed the critical fragmentation threshold energy Eloss of 6.4 eV and that can therefore dissociate a-C(:H) nanoparticles.
With the THEMIS nanoparticles we are dealing with structures that are much less rigid than PAHs, that clearly exhibit IR emission modes in addition to their aromatic modes (i.e. aliphatic and olefinic CC and CH emission bands), and that, in their much floppier states, it is here postulated that they are likely to be more efficient IR photon emitters. In contrast to Montillaud et al. (2013), we consider that it is the particle internal temperature that is the critical parameter, we adopt a temperature-dependent IR photon emission rate kIR(T) = 0.02 × Ts−1. The pre-temperature factor of 0.02 was chosen so as to give a reasonable comparison with the results of Montillaud et al. (2013) and yields kIR(T) = 2, 10, 20, and 60s−1 at 100, 500, 1000, and 3000 K, respectively. Note that we did not include an explicit size dependence into kIR but left this to enter implicitly through the derived, size-dependent internal temperatures.
It seemed reasonable to assume that the energy of the emitted IR photons, EIR, must also have some dependence on the nanoparticle temperature and so we assumed an equivalence between the particle internal temperature and the wavelength of the emitted IR photons, implicitly assuming that the particle emits as a blackbody. We therefore temperature-sliced the EIR values as shown in Table 3. The energy dependence of kIR was not considered by Micelotta et al. (2010a).
We now consider the competition between the channels for energy loss via IR photon emission, kIR, and dissociative fragmentation, kdiss. Following the methodology of Micelotta et al. (2010a) the (un-normalized) nanoparticle fragmentation probability between the emission of the nth and the (n + 1)th IR photons can be expressed as pi = kdiss(Ei)/kIR(Ei), where Ei = (Ehν - i × EIR(T)) (in the nomenclature adopted here). However, as Micelotta et al. (2010a) pointed out in their Section 4.1 it is difficult to solve the associated equations (their Eqs. (15)-(17)) in closed form and therefore requires some simplifying assumptions. Hence, and as per Micelotta et al. (2010a), assuming that pi in invariant and given by the average probability, pav, the total un-normalised probability of dissociation, P(nmax), is
where nmax = 0.2 NC19 and taking the average temperature to be the geometric mean Tav = (T(Ehv) × Tnmax)0.5. Here T(Ehv) is the initial temperature after UV photon absorption and Tnmax = T(Eint - nmax × EIR) is that after the emission of nmax IR photons. We considered discrete cooling steps until such time as the internal energy has dropped to the minimum IR photon energy (i.e. Eint = 0.1 eV, see Table 3). Any given cooling step where Eint is greater than E0 results in the loss of 6.4 eV of internal energy from the particle due the bond breaking resulting in the loss of a CnHk fragment. Otherwise each cooling step results it the loss of an energy EIR(T), that is the energy of the temperature appropriate IR photon (see Table 3). Only for the smallest particles and for the initial cooling events following energetic UV photon absorption (Ehν ≃ 8 eV) can fragment loss occur. For ionising photons (E ⩾ 13.6 eV) this may result in the loss of two fragments in the first two consecutive cooling events because 13.6 eV > 2 × Eloss = 12.8 eV. This approach would appear to be physically reasonable given that thermal dissociation is driven by the highest internal temperatures, which occur immediately after UV photon absorption.
In our study we adopted k0 = 1016 s−1 (similar to k0 = 1.4 × 1016 s−1 of Micelotta et al. 2010a)20 and E0 = 6.4 eV for a single bridging link21. The ejection of an aromatic domain is less likely because its dissociation energy could be as high as ~15 eV if for example, as shown previously, it were linked into the nanoparticle network by four aliphatic CC bonds. Hence, the motivation for considering that a-C nanoparticle destruction is instead triggered by the progressive and dissociative loss of the weaker bridging links.
The rate constants for dissociation and IR photon emission are shown in Fig. 3 for grain radii from 0.3 to 0.74 nm and can be compared with those of Montillaud et al. (2013). In Fig. 3 the dashed lines indicate the dissociation rate constants for particles with NC = 23 and 61, that is those closest in number of carbon atoms to the PAHs coronene, C24H12, and circumcorene, C66H20, presented in Fig. 3 of Montillaud et al. (2013). The dissociation rate constants calculated with the method presented here appear to be good agreement for the larger species but are significantly higher for smaller species. In other words we predict significantly higher photo-dissociation rates for the THEMIS a-C(:H) nanoparticles than for perfect planar PAHs, which is perhaps not surprising given the seemingly more fragile nature of the THEMIS nanograin structures (see Fig. 2).
The nanoparticle UV photon absorption timescale is
where Qabs(Eg, a, λ) is the absorption efficiency factor, a is the nanoparticle radius, FUV is the UV photon flux, the exponential factor is the UV extinction factor, taken to be ~2.5 × AV (assuming the average Galactic extinction curve from Fitzpatrick & Massa 2007), and G0 is the interstellar radiation field (ISRF) scaling factor. We took the nanoparticle photo-fragmentation lifetime, tpf, to be
where Nar is the number of aromatic domains per nanoparticle the factor 2 is due to the equivalent need to liberate two aliphatic-olefinic bridges (2 × E0 = 6.4 eV) or, that is, to break four C-C bonds (4 × 3.2 eV) and thus to liberate an aromatic domain (see Fig. 2 and Section 3). This lifetime calculation makes the simplifying assumption that the particle properties are independent of photon absorption events, that is, the progressive erosion is not taken into account. With this assumption it is evident that the derived lifetimes are therefore upper limits. Nevertheless, this limitation is probably counteracted by processes that lead to particle annealing by bond (re-)formation and/or the accretion of atoms from the gas. It should, however, be pointed out that the dissociative erosion of nanoparticles leads to smaller particles that have even shorter lifetimes, as is clearly evident in Fig. 4, because tpf decreases steeply with NC.
Some example results are shown in Fig. 4 for fluxes corresponding to Ehν = 8,10, and 12eV photons, the dotted, short, and long dashed lines, respectively, with the local UV fluxes taken from Henry (2002). This figure shows that a million year lifetime is compatible with the minimum grain size, a- ~ 0.4 nm (NC - 40), as per the THEMIS diffuse ISM model (Jones et al. 2013, 2017). Also shown is an illustrative example that leads to the photo-destruction of all particles with less than 160200 C atoms (a < 0.7-0.8 nm, as per Schirmer et al. 2022), which requires an excitation or absorbed energy per particle of -30 eV. Such a high excitation energy could be achieved by hard photons (Ehν = 30 eV) in a harsh ionising ISRF or through the effects of multi-photon absorption events (e.g. Montillaud et al. 2013), indicating that the destruction of a-C nanoparticles with hundreds of carbon atoms requires extremely high internal excitation energies. In their detailed JWST spectroscopic data analysis Elyajouri et al. (2024) determined a minimum grain size (a- ~ 0.4 nm) for the Orion Bar that is compatible with the THEMIS diffuse ISM model (Jones et al. 2013, 2017) but significantly smaller that that found by Schirmer et al. (2022) using Spitzer and Herschel photometric data.
We found that for our adopted photo-fragmentation scheme it was both the intensity (possibly leading to multi-photon absorption events) and the hardness (the absorption of extreme UV photons) of the ISRF that were critical. In these calculations the nanoparticle lifetimes were determined by assuming the breaking of four C-C aliphatic-olefinic bridge bonds per aromatic domain equivalent to the ejection of two complete aliphatic-olefinic bridges.
Unfortunately, the values of k0 and E0 that were adopted here are rather uncertain for a-C(:H) nanoparticles, and more so than for PAHs, for which there is some experimental evidence. Hence the current results should be regarded as order of magnitude estimates for the photo-fragmentation rates of the THEMIS a-C(:H) nanoparticles until such time as relevant experimental data and/or more rigorous models become available.
Emitted IR photon energies, EIR, and wavelengths, λIR, as a function of particle temperature, T, and wavelength ranges, λ.
 |
Fig. 3 THEMIS a-C(:H) nanoparticle rates constants for dissociation, kdiss (upper plot), and IR photon emission, kIR (lower plot), as a function of the internal energy Eint and particle radius from 0.3 to 0.74 nm, thinner to thicker lines, respectively. The dashed lines indicate particles with NC = 23 and 61 (see text for explanation). |
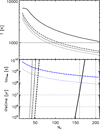 |
Fig. 4 THEMIS a-C(:H) nanoparticle initial temperatures (upper plot), and in the lower plot photon absorption timescales (blue), and lifetimes (black) for the ISRF conditions (G0, FUV Ehν, and AV) given in Table 4. The thin vertical dashed lines indicate the THEMIS minimum grain size in the diffuse ISM (a ~ 0.4-0.5 nm), and the derived limit for harsh PDR environments (a- ≲ 0.7-0.8 nm, IC63 and Orion Bar, Schirmer et al. 2022) and (a- ~ 0.4 nm, Orion Bar, Elyajouri et al. 2024). The horizontal dashed lines mark the million year lifetime (lower plot) and T = 103 K (upper plot). |
5 Coulomb fragmentation
In amorphous semi-conductors such as a-C(:H), conduction is excitation-induced with the charge carriers (electrons or holes) bound to, and promoted between, the aromatic domains. In finite-sized a-C(:H) particles the charges will therefore be localised on the aromatic sub-structures and, in multiply-charged a-C(:H) nanoparticles with a total charge ⩾2e, the charge carriers will tend to reside on different aromatic domains because of Coulomb repulsion. The maximum distance between the charged aromatic domains, in a cage-like a-C(:H) nanoparticle, is the diameter of the particle, which is likely to be of the order of 0.51 nm for the types of particles where Coulomb fragmentation might be important (e.g. Micelotta et al. 2012).
From the above discussion and calculations we reasonably assumed (on a statistical basis) that a typical aromatic domain consists of -14 C atoms (≡ NR = 3) and that it is linked within the a-C(:H) grain network by four bridging structures, which will dissociate upon multi-cation induced Coulomb fragmentation (MCF) and such an occurence will result in the loss of -20 C atoms from the particle. In this case the extra-aromatic C atoms result from the disruption of some of the aliphatic-olefinic inter-domain bridges (e.g. Jones & Habart 2015).
As shown earlier, the number of aromatic domains in these shell-like structures increases with radius (see Eq. (20)). Nevertheless, for a given size particle, as the number of charges increases the distance between the charge carrying domains must necessarily decrease. In fact, the minimum distance between the aromatic domains in an a-C(:H) nanoparticle is -0.4-0.5 nm.
Within an a-C(:H) nanoparticle the Coulomb force, FC, and electrostatic potential, UC, between two charged aromatic, subparticle domains, with charges Z1 and Z2, are given by
respectively, where e can be expressed in e.s.u. and dar in cm. MCF can occur if the Coulomb repulsive force between these charged aromatic domains exceeds the tensile strength that holds either of them within the network, that is, if the repulsive force is greater than the sum of the bond energies binding one of the domains within the contiguous network. As shown above, assuming an aromatic domain is bound by four single aliphatic bridge bonds (see Fig. 2 and Section 3.1), the binding energy for an aromatic domain is then ≃4 Ebr, where Ebr ≃ 3.2eV is the binding energy of a single aliphatic bond that links an aromatic domains into the network. Thus, the energy required to liberate an aromatic domain is of the order of 12.8 eV.
If we assume that particles with radii of 0.2, 0.25, 0.3, 0.35, and 0.4 nm contain, on average, 2, 2, 3, 3, and 4 aromatic domains, and that the distance between these domains is ≃0.4 nm, then charges of +2 or +3 on adjacent aromatic domains are enough to drive one of those domains from the nanoparticle and therefore to significantly disrupt it (i.e. E > 12.8 eV). To arrive at this catastrophic situation requires that the other aromatic domains in the particle are almost equally charged, leading to a situation in which the total charge state for MCF increases with particle size. For the above parameters, MCF would occur for particles with radii of 0.2 and 0.25 nm with each of the two constituent aromatic domains charged to +2 or +3 or a total particle charge of +4 or +6, respectively. Where the nanoparticles contain three [four] aromatic domains the charge states required for MCF would be +2/+3/+3 (total +8) [+2/+2/+3/+3 (total +10)]. These example charge states would appear to be significantly higher than those typically found on interstellar grains (e.g. Ibáñez-Mejía et al. 2019), even in PDRs, which would seem to argue against charge-induced effects being at the heart of carbonaceous nanoparticle destruction in high excitation regions. Given that the nanoparticle charge states required to induce MCF are rather extreme, it would appear that destructive charge effects on nanoparticles are subordinate to the photo-fragmentation effects discussed in the preceding sections.
6 Conclusions
The heterogeneous structural properties of semiconducting, hydrogenated amorphous carbon materials, a-C(:H), pose a challenge to the investigation of their survival in the ISM and in PDRs, especially in the most highly excitation regions. Following a detailed study of the chemical bonding makeup of a-C(:H) nanoparticles, that took their intrinsic heterogeneity into account, this work modelled their photo- and charge-stability in the ISM by developing a detailed understanding of the nature of their constituent aliphatic-olefinic and aromatic domain sub-structures. The important developmental aspects and major conclusions of this work are:
Using a statistical approach, we estimated the aromatic domain sizes, their size distribution, how they are bonded into a contiguous 3D a-C(:H) network, and where they are found within these structures as a function of the particle size;
We found that, as constrained by network structure and H atom fraction considerations, single aromatic ring systems (NR = 1 with NC = 6, i.e. benzene-like rings) are not favoured in the smallest nanoparticles (Nc < 80). In general, aromatic domains with NR = 2-3 are the most common in a-C(:H) nanoparticle structures containing 40-80 carbon atoms;
About one half of the peripheral bonding sites on aromatic domains are network bonded, and about one half are hydrogenated, exhibiting aromatic CH bonds, which will, statistically, tend to solo-type CH configurations;
Aromatic domains are linked into the 3D structure via aliphatic-olefinic bridges or chains with typically 4-6 carbon atoms. Non-aromatic cyclic domain linking structures are also possible and would appear to be essential in explaining the aromatisation of hydrogenated amorphous carbons;
In bulk a-C(:H) materials, where a power law aromatic domain size distribution favours the smaller domains and the optical properties are determined by the largest. In nanoparticles the aromatic domains tend towards the largest possible;
In a-C(:H) nanoparticles the sizes (diameters) of the aromatic domains must be, at most, similar to the particle radius in order to preserve a contiguous 3D structure. This makes sense physically because sub-nm sized a-C(:H) particles tend to exhibit cage- or shell-like structures22.
Interestingly, and perhaps counter intuitively, within mixed aliphatic, olefinic, and aromatic 3D structural networks, the weakest bonds are not the CH bonds (DcH ~ 4.3 eV) nor the aliphatic CC bonds (DCC ~ 3.8 eV). This prize goes to allyl-adjacent aliphatic C-≀-C bonds (-C-≀-C-C=C-, DC-≀-C ~ 3.2 eV) in mixed aliphatic and olefinic chains;
Aliphatic chains (e.g. -C-C-C-C-) between aromatic domains are more resistant to photodissociation than their partially dehydrogenated products (e.g. -C-C-C=C-). Dehydrogenation therefore tends to weaken a-C(:H) nanoparticle structures before strengthening them by aromatisation;
We considered the effects of thermal excitation and photodissociation on a-C(:H) nanoparticles using an approach based on photo-thermo-dissociation methodologies, allowing us to predict the fragmentation timescales for the UV photon-driven photodissociation of CC bonds;
We estimated a-C(:H) nanoparticle lifetimes in the ISM and in PDRs of the order of 106-107 yr, depending on the local ISRF, for particles with radii of 0.4-0.5 nm (Nc = 4060), sizes that are consistent with the smallest nanoparticles predicted by THEMIS;
As concluded in studies of PAH survival, we found that particles with less than ≲ 50 carbon atoms are unstable in the diffuse ISM where the mean UV photn energy is 8-10 eV;
In H II regions, where hard UV photons (Ehν > 13.6 eV) are present and multiple UV photon absorption events can occur, only particles with radii greater than 0.7nm (≳150 carbon atoms) are likely to survive;
Energetic photon absorption leading to charge-induced Coulomb fragmentation was shown to be an unimportant dust destruction process, except in the case of extremely large grain charges on small grains where each of the constituent aromatic domains carry charges of ⩾ + 2 or +3.
Acknowledgements
The authors would like to thank the referee for a very thorough, careful and detailed review, which helped to greatly improve the paper.
References
- Alata, I., Cruz-Diaz, G. A., Muñoz Caro, G. M., & Dartois, E. 2014, A&A, 569, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alata, I., Jallat, A., Gavilan, L., et al. 2015, A&A, 584, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allain, T., Sedlmayr, E., & Leach, S. 1995, Ap&SS, 224, 417 [Google Scholar]
- Allain, T., Leach, S., & Sedlmayr, E. 1996a, A&A, 305, 602 [Google Scholar]
- Allain, T., Leach, S., & Sedlmayr, E. 1996b, A&A, 305, 616 [Google Scholar]
- Arab, H., Abergel, A., Habart, E., et al. 2012, A&A, 541, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bocchio, M., Jones, A. P., & Slavin, J. D. 2014, A&A, 570, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bossion, D., Sarangi, A., Aalto, S., et al. 2024, A&A, 692, A249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boutéraon, T., Habart, E., Ysard, N., et al. 2019, A&A, 623, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carpentier, Y., Féraud, G., Dartois, E., et al. 2012, A&A, 548, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Compiègne, M., Abergel, A., Verstraete, L., & Habart, E. 2008, A&A, 491, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Muñoz Caro, G. M., Deboffle, D., & d’Hendecourt, L. 2004, A&A, 423, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Muñoz Caro, G. M., Deboffle, D., Montagnac, G., & D’Hendecourt, L. 2005, A&A, 432, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Döhler, G. H., Dandaloff, R., & Bilz, H. 1980, J. Noncryst. Solids, 42, 87 [Google Scholar]
- Elyajouri, M., Ysard, N., Abergel, A., et al. 2024, A&A, 685, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrari, A. C., & Robertson, J. 2000, Phys. Rev. B, 61, 14095 [Google Scholar]
- Ferrari, A. C., & Robertson, J. 2004, Philos. Trans. R. Soc. Lond. A, 362, 2477 [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [Google Scholar]
- Galliano, F., Dwek, E., & Chanial, P. 2008, ApJ, 672, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Galametz, M., & Jones, A. P. 2018, ARA&A, 56, 673 [Google Scholar]
- Guzmán, V. V., Pety, J., Goicoechea, J. R., et al. 2015, ApJ, 800, L33 [CrossRef] [Google Scholar]
- Habart, E., Boutéraon, T., Brauer, R., et al. 2021, A&A, 649, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, R. C. 2002, ApJ, 570, 697 [Google Scholar]
- Ibáñez-Mejía, J. C., Walch, S., Ivlev, A. V., et al. 2019, MNRAS, 485, 1220 [CrossRef] [Google Scholar]
- Jochims, H. W., Ruhl, E., Baumgartel, H., Tobita, S., & Leach, S. 1994, ApJ, 420, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Jochims, H. W., Baumgärtel, H., & Leach, S. 1999, ApJ, 512, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P. 1990, MNRAS, 247, 305 [NASA ADS] [Google Scholar]
- Jones, A. P. 2012a, A&A, 540, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P. 2012b, A&A, 540, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P. 2012c, A&A, 542, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P. 2013, A&A, 555, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P. 2016a, Roy. Soc. Open Sci., 3, 160221 [Google Scholar]
- Jones, A. P. 2016b, Roy. Soc. Open Sci., 3, 160223 [Google Scholar]
- Jones, A. P. 2016c, Roy. Soc. Open Sci., 3, 160224 [Google Scholar]
- Jones, A. P., & Habart, E. 2015, A&A, 581, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., & Nuth, J. A. 2011, A&A, 530, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., & Ysard, N. 2019, A&A, 627, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Ysard, N., Köhler, M., et al. 2014, RSC Faraday Discuss., 168, 313 [Google Scholar]
- Jones, A. P., Köhler, M., Ysard, N., et al. 2016, A&A, 588, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Köhler, M., Ysard, N., Bocchio, M., & Verstraete, L. 2017, A&A, 602, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kimura, H. 2016, MNRAS, 459, 2751 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, M., Jones, A., & Ysard, N. 2014, A&A, 565, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leger, A., D’Hendecourt, L., Boissel, P., & Desert, F. X. 1989, A&A, 213, 351 [NASA ADS] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010a, A&A, 510, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010b, A&A, 510, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2011, A&A, 526, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., Cami, J., et al. 2012, ApJ, 761, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Montillaud, J., Joblin, C., & Toublanc, D. 2013, A&A, 552, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Teyssier, D., Fossé, D., et al. 2005, A&A, 435, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Gratier, P., Guzmán, V., et al. 2012, A&A, 548, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phillips, J. C. 1979, Phys. Rev. Lett., 42, 1151 [Google Scholar]
- Quan-De Wang. 2017, Computat. Theor. Chem., 1115, 45 [Google Scholar]
- Robertson, J. 1986, Adv. Phys., 35, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, J. 1988, Philos. Mag. Lett., 57, 143 [Google Scholar]
- Robertson, J. 1991, Prog. Solid State Chem., 21, 199 [Google Scholar]
- Robertson, J. 2001, Physica Status Solidi Appl. Res., 186, 1521 [Google Scholar]
- Robertson, J. 2002, Mater. Sci. Eng., 37, 129 [Google Scholar]
- Robertson, J., & O’Reilly, E. P. 1987, Phys. Rev. B, 35, 2946 [NASA ADS] [CrossRef] [Google Scholar]
- Schirmer, T., Abergel, A., Verstraete, L., et al. 2020, A&A, 639, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schirmer, T., Habart, E., Ysard, N., et al. 2021, A&A, 649, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schirmer, T., Ysard, N., Habart, E., et al. 2022, A&A, 666, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slavin, J. D. 2009, Space Sci. Rev., 143, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B.-C., Wang, H.-W., Chang, J.-C., Tso, H.-C., & Chou, Y.-M. 2001, J. Mol. Struct. THEOCHEM, 540, 171 [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJS, 134, 263 [CrossRef] [Google Scholar]
- Weingartner, J. C., Draine, B. T., & Barr, D. K. 2006, ApJ, 645, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., Köhler, M., Jones, A., et al. 2015, A&A, 577, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Jones, A. P., Guillet, V., et al. 2024, A&A, 684, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
As per Jones (2012c) f = fmax/[e(xh-xHc)/6 + 1], where the maximum fraction of sp2 carbon atoms that can be incorporated into aromatic clusters fmax = 0.6 [= 0] at low [high] Xh, XHc = 0.33 and δ = 0.07 defines the steepness of the transition between high and low f.
This approximation is derived from Eq. (24) of Jones (2012a), viz. Xsp2 = (8 - 13Xh)/2(7 - 0.5[7 - b]), with the substitutions b = 0.5(7 -Yf ) and Yf = (7 - 2Z)f, as stated just before Eq. (40). Z is given by Eq. (A.1) of Jones (2012a) and for NR = 1-3 yields Z = 2 to the nearest integer and the denominator simplifies to 2(7 - 0.5[7 - 3f ]).
N.B. For Eg ≃ 0.1 eV bulk materials Eq. (1) predicts aromatic domains with NR ≥ 3000 and radii ≥7 nm that would be significantly larger than the IR band emitting carriers in THEMIS (a ~ 0.4-3 nm). Hence the need to consider a size-dependent effective band gap of 2.5 eV (see Jones 2012c, Fig. 2), which yields NR ~ 5.
The bond lengths are taken from the National Institute of Standards and Technology (NIST) Computational Chemistry Comparison and Benchmark DataBase (CCCBDB) and are those for benzene, cylcohexene and adamantane. https://cccbdb.nist.gov/expbondlengths1x.asp
In the atomic region of the Orion PDR the a-C(:H) nanoparticle band gap is reduced to 0.03 eV (Elyajouri et al. 2024).
The aromatic cluster power-law, p, for bulk a-C(:H) materials is given by 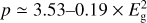 (Jones 2012c, Eq. (B.9)).
(Jones 2012c, Eq. (B.9)).
Equivalent to the finding of Micelotta et al. (2010a), expressed on their page 5, that “nmax = 10, 20, and 40 for Nc = 50, 100, and 200 respectively.”
We note that in their modelling Bossion et al. (2024) derive a binding energy of 7.55 ± 0.01 eV for C atoms within an amorphous carbonaceous structure but do not consider allyl adjacent bonding configurations.
All Tables
Number aromatic rings, NR, cluster coordination number, mcluster, and number of network linking bonds, nlink.
Typical hydrocarbon bond-breaking energies. In the polyatomics, the energies are for the single C-C bonds indicated by -≀-.
Emitted IR photon energies, EIR, and wavelengths, λIR, as a function of particle temperature, T, and wavelength ranges, λ.
All Figures
 |
Fig. 1 Aromatic clusters coordination numbers, mcluster (red lines, upper and lower limits shown dashed), and number of network linking bonds, nlink, in a-C(:H) nanoparticles as a function of NR and radius (0.4, 0.6, 0.8, 1.0, 1.2 nm, thin to thick black and grey lines, respectively). For each particle radius (same line thickness) the blue cross ordinate indicates the size-dependent hydrogen to carbon atomic ratios, [H]/[C], multiplied by 10. |
| In the text | |
 |
Fig. 2 Schematic structure of an idealised, simplified, and unfolded, shell-like a-C nanoparticle, C43H40, which could also be a substructure within a larger a-C(:H) nanoparticle network. The dashed green arrows indicate the common linking bonds that close the shell structure. The red dots indicate the equally probable (i.e. lowest energy) bond cleavage sites. The unadorned, dangling bonds mark the positions of H atoms. |
| In the text | |
 |
Fig. 3 THEMIS a-C(:H) nanoparticle rates constants for dissociation, kdiss (upper plot), and IR photon emission, kIR (lower plot), as a function of the internal energy Eint and particle radius from 0.3 to 0.74 nm, thinner to thicker lines, respectively. The dashed lines indicate particles with NC = 23 and 61 (see text for explanation). |
| In the text | |
 |
Fig. 4 THEMIS a-C(:H) nanoparticle initial temperatures (upper plot), and in the lower plot photon absorption timescales (blue), and lifetimes (black) for the ISRF conditions (G0, FUV Ehν, and AV) given in Table 4. The thin vertical dashed lines indicate the THEMIS minimum grain size in the diffuse ISM (a ~ 0.4-0.5 nm), and the derived limit for harsh PDR environments (a- ≲ 0.7-0.8 nm, IC63 and Orion Bar, Schirmer et al. 2022) and (a- ~ 0.4 nm, Orion Bar, Elyajouri et al. 2024). The horizontal dashed lines mark the million year lifetime (lower plot) and T = 103 K (upper plot). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![N_{\rm R} \simeq \left( 5.8 / E_{\rm g}[{\rm eV}] \right)^2.](/articles/aa/full_html/2025/12/aa55203-25/aa55203-25-eq1.png)
![L_{\rm a}[{\rm nm}] \simeq ( 0.77 \, N_{\rm R}^{0.5} ) / 5.8 = 0.13 \, N_{\rm R}^{0.5}.](/articles/aa/full_html/2025/12/aa55203-25/aa55203-25-eq2.png)
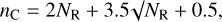
![a_{\rm R} = 0.09 \left[2 N_{\rm R} + \surd N_{\rm R} + 0.5 \right]^{0.5} {\rm nm}.](/articles/aa/full_html/2025/12/aa55203-25/aa55203-25-eq4.png)
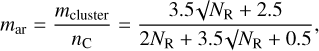
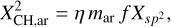
![X_{sp^2} = \frac{(8-13 X_{\rm H})}{2(7-0.5[7-3f])},](/articles/aa/full_html/2025/12/aa55203-25/aa55203-25-eq8.png)
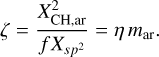
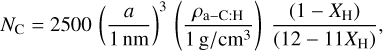
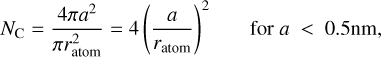
![\eta = \frac{[H]}{[C]} = \frac{X_{\rm H}^\prime}{(1-X_{\rm H})},](/articles/aa/full_html/2025/12/aa55203-25/aa55203-25-eq12.png)
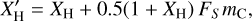
![F_S = \Bigg\{ 1 - \left[ 1 - \left( \frac{2 \, r_{\rm atom}}{a} \right) \right]^3 \Bigg\}.](/articles/aa/full_html/2025/12/aa55203-25/aa55203-25-eq14.png)
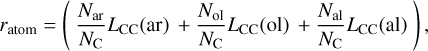
![m_{\rm C} = \frac{(20-15 X_{\rm H}) + 4 \, [7-2Z] f \, (1-X_{\rm H})}{(7+ [7-2Z] f) \, (1-X_{\rm H})},](/articles/aa/full_html/2025/12/aa55203-25/aa55203-25-eq16.png)
![Z = \left[ \frac{5}{4} (7 \surd \langle{N_{\rm R} \rangle} +5) - 3 \right] \frac{1}{N_{\rm ar}},](/articles/aa/full_html/2025/12/aa55203-25/aa55203-25-eq17.png)
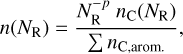
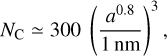
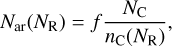
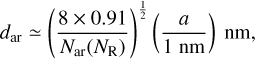
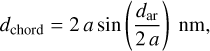
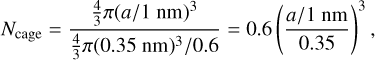
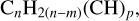
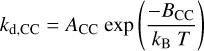
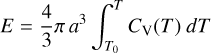
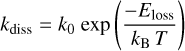
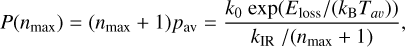
![\tau_{\rm abs} = \left[ Q_{\rm abs}(E_{\rm g},a, \lambda) \ \pi a^2 \ F_{\rm UV} \ {\rm exp}(- 2.5 \, A_{\rm V}) \ G_0 \right]^{-1}](/articles/aa/full_html/2025/12/aa55203-25/aa55203-25-eq29.png)