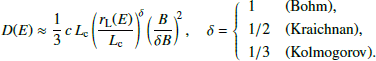| Issue |
A&A
Volume 705, January 2026
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202557202 | |
| Published online | 08 January 2026 | |
Letter to the Editor
Microquasar remnants as hidden PeVatrons
1
Instituto Argentino de Radioastronomía (CCT La Plata, CONICET; CICPBA; UNLP), C.C.5, (1894), Villa Elisa, Argentina
2
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, B1900FWA La Plata, Argentina
3
Departament de Física Quàntica i Astrofísica, Institut de Ciències del Cosmos (ICC), Universitat de Barcelona (IEEC-UB), Martí i Franquès 1, E08028 Barcelona, Spain
⋆ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
11
September
2025
Accepted:
8
December
2025
The Large High Altitude Air Shower Observatory (LHAASO) has revealed numerous ultrahigh-energy gamma-ray sources of unknown origin. We propose that a fraction of them can be explained by microquasar remnants, i.e., binary systems where mass transfer has ceased and the central engine is quenched. Cosmic rays injected during the active phase of a microquasar may remain confined within its cocoon and subsequently interact with nearby molecular clouds, producing bright gamma-ray emission through pp collisions. Remnants of former super-Eddington systems can act as dark PeVatrons, releasing particles up to ∼10 PeV that illuminate surrounding clouds producing gamma rays reaching hundreds of tera-electron volts. This scenario provides a natural explanation for several unidentified Galactic LHAASO sources.
Key words: acceleration of particles / radiation mechanisms: non-thermal / relativistic processes
© The Authors 2026
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1. Introduction
The terminal regions of microquasar (MQ) jets are efficient sites of particle acceleration to relativistic energies (Heinz & Sunyaev 2002; Bosch-Ramon et al. 2005b; Romero & Vila 2008; Bordas et al. 2009). Recent studies have shown that super-Eddington MQs and binaries can accelerate particles up to ≳10 PeV (Abaroa et al. 2024; Yue et al. 2024; Peretti et al. 2025; Zhang et al. 2025). Energetic arguments further indicate that transrelativistic jets and winds with kinetic power ≳1039 erg s−1 are the most likely Galactic PeVatrons (Wang et al. 2025), strengthening the case for MQs as sources of cosmic rays (CRs) beyond the knee. These predictions are consistent with the ultrahigh-energy (UHE) gamma rays recently detected by the Large High Altitude Air Shower Observatory (LHAASO) (Cao et al. 2024; LHAASO Collaboration 2024a, 2024b).
Several UHE sources detected by LHAASO are associated with MQs. Most of these sources are believed to host compact objects that accrete matter at super-Eddington rates, either permanently or during certain phases of their activity (LHAASO Collaboration 2024a). This connection suggests that not only active MQs but also their long-lived remnants could contribute to the unidentified LHAASO population.
In this Letter, we propose that microquasar remnants (MQRs) can act as hidden PeVatrons. In an MQR, mass transfer from the companion star to the black hole (BH) ceases permanently. This may occur if the system loses angular momentum, widening the orbit from semi-detached to detached (Willcox et al. 2023); if a massive companion (M* > 40 M⊙) collapses directly into a BH without a supernova (Belczynski et al. 2016); or if the strong wind from a supercritical accretion disk expels the stellar envelope (Ohsuga et al. 2005; Abaroa et al. 2023; Abaroa & Romero 2024).
Once the central engine shuts down, the only fossil is the non-interacting binary at the center of the cocoon inflated by the jets during the MQ’s lifetime. This structure resembles Fanaroff-Riley II cocoons (Begelman & Cioffi 1989), but on smaller scales (Bordas et al. 2009; Abaroa et al. 2024).
Ultra-relativistic CRs injected throughout the MQ’s active phase can irradiate dense clumps or cloud fragments engulfed by the cocoon, producing gamma rays via pp interactions. A schematic of this scenario is shown in Fig. 1.
 |
Fig. 1. Conceptual scheme, not to scale. Left panel: Microquasar (t < t0). The stellar-mass BH and the star are in the core. The backward shock at the end of the jets accelerates particles to relativistic energies. An overpressured cocoon evolves with the jets and envelops the entire system. Right panel: Microquasar remnant (t > t0). The central engine shuts down, and an MQR forms. Cosmic rays distributed within the survivor cocoon interact with a fragment of a molecular cloud that enters the MQR, illuminating it. |
Cosmic ray diffusion timescales depend on the diffusion coefficient τ = R2/D(E), where D(E)∝Eδ (δ = 1 in the Bohm limit), so the highest-energy protons diffuse more rapidly and reach the clouds first. The duration of cloud irradiation and the resulting gamma-ray spectrum depend on several parameters, while escaping CRs can propagate through the interstellar medium (ISM) and interact with more distant molecular clouds, potentially producing multiple spatially separated gamma-ray sources with spectra set by the diffusion coefficient (Aharonian & Atoyan 1996; Bosch-Ramon et al. 2005a).
In the following sections of this Letter, we first present a model for MQRs (Sect. 2) and then the CR propagation model (Sect. 3). We show the results of CR–cloud interactions (Sect. 4), and we conclude with a discussion (Sect. 5).
2. The microquasar remnant
We assumed that the MQ remains active for t0 = 105 yr, injecting power through twin jets into the ISM and carving out a dilute bubble that is subsequently filled with relativistic particles accelerated in the shocks formed at the jet termination regions. This dilute bubble corresponds to the hot cocoon inflated by the bow shocks, which are driven by the jets as they propagate through the ISM. Such jet-inflated bubbles have been extensively studied and observed in both radio galaxies and MQs, supporting the adopted physical picture (Begelman & Cioffi 1989; Kaiser & Alexander 1997; Heinz & Sunyaev 2002; Kino & Kawakatu 2005; Bordas et al. 2009; Pakull et al. 2010; Soria et al. 2010; Martí et al. 2015, 2017; Abaroa et al. 2024).
Once the injection ceases, the system evolves into an MQR. We adopted a BH mass of 10 M⊙ accreting (for t < t0) at super-Eddington rates with an accretion power at the jet launch radius of Lacc ≈ 1041 erg s−1. Table A.1 in Appendix A.1 lists the main parameters of our model.
2.1. Jet
According to the disk–jet coupling hypothesis (e.g., Falcke & Biermann 1995), the kinetic power of each jet is assumed to be a fraction of the accretion power at the launching radius, Lj = qjLacc. Typical jet powers of Galactic and extragalactic MQs range from 1037 to 1041 erg s−1 (e.g., Heinz & Sunyaev 2002; Pakull et al. 2010). We adopted qj = 0.1, yielding Lj = 1040 erg s−1 per jet as a representative value supported by observations of powerful systems such as SS 433 and S26 in NGC 7793, whose large-scale radio and X-ray bubbles imply sustained kinetic luminosities of > 1040 erg s−1 over > 105 yr. Such powers are naturally explained by super-Eddington accretion onto the compact object. We also assumed a moderate value for the jet Lorentz factor, γj = (1 − vj2/c2)−1/2 = 3, which corresponds to a velocity of vj ≈ 0.943 c (Heinz & Sunyaev 2002).
The jet head propagates through the ISM, and its length, lj, at a time t ( < t0), is approximated here as lj = (Lj/ρISM)1/5 t3/5 (Kaiser & Alexander 1997), where the typical intercloud ISM density is ρISM = 1.7 × 10−25 g cm−3 (Spitzer 1978). At t = t0, the jet length is ≈2.8 × 1020 cm ≈ 95 pc. The longitudinal velocity of the jet head is vl = dlj/dt = 3lj/5t, which at t = t0 gives 5.4 × 107 cm s−1. An adiabatic reverse shock (RS) develops at the jet termination region, where it accelerates particles that are then advected by the bowshock backflows and subsequently injected into the cocoon. Once accelerated at the RS, relativistic particles are entrained in the downstream flow of the shocked jet material. This post-shock plasma streams backward along the cocoon, advecting and mixing the relativistic particles throughout its volume, where they can remain confined for long times before diffusing out.
The RS is a strong relativistic shock capable of efficient diffusive shock acceleration, as inferred in large-scale jet termination regions. Observations of non-thermal lobes in several MQs (e.g., Pakull et al. 2010; Alfaro et al. 2024) have demonstrated that particles can indeed be accelerated at such termination shocks and later advected into the cocoon.
Shortly after mass transfer stops, the BH accretes all matter from the accretion disk. Once the accretion stops, the system can no longer produce jets.
2.2. Cocoon
The cocoon is a cavity inflated by the jet that remains overpressured and expands into the ISM with an ellipsoidal geometry if the medium is approximately homogeneous. Its semimajor axis equals the jet length during the active MQ phase, lc(t < t0)=lj(t < t0), while the semiminor axis at any t is wc ∼ lc/3. This aspect ratio for the cocoon is consistent with analytical and observational results for jet-driven lobes (e.g., Begelman et al. 1984; Kaiser & Alexander 1997; Bordas et al. 2009; Soria et al. 2010). Here, the cocoon volume is taken to be Vc(t)=4πlc(t)3/27.
After t0, when accretion ceases and the jets no longer propagate, the cocoon continues to expand as an adiabatic bubble powered by an impulsive energy injection. Its longitudinal evolution is approximated as lc(t > t0)=(Lj t0/ρISM)1/5 t2/5, with a corresponding expansion velocity of vc = dlc/dt. This adiabatic phase lasts until the onset of the radiative phase (trad; see Appendix A.2).
3. Production and distribution of cosmic rays
A fraction, qrel ≈ 0.1, of the jet power is assumed to be converted to relativistic particles: Lrel = qrel Lj. We include both the hadronic and leptonic populations, Lrel = Lp + Le. The energy distribution between hadrons and leptons is unknown. We assumed a hadron-dominated scenario (Lp = 100 Le), meaning that 99% of the non-thermal power resides in protons, while only 1% is carried by electrons. This assumption is consistent with shock acceleration efficiencies inferred in supernova remnants and MQ jets (e.g., Romero & Vila 2008), and it is also supported by particle-in-cell simulations (Caprioli & Spitkovsky 2014).
The diffusive acceleration rate of the particles is given by 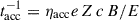 , where e is the electric charge, Z is the atomic number, c is the speed of light, B is the magnetic field, and E is the energy of the particle. We assumed an equipartition fraction of ∼0.1 between the magnetic pressure and thermal pressure to determine the strength of the magnetic field in the post-shock region (B ∼ 10 μG). We note that our results remain essentially the same if we vary the value of B in a reasonable parameter range. We also note that this value corresponds to a few times the compressed interstellar value and is well below equipartition with the jet luminosity. This ensures efficient acceleration without requiring unrealistically strong fields. On the other hand, the upstream medium is expected to have a weaker field and a larger diffusion coefficient. Since particle confinement is primarily limited by advection through the downstream region, we used the downstream B to estimate Emax.
, where e is the electric charge, Z is the atomic number, c is the speed of light, B is the magnetic field, and E is the energy of the particle. We assumed an equipartition fraction of ∼0.1 between the magnetic pressure and thermal pressure to determine the strength of the magnetic field in the post-shock region (B ∼ 10 μG). We note that our results remain essentially the same if we vary the value of B in a reasonable parameter range. We also note that this value corresponds to a few times the compressed interstellar value and is well below equipartition with the jet luminosity. This ensures efficient acceleration without requiring unrealistically strong fields. On the other hand, the upstream medium is expected to have a weaker field and a larger diffusion coefficient. Since particle confinement is primarily limited by advection through the downstream region, we used the downstream B to estimate Emax.
The acceleration efficiency of the process in the non-relativistic limit can be estimated as ηacc ≃ 3βsh2/8 (Drury 1983), where we adopted Bohm diffusion1 at the shocks and where βsh = vsh/c (with vsh as the shock velocity; see Table A.1). These values lead to ηacc ≈ 0.1. Escape is advective in the terminal region of the jet, 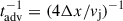 , and diffusive in the cocoon,
, and diffusive in the cocoon, 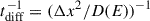 , where Δx is the size of the corresponding region. Here, D(E) is the diffusion coefficient, considered as a factor ζ of the Bohm coefficient: D(E)=ζDB(E)=ζE c/3 B e. To make some numerical estimates, we adopted ζ = 5 in the interior of the cocoon. This choice reflects the expected turbulence of the shocked jet plasma, which is likely filled with magnetic irregularities that strongly scatter CRs. Such a suppressed diffusion, while not strictly Bohmian, is consistent with conditions inferred in analogous systems such as radio-galaxy lobes and the Galactic Fermi bubbles, where relativistic particles appear confined for extended periods of time (Crocker & Aharonian 2011).
, where Δx is the size of the corresponding region. Here, D(E) is the diffusion coefficient, considered as a factor ζ of the Bohm coefficient: D(E)=ζDB(E)=ζE c/3 B e. To make some numerical estimates, we adopted ζ = 5 in the interior of the cocoon. This choice reflects the expected turbulence of the shocked jet plasma, which is likely filled with magnetic irregularities that strongly scatter CRs. Such a suppressed diffusion, while not strictly Bohmian, is consistent with conditions inferred in analogous systems such as radio-galaxy lobes and the Galactic Fermi bubbles, where relativistic particles appear confined for extended periods of time (Crocker & Aharonian 2011).
For simplicity, we neglected further acceleration mechanisms that might occur within the cocoon, such as Fermi type II or reacceleration due to the interaction between the CRs and the cocoon’s shell. In other words, all acceleration occurs at the RS, and the cocoon merely serves as a reservoir that traps the particles that have already been accelerated.
Relativistic particles cool via nonthermal processes arising from interactions with radiation, magnetic fields, and matter, and they also experience adiabatic losses in the RS and cocoon due to work done during their expansion. The following subsections describe the particle distribution in the cocoon during the MQ and MQR phases and CR propagation through the ISM. From this point onward, we focus on protons, as electrons are expected to cool rapidly via synchrotron losses.
The relativistic particles are accelerated at the RS in the moving head of the jets. We estimated this population by solving the time-dependent transport equation in the RS during the lifetime of the MQ (t < t0). The injection function for the source, QRS(E, t)=Q0(t)E−pexp( − E/Emax(t)), is a power-law in energy with an exponential cutoff and a spectral index of p = 2, which is characteristic of the Fermi first-order acceleration mechanism (see, e.g., Drury 1983).
At t0, the particle injection stops (Q0 = 0), and the fluid rapidly evacuates the acceleration region by advection (tesc, RS ≡ tadv). Thus, the particle distribution is completely suppressed for t ≳ t0. We note that to achieve energies greater than 1 PeV, the source must be active for at least 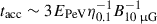 yr. This means that if the source is sporadic, it should have a high duty cycle to secure the necessary total power, with active periods lasting several years to reach adequate energies. In Appendix B.1 we detail the equation for particle transport in the cocoon.
yr. This means that if the source is sporadic, it should have a high duty cycle to secure the necessary total power, with active periods lasting several years to reach adequate energies. In Appendix B.1 we detail the equation for particle transport in the cocoon.
Figure 2 (top) shows the evolution of the proton distribution in the cocoon up to t = 5 × 105 yr. It can be seen that even hundreds of thousands of years after the MQ is turned off, particles with energies greater than 1 PeV remain within the cocoon. The maximum energy of the particles depends on time, and we find that under the Bohm regime and at t0, Emax ≈ 25 PeV.
 |
Fig. 2. Evolution of proton distributions. Top: Cosmic rays within the cocoon. The color bar distinguishes the MQ (t < t0, orange) and MQR (t > t0, blue) phases. Bottom: Cosmic ray propagation to a distance of 100 pc from the MQR over time for a source with a continuous injection of particles. |
4. Irradiation of clouds
Long after the MQ activity ceases, the relativistic particles accumulated in the cocoon begin to leak into the ISM. These escaping CRs diffuse outward and can interact with nearby molecular material, leading to delayed gamma-ray emission. Figure 2 (bottom) shows the proton distribution at a fixed distance of 100 pc from the MQR for different arrival times of the CRs.
Figure 3 shows the spectral energy distributions (SEDs) of irradiated clouds inside the MQR (top) and 100 pc away from the MQR (bottom). In both cases, we calculated the emission at different times (see the color bar). It can be seen that, even for t ≫ t0, UHE gamma rays are produced in the CR-cloud interaction with enough power to be detected by LHAASO for a source at 5 kpc from Earth (see Appendix B.2 for details on particle transport in the ISM and cloud irradiation).
 |
Fig. 3. Spectral energy distributions of the illuminated clouds at different times (see color bar). Leptonic emission is produced by secondary pairs created in the cloud via pp interactions. Thick dashed lines show the sensitivity curves of Fermi (10 yr, gray), SWGO (5 yr, light blue), and LHAASO (1 yr, green) for a Galactic MQR at 5 kpc. Top: Cloud in the MQR. Bottom: Cloud at 100 pc from the MQR (continuous scenario). |
5. Discussion and conclusion
Irradiated clouds would appear as very high energy (VHE) gamma-ray sources, while the PeVatron accelerating the CRs could remain undetected. At 5 kpc, the MQR would span ∼2°, but its radio surface brightness, produced by the primary electrons, would be below that of a bright supernova remnant, making it invisible to interferometers and hard to detect for single-dish surveys unless the large-scale Galactic diffuse emission is efficiently subtracted (e.g., Combi et al. 1998). We estimate a moderate radio surface brightness of Σ1.4 GHz ∼ 10−21 W m−2 Hz−1 sr−1 for most of the MQR phase, assuming a magnetic field of 2.5 μG in the cocoon. This low surface brightness arises from two complementary effects. First, only about one percent of the non-thermal power is injected into electrons, which is consistent with the adopted proton-to-electron energy ratio (Sect. 3). Second, the source is very extended, and therefore the emissivity per unit area is very low. This explains why most MQ bubbles exhibit only faint extended radio emission despite their large kinetic powers.
A single MQR could also generate multiple gamma-ray sources if located in a dense and structured ISM, suggesting a strategy to search for weak, extended radio counterparts in regions of clustered VHE emission. Clouds at different distances from the CR reservoir show spectra modified by energy-dependent diffusion, with steepening at larger distances (Aharonian & Atoyan 1996). This behavior (see Eq. (B.2)) can be used to constrain the ISM diffusion coefficient.
The MQR lifetime is set by its ability to confine CRs since the escape timescale grows as diffusion decreases. Cocoons approaching the Bohm limit (ζ = 5 here, but smaller values yield longer lifetimes) act as long-lived CR reservoirs. Even after the MQR dissipates, low diffusion in the environment can still generate a sequence of UHE, VHE, and high energy gamma-ray sources at different distances from the remnant if a cloudy medium is present.
Our conclusions rely on the assumption of quasi-Bohm diffusion inside the cocoon. If diffusion is faster, the CRs escape more rapidly and the γ-ray emission fades on shorter timescales. To test the robustness of this assumption, we explored alternative turbulence regimes (Kolmogorov and Kraichnan; see Appendix C). In these cases, the hard power-law energy dependence of the diffusion coefficient reduces particle confinement so that the MQR acts as a PeVatron for a shorter period than in the Bohm scenario. The resulting particle spectra lead to weaker non-thermal emission from the clouds in the cocoon and in the ISM. Consequently the γ-ray output shifts to lower energies, and the UHE component becomes strongly suppressed. These effects depend on the poorly constrained turbulence spectrum of MQ cocoons, but they could be partially mitigated if higher magnetic fields or denser nearby clouds are assumed.
The MQ type considered here is a super-Eddington system with powerful jets and hot spots for particle acceleration, exemplified by S26 in NGC 7793 (Abaroa et al. 2024), and it resembles FRII radio galaxies. A second class of MQs, with comparable power but slower jets (vj ∼ 0.3 c), resembles FRI galaxies and lacks bright terminal regions. SS 433 is a well-known case, detected by LHAASO at > 200 TeV. In such systems, particle acceleration likely occurs at recollimation shocks, where lateral jet expansion is confined by external pressure. In SS 433, this happens at ∼30 pc from the central engine (Abeysekara et al. 2018; H.E.S.S. Collaboration 2024). The scenario discussed here applies to these sources with only minor modifications, and the overall conclusions remain valid.
In summary, we suggest that undetected remnants of extinct super-Eddington MQs may act as CR reservoirs illuminating nearby clouds, potentially explaining many unidentified LHAASO sources in the Galactic plane. Given the presence of active super-Eddington MQs in the Galaxy, such remnants are likely, and we have outlined their possible manifestations.
This assumption is usually done in the acceleration regions of jets (e.g., Abeysekara et al. 2018; H.E.S.S. Collaboration 2024).
Acknowledgments
We thank the referee for his/her comments. LA thanks the UNLP. GER and VBR were funded by PID2022-136828NB-C41/AEI/10.13039/501100011033/ and through the “Unit of Excellence María de Maeztu” award to the Institute of Cosmos Sciences (CEX2019-000918-M, CEX2024-001451-M). VB-R is Correspondent Researcher at the IAR.
References
- Abaroa, L., & Romero, G. E. 2024, Rev. Mex. Astron. Astrofis. Conf. Ser., 56, 39 [NASA ADS] [Google Scholar]
- Abaroa, L., Romero, G. E., & Sotomayor, P. 2023, A&A, 671, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abaroa, L., Romero, G. E., Mancuso, G. C., & Rizzo, F. N. 2024, A&A, 691, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abeysekara, A. U., Albert, A., Alfaro, R., et al. 2018, Nature, 562, 82 [CrossRef] [Google Scholar]
- Aharonian, F. A., & Atoyan, A. M. 1996, A&A, 309, 917 [Google Scholar]
- Alfaro, R., Alvarez, C., Arteaga-Velázquez, J. C., et al. 2024, Nature, 634, 557 [Google Scholar]
- Begelman, M. C., & Cioffi, D. F. 1989, ApJ, 345, L21 [CrossRef] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1984, Rev. Mod. Phys., 56, 255 [Google Scholar]
- Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [Google Scholar]
- Bordas, P., Bosch-Ramon, V., Paredes, J. M., & Perucho, M. 2009, A&A, 497, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., Aharonian, F. A., & Paredes, J. M. 2005a, A&A, 432, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., Romero, G. E., & Paredes, J. M. 2005b, A&A, 429, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, Z., Aharonian, F., An, Q., et al. 2024, ApJS, 271, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., & Spitkovsky, A. 2014, ApJ, 783, 91 [CrossRef] [Google Scholar]
- Combi, J. A., Romero, G. E., & Benaglia, P. 1998, A&A, 333, L91 [NASA ADS] [Google Scholar]
- Crocker, R. M., & Aharonian, F. 2011, Phys. Rev. Lett., 106, 101102 [Google Scholar]
- Crutcher, R. M. 2012, ARA&A, 50, 29 [Google Scholar]
- Drury, L. O. 1983, Rep. Progr. Phys., 46, 973 [Google Scholar]
- Falcke, H., & Biermann, P. L. 1995, A&A, 293, 665 [NASA ADS] [Google Scholar]
- H. E. S. S. Collaboration (Olivera-Nieto, L., et al.) 2024, Science, 383, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Heinz, S., & Sunyaev, R. 2002, A&A, 390, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaiser, C. R., & Alexander, P. 1997, MNRAS, 286, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Kino, M., & Kawakatu, N. 2005, MNRAS, 364, 659 [NASA ADS] [Google Scholar]
- Klein, R. I., McKee, C. F., & Colella, P. 1994, ApJ, 420, 213 [Google Scholar]
- LHAASO Collaboration 2024a, arXiv e-prints [arXiv:2410.08988] [Google Scholar]
- LHAASO Collaboration 2024b, Sci. Bull., 69, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Martí, J., Luque-Escamilla, P. L., Romero, G. E., Sánchez-Sutil, J. R., & Muñoz-Arjonilla, Á. J. 2015, A&A, 578, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martí, J., Luque-Escamilla, P. L., Bosch-Ramon, V., & Paredes, J. M. 2017, Nat. Commun., 8, 1757 [CrossRef] [Google Scholar]
- McCourt, M., O’Leary, R. M., Madigan, A.-M., & Quataert, E. 2015, MNRAS, 449, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Ohsuga, K., Mori, M., Nakamoto, T., & Mineshige, S. 2005, ApJ, 628, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Pakull, M. W., Soria, R., & Motch, C. 2010, Nature, 466, 209 [Google Scholar]
- Peretti, E., Petropoulou, M., Vasilopoulos, G., & Gabici, S. 2025, A&A, 698, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ptuskin, V. 2012, Astropart. Phys., 39, 44 [Google Scholar]
- Romero, G. E., & Vila, G. S. 2008, A&A, 485, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soria, R., Pakull, M. W., Broderick, J. W., Corbel, S., & Motch, C. 2010, MNRAS, 409, 541 [CrossRef] [Google Scholar]
- Spitzer, L. 1978, Physical Processes in the Interstellar Medium (A Wiley-Interscience Publication, New York: Wiley) [Google Scholar]
- Wang, J., Reville, B., & Aharonian, F. A. 2025, ApJ, 989, L25 [Google Scholar]
- Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [Google Scholar]
- Willcox, R., MacLeod, M., Mandel, I., & Hirai, R. 2023, ApJ, 958, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Yue, H., Zhang, J., Ge, Y., et al. 2024, arXiv e-prints [arXiv:2412.13889] [Google Scholar]
- Zhang, B. T., Kimura, S. S., & Murase, K. 2025, Phys. Rev. D, 112, 123015 [Google Scholar]
Appendix A: System parameterization
A.1. General parameters
In the Table A.1, we provide the main parameters of our model for the jet, cocoon, and clouds. These values define the fiducial setup adopted throughout the calculations.
Parameters of the model.
A.2. Cocoon survival
Here, we describe the characterization of the cocoon as it expands into the ISM and the conditions for survival. The cocoon begins to break and to mix with the ISM in the transition between the adiabatic and radiative phases.
The transition occurs when the cooling time tcool(t)=3kBT(t)/nΛ(T(t)) becomes equal to t (Weaver et al. 1977). Here, kB is the Boltzmann constant, Λ is the cooling function, and n is the electron density (we assumed a plasma of pure hydrogen so that the mean molecular weight in the ionized medium is μ = 0.5). The temperature in the cocoon is given by Tc(t)=2Eint(t)/3ncocoonVc(t)kB, where Eint(t)∼0.5Ljt. At t = t0, we obtained Tc ≈ 6 × 108 K. As expected for jet-inflated bubbles, this implies that roughly half of the jet’s kinetic energy is converted into the cocoon’s internal energy, rather than representing an independent energy channel, as is the case in purely wind-driven outflows (Peretti et al. 2025). The temperature for the expanding shell is Ts(t)=3μmpvc2/16kB (where mp is the proton mass). At t = t0, we get Ts ≈ 3.3 × 106 K. Considering a post-shock density of 0.4 cm−3 and a cooling function value of Λ(T)∼2 × 10−22 erg cm3 s−1 for the temperature, Ts, above, we obtained tcool ≈ 5 × 105 yr for the shell, i.e., trad ≈ 5t0.
A.3. Engulfment of clouds
The cocoon expansion can lead to the engulfment of nearby clouds (see Table A.1 for cloud parameters). We followed the criteria of Klein et al. (1994) to assess whether a cloud engulfed by the expanding cocoon would survive.
We compared the timescales associated with crushing due to Kelvin-Helmholtz or Rayleigh-Taylor instabilities (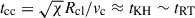 , where χ = ncl/nISM = 104, where vc is the expansion velocity of the cocoon and Rcl the cloud radius), shredding (tsh = Ntcc, with N > 1 as a dimensionless factor that depends on the cloud’s magnetic field), and dragging (tdrag = χtcc). The magnetic Mach number is given by MA = vsc/vA, where
, where χ = ncl/nISM = 104, where vc is the expansion velocity of the cocoon and Rcl the cloud radius), shredding (tsh = Ntcc, with N > 1 as a dimensionless factor that depends on the cloud’s magnetic field), and dragging (tdrag = χtcc). The magnetic Mach number is given by MA = vsc/vA, where 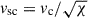 is the shock velocity in the cloud and
is the shock velocity in the cloud and 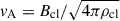 is the Alfvén velocity. If MA < 1, the shock is sub-Alfvénic, and the magnetic field drapes the cloud and suppresses hydrodynamic instabilities in the direction perpendicular to the local field lines (McCourt et al. 2015). The post-shock temperature is given by
is the Alfvén velocity. If MA < 1, the shock is sub-Alfvénic, and the magnetic field drapes the cloud and suppresses hydrodynamic instabilities in the direction perpendicular to the local field lines (McCourt et al. 2015). The post-shock temperature is given by 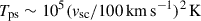 . If we suppose that the cloud is engulfed at t = t0, we have
. If we suppose that the cloud is engulfed at t = t0, we have 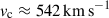 , tcc ≈ 5.5 × 1012 s ∼ 2 t0, tsh ≈ 5.5 × 1013 s, tdrag ≈ 5.5 × 1016 s,
, tcc ≈ 5.5 × 1012 s ∼ 2 t0, tsh ≈ 5.5 × 1013 s, tdrag ≈ 5.5 × 1016 s, 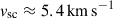 ,
, 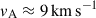 , MA ≈ 0.6, and Tps ≈ 291 K. Therefore, the cloud survives the engulfment (tsh ≫ tcc), it is not dragged (tdrag ≫ tcc), and we can neglect the cloud ionization (Tps ≪ 104 K).
, MA ≈ 0.6, and Tps ≈ 291 K. Therefore, the cloud survives the engulfment (tsh ≫ tcc), it is not dragged (tdrag ≫ tcc), and we can neglect the cloud ionization (Tps ≪ 104 K).
Appendix B: Particle transport
B.1. Transport in the cocoon
We injected the relativistic particles from the RS in the cocoon and determine their evolution by solving the time-dependent transport equation in the one-zone approximation:
Here, the injection is given by Qc(E, t)=nRS(E, t)VRS(t)/tesc, RS(t)Vc(t), where VRS ∼ Δx3 and Vc are the volumes of each zone, and nRS is the proton distribution in the RS. Escape of the cocoon is diffusive (tesc, c ≡ tdiff).
B.2. Transport in the interstellar medium
Equation (B.2) below expresses the transport of CRs in the ISM once they have escaped the cocoon, following the formalism of Aharonian & Atoyan (1996). Considering propagation in the spherically symmetric case, the transport equation of protons reads as
where the injection function is Q(E, R, t)=Q0(E, t)δ(R). Here, Q0(E, t)=nc(E, t)Vc(t)/tesc, c(E, t) and δ(R) is a delta function in space. A solution to this equation is provided by Aharonian & Atoyan (1996). We considered the scenario of a continuous injection of energy.
The diffusion coefficient in the ISM is given by D(E)=D0Eδ, where we assumed that δ = 0.5 and that the diffusion coefficient normalization constant is D0 = D(10 GeV)=1026 cm2 s−1 (e.g., Aharonian & Atoyan 1996). This value is a suppressed version of the average Galactic coefficient (D = χDgal, with χ = 10−2 and Dgal(10 GeV)≈1028 cm s−1), as the environment surrounding a former MQ is expected to be more turbulent and magnetically irregular. Such conditions may locally suppress diffusion because of the Alfvén-wave excitation by the escaping CRs themselves. This leads to a slow-diffusion zone analogous to those inferred around other compact accelerators (Aharonian & Atoyan 1996). This assumption allows the CRs to remain concentrated near the source and improves their probability of interaction with nearby clouds.
Proton-proton interactions between CRs and clouds lead to the production of neutral pions, which decay into gamma rays (π0 → 2γ), and charged pions, which in turn decay into electron-positron pairs (π± → μ± + νμ → e± + neutrinos). These secondary pairs then interact with matter and magnetic fields, producing synchrotron and Bremsstrahlung radiation. Inverse Compton radiation can be neglected (see Bosch-Ramon et al. 2005a).
Appendix C: Non-Bohmian diffusion
To test the sensitivity of our results to the assumed turbulence regime, we examined diffusion coefficients following Kolmogorov and Kraichnan scalings. The particle diffusion coefficient can be written as (Ptuskin 2012; Peretti et al. 2025)
Here, rL(E)=E/eB is the Larmor radius of a relativistic particle with energy E, B is the mean magnetic field, δB its turbulent component, and Lc the coherence (or injection) scale of turbulence, where most of the magnetic energy is contained. In the Bohm limit (δ = 1) the diffusion coefficient reaches its minimum value.
For non-Bohmian regimes (δ = 1/2, 1/3), we adopt Lc ∼ 10−2 lc at each time t, corresponding to the expected correlation length of turbulence within the cocoon (a small but reasonable fraction of its radius; see Zhang et al. 2025). This parameterization enables comparison among different turbulence spectra, while assuming that the acceleration process–occurring at the relativistic jet termination shock–operates near the Bohm regime, which sets the maximum particle energy Emax in our model.
As an illustrative example, Figs. C.1 and C.2 show the proton distributions (in the cocoon and ISM) and the corresponding SEDs (for the MQR and ISM clouds) for Kolmogorov diffusion with δB/B = 0.3. In this case, the MQR cloud emits detectable γ-rays up to ∼10 TeV for ≲105 yr after the MQ shuts down, although the emission at UHEs is markedly suppressed. The ISM cloud also shows a noticeable change: its γ-ray spectrum shifts to slightly lower energies and the overall luminosity decreases compared to the Bohm case, although the effect is less pronounced than in the MQR cloud. We also tested the Kraichnan regime and different turbulence levels (not shown here). The qualitative behavior remains similar, although Kraichnan diffusion is slightly more favorable to UHE emission.
All Tables
All Figures
 |
Fig. 1. Conceptual scheme, not to scale. Left panel: Microquasar (t < t0). The stellar-mass BH and the star are in the core. The backward shock at the end of the jets accelerates particles to relativistic energies. An overpressured cocoon evolves with the jets and envelops the entire system. Right panel: Microquasar remnant (t > t0). The central engine shuts down, and an MQR forms. Cosmic rays distributed within the survivor cocoon interact with a fragment of a molecular cloud that enters the MQR, illuminating it. |
| In the text | |
 |
Fig. 2. Evolution of proton distributions. Top: Cosmic rays within the cocoon. The color bar distinguishes the MQ (t < t0, orange) and MQR (t > t0, blue) phases. Bottom: Cosmic ray propagation to a distance of 100 pc from the MQR over time for a source with a continuous injection of particles. |
| In the text | |
 |
Fig. 3. Spectral energy distributions of the illuminated clouds at different times (see color bar). Leptonic emission is produced by secondary pairs created in the cloud via pp interactions. Thick dashed lines show the sensitivity curves of Fermi (10 yr, gray), SWGO (5 yr, light blue), and LHAASO (1 yr, green) for a Galactic MQR at 5 kpc. Top: Cloud in the MQR. Bottom: Cloud at 100 pc from the MQR (continuous scenario). |
| In the text | |
 |
Fig. C.1. Same as in Fig.2 but assuming Kolmogorov diffusion inside the cocoon. |
| In the text | |
 |
Fig. C.2. Same as in Fig. 3 but assuming Kolmogorov diffusion inside the cocoon. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \frac{{\partial n_{\rm c}(E,t)}}{\partial t}+ \frac{\partial }{\partial E}\left[\frac{\mathrm{d}E}{\mathrm{d}t} n_{\rm c}(E,t)\right]+\frac{n_{\rm c}(E,t)}{t_{\rm esc, c}(E,t)}=Q_{\rm c}(E,t). \end{aligned} $$](/articles/aa/full_html/2026/01/aa57202-25/aa57202-25-eq12.gif)
![$$ \begin{aligned} \dfrac{\partial n_{\rm I}(E,R,t)}{\partial t}&=\dfrac{D(E)}{R^2}\dfrac{\partial }{\partial R}\left[R^2 \dfrac{\partial n_{\rm I}(E,R,t)}{\partial R}\right]+\nonumber \\&\quad +\dfrac{\partial }{\partial E}\left[\left(-\dfrac{\mathrm{d}E}{\mathrm{d}t}\right)\,n_{\rm I}(E,R,t)\right]+Q(E,R,t), \end{aligned} $$](/articles/aa/full_html/2026/01/aa57202-25/aa57202-25-eq13.gif)