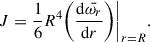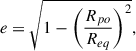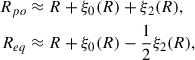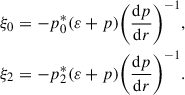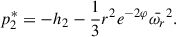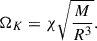| Issue |
A&A
Volume 706, February 2026
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202452766 | |
| Published online | 05 February 2026 | |
Symmetry energy effect on rotating neutron stars
1
Key Laboratory for Microstructural Material Physics of Hebei Province, School of Science, Yanshan University Qinhuangdao 066004, China
2
School of Physics and Information Engineering, Shanxi Normal University Taiyuan 030031, China
3
School of Science, China University of Petroleum (East China) Qingdao 266580, China
4
School of Physics, Nankai University Tianjin 300071, China
★ Corresponding authors: This email address is being protected from spambots. You need JavaScript enabled to view it.
, This email address is being protected from spambots. You need JavaScript enabled to view it.
, This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
27
October
2024
Accepted:
1
December
2025
We explore the symmetry energy effect on the bulk properties of static neutron stars and rotating millisecond pulsars (MSPs). The unified equations of state (EOSs) are constructed self-consistently within the relativistic mean-field framework from the inner crust to the outer core. To investigate the impact of a unified EOS, which uses the same nuclear interaction for both the crust and core, we compared the results of MSPs with those obtained using non-unified EOSs. These non-unified EOSs match the crust and core EOSs, which have different slopes of symmetry energy. For a given rotational period, we examined how symmetry energy influences the maximum mass, equatorial radius, and deformation from sphericity in MSPs. Our findings indicate that a softer EOS is favored by a higher Keplerian frequency, which corresponds to a smaller L for unified EOSs, but a larger L for the crust in matching EOSs. However, under the slow rotation approximation, there is no significant effect from the symmetry energy slope on the bulk properties of 2 M⊙ MSPs. In contrast, clear differences are observed for those around and below 1.4 M⊙.
Key words: dense matter / equation of state / stars: neutron / stars: rotation
© The Authors 2026
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1. Introduction
A millisecond pulsar (MSP) is a neutron star (NS) with a rotational period less than about 10 milliseconds (ms), exhibiting significantly faster spin rates than ordinary pulsars. Millisecond pulsars are generally older than standard pulsars. They have formed through a prolonged period of accretion from a companion star, which spins them up to periods less than about 10 ms (Nagase 1989). This mass transfer process causes the NS to spin faster and leads to a reduction in its magnetic field. A significant proportion of MSPs are observed in binary star systems (Bhattacharyya & Roy 2022). Their masses typically range from 1 to 2 M⊙ (M⊙ ≃ 1.989 × 1033 g is the mass of the Sun), while their radii generally fall within the range of 10 to 14 km. Recently, a large population of MSPs has been discovered in globular clusters (GCs) (Pan et al. 2021; Ridolfi et al. 2021; DeCesar et al. 2015; Wang et al. 2020), which have been shown to undergo a process of accretion acceleration. The first MSP, PSR B1937+21, was discovered in 1982 (Backer et al. 1982), with a period of 1.558 ms (642 Hz), once known as the second fastest-spinning pulsar. Currently, PSR J1748-2446ad is recognized as the fastest-spinning pulsar known, with a frequency of 716 Hz (1.397 ms) (Hessels et al. 2006). M14A is a black widow pulsar with a rotational period of approximately 1.98 ms (Pan et al. 2021). It is the second fastest-spinning black widow pulsar in GCs, after the one found in GC Terzan 5 (1.67 ms) (Ransom et al. 2005). Another remarkable MSP is the black widow pulsar PSR J0952-0607, which is not only the second fastest-spinning pulsar now, with a period of 1.41 ms (707 Hz), but it may also be the heaviest NS ever known, with a mass of 2.35 ± 0.17 M⊙ (Bassa et al. 2017; Romani et al. 2022).
FAST (Five-hundred-meter Aperture Spherical radio Telescope) is the most sensitive single-antenna radio telescope in the world today (Li et al. 2018). It has identified a lot of new pulsars since its commissioning, including MSPs (Han 2025). Specific work includes the Galactic Plane Pulsar Snapshot (GPPS) survey, which discovered 201 pulsars, of which 40 are MSPs (Han et al. 2021). More than 30 GC pulsars were discovered between 2017 and 2021 (Pan et al. 2020; Wang et al. 2020). PSR J1717+4307A was the first pulsar discovered in the GC Messier 92 (M92), with a spin period of 3.16 ms (316.5 Hz) (Pan et al. 2020). PSR J1853-0842A, found through high-sensitivity searches using FAST, has a period of 2.15 ms and is part of a black widow system (Yan et al. 2021). Motivated by these findings, in this work we study the effects of nuclear symmetry energy and its slope on the bulk properties of MSPs.
The reasonable range of symmetry energy and its slope have been widely discussed (Tews et al. 2017; Holt & Kaiser 2017; Reed et al. 2021; Essick et al. 2021; Tagami et al. 2022), incorporating both nuclear experimental constraints and astrophysical observations. However, this remains an open problem, particularly since the PREX II results (Reed et al. 2021) do not overlap with those from other constraints. It is well known that the nuclear symmetry energy and its slope have significant effects on the global properties of NSs (Cavagnoli et al. 2011; Baldo & Burgio 2016; Margueron et al. 2018; Wu & Shen 2019; Hu et al. 2020; Wu et al. 2021; Wang et al. 2024), but most studies on this topic focus on static NSs. Cavagnoli et al. (2011) demonstrated that for NSs with masses exceeding 1 M⊙, the radius exhibits a linear relationship with the symmetry energy slope. Utilizing a Bayesian statistical approach, Margueron et al. (2018) found that symmetry energy slope and curvature play an important role in determining the radius of NSs. Tsaloukidis et al. (2019) examined the effects of symmetry energy on the transition density and r-mode instability of a rotating NS. Li et al. (2020) investigated how the isoscalar skewness coefficient and the symmetry energy slope influence the masses of rapidly rotating NSs. Lopes (2024) studied how the symmetry energy slope of the core EOS affect the properties of static and slowly rotating NSs using non-unified EOSs with a fixed crust segment. In most calculations of NS properties, a non-unified EOS is employed, i.e., the core EOS is matched to a crust EOS obtained from different models (Read et al. 2009; Koliogiannis & Moustakidis 2021; Lopes 2024). However, it should be more advantageous to calculate the structures of static NSs and MSPs using a unified EOS, whereby both the core and crust EOS are based on the same theoretical framework. The interior of a NS has three qualitatively different domains: the outer crust, the inner crust, and the core, separated by phase transition boundaries, namely the neutron drip density (interface between the outer crust and the inner crust) and the crust-core interface. The outer crust is mainly determined by masses of neutron-rich nuclei (Baym et al. 1971; Haensel et al. 2007; Fortin et al. 2016), and its properties are described in this work by the EOS of Baym et al. 1971 (Baym et al. 1971), referred to as BPS. The inner crust has to be studied using phenomenological models due to the presence of inhomogeneous nuclear matter. The unified EOS is obtained from the same Lagrangian to describe the neutron drip density, the inner crust, and the core. The use of a unified EOS allows for a self-consistent treatment of the core-crust transition. It has been reported that the EOS of the crust significantly impacts NS properties (Fortin et al. 2016; Ji et al. 2019; Suleiman et al. 2021; Huang et al. 2024). In this work, we compare the results using unified EOSs with those using non-unified EOSs, and explore the effects of the symmetry energy and its slope using the parameter family TM1 introduced in Bao et al. (2014), in which the self-consistent Thomas-Fermi approximation has been employed to calculate the inner crust structure. A similar calculation using the family IUFSU (Bao et al. 2014) was also performed to check the symmetry energy dependence of our results. The original TM1 and IUFSU parameter sets describe the properties of finite nuclei and the saturation properties of nuclear matter very well (Sugahara & Toki 1994; Fattoyev et al. 2010). The TM1 and IUFSU families predict similar ground-state properties of finite nuclei, whereas they affect the interface densities between the crust and core and the crust composition due to their different symmetry energy slopes. The unified EOS utilizes a consistent model for both the crust and core, while for the non-unified EOS, we adopt the same TM1e or original IUFSU EOS for the core (Shen et al. 2020; Fattoyev et al. 2010), but the crust features different symmetry energy slopes within the same parameter family.
The NS/MSP observations are crucial for understanding symmetry energy and its slope, especially the NS radius. The mass measurement of MSP J1614+2230 (P = 3.15 ms) indicates a mass of M = 1.97 ± 0.04 M⊙ (Demorest et al. 2010), with an updated result of M = 1.908 ± 0.016 M⊙ (Arzoumanian et al. 2018). This finding raised the observational limit of NS mass to approximately 2 M⊙. In 2013, PSR J0348+0432 (P = 39.12 ms) was reported to have a mass of M = 2.01 ± 0.04 M⊙ (Antoniadis et al. 2013). Later, in 2019, PSR J0740+6620 with a spin period of about 2.88 ms was found to have a mass of M = 2.08 ± 0.07 M⊙ (Cromartie et al. 2020; Fonseca et al. 2021), which is recognized as the most massive MSP measured precisely through pulse timing observations and detailed assessments of general relativistic effects. The Neutron Star Interior Composition Explorer (NICER) has enabled simultaneous measurements of mass and radius. For PSR J0740+6620, the measurements yield a mass of M = 2.08 ± 0.07 M⊙, and a radius of 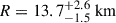 (Miller et al. 2021). An alternatively result is a mass of
(Miller et al. 2021). An alternatively result is a mass of 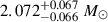 with a radius of
with a radius of 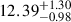 km (Riley et al. 2021). For PSR J0030+0451, its spin period is known to be 4.87 ms, and its mass was determined to be
km (Riley et al. 2021). For PSR J0030+0451, its spin period is known to be 4.87 ms, and its mass was determined to be 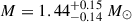 with a radius of
with a radius of 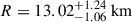 (Miller et al. 2019), or alternatively,
(Miller et al. 2019), or alternatively, 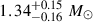 with a radius of
with a radius of 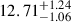 km (Miller et al. 2019; Riley et al. 2019).
km (Miller et al. 2019; Riley et al. 2019).
To infer the radii of NSs, NICER observes the X-ray pulse profiles emitted by hot spots on the surfaces of rotating NSs (Raaijmakers et al. 2019). A critical ingredient in the pulse profile model is the oblate shape of the star. The shape eccentricity introduced by rotation could impact the X-ray light curve from rotating pulsars (Morsink et al. 2007). To reduce the number of parameters used to describe the shape and multipoles of rotating NSs, Bauböck et al. (2013) established a universal relation between the eccentricity and the compactness. Gao et al. (2023) proposed a universal relation that connects the eccentricity to the radius and moment of inertia of rotating NSs. In this work, we also discuss the dependence of the eccentricity and moment of inertia of MSPs on the symmetry energy slope, L, and the spin period, P.
This paper is organized as follows. Section 2 provides a brief description of the relativistic mean-field (RMF) model and the unified EOSs, while the non-unified connection of the crust and core EOSs is also introduced. Additionally, the Hartle-Thorne slow-rotation approximation is reviewed briefly. In Section 3, we present our main results regarding the effects of symmetry energy on the properties of rotating MSPs. Finally, Section 4 is devoted to the conclusions.
2. Models
We employed the RMF model to construct the EOSs. In this framework, nucleons interact through the exchange of mesons, including scalar σ, vector ω, and isovector ρ mesons. The model also includes nonlinear terms for the σ and ω mesons, as well as an additional ω − ρ coupling term (Bao et al. 2014; Shen et al. 2020). The Lagrangian density of NS matter is written as
where Wμν and Rαμν are the antisymmetric field tensors corresponding to ωμ and ρaμ, respectively.
In order to explore the influence of symmetry energy on rotating MSPs, we provide a brief description of the symmetry energy, Esym, and its slope, L. The symmetry energy of nuclear matter is defined as
where ρB is the baryon number density, and δ is the isospin asymmetry defined as δ = (ρn − ρp)/(ρn + ρp), with ρn and ρp being the neutron and proton number densities, respectively. ε(ρB, δ)/ρB is the energy per baryon. Under the RMF framework, the symmetry energy expression can be derived from Bao et al. (2014), Hu et al. (2020)
kF is the Fermi momentum of symmetric nuclear matter and MN* = MN + gσσ is the effective nucleon mass, with MN being the free nucleon mass. The symmetry energy slope is given as
where ρ0 is the saturation density. We used a series of EOSs based on the TM1/IUFSU parameter set, which exhibit different Esym and L at the saturation density, while keeping the same values for the other saturation properties. These EOSs feature a uniform symmetry energy at a subsaturation density of 0.11 fm−3 (Esym(0.11 fm−3) = 28.05 MeV (TM1), Esym(0.11 fm−3) = 26.78 MeV (IUFSU)) (Bao et al. 2014). Therefore, the symmetry energy coefficient at saturation density ρ0, Esym(ρ0), is also affected by the change in the symmetry energy slope. Through this approach, we can focus on the effect of a single variable among the saturation parameters, the symmetry energy slope, L. In Table 1, we present the mass and coupling constants of the nucleon and mesons in the original TM1 and IUFSU model. Table 2 lists the saturation properties, while Tables 3 and 4 list the corresponding coupling constants for generated models. It is shown that the parameters in this TM1 series yield different symmetry energies at ρ0, while a smaller L corresponds to a smaller Esym(ρ0). The configuration with a symmetry energy slope of L = 40 MeV is commonly referred to as TM1e, which is more compatible with the GW170817 constraint compared to other values of L (Ji et al. 2019). The detailed EOS table obtained with TM1e can be found in Shen et al. (2020). In this work, we utilize unified EOSs in which both the core and crust EOSs share the same value of symmetry energy slope, L. To investigate the effects of unified EOSs, we also compare with the results using non-unified EOSs that match the crust with different L values and maintain the same core EOS by using TM1e.
Parameter sets of the RMF models.
Nuclear matter saturation properties.
TM1 family for different slopes, L.
IUFSU family for different slopes, L.
For nonrotating NSs, the equations of the hydrostatic equilibrium are the Tolman-Oppenheimer-Volkof (TOV) equations, which read
where p(r) and ε(r) represent the pressure and total energy density (including the rest-mass energy) at radius r, respectively. M(r) denotes the mass enclosed within a radius, r. In the following, we adopt the units G = c = 1.
The rotation of massive NSs would distort the spacetime metric, and produces the frame-dragging effect, which leads to an increase in the static mass. Since the observed MSPs have periods on the order of milliseconds rather than sub-milliseconds, we adopted the slow-rotation Hartle-Thorne approximation, where the spin is expanded to quadratic order (Hartle & Thorne 1968; Berti et al. 2005; Ordaz 2019; Lopes 2024). The parameter ωr = ωr(r) = dϕ/dt represents the angular velocity acquired by a free-falling observer due to the dragging of the inertial frame. The perturbed Schwarzschield metric for a slowly rotating star is written as
in which the metric function, φ, fulfills the equation
h(r, θ), m(r, θ), and k(r, θ) can be considered to be the perturbation terms. Expanding them up to the second order, one obtains:
in which P2(cos(θ) is the Legendre polynominal. The monopole pressure perturbation, p0*, and the quadrupole pressure perturbation, p2*, are defined in
Δp denotes the pressure change induced by rotation at a fixed point in the frame corotating with the star. The corresponding perturbed energy density, Δε, and perturbed number density, Δn, reads
The perturbative terms, m0, p0*, and metric functions, ν2 ≡ h2 + k2, h2, were obtained by applying Einstein’s field equations:
with the boundary conditions: m0(0) = p0*(0) = h2(0) = ν2(0) = 0.
At the first order in spin, we could extract the angular momentum. The angular velocity of the star relative to the local inertial frame, 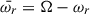 , satisfies the equation (Hartle 1967)
, satisfies the equation (Hartle 1967)
with
The angular momentum (J) of a spherical symmetrical star with radius R is given by
At the second order in spin, the rotation causes the NSs to become ellipsoids. The eccentricity is defined as
where Rpo and Req are the polar and equator radii, respectively. Thus, e = 0 refers to the spherical limit and 0 < e < 1 corresponds to oblate sphere for rotating NSs. In the Hartle-Thorne approach, the polar and equatorial radii are obtained from the nonrotating star radius, R,
in which ξ0 and ξ2 are referred to the spherical and quadrupole stretching functions,
The quadrupole pressure perturbation, p2*, is given by
3. Results
In Fig. 1, the pressures of pure neutron matter (PNM) and symmetric nuclear matter (SNM) are plotted applying, respectively, the TM1 and IUFSU parameter families. The family TM1 parameter sets with L = 40, 60, 80, 111 MeV are applied, while the IUFSU family adopt L = 47.2, 60, 80, 110 MeV. The ab initio calculations (Hebeler et al. 2013) and experimental constraints obtained from collective flow data in heavy-ion collisions (Danielewicz et al. 2002) are included in colored areas. The PNM constraint favors smaller values of L at higher densities (ρB > 0.06 fm−3), but at lower densities, smaller L in turn leads to higher pressure. In the right panel of SNM, the pressure, p, is independent of the symmetry energy slope, L. The SNM constraint area prefers the softer IUFSU family, while the TM1 result lies very close to the edge of the constraint. Both the TM1 and IUFSU parameter families are adjusted based on the properties of finite nuclei and fulfill the saturation property ranges. These parameter sets can help to understand the effect of symmetry energy on the properties of rotating NSs, though some of them exceed the constraint area.
 |
Fig. 1. Pressure as a function of baryon density, ρB, for PNM and SNM. The unit of L is mega-electronvolts. Ab initio results from Hebeler et al. (2013) for PNM and the experimental flow constraint from Danielewicz et al. (2002) for SNM are shown. |
In Fig. 2(a), the mass radius relations for different TM1 EOSs are displayed (these results can also be found in Ji et al. 2019; Hu et al. 2020). These results were obtained by using the unified EOSs with L = 40, 60, 80, 111 MeV and the non-unified ones with a core L = 40 MeV matched to crusts with L = 60, 80, 111 MeV. The constraints from recent observations are also shown, including those from PSR J0740+6620 (Riley et al. 2021), PSR J0030+0451 (Riley et al. 2019), PSR J1614-2230 (Arzoumanian et al. 2018), and PSR J0348+0432 (Antoniadis et al. 2013). We find that in the case of the maximum-mass NS, symmetry energy effects are nearly negligible, except for the original TM1 model, which has L = 111 MeV. However, the results with L = 111 MeV exceed the constraint derived from PSR J0030+0451, and therefore the unified EOS with L = 111 MeV is not included in the following discussion. Other EOSs in Fig. 2 (a) lead to very similar maximum masses: approximately Mmax ≈ 2.125 M⊙ for unified EOS with L = 40 MeV and all the non-unified EOSs, and Mmax ≈ 2.120 M⊙ for the unified EOSs with L = 60 and 80 MeV. On the other hand, significant differences can be observed in the radius, especially for NSs with smaller masses. It is shown that the differences between these EOSs increase as the mass of NSs decreases. For the unified EOSs, a smaller slope, L, corresponds to a smaller radius. In contrast, for the non-unified EOSs with the same core EOS (L = 40 MeV) but different crusts, a larger L for the crust EOS corresponds to a smaller radius. This behavior is discussed in Ji et al. (2019), where it is pointed out that a larger L for the crust corresponds to a softer EOS. For a unified EOS, if it has a stiff core, the crust is softer. This L-driven crust EOS stiffness effect on the NS radius is consistent with the results in Fortin et al. (2016), Suleiman et al. (2021), in which the crust EOS differences stem from the glue-density choice. In Fig. 2 (b), we performed a similar calculation using the family IUFSU parameter sets to assess the model dependence. The original IUFSU parameter gives L = 47.2 MeV. Whether the symmetry energy slope, L, is varied within unified or non-unified schemes, the maximum mass of static NSs and the corresponding radius are almost unchanged. The L dependence of the radius is consistent with that found for the TM1 parameter sets. Fig. 2 (c) and (d) show the relative radius differences with respect to the unified EOS L = 40 MeV for family TM1 parameter sets and unified EOS L = 47.2 MeV for family IUFSU parameter sets. A different L results in almost the same maximum mass and a less than 2% difference in radius for the maximum-mass NSs. Even for the 1.4 M⊙ NSs, the radius relative difference is less than 5%.
 |
Fig. 2. Mass-radius relations for different symmetry energy slopes, L (upper panel). Uncertainties on the radius due to the use of EOSs with different L (lower panel). The unit of L is mega-electronvolts. Results from unified (L (crust) = L (core)) and non-unified EOSs (L (crust)≠ L (core)) are shown. |
We now concentrate our study on the bulk properties of rotating MSPs. We implemented numerical codes to solve the mass-radius relation equations by fixing the period, P, with various EOSs, in order to study the effects of the symmetry energy slope, L, on rotating MSPs. In Fig. 3, we present the relationship between the Kepler frequency (mass-shedding limit), 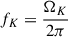 , and the static mass (gravitational mass of nonrotating NS) of NSs, using an empirical formula for relativistic stars (Haensel & Zdunik 1989; Friedman et al. 1989; Lopes 2024),
, and the static mass (gravitational mass of nonrotating NS) of NSs, using an empirical formula for relativistic stars (Haensel & Zdunik 1989; Friedman et al. 1989; Lopes 2024),
 |
Fig. 3. Kepler frequency as a function of the NSs static mass for different EOSs. The horizontal lines correspond to the periods of 1 ms, 2 ms, and 5 ms, and the fastest observed MSP frequency of 716 Hz. The vertical line indicates the canonical mass of 1.4 M⊙. |
Under the Newtonian limit, the value of χ is 1, while under the effect of general relativity, it satisfies the condition χ < 1 (Paschalidis & Stergioulas 2017). Haensel et al. (2009) discussed the value of the parameter χ, whose error holds within a few percent for rotating NSs. In this figure, χ = 0.67 is used, following Paschalidis & Stergioulas (2017). For a canonical 1.4 M⊙ NS, the period corresponding to the limit frequency will not exceed 1 ms, except for the unified L = 80 MeV result in the right panel, and remain safe at f = 716 Hz. For NSs with static masses of around ∼2 M⊙, the period can be less than 1 ms while still remaining stable; this is suitable for both TM1 and IUFSU families. A softer EOS, characterized by a smaller slope for unified EOSs or a larger crust slope for non-unified EOSs, results in a larger Kepler frequency. For static mass of M > 0.5 M⊙, MSPs can be stable with a period of P = 2 ms. However, to achieve P = 1 ms, the stable MSP must have a static mass of M > 1.6 M⊙ for L = 80 MeV (unified, TM1) and M > 1.5 M⊙ for L = 40 MeV (unified, TM1). For the non-unified EOS with L = 111 + 40 MeV (crust+core, TM1), the stable static mass lower limit for MSPs is M > 1.4 M⊙ to achieve P = 1 ms. Comparatively, family IUFSU could support a higher frequency limit with the same static mass and L. This indicates that the minimum stable mass for MSPs decreases with decreasing L or softer EOSs for unified EOSs. From this figure, we can conclude that softer EOSs correspond to a smaller minimum stable static mass for the same period, P. With varying L, the curves exhibit no intersection points for M > 0.15 M⊙, which differs from the findings in Lopes (2024). However, the above relationship between EOS stiffness and minimum stable static mass for the same P remains consistent with Lopes (2024).
To examine the effects of symmetry energy and its slope on the bulk properties of MSPs, we solved the TOV equations and the equations in Hartle’s formalism. For a given period, a stable mass-radius curve extends from the minimum mass at which mass-shedding instability occurs to the maximum mass. Beyond this maximum mass, MSPs become unstable with respect to axi-symmetric perturbations (Bejger et al. 2007). In Fig. 4, we display the equatorial radius as a function of the gravitational mass for MSPs with fixed period P = 1 ∼ 5 ms (left panels) and the MSP mass as a function of the central density, ρc (right panels), using unified TM1 EOSs. In the right panel, the region of high densities beyond the maximum mass point is unstable. As is shown in Appendix A, the results of P = 1 ms are beyond the slow rotation limit. However, they can still be considered as a first estimate of the trend with the rotational period, and the actual effect is expected to be more significant. The purple crosses mark the rotational mass (gravitational mass of rotating NS) at the Kepler limit. The results for static NSs are also shown for comparison. Different values of the slope in unified EOSs, L = 40, 60, 80 MeV, are presented in the upper, middle, and lower panels, respectively. With the same period, P, and rotational mass, the effect of the symmetry energy slope, L, on the equatorial radius, Req, is similar to that on the static NS radius. The EOSs with larger L result in a slightly larger Req. This effect decreases with increasing rotational mass. Fig. 5 is the same as Fig. 4, but it uses non-unified TM1 EOSs, which share the same core with L = 40 MeV and different crusts with L = 111, 80, 60 MeV in the upper, middle, and lower panels. Since there are only differences in the crust that correspond to the sub-saturation density range, the effect of L on the Mrot − Req relation (with same P) is mainly reflected in low-mass MSPs, specifically those with Mrot ≲ 0.5 M⊙, which could be stable with P ≥ 2 ms. Both Fig. 4 and Fig. 5 indicate that the rotational mass-central density relations (Mrot − ρc) show no clear L dependence for Mrot ≳ 1 M⊙. It is shown that, as the spin period decreases, the curves shift toward a higher mass and larger radius. The results indicate that with faster rotation, the change in the mass with respect to the nonrotating configuration also grows faster. The relevant quantities (ΔM, ΔR) are summarized in Table B.1 and Table B.2. The rotation effect leads to an increase in both the maximum mass (Mmax) and the equatorial radius at the maximum mass, Req(max), while lowering the central density, ρc. The radius of a 1.4 M⊙ star, denoted as R(1.4), is significantly influenced by the rotation effect. For a unified EOS with L = 40 MeV, the equatorial radius of the canonical 1.4 M⊙ star increases from 13.157 km to 13.605 km at a period of P = 2 ms (note that P = 1 ms exceeds the Kepler limit). In the case of a 2 M⊙ star, the equatorial radius increases from 12.704 km to 13.017 km for P = 2 ms. The change in maximum mass, ΔM, for different L cases shows little variation. The rotation lowers the central density of maximum mass MSPs, ρc(max), but the effect is minimal until P < 2 ms.
 |
Fig. 4. Rotational mass-equatorial radius relations and central-density dependence. Left panels show rotational mass-equatorial radius sequences for unified TM1 EOSs with varying symmetry energy slope, L, and spin period, P. Right panels give the rotational mass, Mrot, as a function of central density, ρc. The purple crosses mark the rotational mass at the Kepler limit. |
In Fig. 6, we show the relationship between the eccentricity, e, of the MSP and the gravitational mass under varying L and period, P. Panels (a), (b), and (c) show results for different periods with a given L = 40, 60, 80 MeV. Panel (d) provides a comparison for different EOSs with the same periods, P = 1, 2, 5 ms. As a measurement of the oblate shape of the star deformation, e = 0 indicates the sphere shape (P = 0). It can be observed that the eccentricity, e, increases as the rotational period, P, decreases for a given mass, and a heavier MSP exhibits a smaller e, indicating less deformation. This trend holds for all masses, but it should be noted that configurations beyond the purple cross-marks exceed the Kepler limit. In particular, for P = 1 ms, the Kepler limit is reached even for canonical NSs. As was mentioned in Fig. 2, the EOSs we used have nearly indistinguishable maximum masses, and there is very little difference among these EOSs on e for MSP with growing mass, especially for those greater than 1.5 M⊙ (heavier than 2 M⊙ for P = 1 ms). For low-mass MSPs, the curves in Fig. 6 are clearly separated with a given P, revealing the enhanced crustal influence on the induced eccentricity. For MSPs with masses less than 1.0 M⊙, a trend emerges that softer EOSs (lower L for unified EOSs, and larger L for the crust) lead to smaller e. When P = 2 ms and Mrot = 1.0 M⊙, the unified EOS with L = 40 MeV results in e = 0.38, while the one with L = 80 MeV yields e = 0.40. In Table B.1 and Table B.2, we summarize the eccentricities of 1.4 M⊙ and 2.0 M⊙ nonrotating NSs and MSPs (e1.4 and e2.0). Overall, both e1.4 and e2.0 slightly increase as the EOS stiffness grows (from top to bottom in Tables B.1 and B.2) with a fixed P. For example, compared to the results for e2.0 with unified L = 80 MeV, those with L = 40 MeV and L = 60 MeV show slightly smaller values of e2.0 for the same period, P, with differences of around 1%.
 |
Fig. 6. Eccentricity, e, as a function of the gravitational mass of the MSPs for the family TM1 parameter set. Panels (a), (b), and (c) represent results from unified EOS with L = 40, 60, 80 MeV, respectively, while panel (d) shows a comparison of different EOSs. |
Fig. 7 depicts the results of moment of inertia 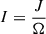 as a function of the rotational mass. Similarly to Fig. 6, panel (a) shows results for different periods with a given L = 40 MeV. Since the I results for P = 3, 4 ms are too close to those for P = 5 ms, panel (b) provides a comparison of different EOSs with the same periods, P = 5 ms. The moment of inertia, I, depends on both the mass and the square of the radius. At a fixed rotational mass, Mrot, a smaller period, P (faster spin), reduces the central density (see Figs. 4 and 5), making the star more dilute; because J increases sub-linearly with Ω, the moment of inertia I = J/Ω decreases (panel (a)). This also explains why the L effect on I is weakened at P = 5 ms (same trend for P = 4 ∼ 1 ms): the shifts in mass and radius produced by rotation are larger than those arising from varying the symmetry energy slope, L. A softer EOS leads to a smaller I mainly due to a smaller radius. These results are consistent with the mass-radius relations discussed above. The constraint
as a function of the rotational mass. Similarly to Fig. 6, panel (a) shows results for different periods with a given L = 40 MeV. Since the I results for P = 3, 4 ms are too close to those for P = 5 ms, panel (b) provides a comparison of different EOSs with the same periods, P = 5 ms. The moment of inertia, I, depends on both the mass and the square of the radius. At a fixed rotational mass, Mrot, a smaller period, P (faster spin), reduces the central density (see Figs. 4 and 5), making the star more dilute; because J increases sub-linearly with Ω, the moment of inertia I = J/Ω decreases (panel (a)). This also explains why the L effect on I is weakened at P = 5 ms (same trend for P = 4 ∼ 1 ms): the shifts in mass and radius produced by rotation are larger than those arising from varying the symmetry energy slope, L. A softer EOS leads to a smaller I mainly due to a smaller radius. These results are consistent with the mass-radius relations discussed above. The constraint 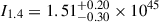 g cm2 (Landry et al. 2020) was derived from measurements of pulsar masses, gravitational wave event GW170817 and GW190425, and X-ray data from NICER.
g cm2 (Landry et al. 2020) was derived from measurements of pulsar masses, gravitational wave event GW170817 and GW190425, and X-ray data from NICER.
 |
Fig. 7. Moment of inertia, I, as a function of the gravitational mass of the MSPs for the family TM1 parameter set. Panel (a) represents results from unified EOS L = 40 MeV, while panel (b) shows a comparison of different EOSs with P = 5 ms. |
4. Conclusions
In this work, we have studied the effect of symmetry energy on the bulk properties of MSPs. We utilized the TM1 parameter set family within the RMF framework for our analysis. The EOSs with a different symmetry energy slope, L, lead to variations in the macroscopic properties of MSPs, such as the maximum mass, central density, Kepler frequency, equatorial radius, eccentricity, and moment of inertia. The IUFSU family exhibits a similar trend to that of the TM1 family on the L dependence. Within the models explored in this work, a soft EOS corresponding to smaller L for a unified EOS or larger L for the crust is favored by the recent observations of NS radius. Additionally, such softer EOSs yield slightly higher Kepler-limit frequencies.
Both the eccentricity, e, and the equatorial radius, Req, are sensitive to the symmetry energy slope, L, and the pulsar period, P, but are not directly coupled to each other. They can be treated as independent observables. Measuring P and compactness (from gravitational wave event) allows one to infer e via the universal relation. Together with observed Req, the two quantities could provide complementary constraints on L. Moreover, the effects of symmetry energy and its slope are particularly pronounced for less massive NSs. Future measurements of low-mass MSPs may help us constrain the symmetry energy slope more effectively.
With large-scale surveys such as FAST, radio telescopes are discovering an increasing number of pulsars. Measurements of period, mass, and eccentricity could potentially provide further constraints on the symmetry energy slope.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grants No. 12305148, No. 12175109, 12505159), Hebei Natural Science Foundation (No. A2023203055), and Fundamental Research Program of ShanxiProvince (No. 202303021211135), and Natural Science Foundation of Shandong Province under Grants No. ZR2023QA112, and Fundamental Research Funds for the Central Universities under Grant No. 22CX06006A.
References
- Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 1233232 [Google Scholar]
- Arzoumanian, Z., Brazier, A., Burke-Spolaor, S., et al. 2018, ApJS, 235, 37 [CrossRef] [Google Scholar]
- Backer, D. C., Kulkarni, S. R., Heiles, C., Davis, M. M., & Goss, W. M. 1982, Nature, 300, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., & Burgio, G. 2016, Prog. Part. Nucl. Phys., 91, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Bao, S. S., Hu, J. N., Zhang, Z. W., & Shen, H. 2014, Phys. Rev. C, 90, 045802 [NASA ADS] [CrossRef] [Google Scholar]
- Bassa, C., Pleunis, Z., Hessels, J., et al. 2017, ApJ, 846, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Bauböck, M., Berti, E., Psaltis, D., & Özel, F. 2013, ApJ, 777, 68 [Google Scholar]
- Baym, G., Pethick, C., & Sutherland, P. 1971, ApJ, 170, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Bejger, M., Haensel, P., & Zdunik, J. L. 2007, A&A, 464, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berti, E., White, F., Maniopoulou, A., & Bruni, M. 2005, MNRAS, 358, 923 [Google Scholar]
- Bhattacharyya, B., & Roy, J. 2022, Radio Millisecond Pulsars (Cham: Springer International Publishing), 1 [Google Scholar]
- Cavagnoli, R., Menezes, D. P., Providência, C. M. C., 2011, Phys. Rev. C, 84, 065810 [CrossRef] [Google Scholar]
- Cromartie, H. T., Fonseca, E., Ransom, S. M., et al. 2020, Nat. Astron., 4, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Danielewicz, P., Lacey, R., & Lynch, W. G. 2002, Science, 298, 1592 [NASA ADS] [CrossRef] [Google Scholar]
- DeCesar, M. E., Ransom, S. M., Kaplan, D. L., Ray, P. S., & Geller, A. M. 2015, ApJ, 807, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [Google Scholar]
- Essick, R., Tews, I., Landry, P., & Schwenk, A. 2021, Phys. Rev. Lett., 127, 192701 [CrossRef] [PubMed] [Google Scholar]
- Fattoyev, F. J., Horowitz, C. J., Piekarewicz, J., & Shen, G. 2010, Phys. Rev. C, 82, 055803 [Google Scholar]
- Fonseca, E., Cromartie, H. T., Pennucci, T. T., et al. 2021, ApJ, 915, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Fortin, M., Providência, C., Raduta, A. R., et al. 2016, Phys. Rev. C, 94, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, J. L., Ipser, J. R., & Parker, L. 1989, Phys. Rev. Lett., 62, 3015 [Google Scholar]
- Gao, Y., Shao, L., & Steinhoff, J. 2023, ApJ, 954, 16 [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1989, Nature, 340, 617 [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron stars 1: Equation of state and structure (New York, USA: Springer), 326 [Google Scholar]
- Haensel, P., Zdunik, J. L., Bejger, M., & Lattimer, J. M. 2009, A&A, 502, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, J. L., et al. 2025, Res. Astron. Astrophys., 25, 014001 [Google Scholar]
- Han, J. L., Wang, C., Wang, P. F., et al. 2021, Res. Astron. Astrophys., 21, 107 [CrossRef] [Google Scholar]
- Hartle, J. B. 1967, ApJ, 150, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Hartle, J. B., & Thorne, K. S. 1968, ApJ, 153, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Hebeler, K., Lattimer, J. M., Pethick, C. J., & Schwenk, A. 2013, ApJ, 773, 11 [CrossRef] [Google Scholar]
- Hessels, J. W. T., Ransom, S. M., Stairs, I. H., et al. 2006, Science, 311, 1901 [CrossRef] [PubMed] [Google Scholar]
- Holt, J. W., & Kaiser, N. 2017, Phys. Rev. C, 95, 034326 [Google Scholar]
- Hu, J., Bao, S., Zhang, Y., et al. 2020, Prog. Part. Nucl. Phys., 2020, 043D01 [Google Scholar]
- Huang, K., Shen, H., Hu, J., & Zhang, Y. 2024, Phys. Rev. D, 109, 043036 [CrossRef] [Google Scholar]
- Ji, F., Hu, J., Bao, S., & Shen, H. 2019, Phys. Rev. C, 100, 045801 [NASA ADS] [CrossRef] [Google Scholar]
- Koliogiannis, P. S., & Moustakidis, C. C. 2021, ApJ, 912, 69 [Google Scholar]
- Landry, P., Essick, R., & Chatziioannou, K. 2020, Phys. Rev. D, 101, 123007 [NASA ADS] [CrossRef] [Google Scholar]
- Li, D., Wang, P., Qian, L., et al. 2018, IEEE Microwave Magazine, 19, 112 [Google Scholar]
- Li, J. J., Sedrakian, A., & Weber, F. 2020, Phys. Lett. B, 810, 135812 [Google Scholar]
- Lopes, L. L. 2024, ApJ, 966, 184 [Google Scholar]
- Margueron, J., Hoffmann Casali, R., & Gulminelli, F. 2018, Phys. Rev. C, 97, 025806 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2019, ApJ, 887, L24 [Google Scholar]
- Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2021, ApJ, 918, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Morsink, S. M., Leahy, D. A., Cadeau, C., & Braga, J. 2007, ApJ, 663, 1244 [NASA ADS] [CrossRef] [Google Scholar]
- Nagase, F. 1989, Astron. Soc. Japan, 41, 1 [Google Scholar]
- Ordaz, A. C. 2019, Ph.D. Thesis, Master’s Thesis presented to the Universitat de Barcelona, Spain [Google Scholar]
- Pan, Z., Ransom, S. M., Lorimer, D. R., et al. 2020, ApJ, 892, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, Z., Qian, L., Ma, X., et al. 2021, ApJ, 915, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Paschalidis, V., & Stergioulas, N. 2017, Liv. Rev. Relativ., 20, 7 [Google Scholar]
- Raaijmakers, G., Riley, T. E., Watts, A. L., et al. 2019, ApJ, 887, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Ransom, S. M., Hessels, J. W. T., Stairs, I. H., et al. 2005, Science, 307, 892 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Read, J. S., Lackey, B. D., Owen, B. J., & Friedman, J. L. 2009, Phys. Rev. D, 79, 124032 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, B. T., Fattoyev, F. J., Horowitz, C. J., & Piekarewicz, J. 2021, Phys. Rev. Lett., 126, 172503 [NASA ADS] [CrossRef] [Google Scholar]
- Ridolfi, A., Gautam, T., Freire, P. C. C., et al. 2021, MNRAS, 504, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Riley, T. E., Watts, A. L., Bogdanov, S., et al. 2019, ApJ, 887, L21 [Google Scholar]
- Riley, T. E., Watts, A. L., Ray, P. S., et al. 2021, ApJ, 918, L27 [CrossRef] [Google Scholar]
- Romani, R. W., Kandel, D., Filippenko, A. V., Brink, T. G., & Zheng, W. 2022, ApJ, 934, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, H., Ji, F., Hu, J., & Sumiyoshi, K. 2020, ApJ, 891, 148 [Google Scholar]
- Stergioulas, N. 2003, Liv. Rev. Relativ., 6, 3 [Google Scholar]
- Stergioulas, N., & Friedman, J. L. 1995, ApJ, 444, 306 [Google Scholar]
- Sugahara, Y., & Toki, H. 1994, Nucl. Phys. A, 579, 557 [Google Scholar]
- Suleiman, L., Fortin, M., Zdunik, J. L., & Haensel, P. 2021, Phys. Rev. C, 104, 015801 [NASA ADS] [CrossRef] [Google Scholar]
- Tagami, S., Wakasa, T., & Yahiro, M. 2022, Results Phys., 43, 106037 [Google Scholar]
- Tews, I., Lattimer, J. M., Ohnishi, A., & Kolomeitsev, E. E. 2017, ApJ, 848, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Tsaloukidis, L., Margaritis, C., & Moustakidis, C. C. 2019, Phys. Rev. C, 99, 015803 [Google Scholar]
- Wang, L., Peng, B., Stappers, B. W., et al. 2020, ApJ, 892, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S.-P., Wang, R., Ye, J.-T., & Chen, L.-W. 2024, Phys. Rev. C, 109, 054623 [Google Scholar]
- Wu, X. H., & Shen, H. 2019, Phys. Rev. C, 99, 065802 [Google Scholar]
- Wu, X., Bao, S., Shen, H., & Xu, R. 2021, Phys. Rev. C, 104, 015802 [Google Scholar]
- Yan, Z., chen Pan, Z., Ransom, S. M., et al. 2021, ApJ, 921, 120 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Comparison with RNS
In appendix A, we compare rotational mass-radius results obtained with the slow rotation approximation to those computed with the RNS code1 (Stergioulas & Friedman 1995; Stergioulas 2003) in Fig. A.1. The results are obtained using unified TM1 parameter sets with L = 40, 60, 80 MeV. The rotational mass-equatorial radius curves obtained using the slow rotation approximation (dash lines) are slightly lower than those from the RNS code (solid lines) with the same period P. The differences are minimal for P = 5 ms, distinguishable for P = 2 ms (Ω ≈ 3141.6 rad/s), and more pronounced when P = 1 ms. Comparatively, with larger gravitational masses, the differences become smaller, especially for the maximum rotational mass MSPs. These differences arise because the rotational-energy contribution to the gravitational mass is only approximate calculated in the Hartle-Thorne treatment. And the gap between approximation and RNS results becomes more pronounced with rapid rotation. This difference manifests primarily in the equatorial radius (and hence in the eccentricity and moment of inertia). Although such differences exist, the slow-rotation approximation has still proven useful for obtaining a quick estimate of rotational effects. In Fig. 4, purple crosses mark the Kepler limit; compared with those in Fig. A.1 (crosses between solid and Kepler lines), they share nearly the same rotational mass but exhibit a clear equatorial radius offset.
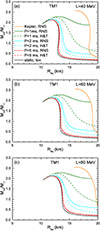 |
Fig. A.1. The rotational mass-equatorial radius relations derived from RNS code and Hartle-Thorne approximation (H&T). |
Appendix B: Properties of rotating MSPs
The following two tables list the properties of nonrotating NSs and rotating MSPs for the TM1 EOSs.
Properties of nonrotating NSs and rotating MSPs for the TM1 family.
Same as Table B.1, but using non-unified TM1 EOS with different crust.
All Tables
All Figures
 |
Fig. 1. Pressure as a function of baryon density, ρB, for PNM and SNM. The unit of L is mega-electronvolts. Ab initio results from Hebeler et al. (2013) for PNM and the experimental flow constraint from Danielewicz et al. (2002) for SNM are shown. |
| In the text | |
 |
Fig. 2. Mass-radius relations for different symmetry energy slopes, L (upper panel). Uncertainties on the radius due to the use of EOSs with different L (lower panel). The unit of L is mega-electronvolts. Results from unified (L (crust) = L (core)) and non-unified EOSs (L (crust)≠ L (core)) are shown. |
| In the text | |
 |
Fig. 3. Kepler frequency as a function of the NSs static mass for different EOSs. The horizontal lines correspond to the periods of 1 ms, 2 ms, and 5 ms, and the fastest observed MSP frequency of 716 Hz. The vertical line indicates the canonical mass of 1.4 M⊙. |
| In the text | |
 |
Fig. 4. Rotational mass-equatorial radius relations and central-density dependence. Left panels show rotational mass-equatorial radius sequences for unified TM1 EOSs with varying symmetry energy slope, L, and spin period, P. Right panels give the rotational mass, Mrot, as a function of central density, ρc. The purple crosses mark the rotational mass at the Kepler limit. |
| In the text | |
 |
Fig. 5. Same as Fig. 4, but using non-unified TM1 EOSs with a different crust. |
| In the text | |
 |
Fig. 6. Eccentricity, e, as a function of the gravitational mass of the MSPs for the family TM1 parameter set. Panels (a), (b), and (c) represent results from unified EOS with L = 40, 60, 80 MeV, respectively, while panel (d) shows a comparison of different EOSs. |
| In the text | |
 |
Fig. 7. Moment of inertia, I, as a function of the gravitational mass of the MSPs for the family TM1 parameter set. Panel (a) represents results from unified EOS L = 40 MeV, while panel (b) shows a comparison of different EOSs with P = 5 ms. |
| In the text | |
 |
Fig. A.1. The rotational mass-equatorial radius relations derived from RNS code and Hartle-Thorne approximation (H&T). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \mathcal{L} _{\mathrm{RMF}}&= \sum _{i=p,n}\bar{\psi }_i \left\{ i\gamma _{\mu }\partial ^{\mu }-\left(M_N+g_{\sigma }\sigma \right) \right.\nonumber \\&\quad \left. -\gamma _{\mu } \left[g_{\omega }\omega ^{\mu } +\frac{g_{\rho }}{2}\tau _a\rho ^{a\mu } \right]\right\} \psi _i \nonumber \\&\quad +\frac{1}{2}\partial _{\mu }\sigma \partial ^{\mu }\sigma -\frac{1}{2} m^2_{\sigma }\sigma ^2-\frac{1}{3}g_{2}\sigma ^{3} -\frac{1}{4}g_{3}\sigma ^{4} \nonumber \\&\quad -\frac{1}{4}W_{\mu \nu }W^{\mu \nu } +\frac{1}{2}m^2_{\omega }\omega _{\mu } \omega ^{\mu } +\frac{1}{4}c_{3}\left(\omega _{\mu }\omega ^{\mu }\right)^2 \nonumber \\&\quad -\frac{1}{4}R^a_{\mu \nu }R^{a\mu \nu } +\frac{1}{2}m^2_{\rho }\rho ^a_{\mu } \rho ^{a\mu } \nonumber \\&\quad +\Lambda _{\mathrm{v}} \left(g_{\omega }^2 \omega _{\mu }\omega ^{\mu }\right) \left(g_{\rho }^2\rho ^a_{\mu }\rho ^{a\mu }\right) \nonumber \\&\quad +\sum _{l=e,\mu }\bar{\psi }_{l} \left( i\gamma _{\mu }\partial ^{\mu }-m_{l}\right)\psi _l, \end{aligned} $$](/articles/aa/full_html/2026/02/aa52766-24/aa52766-24-eq8.gif)
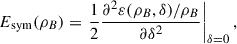
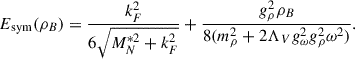
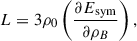
![$$ \begin{aligned} \frac{\mathrm{d}p(r)}{\mathrm{d}r}&= \frac{-GM(r)\varepsilon (r)}{r^2 c^2} \bigg [ 1 + \frac{p(r)}{\varepsilon (r)} \bigg ] \bigg [ 1 + \frac{4\pi p(r)r^3}{M(r) c^2} \bigg ] \bigg [ 1 - \frac{2GM(r)}{c^2 r} \bigg ]^{-1},\nonumber \\ \frac{\mathrm{d}M(r)}{\mathrm{d}r}&= 4\pi r^2 \frac{\varepsilon (r)}{c^2}, \end{aligned} $$](/articles/aa/full_html/2026/02/aa52766-24/aa52766-24-eq12.gif)
![$$ \begin{aligned} \mathrm{d}s^2&= -e^{2\varphi }(1 + 2h(r,\theta ))\mathrm{d}t^2 \nonumber \\&\quad + \bigg [1 + \frac{2m(r,\theta )}{r - 2M(r)} \bigg ] \bigg [ 1 - \frac{2M(r)}{r} \bigg ]^{-1}\mathrm{d}r^2 \nonumber \\&\quad + r^2(1 + 2k(r,\theta ))[\mathrm{d}\theta ^2 + \sin ^2\theta (\mathrm{d}\phi - \omega _r \mathrm{d}t)^2] , \end{aligned} $$](/articles/aa/full_html/2026/02/aa52766-24/aa52766-24-eq13.gif)
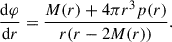
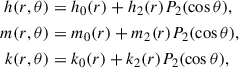
![$$ \begin{aligned} \Delta p = (\varepsilon +p)[p_0^* + p_2^*P_2(\cos (\theta )] .\end{aligned} $$](/articles/aa/full_html/2026/02/aa52766-24/aa52766-24-eq16.gif)
 , \nonumber \\ \Delta n&= (\varepsilon +p)[p_0^* + p_2^*P_2(\cos (\theta )](\mathrm{d}n/\mathrm{d}p) . \end{aligned} $$](/articles/aa/full_html/2026/02/aa52766-24/aa52766-24-eq17.gif)
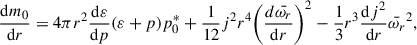
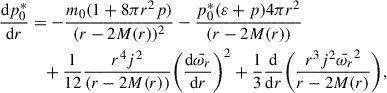
![$$ \begin{aligned} \frac{\mathrm{d}\nu _2}{\mathrm{d}r}&= -2h_2 \bigg ( \frac{\mathrm{d}\varphi }{\mathrm{d}r} \bigg ) + \bigg ( \frac{1}{r} +\frac{\mathrm{d}\varphi }{\mathrm{d}r} \bigg ) \bigg [- \frac{1}{3} r^3 \frac{\mathrm{d}j^2}{\mathrm{d}r} \bar{\omega _r}^2 + \frac{1}{6} j^2r^4 \bigg (\frac{\mathrm{d} \bar{\omega _r}}{\mathrm{d}r} \bigg )^2 \bigg ] , \nonumber \\ \end{aligned} $$](/articles/aa/full_html/2026/02/aa52766-24/aa52766-24-eq20.gif)
![$$ \begin{aligned} \frac{\mathrm{d}h_2}{\mathrm{d}r}&= -2h_2 \bigg ( \frac{\mathrm{d}\varphi }{\mathrm{d}r} \bigg ) + \frac{r}{r - 2M(r)} \bigg (2 \frac{\mathrm{d}\varphi }{\mathrm{d}r} \bigg )^{-1} \bigg [ 8\pi (\varepsilon + p) - \frac{4M(r)}{r^3} \bigg ]h_2 \nonumber \\&\quad - \frac{4\nu _2}{r(r -2M(r))} \bigg (2 \frac{\mathrm{d}\varphi }{\mathrm{d}r} \bigg )^{-1} \nonumber \\&\quad + \frac{1}{6} \bigg [ \frac{\mathrm{d}\varphi }{\mathrm{d}r}r - \frac{1}{r -2M(r)} \bigg (2 \frac{\mathrm{d}\varphi }{\mathrm{d}r} \bigg )^{-1}\bigg ]r^3j^2 \bigg (\frac{\mathrm{d} \bar{\omega _r}}{\mathrm{d}r} \bigg )^2 \nonumber \\&\quad - \frac{1}{3} \bigg [ \frac{\mathrm{d}\varphi }{\mathrm{d}r}r - \frac{1}{r -2M(r)} \bigg (2 \frac{\mathrm{d}\varphi }{\mathrm{d}r} \bigg )^{-1}\bigg ] r^2 \bigg (\frac{\mathrm{d}j^2}{\mathrm{d}r} \bigg ) \bar{\omega _r}^2 , \end{aligned} $$](/articles/aa/full_html/2026/02/aa52766-24/aa52766-24-eq21.gif)
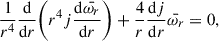
![$$ \begin{aligned} j = j(r) = e^{-\varphi } \bigg [1 - \frac{2M(r)}{r} \bigg ]^{1/2}. \end{aligned} $$](/articles/aa/full_html/2026/02/aa52766-24/aa52766-24-eq24.gif)