EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 706 (February 2026) A&A, 706 (2026) L7 Full HTML
Open Access
Issue
A&A
Volume 706, February 2026
Article Number L7
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202558173
Published online 30 January 2026

© The Authors 2026

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.

1. Introduction

The formation of the Galilean satellites (Io, Europa, Ganymede, and Callisto) is a cornerstone problem in planetary theory that offers a scaled-down analog of planetary system formation. Paralleling this process, the moons are thought to have formed via a bottom-up accretion process within the solids-rich primordial circumplanetary disk of Jupiter (Lunine & Stevenson 1982; Coradini et al. 1995; Peale 1999), analogous to the initial phase of planet formation (Pollack et al. 1996).

While foundational models such as those by Canup & Ward (2002) and Mosqueira & Estrada (2003a) successfully predict the total mass and compositional gradient of the system, these frameworks have long been crippled by the Type I migration catastrophe. This describes the tendency of gravitational torques from the massive gaseous phase of the circumjovian disk to rapidly drive protomoons inward (Goldreich & Tremaine 1980; Ward 1997), which results in their destruction (Mosqueira & Estrada 2003b; Canup & Ward 2006; Sasaki et al. 2010; Ogihara & Ida 2012; Miguel & Ida 2016). Thus, the survival of a moon depends on whether it can counteract this rapid inward migration.

A promising mechanism that can mitigate the inward migration naturally emerges from the aerodynamics of solids (Benítez-Llambay & Pessah 2018). The scattering of solids by the gravitational potential of the satellite can drive large asymmetries in the flow, which critically affects the net torques exerted on the satellite. The implications of this migration regulated by solids have been addressed solely in the context of planet formation, however (e.g., Regály 2020; Chrenko et al. 2024; Hou & Yu 2024).

We present the first systematic investigation of the migration of the Galilean moons that incorporates self-consistent solids dynamics. We demonstrate that torques arising from solids dynamics fundamentally alter the net torque on the satellites by causing it to deviate significantly from gas-only models. This effect is decisive for the migration history of the Galilean moons because it can slow, accelerate, or even reverse the migration, depending on the local dust-to-gas ratio and particle Stokes number. We summarize our findings in Figure 1, which shows the solids torque relative to the gaseous torque as exerted by the circumjovian disk on satellites with the mass of Europa and Ganymede.

thumbnail Fig. 1.

Normalized time-averaged net torque for all the models we considered as a function of the initial dust-to-gas density ratio and Stokes number. From left to right, the mass of the satellite corresponds to Ms = 1.25 × 10−5 MJ, Ms = 2.53 × 10−5 MJ, and Ms = 7.82 × 10−5 MJ. Blue indicates a net positive torque (outward orbital migration). The normalization, Γgas0, corresponds to the net torque when ϵ = 0. From left to right, Γgas0 = −3.63Γ0, Γgas0 = −3.33Γ0, and Γgas0 = −2.83Γ0, with Γ0 = (Ms/MJ)2Σ0 h−2r04Ω02.

2. Disk Model

We utilized the FARGO3D code and performed two-fluid simulations of a disk around a central mass MJ (numerical details are included in Appendix A). The gaseous phase of the disk is locally isothermal, with an aspect ratio h = 0.1 (Brunton & Batygin 2025) and viscosity ν = αcshr with α = 10−3. Its initial surface density is Σ(r) = Σ0(r/r0)−1/2, where Σ0 = 6 × 10−4 MJ/r02. The locally isothermal assumption was adopted for computational feasibility, but we acknowledge that it neglects complex thermodynamic effects such as cold thermal torques and heating torques, which can significantly affect the gaseous torque (Lega et al. 2014; Benítez-Llambay et al. 2015; Masset 2017). The dust component was initialized with a constant dust-to-gas mass ratio ϵ and was coupled to the gas via a drag force consistent with the Epstein and Stokes regimes. (Weidenschilling 1977). Dust back-reaction onto the gas was enabled by default.

In our exploration, we considered nine Stokes numbers1Ts = [0.01, 0.05, 0.1, 0.2, 0.35, 0.63, 1.12, 2, 5] and seven different dust-to-gas mass ratios ϵ = [0, 0.005, 0.01, 0.025, 0.05, 0.1, 0.5], which are consistent with subsolar to supersolar metallicity values. For all these parameters, we considered three different moon masses that were consistent with a protomoon (Ms = 1.25 × 10−5 MJ), Europa (Ms = 2.53 × 10−5 MJ), and Ganymede (Ms = 7.82 × 10−5 MJ). We focused on the late stages of moon formation, and we therefore did not explore satellite masses below Ms ≲ 1.25 × 10−5 MJ. Nevertheless, based on results from previous work, dust torques are positive and dominant for low-mass bodies, which is consistent with those we did not consider here (Benítez-Llambay & Pessah 2018).

3. Torque maps for Jovian disks

We present the main results of our numerical exploration in Figure 1. Each panel summarizes our results for a different satellite mass. The colors represent the net (gas + dust) torque exerted by the circumjovian disk, normalized by the torque measured in a simulation in which the solid phase is not taken into account. The total torque includes contributions from the disk potential and the indirect potential arising from the noninertial frame (see, e.g., Eqs. (5)–(7) Crida et al. 2025). While the torque in most cases reached a steady-state value within the integration time, it is not strictly steady for high dust-to-gas mass ratios. We therefore characterized the torque by its time-averaged value over the final orbital period of the integration. We present our main results below.

3.1. Positive torques are ubiquitous.

A first striking result of our exploration is that solids can induce positive torques (hence outward migration) for all satellite masses we considered when the Stokes number (Ts) and dust-to-gas mass ratio (ϵ) exceed certain thresholds. This dependence is clearest for the protomoon and Europa. For these bodies, positive torque at low solids fractions (e.g., ϵ < 0.01) requires high Stokes numbers (Ts ≳ 2). As the solid fraction ϵ increases, this requirement on Ts relaxes, and models with progressively lower Stokes numbers also yield positive torques. The behavior of the protomoon closely mirrors that of Europa, although its transition to outward migration occurs at slightly higher Stokes numbers. The conditions are slightly more restrictive for the more massive Ganymede because outward migration is only possible when ϵ ≳ 0.025 and Ts ≳ 1.

3.2. Torques differ from those in gas-only disks.

In most cases we explored, the net torque is affected by the presence of dust whenever Ts > 0.01. Critically, we find a dramatic enhancement of negative torques for the protomoon. This is a key result: Within the regime of intermediate Stokes numbers (0.1 ≲ Ts ≲ 1), we find a net torque magnitude |Γ|∼3 − 7 × |Γg0| even at subsolar metallicities. Here, Γg0 corresponds to the net torque in our dust-free models. While stronger negative torques can accelerate the orbital loss for protomoons, this effect depends on the local Stokes number and solids fraction. When accretion allows the moon to grow faster than it migrates, it can bypass this unstable regime to reach higher masses (e.g., Europa or Ganymede), where outward migration and orbital stalling become possible. A second striking feature, shown in Figure 1, is the strong positive torque achieved at high metallicity (ϵ ∼ 0.5). This torque is stronger by more than two orders of magnitude than in a gas-only model. We found this regime to be strongly affected by dust feedback because vortices that form in the horseshoe region induce stochastic fluctuations in the dust torque. This is consistent with findings by Chen & Lin (2018) in disks with very high dust-to-gas mass ratios.

4. Discussion

The dust torque affects satellite migration significantly by either promoting outward migration or by critically accelerating inward migration within specific parameter regimes. The division between these two migration behaviors is fundamentally determined by the satellite mass, the particle Stokes number, and the solids mass fraction. A general trend that is shown in Figure 1 is that outward migration typically occurs for high Stokes numbers and moderate to high gas-to-dust mass ratios. Because our torque measurements were made on a fixed planetary orbit, the sign of the torques are independent of the disk surface density Σ. The migration regimes highlighted in Figure 1 are therefore applicable across a wide range of formation scenarios, including gas-starved disk models (Canup & Ward 2002) and minimum-mass subnebula models (Lunine & Stevenson 1982; Mosqueira & Estrada 2003a) as long as the migration rate remains lower than the radial drift of solids. In the following, we discuss potential implications or modifications of our findings under more realistic physical modeling.

4.1. Implications for circumjovian disk models

In gas-starved disk models, the solid-to-gas ratio has been suggested to increase significantly and to even potentially approach unity (Canup & Ward 2002). Our results indicate that if Ts > 0.1, a scenario like this would robustly lead to an outward-migration regime of the regular satellites as they grow beyond Ms ∼ 10−5 MJ. Because the typical average surface densities in these models (Σ ∼ 10 − 1000 g/cm2) are consistent with Ts ≳ 0.1 for solids in the range of centimeters to meters, this outward migration is a highly plausible outcome. This means that solids-driven migration directly affects the orbital evolution and final formation locations of the Galilean moons.

For models with augmented solids fractions that are still well below unity (e.g., Solid Enhanced Minimum Mass disk Estrada et al. 2009), outward migration is triggered as the Stokes number exceeds unity (Ts > 1). In these models, the average gas surface densities can exceed Σ ∼ 1000 g/cm2, however, and solids larger than a meter are therefore required to reach Ts ∼ 1 until the gas starts to dissipate. Thus, when the particle size distribution in the primordial circumjovian disk is limited below the meter barrier, the solids are instead likely to drive fast inward migration. Furthermore, our results are consistent with rapid inward migration under subsolar metallicity conditions, such as the torques shown for ϵ = 0.005 in Figure 1 only for the protomoon and Europa. This finding suggests that migration rates in existing formation models that are based purely on pebble accretion might be significantly underestimated (Shibaike et al. 2019; Ronnet & Johansen 2020; Madeira et al. 2021). Overall, the complex and nontrivial dependence of the net torque on ϵ and Ts means that modern formation models (e.g., Shibaike & Alibert 2025) must now incorporate the time-evolving solids component as a critical source of migration to accurately track the orbital evolution of the satellite.

The possibility of outward migration or stalling naturally raises the question of mass regulation. If solid driven torques prevent orbital decay, we propose that mass regulation is dictated by the solid reservoir or by the dissipative timescale of the circumplanetary disk. In this scenario, growth concludes when the available solids in the feeding zone are exhausted or when the gas disk (which mediates these torques) dissipates. This shifts the focus from a continuous flux model to a reservoir-limited scenario in which the final system architecture is primarily determined by the total solid budget.

4.2. Differential migration of the Galilean moons

The differing migration regimes found for Ganymede and Europa are a strong indication that solids provide a viable source of differential migration. This is a crucial requirement for locking the regular satellites into their observed mean-motion resonances. Outward migration for Ganymede occurs when the conditions are Ts ≳ 0.1 and ϵ ≳ 0.02. Although Ganymede is typically prone to the fastest inward migration in gas-only models, this rapid decline is efficiently mitigated if it reached its final mass within a region characterized by a solids fraction augmented by a few percent. On the other hand, the transition to outward migration for Europa occurs even for lower dust-to-gas ratios of ϵ ∼ 0.005 if the Stokes number is high enough (Ts ≳ 5). This suggests that Europa might require local disk conditions with larger particle sizes and/or higher solid-to-gas densities than Ganymede to reach an outward-migration regime. Although Figure 1 uses a mass-dependent normalization, the transition between inward and outward migration varies for Europa and Ganymede in the (ϵ, Ts) parameter space. This mass-dependent response enables the differential migration that is required to reach mean-motion resonances. For instance, in a fixed-disk model, a more massive Ganymede might experience reduced inward migration, while a smaller Europa stalls or moves outward. This facilitates orbital convergence. While detailed simulations for Io and Callisto are beyond the scope of this Letter, their intermediate masses suggest that they would experience comparable intermediate trends. This further supports the general applicability of solids-driven migration for the entire system.

4.3. The role of solids accretion

While we calculated steady-state torques on fixed nonaccreting satellites, the formation of the Galilean moons strongly relies on accretion of solids (see e.g., Ormel 2024). This process fundamentally alters the total torque in two ways. First, accretion modifies the spatial distribution of solids by removing material close to the moon, which tends to accentuate the asymmetry in the solid distribution (Regály 2020; Chrenko et al. 2024). This strengthening effect means that the magnitude of the torque exerted by solids can increase with the accretion strength. For satellite masses lower than those we considered, the torque exerted by solids can significantly exceed the gas torque through accretion (Chrenko et al. 2024) or for higher masses if the metallicity is high enough, as we showed above. Second, accretion introduces the so-called accretion torque, which is produced by the angular momentum carried by the accreted solids (Chrenko et al. 2024). This torque can be a substantial component that can either diminish the net torque by solids or strengthen it, depending on the Stokes number. Studies incorporating self-consistent accretion in the context of planet formation demonstrated that the positive magnitude of the dust torque is notably higher for low-mass bodies and low Stokes numbers when accretion is included (Guilera et al. 2025). These findings strengthen the conclusion that outward migration can be a natural outcome for moons that form via solid accretion not only at late stages, but more importantly, during their formation stage.

4.4. Thermal torques

Our analysis relied on a locally isothermal disk model that simplified the computation of gas torques. Realistic disk thermodynamics introduces critical nonisothermal effects that directly interact with the dust dynamics and exert additional and substantial torques, however. One such effect is the so-called cold thermal torque (Lega et al. 2014), which arises from thermal diffusion close to the moon. The thermal structure is inherently connected to the dust component, however. Dust feedback can significantly reshape the cold, dense lobes around the planet that are the source of the thermal torque (Chametla et al. 2025). Furthermore, the release of energy during accretion generates a heating torque (Benítez-Llambay et al. 2015). The strong asymmetries in the dust distribution around the planet might alter the local opacity, which in turn might lead to an asymmetric thermal diffusivity near the moons. This effect might affect the net thermal torque that acts on the satellite. A comprehensive picture of Galilean moon migration therefore requires integration of these nonisothermal physics because the gravitational torque from solids and thermal torques operates under coupled conditions.

4.5. Caveats and future directions

Our primary finding is that torques arising from solids dynamics cannot be neglected when the migration history of the Galilean moons is to be understood. While simplified, our 2D framework facilitates a broad and systematic parameter exploration with self-consistent solids dynamics. Two-dimensional simulations might overestimate dust-feedback torques compared to three-dimensional disks at the same dust-to-gas ratio, however (Hsieh & Lin 2020). Moreover, disk asymmetries and filaments are sensitive to turbulent diffusion and vertical settling, which likely affect the net torque and might lead to nonsteady migration (Chametla et al. 2025). In addition, 3D models are required to validate the effect of the gravitational softening, which can artificially enhance a gaseous torque while suppressing a dusty torque, although recent work suggests a weak sensitivity for low Stokes numbers (Chametla et al. 2025). Finally, our torque values assumed a fixed circular orbit and neglected mass growth. Realistic evolutionary tracks demand coupled migration and accretion simulations that include the accretion torque (Chrenko et al. 2024), which can substantially alter the total torque. Migration itself modifies relative dust–moon velocities, which further affects the torque asymmetry. We assumed circular orbits because the eccentricity of the Galilean moons is low. Thermal forces and dust feedback can excite eccentricity, however (Eklund & Masset 2017), which strongly affects the asymmetry morphology and torque magnitude. Future models must solve the nonisothermal energy equation to capture the eccentricity growth and its interplay with dust-feedback torques self-consistently.

5. Conclusions

We presented the first systematic investigation into the effect of solids dynamics on the orbital evolution of Galilean moons of Jupiter. We suggest that torques arising from the solid component are a critical element that must be integrated into future satellite formation models to achieve a complete picture of their evolution. Our results demonstrate that the total torque experienced by forming satellites deviates significantly from gas-only models in a wide range of parameters. These findings elucidate a self-consistent migration mechanism that agrees seamlessly with classical and contemporary Jovian disk models that assumed higher dust-to-gas mass fractions (e.g., Cilibrasi et al. 2018; Batygin & Morbidelli 2020; Schneeberger & Mousis 2025). Crucially, the differing migration regimes we found for the moons provide a viable source of differential migration. A successful model must identify parameters that not only reproduce the differential migration needed to capture Io, Europa, and Ganymede in Laplace resonances (Peale & Lee 2002), but must also simultaneously explain the compositional gradient of the moons (Kuskov & Kronrod 2005; Canup & Ward 2009). Finally, while we focused on Jovian moons, solids-driven migration might be pivotal in shaping exomoon systems (Heller et al. 2014; Kipping et al. 2022) and other regular satellites in our Solar System (Coradini et al. 1995; Alibert & Mousis 2007). These insights underscore that coupling the time-evolving solids component with gas dynamics, a key aspect of circumplanetary disk models (Krapp et al. 2024), is mandatory for accurately tracking the orbital evolution of the satellite and for developing a comprehensive understanding of satellite system architectures in diverse planetary environments.

Acknowledgments

L. K. thanks Robin Canup, Yuri Fujii, and Konstantin Batygin for inspiring discussion that led to this publication during the Circumplanetary Disks and Satellite Formation III conference in Kyoto, Japan. L. K. acknowledges support from the Heising-Simons Foundation, ANID Fondecyt Iniciacion (project 11250447), ANID-Quimal 220002, and ANID BASAL project FB21003. L. K. acknowledges High Performance Computing resources supported by the University of Arizona TRIF, UITS, and Research, Innovation, and Impact (RII) and maintained by the UArizona Research Technologies department. P. B. L. acknowledges support from ANID, QUIMAL fund ASTRO21-0039 and FONDECYT project 1231205.

References

  1. Alibert, Y., & Mousis, O. 2007, A&A, 465, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Batygin, K., & Morbidelli, A. 2020, ApJ, 894, 143 [NASA ADS] [CrossRef] [Google Scholar]
  3. Benítez-Llambay, P., & Masset, F. S. 2016, ApJS, 223, 11 [Google Scholar]
  4. Benítez-Llambay, P., & Pessah, M. E. 2018, ApJ, 855, L28 [Google Scholar]
  5. Benítez-Llambay, P., Masset, F., Koenigsberger, G., & Szulágyi, J. 2015, Nature, 520, 63 [Google Scholar]
  6. Benítez-Llambay, P., Krapp, L., & Pessah, M. E. 2019, ApJS, 241, 25 [Google Scholar]
  7. Brunton, I. R., & Batygin, K. 2025, ApJ, 991, 15 [Google Scholar]
  8. Canup, R. M., & Ward, W. R. 2002, AJ, 124, 3404 [Google Scholar]
  9. Canup, R. M., & Ward, W. R. 2006, Nature, 441, 834 [NASA ADS] [CrossRef] [Google Scholar]
  10. Canup, R. M., & Ward, W. R. 2009, in Europa, eds. R. T. Pappalardo, W. B. McKinnon, & K. K. Khurana, 59 [Google Scholar]
  11. Chametla, R. O., Chrenko, O., Sánchez-Salcedo, F. J., et al. 2025, A&A, 704, A207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Chen, J.-W., & Lin, M.-K. 2018, MNRAS, 478, 2737 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chrenko, O., Chametla, R. O., Masset, F. S., Baruteau, C., & Brož, M. 2024, A&A, 690, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Cilibrasi, M., Szulágyi, J., Mayer, L., et al. 2018, MNRAS, 480, 4355 [NASA ADS] [Google Scholar]
  15. Coradini, A., Federico, C., Forni, O., & Magni, G. 1995, Surv. Geophys., 16, 533 [Google Scholar]
  16. Crida, A., Baruteau, C., Griveaud, P., et al. 2025, Open J. Astrophys., 8, 84 [Google Scholar]
  17. Eklund, H., & Masset, F. S. 2017, MNRAS, 469, 206 [NASA ADS] [CrossRef] [Google Scholar]
  18. Estrada, P. R., Mosqueira, I., Lissauer, J. J., D’Angelo, G., & Cruikshank, D. P. 2009, in Europa, eds. R. T. Pappalardo, W. B. McKinnon, & K. K. Khurana, 27 [Google Scholar]
  19. Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [Google Scholar]
  20. Guilera, O. M., Benitez-Llambay, P., Miller Bertolami, M. M., & Pessah, M. E. 2025, ApJ, 986, 199 [Google Scholar]
  21. Heller, R., Williams, D., Kipping, D., et al. 2014, Astrobiology, 14, 798 [CrossRef] [Google Scholar]
  22. Hou, Q., & Yu, C. 2024, ApJ, 972, 152 [Google Scholar]
  23. Hsieh, H.-F., & Lin, M.-K. 2020, MNRAS, 497, 2425 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kipping, D., Bryson, S., Burke, C., et al. 2022, Nat. Astron., 6, 367 [NASA ADS] [CrossRef] [Google Scholar]
  25. Krapp, L., Kratter, K. M., Youdin, A. N., et al. 2024, ApJ, 973, 153 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kuskov, O. L., & Kronrod, V. A. 2005, Sol. Syst. Res., 39, 283 [Google Scholar]
  27. Lega, E., Crida, A., Bitsch, B., & Morbidelli, A. 2014, MNRAS, 440, 683 [Google Scholar]
  28. Lunine, J. I., & Stevenson, D. J. 1982, Icarus, 52, 14 [NASA ADS] [CrossRef] [Google Scholar]
  29. Madeira, G., Izidoro, A., & Giuliatti Winter, S. M. 2021, MNRAS, 504, 1854 [NASA ADS] [CrossRef] [Google Scholar]
  30. Masset, F. S. 2017, MNRAS, 472, 4204 [NASA ADS] [CrossRef] [Google Scholar]
  31. Miguel, Y., & Ida, S. 2016, Icarus, 266, 1 [NASA ADS] [CrossRef] [Google Scholar]
  32. Mosqueira, I., & Estrada, P. R. 2003a, Icarus, 163, 198 [NASA ADS] [CrossRef] [Google Scholar]
  33. Mosqueira, I., & Estrada, P. R. 2003b, Icarus, 163, 232 [NASA ADS] [CrossRef] [Google Scholar]
  34. Ogihara, M., & Ida, S. 2012, ApJ, 753, 60 [NASA ADS] [CrossRef] [Google Scholar]
  35. Ormel, C. W. 2024, ArXiv e-prints [arXiv:2411.14643] [Google Scholar]
  36. Peale, S. 1999, ARA&A, 37, 533 [NASA ADS] [CrossRef] [Google Scholar]
  37. Peale, S. J., & Lee, M. H. 2002, Science, 298, 593 [NASA ADS] [CrossRef] [Google Scholar]
  38. Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
  39. Regály, Z. 2020, MNRAS, 497, 5540 [CrossRef] [Google Scholar]
  40. Ronnet, T., & Johansen, A. 2020, A&A, 633, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Sasaki, T., Stewart, G. R., & Ida, S. 2010, ApJ, 714, 1052 [NASA ADS] [CrossRef] [Google Scholar]
  42. Schneeberger, A., & Mousis, O. 2025, Planet. Sci. J., 6, 23 [Google Scholar]
  43. Shibaike, Y., & Alibert, Y. 2025, ArXiv e-prints [arXiv:2508.05932] [Google Scholar]
  44. Shibaike, Y., Ormel, C. W., Ida, S., Okuzumi, S., & Sasaki, T. 2019, ApJ, 885, 79 [NASA ADS] [CrossRef] [Google Scholar]
  45. Ward, W. R. 1997, Icarus, 126, 261 [Google Scholar]
  46. Weidenschilling, S. J. 1977, MNRAS, 180, 57 [Google Scholar]
1

We defined the Stokes number as the dimensionless stopping time, expressed in units of the local Keplerian frequency of the disk.

Appendix A: Numerical methods

We performed two-fluid simulations with the code FARGO3D (Benítez-Llambay & Masset 2016; Benítez-Llambay et al. 2019) on a 2D polar grid (r, ϕ) with 768 × 4096 cells spanning r ∈ [0.5r0, 1.5r0], which is enough to account for the main source of the gaseous torque. A satellite with a mass Ms is on a circular orbit around a central planet with a mass MJ, with semimajor axis rs and an orbital frequency Ωs. We adopted a planetocentric frame and included the indirect terms arising from the planet and the disk (dust+gas) (Crida et al. 2025). We adopted units such that our reference time, mass, and distance units were Ω0−1 = 1, M0 = 1, and r0 = 1, respectively. We set MJ = M0, rs = r0, which implies Ωs = Ω0. The size of each cell in the hydrodynamical grid was ∼1.3 × 10−3r0, which is also enough to resolve the small-scale substructure induced by the gravitational perturbation of the moon on the solid phase of the disk. The satellite potential was modeled as a Plummer potential with a smoothing length equal to the Hill radius of the moon. The initial and boundary conditions were taken from (Benítez-Llambay & Pessah 2018). We integrated the system until the torque reached steady state, which varied between 28 to 56 satellite orbits, depending on the parameters.

Appendix B: Dust Density and Torque Contributions

The contribution of the solid material to the net torque is driven by an asymmetric density distribution in the horseshoe region. This asymmetry results from the satellite scattering solids as they drift through the disk. As a result of this scattering, a complex structure develops. For large Stokes Numbers this typically resembles an under-dense cavity with a lower density in the region trailing the satellite, which is itself asymmetric, and an over-dense stream of dust leading the satellite’s orbit. The outcome of these complex asymmetric flows is generally a positive torque. However, this is not always the case; as shown in Figure 1, solids can also increase the net negative torque (Benítez-Llambay & Pessah 2018).

We illustrate this density structure in Figures B.1 (protomoon) and B.2 (Ganymede). The overlaid gas and dust streamlines highlight the key dynamical processes responsible for this distribution: the radial drift of dust particles and the asymmetric flows in the co-orbital region. In the protomoon case, only a small dust cavity forms. As a result, the dust torque is dominated by the radially drifting dust stream interior to the orbit, yielding a strongly negative dust torque contribution and thus a net negative torque on the satellite. In contrast, the more massive Ganymede forms a much larger dust cavity. This allows the positive dust torque to dominate, whose absolute value is larger than the gas torque (depending on the dust-to-gas mass fraction), resulting in a net positive torque. The bottom panels of Figures B.1 and B.2 show the time evolution of the total torque for both cases. For reference, we also include the torque obtained from dust-free simulations. In both the Protomoon and Ganymede cases, the presence of dust substantially modifies the gas torque through dust and gas backreaction, underscoring the critical importance of dust feedback in these models.

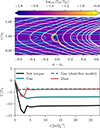thumbnail Fig. B.1.

Top row: Dust surface density (color) with superimposed gas (cyan) and dust (white) velocity streamlines. Bottom row: Time evolution of the normalized torques exerted on the embedded moon. The solid black curve shows the net (gas + dust) torque, while the red and green curves correspond to the dust and gas contributions, respectively. The dashed green curve indicates the net gas torque in the corresponding dust-free reference simulation. Simulation corresponds to protomoon with ϵ = 0.025 and Ts = 0.35.

thumbnail Fig. B.2.

Same as Figure B.1 but for Ganymede with ϵ = 0.05 and Ts = 0.35.

All Figures

thumbnail Fig. 1.

Normalized time-averaged net torque for all the models we considered as a function of the initial dust-to-gas density ratio and Stokes number. From left to right, the mass of the satellite corresponds to Ms = 1.25 × 10−5 MJ, Ms = 2.53 × 10−5 MJ, and Ms = 7.82 × 10−5 MJ. Blue indicates a net positive torque (outward orbital migration). The normalization, Γgas0, corresponds to the net torque when ϵ = 0. From left to right, Γgas0 = −3.63Γ0, Γgas0 = −3.33Γ0, and Γgas0 = −2.83Γ0, with Γ0 = (Ms/MJ)2Σ0 h−2r04Ω02.
In the text
thumbnail Fig. B.1.

Top row: Dust surface density (color) with superimposed gas (cyan) and dust (white) velocity streamlines. Bottom row: Time evolution of the normalized torques exerted on the embedded moon. The solid black curve shows the net (gas + dust) torque, while the red and green curves correspond to the dust and gas contributions, respectively. The dashed green curve indicates the net gas torque in the corresponding dust-free reference simulation. Simulation corresponds to protomoon with ϵ = 0.025 and Ts = 0.35.
In the text
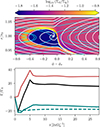thumbnail Fig. B.2.

Same as Figure B.1 but for Ganymede with ϵ = 0.05 and Ts = 0.35.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.