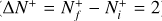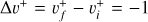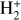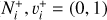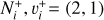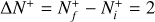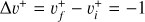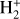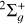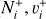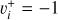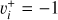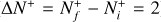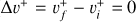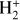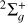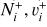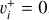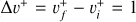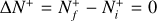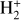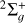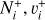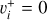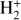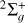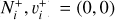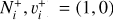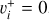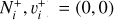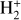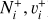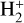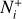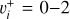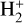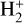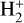EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 703 (November 2025) A&A, 703 (2025) A220 Full HTML
Open Access
Issue
A&A
Volume 703, November 2025
Article Number A220
Number of page(s) 8
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202556510
Published online 20 November 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Molecular hydrogen and its cation are among the first species formed in the early Universe (for a review, see, e.g., Galli & Palla 2013). Due to the lack of a dipole moment, in the absence of catalyzing dust grains, the homonuclear molecule H2 cannot be formed by radiative association of two hydrogen atoms, and its production in a gas of primordial composition proceeds via the intermediary species H−and 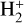H2+$\mathrm{H}_{2}^{+}$ (see, e.g., Lepp et al. 2002; Coppola et al. 2011; Gay et al. 2012). The latter channel is the dominant one at high temperature, and is limited by the destruction of 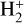H2+$\mathrm{H}_{2}^{+}$ by photodissociation, charge exchange with H atoms, and dissociative recombination (DR) with electrons. In dense molecular clouds where ultraviolet radiation is efficiently absorbed by dust grains, 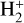H2+$\mathrm{H}_{2}^{+}$ is formed in excited vibrational states by cosmic-ray ionization of H2 (Glassgold & Langer 1973) and rapidly transformed into 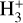H3+$\mathrm{H}_{3}^{+}$, which is the starting point of gas phase ion-molecule reaction chemistry (see, e.g., Tielens 2013). In addition, due to the high electron densities, DR of 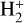H2+$\mathrm{H}_{2}^{+}$ plays an important role also in brown dwarfs atmospheres (Gibbs & Fitzgerald 2022; Pineda et al. 2024), planetary nebulae (Black 1978), and HII regions (Aleman & Gruenwald 2004).

The molecular hydrogen cation is also the primary molecular ion formed by photoionization of H2 in the upper atmospheres and ionospheres of outer gaseous planets in the Solar System and extrasolar giant planets (see, e.g., Chadney et al. 2016). In this context, the recombination of 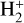H2+$\mathrm{H}_{2}^{+}$with electrons has also been studied as a source of excited states of atomic hydrogen, in particular H(2p), in models of the ultraviolet emission of Jupiter’s upper atmosphere, where it competes with the energy transfer between free protons and H(2s) (Shemansky 1985).

Dissociative recombination is also an important reaction in laboratory astrophysics (Parigger et al. 2018) because it affects the diagnostics of electric discharges in hydrogen and deuterium mixtures based on the line profile of the hydrogen Balmer series, where this recombination process becomes dominant. The effect has been studied in particular in recombining plasmas where the electron temperature is below 1 eV (Wünderlich et al. 2009; Friedl et al. 2020) and therefore relevant for the interstellar medium. The effect of DR on diagnostics was also studied using the Monte Carlo DEGAS2 model (Stotler & Karney 1994), applied to the simulation of MAP-II (materials and plasma) columnar plasma sources (Tanaka et al. 2000), used to study edge recombination. In this type of source, the plasma has two mixed but not balanced components: one has a temperature of the order of 1 eV, and a second has a higher temperature. Krasheninnikov et al. (1997) used a collisional-radiative model to show that, due to this reaction too, the formation of molecular ions has a significant effect on the recombination rate of a hydrogen plasma.

In all these environments, in which the ionization fraction is significant, the electron-impact induced ro-vibrational transitions (RVT), strong competitors of the DR, provide the dominant path to excitation and de-excitation process of 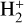H2+$\mathrm{H}_{2}^{+}$(Black & Van Dishoeck 1987; Le Petit et al. 2002; Agundez et al. 2010). 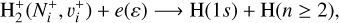The aim of the present paper is to provide accurate cross sections and rate coefficients for electron-impact induced RVT, H2+(Ni+,vi+)+e(ε)⟶H2+(Nf+,vf+)+e(ε'),$\mathrm{H}_{2}^{+}\left(N_{i}^{+}, v_{i}^{+}\right)+e(\varepsilon) \longrightarrow \mathrm{H}_{2}^{+}\left(N_{f}^{+}, v_{f}^{+}\right)+e\left(\varepsilon^{\prime}\right),$(1) and DR reactions, H2+(Ni+,vi+)+e(ε)⟶H(1s)+H(n≥2),$\mathrm{H}_{2}^{+}\left(N_{i}^{+}, v_{i}^{+}\right)+e(\varepsilon) \longrightarrow \mathrm{H}(1 s)+\mathrm{H}(n \geq 2),$(2) of H2+$\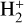mathrm{H}_{2}^{+}$and its isotopolog HD+, including all relevant ro-vibrational levels. 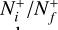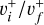In reactions (1) and (2), Ni+/Nf+$N_{i}^{+} / N_{f}^{+}$ and vi+/vf+$v_{i}^{+} / v_{f}^{+}$ are the initial and final rotational and vibrational quantum numbers of the target ion, respectively, ɛ/ɛ′ is the energy of the incident and scattered electron, and n the principal quantum number of the excited atom resulting from dissociation. RVT can be further characterized as resonant elastic collisions, inelastic collisions and super-elastic collisions when the energy ɛ′ of the scattered electron is equal to, smaller, or larger than the energy ɛ of the incident electron. The spectroscopic information, given by the output of reactions (1)-(2), is sensitive to the initial (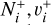Ni+,vi+$N_{i}^{+}, v_{i}^{+}$) and final (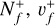Nf+,vf+$N_{f}^{+}, v_{f}^{+}$) quantum numbers of the target ions and consequently provides the structure of the ionized media.

This study was initiated in previous publications by our group (Motapon et al. 2014; Epée Epée et al. 2016; Djuissi et al. 2020; Epée Epée et al. 2022). We notice that, whereas for 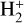H2+$\mathrm{H}_{2}^{+}$ the rotational transitions involve rotational quantum numbers of strictly the same parity (“gerade” or “ungerade”), this rule is not valid for the deuterated variant. However, we assumed it for HD+ too, since no data are currently available for the gerade/ungerade mixing, and since the transitions between rotational quantum numbers of different parity are much less intense than the others (Shafir et al. 2009).

This paper is organized as follows: in Sect. 2 we describe our theoretical method. In Sect. 3, we present our results in terms of cross sections and rate coefficients. In Sect. 4, we discuss the applications in the media of astro-chemical interest. And, finally, in Sect. 5 we summarize our conclusions.

2 Theoretical method

The electron-induced reactions (1) and (2) for 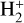H2+$\mathrm{H}_{2}^{+}$and HD+ are studied by a step-wise version of the multichannel quantum defect theory (MQDT), which we successfully applied to calculate DR, ro-vibrational and dissociative excitation cross sections for molecular cations such as 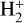H2+$\mathrm{H}_{2}^{+}$and its isotopolog (Waffeu Tamo et al. 2011; Chakrabarti et al. 2013; Motapon et al. 2014; Epée Epée et al. 2016, 2022), CH+(Mezei et al. 2019), SH+(Kashinski et al. 2017), BeH+and its isotopologs (Niyonzima et al. 2017, 2018; Pop et al. 2021).

A detailed description of the method has been given in previous articles (Motapon et al. 2014; Mezei et al. 2019), and we list below only the main steps of our current MQDT treatment:

  1. Building the interaction matrix based on the couplings between ionization channels – associated with the ro-vibrational levels N+, v+of the cation and with the orbital quantum number l of the incident (Rydberg) electron – and the dissociation channels.

  2. Computation of the reaction matrix K as a second-order perturbative solution of the Lippmann-Schwinger integral equation (Ngassam et al. 2003).

  3. Diagonalization of the reaction matrix by building the short-range representation of the eigenchannel.

  4. Frame transformation from the Born-Oppenheimer (shortrange) representation—characterized by quantum numbers N, v, Λ, and l—to the close-coupling (long-range) representation, defined by N+, v+, and l. Here, N and N+denote the total rotational quantum numbers of the neutral system and the ion, respectively, v and v+are the corresponding vibrational quantum numbers, and l is the orbital angular momentum of the incoming, outgoing, or scattered electron.

  5. Building of the generalized scattering matrix based on the frame-transformation coefficients organized in blocks associated with energetically open (o) and/or closed (c) channels: 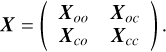X=(XooXocXcoXcc).$ \boldsymbol{X}=\left(\begin{array}{ll} \boldsymbol{X}_{o o} & \boldsymbol{X}_{o c}\\ \boldsymbol{X}_{c o} & \boldsymbol{X}_{c c} \end{array}\right). $(3)

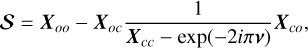  6. Building of the physical scattering matrix: S=Xoo-Xoc1Xcc-exp(-2iπv)Xco,$\boldsymbol{S}=\boldsymbol{X}_{o o}-\boldsymbol{X}_{o c} \frac{1}{\boldsymbol{X}_{c c}-\exp (-2 i \pi \boldsymbol{v})} \boldsymbol{X}_{c o},$(4) obtained by the so-called “elimination of closed channel” (Seaton 1983). The diagonal matrix v in the denominator contains the effective quantum numbers corresponding to the vibrational thresholds of the closed ionization channels at the current total energy of the system.

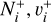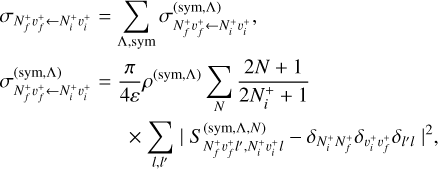  7. Computation of the cross sections for the target initially in a state characterized by the quantum numbers Ni+,vi+$N_{i}^{+}, v_{i}^{+}$, and for the energy of the incident electron ɛ, the RVT and the DR global cross sections read, respectively, σNf+vf+←Ni+vi+=∑Λ,symσNf+vf+←Ni+vi+(sym,Λ)σNf+vf+←Ni+vi+(sym,Λ)=π4ερ(sym,Λ)∑N2N+12Ni++1×∑l,l′|SNf+vf+l′,Ni+vi+l(sym,Λ)−δNi+Nf+δvi+vf+δl′l|2$ \begin{align*} \sigma_{N_{f}^{+} v_{f}^{+} \leftarrow N_{i}^{+} v_{i}^{+}}= & \sum_{\Lambda, \mathrm{sym}} \sigma_{N_{f}^{+} v_{f}^{+} \leftarrow N_{i}^{+} v_{i}^{+}}^{(\mathrm{sym}, \Lambda)}\\ \sigma_{N_{f}^{+} v_{f}^{+} \leftarrow N_{i}^{+} v_{i}^{+}}^{(\mathrm{sym}, \Lambda)}= & \frac{\pi}{4 \varepsilon} \rho^{(\mathrm{sym}, \Lambda)} \sum_{N} \frac{2 N+1}{2 N_{i}^{+}+1} \\ & \times \sum_{l, l^{\prime}}\left|S_{N_{f}^{+} v_{f}^{+} l^{\prime}, N_{i}^{+} v_{i}^{+} l}^{(\mathrm{sym}, \Lambda)}-\delta_{N_{i}^{+} N_{f}^{+}} \delta_{v_{i}^{+} v_{f}^{+}} \delta_{l^{\prime} l}\right|^{2} \end{align*} $(5) σdiss←Ni+vi+=∑Λ,symσdiss←Ni+vi+(sym,Λ)$\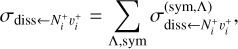sigma_{\text {diss} \leftarrow N_{i}^{+} v_{i}^{+}}= \sum_{\Lambda, \text { sym }} \sigma_{\text {diss } \leftarrow N_{i}^{+} v_{i}^{+}}^{(\text {sym }, \Lambda)}$(6) σdiss ←Ni+vi+(sym ,Λ)=π4ερ(sym ,Λ)∑N2N+12Ni++1×∑l,j|Sdj,Ni+vi+l(sym ,Λ,N)|2,$ \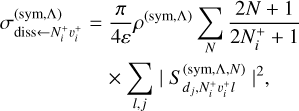begin{align*} \sigma_{\text {diss } \leftarrow N_{i}^{+} v_{i}^{+}}^{(\text {sym }, \Lambda)}= & \frac{\pi}{4 \varepsilon} \rho^{(\text {sym }, \Lambda)} \sum_{N} \frac{2 N+1}{2 N_{i}^{+}+1} \\ & \times \sum_{l, j}\left|S_{d_{j}, N_{i}^{+} v_{i}^{+} l}^{(\text {sym }, \Lambda, N)}\right|^{2}, \end{align*} $(7) where sym refers to the inversion symmetry – gerade/ungerade – and to the spin quantum number of the neutral system, Λ is the projection of the electronic orbital angular momentum on the molecular axis, and ρ(sym, Λ) is the ratio between the spin multiplicities of the neutral system and that of the ion.

This work extends our previous studies performed on HD+ (Waffeu Tamo et al. 2011; Motapon et al. 2014) and 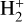H2+$\mathrm{H}_{2}^{+}$(Epée Epée et al. 2016) for low collision energies relevant for kinetics modeling in astrochemistry, by considering simultaneous rotational and vibrational transitions (excitations and/or deexcitations) and by increasing the range of the incident energy of the electron. We used the same molecular structure data sets as those from our previous studies (Waffeu Tamo et al. 2011; Motapon et al. 2014; Epée Epée et al. 2016; Djuissi et al. 2020; Epée Epée et al. 2022). The energies of the first 30 ro-vibrational levels of the 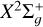X2Σg+$X^{2} \Sigma_{g}^{+}$ electronic state of 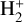H2+$\mathrm{H}_{2}^{+}$and HD+relative to the ground level 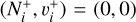(Ni+,vi+)=(0,0)$\left(N_{i}^{+}, v_{i}^{+}\right)=(0, 0)$ are listed in Table 1. The molecular states of the neutral (H2, HD) systems taken into account were of 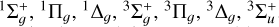1Σg+,1Πg,1Δg,3Σg+,3Πg,3Δg,3Σu+${ }^{1} \Sigma_{g}^{+},{ }^{1} \Pi_{g},{ }^{1} \Delta_{g},{ }^{3} \Sigma_{g}^{+},{ }^{3} \Pi_{g},{ }^{3} \Delta_{g},{ }^{3} \Sigma_{u}^{+}$, and 3Πu symmetries. Consequently, the partial waves considered for the incident electron were s and d for the 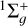1Σg+${ }^{1} \Sigma_{g}^{+}$ states, d for 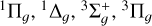1Πg,1Δg,3Σg+,3Πg${ }^{1} \Pi_{g},{ }^{1} \Delta_{g},{ }^{3} \Sigma_{g}^{+},{ }^{3} \Pi_{g}$ and 3Δg, and 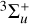3Σu+${ }^{3} \Sigma_{u}^{+}$, and 3Πu.

Table 1

First 30 ro-vibrational levels of 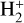H2+$\mathrm{H}_{2}^{+}$and HD+.

3 Results and discussions

We computed the RVT cross sections for the lowest 30 rovibrational levels of 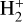H2+$\mathrm{H}_{2}^{+}$and HD+in their ground 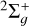2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state, and for collision energies ranging between 10−5−1.09 eV–this latter value corresponding to the opening of the following dissociation channel – with an energy step of 0.01 meV. We considered both “direct” and “indirect” mechanisms – i.e., including “open” and “closed” channels, respectively. The reaction matrix was evaluated to second order in perturbation theory.

Thermally averaged rate coefficients were obtained by convolution of the cross sections with the isotropic Maxwell distribution function of the kinetic energy of the incident electrons: 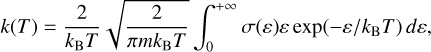k(T)=2kBT2πmkBT∫0+∞σ(ε)εexp(-ε/kBT)dε$k(T)=\frac{2}{k_{\mathrm{B}} T} \sqrt{\frac{2}{\pi m k_{\mathrm{B}} T}} \int_{0}^{+\infty} \sigma(\varepsilon) \varepsilon \exp \left(-\varepsilon / k_{\mathrm{B}} T\right) d \varepsilon$(8) where σ(ɛ) are the cross sections calculated according to Eqs. (5)–(8) and kB is the Boltzmann constant.

Figures 1 4 display representative samples of RVT cross sections and thermal rate coefficients. 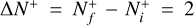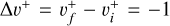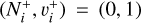More specifically, Figure 1 displays the cross sections of simultaneous electron-impact rotational excitation (ΔN+=Nf+-Ni+=2$\Delta N^{+}=N_{f}^{+}-N_{i}^{+}=2$) and vibrational de-excitation (Δv+=vf+-vi+=-1$\Delta v^{+}=v_{f}^{+}-v_{i}^{+}=-1$) from the ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state and initial ro-vibrational levels (Ni+,vi+)=(0,1)$\left(N_{i}^{+}, v_{i}^{+}\right)=(0,1)$ and (Ni+,vi+)=(2,1)$\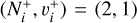left(N_{i}^{+}, v_{i}^{+}\right)=(2,1)$. Figure 2 displays the corresponding rate coefficients for ten ro-vibrational levels of the target, ranging from (0, 1) to (9, 1). Figure 3 presents rate coefficients for pure rotational excitation (Δ N+=2, Δ v+=0) from levels (0, 0) to (9, 0), while Figure 4 shows rate coefficients for pure vibrational excitation (Δ N+=0, Δ v+=1) over the same set of initial levels.

In parallel, we computed DR cross sections under the same conditions as those used for the RVT calculations. Figure 5 presents the results for the two lowest initial levels, (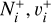Ni+,vi+$N_{i}^{+}, v_{i}^{+}$) = (0, 0) and (1, 0). In the most recent calculations performed by Hvizdoš et al. (2025) and Hörnquist et al. (2024), only the 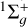1Σg+${ }^{1} \Sigma_{g}^{+}$ symmetry of the neutral was considered, which leads to smaller cross sections than ours. Moreover, Hvizdoš et al. (2025) is using a simplified rotationless model. Our corresponding DR rate coefficients, derived from the full set of 30 levels, are shown in Figure 6 up to an electron temperature of 4000 K, along with the thermally averaged values. The latter incorporates the temperature-dependent population distributions and the ortho–para statistical weights (relevant only for 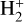H2+$\mathrm{H}_{2}^{+}$). The results were fit using the following expression: 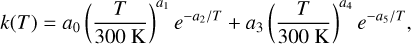k(T)=a0(T300K)a1e-a2/T+a3(T300K)a4e-a5/T,$k(T)=a_{0}\left(\frac{T}{300 \mathrm{~K}}\right)^{a_{1}} e^{-a_{2} / T}+a_{3}\left(\frac{T}{300 \mathrm{~K}}\right)^{a_{4}} e^{-a_{5} / T},$(9) where the coefficients {a0, a5} have the values listed in Table 2. The last column lists the root-mean-square relative deviation between the calculated and fit rates, RMS =n-1∑i[(ki-kfit)/ki]2$= \sqrt{n^{-1} \sum_{i}\left[\left(k_{i}-k^{\text {fit}}\right) / k_{i}\right]^{2}}$. The reported values (0.09-0.27) correspond to typical average deviations of about 9−27% over the full temperature range, indicating that the fits reproduce the numerical data with sufficient accuracy for astrophysical applications.

In the ISM, as in laboratory experiments, electron impact ionization of H2 produces vibrationally excited 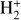H2+$\mathrm{H}_{2}^{+}$ions with a non-Boltzmann distribution of energy levels that can be estimated by applying the Franck-Condon principle. In its most elementary form, this principle assumes that the transition matrix element varies slowly enough with internuclear separation that it can be factored in the calculation of the relative transition strength to various vibrational levels. In ion trap experiments, the vibrational level populations of 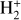H2+$\mathrm{H}_{2}^{+}$formed by electron impact ionization of thermal H2 are in good agreement with the prediction of the Franck-Condon principle (see, e.g., Von Busch & Dunn 1972; Weijun et al. 1993; Abdellahi El Ghazaly et al. 2004). For these reasons, it is expected that 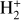H2+$\mathrm{H}_{2}^{+}$ions produced in the ISM by cosmic rays (protons, nuclei and electrons) impacting ambient H2 are formed with a population of excited vibrational states close to the distribution of Franck-Condon factors (Shuter et al. 1986). These vibrationally excited levels have long lifetimes, since dipole transitions within the ground electronic state of 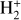H2+$\mathrm{H}_{2}^{+}$are forbidden. Thus, even though non-reactive collisions of 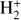H2+$\mathrm{H}_{2}^{+}$with ambient electrons and other species will eventually establish a thermal Boltzmann distribution of level populations, averaging over a Franck-Condon distribution can be appropriate for the low density conditions of the ISM. Fitting parameters corresponding to the Franck-Condon averaged rate coefficients, for initial vibrational levels 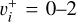vi+=0-2$v_{i}^{+}=0-2$, were obtained using the population weighting factors listed in Weijun et al. (1993).

Figure 7 presents the fit curves for the thermally averaged and Franck-Condon averaged DR rate coefficients of 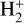H2+$\mathrm{H}_{2}^{+}$(red curves), along with the fits of the thermally averaged DR rate coefficients of HD+(black curves), for initial vibrational levels 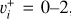vi+=0,1$v_{i}^{+}=0, 1$, and 2, up to an electron temperature of 4000 K.

thumbnail Fig. 1

Left panel: electron-impact rotational excitation (ΔN+=Nf+-Ni+=2$\Delta N^{+}=N_{f}^{+}-N_{i}^{+}=2$) and vibrational de-excitation (Δv+=vf+-vi+=-1$\Delta v^{+}=v_{f}^{+}-v_{i}^{+}=-1$) cross sections of H2+$\mathrm{H}_{2}^{+}$from its ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state and initial ro-vibrational levels (Ni+,vi+)=(0,1)$\left(N_{i}^{+}, v_{i}^{+}\right)=(0, 1)$, black line, and (Ni+,vi+)=(2,1)$\left(N_{i}^{+}, v_{i}^{+}\right)=(2, 1)$, red line. Right panel: same for HD+.
thumbnail Fig. 2

Left panel: electron-impact rotational excitation (ΔN+=Nf+-Ni+=2$\Delta N^{+}=N_{f}^{+}-N_{i}^{+}=2$) and vibrational de-excitation (Δv+=vf+-vi+=-1$\Delta v^{+}=v_{f}^{+}-v_{i}^{+}=-1$) rate coefficients of H2+$\mathrm{H}_{2}^{+}$from its ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state for ten initial ro-vibrational levels ( Ni+,vi+$N_{i}^{+}, v_{i}^{+}$), where vi+=1$v_{i}^{+}=1$), where vi+=1$v_{i}^{+}=1$. Right panel: same for HD+.
thumbnail Fig. 3

Left panel: electron-impact rotational excitation (ΔN+=Nf+-Ni+=2$\Delta N^{+}=N_{f}^{+}-N_{i}^{+}=2$), (Δv+=vf+-vi+=0$\Delta v^{+}=v_{f}^{+}-v_{i}^{+}=0$) rate coefficients of H2+$\mathrm{H}_{2}^{+}$from its ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state and for the first ten initial ro-vibrational levels (Ni+,vi+$N_{i}^{+}, v_{i}^{+}$), where vi+=0$v_{i}^{+}=0$. Right panel: same for HD+.
thumbnail Fig. 4

Left panel: electron-impact vibrational excitation (Δv+=vf+-vi+=1$\Delta v^{+}=v_{f}^{+}-v_{i}^{+}=1$), (ΔN+=Nf+-Ni+=0$\Delta N^{+}=N_{f}^{+}-N_{i}^{+}=0$) rate coefficients of H2+$\mathrm{H}_{2}^{+}$from its ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state and for the first ten initial ro-vibrational levels (Ni+,vi+$N_{i}^{+}, v_{i}^{+}$), where vi+=0$v_{i}^{+}=0$. Right panel: same for HD+.
thumbnail Fig. 5

Left panel: DR cross sections of H2+$\mathrm{H}_{2}^{+}$from its ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state, and the two lowest initial ro-vibrational levels: (Ni+,vi+)=(0,0)$\left(N_{i}^{+}, v_{i}^{+}\right)=(0, 0)$, black line, and (Ni+,vi+)=(1,0)$\left(N_{i}^{+}, v_{i}^{+}\right)=(1, 0)$, red line. Cross sections by Hvizdoš et al. (2025): vi+=0$v_{i}^{+}=0$, orange line, and Hörnquist et al. (2024): (Ni+,vi+)=(0,0)$\left(N_{i}^{+}, v_{i}^{+}\right)=(0, 0)$, magenta line. Right panel: same for HD+.
thumbnail Fig. 6

Left panel: thermal rate coefficient for the DR of H2+$\mathrm{H}_{2}^{+}$summed over all five relevant molecular symmetries of the neutral up to an electron temperature of T=4000 K. The colored thin lines show the rate coefficient for the first 30 ro-vibrational levels (Ni+,vi+$N_{i}^{+}, v_{i}^{+}$) listed in the legend, while the thick black line shows the thermally averaged rate coefficient by considering the temperature-dependent level population distributions and the ortho-para statistical weights. Right panel: same for HD+without ortho-para weights.
Table 2

Fitting parameters for DR rate coefficients of 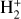H2+$\mathrm{H}_{2}^{+}$and HD+.

thumbnail Fig. 7

Thermally averaged and Franck-Condon averaged rate coefficients for DR of H2+$\mathrm{H}_{2}^{+}$(red lines) and HD+ (black lines) for every rotational level Ni+$N_{i}^{+}$, with vi+=0-2$v_{i}^{+}=0-2$ using the fitting parameters given in Table 2. Electron temperature is between 10 and 4000 K.

4 Astrophysical applications

Figure 8 shows a comparison of the thermal rate coefficients of 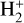H2+$\mathrm{H}_{2}^{+}$and HD+adopted in models of the chemistry of primordial gas, compared to our results. The calculations presented in this paper (black curves) resolve considerable discrepancies in previous evaluations of the DR rate of 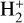H2+$\mathrm{H}_{2}^{+}$and HD+, and extend the results to temperatures below ∼ 100 K, where all available estimates of the DR rate significantly underestimate its importance.

In the early Universe, DR of 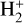H2+$\mathrm{H}_{2}^{+}$and HD+competes with photodissociation (at z ≳ 300) and charge exchange with H (at z ≲ 300) in the destruction of these species. At low redshifts (z ≲ 100) the significant increase in DR at low temperatures evidenced in the current work implies a larger effect of DR with respect to previous results obtained with the DR rate by Schneider et al. (1994): at z ≈ 10−20, the contribution of DR of 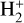H2+$\mathrm{H}_{2}^{+}$and HD+increases from ∼ 2% to ∼ 12% and from ∼ 1% to ∼ 5% of the total destruction rate, respectively. However, because of the low electron fraction, the destruction of both cations at low redshift remains dominated by charge-exchange reactions with the more abundant H atoms.

As was mentioned in the Introduction, 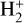H2+$\mathrm{H}_{2}^{+}$ions produced by cosmic-ray ionization in dense molecular clouds shielded from UV radiation are rapidly converted into 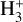H3+$\mathrm{H}_{3}^{+}$ions by charge transfer reactions with ambient H2. Given the importance of 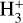H3+$\mathrm{H}_{3}^{+}$as a cornerstone of interstellar chemistry, one may wonder to what extent the DR of 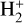H2+$\mathrm{H}_{2}^{+}$can affect the abundance of 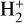H3+$\mathrm{H}_{3}^{+}$. In pre-dominantly neutral clouds, DR is generally less important than charge transfer reactions of 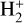H2+$\mathrm{H}_{2}^{+}$with atomic or molecular hydrogen, which are quite fast. Therefore, it is not expected that the equilibrium abundance of 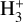H3+$\mathrm{H}_{3}^{+}$in molecular clouds depends on DR of 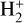H2+$\mathrm{H}_{2}^{+}$. However, in low-density, highly ionized nebular gas, such as planetary nebulae, planetary ionospheres, and supernova remnants, where 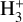H3+$\mathrm{H}_{3}^{+}$has been detected or predicted to be present (see, e.g., Tennyson & Miller 2019), the abundance of 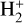H2+$\mathrm{H}_{2}^{+}$(and, as a consequence, that of 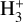H3+$\mathrm{H}_{3}^{+}$) is entirely controlled by DR.

Another process competing with DR in the destruction of 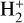H2+$\mathrm{H}_{2}^{+}$ ions is photodissociation. In the early Universe, at high redshift, the intense cosmic radiation background is by far the dominant destruction process for all molecular ions, and DR of 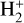H2+$\mathrm{H}_{2}^{+}$plays no role. This is not the case when the radiation field is produced by a point source, as in the case of planetary nebulae (Black 1978) and Hii regions (Aleman & Gruenwald 2004), due to the geometric dilution of radiation with distance from the source. In addition, DR in nebulae is also favored by the high abundance of free electrons. In this situation, the abundance of 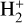H2+$\mathrm{H}_{2}^{+}$is basically controlled by the balance of formation by radiative association of H and H+(with rate kra) and destruction by DR (with rate kdr), and it is given by 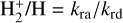H2+/H=k ra /k rd $\mathrm{H}_{2}^{+} / \mathrm{H}=k_{\mathrm{ra}} / k_{\mathrm{rd}}$ (see, e.g., Cecchi Pestellini & Dalgarno 1993).

Shock waves could also lead to high 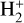H2+$\mathrm{H}_{2}^{+}$and electron abundances. For this reason, accurate and state-to-state resolved DR reaction rates are needed (Shapiro & Kang 1987; Takagi 2002; Shchekinov & Vasiliev 2006; Coppola et al. 2016). The updated DR reaction rates in the chemical evolution of shock waves through gas at high redshift, lead to changes in the fractional abundances of 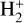H2+$\mathrm{H}_{2}^{+}$and HD+.

Figure 9 shows the results of simulations of shocks propagating with velocity vs=20 km s−1, compatible with typical supernova explosions, in a gas of primordial composition at redshift z = 10, 20, and 30 (see Coppola et al. 2016, for a description of the shock model). For T > 4000 K, beyond the range of validity of Eq. (10), we adopted a constant value equal to the rate at T=4000 K. Since the DR rate decreases with T above a few × 103 K, this choice may overestimate the true rate and thus provides a conservative lower bound on the abundances. In this context, the results demonstrate that, as is discussed in Section 4, when the ionization fraction is significant (as in shocks, ∼ 10−2−10−1 in these models), DR becomes an important channel for the destruction of 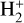H2+$\mathrm{H}_{2}^{+}$and HD+, competing with the fast charge exchange reactions that usually dominate in a nearly neutral medium. For example, in the high temperature range relevant for a high-speed shock, the DR rate of 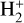H2+$\mathrm{H}_{2}^{+}$computed in this paper is a factor of ∼ 8−10 lower than the DR rate coefficient adopted by Coppola et al. (2016) on the basis of the cross sections calculated by Takagi (2002). Consequently, the abundance of 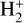H2+$\mathrm{H}_{2}^{+}$is a factor of ∼ 2−3 higher than that obtained by Coppola et al. (2016). On the other hand, at temperatures of a few ∼ 103 K the newly calculated DR rate of HD+is a factor of ∼ 2−3 higher than the value previously adopted, and consequently the abundance of HD+is slightly reduced.

thumbnail Fig. 8

Comparison of thermal rate coefficients for the DR of H2+$\mathrm{H}_{2}^{+}$and HD+. Left panel: DR of H2+$\mathrm{H}_{2}^{+}$. dashed blue and dashed red lines: fits by Galli & Palla (1998) and Stancil et al. (1998), respectively, of the thermal rate coefficient computed by Schneider et al. (1994) (triangles); dash-dotted green line: fit of the rate computed by Coppola et al. (2011) from the cross sections by Takagi (2002); solid black line: thermal rate, this work; dashed black line: Frank-Condon averaged rate, this work. Right panel: same for HD+. dashed blue and dashed red lines: extrapolations by Galli & Palla (1998) and Stancil et al. (1998), respectively, of the thermal rate coefficient computed from the experimental cross section by Strömholm et al. (1995) (dots).
thumbnail Fig. 9

Fractional abundances of H2+$\mathrm{H}_{2}^{+}$(left panel) and HD+(right panel) for a shock wave propagating through a gas of primordial composition at redshift z=10, 20, and 30 and at a speed vs=20 km s−1. The dotted curves show the fractional abundances obtained adopting the DR reaction rates of Coppola et al. (2011) and Galli & Palla (1998), respectively.

5 Conclusions

We computed cross sections and thermally averaged rate coefficients summed for all five relevant molecular symmetries of the neutral from T=1 K up to T=4000 K electron temperatures considering temperature-dependent level population distributions. These new cross sections and rate coefficients can be adopted to model the kinetics of hydrogen-rich media in which the ionization fraction is significant. A primary field of application is planetary atmospheres and astrophysical plasmas in general, either in conditions typical of the early Universe (absence of metals and dust grains) or in the present-day partially ionized interstellar medium (as, for example, in planetary nebulae and HII regions). In all these environments, electronimpact induced RVT are the dominant excitation process of 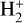H2+$\mathrm{H}_{2}^{+}$ and HD+, and DR is one of their main destruction channels. Our main findings are summarized as follows:

  1. With the new cross sections, significant differences with previously adopted thermal rate coefficients of DR are found (see Sect. 4 and Fig. 9);

  2. The new rates produce substantial differences with respect to earlier results when introduced in astrochemical models, for example in models for the shock-induced chemistry of hydrogen and deuterium in a zero-metal gas (see Fig. 8).

Data availability

The data supporting the findings of this study are available on Zenodo at https://doi.org/10.5281/zenodo.17344099.

Acknowledgements

The authors acknowledge support from the Agence nationale de la recherche (ANR) via the project MONA; the Centre national de la recherche scientifique (CNRS) via the GdR TheMS; the PCMI program of INSU (ColEM project, co-funded by CEA and CNES); the PHC Galilée programme between France and Italy; the DYMCOM project; the Fédération de Recherche “Fusion par Confinement Magnétique” (CNRS, CEA, and EUROfusion); Région Normandie, the European Regional Development Fund (FEDER), and LabEx EMC3 via the projects Bioengine, EMoPlaF, CO2-VIRIDIS, and PTOLEMEE; COMUE Normandie Université; the Institute for Energy, Propulsion and Environment (FR-IEPE); the International Atomic Energy Agency (IAEA) via the Coordinated Research Project “The Formation and Properties of Molecules in Edge Plasmas”; and the European Union via COST (European Cooperation in Science and Technology) Actions TUMIEE (CA17126), MW-GAIA (CA18104), MD-GAS (CA18212), COSY (CA21101), PLANET (CA22133), PROBONO (CA21128), PhoBioS (CA21159), DAEMON (CA22154), and DYNALIFE (CA21169). ERASMUS+ agreements between Université Le Havre Normandie and Politehnica University Timișoara, West University of Timișoara, and University College London are also gratefully acknowledged. IFS and MA acknowledge support from the French PEPR SPLEEN consortium via the project PLASMA-N-ACT. NP and IFS are grateful for support from the Romanian Ministry of Research and Innovation, project no. 10PFE/16.10.2018 (PERFORM-TECH-UPT) and “Mobility for the experienced researchers from diaspora” (MCD). JZsM thanks the National Research, Development and Innovation Fund of Hungary for support under the FK-19 and Advanced-24 funding schemes (project nos. FK-132989 and 151196), and acknowledges support from the Program Hubert Curien “BALATON” (Campus France grant no. 49848TC) and NKFIH TÉT-FR 2023-2024 (2021-1.2.4-TÉT-2022-00069). JZsM is also grateful for the France Excellence Hongrie fellowship. DG acknowledges support from INAF grant PACIFISM. MA acknowledges support from French state aid under France 2030 (QuanTEdu-France; ANR-22-CMAS-0001). We thank A. Larson and D. Hvizdos for having provided some of their results for comparison with ours.

References

  1. Abdellahi El Ghazaly, M. O., Jureta, J., Urbain, X., & Defrance, P., 2004, J. Phys. B, 37, 2467 [Google Scholar]
  2. Agundez, M., Goicochea, J. R., Cernicharo, J., Faure A., & Roueff E., 2010, ApJ, 713, 662 [CrossRef] [Google Scholar]
  3. Aleman, I., & Gruenwald, R., 2004, ApJ, 607, 865 [Google Scholar]
  4. Black, J. H., 1978, ApJ, 222, 125 [NASA ADS] [CrossRef] [Google Scholar]
  5. Black, J. H., & Van Dishoeck, E. F., 1987, ApJ, 322, 412 [Google Scholar]
  6. Cecchi, Pestellini C., & Dalgarno, A., 1993, ApJ, 413, 611 [Google Scholar]
  7. Chadney, J. M., Galand, M., Koskinen, T. T., et al. 2016, A&A, 687, A87 [Google Scholar]
  8. Chakrabarti, K., Backodissa-Kiminou, D. R., Pop, N., et al. 2013, Phys. Rev. A, 87, 022702 [Google Scholar]
  9. Coppola, C. M., Longo, S., Capitelli, M., Palla, F., & Galli, D., 2011, ApJS, 193, 7 [Google Scholar]
  10. Coppola, C. M., Mizzi, G., Bruno, D., et al. 2016, MNRAS, 457, 3732 [Google Scholar]
  11. Djuissi, E., Bogdan, R., Abdoulanziz, A., et al. 2020, Rom. Astron. J., 30, 101 [Google Scholar]
  12. Epée Epée, M. D., Mezei, J. Zs, Motapon, O., Pop, N., & Schneider, I. F. 2016, MNRAS, 455, 276 [Google Scholar]
  13. Epée Epée, M. D., Motapon, O., Pop, N., et al. 2022, MNRAS, 512, 424 [Google Scholar]
  14. Friedl, R., Rauner, D., Heiler, A., & Fantz, U., 2020, PSST, 29, 015014 [Google Scholar]
  15. Galli, D., & Palla, F., 1998, A&A, 335, 403 [NASA ADS] [Google Scholar]
  16. Galli, D., & Palla, F., 2013, ARA&A, 51, 163 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gay, C. D., Abel, N. P., Porter, R. L., et al. 2012, ApJ, 746, 78 [Google Scholar]
  18. Gibbs, A., & Fitzgerald, M. P., 2022, ApJ, 164, 63 [Google Scholar]
  19. Glassgold, A. E., & Langer, W. D., 1973, ApJ, 186, 859 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hörnquist, J., Orel, A. E., & Larson, A., 2024, Phys. Rev. A, 109, 052806 [Google Scholar]
  21. Hvizdoš, D., Čurík, R., & Greene, C. H., 2025, Phys. Rev. A, 111, 012805 [Google Scholar]
  22. Kashinski, D. O., Talbi, D., Hickman, A. P., et al. 2017, J. Chem. Phys., 146, 204109 [Google Scholar]
  23. Krasheninnikov, S. I., Pigarov, A. Y., Soboleva, T. K., & Sigmar, D. J., 1997, J. Nucl. Mater., 241, 283 [Google Scholar]
  24. Le Petit, F., Roueff, E., & Le Bourlot, J., 2002, A&A, 390, 369 [CrossRef] [EDP Sciences] [Google Scholar]
  25. Lepp, S., Stancil, P. C., & Dalgarno, A., 2002, J. Phys. B, R57, 35 [Google Scholar]
  26. Mezei, J. Zs., Epée Epée, M. D., Motapon, O., & Schneider, I. F. 2019, Atoms, 7, 82 [Google Scholar]
  27. Motapon, O., Pop, N., Argoubi, F., et al. 2014, Phys. Rev. A, 90, 012706 [Google Scholar]
  28. Ngassam, V., Florescu, A., Pichl, L., et al. 2003, Eur. Phys. J. D, 26, 165 [Google Scholar]
  29. Niyonzima, S., Ilie, S., Pop, N., et al. 2017, At. Data Nucl. Data Tables, 115, 287 [Google Scholar]
  30. Niyonzima, S., Pop, N., Iacob, F., et al. 2018, PSST, 27, 025015 [Google Scholar]
  31. Parigger, C. G., Drake, K. A., Helstern, C. M., & Gautam, G., 2018, Atoms, 6, 36 [Google Scholar]
  32. Pineda, J. S., Hallinan, G., Desert, J. M., & Harding, L. K., 2024, ApJ, 966, 58 [Google Scholar]
  33. Pop, N., Iacob, F., Niyonzima, S., et al. 2021, At. Data Nucl. Data Tables, 139, 101414 [Google Scholar]
  34. Schneider, I. F., Dulieu, O., Giusti-Suzor, A., & Roueff, E., 1994, ApJ, 424, 983 [NASA ADS] [CrossRef] [Google Scholar]
  35. Seaton, M. J., 1983, Rep. Prog. Phys. 46, 167 [Google Scholar]
  36. Shafir, D., Novotny, S., Buhr, H., et al. 2009, Phys. Rev. Lett., 102, 223202 [Google Scholar]
  37. Shchekinov, Y. A., & Vasiliev, E. O., 2006, MNRAS, 368, 454 [Google Scholar]
  38. Shapiro, P. R., & Kang, H., 1987, ApJ, 318, 32 [Google Scholar]
  39. Shemansky, D. E., 1985, J. Geophys. Res. Space Phys., 90, 2673 [Google Scholar]
  40. Shuter, W. L. H., Williams, D. R. W., Kulkarni, S. R., & Heiles, C., 1986, ApJ, 306, 255 [Google Scholar]
  41. Stancil, P. C., Lepp, S., & Dalgarno, A., 1998, ApJ, 509, 1 [Google Scholar]
  42. Stotler, D., & Karney, C., 1994, Contrib. Plasma Phys., 34, 392 [Google Scholar]
  43. Strömholm, C., Schneider, I. F., Sundström, G., et al. 1995, Phys. Rev. A, 52, R320 [Google Scholar]
  44. Takagi, H., 2002, Phys. Scr., T96, 52 [Google Scholar]
  45. Tanaka, S., Xiao, B., Kazuki, K., & Morira, M., 2000, Plasma. Phys. Contr. F., 42, 1091 [Google Scholar]
  46. Tennyson, J., & Miller, S., 2019, Phil. Trans. Roy. Soc. London Ser. A, 377, 2154 [Google Scholar]
  47. Tielens, A. G. G. M., 2013, Rev. Mod. Phys., 85, 1021 [NASA ADS] [CrossRef] [Google Scholar]
  48. von Busch, F., & Dunn, G. H., 1972, Phys. Rev. A, 5, 1726 [Google Scholar]
  49. Waffeu Tamo, F. O., Buhr, H., Motapon, O., et al. 2011, Phys. Rev. A, 84, 022710 [Google Scholar]
  50. Weijun, Y., Alheit, R., & Werth, G., 1993, Z. Phys., 28, 87 [Google Scholar]
  51. Wünderlich, D., Dietrich, S., & Fantz, U., 2009, J. Quant. Spectrosc. Radiat. Transf., 110, 62 [Google Scholar]

All Tables

Table 1

First 30 ro-vibrational levels of H2+$\mathrm{H}_{2}^{+}$and HD+.

In the text
Table 2

Fitting parameters for DR rate coefficients of H2+$\mathrm{H}_{2}^{+}$and HD+.

In the text

All Figures

thumbnail Fig. 1

Left panel: electron-impact rotational excitation (ΔN+=Nf+-Ni+=2$\Delta N^{+}=N_{f}^{+}-N_{i}^{+}=2$) and vibrational de-excitation (Δv+=vf+-vi+=-1$\Delta v^{+}=v_{f}^{+}-v_{i}^{+}=-1$) cross sections of H2+$\mathrm{H}_{2}^{+}$from its ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state and initial ro-vibrational levels (Ni+,vi+)=(0,1)$\left(N_{i}^{+}, v_{i}^{+}\right)=(0, 1)$, black line, and (Ni+,vi+)=(2,1)$\left(N_{i}^{+}, v_{i}^{+}\right)=(2, 1)$, red line. Right panel: same for HD+.
In the text
thumbnail Fig. 2

Left panel: electron-impact rotational excitation (ΔN+=Nf+-Ni+=2$\Delta N^{+}=N_{f}^{+}-N_{i}^{+}=2$) and vibrational de-excitation (Δv+=vf+-vi+=-1$\Delta v^{+}=v_{f}^{+}-v_{i}^{+}=-1$) rate coefficients of H2+$\mathrm{H}_{2}^{+}$from its ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state for ten initial ro-vibrational levels ( Ni+,vi+$N_{i}^{+}, v_{i}^{+}$), where vi+=1$v_{i}^{+}=1$), where vi+=1$v_{i}^{+}=1$. Right panel: same for HD+.
In the text
thumbnail Fig. 3

Left panel: electron-impact rotational excitation (ΔN+=Nf+-Ni+=2$\Delta N^{+}=N_{f}^{+}-N_{i}^{+}=2$), (Δv+=vf+-vi+=0$\Delta v^{+}=v_{f}^{+}-v_{i}^{+}=0$) rate coefficients of H2+$\mathrm{H}_{2}^{+}$from its ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state and for the first ten initial ro-vibrational levels (Ni+,vi+$N_{i}^{+}, v_{i}^{+}$), where vi+=0$v_{i}^{+}=0$. Right panel: same for HD+.
In the text
thumbnail Fig. 4

Left panel: electron-impact vibrational excitation (Δv+=vf+-vi+=1$\Delta v^{+}=v_{f}^{+}-v_{i}^{+}=1$), (ΔN+=Nf+-Ni+=0$\Delta N^{+}=N_{f}^{+}-N_{i}^{+}=0$) rate coefficients of H2+$\mathrm{H}_{2}^{+}$from its ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state and for the first ten initial ro-vibrational levels (Ni+,vi+$N_{i}^{+}, v_{i}^{+}$), where vi+=0$v_{i}^{+}=0$. Right panel: same for HD+.
In the text
thumbnail Fig. 5

Left panel: DR cross sections of H2+$\mathrm{H}_{2}^{+}$from its ground 2Σg+${ }^{2} \Sigma_{g}^{+}$ electronic state, and the two lowest initial ro-vibrational levels: (Ni+,vi+)=(0,0)$\left(N_{i}^{+}, v_{i}^{+}\right)=(0, 0)$, black line, and (Ni+,vi+)=(1,0)$\left(N_{i}^{+}, v_{i}^{+}\right)=(1, 0)$, red line. Cross sections by Hvizdoš et al. (2025): vi+=0$v_{i}^{+}=0$, orange line, and Hörnquist et al. (2024): (Ni+,vi+)=(0,0)$\left(N_{i}^{+}, v_{i}^{+}\right)=(0, 0)$, magenta line. Right panel: same for HD+.
In the text
thumbnail Fig. 6

Left panel: thermal rate coefficient for the DR of H2+$\mathrm{H}_{2}^{+}$summed over all five relevant molecular symmetries of the neutral up to an electron temperature of T=4000 K. The colored thin lines show the rate coefficient for the first 30 ro-vibrational levels (Ni+,vi+$N_{i}^{+}, v_{i}^{+}$) listed in the legend, while the thick black line shows the thermally averaged rate coefficient by considering the temperature-dependent level population distributions and the ortho-para statistical weights. Right panel: same for HD+without ortho-para weights.
In the text
thumbnail Fig. 7

Thermally averaged and Franck-Condon averaged rate coefficients for DR of H2+$\mathrm{H}_{2}^{+}$(red lines) and HD+ (black lines) for every rotational level Ni+$N_{i}^{+}$, with vi+=0-2$v_{i}^{+}=0-2$ using the fitting parameters given in Table 2. Electron temperature is between 10 and 4000 K.
In the text
thumbnail Fig. 8

Comparison of thermal rate coefficients for the DR of H2+$\mathrm{H}_{2}^{+}$and HD+. Left panel: DR of H2+$\mathrm{H}_{2}^{+}$. dashed blue and dashed red lines: fits by Galli & Palla (1998) and Stancil et al. (1998), respectively, of the thermal rate coefficient computed by Schneider et al. (1994) (triangles); dash-dotted green line: fit of the rate computed by Coppola et al. (2011) from the cross sections by Takagi (2002); solid black line: thermal rate, this work; dashed black line: Frank-Condon averaged rate, this work. Right panel: same for HD+. dashed blue and dashed red lines: extrapolations by Galli & Palla (1998) and Stancil et al. (1998), respectively, of the thermal rate coefficient computed from the experimental cross section by Strömholm et al. (1995) (dots).
In the text
thumbnail Fig. 9

Fractional abundances of H2+$\mathrm{H}_{2}^{+}$(left panel) and HD+(right panel) for a shock wave propagating through a gas of primordial composition at redshift z=10, 20, and 30 and at a speed vs=20 km s−1. The dotted curves show the fractional abundances obtained adopting the DR reaction rates of Coppola et al. (2011) and Galli & Palla (1998), respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.