| Issue |
A&A
Volume 704, December 2025
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 6 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202557288 | |
| Published online | 05 December 2025 | |
Charge transfer in C + O+ collisions and its impact on supernova spectra
1
Theoretical Astrophysics, Department of Physics and Astronomy, Uppsala University,
Box 516,
751 20
Uppsala,
Sweden
2
The Oskar Klein Centre, Department of Astronomy, Stockholm University, AlbaNova,
10691
Stockholm,
Sweden
★ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
17
September
2025
Accepted:
17
October
2025
The charge-transfer process C + O+ → C+ + O (1D) has been found in previous modelling to be important in neutralising oxygen ions in supernova (SN) ejecta, as well as in determining the strength of the [O I] doublet at 6300 and 6364 Å. This conclusion is, however, based on a highly uncertain simple estimate of the rate coefficient. In this work, calculations of the cross-sections at low energy (0–10 eV) are performed using quantum mechanical methods. The rate coefficients at temperatures up to 10 000 K are determined and found to be significantly lower than the simple estimate. Using spectral modelling of SN ejecta, we show that the new rates change model predictions for [O I] λλ6300, 6364 and [C I] λλ9824, 9850 by ~10% in the early, warm nebular phases, and by yet larger factors in the late, cold phases, with direct impact on inferences of carbon and oxygen masses.
Key words: atomic data / atomic processes / supernovae: general
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1 Introduction
Carbon and oxygen are the most abundant elements in the Universe after hydrogen and helium, and both have been identified in the spectra of supernovae (SNe), including the nearby supernova 1987A (SN 1987A; e.g. Jerkstrand et al. 2011). In SN ejecta, C and O are expected, based on stellar evolution models, to be found together in regions that are poor in H and He. For example, the 19 M⊙ explosion model from Woosley & Heger (2007), predicts regions dominated by O, Ne, Mg, and C.
The importance of charge-transfer, where one or more electrons is transferred between atoms, in supernovae has long been known (e.g. Meyerott 1978). SN 1987A has made it possible to study the ejecta of this supernova in great detail, even at very late times, and modelling has also shown the importance of chargetransfer processes (see Jerkstrand et al. 2011, and Fig. 2 therein). In particular, the process
![$\[\mathrm{C}+\mathrm{O}^{+} \rightleftharpoons \mathrm{C}^{+}+\mathrm{O}\left({ }^1 \mathrm{D}\right)+0.39 ~\mathrm{eV}\]$](/articles/aa/full_html/2025/12/aa57288-25/aa57288-25-eq1.png) (1)
(1)
was identified as being the dominant reaction for neutralising oxygen ions. Further, it should be noted that the process produces neutral oxygen atoms in the excited 1D state, which produces the observed [O I] doublet at 6300 and 6364 Å. However, these models are dependent on uncertain rates for charge-transfer processes. This process is included via a ‘simple rule for guessing the rate coefficients’ from Péquignot & Aldrovandi (1986), based on the classical Langevin orbiting model and some experimental results.
Charge transfer involving a singly charged positive ion and a neutral atom at low energy represents a particular challenge, as in general there is no easily identifiable single dominant mechanism, and thus there is presently no reliable way to make simple theoretical estimates (Stancil 2001). Setting aside the well-studied case of resonant charge-transfer in H+H+, there are only a small number of specific cases involving heavier targets where data are available from fully quantum-mechanical calculations; i.e. molecular structure and quantum scattering: O++H (Stancil et al. 1999; Chambaud et al. 1980), Cl+H+ (Pradhan & Dalgarno 1994), C+H+ (Stancil et al. 1998), and S+C+ (Chenel et al. 2010). All but the last involve hydrogen, and thus there is a particular scarcity of data for ion-atom charge-transfer between heavier atoms. Yet, these are the crucial reactions for the nucleosynthesis layers in supernovae, which lack both H and He. The main bottleneck here is the ab initio calculation of required potential energy curves (PECs) and couplings for the relevant states of the molecular ion system.
Potential energy curves of the molecular system CO+ were reported by Krupenie & Weissman (1965) and Singh & Rai (1966) using a version of the semi-empirical Rydberg–Klein–Rees method, but it only provides PECs for bound molecular states and those in the region of the potential well. Honjou & Sasaki (1979) performed ab initio PEC calculations of 25 lowlying states. Okada & Iwata (2000) later performed calculations for PECs, dipole moment functions, and transition moments, and Shi et al. (2011) performed a study of PECs and spectroscopic and molecular properties for nine low-lying electronic states. A study of 21 low-lying electronic states by Xing et al. (2018) includes PECs, spectroscopic parameters, transition dipoles, and transition probabilities.
None of these studies is sufficient for the calculation of the charge-transfer process of Eq. (1), as in all cases they do not provide the required couplings needed for collision-dynamics calculations. In addition, some of the studies do not cover all required molecular states, or they have a too limited internucleardistance range. In this paper, we describe calculation of the cross-sections and rates for process (1). In Sect. 2, we describe the theory used and present the calculations, specifically the molecular structure and collision dynamics. In Sect. 3, the results are presented and discussed. In Sect. 4, we present a first astrophysical application in modelling the spectrum of a SN ejecta.
Low-lying ground and excited electronic states of CO+ resulting from the combination of asymptotic atomic states.
2 Theory and calculations
The astrophysical environments of interest have temperatures of the order of a few thousand Kelvin, and thus we are particularly interested in centre-of-mass energies of the order of 0.1 to 1 eV. To reliably calculate the cross-sections for process (1) at low energy requires a fully quantum-mechanical theoretical description (e.g. Bransden & McDowell 1992; Stancil 2001). This means molecular electronic structure calculations based on molecular orbital methods, providing PECs and relevant couplings as input for collision dynamics based on the solution of the coupled-channel equations describing quantum scattering. We performed detailed quantum-chemistry calculations including PECs of 32 low-lying electronic states for the molecular ion CO+ covering all relevant channels for the charge-transfer process, and all neighbouring channels, from small to large internuclear distance. The states covered are listed in Table 1, which includes 19 doublet, 11 quartet, and 2 sextet spin states, dissociating into five different sets of asymptotic atomic states. From the calculated PECs, we identified the expected mechanisms and channels involved in the charge-transfer process, and relevant radial and rotational couplings calculated. These molecular-structure calculations are described in Sect. 2.1. The collision dynamics calculations are described in Sect. 2.2.
2.1 Molecular structure
The ab initio MOLPRO quantum-chemistry suite of programs (Werner et al. 2022) was used for the molecular-structure computations. The calculations were performed within the multi-reference configuration interaction (MRCI) level of theory using Dunning’s correlation-consistent basis sets aug-cc-pVQZ (Dunning Jr 1989) in C2v in doublet spin symmetry. Calculations were carried out using a complete active-space self-consistent field (CASSCF; Werner & Meyer 1981; Werner & Knowles 1985) as a reference space followed by MRCI. For the molecular system CO+, 13 electrons were distributed as four core electrons and nine valence electrons. We computed first-order radial couplings ![$\[\left\langle\psi_{j}\right| \frac{\partial}{\partial R}\left|\psi_{i}\right\rangle\]$](/articles/aa/full_html/2025/12/aa57288-25/aa57288-25-eq2.png) , where R is the internuclear distance and |ψ⟩ are adiabatic wave functions, using the finite-difference method with ΔR = 0.0002 a.u., which was sufficient to yield numerical convergence. Phases were determined by employing a biorthogonalisation procedure. Non-adiabatic rotational coupling matrix elements, ⟨ψj|L±|ψi⟩, were also computed. The adiabatic potentials and couplings are available (see the data availability statement).
, where R is the internuclear distance and |ψ⟩ are adiabatic wave functions, using the finite-difference method with ΔR = 0.0002 a.u., which was sufficient to yield numerical convergence. Phases were determined by employing a biorthogonalisation procedure. Non-adiabatic rotational coupling matrix elements, ⟨ψj|L±|ψi⟩, were also computed. The adiabatic potentials and couplings are available (see the data availability statement).
The PECs of all doublet electronic states are shown in Fig. 1a, and all quartet and sextet electronic states in Fig. 1b. For non-adiabatic processes to be efficient and the cross-section significant, it is necessary for potentials to approach each other at a reasonably large internuclear distance. A detailed examination of these potentials and consideration of the selection rules for transitions between electronic states (e.g. Nikitin & Umanskii 1984, Sect. 3.4) reveal two avoided crossings between states corresponding to the initial and final channels of interest that are expected to be important. The first is between 3 2Σ+ and 4 2Σ+ at around 3.8 a.u., and the second is between 5 and 6 2Π, at around 3.5 a.u. Such avoided crossings between states of the same symmetry imply a radial coupling mechanism.
We note that no avoided crossings are seen between the initial channels and the low-lying manifold of electronic states corresponding asymptotically to C+ (2P0) + O (3P), 2.36 eV below the initial channels. Real crossings between the repulsive states arising from the low-lying manifold occur, but such a transition must proceed via spin-orbit coupling, and we estimate these mechanisms to be less important than the radial coupling discussed above (see also Stancil 2001). Thus, we expect chargetransfer into these channels to be negligible. Though there are crossings with states dissociating to higher lying asymptotic states, these are endoergic with 1.26 and 1.83 eV, and they will not have significant rates at the temperatures and corresponding collision energies of interest. Also, the first of these reactions would lead to excitation of C, not charge-transfer.
Thus, we focused on the 4–3 2Σ+and 6–5 2Π states, the adiabatic PECs for which are shown in Figs. 2a and 2b (solid lines), respectively. The radial couplings ![$\[\tau_{43}=\left\langle 4^{2} \Sigma^{+}\right| \frac{\partial}{\partial R}\left|3^{2} \Sigma^{+}\right\rangle\]$](/articles/aa/full_html/2025/12/aa57288-25/aa57288-25-eq4.png) and
and ![$\[\tau_{65}=\left\langle 6^{2} \Pi\right| \frac{\partial}{\partial R}\left|5^{2} \Pi\right\rangle\]$](/articles/aa/full_html/2025/12/aa57288-25/aa57288-25-eq5.png) are shown in Fig. 2c. For τ43, peaks are seen at around 2.8 and 4.0 a.u., the latter corresponding to the outer avoided crossing. For τ65, multiple peaks of high magnitude in the range of R = 2.0–4.0 a.u. are seen, the outermost again corresponding to the outer avoided crossing. These radial couplings are expected to provide the dominant mechanisms for the charge-transfer process of interest. Rotational couplings between the 2Σ+ and 2Π states could potentially mix these processes and were also calculated.
are shown in Fig. 2c. For τ43, peaks are seen at around 2.8 and 4.0 a.u., the latter corresponding to the outer avoided crossing. For τ65, multiple peaks of high magnitude in the range of R = 2.0–4.0 a.u. are seen, the outermost again corresponding to the outer avoided crossing. These radial couplings are expected to provide the dominant mechanisms for the charge-transfer process of interest. Rotational couplings between the 2Σ+ and 2Π states could potentially mix these processes and were also calculated.
 |
Fig. 1 Adiabatic PECs of doublet (panel a; 1–5 2Σ+: red line, 1–7 2Π: blue line, 1 2Φ: violet line, 1–3 2Δ: black line, 1–3 2Σ−: green line), quartet (panel b; 1–2 4Σ+: red line, 1–4 4Π: blue line, 1–2 4Δ: black line, 1–3 4Σ−: green line), and sextet (1 6Σ+: brown line, 1 6Π: violet line) spin states of CO+ molecular ion as a function of internuclear distance R. All are given in atomic units (a.u.). |
 |
Fig. 2 Adiabatic (solid lines) and diabatic (dash-dotted lines) PECs of 3 and 4 2Σ+ (panel a) and 5 and 6 2Π (panel b), of the CO+ molecular ion as a function of internuclear distance R. Panel c: non-adiabatic radial coupling matrix elements |
2.2 Dynamics
To describe the collision dynamics and calculate cross-sections, we used scattering theory in the diabatic representation following that conveniently summarised in Chapter 4 of Bransden & McDowell (1992). In practice, this is achieved using a significantly developed version of the QUANTXS code (Allan 1999) written in FORTRAN, employing the improved log-derivative method (Johnson 1973; Manolopoulos 1986), for a solution to the coupled channel equations. Appropriate asymptotic nuclear wave functions for open channels are Ricatti–Bessel functions, and they were calculated with codes from Barnett (1982, 1996).
Since adiabatic radial couplings vary rapidly with internuclear distance, as seen in Fig. 2c, it is often numerically preferable to perform the collision dynamics calculations in a diabatic representation so that couplings vary more smoothly. Specifically, we transformed them on a basis where the radial coupling is zero at all internuclear distances (Smith et al. 1969; Heil et al. 1981); see also Bransden & McDowell (1992), Sect. 4.4. The diabatic PECs were computed for the 4–3 2Σ+and 6–5 2Π states. The diabatic PECs, the diagonal matrix elements of the electronic Hamiltonian, corresponding to the 4–3 2Σ+and 6–5 2Π states are shown in Figs. 2a and 2b (dash-dotted lines), respectively. The PECs in this representation show real crossings rather than avoided ones, and the coupling between states is captured through non-zero off-diagonal matrix elements of the electronic Hamiltonian. We note that the rotational-coupling matrix elements must also be transformed from the adiabatic to the diabatic representation.
To cover the temperature range of interest, we performed cross-section calculations for centre-of-mass energies ranging from 0 to 10 eV, with a step of 0.01. The coupled channel equations are integrated from 0.1 to 10 a.u. using a radial step depending on relevant de Broglie wavelengths, and thus on collision energy, ensuring at least 20 radial points per wavelength in all channels. The radial step is always of the order of 10−3 a.u. across our considered energy range. Partial waves up to J = 5000 were calculated. In all cases, we verified that the results were converged to better than 0.1%, well below the expected physical accuracy of the results, with increased integration limits, finer radial step sizes, or the inclusion of more partial waves.
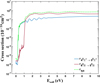 |
Fig. 3 Total cross-section for process (1) (σtot) and cross-sections for the two most important partial processes, as a function of collision energy in the centre-of-mass frame (Ecoll). Statistical weights of the initial channels are included in the cross-sections. |
3 Result and discussion
The total cross-sections for process (1) and cross-sections for relevant partial processes between molecular states, including statistical weights of the initial channels, are shown in Fig. 3. Though partial processes, 4 → 3 2Σ+ and 6 → 5 2Π are exoergic, they both show a threshold-like behaviour due to the repulsive potential barriers in the initial channels; see Fig. 2. In the 2Π case, this barrier is roughly 1 eV, and the very small cross-section between zero and ~1 eV (~10−5 to 10−4 Å2) is a result of rotational coupling mixing the processes in each symmetry. Thus, below ~1 eV, the mechanism in the 2Σ+ symmetry is dominant, while above ~1 eV the mechanism in the 2Π symmetry dominates. The oscillatory structures observed in the cross-sections occur due to the quantum interference effects and sharp peaks at low energy due to tunnelling effects; these are the so-called orbiting resonances.
The cross-sections were then integrated over a Maxwellian speed distribution to produce rate coefficients from zero to 10 000 K, which are shown in Fig. 4. Due to the behaviour of the cross-sections described above, the total rate is dominated by charge-transfer in the 2Σ+ symmetry at temperatures up to around 4000 K, above which it is dominated by the 2Π symmetry. This leads to different behaviours of the total rate coefficient above and below 4000 K. A fit to the total rate coefficient (k) is provided by a modified Arrhenius equation:
![$\[k=\exp \left(a_1+a_2 / T+a_3 T\right).\]$](/articles/aa/full_html/2025/12/aa57288-25/aa57288-25-eq6.png) (2)
(2)
For T = 400–4000 K, the fit parameters are a1 = −2.8097 × 101, a2 = −3.3368 × 103, and a3 = 5.8046 × 10−4. For T = 4001–10 000 K, they are a1 = −2.4299 × 101, a2 = −1.0391 × 104, and a3 = 5.3615 × 10−5. The coefficients all have estimated accuracies better than 0.3%. Figure 4 shows these fits reproduce the data well. The total cross-section and rate coefficient data are also made available (see the data availability statement).
We may compare our rates coefficients with various methods for obtaining estimates, such as those discussed by Stancil (2001). The simple estimate of Péquignot & Aldrovandi (1986), used by Jerkstrand et al. (2011), gives a constant rate coefficient of 10−9 cm3/s at all temperatures. The classical Langevin rate coefficient is 5.8 × 10−10 cm3/s, which is also independent of temperature. We see both these values are significantly higher than the values obtained in this work, which are 10−13 to 10−11 cm3/s at the temperatures of interest (a few thousand Kelvin). The inclusion of an approach probability, accounting for the Wigner-Witmer rules for the molecular states (Herzberg 1950, Sect. VI.1) and the selection rules for coupling between states (Nikitin & Umanskii 1984, Sect. 3.4), would introduce a factor of 1/6 for radial coupling. Though this would improve agreement, the estimates are still significantly too large. An estimate based on the Olson-Demkov model (Demkov 1964; Olson et al. 1971; Olson 1972; Swartz 1994), including the approach probability, gives rate coefficients of 2.3×10−18, 1.8×10−14, and 2.4×10−13 cm3/s, for temperatures of 1000, 5000, and 10 000 K, respectively. Though these estimates better reflect the temperature dependence of the rate coefficient, they are much too small. Note that, from a physical point of view, our calculations do not indicate a Demkov-type interaction (radial coupling between parallel potentials), but rather Landau-Zener-type interactions (radial coupling at well-localised avoided crossings).
 |
Fig. 4 Total rate coefficient as a function of temperature for process (1), as well as for the most important partial processes. Fitted rate coefficients (red dotted line) for T = 400–10 000 K. |
4 Astrophysical application
As discussed in Sect. 1, the charge-transfer process C + O+ → C++O (1D) is of particular interest in the astrophysical context of nebular SN spectra. The strength of the [O I] λλ6300, 6364 emission line (which can be directly influenced by the process; Jerkstrand et al. 2011) has been shown to be a diagnostic for the mass of SN progenitors. (Elmhamdi 2011; Maguire et al. 2012). Calibration of a given line luminosity to a progenitor mass requires detailed spectral modelling, as was done using the SUMO code by Jerkstrand et al. (2012, 2015). However, to calculate the spectral models, the authors implemented a constant temperature-independent rate of 10−9 cm3 s−1, which we find here is multiple orders of magnitude too large. This mismatch could mean that the calibrations made in Jerkstrand et al. (2012) and Jerkstrand et al. (2015) require some modification.
In Fig. 5, we present a comparison between three SUMO models1 implementing different rates for the C + O+ → C++O (1D) process to study its effect on the [O I] λλ6300, 6364 line strength. The figure shows that for stripped-envelope supernovae (SESN), the [O I] λλ6300, 6364 luminosity would be overestimated on the 10% level when using the constant rate compared to the rate computed in this work. Physically, this overestimation in flux is mostly caused by an increased neutral O fraction in the [O I] λ26300, 6364 emitting zones.
Although not tested here, a similar impact could be expected for Type II SNe. The recent work by Fang et al. (2025) uses the calibrated relations in Jerkstrand et al. (2012) to study the socalled red supergiant (RSG) problem (Smartt et al. 2009) from the perspective of [O I] line strength. The mass estimates they obtain for 50 Type II SN progenitors would all shift to somewhat higher masses if our new rate were to be implemented (assuming it somewhat damps [O I], as in the SESN case).
The right panel of Fig. 5 shows another line for which luminosity is influenced by the updated reaction rate, namely [C I] λλ9824, 9850. The [C I] λλ9824, 9850 line recently received increased attention; Liu et al. (2025) presented the first ever observations of this line in a Type Ia SN (SN 2022pul), while Barmentloo & Jerkstrand (2025) modelled this line for SESNe and investigated its diagnostic potential. In the latter work, the authors found an overproduction of [C I] λλ9824, 9850 in their model spectra when comparing to observed SNe. However, their simulations did not include any charge-transfer processes. With our updated, more robust rates we can now state that some of this overproduction (but not all) may be caused by not including charge-transfer in their simulations.
Finally, it should be noted that the importance of our updated rates becomes even more significant at later epochs. To illustrate this, Fig. 6 shows the same model as in Fig. 5, but evaluated at 1000d post explosion. The much lower temperatures in the ejecta at this epoch means that the discrepancy between the simple, constant estimate of Péquignot & Aldrovandi (1986) and the rates calculated is even larger than at earlier epochs. At this epoch, the new rates predict the feature around 6300 Å to be dominated by Fe I, contrary to the old rate that predicts [O I] domination. This also implies that the observed [O I] 6300, 6364 luminosity in SN 1987A at an age of 8y remains to be explained – previous models have relied on an assumed large CT rate to obtain sufficient luminosity for this line (Jerkstrand et al. 2011). Another excitation mechanism must be operating than thermal excitations (ejecta much too cold at only a few hundred degrees), non-thermal excitation or (radiative or dielectronic) recombination (modelled in detail and insufficient), or charge-transfer pumping via the C + O+ reaction.
 |
Fig. 5 Left panel: comparison of the [O I] λλ6300, 6364 line strength for three different rates for C + O+ → C+ + O (1D). The simulated model is the he4p0 model from Barmentloo & Jerkstrand (2025), evaluated at 300 days after explosion. Line strengths decrease by about 10% compared to the model with the rate used in Jerkstrand et al. (2011). Right panel: same models as in the left panel, but now comparing the strengths of [C I] λλ9824, 9850. Note that the high Doppler blending makes the doublets appear as single, broad features. |
 |
Fig. 6 Zoomed-in view around the [O I] λλ6300, 6364 region for the models in Fig. 5, now evaluated at 1000d post explosion. In the model with the new rate, it is Fe I lines rather than [O I] λλ6300, 6364 that dominate the emission in this region. |
Data availability
The potentials, couplings, total cross-sections, and rate coefficients are all made available at Github: https://github.com/debokireja/Datasets_for_CO_cation.git.
Acknowledgements
D.R. acknowledges support from the Wenner-Gren foundation. The computations and data handling were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS), partially funded by the Swedish Research Council through grant agreement no. 2022-06725. P.S.B. acknowledges support from the Swedish Research Council (VR 2020-03404). S.B. and A.J. acknowledge support by the Swedish Research Council, grant 2018-07399.
References
- Allan, R. J. 1999, in New Directions in Atomic Physics, eds. C. T. Whelan, R. M. Dreizler, J. H. Macek, & H. R. J. Walters, Physics of Atoms and Molecules (Boston, MA: Springer US), 281 [Google Scholar]
- Barmentloo, S., & Jerkstrand, A. 2025, arXiv e-prints [arXiv:2509.19438] [Google Scholar]
- Barnett, A. R. 1982, Comput. Phys. Commun., 27, 147 [Google Scholar]
- Barnett, A. R. 1996, in Computational Atomic Physics: Electron and Positron Collisions with Atoms and Ions, ed. K. Bartschat (Berlin, Heidelberg: Springer), 181 [Google Scholar]
- Bransden, B. H., & McDowell, M. R. C. 1992, Charge Exchange and the Theory of Ion-Atom Collisions (Oxford University Press) [Google Scholar]
- Chambaud, G., Levy, B., Millie, P., et al. 1980, J. Phys. B: At. Mol. Phys., 13, 4205 [Google Scholar]
- Chenel, A., Mangaud, E., Justum, Y., et al. 2010, J. Phys. B: At. Mol. Phys., 43, 245701 [Google Scholar]
- Demkov, Y. N. 1964, JETP, 18, 138 [Google Scholar]
- Dunning Jr, T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Elmhamdi, A. 2011, Acta Astron., 61, 179 [NASA ADS] [Google Scholar]
- Fang, Q., Moriya, T. J., & Maeda, K. 2025, ApJ, 986, 39 [Google Scholar]
- Heil, T. G., Butler, S. E., & Dalgarno, A. 1981, Phys. Rev. A, 23, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Herzberg, G. 1950, Molecular Spectra and Molecular Structure. 1: Spectra of Diatomic Molecules (New York: Van Nostrand Reinhold) [Google Scholar]
- Honjou, N., & Sasaki, F. 1979, Mol. Phys., 37, 1593 [Google Scholar]
- Jerkstrand, A., Fransson, C., & Kozma, C. 2011, A&A, 530, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jerkstrand, A., Fransson, C., Maguire, K., et al. 2012, A&A, 546, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jerkstrand, A., Ergon, M., Smartt, S. J., et al. 2015, A&A, 573, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, B. R. 1973, J. Comp. Phys., 13, 445 [Google Scholar]
- Krupenie, P. H., & Weissman, S. 1965, J. Chem. Phys., 43, 1529 [Google Scholar]
- Liu, J., Wang, X., Yang, Y., et al. 2025, ApJ, 982, L18 [Google Scholar]
- Maguire, K., Jerkstrand, A., Smartt, S. J., et al. 2012, MNRAS, 420, 3451 [Google Scholar]
- Manolopoulos, D. E. 1986, J. Chem. Phys., 85, 6425 [Google Scholar]
- Meyerott, R. E. 1978, ApJ, 221, 975 [Google Scholar]
- Nikitin, E. E., & Umanskii, S. I. 1984, Springer Series in Chemical Physics, 30: Theory of Slow Atomic Collisions (Berlin and New York: Springer) [Google Scholar]
- Okada, K., & Iwata, S. 2000, J. Chem. Phys., 112, 1804 [Google Scholar]
- Olson, R. E. 1972, Phys. Rev. A, 6, 1822 [Google Scholar]
- Olson, R. E., Smith, F. T., & Bauer, E. 1971, Appl. Opt., 10, 1848 [NASA ADS] [CrossRef] [Google Scholar]
- Péquignot, D., & Aldrovandi, S. M. V. 1986, A&A, 161, 169 [NASA ADS] [Google Scholar]
- Pradhan, A., & Dalgarno, A. 1994, Phys. Rev. A, 49, 960 [Google Scholar]
- Shi, D., Li, W., Sun, J., Zhu, Z., & Liu, Y. 2011, Comput. Theor. Chem., 978, 126 [Google Scholar]
- Singh, R. B., & Rai, D. 1966, J. Mol. Spectrosc., 19, 424 [Google Scholar]
- Smartt, S. J., Eldridge, J. J., Crockett, R. M., & Maund, J. R. 2009, MNRAS, 395, 1409 [CrossRef] [Google Scholar]
- Smith, E. W., Cooper, J., & Vidal, C. R. 1969, Phys. Rev., 185, 140 [Google Scholar]
- Stancil, P. C. 2001, ASP Conf. Ser., 247, 3 [Google Scholar]
- Stancil, P. C., Havener, C. C., Krstić, P. S., et al. 1998, ApJ, 502, 1006 [Google Scholar]
- Stancil, P. C., Schultz, D. R., Kimura, M., et al. 1999, A&AS, 140, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swartz, D. A. 1994, ApJ, 428, 267 [Google Scholar]
- Werner, H.-J., & Meyer, W. 1981, J. Chem. Phys., 74, 5802 [CrossRef] [Google Scholar]
- Werner, H.-J., & Knowles, P. J. 1985, J. Chem. Phys., 82, 5053 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H., Knowles, P., Knizia, G., et al. 2022, See http://www.molpro.Net [Google Scholar]
- Woosley, S. E., & Heger, A. 2007, Phys. Rep., 442, 269 [Google Scholar]
- Xing, W., Shi, D., Zhang, J., Sun, J., & Zhu, Z. 2018, J. Quant. Spectrosc. Radiat. Transf., 210, 62 [Google Scholar]
All Tables
Low-lying ground and excited electronic states of CO+ resulting from the combination of asymptotic atomic states.
All Figures
 |
Fig. 1 Adiabatic PECs of doublet (panel a; 1–5 2Σ+: red line, 1–7 2Π: blue line, 1 2Φ: violet line, 1–3 2Δ: black line, 1–3 2Σ−: green line), quartet (panel b; 1–2 4Σ+: red line, 1–4 4Π: blue line, 1–2 4Δ: black line, 1–3 4Σ−: green line), and sextet (1 6Σ+: brown line, 1 6Π: violet line) spin states of CO+ molecular ion as a function of internuclear distance R. All are given in atomic units (a.u.). |
| In the text | |
 |
Fig. 2 Adiabatic (solid lines) and diabatic (dash-dotted lines) PECs of 3 and 4 2Σ+ (panel a) and 5 and 6 2Π (panel b), of the CO+ molecular ion as a function of internuclear distance R. Panel c: non-adiabatic radial coupling matrix elements |
| In the text | |
 |
Fig. 3 Total cross-section for process (1) (σtot) and cross-sections for the two most important partial processes, as a function of collision energy in the centre-of-mass frame (Ecoll). Statistical weights of the initial channels are included in the cross-sections. |
| In the text | |
 |
Fig. 4 Total rate coefficient as a function of temperature for process (1), as well as for the most important partial processes. Fitted rate coefficients (red dotted line) for T = 400–10 000 K. |
| In the text | |
 |
Fig. 5 Left panel: comparison of the [O I] λλ6300, 6364 line strength for three different rates for C + O+ → C+ + O (1D). The simulated model is the he4p0 model from Barmentloo & Jerkstrand (2025), evaluated at 300 days after explosion. Line strengths decrease by about 10% compared to the model with the rate used in Jerkstrand et al. (2011). Right panel: same models as in the left panel, but now comparing the strengths of [C I] λλ9824, 9850. Note that the high Doppler blending makes the doublets appear as single, broad features. |
| In the text | |
 |
Fig. 6 Zoomed-in view around the [O I] λλ6300, 6364 region for the models in Fig. 5, now evaluated at 1000d post explosion. In the model with the new rate, it is Fe I lines rather than [O I] λλ6300, 6364 that dominate the emission in this region. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\[\left.\left(|\langle 4^2 \Sigma^{+}| \frac{\partial}{\partial R}| 3^2 \Sigma^{+}\rangle|,|\langle 6^2 \Pi| \frac{\partial}{\partial R}| 5^2 \Pi\rangle \rvert\,\right)\right)\]$](/articles/aa/full_html/2025/12/aa57288-25/aa57288-25-eq3.png)