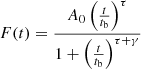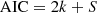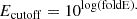| Issue |
A&A
Volume 700, August 2025
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 28 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202553801 | |
| Published online | 08 August 2025 | |
Gamma-ray burst prompt emission spectra at high energies
1
Gran Sasso Science Institute, Viale F. Crispi 7, I-67100 L’Aquila (AQ), Italy
2
INFN – Laboratori Nazionali del Gran Sasso, I-67100 L’Aquila (AQ), Italy
3
INAF – Osservatorio Astronomico d’Abruzzo, Via M. Maggini snc, I-64100 Teramo, Italy
⋆ Corresponding author: samanta.macera@gssi.it
Received:
17
January
2025
Accepted:
25
May
2025
Despite more than fifty years of gamma-ray burst (GRB) observations, several questions regarding the origin of the prompt emission, particularly at high energies, remain unresolved. We present a comprehensive analysis of 35 GRBs observed by Fermi/GBM and Fermi/LAT over the past 15 years, focusing on the nature of high-energy (HE, E > 100 MeV) emission during the prompt emission phase. Our study combines temporal and spectral analyses to investigate the synchrotron origin of the observed emission spanning the energy range from 10 keV to 100 GeV and explore the possible contribution of additional spectral components. Temporal modeling of Fermi/LAT light curves for 12 GRBs in our sample reveals deviations from standard afterglow scenarios during the early phases, suggesting a significant contamination from prompt emission. We find that most GRB spectra align with synchrotron emission extending to GeV energies, with the slope p of the non-thermal electron distribution clustering around p ∼ 2.7, consistently with theoretical predictions. For three GRBs, an additional power law component is required to explain the high-energy emission, but the nature and temporal evolution of this component remain unclear due to the limited quality of Fermi/LAT data. When the power law component is needed, the synchrotron spectrum shows a sharp MeV suppression. It could be explained by the pair loading effects in the early afterglow. These findings emphasize the importance of multi-wavelength observations in unveiling the mechanisms driving early HE prompt emission in GRBs. We briefly discuss the implications of our findings for future very-high-energy (VHE, E > 100 GeV) gamma-ray observatories, such as the Cherenkov Telescope Array, and address the detection prospects of additional non-thermal components in GRB spectra.
Key words: astroparticle physics / radiation mechanisms: non-thermal / relativistic processes / gamma-ray burst: general / gamma rays: general
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Gamma-ray burst (GRB) prompt emission consists of brief flashes of MeV radiation lasting fractions of a second. Due to its short duration, typically spanning seconds to minutes, it is predominantly observed in the 10 keV–10 MeV energy range, as determined by the sensitivity of the triggering instruments. This emission is thought to be produced by non-thermal particles accelerated in the dissipative zones within the relativistic jets (e.g. Rees & Meszaros 1994; Sari & Piran 1997; Paczynski & Xu 1994; Daigne & Mochkovitch 2000). Due to the lack of knowledge on the GRB jet composition from first principles, the dissipative processes responsible for the GRB production cannot a priori be determined (Meszaros & Rees 1997). Two main prompt emission sites are typically proposed: optically thick regions below the photosphere (Meszaros & Rees 2000) and optically thin regions above it. Either mildly relativistic shocks or magnetic reconnection (Thompson 1994; Spruit et al. 2001) processes could be responsible for the heating of charged particles that power the observed radiation.
In the standard GRB model, dissipation of the relativistic unsteady jet above the photosphere produces non-thermal electrons via internal shocks. In this scenario, the prompt emission is produced by the synchrotron radiation of shock-accelerated electrons (Rees & Meszaros 1994; Tavani 1996). However, the apparent inconsistency of the low-energy spectra of GRBs with the expected fast-cooling synchrotron spectral shape (Crider et al. 1997; Preece et al. 1998; Ghisellini et al. 2000; Ghirlanda et al. 2002; Kaneko et al. 2006; Nava et al. 2011; Gruber et al. 2014) has opened up more complex scenarios. Several solutions within the synchrotron radiation model have been proposed (i.e. Lloyd & Petrosian 2000; Pe’er & Zhang 2006; Burgess et al. 2019), including the effects of incomplete cooling of electrons (Kumar et al. 2008; Daigne et al. 2011; Beniamini & Piran 2013; Daigne & Bošnjak 2025). Alternatively, some authors suggest that the GRB spectra are formed in optically thick media, where dissipative photospheres provide hot electrons that enable multiple Compton scatterings of low-energy photons (Ghisellini & Celotti 1999; Pe’er & Waxman 2004; Rees & Meszaros 2005; Giannios 2012).
For a long time, the prompt emission spectra of long GRBs were best characterised by the Band function (Band et al. 1993). This model consists of two smoothly connected power law segments, with a characteristic energy falling in the range ∼100 keV−1 MeV. Typically, the photon indices below and above the peak energy in the νFν spectrum are −1 and −2.3, respectively. This empirical model can effectively describe most GRB prompt spectra. However, despite extensive observations and modelling, a physical interpretation of the Band function remains elusive. As an empirical model, the parameters of the Band function are not constrained by physical assumptions. Furthermore, due to its simplicity, the Band function, with its two power law segments, cannot capture many significant features of the GRB spectrum, such as possible energy breaks.
In some GRBs observations, the spectrum significantly deviates from a Band function, particularly with an excess of low-energy photons (≤30 keV). These deviations have led to suggestions of a thermal (blackbody) component superimposed on the Band function (Ghirlanda et al. 2003; Ryde 2004; Guiriec et al. 2015).
Recently, breaks in the GRB prompt emission spectra have been found (Ravasio et al. 2019a) also with the help of the inclusion of X-ray and optical data (Oganesyan et al. 2017, 2019). This finding necessitated the addition of a third low-energy power law segment. Consequently, the spectra are now best described by three smoothly connected power law segments with indices α1, α2, and β, where the break energy, Eb, ranges from a few keV to hundreds of keV. The values of α1 and α2 have been found to be consistent with marginally fast cooling synchrotron radiation (Ravasio et al. 2019a).
The main challenge in identifying GRB prompt emission mechanisms lies mainly in the lack of early multi-wavelength (MWL) observations. Observations at lower energies (optical and X-rays) and in the MeV gamma-ray range suggest that some GRB spectra are consistent with moderately fast-cooling synchrotron radiation models (Oganesyan et al. 2017, 2018; Ravasio et al. 2019a). Systematic modelling of GRB spectra using physically motivated synchrotron models is essential to advance our understanding of these enigmatic emissions.
In general, the high-energy part of the spectrum is crucial for distinguishing between different GRB emission mechanisms, as different models provide different predictions in this energy range (Rees & Meszaros 1994, 2005; Peér 2008). In particular, in the synchrotron scenario the high-energy spectrum is essential for constraining the particle energy distribution. In the optically thin scenarios (both in internal shocks or reconnection), the highest-energy photons are strictly related to the size of the emitting region, and very-high-energy (VHE) photons can, in principle, be produced by inverse Compton scattering (see Banerjee et al. 2023, for a description of possible scenarios). However, it is important to consider that this part of the spectrum can also be influenced by other processes, such as pair annihilation, which may alter its observed characteristics. Furthermore, it remains uncertain whether the synchrotron model alone can fully account for the overall shape of the GRB spectrum, including its width and transition to higher energies (van Eerten 2015; Burgess & Ryde 2015). In the optically thick models, the highest-energy photons are limited by the opacity of the last scattering surface. Therefore, it is essential to characterise the high and VHE portions of the prompt emission. Little is known about the prompt emission spectra at the high-energy (HE) and VHE gamma-rays. Only recently, for GRB 221009A, early emission from GRBs in the VHE domain (from 0.3 to above 5 TeV) has been discovered, thanks to the observation by the Large High Altitude Air Shower Observatory (LHAASO) (Cao et al. 2023a,b). The detection of the VHE emission overlaps with the prompt emission detected by Fermi/GBM. One of the possible explanations for multi-TeV emission is synchrotron self-Compton radiation from the afterglow (SSC; Derishev & Piran 2024; Banerjee et al. 2024), since no evidence of TeV light curve variability associated with the prompt emission has been found (Cao et al. 2023a).
The Large Area Telescope (LAT; Atwood et al. 2009) on board the Fermi Observatory enables a wide field coverage of the sky in the 30 MeV–300 GeV energy range. The large effective area of LAT allows for the detection of short-lasting (∼10 s) HE and VHE sources at a level of ∼10 mCrab. Provided that each point in the sky is observed by LAT every 3 hours, many GRBs have been covered during their prompt emission phase over the past 15 years. The HE emission of GRBs has been extensively studied by many authors (e.g. Hascoët et al. 2012; Vianello et al. 2018; Chand et al. 2020; Mei et al. 2022b; Ravasio et al. 2024). In most cases, the long-lasting (up to 104 s) GeV emission discovered by LAT was attributed to synchrotron radiation from the electrons accelerated in the external shock (afterglow radiation) (e.g. Ackermann et al. 2013; Ajello et al. 2020). Some authors found early GeV radiation to be consistent with the high-energy extension of the prompt emission spectrum (Nava et al. 2014; Nava 2018; Miceli & Nava 2022, and references therein). Usually, the prompt GeV spectrum is soft and is interpreted as suppressed by the photon annihilation. In these studies the prompt emission spectra are modelled by the empirical two-power law functions, and the afterglow emission component is treated separately. The fundamental problem in identifying the origin of the early GeV radiation is the limitation of the LAT sensitivity. It is difficult to trace the temporal evolution of the GeV emission and therefore to distinguish the onset of the afterglow from a possible prompt emission contribution.
In this paper, we consider the high-energy emission that is temporally coincident with the prompt emission of GRBs detected over the past 15 years. We make use of the publicly available data from the Fermi Gamma-ray Burst Monitor (GBM; 8 keV–40 MeV; Meegan et al. 2009) and Fermi-LAT (∼30 MeV–300 GeV). We investigated the nature of the early GeV emission in the context of a synchrotron radiation model. We also searched for an additional HE and VHE spectral component in the Fermi-LAT data in the prompt emission phase. This paper is organised as follows: in Section 2, we describe the joint keV–GeV sample selection criteria. In Section 3, we provide details on the acquisition and treatment of the data. The temporal analysis of the GeV emission is provided in Section 4. The description and the implementation of the tested models for the joint keV–GeV spectra is reported in Section 5. The outcome of the MWL prompt emission modelling is presented in Section 6 and discussed in Section 7. We draw conclusions in Section 8 of our work.
2. Sample selection
The GRBs included in our study are primarily detected by Fermi/GBM. We selected GRBs from the GBM trigger catalog1, ensuring that the probability of the trigger being a GRB exceeds 95% (the probability that the GBM flight system classified the trigger as a GRB is more than 95%). We further refined our selection to include GRBs with a localisation accuracy below 0.5°, aligning with the point spread function of LAT at around 1 GeV. From this refined sample, we chose those that demonstrate detection with LAT within their prompt phase of emission (within T90) and detected with a test statistic TS > 25, indicating a detection significance greater than 5σ. A significant fraction of these GRBs were not within the FoV of LAT during the prompt emission phase (within T90). Hence, they were not included in the sample. This selection described above resulted in 35 GRBs, observed from July 2008 to October 2022. Among these, 19 GRBs were localised by Swift, of which 16 were localised by Swift/XRT. Furthermore, Fermi/LAT localised 15 GRBs, and GRB 110721A was localised through IPN triangulation.
Since the goal of this work is to characterise the high-energy emission during the prompt emission phase, the temporal binning of the combined keV–GeV dataset is driven by the Fermi/LAT data because of its limited sensitivity. We defined time intervals according to their LAT likelihood ratio, i.e. test statistics (TS). We selected time-bins where TS ≥ 10, which correspond to a LAT detection significance > 3σ, as detailed in Section 3. Twelve out of the 35 GRBs in the initial sample exhibit a joint keV–GeV emission which enables us to identify at least two time bins where both GBM and LAT data are available, according to our LAT selection criterion previously described. We refer to these GRBs as the Sample-1 and report them in Table 1. Given the identification of multiple time-bins for each GRB in Sample-1, we carried out a temporal and (time-resolved) spectral analysis for a total of 67 spectra. The time-resolved GRBs, the respective T90, and redshift (when available) are reported in Table 1.
Properties of GRBs in Sample-1.
For the remaining 23 GRBs, it was possible to identify only a single bin with joint GBM-LAT detection. We refer to these GRBs as Sample-2, which is reported in the Table 2. In the case of the GRBs in Sample-2, the presence of a single bin prevents a temporal analysis.
3. Data extraction and analysis
3.1. Fermi-GBM data
For each GRB in our sample, we retrieved the Fermi/GBM (8 keV–40 MeV) data from the Fermi GBM Burst catalog2 and performed a standard reduction using the Fermi science tool GTBURST3. We considered data from the two sodium iodide (NaI, 8–900 keV) and one bismuth germanate (BGO, 0.3–40 MeV) detectors with the lowest viewing angles. The background analysis was performed by choosing custom background intervals that lead to a convergent polynomial fit. Source intervals were chosen according to the LAT time-bins, in order to perform a simultaneous Fermi/GBM and Fermi/LAT spectral analysis. The data reduction outputs are the source spectra, background spectra and the weighted response files that are later used for the spectral analys is through the XSPEC software4 provided by the High Energy Astrophysics Science Archive Research Center (HEASARC). We ignored the energy channels outside 8–900 keV for the NaI detectors, together with the 30–40 keV interval to avoid the iodine K-edge line at 33.17 keV. For the BGO detectors, we ignored the channels outside the 300 keV–40 MeV interval. For the spectral analysis of this dataset, we applied a Poisson-Gaussian statistics (pgstat).
3.2. Fermi-LAT data
We used the GTBURST software from the official Fermi tools to extract and analyse the data from the GRBs listed in Tables 1 and 2, Section 2. The high-energy data within the 0.1–10 GeV energy band were extracted from a 12° region of interest (ROI) around the source location of the GRB. The source location (RA, Dec) and trigger time were obtained from the GBM online trigger catalog. A zenith angle cut of 100° was applied to minimise contamination from gamma-ray photons originating from the Earth’s limb as a sanity measure.
Properties of GRBs in Sample-2.
The GRBs were selected ensuring a detection significance of more than 3 sigma in high-energy gamma-rays. The temporal bins for each GRB were chosen so that the total number of high-energy gamma-ray photons within a 5° radius around the GRB location is at least 15. Thus, ensuring a higher detection significance. We considered a spectral model of type ‘powerlaw2’ for the analysis throughout along with ‘isotr_template’ and ‘template’ (fixed norm) for the particle background and the Galactic component, respectively. An ‘unbinned likelihood analysis’ is considered with a minimum test statistic (TSmin) of 10, which denotes the detection significance (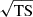 ) of more than 3. The selection of the instrument response function was made based on the duration. We used the response function ‘P8R3_TRANSIENT010E_V2’ until 1000 s from the trigger time following the analysis methods described in Ajello et al. (2019). The Fermi/LAT data spectral products are produced through GTBURST using the standard ScienceTool5 and gtbin pipeline. In addition, we produced background counts and response files using gtbkg and gtrspgen, respectively (for details see Ajello et al. 2019). A cut in the angle of the off-axis source of 90° was considered to produce the spectral files in the six energy bins between 100 MeV and 100 GeV. We fitted the Fermi/LAT spectrum in XSPEC using Cash statistics. For each time bin, we further searched for the highest-energy photon (Emax, GeV) using the gtsrcprob tool, which has a probability of association with the GRB greater than 0.9. We perform two independent analysis a) 0.1–100 GeV, and b) 100 MeV–Emax. The spectral points presented in Figures 2, 4 and 5, were made following the strategy (a), whereas the spectral butter-fly plots were made with the analysis described in (b).
) of more than 3. The selection of the instrument response function was made based on the duration. We used the response function ‘P8R3_TRANSIENT010E_V2’ until 1000 s from the trigger time following the analysis methods described in Ajello et al. (2019). The Fermi/LAT data spectral products are produced through GTBURST using the standard ScienceTool5 and gtbin pipeline. In addition, we produced background counts and response files using gtbkg and gtrspgen, respectively (for details see Ajello et al. 2019). A cut in the angle of the off-axis source of 90° was considered to produce the spectral files in the six energy bins between 100 MeV and 100 GeV. We fitted the Fermi/LAT spectrum in XSPEC using Cash statistics. For each time bin, we further searched for the highest-energy photon (Emax, GeV) using the gtsrcprob tool, which has a probability of association with the GRB greater than 0.9. We perform two independent analysis a) 0.1–100 GeV, and b) 100 MeV–Emax. The spectral points presented in Figures 2, 4 and 5, were made following the strategy (a), whereas the spectral butter-fly plots were made with the analysis described in (b).
3.3. Fermi-LLE data
The GRBs listed in Samples-1 and -2 were detected by Fermi/LAT during the prompt emission and thus led to the possibility of detection in 30–100 MeV. We searched for the availability of LLE data (Pelassa et al. 2010). We downloaded data from the Fermi LAT Low-Energy Events Catalog6. LLE data were reduced using the same tools employed in the Fermi/GBM analysis, selecting the source in the same time-bin to perform a simultaneous joint time-resolved analysis. In the spectral analysis, we excluded all channels outside the 30–100 MeV interval. For this dataset fit, we employed a Cash statistics (cstat). The column ‘LLE’ in Tables 1 and 2 indicates the availability of the LLE data.
4. Timing analysis
To explore the origin of the HE emission observed by Fermi/LAT, we empirically modelled the light curves in terms of the observed flux. In the standard forward shock model, excluding the effects of continuous energy injection, the bolometric light curve of the afterglow is expected to rise proportionally to tτ until the deceleration time, after which it follows a power law decline t−γ (Sari et al. 1998). To model the light curve empirically, we used the following function adopted from Ghirlanda et al. (2010):
where A0 is the flux normalisation, tb is the characteristic break time, and τ and γ are the temporal rise and decay indices, respectively. In our calculation, we fixed τ = 2 and explored the posterior distribution of the model parameters. We derive the peak time as 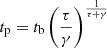 .
.
We built a likelihood based on the model function, comparing it with the observed Fermi/LAT light curves. Logarithmic priors for the parameters A0, tp, γ were chosen in ranges [ − 8.0, −4.0], [ − 0.8, 4.0], [1.0, 5.0], respectively. We performed an MCMC sampling using the Python package EMCEE (Foreman-Mackey et al. 2013) to estimate the posterior distribution of the parameters.
We defined the best-fit values of the parameters as the median of their posterior distribution. The uncertainty for each parameter was expressed as the range between the 16th and 84th percentiles of the posterior distribution, representing the range within which the true value of each parameter is expected to lie with a probability of 68%, given the model and the data. The best-fit values of the parameters and their uncertainties for each Fermi/LAT light curve analysed are reported in Table 1. Some of the time bins selected through the method reported in Sect. 2 are simultaneous with the relative prompt emission, as highlighted by Fermi/GBM duration. When fitting the afterglow light curve model to the LAT data, we find that some GRBs exhibit data points at early times in excess with respect to the best-fit afterglow light curve. The latter is mainly driven by the fit of late time data points, which are produced with a large temporal delay with respect to the GBM trigger, when the prompt emission component is largely sub-dominant. Therefore, the excess observed at early times might be caused by the superposition of both prompt and afterglow emissions. However, given the uncertainties of the ratio between the data and the model, it is difficult to distinguish the prompt and/or the afterglow contribution in the early GeV data. Hence, we performed a more detailed spectral analysis, described in the following section.
5. Spectral analysis
A temporal analysis alone is not sufficient to determine the origin of the early GeV emission. In this study, we performed a detailed spectral analysis of GRB prompt emission, adopting a physical model based on the assumption that prompt emission is produced by synchrotron radiation. For the synchrotron component, since no built-in synchrotron model is available in XSPEC for spectral fitting, we used a table model as described in Oganesyan et al. (2019). Synchrotron emission arises from non-thermal electrons distributed according to a power law 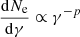 , where γm denotes the minimum Lorentz factor. The resulting table spectra were generated by combining the single-electron emission spectrum with the electron distribution after cooling via synchrotron radiation down to the cooling Lorentz factor γc. The table spectra were constructed to account for both the fast γm > γc and slow γm < γc cooling regimes of synchrotron radiation. These tables were then stored in a FITS file, which can be used as a tabulated multiplicative model on XSPEC. In the table spectra, the energies were normalised in such a way that the cooling frequency νc was always at 1 keV. Therefore, we used the XSPEC convolution model zmshift, which shifts the spectrum along the energy axis introducing one additional parameter and from which we can determine the actual cooling frequency. The resulting parameters of the model are: pindex, log(γm/γc), zshift and the normalisation NSync. Spectra that reach GeV energies require an empirical high-energy cut-off to consider the potential spectral attenuation attributed to pair production (Vianello et al. 2018; Mei et al. 2022a; Ravasio et al. 2024). The energy resolution and sensitivity of LAT prevent an accurate characterisation of the GeV spectrum. The addition of the HE cut-off allows for a proper description of the putative pair-attenuation, without strong assumptions on the spectral shape. This table model with the additional high-energy cut-off is named Model-1, hereafter. To account for a potential additional high-energy component, we tested models with both a power law and a cut-off power law. For these cases, the added parameters included the power law photon index (phindex) and normalisation. We term this as Model-2. On rare occasions, the data also require a high-energy cut-off. This third category is termed Model-3. The models and the relevant quantities are presented in Fig. 1. For comparison, we fitted all GRBs in our sample using the Band model in the standard MeV range. This allowed us to evaluate how the results differ when using a physical model instead of the empirical approach applied to most GRBs in our sample.
, where γm denotes the minimum Lorentz factor. The resulting table spectra were generated by combining the single-electron emission spectrum with the electron distribution after cooling via synchrotron radiation down to the cooling Lorentz factor γc. The table spectra were constructed to account for both the fast γm > γc and slow γm < γc cooling regimes of synchrotron radiation. These tables were then stored in a FITS file, which can be used as a tabulated multiplicative model on XSPEC. In the table spectra, the energies were normalised in such a way that the cooling frequency νc was always at 1 keV. Therefore, we used the XSPEC convolution model zmshift, which shifts the spectrum along the energy axis introducing one additional parameter and from which we can determine the actual cooling frequency. The resulting parameters of the model are: pindex, log(γm/γc), zshift and the normalisation NSync. Spectra that reach GeV energies require an empirical high-energy cut-off to consider the potential spectral attenuation attributed to pair production (Vianello et al. 2018; Mei et al. 2022a; Ravasio et al. 2024). The energy resolution and sensitivity of LAT prevent an accurate characterisation of the GeV spectrum. The addition of the HE cut-off allows for a proper description of the putative pair-attenuation, without strong assumptions on the spectral shape. This table model with the additional high-energy cut-off is named Model-1, hereafter. To account for a potential additional high-energy component, we tested models with both a power law and a cut-off power law. For these cases, the added parameters included the power law photon index (phindex) and normalisation. We term this as Model-2. On rare occasions, the data also require a high-energy cut-off. This third category is termed Model-3. The models and the relevant quantities are presented in Fig. 1. For comparison, we fitted all GRBs in our sample using the Band model in the standard MeV range. This allowed us to evaluate how the results differ when using a physical model instead of the empirical approach applied to most GRBs in our sample.
 |
Fig. 1. Model-1: synchrotron emission only. Model-2: additional power law included. Model-3: Model-2 with a high energy cut off in the spectrum. The characteristic frequencies (νc and νm), and the cut-off energy (Ecut) are indicated by the vertical lines. For a detailed description, see Section 5. |
5.1. Implementation of the models and spectral analysis
We performed a joint spectral analysis using Fermi/GBM, Fermi/LLE, and Fermi/LAT data, applying the three physical models described in Section 5 and shown in Fig. 1. The fitting process was carried out using XSPEC (v12.13.0c). In Model-1 (table synchrotron model), we combined an additional feature, the multiplicative component highecut, that includes two parameters: Eb, fixed at 300 keV, and the fold energy foldE, which remains a free parameter. For Model-2 (synchrotron and power law combined) and Model-3 (synchrotron and cut-off power law components), in addition to Model-1, we added the built-in XSPEC models powerlaw and cutoffpl, respectively. These models introduced additional parameters: normalisation, photon index (phindex), and, for the cut-off model, the folding energy (foldE). In the case of the conventional Band model, we used the grbm model, with parameters comprising the two photon indices α and β, the characteristic energy Ec, and normalisation.
5.2. Model comparison: The Akaike information criterion
To select the best fit model among Model 1 and Model 2 for the GRBs in Sample 1, we used the Akaike Information Criterion (AIC; Akaike 1974). The AIC helps in evaluating and comparing different models. Specifically, AIC takes into account the number of degrees of freedom and the statistic values for each model fit. In practice, we evaluated the quantity
for each model fitted to each spectrum, where k is the number of model parameters and S is the statistic value, which in this case consists of a combination of pgstat and cstat. We then computed the difference ΔAIC = AIC2 − AIC1, where AIC2 is the more complex model, i.e. with more model parameters k. We selected the more complex model as the best-fit model if ΔAIC ≥ 4, which corresponds to a statistical improvement of 1σ (Burnham & Anderson 2004). We did not perform model comparison between the Band and synchrotron model. Band, being a phenomenological model, is able to easily accommodate the majority of the GRB spectra, without any insight on the physical processes behind. On the other hand, the synchrotron model allows us to investigate the physical framework (with the same number of free parameters), but with less freedom in describing the spectral data. Instead, our goal is to study whether the synchrotron emission can model the prompt spectrum up to HE with or without the addition of extra components.
5.3. Parameter estimation: BXA
Once the best-fit model was determined with the AIC test, we used the Bayesian X-ray analysis tool BXA7 together with PyXSPEC for precise parameter estimation. BXA is particularly advantageous for parameter estimation due to its integration of Bayesian inference with the nested sampling algorithm (like UltraNest), enabling the thorough exploration of the parameter space and delivering reliable estimates and uncertainties for the model parameters. First, we implemented the best-fit model, as identified by the AIC test, in PyXSPEC. We then defined non-informative priors for the free parameters of the model. Specifically, we applied logarithmic priors for the normalisation of the synchrotron and power law components (where needed) and for the fold energy of the cut-off component, while using uniform priors for the p-index (2, 5), log(γm/γc) (−1, 2), zshift (−0.999, 10), and the photon index of the power law phindex (−3, 10). From the samples of the parameters log(γm/γc), zshift and the fold energy, we obtained ‘secondary’ samples for the physical quantities of interest νm, νc, and Ecut in the following way:
We defined the median of the posterior distribution as the mean value of each parameter and determine credible intervals as the range from the 16th to the 84th quantile. The values of the flux and the relative errors were computed directly from PyXspec. The resulting values of all the parameters for each analysed spectrum are reported in Table A.1 for GRB 080916C, Table A.2 for GRB 090902B, Table A.3 for GRB 221023A, and Table A.4 for GRB 190114C. All remaining tables for the other GRBs analysed in this work are provided in Table A.5 and in Table 2.
6. Results
In this work, we performed a temporal analysis of the Fermi/LAT light curves of 12 GRBs and a time-resolved spectral analysis of 35 GRBs, encompassing a total of 90 spectra.
6.1. Temporal analysis
For Sample-1, we conducted a timing analysis, to study the evolution of Fermi/LAT light curves. Our analysis shows that, in most cases, the empirical model (Eq. (1)) adequately represents the Fermi/LAT light curve, with some exceptions. Fig. 2 presents the results of this analysis, using GRB 080916C as an illustrative example. In the top panel, we show the afterglow model fitted to the data. The synchrotron process within the external shock model establishes a connection between the temporal decay index (γ) of the light curve and the energy spectral index (ϕ), referred to as the closure relations (Kumar & Duran 2010; Ghisellini et al. 2010). These relations provide a convenient method to verify whether the observed radiation originates from the external shock. In particular, high-energy emission is often associated with the synchrotron radiation from the forward shock accelerated electrons beyond the synchrotron cooling frequency. If so, then the spectrum should be ∝ν−p/2, while the light curve in the external shock scenario should decay as ∝t−(3p − 2)/4 (Panaitescu & Kumar 2000; Beniamini et al. 2015, 2016). From this, we can derive the closure relation ϕ = −(2γ + 4)/3. Therefore, from the fit of the decay temporal index γ, we derive the predicted spectral index ϕ, which is shown with its uncertainties as a shaded grey area in the central panel of Fig. 2, together with the observed spectral indices. The bottom panel presents the Residuals, indicating the deviation of the light curve from the afterglow model. The majority of data points which show an excess are clustering around the peak of the Fermi/LAT light curve, and within the duration of the burst (T90 measured by the Fermi/GBM) ensuring the emission in GeV energies during the prompt phase. However, we did not observe any significant excess over 5σ. We also computed the quantity tpeak/T90, which indicates what fraction of the duration occurs during prompt and which one is more likely afterglow-related. The median values for tpeak/T90 and γ found in our sample are 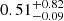 and
and 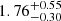 respectively.
respectively.
 |
Fig. 2. Time-resolved spectral analysis of GRB 080916C. The upper-left panel shows the fit of the LAT light curve (0.1–10 GeV) with the model from Eq. 1, along with GBM light curves (BGO and NaI). The middle panel compares the inferred spectral index (ϕ) with the observed spectral index, with the shaded grey area representing uncertainties on the predicted index, derived from the decay temporal index fit. The bottom panel shows the residuals, indicating the deviation of the light curve from the model. The remaining panels show the time-resolved spectral fits. Details are provided in Table A.1. |
6.2. Spectral analysis
To better understand the nature of the HE emission, we performed a spectral analysis. For Sample-1, which includes time-resolved spectra, Model-1 (only synchrotron emission and high-energy cut-off) and Model-2 (a combination of synchrotron and power law) are employed. When Model-2 is selected as best-fit model by the Akaike test, further evaluation is performed using Model-3 (synchrotron and power law with high-energy cut-off). Meanwhile, for Sample-2, due to the absence of significant GeV excess beyond synchrotron emission, we limit our analysis to Model-1, without the addition of a high-energy cut-off. The subsequent sections highlight the most suitable model category and are illustrated with examples.
6.2.1. Model-1: Synchrotron-dominated spectra
In total, 32 GRBs are best-fitted by a pure synchrotron with a high-energy cut-off (Model-1), resulting in a total of 75 spectra for which the HE emission is well explained by synchrotron radiation in a marginally fast-cooling regime. In particular, in the illustrative case of GRB 080916C, the cooling regime shows an evolution: during the first time-bin, at the onset of the prompt emission, the synchrotron frequencies  keV and
keV and 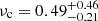 MeV are particularly close (see Fig. 2 and Table A.1 for details). However, in subsequent time bins, they become distinct and well-constrained. Additionally, the post-peak spectrum hardens over time, with the spectral index p evolving from 2.85 in the 0.0 − 5.27 s time bin to 2.18 in the 5.95 − 6.63 s time bin, before softening again at later times. Moreover, the model provides tight constraints on the cut-off energy, Ecutoff, in all the time bins analysed (see Table A.1).
MeV are particularly close (see Fig. 2 and Table A.1 for details). However, in subsequent time bins, they become distinct and well-constrained. Additionally, the post-peak spectrum hardens over time, with the spectral index p evolving from 2.85 in the 0.0 − 5.27 s time bin to 2.18 in the 5.95 − 6.63 s time bin, before softening again at later times. Moreover, the model provides tight constraints on the cut-off energy, Ecutoff, in all the time bins analysed (see Table A.1).
The inclusion of Fermi/LAT and LLE data significantly improved the constraints on the p index. To show this, we fitted three physical models all based on the synchrotron emission to all the GRBs in both samples, with and without Fermi/LAT data (Fig. 4). The improvement in constraints is shown in Figure 4. We observe that the fit of GRB spectra without high-energy data returns unconstrained values of pindex (grey bins). In contrast, the inclusion of MWL data between 30 MeV and 10 GeV helps to constrain the parameter, returning a median value of p ≃ 2.7.
6.2.2. Model-2: Synchrotron plus power law dominated spectra
From our analysis, we identified a total of 14 spectra requiring the addition of a secondary power law component superimposed to the main synchrotron model. In this section, we report two GRBs as examples, namely GRB 221023A and GRB 090902B.
In the case of GRB 221023A, as can be seen in Fig. A.2, the power law component emerges at later times, around ∼25 s after the burst, and subsequently it fades away. Interestingly, the onset of the power law coincides with a softening of the synchrotron emission, which exhibits a particularly soft electron distribution index p ≃ 3.5. In these cases, as well as in the case of GRB 190114C, descibed in Section 6.2.3, the synchrotron radiation alone is not capable to describe the curvature around the peak of the spectrum. To fully characterise the spectral softening, we include an additional cut-off component to the synchrotron component in the energy range 100 keV–1 MeV.
In the case of GRB 090902B, the power law component is present throughout the entire duration of the prompt emission (Fig. A.1). It extends to lower energies, influencing the synchrotron spectrum even at a few keV, and has a larger impact compared to the case of GRB 221023A. Moreover, in GRB 090902B, the flux of the power law component closely tracks the time evolution of the synchrotron one, indicating a possible connection between the two emission processes. For GRB 221023A, the power law component appears only in a few time bins, making it difficult to probe its time evolution and to establish a consistent physical scenario.
6.2.3. Model-3: Synchrotron plus cut-off power law dominated spectra
In the case of GRB 190114C, during its first time bin (0–4.6 s) the spectrum clearly requires the addition of a HE cut-off to the power law component superimposed to the synchrotron spectrum, described in Model-2. This new model, named Model-3, allows us to constrain the peak of the power law component at higher energies, thanks to the availability of data from LLE and LAT. In all the time bins, the synchrotron component appears to be narrow, with both νm and νc unconstrained. Indeed, all the spectra show a strong softening observed by BGO. Previous studies also showed that a cut-off in the MeV energies is required to explain the observed spectra (Ajello et al. 2019).
The second spectral component represented by a cut-off power law in addition to the synchrotron component peaks at approximately 46 MeV, representing a rare instance where the high-energy peak can be identified. However, in the subsequent time bins, the high-energy cut-off is not required, resulting in a harder power law index (Fig. A.3).
7. Discussion
7.1. Temporal properties
In this paper, we analysed GRBs jointly detected by Fermi/LAT and Fermi/GBM. The selected GRBs are divided into two subgroups, Sample-1 and Sample-2.
The GRBs in Sample-1 have more than one temporal bin with significant detection in GeV energies and hence allow us to perform a temporal analysis of the HE light curve (0.1–10 GeV). We fit an analytical function describing an afterglow light curve (F0.1 − 10 GeV ∝ t−γ) to the Fermi/LAT dataset, which extends up to more than 1000 s beyond Fermi/GBM prompt duration, 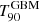 . During the early prompt phase, the data points deviate from the afterglow model. However, this excess is not significant enough to rule out an afterglow origin. Thus, the origin of the HE emission is rather inconclusive from the temporal fitting of the light curve to claim an association with prompt or afterglowemissions.
. During the early prompt phase, the data points deviate from the afterglow model. However, this excess is not significant enough to rule out an afterglow origin. Thus, the origin of the HE emission is rather inconclusive from the temporal fitting of the light curve to claim an association with prompt or afterglowemissions.
However, the temporal decay index γ yields an average value of approximately 1.5. To produce photons with E > 0.1 GeV, the associated electrons must be in the fast-cooling regime. Following the deceleration time, the afterglow flux is expected to decay as γ = −(3p − 2)/4, where p is the slope of the electron distribution function, as described in Nava et al. (2017). Using the inferred temporal index, a spectral index can be estimated using ϕ = −p/2 − 1. The derived spectral index most often is in accordance with the values observed in LAT spectra. However, there are some GRBs (e.g., GRB 090902B, see Fig. A.1), where the observed spectral index at GeV energies deviates from the predicted one derived from the temporal index. In these cases, the observed spectral indices at GeV energies are harder than the ones expected (see Figs. A.1 and A.2). At early times, such hardening is consistent with the emergence of a power law component, as observed in GRB 090902B and GRB 221023A. At later times, spectral hardening could suggest the presence of a potential SSC component of the afterglow. The energy range covered in our analysis, up to ∼100 GeV, does not identify the presence of the peak of this SSC component mostly due to the low-sensitivity of LAT. This further suggests that the appearance of the peak of the SSC component might be expected beyond 100 GeV (in the VHE gamma-rays). In addition, we also find that in many cases the HE photons seem to be delayed with respect to the keV–MeV emission. This delay was reported by many authors for different GRBs (i.e. Ackermann et al. 2013; Castignani et al. 2014; Ajello et al. 2019).
7.2. Spectral analysis
We investigated the nature of early high-energy emission by performing a detailed time-resolved spectral analysis for GRBs in Sample-1. Several studies previously argued that GRB spectra cannot be explained by synchrotron radiation from a distribution of non-thermal electrons (e.g., Beloborodov 2013; Axelsson & Borgonovo 2015; Burgess 2019), since GRB prompt spectra are in general much narrower than what predicted by synchrotron processes. However, our analysis extends the spectral coverage to energies exceeding 30 MeV by including LLE and LAT data. Such a large energy range (10 keV up to ∼10 GeV) reveals a unique perspective: most of the prompt GRB spectra we analysed appear significantly broader than previously expected, making them consistent with a synchrotron origin. Several of the GRBs analysed in this work have been the subject of extensive studies across a broad energy range. For instance, GRB 080916C was shown by Abdo et al. (2009b) to exhibit a prompt emission spectrum well described by a Band function extending up to GeV energies, consistent with a synchrotron origin. GRB 090902B has also been extensively studied due to its unusual prompt emission spectrum, which displays two distinct components (Abdo et al. 2009a). While this has often been interpreted as a combination of thermal and non-thermal emission (e.g. in Pe’er et al. 2012) our analysis does not invoke a thermal origin. Instead, within the synchrotron framework, we reproduce the observed spectrum by introducing a sharp cut-off in the MeV range, providing an alternative explanation for its spectral shape. In the case of GRB 090926A (see Fig. A.4 in the appendix), Ackermann et al. (2011) identified an additional power-law component with a high-energy cut-off in the GeV range. However, our analysis finds that the spectrum can be consistently interpreted as a single synchrotron component extending to GeV energies. A similar conclusion is drawn for GRB 090510 (Fig. A.5), where previous studies such as Ackermann et al. (2010) reported a distinct power-law, but our synchrotron modelling suggests a unified, single-component spectrum. GRB 160625B presents an interesting case where Ravasio et al. (2018) showed that the prompt emission spectrum can be successfully fitted with a three smoothly connected power laws function, interpreted as consistent with synchrotron emission. In this work, we find a similar agreement, supporting the synchrotron origin of the emission. Conversely, for GRB 190114C, our analysis confirms the presence of an additional component with a distinct spectral peak, in line with earlier findings (Ajello et al. 2020). It is worth emphasising the critical role of LAT Low-Energy (LLE) data, which often probes crucial informations in constraining the spectral shape and, in many cases, leads to different physical interpretations.
Specifically, in Sample-1, 52 spectra (10 GRBs) are well described by a pure synchrotron model that incorporates a high-energy cut-off, which effectively describes the high-energy emission. In contrast, the spectra of 23 GRBs in Sample-2 are well-fitted with a synchrotron model without requiring a high-energy cut-off. This is because the data for Sample-2 exhibit a lower bolometric flux compared to Sample-1 (as illustrated in Fig. 3), returning spectral parameters not well-constrained.
 |
Fig. 3. Histogram of the bolometric flux of GRBs. The bolometric fluxes are calculated in the energy band of 10 keV–10 GeV. The histogram hints towards the fact that the GRBs considered in Sample-1 are predominantly brighter than Sample-2. Therefore, Sample-1 is associated with significant data in both LLE and LAT. |
However, Fermi/LAT data remain consistent with the synchrotron model across all the analysed spectra. In addition, the availability of significant BGO and LLE data significantly impacts the estimation of the slope of the high-energy emission. This effect is more prominent in Sample-2, where we rarely have GRBs, which are bright in BGO energy range, and only 7 GRBs have available LLE data. For these reasons, the p index in this sample is poorly constrained.
It should be noted that, in most cases, synchrotron emission is in an intermediate cooling regime, where the values of the characteristic frequencies νm and νc are close, or even nearly identical (1 < νm/νc < 3). This is clearly demonstrated in Fig. 5, where most of the data points show a frequency ratio νm/νc ∼ 1. Specifically, when the two frequencies are approximately equal, the slope of the low-energy portion of the spectrum (i.e. before the break) still matches the expected behaviour of a synchrotron spectrum. There are 15 cases (3 GRBs) in Sample-1 where the spectra appear significantly narrower, with the electron spectral index p > 4, consistent with findings reported in previous works (see e.g. Burgess 2019). In these cases, an additional power law component is necessary to describe the high-energy data. In order to fully explain such spectra within thesynchrotron model framework, the introduction of a cut-off at lower energies is required, typically around a few MeV. In particular, this cut-off is consistently observed whenever a power law component is present in the prompt spectrum. Interestingly, a cut-off around 5 MeV is physically anticipated in the pair-loading afterglow scenario, as proposed by Beloborodov (2002).
In particular, we notice peculiarity in the time resolved spectra of three GRBs: GRB 090902B, GRB 190114C, and GRB 221023A. For GRB 090902B, the power law component persists throughout the entire prompt phase, exhibiting spectral evolution that appears consistent with the variability observed in the GBM data. This suggests that the GeV component is most likely associated with the prompt emission. In contrast, for GRB 221023A, the power law emerges only at later times, specifically during the final stages of the prompt emission, when the GBM flux is comparatively lower. This indicates that, in this case, the power law is more likely linked to the afterglow, which begins to overlap with and influence the prompt phase. For the spectrum of GRB 190114C during the time interval from 0.0 to 4.62 seconds, where a secondary component peaking at approximately 46 MeV is observed, our findings align with those reported by Ajello et al. (2019). However, we interpret the first spectral component as synchrotron emission with a MeV cut-off. The second component is distinctly identifiable only in the initial time bin analysed, when its peak energy is low enough to appear at high energies, before evolving into a power law in subsequent bins. This evolution suggests that the peak shifts to higher energies while the keV–MeV component decreases in flux, eventually adopting a power law-like appearance. This behaviour indicates that the HE emission in this case may originate from the afterglow, which begins to dominate during the latter part of the prompt phase. Consequently, the entire keV–GeV emission could represent a transition from the prompt to the afterglow phase, as suggested by Ravasio et al. (2019b). However, due to the sensitivity limitations of Fermi/LAT and the resulting poor spectral resolution, we are unable to precisely determine the nature and temporal evolution of this distinct power law component.
To compare our findings with previous studies, we also fitted the synchrotron model within the keV–MeV range, and therefore used only GBM data. In this limited range, the p index distribution is much broader, yielding less precise constraints. The use of LLE data was essential to have a better picture of the prompt spectrum after the peak. In fact, this methodology allowed us to place tighter constraints on the electron spectral index p, which exhibits a distribution that peaks around 2.7, as shown in Fig. 4. This aligns well with theoretical predictions from the particle acceleration mechanisms (for a recent review Sironi et al. 2015).
 |
Fig. 4. Comparison between the p index obtained from the spectral analysis between 8 keV and 10 GeV and using only the GBM data for Sample-1 and their corresponding uncertainties. The histogram on the sides provide a distribution of the indices for each case. The index while adding the GeV data provides significant constraints. |
It is interesting to note the evolution of the frequencies νm and νc for the GRBs in Sample-1. Since all the analysed spectra appear to be in a fast-cooling regime, νm consistently represents the spectral peak energy. In some cases, such as GRB 080916C, νm and νc are well-separated (νm/νc > 1) with the peak energy closely following the flux evolution, in other words, shifting to higher energies as the flux increases. However, in other cases such as GRB 090926A (see Fig. A.4), the two frequencies are indistinguishable, and the peak energy remains constant over time. In these cases, the high-energy slope becomes harder as the flux increases. Thus, there is no universal pattern for the evolution of the peak energy in the prompt spectrum, as the behaviour varies case to case.
We calculated the bolometric flux within the energy range spanning 10 keV to 10 MeV for the time-resolved spectra of GRBs in Sample-1, specifically when the spectra are optimally fitted using Model-1 and Model-2. Figure 6 illustrates the relationship between bolometric flux and the maximum photon energy in the co-moving frame in those temporal bins. Spectra with higher flux levels tend to exhibit a softer LAT index, which indicates an early prompt emission phase, and consequently shows a lower maximum photon energy because of the spectral cut-off previously described. Conversely, spectra with lower bolometric flux lead to the production of photons with higher energies. This could be due to the emergence of the afterglow component around the end of the prompt emission. However, the association of this HE emission, exhibiting harder photon indices, with the afterglow is particularly challenging, given the poor sensitivity of Fermi/LAT.
7.3. Comparison with the Band model
We investigated the impact of physical models in describing prompt emission spectra. To do so, we fitted our dataset not only with a synchrotron model, but also with the empirical Band function, which was already adopted in previous studies. We focused on the comparison between the Band function’s spectral index before the peak, α, with the frequencies ratio νm/νc. This comparison is illustrated in Fig. 5.
 |
Fig. 5. Spectral index, α, from the Band model compared to the ratio of the two characteristic frequencies, νm and νc, derived from the synchrotron model. The ratio, νm/νc, indicates the cooling regime, where a value greater or less than one represents the fast or slow cooling regime, respectively. The majority of the spectra are found to be in the fast- or marginally fast cooling regime. |
 |
Fig. 6. Bolometric flux vs. Emax for the GRBs in Sample-1. Each entry in the plot represents a spectrum of Sample-1. The best-fitted models (Model-1 or Model-2) of the individual spectrum are indicated with different markers. The colour bar indicates the corresponding spectral index for each spectrum (represented by each point in the graph) in the high-energy gamma-rays detected with LAT. The highest-energy photons are represented in the co-moving frame. For each spectrum the corresponding LAT photon index in the energy range 0.1–10 GeV is indicated by a colour gradient. |
We observe that when the ratio νm/νc > 1, the corresponding α tends to be softer, i.e. α < −0.8. The larger νm/νc is, the more α approaches the value of ∼ − 1.5, which is the slope expected in a fast-cooling regime. In contrast, when νm/νc ∼ 1, α ∼ −0.6, typical of the slow-cooling regime. These findings are consistent with previous studies both involving the Band function (Band et al. 1993) and exploring the synchrotron mechanism (Mei et al. 2025), further confirming the robustness of our approach. Additionally, in some spectra, the peak energy shifts to higher energies when fitted with a synchrotron model. However, when νm/νc ∼ 1, the spectrum is well-described by the Band function, since the exhibits a single energy break which corresponds to the peak energy. In these cases, the synchrotron model and the Band one lead to similar results.
We also compare the synchrotron spectral index p with the high-energy spectral index of the Band model, β. When fitted with the synchrotron model, the GRBs in our sample predominantly show a spectrum in the fast-cooling regime, when the photon index after the peak depends on p as β = −p/2 − 1. Our analysis in most cases shows the consistency between these two parameters. Although, the uncertainties obtained from the Band model are significantly larger, which do not lead to constraints on the spectra.
8. Conclusions
In this study, we performed a detailed analysis of GRBs detected simultaneously by Fermi/LAT and Fermi/GBM, focusing on the temporal and spectral features of their high-energy emission within the synchrotron scenario. The temporal analysis of the Fermi/LAT data was conducted under the assumption of an afterglow origin for the late-time HE component. We compared the spectral index inferred from the analysis of the light curves and the observed spectral index in the GeV band, in order to examine their consistency with the afterglow modelling. Our results show that the early LAT emission, particularly during the prompt phase, deviate from the expectations of standard afterglow scenarios. To further investigate these discrepancies, we performed MWL spectral modelling based on synchrotron emission, deriving key physical parameters such as the characteristic frequencies, νm and νc, and the slope of the electron distribution, p. These findings provide important insights into the origin of the early GeV emission observed in these bursts. Below, we summarise our strategy and keyfindings:
-
GRBs selected in this work: We searched for GRBs jointly detected by Fermi/GBM and Fermi/LAT, localised by Swift/BAT, with and without redshift up to year 2023. Our binning is driven by LAT time bins, for which we require a test statistic value exceeding ten. We examined two distinct samples: 1) GRBs with at least two consecutive time bins jointly detected (Sample-1) and 2) GRBs with single-bin detections (Sample-2). For Sample-1, we obtain a total of 12 GRBs; and for Sample-2, we obtain 23 GRBs, resulting in a total sample of 35 GRBs and 90 spectra, analysed in the energy range from 10 keV up to the highest-energy photon detected (∼GeV).
-
Modelling of the high-energy light curve and spectral prediction: For GRBs in Sample-1, the evolution of their LAT light curve can typically be modelled as an afterglow with a temporal decay index of γ ∼ 1.5. This value is roughly consistent with predictions of afterglow light curves from synchrotron radiation above the cooling frequency. However, deviations from the afterglow model, particularly near the peaks of the Fermi/LAT light curves show potential contributions from the prompt phase. Nonetheless, these deviations are not statistically significant enough to confirm the presence of prompt emission contamination. The spectral indices inferred during the temporal decay are generally consistent with those observed in the LAT energy range, reinforcing the link between the temporal and spectral properties. In some cases, a spectral hardening is observed at later times, suggesting the possible emergence of an SSC component in the afterglow phase, which may peak beyond the sensitivity range of the LAT.
-
Modelling of MWL spectra with synchrotron emission and inferences of the characteristic frequencies: We assumed a synchrotron origin for the prompt emission and fitted all the spectra in our sample using a synchrotron model. The spectral analysis provides distinct insights from those revealed by the temporal analysis: while the temporal features suggest an afterglow origin for the GeV photons, the spectral properties indicate that they are more likely associated with the prompt emission. This discrepancy shows the critical importance of combining spectral and temporal analyses, as relying solely on temporal data may lead to incorrect conclusions about the origin of high-energy photons. Our spectral investigation reveals that most GRB spectra align with synchrotron emission extending into the GeV range. A significant portion of GRBs in Sample-1 (52 spectra) is well-represented by a synchrotron model featuring a high-energy softening. For Sample-2, where the LAT data quality is comparatively lower, the spectra also remain consistent with synchrotron emission, though constraints on parameters such as the pindex are less precise. This highlights the importance of high-energy data in refining physicalmodels.
-
Best fitted models to characterise the observed spectra: We find that the majority of GRB spectra collected in this work can be described with a synchrotron model with a high-energy cut-off due to pair annihilation (Model-1). The two characteristic frequencies νm and νc are well constrained in the majority of cases, and a large number of spectra seem to be very close to each other or almost identical, pointing towards a marginally fast cooling synchrotron regime. However, for some GRBs, we find that the model needs to be accompanied by additional features. For example, in some cases, and in particular GRB 090902B, the spectra require both a cut-off in the spectra around a few MeV and an additional broad-band power law component. These are necessary to describe the high-energy behaviour (Model-2). The power law component is rather constrained by the low-energy data below 50 keV, as the emission cannot be higher than the flux observed at those energies. Moreover, for GRB 190114C, the data require an additional cut-off in the high-energy gamma-rays, defining the peak of an additional component around 50 MeV. It is important to state that in all the cases, which require an additional power law, the spectra require an MeV suppression (which is predicted in the pair-loaded afterglow scenario) in order to be consistent with the synchrotron emission.
-
Observation of a broader synchrotron component: Synchrotron fits return a value of the electron spectral index p ≃ 2.7, consistent with theoretical predictions for shock acceleration and reconnection processes (Sironi et al. 2015). The inclusion of Fermi/LLE and Fermi/LAT data significantly improves the constraints on p compared to fits limited to the Fermi/GBM range. The temporal and spectral properties of the high-energy emission provide strong evidence for synchrotron radiation as the dominant mechanism during the prompt phase of most GRBs. The spectral broadening observed when including LAT data reconciles previous discrepancies between observations and synchrotron model predictions, which were based on narrower energy ranges.
-
Emergence of a power law component at high-energies: For a subset of GRBs, an additional power law component (Model-2) is necessary to explain the observed spectra. When this component is included, the synchrotron spectral component often exhibits an MeV cut-off, potentially linked to a pair-loaded afterglow. This extra component is notably present in GRBs, such as GRB 090902B, GRB 221023A, and GRB 190114C, suggesting the involvement of an additional high-energy mechanism. In some cases, this component extends to lower energies, potentially contaminating the synchrotron spectrum. However, due to limited high-energy spectral data quality, the exact nature of this power law component remains uncertain. It may originate from the prompt phase in some bursts and from the afterglow phase in others.
-
Inference from the highest photon energy during prompt emission: Photons with the highest energies observed in the GRBs reported in the work range between 0.1 and 100 GeV. We observed that the initial bright emission phases (higher bolometric flux) are associated with softer spectra in the high-energy gamma-rays and hence lower photon energies. On the contrary, the states with low bolometric fluxes are associated with later time emission (close to the end of the prompt emission) and are most often represented by a harder (around spectral index of −2) spectral index in the high-energy gamma-rays. Observation of a high-energy photon from a spectrum, in particular beyond the high-energy spectral cut-off, might indicate an afterglow contamination. However, the poor sensitivity in LAT does not allow us to identify the presence of an afterglow emission component, if present. This is particularly relevant for the observation of the GRBs in prompt phases with current and future ground based telescopes, such as theMajor Atmospheric Gamma-ray Imaging Cherenkov Telescope (MAGIC) and Cherenkov Telescope Array Observatory (CTAO)- Large-sized Telescope (LST). An early observation of any very high-energy component can confirm the origin of this high-energy component.
-
Comparison with Band modelling: We fitted all the GRBs spectra in our sample using both the empirical Band model and the physical synchrotron model. The Band model is a simple analytical model that consists of two power laws smoothly connected at a characteristic frequency, which represents the peak energy in the νFν representation. In contrast, the synchrotron model, together with the high-energy cut-off, is able to identify the presence of spectral breaks. These breaks, together with the addition of the high-energy data (above 30 MeV), implies a comprehensive characterisation of MWL prompt spectra. This helps us identify the origin of the high-energy emission, whether it is a separate spectral component (i.e. an additional power law) or an extension of the synchrotron emission. Moreover, the high-energy part of the spectrum, while fitted with synchrotron, provides directly constraints on the particle distribution.
-
Detection of prompt emission in VHE Gamma-Rays: Ground-based Imaging Atmospheric Cherenkov Telescopes (IACTs) such as MAGIC, H.E.S.S., and the forthcoming Cherenkov Telescope Array Observatory (CTAO) need at least 20 seconds to reposition and target the transient discovered by localising keV/MeV telescopes (such as Swift/BAT and Fermi/GBM). The operations of IACTs are further constrained by a duty cycle of about 10–15%. In addition, the time needed for inter-telescope communication (usually in the range of tens of seconds) relies on the triggering instrument. For instance, the Fermi/GBM identifies a large number of bursts (around 240 GRBs per year), but the localisation (larger than 100 deg2 considering systematic and statistical uncertainties) it provides at trigger time, or via follow-up notices, is considerably larger than the field of view (FoV) of the IACTs (e.g., ∼5 deg2). One strategy that is potentially important involves conducting a tiling observation of the GRB localisation to capture the VHE transient signal. In a conservative scenario, the expected flux due to synchrotron emission within the 0.03–1.0 TeV energy range is approximately 10−12 erg cm−2 s−1. The sensitivity of the CTAO/LST for brief observations lasting about 10 seconds (or nearly 100 seconds) is roughly 10−9 (or 10−10) erg cm−2 s−1. Nonetheless, instances of a power law component emerging in several cases in our sample offer a promising opportunity to detect VHE gamma-ray emission either during ongoing prompt emission or in the early afterglow phase. This suggests that the most favourable scenario for detecting the VHE component of GRBs from the onset of prompt emission is achievable only with telescopes that have a larger FoV and higher duty cycles (about more than 80%). Consequently, LHAASO and High Altitude Water Cherenkov observatory (HAWC) are prime candidates for discovering the VHE counterpart during the prompt emission phase. However, a limitation of these instruments is their high-energy threshold, which is above a few hundred of GeV (unlike IACTs, which have a threshold of approximately a few tens of GeV), and their limited sensitivity at these higher energies.
In conclusion, the temporal and spectral properties of the high-energy emission provide strong evidence for synchrotron radiation as the dominant mechanism for the prompt phase of most GRBs. The requirement for an additional power law component in some GRBs points to the potential presence of additional physical processes (such as inverse Compton scattering, prompt or afterglow related). Further investigation of these cases, especially with MWL observations extending beyond the LAT energy range, at very high energies, is necessary to clarify the nature of these components. Overall, our analysis highlights the importance of extending GRB spectral studies to higher energies and emphasises the need for simultaneous MWL observations to disentangle the complex interplay between the prompt and afterglow emissions.
Acknowledgments
BB and MB acknowledge financial support from the Italian Ministry of University and Research (MUR) for the PRIN grant METE under contract no. 2020KB33TP. The authors thank the Director and the Computing and Network Service of the Laboratori Nazionali del Gran Sasso (LNGS-INFN). This research used resources of the LNGS HPC cluster realised in the framework of Spoke 0 and Spoke 5 of the ICSC project – Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing, funded by the NextGenerationEU European initiative through the Italian Ministry of University and Research, PNRR Mission 4, Component 2: Investment 1.4, Project code CN00000013 – CUP I53C21000340006. We acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources and support
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJ, 706, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Arimoto, M., et al. 2009b, Science, 323, 1688 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Asano, K., Atwood, W., et al. 2010, ApJ, 716, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Asano, K., et al. 2011, ApJ, 729, 114 [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Asano, K., et al. 2013, ApJS, 209, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Arimoto, M., Axelsson, M., et al. 2019, ApJ, 878, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Arimoto, M., Axelsson, M., et al. 2020, ApJ, 890, 9 [Google Scholar]
- Akaike, H. 1974, IEEE Trans. Automatic Control, 19, 716 [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [CrossRef] [Google Scholar]
- Axelsson, M., & Borgonovo, L. 2015, MNRAS, 447, 3150 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [Google Scholar]
- Banerjee, B., Oganesyan, G., Branchesi, M., et al. 2023, A&A, 678, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banerjee, B., Macera, S., De Santis, A. L., et al. 2024, arXiv e-prints [arXiv:2405.15855] [Google Scholar]
- Beloborodov, A. M. 2002, ApJ, 565, 808 [Google Scholar]
- Beloborodov, A. M. 2013, ApJ, 764, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., Nava, L., & Piran, T. 2016, MNRAS, 461, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., & Piran, T. 2013, ApJ, 769, 69 [Google Scholar]
- Beniamini, P., Nava, L., Barniol Duran, R., & Piran, T. 2015, MNRAS, 454, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, J. M. 2019, A&A, 629, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgess, J. M., & Ryde, F. 2015, MNRAS, 447, 3087 [Google Scholar]
- Burgess, J. M., Bégué, D., Bacelj, A., et al. 2019, Nat. Astron., 4, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Burnham, K. P., & Anderson, D. R. 2004, Sociol. Methods Res., 33, 261 [Google Scholar]
- Cao, Z., Aharonian, F., An, Q., et al. 2023a, Science, 380, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, Z., Aharonian, F., An, Q., et al. 2023b, Sci. Adv., 9, 46 [Google Scholar]
- Castignani, G., Guetta, D., Pian, E., et al. 2014, A&A, 565, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chand, V., Pal, P. S., Banerjee, A., et al. 2020, ApJ, 903, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Crider, A., Liang, E. P., Smith, I. A., et al. 1997, ApJ, 479, 39 [Google Scholar]
- Daigne, F., & Bošnjak, Ž. 2025, A&A, 693, A320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daigne, F., & Mochkovitch, R. 2000, A&A, 358, 1157 [NASA ADS] [Google Scholar]
- Daigne, F., Bosnjak, Z., & Dubus, G. 2011, A&A, 526, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derishev, E., & Piran, T. 2024, MNRAS, 530, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Ghirlanda, G., Celotti, A., & Ghisellini, G. 2002, A&A, 393, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghirlanda, G., Celotti, A., & Ghisellini, G. 2003, A&A, 406, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghirlanda, G., Ghisellini, G., & Nava, L. 2010, A&A, 510, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., & Celotti, A. 1999, A&AS, 138, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Celotti, A., & Lazzati, D. 2000, MNRAS, 313, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Ghirlanda, G., & Nava, L. 2010, MNRAS, 403, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Giannios, D. 2012, MNRAS, 422, 3092 [Google Scholar]
- Gruber, D., Goldstein, A., Weller von Ahlefeld, V., et al. 2014, ApJS, 211, 12 [Google Scholar]
- Guiriec, S., Kouveliotou, C., Daigne, F., et al. 2015, ApJ, 807, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Hascoët, R., Daigne, F., Mochkovitch, R., & Vennin, V. 2012, MNRAS, 421, 525 [NASA ADS] [Google Scholar]
- Kaneko, Y., Preece, R. D., Briggs, M. S., et al. 2006, AIP Conf. Proc., 836, 133 [Google Scholar]
- Kumar, P., & Duran, R. B. 2010, MNRAS, 409, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., McMahon, E., & Austin, U. 2008, MNRAS, 384, 33 [Google Scholar]
- Lloyd, N. M., & Petrosian, V. 2000, ApJ, 543, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Meegan, C., Lichti, G., Bhat, P. N., et al. 2009, ApJ, 702, 791 [Google Scholar]
- Mei, A., Oganesyan, G., Tsvetkova, A., et al. 2022a, ApJ, 941, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, A., Banerjee, B., Oganesyan, G., et al. 2022b, Nature, 612, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, A., Oganesyan, G., & Macera, S. 2025, A&A, 693, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meszaros, P., & Rees, M. J. 1997, ApJ, 476, 232 [CrossRef] [Google Scholar]
- Meszaros, P., & Rees, M. J. 2000, ApJ, 530, 292 [Google Scholar]
- Miceli, D., & Nava, L. 2022, Galaxies, 10, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L. 2018, IJMPD, 27, 1842003 [Google Scholar]
- Nava, L., Desiante, R., Longo, F., et al. 2017, MNRAS, 465, 811 [Google Scholar]
- Nava, L., Ghirlanda, G., Ghisellini, G., & Celotti, A. 2011, A&A, 530, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nava, L., Vianello, G., Omodei, N., et al. 2014, MNRAS, 443, 3578 [NASA ADS] [CrossRef] [Google Scholar]
- Oganesyan, G., Nava, L., Ghirlanda, G., & Celotti, A. 2017, ApJ, 846, 137 [Google Scholar]
- Oganesyan, G., Nava, L., Ghirlanda, G., & Celotti, A. 2018, A&A, 616, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oganesyan, G., Nava, L., Ghirlanda, G., Melandri, A., & Celotti, A. 2019, A&A, 628, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paczynski, B., & Xu, G. 1994, ApJ, 427, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2000, ApJ, 543, 66 [Google Scholar]
- Peér, A. 2008, ApJ, 682, 463 [Google Scholar]
- Pe’er, A., & Waxman, E. 2004, ApJ, 613, 448 [CrossRef] [Google Scholar]
- Pe’er, A., & Zhang, B. 2006, ApJ, 653, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Pe’er, A., Zhang, B.-B., Ryde, F., et al. 2012, MNRAS, 420, 468 [Google Scholar]
- Pelassa, V., Preece, R., Piron, F., Omodei, N., & Guiriec, S. 2010, arXiv e-prints [arXiv:1002.2617] [Google Scholar]
- Preece, R. D., Briggs, M. S., Mallozzi, R. S., et al. 1998, ApJ, 506, L23 [Google Scholar]
- Ravasio, M. E., Oganesyan, G., Ghirlanda, G., et al. 2018, A&A, 613, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ravasio, M. E., Ghirlanda, G., Nava, L., & Ghisellini, G. 2019a, A&A, 625, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ravasio, M. E., Oganesyan, G., Salafia, O. S., et al. 2019b, A&A, 626, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ravasio, M. E., Ghirlanda, G., & Ghisellini, G. 2024, A&A, 685, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rees, M. J., & Meszaros, P. 1994, ApJ, 430, L93 [Google Scholar]
- Rees, M. J., & Meszaros, P. 2005, ApJ, 628, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Ryde, F. 2004, ApJ, 614, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., & Piran, T. 1997, ApJ, 485, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [Google Scholar]
- Sironi, L., Keshet, U., & Lemoine, M. 2015, Space Sci. Rev., 191, 519 [CrossRef] [Google Scholar]
- Spruit, H. C., Daigne, F., & Drenkhahn, G. 2001, A&A, 369, 694 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tavani, M. 1996, ApJ, 466, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C. 1994, MNRAS, 270, 480 [NASA ADS] [CrossRef] [Google Scholar]
- van Eerten, H. 2015, JHEAp, 7, 23 [Google Scholar]
- Vianello, G., Gill, R., Granot, J., et al. 2018, ApJ, 864, 163 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: GRBs in Sample-1
In this section, we present the results of our analysis for the time-resolved GRB sample. The results of the analysis of GRB 080916C, GRB 090902B, GRB 221023A, GRB 190114C are summarised in Tables A1 - A4, and in the plots A1-A4. The physical parameters for the rest of the GRBs in Sample 1 are summarised in Table A4. Additionally, the spectra for each time interval, along with the LAT and GBM light curves (as shown in Figure 2 of the main text), are displayed in Figures A4–A11.
Synchrotron parameters for individual time bins of GRB 080916C, along with the bolometric flux and the highest-energy photon detected by Fermi/LAT.
Synchrotron parameters for each analysed time bin of GRB 090902B, along with the bolometric flux and the highest-energy photon detected by Fermi/LAT.
Synchrotron parameters for each analysed time bin of GRB 221023A, along with the bolometric flux and the highest-energy photon detected by Fermi/LAT.
Synchrotron parameters for each analysed time bin of GRB 190114C, along with the bolometric flux and the highest-energy photon detected by Fermi/LAT.
 |
Fig. A.1. Same as Fig.2, but for GRB 090902B. The upper-left panel shows the LAT and the GBM light curves. The middle panel compares the inferred spectral index ϕ with the observed one. The bottom panel presents residuals. The remaining panels display the time-resolved spectral fits. See Table A.2 for the spectral fit parameters. |
 |
Fig. A.2. Same as Fig.2, but for GRB 221023A. The upper-left panel shows the LAT and the GBM light curves. The middle panel compares the inferred spectral index ϕ with the observed one. The bottom panel presents residuals. The remaining panels display the time-resolved spectral fits. See Table A.3 for the spectral fit parameters. |
 |
Fig. A.3. Same as Fig.2, but for GRB 190114C. The upper-left panel shows the LAT and the GBM light curves. The middle panel compares the inferred spectral index ϕ with the observed one. The bottom panel presents residuals. The remaining panels display the time-resolved spectral fits. See Table A.4 for the spectral fit parameters. |
Spectral analysis results for GRBs in Sample-1. This table presents the synchrotron parameters obtained from our analysis of the full time-resolved GRB sample, listed for each analysed time interval. For each time bin, the table includes the derived synchrotron parameters, the bolometric flux, and the maximum energy photon.
 |
Fig. A.4. Lightcurves and spectra of GRB 090926A. |
 |
Fig. A.5. Light curves and spectra of GRB 090510. |
 |
Fig. A.6. Light curves and spectra of GRB 110731A. |
 |
Fig. A.7. Lightcurves and spectra of GRB 130427A |
 |
Fig. A.8. Lightcurves and spectra of GRB 131108A. |
 |
Fig. A.9. Lightcurves and spectra of GRB 160509A. |
 |
Fig. A.10. Lightcurves and spectra of GRB 160625B. |
 |
Fig. A.11. Lightcurves and spectra of GRB 170214A. |
Appendix B: GRBs in Sample-2
In this section, we present the spectra for the single-bin GRB sample. The physical parameters derived from our fits are summarised in Table 2.
 |
Fig. B.2. All GRBs in Sample-2, continued. |
All Tables
Synchrotron parameters for individual time bins of GRB 080916C, along with the bolometric flux and the highest-energy photon detected by Fermi/LAT.
Synchrotron parameters for each analysed time bin of GRB 090902B, along with the bolometric flux and the highest-energy photon detected by Fermi/LAT.
Synchrotron parameters for each analysed time bin of GRB 221023A, along with the bolometric flux and the highest-energy photon detected by Fermi/LAT.
Synchrotron parameters for each analysed time bin of GRB 190114C, along with the bolometric flux and the highest-energy photon detected by Fermi/LAT.
Spectral analysis results for GRBs in Sample-1. This table presents the synchrotron parameters obtained from our analysis of the full time-resolved GRB sample, listed for each analysed time interval. For each time bin, the table includes the derived synchrotron parameters, the bolometric flux, and the maximum energy photon.
All Figures
 |
Fig. 1. Model-1: synchrotron emission only. Model-2: additional power law included. Model-3: Model-2 with a high energy cut off in the spectrum. The characteristic frequencies (νc and νm), and the cut-off energy (Ecut) are indicated by the vertical lines. For a detailed description, see Section 5. |
| In the text | |
 |
Fig. 2. Time-resolved spectral analysis of GRB 080916C. The upper-left panel shows the fit of the LAT light curve (0.1–10 GeV) with the model from Eq. 1, along with GBM light curves (BGO and NaI). The middle panel compares the inferred spectral index (ϕ) with the observed spectral index, with the shaded grey area representing uncertainties on the predicted index, derived from the decay temporal index fit. The bottom panel shows the residuals, indicating the deviation of the light curve from the model. The remaining panels show the time-resolved spectral fits. Details are provided in Table A.1. |
| In the text | |
 |
Fig. 3. Histogram of the bolometric flux of GRBs. The bolometric fluxes are calculated in the energy band of 10 keV–10 GeV. The histogram hints towards the fact that the GRBs considered in Sample-1 are predominantly brighter than Sample-2. Therefore, Sample-1 is associated with significant data in both LLE and LAT. |
| In the text | |
 |
Fig. 4. Comparison between the p index obtained from the spectral analysis between 8 keV and 10 GeV and using only the GBM data for Sample-1 and their corresponding uncertainties. The histogram on the sides provide a distribution of the indices for each case. The index while adding the GeV data provides significant constraints. |
| In the text | |
 |
Fig. 5. Spectral index, α, from the Band model compared to the ratio of the two characteristic frequencies, νm and νc, derived from the synchrotron model. The ratio, νm/νc, indicates the cooling regime, where a value greater or less than one represents the fast or slow cooling regime, respectively. The majority of the spectra are found to be in the fast- or marginally fast cooling regime. |
| In the text | |
 |
Fig. 6. Bolometric flux vs. Emax for the GRBs in Sample-1. Each entry in the plot represents a spectrum of Sample-1. The best-fitted models (Model-1 or Model-2) of the individual spectrum are indicated with different markers. The colour bar indicates the corresponding spectral index for each spectrum (represented by each point in the graph) in the high-energy gamma-rays detected with LAT. The highest-energy photons are represented in the co-moving frame. For each spectrum the corresponding LAT photon index in the energy range 0.1–10 GeV is indicated by a colour gradient. |
| In the text | |
 |
Fig. A.1. Same as Fig.2, but for GRB 090902B. The upper-left panel shows the LAT and the GBM light curves. The middle panel compares the inferred spectral index ϕ with the observed one. The bottom panel presents residuals. The remaining panels display the time-resolved spectral fits. See Table A.2 for the spectral fit parameters. |
| In the text | |
 |
Fig. A.2. Same as Fig.2, but for GRB 221023A. The upper-left panel shows the LAT and the GBM light curves. The middle panel compares the inferred spectral index ϕ with the observed one. The bottom panel presents residuals. The remaining panels display the time-resolved spectral fits. See Table A.3 for the spectral fit parameters. |
| In the text | |
 |
Fig. A.3. Same as Fig.2, but for GRB 190114C. The upper-left panel shows the LAT and the GBM light curves. The middle panel compares the inferred spectral index ϕ with the observed one. The bottom panel presents residuals. The remaining panels display the time-resolved spectral fits. See Table A.4 for the spectral fit parameters. |
| In the text | |
 |
Fig. A.4. Lightcurves and spectra of GRB 090926A. |
| In the text | |
 |
Fig. A.5. Light curves and spectra of GRB 090510. |
| In the text | |
 |
Fig. A.6. Light curves and spectra of GRB 110731A. |
| In the text | |
 |
Fig. A.7. Lightcurves and spectra of GRB 130427A |
| In the text | |
 |
Fig. A.8. Lightcurves and spectra of GRB 131108A. |
| In the text | |
 |
Fig. A.9. Lightcurves and spectra of GRB 160509A. |
| In the text | |
 |
Fig. A.10. Lightcurves and spectra of GRB 160625B. |
| In the text | |
 |
Fig. A.11. Lightcurves and spectra of GRB 170214A. |
| In the text | |
 |
Fig. B.1. Spectral fitting of the GRBs in Sample-2. See Table 2 for details. |
| In the text | |
 |
Fig. B.2. All GRBs in Sample-2, continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.