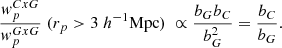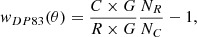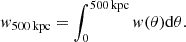EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 700 (August 2025) A&A, 700 (2025) A271 Full HTML
Open Access
Issue
A&A
Volume 700, August 2025
Article Number A271
Number of page(s) 10
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/202555287
Published online 28 August 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open Access funding provided by Max Planck Society.

1. Introduction

The galaxy red sequence is a tight correlation observed in color-magnitude diagrams of galaxies, where more luminous galaxies tend to be redder. It represents a population of massive, old, and quiescent (non-star-forming) galaxies, primarily composed of older stars that have exhausted most of their gas for star formation (Bell et al. 2004; Nelan et al. 2005; Faber et al. 2007). Red-sequence galaxies dominate the population in clusters of galaxies, particularly in the densest central regions. In particular, detecting and measuring the photometric redshift of galaxy clusters using the red-sequence technique is efficient and widely used (Gladders & Yee 2000; Koester et al. 2007; Rykoff et al. 2014; Clerc et al. 2020; Kluge et al. 2024).

The definition of the red sequence in galaxy clusters stems from the combination of photometric and spectroscopic surveys. With the photometric survey, we evaluate the color of each galaxy, while with the spectroscopic survey we measure its redshift and decide if it belongs to a cluster. The average color of galaxies in clusters is red, and only shows a small dispersion. Importantly, the value of the color directly correlates the with redshift with a small scatter, so the measurement of the color can be used as a proxy for redshift. Central to the definition of red-sequence models (and their scatter) is their need for (i) stellar population synthesis models, (ii) highly complete spectroscopic follow-up, and (iii) iteration to evaluate membership, including the removal of probable members that are outliers in color (Rykoff et al. 2014). Such training sets are not necessarily available at all redshifts.

In this article, we present a method to retrieve the red sequence as a function of redshift via cross-correlation between clusters and galaxies. The cross-correlation between galaxies and clusters has been widely used. Initially, Peebles (1974) and Lilje & Efstathiou (1988) measured a significant angular cross-correlation between Abell clusters and galaxy catalogs. Later, using the APM survey of galaxies and galaxy clusters, Maddox et al. (1990), Dalton et al. (1997), Croft et al. (1999) inferred the linear bias of the galaxy population and the matter density. Sánchez et al. (2005) subsequently measured the cross-correlation between X-ray-selected clusters (REFLEX, Böhringer et al. 2004) and galaxies from APM and 2MASS (Jarrett et al. 2000), which is the earliest precursor to this study. They measured, with significance, the presence of both the one-halo and two-halo terms in the cross-correlation signal and how it increases with the X-ray luminosity threshold. This measurement (and, more generally, any cross-correlation summary statistic; Banerjee & Abel 2021) has been shown to be sensitive to cosmological parameters (Hütsi & Lahav 2008; Fedeli et al. 2011; Salcedo et al. 2020), and of interest for future surveys such as Euclid and LSST (Laureijs et al. 2011; Euclid Collaboration: Mellier et al. 2025; Ivezić et al. 2019). Zu & Weinberg (2013) measured and modeled the cross-correlation between optically selected galaxy groups (Yang et al. 2007) and SDSS (Sloan Digital Sky Survey) galaxies (York et al. 2000). They constrained their model of galaxy infall kinematics (GIK), arguing that the large-scale infall of galaxies around massive clusters may be a powerful diagnostic of structure growth, dark energy, or deviations from general relativity. Robertson et al. (2024) recently refined the GIK model using the INDRA simulations (Falck et al. 2021) for possible precision cosmology inference. Paech et al. (2017) inferred the large-scale halo bias of optically selected galaxy clusters Rykoff et al. (2014) by cross-correlating them (in Fourier space) with photometric galaxies from SDSS (York et al. 2000).

Although the signal-to-noise ratio in the previously measured summary statistics was high, only a few studies explored possible trends as a function of galaxy properties, such as color or star formation rate (e.g., Baxter et al. 2017; Adhikari et al. 2021). In addition, recent lensing surveys have measured the profile of red-sequence and blue cloud galaxies in clusters (Hennig et al. 2017; Nishizawa et al. 2018). In a sense, these profile measurements represent a cross-correlation between the cluster and galaxy positions. They measure the dominance of red galaxies in the inner parts of clusters.

This article further explores this parameter space with the cross-correlation measurement as a tool. This approach attempts to go beyond the analysis of galaxy fractions as a function of the cluster-centric radius (e.g., van der Wel 2008; Bianconi et al. 2020; Vulcani et al. 2023).

In addition, a related cross-correlation between a hot gas measure (X-ray or SZ) and galaxies is a well-known signpost of feedback (Davies et al. 2019; Kukstas et al. 2020; Truong et al. 2020, 2021; Moser et al. 2022; Grayson et al. 2023; Lau et al. 2024; Sorini et al. 2024). Such cross-correlation measurements, aimed at constraining galaxy evolution models using the X-ray or SZ (Sunyaev-Zel’dovich) field, have been refined through ongoing observations in SZ (Yan et al. 2021; Amodeo et al. 2021; Ibitoye et al. 2022; Pandey et al. 2022; Sánchez et al. 2023; Das et al. 2023; Oren et al. 2024) and X-rays (Comparat et al. 2022; Zhang et al. 2024a,b, 2025; La Posta et al. 2024; Li et al. 2024; Popesso et al. 2024; Dev et al. 2024; Comparat et al. 2025).

Here, we focus on the cross-correlation between X-ray-selected galaxy clusters and galaxies. We use the extended ROentgen Survey with an Imaging Telescope Array (eROSITA) cluster catalogs derived from its first all-sky survey (eRASS1, Merloni et al. 2024; Bulbul et al. 2024). eROSITA is a wide-field X-ray telescope onboard the Russian-German “Spectrum-Roentgen-Gamma” (SRG) observatory, and it is currently the best X-ray instrument for constructing cluster samples (Merloni et al. 2012; Predehl et al. 2021; Sunyaev et al. 2021). We combine it with galaxies selected from the Legacy Survey (Dey et al. 2019), which currently provides the best match in depth and area coverage to the eROSITA cluster sample.

In this article, we extend the statistical study of the cross-correlation between clusters and galaxies as a function of galaxy color. We describe the observations used in Section 2 and the cross-correlation measurements in Section 3. We discuss our findings in Section 4.

2. Observations

In this section, we describe the X-ray-selected cluster catalogs (Sect. 2.1) and the galaxy catalogs (Sect. 2.2).

2.1. Volume-limited cluster sample from eROSITA (eRASS:1)

The eROSITA telescope, equipped with seven identical Wolter-1 mirror modules, is a sensitive wide-field X-ray instrument capable of delivering deep, sharp images over vast sky areas in the 0.2–8 keV energy range, with maximum sensitivity between 0.3 and 2.3 keV. In its first survey, released in 20241 (Merloni et al. 2024), the German eROSITA consortium observed the western Galactic hemisphere. Approximately 12 247 clusters were detected as extended sources in X-rays and confirmed optically (Bulbul et al. 2024). Photometric redshifts were measured using the redMaPPer algorithm in scan mode (Rykoff et al. 2014; Kluge et al. 2024). Seppi et al. (2024) extracted volume-limited samples from this flux-limited survey to perform a detailed clustering analysis. We used three of these volume-limited cluster and random catalogs: the C0, C1, and C2 samples (containing 1650, 2993, and 3732 sources, respectively). These samples span redshifts above 0.1 and below 0.2 (0.3, 0.4), and have log10 soft X-ray luminosities larger than 42.7, 43.1, and 43.4, respectively The mean redshifts of the samples are 0.153, 0.206, and 0.264. The mean X-ray luminosities are 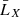L ¯ X $ \bar{L}_X $ = 4.63 ± 0.97, 7.38 ± 0.98, and 10.21 ± 0.98) ×1043 erg s−1. The purity of the samples exceeds 95%. Seppi et al. (2024) measured and modeled the correlation functions of these samples using a halo occupational distribution (HOD; Cooray & Sheth 2002; More et al. 2015). They find satellite cluster fractions consistent with zero: fsat <  14.9% (< 9.3%, < 9.9%), indicating that the cluster samples predominantly consist of distinct halos. The deduced large-scale halo bias increases with the applied luminosity threshold (and mean luminosity) b = 2.95 ± 0.21, 3.35 ± 0.23, and 3.69 ± 0.27 (see their Fig. 8). Equivalently, the mean halo masses, 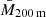M ¯ 200 m $ \bar{M}_{\mathrm{200\,m}} $ = 3.09 ± 0.48, 3.54 ± 0.51, and 3.83 ± 0.55 ×1014 M⊙, correlate with the average X-ray luminosity. These characteristics set the scene for the clusters fed into the cross-correlation.

The choice of cluster samples depends on the available galaxy samples. As detailed below, the galaxy samples considered here extend to a maximum redshift of 0.4. This limit justifies our focus on these three low-redshift cluster samples rather than on higher-redshift samples.

2.2. Legacy Survey DR10.1 galaxies

We used the Legacy Survey tenth data release (LS10 hereafter) to select a flux-limited galaxy sample (Dey et al. 2019). This sample is described in detail in Comparat et al. (2025). We summarize the main information here. In LS10, source catalogs are available for Dec < 32°; from these, we selected low-redshift galaxies using an algorithm similar to that of the DESI Bright Galaxy Sample (BGS) (Hahn et al. 2023), applying a magnitude cut rAB <  19.5. The main difference between our re-implementation of the BGS selection and the original is that we applied stricter MASKBITS and color cuts in order to increase the purity of the photometric sample and guarantee an unbiased clustering estimate when using photometric redshifts. The BGS spectroscopic sample naturally removes contaminants; therefore, its selection cuts can be slightly looser, and thus increasing completeness without impacting purity. However, in the western Galactic hemisphere observed by the German eROSITA consortium, only limited spectroscopy is available, so we applied stricter criteria when defining the galaxy sample. Following the BGS selection criteria, we separated stars from galaxies and selected galaxies with 13 <  rAB <  19.5 to obtain a set of BGS-like galaxies. We required low Galactic reddening (E(B-V) < 0.1) and at least one observation in each of the g, r, and z bands. Using MASKBITS , we removed secondary detections (MASKBIT 0), sources overlapping Tycho sources with MAG_VT < 13, or Gaia stars with G < 13 (MASKBIT 1), and sources that touch pixels in globular clusters (MASKBIT 13). We also removed sources for which FITBITS 1, 6, 10, 11, 12, and 13 are turned on. Finally, we removed Gaia duplicates (TYPE="DUP"). We followed the BGS selection to discard artifacts, but with a stricter criterion in color-color space, retaining sources with −0.2 <  g − r <  2 and −0.2 <  r − z <  1.6. The resulting galaxy sample has a completeness greater than 90%. It contains 13 881 761 sources over a footprint of 16,796 square degrees and extends up to redshift 0.5.

2.3. Sample combinations

In this analysis, we considered two cases for the cross-correlation: (i) clusters crossed with the general population of galaxies, split into red-sequence and blue-cloud galaxies, and (ii) clusters crossed with galaxies in narrow color bins. Table 1 summarizes the sample combinations considered.

Table 1.

Description of the galaxy and cluster sample combinations considered.

For the first case, a volume-limited set of galaxies is required to enable a clear interpretation, so we used those designed and analyzed in Comparat et al. (2025). We selected cluster-galaxy sample pairs so that the galaxy sample completely covers the redshift interval of clusters. Among the possible galaxy samples, we used the one with the most significant number of galaxies, i.e., the one with the lowest stellar mass threshold. Among the cluster samples, only the C0 (0.1 <  z <  0.2) and C1 (0.1 <  z <  0.3) cluster samples have their redshift intervals covered by the galaxy samples considered. The samples covering at least the cluster redshift range and maximizing the number of galaxies are: G1025,selected with 10.25 <  log10(M*[M⊙]) <  12 and 0.05 <  z <  0.22 for C0; and G1075, with 10.75 <  log10(M*[M⊙]) <  12 and 0.05 <  z <  0.31 for C1. We refer to these combinations C0xG1025 and C1xG1075. In Comparat et al. (2025), we measured the autocorrelation function of these galaxy samples and fitted a HOD model to them. The G1025 (G1075) sample comprises 3 280 777 (2 768 066) galaxies; it has a mean redshift of 0.162 (0.226) and a mean stellar mass (log10(M*/M⊙)) of 10.66 (11.02). The redshift selection, 0.1 <  z <  0.2 (0.1 <  z <  0.3), to match that of the cluster samples C0 (C1) reduces the total number of galaxies to 2 255 070 (1 480 941) for the G1025 (G1075) sample. From the HOD fits, we derived a large-scale halo bias value of 1.29 (1.43) and a mean halo mass hosting central galaxies of log10(M200m/M⊙)=12.8 (13).

For the second case, we required the largest number of galaxies to enable fine binning as a function of color. Therefore, we used the complete sample described above (BGS). We used the cluster sample with the largest overlapping redshift range, sample C2 (0.1 <  z <  0.4), and we refer to this combination as C2xBGS.

3. Cross-correlation between individual galaxies and X-ray selected clusters

We describe the cross-correlation between clusters and the general galaxy population, as well as the split into red-sequence and blue-cloud galaxies, in Sect. 3.1. In Sect. 3.2, we investigate how the cross-correlation measurement varies with the g − r color of galaxies and the cluster redshifts.

3.1. Cross-correlation between red-sequence, blue-cloud galaxies, and X-ray-selected clusters

The projected cross-correlation, wp(rp), was computed using the estimator from Landy & Szalay (1993). This measurement used a galaxy sample with its associated random sample (both described in Comparat et al. 2025), as well as a cluster sample and its random sample (both described in Seppi et al. 2024). These constituted two distinct data samples and two distinct random samples, each with its own photometric redshift measurements. We estimated uncertainties by repeating the calculation 1000 times, each time removing 10% of the area by discarding a distinct set of healpix pixels. Another challenge with this photometric-redshift-defined galaxy sample was controlling systematic variations in galaxy number density due to external variables. We found a remaining 1–2% variation that was not captured in the random catalogs for these two samples. Quantitatively addressing these small discrepancies would require extensive spectroscopy. Until additional spectroscopic data become available in the southern hemisphere? (e.g., in five years with 4MOST; de Jong et al. 2019), we will continue to apply a systematic uncertainty floor of 2% to the correlation function measurements.

Figures1 and 2 present the auto- and cross-correlation functions for C1xG1075 and C0xG1025, respectively. The galaxy autocorrelation, split into red-sequence and blue-cloud, was accurately measured, with sub-percent statistical uncertainties (see middle panels, dashed lines). The cluster-galaxy cross-correlation functions also show small relative uncertainties in the range of 2–10% (see middle panels, solid lines). This represents a clear improvement compared to the previous estimate of Zu & Weinberg (2013), who crossed the groups from Yang et al. (2007) with all SDSS galaxies to obtain relative uncertainties in the range of 10%–50%. The gain in signal-to-noise ratio arises from the use of galaxy samples that are 5–10 times denser.

thumbnail Fig. 1.

Correlation functions for the C1xG1075 sample, using C1 clusters (0.1 <  z <  0.3, log10(LX [erg/s]) >  43.1) and G1075 galaxies (10.75 <  log10(M*[M⊙]) <  12). Left: Projected autocorrelation functions of galaxies (and clusters), split into red-sequence (red) and blue-cloud (blue) are shown with dashed lines; projected cluster-galaxy cross-correlation functions are shown as solid lines. This signal is dominated by the red sequence galaxies: the red lines are significantly higher than the blue lines. For comparison, we show the measurement from Zu & Weinberg (2013), who cross-correlated SDSS galaxies with galaxy groups from Yang et al. (2007), whose brightest group galaxy has a stellar mass in the range (11.4 <  log10(MBGG*[M⊙]) <  11.9). This measurement is shown as a green dotted line. In this analysis, we trust the measurements up to 15 h−1Mpc (to the left of the shaded area), beyond which they may be affected by systematics uncertainties. Right: Ratio between the galaxy-cluster cross-correlation and the corresponding galaxy autocorrelations. This comparison shows the strength of the clustering in the cluster environment relative to that of all galaxies (i.e. galaxies in any environment). The ratio is above one, indicating that galaxies cluster more strongly near galaxy clusters. For red-sequence galaxies, the extra power in clustering increases when scales decrease. For blue-cloud galaxies, the clustering increases towards small scales down to 0.3 Mpc/h, where it stalls and decreases below 0.2 Mpc/h. The green horizontal line indicates the ratio of large-scale halo biases determined in Seppi et al. (2024) and Comparat et al. (2025), which aligns with the ratio of correlation functions on large scales, as expected. Bottom: Results of the Jackknife procedure. Left: Relative uncertainties for cross-correlation functions. Right: Cross-correlation coefficient for the C1xG1075 sample. Relative uncertainties range from 1% to 10%; previous SDSS measurement showed 10%-30% uncertainties. The high density of galaxies in LS10 enables increased measurement precision.

thumbnail Fig. 2.

Correlation functions for the C0xG1025 sample, continued from Fig. 1. These are measured using the C0 cluster sample (0.1 <  z <  0.2, log10(LX [erg/s]) >  42.7) in combination with the G1025 galaxy sample (10.25 <  log10(M*[M⊙]) <  12). A comparison is provided using the measurement from Zu & Weinberg (2013), showing the group-galaxy cross-correlation for the sample of Yang et al. (2007), with brightest group galaxies in the stellar mass range (11.2 <  log10(MBGG*[M⊙]) <  11.4) and all SDSS galaxies. This result is shown as a dotted line.

When considering all galaxies, the split in red and blue populations is clear. In the cross-correlation, the blue galaxies depart from the average cross-correlation, while the red galaxies closely follow the average. This indicates that the red galaxies dominate the cross-correlation signal. This description applies to the two sample combinations studied. We did not observe a significant trend when increasing the redshift range from 0.1 <  z <  0.2 to 0.1 <  z <  0.3 and the luminosity threshold from 42.7 to 43.1. These findings are in qualitative agreement with previous studies of the occupation of red and blue galaxies in clusters (Hennig et al. 2017; Nishizawa et al. 2018) and the established fact that red-sequence galaxies dominate at high halo masses and low redshift (e.g., Zu & Mandelbaum 2015, 2016).

Since X-ray luminosity correlates with halo mass (with a scatter of 0.3 dex), this cross-correlation directly probes the galaxy population in high-mass dark matter haloes. The ratio of the cross-correlation between galaxies and clusters (wpCxG) to the galaxy-galaxy autocorrelation (wGxG) (see right panels of Figs. 1 and 2) reveals the extra power from the massive haloes. This ratio serves as a direct probe of how the environment influences different classes of galaxies.

On large scales (rp >  3 h−1Mpc), this correlation-function ratio is expected to reflect the ratio of large-scale halo biases:

w p CxG w p GxG ( r p > 3 h − 1 Mpc ) ∝ b G b C b G 2 = b C b G . $$ \begin{aligned} \frac{{ w}^{CxG}_p}{{ w}^{GxG}_p}\; (r_p>3\; h^{-1} \mathrm{Mpc} )\; \propto \frac{b_{G}b_{C}}{b^2_{G}}=\frac{b_{C}}{b_{G}}. \end{aligned} $$(1)

Indeed, we find that the correlation-function ratio is in agreement with the ratio of large-scale halo biases inferred by Seppi et al. (2024) for the clusters and by Comparat et al. (2025) for the galaxies (see the green shaded region in the right panels of Figs. 1 and 2).

We now focus on smaller scales, within the one-halo term. For the red-sequence galaxies, the ratio between cross-correlation and autocorrelation steadily increases as the separation decreases, from 2h−1 Mpc down to 50h−1 kpc. For blue-cloud galaxies, the ratio between cross-correlation and autocorrelation increases toward smaller separation from 2h−1 Mpc down to 0.3h−1 Mpc, where it stalls and turns over below 0.2h−1 Mpc. This turnover corresponds to the absence of blue-cloud galaxies towards the centers of clusters. These results provide evidence for an infalling population of blue-cloud galaxies that eventually get ram-pressure stripped and disappear upon entering the clusters.

3.1.1. Comparison with models

We compared these results with a prediction constructed using the publicly available UNIVERSEMACHINE model from (Behroozi et al. 2019; Aung et al. 2023) run on the Uchuu simulation (Ishiyama et al. 2021). We selected the two snapshots near the mean redshifts of the samples considered (z = 0.14, z = 0.19), applied the same cuts as in observations, and predicted the equivalent summary statistic (see Fig. 3). To do so, we applied the method of Comparat et al. (2020) and Seppi et al. (2022) to predict X-ray luminosities to each dark matter halo. The models agree with observations on a large scale, indicating that they reproduce the large-scale structure accurately.

thumbnail Fig. 3.

Galaxy-cluster cross-correlation functions compared to model predictions from the Uchuu+UniverseMachine (UM) model (Aung et al. 2023, left column) and LGAL model (Ayromlou et al. 2021 right column). Results are shown for the compared to the C1xG1075 (top) and C0xG1025 (bottom) combinations Model prediction are shown in orange for red-sequence galaxies and in pink for blue-cloud galaxies. The UM model agrees well with the C1xG1075 observations. At lower redshift, for lower stellar mass galaxies, the UM model exhibits a mild discrepancy with the observations, suggesting that the quiescent fraction of cluster galaxies with stellar mass of ∼10.5 may be underestimated. The LGAL model agrees with the measurements of the complete galaxy population (gray lines) and red galaxies (red and orange lines) for both he C1xG1075 and the C0xG1025 combinations, down to 0.5 Mpc/h. The LGAL blue-cloud galaxies show excess power on small scales compared to the observations.

We find excellent agreement between the model and the C1xG1075 measurements at small separations, suggesting that the quiescent fraction in the model is sensitive to galaxies with a log10 stellar mass greater than 10.75 in clusters. At face value, this fraction reaches 90% in the inner regions of the halos (see Fig. 11, Aung et al. 2023). For C0xG1025, which samples lower stellar masses and lower redshifts, we find slight discrepancies at the 1σ level. To match the observations, the model must have a higher fraction of quiescent galaxies in the 10.25 to 10.75 range. The model quiescent fraction for such galaxies, about 80% in the center (see Fig. 11, Aung et al. 2023), may need to be increased. The observed cross-correlation therefore serves as a benchmark to further constrain a model of the quiescent fraction as a function of cluster-centric radius.

In addition, we compared the measurements with predictions from the latest version of the L-Galaxies semi-analytical model (Ayromlou et al. 2021). This model runs on subhalo merger trees from the Millennium simulation (box size ∼ 500 Mpc/h; Springel et al. 2005) and incorporates key physical processes, including gas accretion into dark matter halos, gas cooling, star formation, stellar feedback, chemical enrichment, and supermassive black hole-related mechanisms such as seeding, growth, and AGN feedback, as well as environmental effects. We used the L-Galaxies snapshot at z ∼ 0.2, which corresponds to the midpoint of our redshift bins.

Overall, L-Galaxies reproduce the one-halo term of the cross-correlation function for the complete galaxy population in the C1xG1075 sample combination quite well. However, the model appears to overpredict the star-forming galaxy population when splitting galaxies into star-forming and quenched populations. It is important to note that the definition of quenching can affect this classification, as demonstrated by Vani et al. (2025), who compared quenched galaxy selections based on specific star formation rate (sSFR) thresholds versus color-based criteria (e.g., rest-frame NUV-r and r-J colors).

A more detailed comparison with predictions from large-volume hydrodynamical simulations (e.g., Pakmor et al. 2023; Schaye et al. 2023; Nelson et al. 2024) should provide further insights into the possible relation between quenching and the thermodynamics of the hot gas in clusters (e.g., Lim et al. 2025).

3.2. Angular cross-correlation between clusters and galaxies as a function of cluster redshift and galaxy color

We extended the cross-correlation analysis from the previous section by further splitting the samples as a function of galaxy color specifically, g − r as measured in the Legacy Survey (with DECam; Flaugher et al. 2015), and cluster redshift as measured by Kluge et al. (2024) using redMaPPer (Rykoff et al. 2014), to retrieve information about the galaxy red sequence as a function of redshift.

The accuracy of the galaxy photometric redshifts (0.05) was insufficient to cleanly separate the galaxy sample into fine and accurate redshift bins. We therefore considered the complete galaxy sample described above (BGS), selected to be brighter than rAB <  19.5 regardless of redshift (see Sect. 2.2). The BGS sample was then divided by its observed g − r color into 44 bins of 0.05 mag width, spanning the range of –0.2 to 2. Since the complete galaxy population extends to redshift 0.4, we used the C2 cluster samples from Seppi et al. (2024), defined by 0.1 <  z <  0.4 and log10(LX [erg/s]) >  43.4. The accuracy of the cluster photometric redshift in this range is approximately 0.005 (Kluge et al. 2024). We split the cluster sample into 30 redshift bins of 0.01 width. The lowest and highest redshift bins of the cluster and random samples may suffer from boundary effects; therefore, we only considered those within the sample in the range 0.15 <  z <  0.35. We then measured the cross-correlation between the 44 galaxy samples and 20 cluster samples, yielding a total of 20 × 44 = 880 cross-correlations. Because we do not have a set of random points for the complete BGS galaxy sample, we could not use the optimal estimator of Landy & Szalay (1993) for the cross-correlation. Instead, we used a stacking technique, counting pairs of clusters and galaxies as a function of their separation, and normalized these counts by the equivalent counts centered at random positions (a random catalog was available for the cluster sample). The stacking was equivalent to the Davis & Peebles (1983) estimator of the angular cross-correlation, which used galaxy-cluster pair counts and required only a random sample for the cluster sample:

w D P 83 ( θ ) = C × G R × G N R N C − 1 , $$ \begin{aligned} { w}_{DP83}(\theta ) = \frac{C\times G}{R\times G}\frac{N_R}{N_C} -1, \end{aligned} $$(2)

where C represents the clusters (with NC their number), G is the galaxies, and R is the cluster randoms with (NR their number).

This estimator accurately estimates the clustering, but will overestimate the variance on large scales (beyond a few arcminutes) compared to the Landy & Szalay (1993) estimator (see details of estimator comparisons in, e.g., Pons-Bordería et al. 1999; Kerscher et al. 2000). However, since we focus here on the one-halo term and its integrated signal (up to 500kpc, corresponding to 2.5 arc minutes at z = 0.2), this estimator is well suited, but it would not be appropriate for estimating the large-scale clustering and its uncertainties, as done in the previous section.

We converted the angles into proper distances at the mean redshift of each cluster sample. The majority of the correlation functions are consistent with zero, showing no signal, whereas a subset shows a strong signal. To illustrate the strength of the correlation in the one-halo term, we integrated all correlation functions up to 500kpc (proper distance) to obtain

w 500 kpc = ∫ 0 500 kpc w ( θ ) d θ . $$ \begin{aligned} { w}_{\rm 500\,kpc} = \int ^{500\,\mathrm{kpc}}_0 { w}(\theta ) \mathrm{d}\theta . \end{aligned} $$(3)

A distance of 500 kpc is well inside the one-halo term of the clusters considered, and away from the two-halo term, thereby capturing the extra power in clustering due to galaxies falling into the cluster potential well (see previous section and figures). The resulting values of w500 kpc are shown in Fig. 4 left and right panels as a function of color for two redshift values, z = 0.185 and z = 0.325.

thumbnail Fig. 4.

Measured integral of the cross-correlation function up to 500 kpc as a function of color at redshift 0.195 (left column) and 0.325 (right column). A Gaussian model was fit to the data points (red) and is compared to the model from Kluge et al. (2024) (in black), showing good agreement.

We find that, at fixed redshift, the integral of the cross-correlation captures the existence of the red sequence without any a priori assumptions about the redshift of these galaxies, their possible membership in the clusters, or stellar population synthesis models. Indeed, compared to the model of Kluge et al. (2024) based on EZgal (Mancone & Gonzalez 2012), we find excellent agreement between the color at which this integral peaks (at a given redshift) and the color of the red sequence (Fig. 4). We fit a Gaussian to the observations (see Fig. 4) to retrieve the color value at which the correlation peaks, as well as its spread, assuming it is Gaussian. The residuals show that the Gaussian approximation adequately captures most of the observed curve. We repeated the fits in each redshift slice as a function of color. Table 2 gives the parameters obtained for each fit. These values are very close to those of the model of Kluge et al. (2024), but are derived independently. We accurately measured the scatter of the red sequence as a function of redshift.

Table 2.

Best-fit g − r red-sequence values and scatter as a function of redshift.

We show the values of w500 kpc obtained for all correlation functions in the color-redshift plane in Fig. 5. Using the fits described above, we located our best-fit red sequence (red dashed) in this plane. There is nearly perfect agreement with the model of Kluge et al. (2024), which is shown in black.

thumbnail Fig. 5.

Redshift vs. g-r color, coded by the integral of the cross-correlation function up to 500 kpc. Colored symbols represent individual cross-correlation functions. Dashed red lines indicate the models derived for each redshift slice. Black lines show the red-sequence model from Kluge et al. (2024). Red sequence and its scatter are accurately recovered.

4. Discussion and outlook

In this study, we measure the cross-correlation between volume-limited samples of galaxies and X-ray-selected clusters with unprecedented signal-to-noise (Sect. 3.1). Owing to this high level of significance, we finely split the samples over a grid of redshift and color to measure the amplitude of the one-halo term via the integral of the cluster-galaxy cross-correlation within 500 kpc (Sect. 3.2).

We report two main findings. Firstly, the cross-correlation between clusters and galaxies, divided into quiescent and star-forming galaxies, contains key information about the infall of blue-cloud galaxies, feedback, and quenching in a high-mass environment (Fig. 1 and 2). The results are in excellent quantitative agreement for stellar masses above log10(M*[M⊙]) >  10.75 with the empirical galaxy evolution model of Behroozi et al. (2019), Aung et al. (2023). The measurements also suggest that in the stellar mass range 10.25 <  log10(M*[M⊙]) <  10.75, the red fraction may be slightly underestimated by the model (Fig. 3). The results are in fair qualitative agreement with the LGAL model (Ayromlou et al. 2021).

Secondly, we find that the integral of the cross-correlation (w500 kpc) between clusters (split in redshifts) and galaxies (split in colors) enables a direct measurement of the red sequence and its scatter in galaxy clusters (Figs. 4 and 5). This measurement is independent of models of galaxy evolution or our ability to classify galaxies as cluster members. This method constitutes an alternative to the calibration of red-sequence models from (Rykoff et al. 2014). Similarly to the method of Rykoff et al. (2014), it requires a well-understood cluster sample with accurate photometric redshifts, which in this case is provided by the X-ray-selected eRASS1 catalog from Seppi et al. (2024) and its volume-limited samples. For the galaxies, this method requires a complete (clean), flux-limited galaxy sample (no redshifts required, only colors and sky positions), here provided by the LS10 sample of Comparat et al. (2025). The Rykoff et al. (2014) method additionally requires a stellar population synthesis model (e.g., Bruzual & Charlot 2003) and a set of known galaxy members (with spectroscopic redshifts) that are in the red sequence (e.g., Clerc et al. 2020).

Discussion

With these new measurements, assuming models of how galaxies populate clusters, one can constrain the relative abundance of red and blue galaxies in clusters, as well as how infall, feedback, and quenching are related (see e.g., De Lucia & Blaizot 2007; Ayromlou et al. 2023; Aung et al. 2023; Lehle et al. 2024).

Alternatively, one could constrain the average profile and concentration of red-sequence and blue-cloud galaxies in galaxy clusters with a halo model. The precision of the summary statistic measured here would allow us to improve upon current constraints from Hennig et al. (2017) and Nishizawa et al. (2018). It may also be possible to constrain the location at which the transition from field to cluster galaxies occurs and to determine at which radius ram-pressure stripping becomes essential.

Outlook

Splitting the cluster samples as a function of halo mass may provide further insights. The situation in low-mass clusters or groups is expected to differ significantly from that of massive clusters. Upcoming cluster samples from eROSITA, Euclid, LSST, and CMB-S4 will provide such analyses. Indeed, ram pressure depends on the square of the infall velocity (see recent review from Boselli et al. 2022).

A similar analysis using SZ-detected clusters (e.g., ACT & Planck; Naess et al. 2020, 2025), or by CMB-S4 in the future (Abazajian et al. 2016), and using the same set of galaxies would be complementary, but is outside the scope of this study.

In the future, with Euclid (Euclid Collaboration: Mellier et al. 2025) and LSST (Ivezić et al. 2019), and their upcoming photometric galaxy samples together with 4MOST and DESI spectroscopic samples (de Jong et al. 2019; DESI Collaboration 2016a,b), we expect the summary statistics presented here to achieve a significant increase in signal-to-noise ratio, particularly at small separations where lowering the stellar mass threshold (by increasing the magnitude limit) is key.

The cross-correlation between clusters selected in X-ray, SZ, optical, and infrared (e.g., Bulbul et al. 2024; Naess et al. 2025; Rykoff et al. 2014; Euclid Collaboration: Bhargava et al. 2025) and a fixed sample galaxy (that is as pure and complete as possible) will provide essential information about the cluster selection function and its relation to large-scale structure (e.g., Clerc et al. 2024). A model for the cluster selection function that reproduces the observed cross-correlation with an external data set should be more robust.

Data availability

The auto- and cross-correlations measured and presented in Sect. 3.1 are available on https://zenodo.org/records/15806800.

References

  1. Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, ArXiv e-prints [arXiv:1610.02743] [Google Scholar]
  2. Adhikari, S., Shin, T.-H., Jain, B., et al. 2021, ApJ, 923, 37 [NASA ADS] [CrossRef] [Google Scholar]
  3. Amodeo, S., Battaglia, N., Schaan, E., et al. 2021, Phys. Rev. D, 103, 063514 [NASA ADS] [CrossRef] [Google Scholar]
  4. Aung, H., Nagai, D., Klypin, A., et al. 2023, MNRAS, 519, 1648 [Google Scholar]
  5. Ayromlou, M., Kauffmann, G., Yates, R. M., Nelson, D., & White, S. D. M. 2021, MNRAS, 505, 492 [NASA ADS] [CrossRef] [Google Scholar]
  6. Ayromlou, M., Kauffmann, G., Anand, A., & White, S. D. M. 2023, MNRAS, 519, 1913 [Google Scholar]
  7. Banerjee, A., & Abel, T. 2021, MNRAS, 504, 2911 [NASA ADS] [CrossRef] [Google Scholar]
  8. Baxter, E., Chang, C., Jain, B., et al. 2017, ApJ, 841, 18 [NASA ADS] [CrossRef] [Google Scholar]
  9. Behroozi, P., Wechsler, R. H., Hearin, A. P., & Conroy, C. 2019, MNRAS, 488, 3143 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bell, E. F., Wolf, C., Meisenheimer, K., et al. 2004, ApJ, 608, 752 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bianconi, M., Smith, G. P., Haines, C. P., et al. 2020, MNRAS, 492, 4599 [Google Scholar]
  12. Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Boselli, A., Fossati, M., & Sun, M. 2022, A&ARv, 30, 3 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bulbul, E., Liu, A., Kluge, M., et al. 2024, A&A, 685, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Clerc, N., Kirkpatrick, C. C., Finoguenov, A., et al. 2020, MNRAS, 497, 3976 [NASA ADS] [CrossRef] [Google Scholar]
  17. Clerc, N., Comparat, J., Seppi, R., et al. 2024, A&A, 687, A238 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Comparat, J., Eckert, D., Finoguenov, A., et al. 2020, Open J. Astrophys., 3, 13 [Google Scholar]
  19. Comparat, J., Truong, N., Merloni, A., et al. 2022, A&A, 666, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Comparat, J., Merloni, A., Ponti, G., et al. 2025, A&A, 697, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [Google Scholar]
  22. Croft, R. A. C., Dalton, G. B., & Efstathiou, G. 1999, MNRAS, 305, 547 [NASA ADS] [CrossRef] [Google Scholar]
  23. Dalton, G. B., Maddox, S. J., Sutherland, W. J., & Efstathiou, G. 1997, MNRAS, 289, 263 [CrossRef] [Google Scholar]
  24. Das, S., Chiang, Y.-K., & Mathur, S. 2023, ApJ, 951, 125 [NASA ADS] [CrossRef] [Google Scholar]
  25. Davies, J. J., Crain, R. A., McCarthy, I. G., et al. 2019, MNRAS, 485, 3783 [NASA ADS] [CrossRef] [Google Scholar]
  26. Davis, M., & Peebles, P. J. E. 1983, ApJ, 267, 465 [Google Scholar]
  27. de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
  28. De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [Google Scholar]
  29. DESI Collaboration (Aghamousa, A., et al.) 2016a, ArXiv e-prints [arXiv:1611.00036] [Google Scholar]
  30. DESI Collaboration (Aghamousa, A., et al.) 2016b, ArXiv e-prints [arXiv:1611.00037] [Google Scholar]
  31. Dev, A., Driver, S. P., Meyer, M., et al. 2024, MNRAS, 535, 2357 [Google Scholar]
  32. Dey, A., Schlegel, D. J., Lang, D., et al. 2019, AJ, 157, 168 [Google Scholar]
  33. Euclid Collaboration (Bhargava, S., et al.) 2025, A&A, in press, https://doi.org/10.1051/0004-6361/202554937 [Google Scholar]
  34. Euclid Collaboration (Mellier, Y., et al.) 2025, A&A, 697, A1 [Google Scholar]
  35. Faber, S. M., Willmer, C. N. A., Wolf, C., et al. 2007, ApJ, 665, 265 [Google Scholar]
  36. Falck, B., Wang, J., Jenkins, A., et al. 2021, MNRAS, 506, 2659 [NASA ADS] [CrossRef] [Google Scholar]
  37. Fedeli, C., Carbone, C., Moscardini, L., & Cimatti, A. 2011, MNRAS, 414, 1545 [Google Scholar]
  38. Flaugher, B., Diehl, H. T., Honscheid, K., et al. 2015, AJ, 150, 150 [Google Scholar]
  39. Gladders, M. D., & Yee, H. K. C. 2000, AJ, 120, 2148 [NASA ADS] [CrossRef] [Google Scholar]
  40. Grayson, S., Scannapieco, E., & Davé, R. 2023, ApJ, 957, 17 [Google Scholar]
  41. Hahn, C., Wilson, M. J., Ruiz-Macias, O., et al. 2023, AJ, 165, 253 [CrossRef] [Google Scholar]
  42. Hennig, C., Mohr, J. J., Zenteno, A., et al. 2017, MNRAS, 467, 4015 [NASA ADS] [Google Scholar]
  43. Hütsi, G., & Lahav, O. 2008, A&A, 492, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Ibitoye, A., Tramonte, D., Ma, Y.-Z., & Dai, W.-M. 2022, ApJ, 935, 18 [NASA ADS] [CrossRef] [Google Scholar]
  45. Ishiyama, T., Prada, F., Klypin, A. A., et al. 2021, MNRAS, 506, 4210 [NASA ADS] [CrossRef] [Google Scholar]
  46. Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [Google Scholar]
  47. Jarrett, T. H., Chester, T., Cutri, R., et al. 2000, AJ, 119, 2498 [Google Scholar]
  48. Kerscher, M., Szapudi, I., & Szalay, A. S. 2000, ApJ, 535, L13 [NASA ADS] [CrossRef] [Google Scholar]
  49. Kluge, M., Comparat, J., Liu, A., et al. 2024, A&A, 688, A210 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 221 [NASA ADS] [CrossRef] [Google Scholar]
  51. Kukstas, E., McCarthy, I. G., Baldry, I. K., & Font, A. S. 2020, MNRAS, 496, 2241 [Google Scholar]
  52. La Posta, A., Alonso, D., Chisari, N. E., Ferreira, T., & García-García, C. 2024, ArXiv e-prints [arXiv:2412.12081] [Google Scholar]
  53. Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [Google Scholar]
  54. Lau, E. T., Nagai, D., Bogdán, et al. 2024, ArXiv e-prints [arXiv:2412.04559] [Google Scholar]
  55. Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
  56. Lehle, K., Nelson, D., Pillepich, A., Truong, N., & Rohr, E. 2024, A&A, 687, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Li, D., Fang, T., Ge, C., et al. 2024, ApJ, 977, L40 [Google Scholar]
  58. Lilje, P. B., & Efstathiou, G. 1988, MNRAS, 231, 635 [Google Scholar]
  59. Lim, S., Tacchella, S., Maiolino, R., Schaye, J., & Schaller, M. 2025, ArXiv e-prints [arXiv:2504.02027] [Google Scholar]
  60. Maddox, S. J., Sutherland, W. J., Efstathiou, G., & Loveday, J. 1990, MNRAS, 243, 692 [NASA ADS] [Google Scholar]
  61. Mancone, C. L., & Gonzalez, A. H. 2012, PASP, 124, 606 [NASA ADS] [CrossRef] [Google Scholar]
  62. Merloni, A., Predehl, P., Becker, W. et al. 2012, ArXiv e-prints [arXiv:1209.3114] [Google Scholar]
  63. Merloni, A., Lamer, G., Liu, T., et al. 2024, A&A, 682, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. More, S., Miyatake, H., Mandelbaum, R., et al. 2015, ApJ, 806, 2 [CrossRef] [Google Scholar]
  65. Moser, E., Battaglia, N., Nagai, D., et al. 2022, ApJ, 933, 133 [NASA ADS] [CrossRef] [Google Scholar]
  66. Naess, S., Aiola, S., Austermann, J. E., et al. 2020, JCAP, 2020, 046 [Google Scholar]
  67. Naess, S., Guan, Y., Duivenvoorden, A. J., et al. 2025, ArXiv e-prints [arXiv:2503.14451] [Google Scholar]
  68. Nelan, J. E., Smith, R. J., Hudson, M. J., et al. 2005, ApJ, 632, 137 [Google Scholar]
  69. Nelson, D., Pillepich, A., Ayromlou, M., et al. 2024, A&A, 686, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Nishizawa, A. J., Oguri, M., Oogi, T., et al. 2018, PASJ, 70, S24 [CrossRef] [Google Scholar]
  71. Oren, Y., Sternberg, A., McKee, C. F., Faerman, Y., & Genel, S. 2024, ApJ, 974, 291 [Google Scholar]
  72. Paech, K., Hamaus, N., Hoyle, B., et al. 2017, MNRAS, 470, 2566 [NASA ADS] [CrossRef] [Google Scholar]
  73. Pakmor, R., Springel, V., Coles, J. P., et al. 2023, MNRAS, 524, 2539 [NASA ADS] [CrossRef] [Google Scholar]
  74. Pandey, S., Gatti, M., Baxter, E., et al. 2022, Phys. Rev. D, 105, 123526 [NASA ADS] [CrossRef] [Google Scholar]
  75. Peebles, P. J. E. 1974, ApJS, 28, 37 [Google Scholar]
  76. Pons-Bordería, M.-J., Martínez, V. J., Stoyan, D., Stoyan, H., & Saar, E. 1999, ApJ, 523, 480 [Google Scholar]
  77. Popesso, P., Marini, I., Dolag, K., et al. 2024, A&A, submitted [arXiv:2411.17120], [Google Scholar]
  78. Predehl, P., Andritschke, R., Arefiev, V., et al. 2021, A&A, 647, A1 [EDP Sciences] [Google Scholar]
  79. Robertson, A., Huff, E., Markovič, K., & Li, B. 2024, MNRAS, 533, 4081 [Google Scholar]
  80. Rykoff, E. S., Rozo, E., Busha, M. T., et al. 2014, ApJ, 785, 104 [Google Scholar]
  81. Salcedo, A. N., Wibking, B. D., Weinberg, D. H., et al. 2020, MNRAS, 491, 3061 [Google Scholar]
  82. Sánchez, A. G., Lambas, D. G., Böhringer, H., & Schuecker, P. 2005, MNRAS, 362, 1225 [Google Scholar]
  83. Sánchez, J., Omori, Y., Chang, C., et al. 2023, MNRAS, 522, 3163 [Google Scholar]
  84. Schaye, J., Kugel, R., Schaller, M., et al. 2023, MNRAS, 526, 4978 [NASA ADS] [CrossRef] [Google Scholar]
  85. Seppi, R., Comparat, J., Bulbul, E., et al. 2022, A&A, 665, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Seppi, R., Comparat, J., Ghirardini, V., et al. 2024, A&A, 686, A196 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Sorini, D., Bose, S., Davé, R., & Anglés-Alcázar, D. 2024, Open J. Astrophys., 7, 115 [Google Scholar]
  88. Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [Google Scholar]
  89. Sunyaev, R., Arefiev, V., Babyshkin, V., et al. 2021, A&A, 656, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Truong, N., Pillepich, A., Werner, N., et al. 2020, MNRAS, 494, 549 [NASA ADS] [CrossRef] [Google Scholar]
  91. Truong, N., Pillepich, A., & Werner, N. 2021, MNRAS, 501, 2210 [NASA ADS] [CrossRef] [Google Scholar]
  92. van der Wel, A. 2008, ApJ, 675, L13 [Google Scholar]
  93. Vani, A., Ayromlou, M., Kauffmann, G., & Springel, V. 2025, MNRAS, 536, 777 [NASA ADS] [Google Scholar]
  94. Vulcani, B., Poggianti, B. M., Gullieuszik, M., et al. 2023, ApJ, 949, 73 [CrossRef] [Google Scholar]
  95. Yan, Z., van Waerbeke, L., Tröster, T., et al. 2021, A&A, 651, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Yang, X., Mo, H. J., van den Bosch, F. C., et al. 2007, ApJ, 671, 153 [Google Scholar]
  97. York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] [Google Scholar]
  98. Zhang, Y., Comparat, J., Ponti, G., et al. 2024a, A&A, 690, A267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Zhang, Y., Comparat, J., Ponti, G., et al. 2024b, A&A, 690, A268 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Zhang, Y., Comparat, J., Ponti, G., et al. 2025, A&A, 693, A197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Zu, Y., & Mandelbaum, R. 2015, MNRAS, 454, 1161 [Google Scholar]
  102. Zu, Y., & Mandelbaum, R. 2016, MNRAS, 457, 4360 [NASA ADS] [CrossRef] [Google Scholar]
  103. Zu, Y., & Weinberg, D. H. 2013, MNRAS, 431, 3319 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Description of the galaxy and cluster sample combinations considered.

In the text
Table 2.

Best-fit g − r red-sequence values and scatter as a function of redshift.

In the text

All Figures

thumbnail Fig. 1.

Correlation functions for the C1xG1075 sample, using C1 clusters (0.1 <  z <  0.3, log10(LX [erg/s]) >  43.1) and G1075 galaxies (10.75 <  log10(M*[M⊙]) <  12). Left: Projected autocorrelation functions of galaxies (and clusters), split into red-sequence (red) and blue-cloud (blue) are shown with dashed lines; projected cluster-galaxy cross-correlation functions are shown as solid lines. This signal is dominated by the red sequence galaxies: the red lines are significantly higher than the blue lines. For comparison, we show the measurement from Zu & Weinberg (2013), who cross-correlated SDSS galaxies with galaxy groups from Yang et al. (2007), whose brightest group galaxy has a stellar mass in the range (11.4 <  log10(MBGG*[M⊙]) <  11.9). This measurement is shown as a green dotted line. In this analysis, we trust the measurements up to 15 h−1Mpc (to the left of the shaded area), beyond which they may be affected by systematics uncertainties. Right: Ratio between the galaxy-cluster cross-correlation and the corresponding galaxy autocorrelations. This comparison shows the strength of the clustering in the cluster environment relative to that of all galaxies (i.e. galaxies in any environment). The ratio is above one, indicating that galaxies cluster more strongly near galaxy clusters. For red-sequence galaxies, the extra power in clustering increases when scales decrease. For blue-cloud galaxies, the clustering increases towards small scales down to 0.3 Mpc/h, where it stalls and decreases below 0.2 Mpc/h. The green horizontal line indicates the ratio of large-scale halo biases determined in Seppi et al. (2024) and Comparat et al. (2025), which aligns with the ratio of correlation functions on large scales, as expected. Bottom: Results of the Jackknife procedure. Left: Relative uncertainties for cross-correlation functions. Right: Cross-correlation coefficient for the C1xG1075 sample. Relative uncertainties range from 1% to 10%; previous SDSS measurement showed 10%-30% uncertainties. The high density of galaxies in LS10 enables increased measurement precision.
In the text
thumbnail Fig. 2.

Correlation functions for the C0xG1025 sample, continued from Fig. 1. These are measured using the C0 cluster sample (0.1 <  z <  0.2, log10(LX [erg/s]) >  42.7) in combination with the G1025 galaxy sample (10.25 <  log10(M*[M⊙]) <  12). A comparison is provided using the measurement from Zu & Weinberg (2013), showing the group-galaxy cross-correlation for the sample of Yang et al. (2007), with brightest group galaxies in the stellar mass range (11.2 <  log10(MBGG*[M⊙]) <  11.4) and all SDSS galaxies. This result is shown as a dotted line.
In the text
thumbnail Fig. 3.

Galaxy-cluster cross-correlation functions compared to model predictions from the Uchuu+UniverseMachine (UM) model (Aung et al. 2023, left column) and LGAL model (Ayromlou et al. 2021 right column). Results are shown for the compared to the C1xG1075 (top) and C0xG1025 (bottom) combinations Model prediction are shown in orange for red-sequence galaxies and in pink for blue-cloud galaxies. The UM model agrees well with the C1xG1075 observations. At lower redshift, for lower stellar mass galaxies, the UM model exhibits a mild discrepancy with the observations, suggesting that the quiescent fraction of cluster galaxies with stellar mass of ∼10.5 may be underestimated. The LGAL model agrees with the measurements of the complete galaxy population (gray lines) and red galaxies (red and orange lines) for both he C1xG1075 and the C0xG1025 combinations, down to 0.5 Mpc/h. The LGAL blue-cloud galaxies show excess power on small scales compared to the observations.
In the text
thumbnail Fig. 4.

Measured integral of the cross-correlation function up to 500 kpc as a function of color at redshift 0.195 (left column) and 0.325 (right column). A Gaussian model was fit to the data points (red) and is compared to the model from Kluge et al. (2024) (in black), showing good agreement.
In the text
thumbnail Fig. 5.

Redshift vs. g-r color, coded by the integral of the cross-correlation function up to 500 kpc. Colored symbols represent individual cross-correlation functions. Dashed red lines indicate the models derived for each redshift slice. Black lines show the red-sequence model from Kluge et al. (2024). Red sequence and its scatter are accurately recovered.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.