| Issue |
A&A
Volume 706, February 2026
|
|
|---|---|---|
| Article Number | A263 | |
| Number of page(s) | 24 | |
| Section | Planets, planetary systems, and small bodies | |
| DOI | https://doi.org/10.1051/0004-6361/202556519 | |
| Published online | 18 February 2026 | |
The bulk metal content of WASP-80 b from joint interior-atmosphere retrievals
Breaking degeneracies and exploring biases with panchromatic spectra
Max Planck Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
★ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
21
July
2025
Accepted:
3
December
2025
The atmospheres of warm gas giants can be readily characterized through transmission and emission spectroscopy. WASP-80 b is one such exoplanet, with an unusually low density that is in tension with the metal-rich composition expected for a planet of this mass. The aim of this work to derive precise constraints on WASP-80 b's bulk metal mass fraction, atmospheric composition, and thermal structure. We conducted a suite of retrievals using three approaches: traditional interior-only, atmosphere-only, and joint interior-atmosphere retrievals. We coupled the open-source model GASTLI to describe the planetary structure and thermal evolution and petitRADTRANS to describe the atmospheric chemistry and clouds. Our retrievals combined the mass and age with panchromatic spectra from JWST and HST in both transmission (0.5−4 μm) and emission (1–12 μm) as observational constraints. We identified two fiducial scenarios. In the first, WASP-80 b has an internal temperature consistent with its age in the absence of external heating sources; in addition, its atmosphere is in chemical equilibrium, with an atmospheric metallicity of M/H = 2.75−0.56+0.88× solar, a bulk metal mass fraction Zplanet = 0.12 ± 0.02, and a core mass Mcore = 3.49−1.59+3.49 M⊕. In the second scenario, WASP-80 b would be inflated by an additional heat source, possibly induced by magnetic fields, with an atmospheric metallicity of M/H = 10.00−4.75+8.20× solar, Zplanet = 0.28 ± 0 .11, and Mcore = 31.8−17.5+21.3 M⊕. The super-solar M/H and sub-solar C/O ratios in both scenarios suggest late pebble or planetesimal accretion, while additional heating is required to reconcile the data with the more massive core predicted by the core accretion paradigm. In general, joint retrievals are inherently affected by a degeneracy between atmospheric chemistry and internal structure. Taken together with flexible cloud treatment and an unweighted likelihood, this leads to larger uncertainties in bulk and atmospheric compositions than had previously been claimed.
Key words: planets and satellites: atmospheres / planets and satellites: composition / planets and satellites: gaseous planets / planets and satellites: interiors / planets and satellites: physical evolution
© The Authors 2026
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
Extrasolar gas giants are composed of two main building blocks: hydrogen and helium (H/He) and metals, which include refractory material (rocks) and ices (e.g., H2O, CH4, NH3). Depending on the specific planet formation mechanism characterizing gas giants, their total metal and H/He mass fractions may vary widely. Two main formation mechanisms have been accepted: core accretion and gravitational instability. In the core accretion scenario, gas giants undergo a first stage where metal-rich material is accreted, leading to the formation of a core. This can be further enriched in more metals by accretion of pebbles and plan-etesimals, until the core reaches a critical mass. Then runaway accretion of a gas-rich (H/He) envelope starts. The more massive the planet is, the more gas it binds gravitationally (Helled & Morbidelli 2021; Helled 2023). Thus, core accretion produces massive planets that are metal-poor and dominated by H/He or Neptune-mass planets rich in rocks and ices. The accretion of metal-rich solids and H/He gas occurs within the same time scale in gravitational instability. Traditional gravitational instability models suggest that gas giants formed via this mechanism would have similar bulk compositions to their protoplanetary disk and host star (Helled & Schubert 2008; Boley et al. 2011). However, if the mass of the disk is not massive enough, or if rings and migration play an important role in disk evolution, gravitational instability can form planet cores as massive as in core accretion (Jiang & Ormel 2023; Rice et al. 2025). This is why determining the bulk composition and atmospheric composition of gas giants simultaneously is key to understand their formation and evolution pathways (Thorngren et al. 2016; Müller & Helled 2025).
The bulk amount of metals can only be estimated by comparing (or retrieving) the observed mass and radius to interior structure calculations. Interior models of gas giants typically assume that the planet is stratified in a metal-rich core and an envelope dominated by H/He (Burrows et al. 2004; Fortney et al. 2007; Baraffe et al. 2008; Leconte & Chabrier 2012; Nettelmann et al. 2013; Thorngren et al. 2016; Müller & Helled 2021; Miguel et al. 2022; Baumeister & Tosi 2023). Age is the third observable variable that constrains the internal composition of gas giants, as these contract due to thermal cooling given their Kelvin-Helmholtz timescale. In addition, the metallicity probed in the upper atmosphere by transmission spectroscopy can be used to narrow the envelope metal mass fraction (Bloot et al. 2023; Acuña et al. 2024), assuming that the composition is constant along the radius in the envelope. In retrievals, the precision of the inferred core mass and the total planet metal mass fraction depends on the precision of these four observable parameters. For gas-rich planets, an increase in radius precision produces greater improvements in bulk metal mass fraction estimates than mass (Otegi et al. 2020). In the case of gaseous giants, the precision of the age is particularly important for young planets (< 1 Gyr) because of how rapidly their radius changes between 100 Myr and 1 Gyr, as well as the degeneracy between the luminosity (or internal temperature) and bulk metal mass fraction (Müller & Helled 2023).
The characterization of the bulk composition of extrasolar gas giants faces challenges coming from the aforementioned degeneracies, as well as tensions between different observable parameters and techniques. Degeneracies can be solved by improving the precision of the age measurement, which depends on the spectral type of the star and their properties. Including additional observables could also reduce degeneracies. For example, a lower limit on the internal temperature was inferred from disequilibrium chemistry for WASP-107 b (Sing et al. 2024; Welbanks et al. 2024), a warm gas giant observed in transmission spectroscopy with JWST. This confirmed that WASP-107 b has a metal-rich core, and obtain a precise core mass estimate. Furthermore, the Love number, which quantifies the gravity field and therefore the internal density distribution (Love 1911), is sensitive to the mass of the core, enabling us to constrain it in retrievals (Kramm et al. 2011, 2012; van Dijk & Miguel 2025). This parameter has been measured for five extrasolar hot Jupiters (Buhler et al. 2016; Hardy et al. 2017; Csizmadia et al. 2019; Hellard et al. 2020; Barros et al. 2022; Bernabò et al. 2024). The number of exoplanets whose internal temperature or Love number are available is limited given the required observational criteria (Akinsanmi et al. 2020; Mukherjee et al. 2025).
Tensions can also exist between the bulk density and the inferred atmospheric metallicity. This is the case of sub-Saturn giants with warm equilibrium temperatures (Teq ≤ 1000 K) whose radii are ~1 RJup, such as HAT-P-12 b (Hartman et al. 2009), HAT-P-18 b (Hartman et al. 2011), WASP-29 b (Hellier et al. 2010), WASP-69 b (Anderson et al. 2014), WASP-67 b (Hellier et al. 2012), WASP-39 b (Faedi et al. 2011), and WASP-80 b (Triaud et al. 2013). These exoplanets are easily characterized via transmission spectroscopy given their large radii (Tsiaras et al. 2018; Pinhas et al. 2019). For example, JWST's panchromatic transmission spectrum of WASP-39 b indicate that its atmospheric metallicity is bimodal between solar and ~100x solar (Ahrer et al. 2023; Alderson et al. 2023; Rustamkulov et al. 2023; Feinstein et al. 2023). To explain simultaneously its low density and high atmospheric metallicity, a core-less internal structure is not sufficient because its observed radius is higher than that of a pure envelope exoplanet with a 100 × solar composition (Fortney et al. 2007).
Reconciling apparent discrepancies between interior and atmospheric analyses requires a combination of additional data and more advanced modeling. In general, these discrepancies could have multiple causes, including biases in the atmospheric retrievals (Bézard et al. 2022; Fisher et al. 2024) or unconstrained internal heating mechanisms that inflate the planet's radius (Thorngren & Fortney 2018). Complementary observables to the exoplanet spectra could help clarify the planet's composition and thermal properties, but obtaining such parameters is difficult. For instance, measuring the Love numbers of warm gas giants is challenging because they are further away from their star than their hot Jupiter counterparts (Hellard et al. 2019). Similarly, access to internal temperature constraints can be limited by clouds or equilibrium chemistry. Thus, a new modeling and data analysis approach is required to investigate the source of the differences in interior and atmospheric models. This tension could be mitigated by combining both retrievals into a joint interior-atmosphere retrieval. A joint interior-atmosphere retrieval analysis uses coupled interior-atmospheric calculations as the forward models and integrates the transmission or emission spectra with the observables parameters associated with the bulk density in the likelihood function of the retrieval. Such a retrieval was applied by Wilkinson et al. (2024) to the mass and a transmission spectrum dataset of WASP-39 b obtained by JWST's instrument NIRSpec-G395H. Nonetheless, their work presents two caveats: first, it did not include the effect of clouds in the transmission spectrum and, secondly, it did not consider emission and transmission spectra simultaneously to further constrain any degeneracies.
The aim of this work is to use joint interior-atmosphere retrievals to test whether this framework has this ability to infer more precise bulk composition estimates than the traditional interior structure retrievals by breaking degeneracies. To do this, we explored a suite of interior, atmosphere, and joint interior-atmosphere retrievals. WASP-39 b and WASP-80 b are the two super-puff warm gas giants with the widest wavelength coverage in their spectra. Of the two, WASP-80 b is the only one with emission spectra available; thus, we subsequently selected it as our science case. In Sect. 2, we compile the observational data for WASP-80 b available for our retrievals. In Sect. 3, we introduce the forward models for the three types of retrievals (interior-only, atmosphere-only, and joint). In Sect. 4, we describe our Bayesian framework, including the priors and the calculation of the likelihood function. We present the results of our suite of retrievals in Sects. 5.1–7. We discuss the benefit of joint retrievals in contrast to previous work and the implications for the interior structure and formation of WASP-80 b in Sect. 8. Finally, our conclusions are given in Sect. 9.
2 WASP-80 b data
WASP-80 b is a warm gas giant (Teq = 825 K) with an intermediate mass between that of Jupiter and Saturn. Its radius is similar to that of Jupiter, but its mass is approximately half of Jupiter's value (see Table 1), making it a puffy gas giant. It orbits a low-mass, late-type star (late K or early M) with an effective temperature of 4145 K at an orbital period of ~3 days. Its mass has been measured via the radial velocity method and its radius has been characterized with transit photometry, with consistent results across different ground-based data analyzes (Triaud et al. 2013; Mancini et al. 2014; Triaud et al. 2015). Table 1 shows the values we adopted for estimating for WASP-80 b's mass and radius, along with their references
In addition, WASP-80's age was estimated via gyrochronology to be ~100 Myr. It also presents chromospheric activity, which is expected in stars at young ages (Triaud et al. 2013). Gallet (2020) discussed how gyrochronology could yield a biased age for young stars (<100 Myr) because they might not yet have converged onto a well-behaved rotation-age sequence. In addition, these authors re-calculated the age of several stars via gyrochronology, including WASP-80, while accounting for star-planet tidal interactions. These interactions can spin up the stellar rotational period, biasing gyrochronology estimates towards younger ages. Thus, in this work, we have adopted the age estimate for WASP-80 from Gallet (2020), which is 1.352±0.222 Gyr.
WASP-80 b's short period and high planet-to-star radius ratio make it an excellent target for atmospheric characterization both in transmission and emission spectroscopy. It has been observed in both geometries by Spitzer photometry (Triaud et al. 2015; Wong et al. 2022). Furthermore, two low-resolution transmission datasets were obtained with the Hubble Space Telescope (HST) using the STIS and WFC3 instruments. These observations revealed absorption features in the 1.4 bandpass, attributed to H2O and/or CH4. The STIS spectrum showed a slope at optical wavelengths, likely caused by aerosols or stellar contamination. Using atmospheric retrievals on these data, Wong et al. (2022) constrained the overall atmospheric metallicity to [M/H] = ~30–100 × solar, suggesting that the envelope is significantly enriched in metals. Similarly, WASP-80 b has been characterized by JWST with the NIRCam instrument both in transmission and emission. The analyzes of the NIRCam datasets have shown a sub-solar C/O ratio and a ~5 × solar metallic-ity. In addition, CH4 was detected at 6σ (Bell et al. 2023). This detection confirmed earlier tentative evidence from ground-based observations (Carleo et al. 2022). Furthermore, Wiser et al. (2025) detect H2O, CH4, CO, and CO2 at a high level of confidence by analyzing WASP-80 b's panchromatic emission spectrum from the JWST data sets. Finally, transmission spectroscopy observations have suggested the presence of condensates in the atmosphere of WASP-80 b. The composition of these condensates can be constrained through eclipse observations at short wavelengths (λ < 3 pm), which are covered by HST's WFC3, and JWST's NIRISS instruments. Such observations with these two instruments have revealed that the composition of the condensates may include Cr, Na2S, KCl, and ZnS, which are expected in warm (Teq < 1000 K) atmospheres (Jacobs et al. 2023). Furthermore, a moderately high Bond albedo was estimated for WASP-80 b, with a 1σ interval of AB = 0.15–0.40 (Morel et al. 2025).
Table 1 summarizes the spectrum datasets we re-analyze in our suite of retrievals with their respective wavelength ranges, references, and instruments. We discarded the photometric datasets, as they cover similar wavelength ranges to the HST and JWST low-resolution spectra. We do not include the emission dataset from Morel et al. (2025) in our retrievals due to the computational cost of reflected light calculations. Nonetheless, we discuss the effect of including reflected light data in our framework in the inference of the interior composition in Sect. 8.3.
All observational data used in our suite of retrievals of WASP-80 b.
3 Forward model
3.1 Interior structure model
We adopted the GASTLI open-source package1 (GAS gianT modeL for Interiors; Acuña et al. 2021, 2025) as an interior structure model. GASTLI stratifies the planetary interior into two layers: a core (50% water and 50% silicate in mass) and an envelope (H/He mixed with water as a proxy for metals). The mass of the core is defined by the mass of the planet, Mpl and the core mass fraction (CMF) as Mcore = Mpl × CMF. Together with the planet mass and the CMF, the envelope metal mass fraction, Zenv, is an input parameter. Thus, the total bulk metal mass fraction of the planet can be computed as Zpl = CMF + (1 – CMF) × Zenv. GASTLI solves for the pressure P(r), temperature T(r), gravity g(r), and enclosed mass m(r) radial profiles by integrating the differential equations that correspond to hydrostatic equilibrium, an adiabatic temperature gradient, Gauss's theorem and conservation of mass (Eqs. (1)–(4))2. The computation of the adiabatic gradient requires the Grüneisen parameter, γ, and the seismic parameter, ϕ, which are calculated using the density, ρ, and internal energy, E (Eq. (5)). These two properties are directly obtained from the equation of state (EOS). The density, internal energy, and entropy of H/He are calculated using additive laws, in addition to a correction for non-ideal effects between H and He in the mixture (Chabrier & Debras 2021; Howard & Guillot 2023a). The properties of the water-rock mixture are derived in a similar manner, by applying the additive laws to the EOS of water (Mazevet et al. 2019) and rock (Lyon 1992; Miguel et al. 2022). The ices accreted by gas giants may not only contain water, but also methane and ammonia. Accounting for non-ideal effects caused by the mixing of rock and ices is challenging because the ice-to-rock mass ratio and the mass fractions of H2O, CH4, and NH3 in the ices are unconstrained (Nettelmann et al. 2016; Miguel & Vazan 2023). In the absence of more detailed observational constraints, the use of ideal additive laws is a reasonable approach.
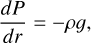 (1)
(1)
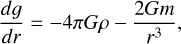 (2)
(2)
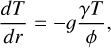 (3)
(3)
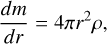 (4)
(4)
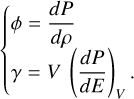 (5)
(5)
To solve for the differential equations that govern the internal structure, the following boundary conditions are defined. First, the gravity at the center of the planet is zero, g(r = 0) = 0. Secondly, the pressure and the temperature need to be specified at the surface interface. This is the external interface of the outermost computational layer in the 1D grid that represents the radius, not the physical surface found in rocky planets. These surface conditions, P(r = Rint) = Psurf and T(r = Rint) = Tsurf, are a flexible input for GASTLI, and can be estimated with pre-computed atmospheric grids in an iterative scheme (see Sect. 3.1.1) or it can be a free parameter (Sect. 3.1.2). The former is required to obtain a grid of mass-radius-age models for the traditional interior retrievals (Sect. 6), while the latter is more appropriate for our approach to the joint interior-atmosphere retrievals (Sect. 7). In the joint retrievals, the surface pressure if fixed to Psurf = 1000 bar.
3.1.1 Grid of mass–radius–age models
We used GASTLI's default grid of atmospheric models, which was precomputed using petitCODE (Mollière et al. 2015, 2017). The grid spans a wide range of planetary surface gravities (log gsurf = 2.6–4.2 cm/s2), equilibrium temperatures (100–1000 K), internal temperatures (50–950 K), metallicities (0.01–250 × solar), and C/O ratios (0.10–0.55), making it well-suited for gas giants such as WASP-80b. In brief, petitCODE computes self-consistent pressure-temperature (P–T) profiles by solving radiative transfer via the correlated-k method, under the assumption of 1D radiative–convective equilibrium. The Bond albedo is calculated self-consistently, based on the energy balance between the emitted and absorbed radiation at the top of the atmosphere. In GASTLI's default atmospheric grid, chemical equilibrium, and cloud-free (clear) atmospheres are assumed. For each coupled model, GASTLI extracts the corresponding P–T profile and computes the atmospheric thickness by integrating the hydrostatic equilibrium equation down to a transit pressure of 20 mbar. This approach enables accurate modeling of observable planetary radii. We refer to Acuña et al. (2024) for more details, including the opacities of atmospheric species and their references.
To achieve consistency between the interior and atmospheric profiles, we used the iterative coupling scheme described in Acuña et al. (2021). In this scheme, we defined the interior radius (Rint) as the radius output by the interior model. An initial guess for Rint determines the planet's surface gravity, which is then used to interpolate a surface temperature from the atmospheric grid. The interpolation is performed at fixed values of planet mass, envelope metallicity, core mass fraction, and internal temperature. The interpolated surface temperature then serves as the boundary condition for the interior model. The new interior radius is recalculated, and the process repeats until convergence in radius and surface temperature is reached. The final mass and radius are calculated consistently by adding its respective atmospheric contributions.
GASTLI calculates the planet's thermal evolution by solving the entropy (S) loss over time (t) due to secular cooling. We computed a sequence of models at different internal temperatures (Tint) – or thermal states. The luminosity, L, at each state is related to the internal temperature and total radius, Rpl, according to Eq. (6). The luminosity is calculated by also using the Stefan-Boltzman constant, σ = 5.67 × 10−8 W m−2 K−4. Entropy as a function of time, S (t), is obtained by integrating the change in entropy ∂S over time, as defined in Eq. (7). This calculation requires us to extract the temperature and enclosed mass profiles, T(r) and m(r), from the interior model to estimate T(m). The resulting S(t) relation enables GASTLI to predict radius and luminosity as functions of age. Here, we adopted GASTLI's default initial entropy, which corresponds to a hot start entropy value S0 = 12 kB mH3. For planets whose age >100 Myr, the choice of the initial entropy does not impact the radius-age and luminosity-age functions (see Figs. 5 and 9 in Spiegel & Burrows 2012; Acuña et al. 2024, respectively). Moreover, hot-start initial entropy conditions are consistent with observations of cold gas giants (Nowak et al. 2020; Trevascus et al. 2025).
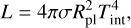 (6)
(6)
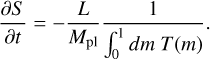 (7)
(7)
In the mass–radius–age grid, we assumed a constant equilibrium temperature at null Bond albedo, equal to that ofWASP-80 b, Teq = 825 K. The definition of this parameter is given in Eq. (8), where T*, R*, and ad are the stellar effective temperature, stellar radius and orbital semi-major axis (Table 1). PetitCODE uses this equilibrium temperature as input and calculates the Bond albedo self-consistently by generating synthetic reflection spectra and integrating over wavelength. We generated a regular grid of GASTLI models across a 4D hyperparameter space by varying the planet mass, CMF, the envelope's log(M/H), and internal temperature (Tint). The input arrays are finely sampled: mass from 0.35 to 0.75 MJup, with ΔM = 0.05 MJup; CMF from 0.0 to 0.90 with ΔCMF = 0.10, plus the value CMF = 0.99 as a last point in the array; log(M/H) is evaluated at −2.0 and 2.4, in addition to the values comprised between 0.0 and 2.0 with Δlog(M/H) = 0.5; Tint is calculated at 50 K, and 100–800 K with ΔTint = 100 K. Thus, our grid contains the planetary radius and age for 5670 models in total. This grid will be interpolated with scipy's function ```RegularGridlnterpolator`` in the traditional interior retrievals in Sect. 6 to evaluate the forward model:
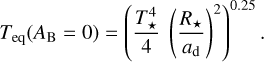 (8)
(8)
3.1.2 Grid for joint retrievals
As discussed in Sect. 3.1, the traditional interior structure retrievals require the interior model to be coupled to a grid of self-consistent atmospheric models to compute the radius and age as a function of internal temperature. However, for the joint interior-spectrum retrievals, we required the atmospheric profiles to be more flexible than the self-consistent grid. The transmission and emission spectrum may show spectral features that can only be explained by physics that deviate from the assumptions of the self-consistent grid, such as clouds or hazes, or a temperature inversion caused by strong optical absorbers in the upper atmosphere.
We coupled the thermal structure analytical model and the new grid of interior structure models. The coupling algorithm is slightly different from the traditional one described in Sect. 3.1.1 and in Acuña et al. (2021). These differences include using additional parameters (i.e., the cloud and thermal structure parameters), adopting an additional step to calculate the mass mixing ratios of the atmospheric species with easyCHEM, and computing the transmission and/or emission spectrum with petitRADTRANS after the coupled model has converged (see Sect. 3.2 for a description of petitRADTRANS and easyCHEM). More details on the modified coupling algorithm are given in Appendix B. In the following, we explain how we obtain the grid for the joint retrievals.
To calculate the grid for joint retrievals, we separated GASTLI's interior module from its atmospheric module. This allowed us to calculate the radius (Rint) and the entropy S(P = 1000 bar) independently of the atmospheric parameters, such as the atmospheric metallicity, log(M/H), or the internal temperature, Tint.
A set of retrievals in our suite requires to calculate the age because it is taken into account as an observable in the calculation of the log-likelihood (see Sect. 4.1). Solving for the Tint-radius-age relations involves computing the function, fS = ∂S/∂t (Eq. (7)). In this equation, the luminosity, L, is dependent on the intrinsic (or internal) temperature (Eq. (6)). Also, Tint is an input to the analytical P–T model that outputs the surface temperature, Tsurf. Consequently, we could not calculate and store the function fS = ∂S/∂t in a grid because the internal temperature was not known a priori. Thus, GASTLI's grid for the joint retrievals cannot contain a multidimensional table of fS. Instead, we defined a new function: 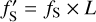 . Then we stored a table for this parameter together with Rint and S(P = 1000 bar). For one instance of a converged coupled interior-atmosphere model, we interpolated the internal radius, entropy and
. Then we stored a table for this parameter together with Rint and S(P = 1000 bar). For one instance of a converged coupled interior-atmosphere model, we interpolated the internal radius, entropy and 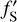 values at different surface temperatures that are obtained by varying the internal temperature Ti in the Guillot (2010) P–T profile, while setting the remaining free parameters constant. We defined the internal temperature in Eq. (6) equal to the intrinsic temperature in the P–T profile, Tint = Ti, to compute its corresponding luminosity array. The arrays containing L(Tint) and
values at different surface temperatures that are obtained by varying the internal temperature Ti in the Guillot (2010) P–T profile, while setting the remaining free parameters constant. We defined the internal temperature in Eq. (6) equal to the intrinsic temperature in the P–T profile, Tint = Ti, to compute its corresponding luminosity array. The arrays containing L(Tint) and 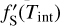 were then used to calculate an array for fS, as they are necessary to solve the differential equation of thermal evolution (Eq. (7)). Consequently, we obtained the radius-age curve that allowed us to evaluate the age at the Ti value proposed by the sampler.
were then used to calculate an array for fS, as they are necessary to solve the differential equation of thermal evolution (Eq. (7)). Consequently, we obtained the radius-age curve that allowed us to evaluate the age at the Ti value proposed by the sampler.
The input variables for GASTLI's joint grid are the planet mass, CMF, the metal mass fraction of the envelope, Zenv, and the surface temperature and pressure. We set the surface pressure to Psurf = 1000 bar, as this is the maximum pressure level appropriate for both our analytical P–T profile and spectrum generator (Sect. 3.2). Similar to our mass-radius-age grid, we generate a rectangular multidimensional grid by evaluating the interior models at the values specified by fixed arrays of the input parameters Mpl, CMF, Zenv, and Tsurf. These arrays consist of Mpl = 0.35-0.75 MJup, with ΔMpl = 0.20 MJup; CMF = 0.0–0.99, with ΔCMF = 0.10; and Tsurf = 700–6000 K, with ΔTsurf = 100 K. For the envelope mass fraction, Zenv = 0.0 to 0.05 at intervals of ΔZenv = 0.01, continued by the ranges Zenv = 0.10–0.30 and Zenv = 0.40–0.80 at intervals of ΔZenv = 0.05 and 0.10, respectively. Detailed models of the joint grid can be found in Appendix B.
3.2 Atmospheric model
As forward atmospheric model to generate transmission and emission spectra, we use petitRADTRANS (pRT, Mollière et al. 2019) version 3.0. pRT is an optimized open-source radiative transfer package that offers flexibility in terms of the P–T profiles, chemistry, cloud treatment, and geometry. The computation of emission spectra requires a measurement the planet-to-star flux ratio; thus, we interpolated pRT's in-built library of PHOENIX stellar spectra (Husser et al. 2013) as described by van Boekel et al. (2012).
To parametrize a flexible P–T profile, we employed the simple analytical model provided by Guillot (2010). It enables us to estimate the thermal structure of irradiated planets by using four free parameters in Eq. (9). The irradiation temperature is defined as 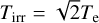 , while the optical depth for a given pressure P is defined as τ = P × κIR/g. Here, Te is denoted as the equilibrium temperature in the model, Ti is the intrinsic temperature, and g is the surface gravity. Finally, κIR corresponds to the mean infrared (gray) opacity, and γ is the optical-to-infrared opacity ratio. These parameters can be physically interpreted, for example we could identify Te = Teq = 825 K, and Ti = Tint as calculated by the thermal evolution in the mass–radius–age models (Sect. 3.1.1). However, this would limit the shape of the P–T profile in the atmosphere-only and joint retrievals, so we treat them as free parameters (see Sect. 4.2 for their priors). We will only physically interpret Ti as the internal temperature Tint in the joint retrievals that include the age as an observable to compute the log-likelihood (see Appendix B and Sect. 4.1). The temperature profile is expressed as:
, while the optical depth for a given pressure P is defined as τ = P × κIR/g. Here, Te is denoted as the equilibrium temperature in the model, Ti is the intrinsic temperature, and g is the surface gravity. Finally, κIR corresponds to the mean infrared (gray) opacity, and γ is the optical-to-infrared opacity ratio. These parameters can be physically interpreted, for example we could identify Te = Teq = 825 K, and Ti = Tint as calculated by the thermal evolution in the mass–radius–age models (Sect. 3.1.1). However, this would limit the shape of the P–T profile in the atmosphere-only and joint retrievals, so we treat them as free parameters (see Sect. 4.2 for their priors). We will only physically interpret Ti as the internal temperature Tint in the joint retrievals that include the age as an observable to compute the log-likelihood (see Appendix B and Sect. 4.1). The temperature profile is expressed as:
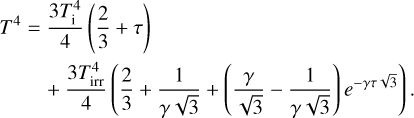 (9)
(9)
We explore both equilibrium chemistry and free chemistry in our suite of retrievals. In equilibrium retrieval, for a given pair of atmospheric metallicity, [M/H], and carbon-to-oxygen ratio, C/O, we calculate the mass fraction abundances by using pRT's pre-computed easyCHEM tables (Mollière et al. 2017; Lei & Mollière 2025). easyCHEM calculates and minimizes the Gibbs free energy of a mixture as a function of pressure, temperature and elemental makeup following the methods described in the Chemical Equilibrium with Applications (CEA) software (Gordon 1994; McBride 1996). We include a variety of chemical species that are expected in warm gas giant atmospheres to generate spectra in our retrievals. Their respective opacity and line list data references are: H2O (Polyansky et al. 2018), CO (Rothman et al. 2010), CO2 (Yurchenko et al. 2020), CH4 (Hargreaves et al. 2020), NH3 (Coles et al. 2019), HCN (Barber et al. 2014), Na (Allard et al. 2019), and K (Mollière et al. 2019).
In our retrievals involving transmission spectra, we include condensates as an opacity source. The parameterization of the cloud opacity, κcloud, of our condensate model is shown in Eq. (10). The cloud model consists of five free parameters (see Sect. 4.2 for their priors). Then, λ0 corresponds to the reference wavelength at which the reference opacity, κ0, is defined. fsed is the cloud scale height decrease factor, and p is the power law coefficient of the opacity with wavelength for λ >> λ0. For pressures higher than the base pressure of the cloud layer (Pbase), the cloud opacity is set to zero as κcloud(λ, P > Pbase) = 0. Our condensate model incorporates the behavior of cloud opacities at different wavelength ranges, which consists of a constant opacity at short wavelengths (λ < λ0) and of a slope at large wavelengths (Dyrek et al. 2024). This is computed as:
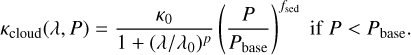 (10)
(10)
4 Bayesian framework
In the atmosphere-only and joint retrievals, we adopted nested sampling (Feroz & Hobson 2008; Feroz et al. 2009; Buchner et al. 2014) to sample the posterior distribution functions, as implemented in the pRT package by Nasedkin et al. (2024). We describe how the log-likelihood function is calculated in these retrievals in Sect. 4.1. In the traditional interior structure retrievals, we employed the Markov chain Monte Carlo (MCMC) ensemble sampler implemented in the emcee package (Foreman-Mackey et al. 2013). The likelihood function was constructed following Eqs. (6) and (14) in Dorn et al. (2015) and Acuña et al. (2021), respectively. The likelihood function is computed by using the observed values of mass, radius, age, and atmospheric metallicity (see Sect. 6). We initialized 32 walkers and ran the chains for 105 iterations. This setup ensures that the chain is sufficiently long to fulfill the MCMC convergence criterion τ << Nchain/50 for a typical interior retrieval autocorrelation time of τ ≃ 100–200 (Acuña et al. 2024).
4.1 Likelihood function
Equation (11) shows the χ2 function used to calculate the log-likelihood function (Eq. (12)). The model parameterization vector, m, contains the input variables of a coupled interior-atmosphere model, which are the mass Mpl and the other 12 parameters shown in Fig. B.2. We separate the data in two vectors: the vector containing the spectral fluxes (transmission, emission or both), dspectra, and the vector containing other observables related to bulk density and evolution information, dbulk. Depending on the retrieval, dbulk may contain the planetary radius (in joint emission retrievals), the planet mass (all joint retrievals) and/or the age. In the retrievals that include the transmission spectra, the planet radius is not included as a bulk observable in dbulk because this information is already contained in the transmission spectrum. In the first term in Eq. (11), the vector si(m) is the spectra binned at the same resolution and central wavelengths as the observed spectra, with corresponding uncertainties σspectra. Similarly, in the second term, gj(m) is the coupled interior-atmosphere model parameters related to bulk density and evolution (mass, radius and age), while σbulk are the uncertainties of the observed mass, radius and age. Nspectra and Nbulk are the number of data points contained in dspectra and dbulk, respectively.
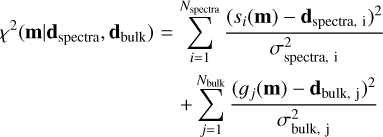 (11)
(11)
The final log-likelihood function, log(ℒ(m|dspectrum, dbulk)), is obtained by adding a normalization constant to χ2 (Eq. (12); see also Eq. (1) in Nasedkin et al. 2024). This constant takes into account the determinant of the covariance matrix, C, which we assume to be diagonal. In previous work, Wilkinson et al. (2024) multiplied the contribution of each data point contained in dbulk in the second term of Eq. (11) by a weight parameter, wj - in the form 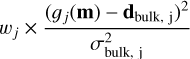 . This weight parameter allows for the importance of an observable in the log-likelihood to be controlled. In our joint interior-atmosphere retrievals, we chose not to weight the bulk observables (mass, radius, and/or age) based on the sensitivity tests discussed in Sect. 8.2.
. This weight parameter allows for the importance of an observable in the log-likelihood to be controlled. In our joint interior-atmosphere retrievals, we chose not to weight the bulk observables (mass, radius, and/or age) based on the sensitivity tests discussed in Sect. 8.2.
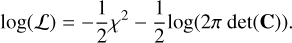 (12)
(12)
Priors used in the interior and equilibrium chemistry atmosphere retrievals.
4.2 Priors
Table 2 indicates the prior distributions used for the free parameters in the interior and equilibrium chemistry atmosphere retrievals. In the interior retrievals, if the atmospheric metallicity is included as an observable in the log-likelihood, the prior on log(M/H) is not uniform (see R3-R6 in Sect. 6). Instead, we use a normal prior whose mean and standard deviation are informed by the imposed value.
For free chemistry retrievals, we assume the same priors of the equilibrium chemistry retrievals except for log(M/H) and C/O since these two parameters do not apply. The mass fraction abundances of the chemical species are free parameters with a prior log(Xspecies) = 𝒰(−10, 0). For consistency, the joint interior-atmosphere retrievals use similar priors for those parameters that are relevant when bulk density data, age and spectra are combined as observables (see caption in Table 2). The reference pressure does not exist as prior in the joint retrievals because it is fixed to Pref = 1000 bar, where the interior-atmosphere interface is located. Similarly, as the planet radius is computed by the interior grid consistently, it does not require a prior in the joint retrievals. Finally, Table 2 shows that the prior on internal temperature is uniform between 0 and 2000 K. In the joint retrievals that include age as an observable, this prior is changed to 𝒰(0,500) K to improve convergence. This prior choice is further motivated by our self-consistent interior-atmosphere models (see Fig. A.1), which show that WASP-80 b's internal temperature does not exceed a few hundred Kelvin in the absence of extra heating sources. The age of WASP-80 b is approximately 1 Gyr, which corresponds to internal temperatures Tint = 100–300 K according to forward models, even in cloudy atmospheres (Poser et al. 2019; Poser & Redmer 2024). Internal temperatures above 900 K hinder convergence towards older ages in our joint retrievals, as they restrict the explored age range to 1-10 Myr.
Our retrievals also include offset parameters between a reference data set and the other data sets in the same geometry. Specifically, the NIRCam data set is our reference in transmission, introducing two free offsets between the NIRCam and STIS, and the NIRCam and WFC3 data sets. In emission, our reference data set is NIRCam F322W2. Thus, we use three free offsets: one for WFC3, one for NIRCam F444W, and one for MIRILRS. These offsets account for differences in instruments and data reductions, for which we adopted Gaussian priors, offsetdataset = 𝒩(0, 100) parts per million (ppm) in transit depth and planet-to-star flux in transmission and emission, respectively. Previous work report offsets of ~200 ppm between JWST and HST data sets (Lothringer et al. 2025), so a normal distribution with a standard deviation of 100 ppm is a reasonable offset prior in our retrievals.
5 Atmosphere spectrum retrievals
5.1 Transmission spectrum retrievals
As a starting point for our transmission-only retrievals, we fit an equilibrium chemistry model. In our retrieval, WASP-80 b's atmospheric composition ranges from sub-solar to solar metallicity, and it is consistent with a solar C/O = 0.55 within 1.3σ. This retrieval obtains an atmospheric metallicity of 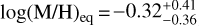 and
and 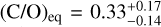 . Our C/O ratio agrees well with similar equilibrium chemistry retrievals by Wong et al. (2022, W22) and Bell et al. (2023, B23), whose 1σ estimates span C/O = 0.20–0.60 (see Fig. 1). In contrast, the equilibrium retrievals by previous work suggest that the atmospheric metallicity is super-solar, with M/H ≃ 3–10 × solar (B23) and M/H ≃25–100 × solar (W22). In summary, our equilibrium chemistry retrieval agrees with previous work on C/O ratio, but obtains a solar-like metallicity in contrast to their super-solar estimates.
. Our C/O ratio agrees well with similar equilibrium chemistry retrievals by Wong et al. (2022, W22) and Bell et al. (2023, B23), whose 1σ estimates span C/O = 0.20–0.60 (see Fig. 1). In contrast, the equilibrium retrievals by previous work suggest that the atmospheric metallicity is super-solar, with M/H ≃ 3–10 × solar (B23) and M/H ≃25–100 × solar (W22). In summary, our equilibrium chemistry retrieval agrees with previous work on C/O ratio, but obtains a solar-like metallicity in contrast to their super-solar estimates.
We also explore free chemistry retrievals to constrain the abundances of individual absorbing species. We obtain tight constraints on the mass fraction abundances of H2O and CH4, 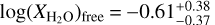 and
and 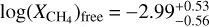 , respectively. CO and CO2 abundances are poorly constrained, spanning more than four orders of magnitude both in our retrievals and B23. Our estimate for CH4 agrees extremely well with that obtained by B23 in their free chemistry retrievals. Our retrieved H2O mass fraction ratio is consistent within 1σ with B23's water abundance estimate.
, respectively. CO and CO2 abundances are poorly constrained, spanning more than four orders of magnitude both in our retrievals and B23. Our estimate for CH4 agrees extremely well with that obtained by B23 in their free chemistry retrievals. Our retrieved H2O mass fraction ratio is consistent within 1σ with B23's water abundance estimate.
Our free retrieval contribution function indicates that the abundances are probed at a pressure Ptransit ≃ 10−3 bar. Thus, we compared our free retrieved abundances to the expected abundances at the transit pressure from our equilibrium chemistry retrieval. We found that the free CH4 abundance is compatible with its expected equilibrium abundance within <2σ. In contrast, water is 4σ more abundant in the free retrieval than in equilibrium.
We estimated the overall atmospheric metallicity and C/O ratio from our free retrieved abundances and obtained 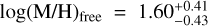 and
and 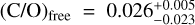 (shown in Fig. 1). This estimate agrees with the scenario presented by B23 in their free retrievals, in which WASP-80 b's atmosphere is super-solar and has a very low C-to-O ratio with
(shown in Fig. 1). This estimate agrees with the scenario presented by B23 in their free retrievals, in which WASP-80 b's atmosphere is super-solar and has a very low C-to-O ratio with 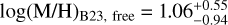 and (C/O)B23, free = 0.004±0.002.
and (C/O)B23, free = 0.004±0.002.
We adopted the equilibrium chemistry retrieval as our fiducial transmission-only model since it has the highest Bayesian evidence (see Table 3). Our free chemistry retrieval and previous analyzes indicate a super-solar metallicity, whereas our fiducial model suggests a sub-solar to solar composition. We explore whether this discrepancy could be explained by different cloud treatments by performing a new retrieval. This retrieval has in common with our fiducial model the equilibrium chemistry, but uses a cloud model that is different from our κcloud model (Eq. (10)). This is a simple cloud model that consists of a gray cloud deck with two free parameters. The first parameter corresponds to the pressure at which the cloud deck is located, Pcloud. This means that the cloud opacity is completely opaque at all wavelengths for P > Pcloud, which is similar to the cloud model assumed in B23. The second free parameter constitutes a haze factor, which scales the Rayleigh scattering opacity characteristic of hazes. With this cloud parameterization, we obtain an atmospheric metallicity and a C-to-O ratio that are super-solar:  and
and 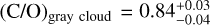 . Thus, we demonstrated that for the particular case of WASP-80 b, the cloud treatment has a significant effect on the estimated composition, particularly the atmospheric metallicity and C/O ratio. Previous work have also found that cloud parameterization can impact the inference of atmospheric composition (Line & Parmentier 2016; MacDonald & Madhusudhan 2017; Fisher & Heng 2018; Lueber et al. 2024; Roy-Perez et al. 2025).
. Thus, we demonstrated that for the particular case of WASP-80 b, the cloud treatment has a significant effect on the estimated composition, particularly the atmospheric metallicity and C/O ratio. Previous work have also found that cloud parameterization can impact the inference of atmospheric composition (Line & Parmentier 2016; MacDonald & Madhusudhan 2017; Fisher & Heng 2018; Lueber et al. 2024; Roy-Perez et al. 2025).
We compared the cloud properties between our nominal equilibrium and free retrievals. All cloud parameters are similar, except for the cloud base pressure, as it is the cloud parameter with the narrowest constraints. The equilibrium retrieval tends to locate the cloud layer at pressures higher than the transit pressure, Pbase, eq = 0.1 to 100 bar (1σ); whereas the free chemistry retrieval locates the cloud base pressure at higher altitudes that are consistent with the transit pressure, Pbase, free = 1.5 × 10−3−3 bar. This suggests that clouds are a greater source of absorption in the free retrieval than the equilibrium one. Thus, in equilibrium chemistry, the opacity is dominated by the species absorption, namely CH4, as the C/O ratio is greater than the free retrieval estimate by ~0.4.
Finally, we compare the Bayesian evidence between the three models: (1) equilibrium chemistry; (2) free chemistry; and (3) equilibrium chemistry, with a gray cloud deck. The equilibrium chemistry model is preferred over the free chemistry one by ln(B12) = ln(Zl) − ln(Z2) = 5.9 and the gray cloud deck equilibrium model by ln(B13) = 12.8. The comparison of these models is not as straightforward as comparing nested testing to estimate the detection confidence of a particular molecule. In this case, the degrees of freedom is different between models, where the most complex models have more free parameters (see Table 3), and the comparison can be more sensitive to the choice of priors. Under this word of caution, we compared the Bayes factors of the two comparisons and estimate lower and upper limits for their confidence levels according to Schmidt et al. (2025) and Trotta (2008), respectively (see also Kipping & Benneke 2025, for a detailed discussion on how to avoid overestimation of confidence levels in Bayesian model comparisons). The first comparison, ln(B12) = 5.9 is equivalent to a confidence level of 1.5–4σ. Similarly, the second comparison ln(B13) = 12.8 corresponds to 1.5–5σ. Even if it is at low confidence, a sub-solar [M/H] with a solar C/O ratio and wavelength-dependent cloud extinction at low altitudes is preferred over a scenario with super-solar [M/H] with very low C/O ratios and high altitude clouds (see Fig. C.1 for the best fit and residuals).
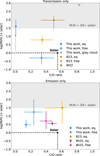 |
Fig. 1 Comparison between our atmospheric composition estimates and previous work from transmission-only (upper panel) and emission-only (lower panel) retrievals. Previous work include Bell et al. (2023, B23, orange), Wong et al. (2022, W22, dark gold), and Wiser et al. (2025, Wi25, violet). The shaded area indicates the region forbidden by our interior-only retrievals at 4σ (see Sect. 6). |
Goodness-of-fit metrics for the three transmission spectrum retrievals.
5.2 Emission spectrum retrievals
In the following, we explore retrievals for the emission spectrum only. Our emission equilibrium chemistry retrieval estimates an atmospheric metallicity of 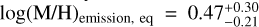 and
and 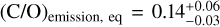 . The emission-only free chemistry retrieval agrees well within 1σ with the emission-only equilibrium estimate,
. The emission-only free chemistry retrieval agrees well within 1σ with the emission-only equilibrium estimate, 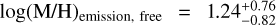 and (C/O)emission, free = 0.24±0.12. Overall, the emission-only retrievals agree well in C/O ratio with our transmission-only retrievals. In contrast, the atmospheric metallicity in emission-only retrievals tends to be slightly super-solar, agreeing well with the free chemistry transmission retrieval (see both panels in Fig. 1).
and (C/O)emission, free = 0.24±0.12. Overall, the emission-only retrievals agree well in C/O ratio with our transmission-only retrievals. In contrast, the atmospheric metallicity in emission-only retrievals tends to be slightly super-solar, agreeing well with the free chemistry transmission retrieval (see both panels in Fig. 1).
We estimate the Bayes factor between the equilibrium and free chemistry emission-only retrievals: ln(B) = ln(Zfree) – ln(Zequiiibrium) = 1538.1 − 1537.0 = 1.1. This value of Bayes factor is well below 1σ, meaning that the emission spectrum alone does not show a preference for equilibrium over free chemistry and viceversa.
Figure 1 (lower panel) shows a comparison of our emission-only estimates and those of previous work. All five estimates agree well within uncertainties in an atmospheric metallicity that ranges between solar and 100× solar. The equilibrium retrievals in Wiser et al. (2025) and our work agree that the atmospheric metallicity is [M/H]~3–10× solar. However, our retrievals constrain C/O < 0.40, while Bell et al. (2023) and Wiser et al. (2025) obtain 1σ intervals C/O = 0.40–0.65. Our lower C/O estimate could be due to our assumption of equilibrium chemistry, while Wiser et al. (2025) consider a free vertical eddy diffusion coefficient, Kzz in their retrievals. Thus, their grid might allow for atmospheric models that have low abundances of carbon-bearing molecules (CH4, CO2, and CO) at moderately high Kzz values without requiring low C/O ratios. In addition, we report a weak correlation between C/O ratio and the offset between the MIRI LRS and NIRCam F322 data sets. For a zero value of this offset, we observe a higher C/O~0.4. Wiser et al. (2025) do not use offsets between the NIRCam and MIRI data sets, which may bias the C/O value to slightly higher estimates.
The emission retrievals also allow us to determine the thermal structure at high altitudes. Figure 2 shows the 1σ confidence regions estimated by both emission-only retrievals. The spectrally weighted contribution function is higher at pressures where the emission spectrum is more sensitive to the thermal structure, indicating the pressures that are probed by the data. These pressures are P = 10−3 − 1 bar, for which the thermal structure is well constrained with T = 700–1000 K. This temperature range is in excellent agreement with that estimated by Bell et al. (2023) and Wiser et al. (2025).
We overplot self-consistent models in our P–T diagram to compare to the retrieved profiles. These models correspond to the clear models provided by Mollière et al. (2017), which agree well with the retrieved profiles at the pressures probed by the emission data. In addition, we show one cloudy model that agrees well, which is model 1 in Table 2 from Mollière et al. (2017). This cloudy model assumes irregular grains via the distribution of hollow spheres (DHS), a standard settling parameter fsed = 3, and includes iron (Fe) clouds. We rule out cloud models with fsed < 1 and atmospheric cloud mass fractions Xmax > 3 × 10−5, as their temperatures (not shown) at pressures P = 1–0.1 bar and P = 10−2–10−3 bar are significantly colder and warmer, respectively, than our retrieved profiles.
 |
Fig. 2 P–T profile of WASP-80 b as constrained by our two emission-only retrievals. The shaded region indicates the 1σ area of the retrieval, while solid lines correspond to the mean. We show self-consistent 1D models from Mollière et al. (2017) for comparison, including cloudy model 1 in their Table 2 (see text). The dotted gray line shows the contribution function from our emission-only retrievals. |
Mean and uncertainties of retrieved compositional parameters in the interior-only retrievals.
6 Interior retrievals
We ran a suite of six interior-only retrievals that take into account the observables traditionally used to characterize planetary interior structure. To assess the effect of each observable, we varied the number of observables included in the retrieval and, in the case of the atmospheric metallicity, we explored the effect of its assumed value. The atmospheric metallicity was not incorporated into the interior retrieval by including the spectrum in the log-likelihood: this approach is applied in Sect. 7 via Eq. (4.1). Instead, we treated the atmospheric metallicity as an independent observable parameter and fit it alongside mass, radius and age using a log-likelihood function with a prior. We considered two scenarios for the atmospheric metallicity: a sub-solar value derived from our transmission-only, equilibrium chemistry retrieval (fiducial), and a super-solar value from our transmission-only, free chemistry retrieval. Table 4 summarizes the observables and shows the mean and uncertainties of the retrieved compositional parameters.
In the retrievals that use a super-solar atmospheric metallicity (R4 and R6), the posterior distribution of the atmospheric metallicity does not agree with the imposed prior distribution. To quantify this discrepancy, we defined the metric |log(M/H)mean PDF – log(M/H)obs|, which quantifies the difference between the posterior mean and the observational mean, expressed in prior standard deviation units (or σ). A value of |log(M/H)mean PDF – log(M/H)obs| > 1σ indicates that R4 and R6 have difficulty fitting log(M/H) and the other observables simultaneously. This tension arises because the density of WASP-80 b is lower than that of a core-less (CMF = 0) planet with a super-solar envelope composition.
In the following, we discuss the maximum atmospheric metallicity allowed by the density of WASP-80 b. R6 shows that if the age is taken into account, the maximum possible metallicity is ~ 10 × solar. This is consistent with the mass-radius-age forward models where a planet with WASP-80 b's mean mass and log(M/H) = 1 requires to have no core (CMF = 0) to match its observed radius at its current age (see Fig. A.1). In the absence of external heat sources and a non-homogeneous interior in WASP-80 b, an atmospheric metallicity that is consistent with the bulk density cannot be [M/H]>10× solar at 1c, and [M/H]>30× solar at 4c. Thus, there is a discrepancy in [M/H] between our interior-only analysis, and our transmission-only, free chemistry retrieval as well as the estimates presented in previous work. We further discuss how free joint interior-atmosphere retrievals show degeneracies between envelope composition and chemistry in Sect. 7.
The retrievals that did not incorporate the atmospheric metallicity as an observable (R1 and R2), and those that use its sub-solar value (R3 and R5), can reproduce all observables within the 1σ uncertainties. This means that the retrieval can find forward models that are physical and fit the values imposed by the observational data. These four retrievals agree well in their retrieved compositional parameters, suggesting that the core mass fraction of WASP-80 b is CMF ~ 0.03–0.19 at 1σ. This CMF range is equivalent to a core mass Mcore = 5.2–33.2 M⊕. Its envelope metal mass fraction is low, with Zenv < 0.07 within 1σ. Thus, the total bulk metal mass fraction of WASP-80 b ranges between 0.10 and 0.15 with standard deviations of 0.05. We compare this estimate to the joint retrieval in Sect. 7 and discuss its implications for WASP-80 b's formation in Sect. 8.7.
7 Joint interior-atmosphere retrievals
The joint interior-atmosphere retrievals presented in this section incorporate both spectra and bulk observables (mass, radius, age) into their likelihood function, as described in Sect. 4.1. In addition, the forward model consists of the coupled interior-atmosphere model described in Sects. 3.1.2, 3.2 and Appendix B. The suite of joint retrievals (JR; see Table 5) consists of six retrievals: two with transmission spectra (JR1, JR2), two with emission spectra (JR3, JR4), and two that combine both geometries (JR5, JR6). We assumed equilibrium chemistry across the suite of joint retrievals because the transmission-only retrievals show a preference for the equilibrium chemistry model (see Sect. 5.1). Additionally, we explored JR1 and JR5 as free chemistry retrievals. Table 5 shows a summary of the compositional parameter estimates (CMF, Zplanet, log(M/H), C/O) from joint retrievals. Furthermore, Fig. 3 shows a summary schematic of JR6, which we adopted as our fiducial joint retrieval (see Sect. 7.3).
Retrieved model parameters in the joint interior-atmosphere retrievals.
7.1 Bulk and atmospheric composition
The compositional parameters derived in the joint retrievals are compared in Fig. 4 with the interior-only retrievals (top panel: CMF and Zplanet) and the atmosphere spectrum retrievals (bottom panel: C/O and M/H). As the joint retrievals combine the observations used in the independent interior and atmosphere retrievals simultaneously, their estimates should be consistent with these. With the exception of JR5, joint retrievals agree within 2σ with the interior-only retrievals, as shown by their overlap in CMF-Zplanet parameter space (Fig. 4, top panel). JR5, which incorporate emission spectra without the age, tends to overestimate the CMF. We discuss the cause of this high-CMF estimate in Sect. 7.4.
The bulk metal and core mass fraction estimates align along the solar envelope line (dashed black line in Fig. 4). We compare the envelope composition estimates in the bottom panel. The joint retrievals that do not include emission spectra (JR1, JR2) retrieve a sub-solar atmospheric metallicity and a solar C/O ratio, consistent with the fiducial transmission-only retrieval. JR3-JR6, which include emission data with bulk properties and/or the transmission spectrum, obtain atmospheric metallicities and C/O ratios in excellent agreement with the emission-only retrievals (Fig. 4, bottom panel). These show that WASP-80 b has a subsolar C/O~0.10–0.20 and [M/H] = 1–20× solar. JR1 and JR2 (transmission) are compatible with solar C/O values, in contrast to the sub-solar C/O in the other joint retrievals.
Overall, we demonstrate that the joint retrievals that include emission spectra are consistent with the emission-only retrievals, while JR1 and JR2 are consistent with the transmission-only retrievals. We observe that the bulk composition derived in the joint retrievals are also consistent with the traditional interior-only retrievals, with the exception of JR5.
7.2 The M/H discrepancy and degeneracies in joint retrievals
We describe in Sect. 5.1 how the atmospheric metallicity derived from the free chemistry, transmission-only retrieval is strongly super-solar and incompatible with the interior-only retrievals that assume secular cooling. To explore this tension, we modified our joint retrieval JR1, which takes into account the transmission spectrum together with the mass as observables, as a free chemistry retrieval. This free chemistry retrieval, JR1*, tends to obtain a lower C/O ratio and higher atmospheric metallicity than its equilibrium counterpart. This decrease in C/O and increase in M/H is consistent with the behavior we observed in the transmission-only retrievals, as the free chemistry retrieval exhibits a preference for a water-rich atmosphere and high-altitude clouds. In contrast to the transmission-only, free retrieval, the atmospheric metallicity has an upper 1σ limit of log(M/H) = 0.89, which is below the 1σ-upper limit derived by the interior-only analysis of 10 × solar. This is caused by the coupling between the reference radius used to generate the transmission spectrum and the interior model. Thus, the coupling between temperature, chemistry (metal content) and radius in joint retrievals effectively demonstrates that there is a degeneracy between the envelope composition (M/H and C/O) and chemistry.
7.3 Clouds
We obtained very similar estimates on the cloud parameters between each joint retrieval, and these and the transmission-only retrievals in Sect. 5.1. For reference, we included the cloud base pressure in Table 5. Most estimates are consistent with a cloud base located at P > 0.1 bar at 1σ. The most data-complete joint retrieval, JR6, suggests that clouds are present at high altitudes P ~ 10−4 bar within 1σ.
In Sect. 5.1, we note the degeneracy between the opacity of carbon- and oxygen-bearing molecules and cloud opacities in spectra. From the least degenerate joint retrieval (JR6), we can conclude that a sub-solar C/O ratio together with an atmospheric metallicity [M/H] = 1–10× solar and high altitude clouds is the most likely scenario for WASP-80 b, as this is compatible with all spectral data sets and the planet bulk density simultaneously, under the assumption of equilibrium chemistry.
7.4 Thermal structure
We show in Fig. 5 the thermal structure profiles constrained by all our joint retrievals (except for JR4) that incorporate emission spectra. These profiles agree well with those derived by the emission-only retrievals (see Sect. 5.2) at pressures P < 1 bar. As demonstrated in Fig. 2 by the contribution function, these are the pressures probed by the emission spectrum. At higher pressures (P = 1–1000 bar), the constrained thermal structure is very dependent on the assumptions and data included in the retrieval. In the following, we discuss how these impact the temperature in the deep envelope and the bulk metal mass fraction.
Including the age in the likelihood improves the constraints on the internal temperature. This can be seen in the central panel of Fig. 5, and by comparing the internal temperatures in Table 5. When the age is not taken into account, the internal temperatures have wide uncertainties (ΔTiat ~ 100–200 K), and their mean values tend to be high (Tint > 200 K). As WASP-80 is a moderately old system (0.99 Gyr), the age's effect in the retrievals is to decrease the internal temperature to Tint = 50–150 K, with uncertainties as low as ΔTint = 12 K in the least degenerate case, JR6. This range of internal temperatures is consistent with the interior-only retrievals that account for the age (RI, R5–R6) and the interior forward models (see Fig. A.1).
Independently of the geometry considered, adding the age to the likelihood reduces the mean value of the retrieved bulk metal mass fraction and the CMF (see Fig. 4, top panel). As discussed above, the age of WASP-80 b decreases the internal temperature, which entails a lower temperature at 1000 bar. Since the interior temperature follows an adiabatic profile, a lower Tsurf correlates to a colder interior. A colder interior adiabat increases the density of the envelope, which lowers the retrieved CMF and Zplanet values.
The inclusion of transmission spectra in the joint retrievals tends to increase the inferred temperature in the deep envelope and reduce its uncertainties. This effect can be seen when comparing Tint in JR1 and JR3 (Table 5), and in the left panel of Fig. 5. When comparing JR1 (transmission without emission) and JR3 (emission without transmission), we find that JR3 yields lower internal temperatures than JRI. JR3 is more sensitive to the temperature at 1 bar – T(P = 1 bar) = 700–900 K (see also Sect. 5.2) –, favoring lower Tint. Similarly, when both transmission and emission are considered (JR5), the temperature increases compared to JR3 (no transmission; see the left panel of Fig. 5). In Sect. 5.1, we noted that the fiducial transmission retrieval tends to retrieve low C/O ratios. We discussed that this could be due to the assumption of equilibrium chemistry, where low C/O ratios and high deep atmospheric temperatures are required to increase the abundance of H2O relative to CH4. Including the transmission spectrum along with the emission spectrum in a joint retrieval further constrains the abundances of H2O and CH4, which drives model in JR5 toward a higher internal temperature (Tint = 500 K). This high deep atmospheric temperature increases the planet radius, yielding a core and bulk metal mass fraction in JR5 that is the highest of all joint retrievals (see Fig. 4, top panel).
Finally, we explored the effect of assuming equilibrium chemistry on the retrieved thermal structure. We compare the P–T profile of JR5 (emission plus transmission, without age) between equilibrium and free chemistry (JR5*). As discussed above, the equilibrium chemistry model requires high temperatures to reproduce the abundance of H20 observed in the spectra. Thus, relaxing the equilibrium assumption in the free chemistry retrieval leads to a decrease in the temperature at high pressures, as shown in the left panel of Fig. 5. The thermal structure of JR5* is compatible with a self-consistent, clear solar model with Tint = 100 K at 1σ, which is the internal temperature predicted by the age of WASP-80 b in the absence of extra heating.
The decrease in deep atmospheric temperature between JR5 and IR5* has a significant impact on the retrieved CMF. In Fig. 4 (top panel), we can see that the CMF decreases from 0.50 (JR5) to ~0.20 (JR5*). Since JR5* (free chemistry) is more consistent with the other retrievals than JR5, it represents a more conservative scenario than JR5. This is especially the case if WASP-80 b's internal temperature is decoupled from its age due to additional heating sources. Thus, we adopted JR5* as our fiducial retrieval, together with JR6. The latter represents a scenario without extra heating sources where age and Tint are coupled.
 |
Fig. 3 Mean forward model from one of our two fiducial interior-atmosphere joint retrievals, JR6, of WASP-80 b. This model corresponds to a core mass fraction (CMF) of 0.02, an atmospheric metallicity of M/H = 2.75 × solar, C/O = 0.12, and Tint = 134 K. Panel a: schematic cross section of the planet; layer thicknesses are to scale. The atmosphere corresponds to pressures below 1000 bar. Panel b: P–T profile of the atmosphere (light blue) and interior (blue and teal). Panel c: transmission spectrum for this model, with the three observed transmission datasets shown for comparison. Panel d: emission spectrum for this model, compared against the four observed emission datasets. Panel e: interior metal mass fraction profile (Z; black) and H/He mass fraction as functions of normalized radius. The atmospheric region (P < 1000 bar) is indicated in light blue. Panel f: atmospheric mass mixing ratios of the molecular species comprising the metals (P < 1000 bar). The region highlighted in orange indicates the pressure range probed by emission spectra, as calculated from the contribution function. |
 |
Fig. 4 Top panel: core and bulk metal mass fraction 1σ estimates obtained by our joint retrievals (JR1-JR6). Joint retrievals that take into account the age have triangle markers. Interior-only retrievals (R1–R3 and R5) are shown as colored boxes for comparison. Bottom panel: atmospheric metallicity and C/O ratio estimates from our suite of joint retrievals. Spectra-only estimates are displayed as colored boxes for comparison. |
7.5 Precision in bulk metal mass fraction, Zplmet
In the following, we compare the CMF and Zplanet estimates shown in Table 5 to discuss how the different observables and data sets can improve the precision in bulk metal mass fraction. For this comparison, our reference uncertainty of the bulk metal mass fraction is ΔZplanet = 0.05, which is the uncertainty of the most-data complete of the traditional, interior-only retrievals, R5-R6.
We note that all three joint retrievals that incorporate the age – JR2, JR4, and JR6 - have bulk metal mass fraction uncertainties of ΔZplanet = 0.02–0.03. This means that a joint retrieval together with age reduces the uncertainties from 0.05 to 0.02 – a factor of 1/2. However, in the absence of an age estimate, a joint retrieval does not guarantee an improvement of the retrieved bulk metal mass fraction relative to the traditional, interior-only retrievals. For example, R3 has a ΔZplanet, R3 = 0.05–0.07, while its joint counterpart in transmission (JR1) shows a similar uncertainty ΔZplanet, JRI = 0.07. Furthermore, the joint counterpart in emission (without transmission), JR3, obtains a larger uncertainty of ΔZplanet, JR3 = 0.16. This is due to the degeneracy between temperature in the deep atmosphere (Tsmt) and CMF, which is mostly solved by the age.
8 Discussion
Wilkinson et al. (2024) conducted a similar analysis using the MCMC method and a coupled interior-atmosphere model on WASP-39 b's transmission spectrum. There are three key differences between their analysis and this work. First, we included a condensate opacity source to simulate the effect of clouds. Second, we did not weight the importance of the bulk density observables (i.e. mass, radius, and age). Third, our retrievals incorporate data in both the near-infrared (nIR) and optical. We examined how the cloud treatment, weighted likelihood, and the spectral wavelength coverage affect the inferred atmospheric and bulk compositions in atmosphere-only and joint retrievals in Sects. 8.1, 8.2, and 8.3, respectively.
Furthermore, we discuss the possible presence of external heating sources and disequilibrium chemistry in WASP-80 b in Sects. 8.4 and 8.5. Finally, we conclude by outlining our model uncertainties and caveats (Sect. 8.6) and by discussing the implications of WASP-80 b's atmospheric and bulk composition for its formation pathways (Sect. 8.7).
8.1 Sensitivity to cloud treatment
The omission of cloud modeling in joint retrievals with transmission spectra may lead to biases in the inference of atmospheric composition and bulk metal mass fraction. In traditional, transmission-only retrievals, the atmospheric metallicity and the cloud top pressure (Pbase) are often correlated (Benneke & Seager 2012; Welbanks & Madhusudhan 2019; Fisher & Heng 2018). To study the impact of not including clouds in our modeling, we run our JR1 retrieval without clouds. We obtain CMFJR1, clear = 0.09±0.05, 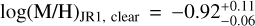 and
and 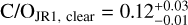 . If we compare these to the fiducial JR1 retrieval, we find that the uncertainties in atmospheric metallicity and C/O ratio are reduced by a factor of 3 and 5, respectively. This bias arises from the reduced parameter space caused by eliminating the degeneracy between chemical abundance and cloud pressure. The CMF mean is decreased from 0.14 to 0.09, while their uncertainties are reduced by a factor of 2. We conclude that not accounting for clouds in joint interior-atmosphere retrievals biases not only the inference of atmospheric composition, but also the inferred CMF and Zplanet. These biases include lower C/O ratio and CMF mean values, and significantly reduced uncertainties for all compositional parameters, by factors of 2–4.
. If we compare these to the fiducial JR1 retrieval, we find that the uncertainties in atmospheric metallicity and C/O ratio are reduced by a factor of 3 and 5, respectively. This bias arises from the reduced parameter space caused by eliminating the degeneracy between chemical abundance and cloud pressure. The CMF mean is decreased from 0.14 to 0.09, while their uncertainties are reduced by a factor of 2. We conclude that not accounting for clouds in joint interior-atmosphere retrievals biases not only the inference of atmospheric composition, but also the inferred CMF and Zplanet. These biases include lower C/O ratio and CMF mean values, and significantly reduced uncertainties for all compositional parameters, by factors of 2–4.
 |
Fig. 5 P–T proflies of WASP-80 b as constrained by four of our joint retrievals. The shaded regions indicate the 1, 2, and 3σ regions of the retrieval, while solid lines correspond to the mean. Black lines highlight self-consistent models from Mollière et al. (2017); Acuña et al. (2024) of a clear atmosphere with solar composition at Tim = 100 (dashed) and 500 K (dotted) for comparison. Left: the difference between JR3 and JR5 shows the effect of adding the transmission spectrum to JR3, which incorporates emission spectra plus the mass and radius. The transmission spectrum reduces significantly the uncertainties in thermal structure. Center, comparing JR6 and JR5 allows us to study the effect of including the age to the retrieval. JR6 is the most data-complete of the joint retrievals, since it incorporates both transmission and emission, plus the mass and age. If the age is removed (JR5), the temperature in the deep atmosphere increases. Right: comparison between JR5 and JR5*, which illustrates the effect of assuming equilibrium chemistry in the joint retrieval. If we relax the assumption of equilibrium chemistry in JR5 by changing to a free chemistry model (JR5*), the temperature decreases in the deep interior. |
8.2 Effect of weighted likelihood
The second key difference from previous work is that we do not scale the terms associated with the bulk density observables in Eq. (11) (dbull) by a weighting factor (wj). Wilkinson et al. (2024) fix wj to a constant value that equalizes the importance of these observables with that of the spectrum. Under this assumption, the weighting factor must be equal to the total number of points in the spectrum. A value wj > 1 is equivalent to reducing the uncertainties of the observables, because the factor 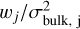 in Eq. (11) can also be written as
in Eq. (11) can also be written as 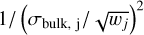 . In volatile-rich planets, reducing mass uncertainties does not improve the precision of inferred bulk composition since the envelope mass contributes a negligible fraction to the total mass (Otegi et al. 2020). However, a reduction in radius and age uncertainties significantly improves the precision of the inferred CMF and Zplanet (Müller & Helled 2023). Consequently, using a weighting factor to give more importance to the bulk density observables relative to the transmission spectrum leads to an underestimation of the uncertainties of core and bulk metal mass fraction. The use of weighting factors adopting a prior wj < 1 may be justified if the flux uncertainties in the transmission and emission spectra are expected to be underestimated. This is not the case for WASP-80 b, as the transmission and emission spectra were obtained contrasting different data reduction pipelines in Bell et al. (2023) and Wiser et al. (2025), showing robustness in their approach.
. In volatile-rich planets, reducing mass uncertainties does not improve the precision of inferred bulk composition since the envelope mass contributes a negligible fraction to the total mass (Otegi et al. 2020). However, a reduction in radius and age uncertainties significantly improves the precision of the inferred CMF and Zplanet (Müller & Helled 2023). Consequently, using a weighting factor to give more importance to the bulk density observables relative to the transmission spectrum leads to an underestimation of the uncertainties of core and bulk metal mass fraction. The use of weighting factors adopting a prior wj < 1 may be justified if the flux uncertainties in the transmission and emission spectra are expected to be underestimated. This is not the case for WASP-80 b, as the transmission and emission spectra were obtained contrasting different data reduction pipelines in Bell et al. (2023) and Wiser et al. (2025), showing robustness in their approach.
8.3 Effect of wavelength coverage in atmospheric spectra
In contrast to WASP-39 b's joint retrievals by Wilkinson et al. (2024), our analysis incorporates both nIR and optical transmission spectra. Transmission spectra retrievals exhibit a normalization degeneracy, in which the molecular abundances relative to H are degenerate with the absolute normalization of the spectrum. The normalization depends on the reference pressure, Pref. This degeneracy can be broken if the spectrum is sensitive to Pref through pressure broadening or collision-induced absorption (CIA). The transmission spectrum contains information about these processes when it spans a wide wavelength range in the nIR, such as that provided by the combined HST and IWST datasets used in our analysis (Fisher & Heng 2018). Additionally, optical data further reduce degeneracies between the chemical abundances and the cloud top pressure (Fairman et al. 2024). The optical wavelength range provides valuable information about condensates in transmission retrievals (Welbanks & Madhusudhan 2019).
We further compare our results to those of Morel et al. (2025), who use reflected light data in traditional, atmosphere-only retrievals. They provide and analyze a dataset of WASP-80 b emission spectra between 0.6 and 3 μm, measured with JWST's NIRISS/SOSS. Their retrievals rule out log(M/H) > 2 and C/O > 0.6, which is in good agreement with our joint retrievals. Their self-consistent cloud modeling concludes that the NIRISS/SOSS data are compatible with cloud species such as chromium (Cr[s]), sodium sulfide (Na2S), potassium chloride (KCl) and Zinc sulfide (ZnS). Morel et al. (2025) also consider the presence of tholins in the atmosphere of WASP-80 b. In this scenario, they estimate a low tholin production rate (<10−11.5 g cm−2 s−1). Tholins tend to cool the envelope due to a high UV extinction, as observed in the sub-Neptune GJ1214 b (Nixon et al. 2024) and as predicted in cold, directly imaged planets (Morley et al. 2015). Our fiducial retrieval (JR6) is compatible within uncertainties with a cool atmosphere (see Fig. 5, central panel). Additionally, our atmosphere-only and joint retrievals further support the presence of condensates in transmission, (see Sects. 5.1 and 7), consistent with the scenario proposed by Morel et al. (2025).
Our analytical parameterization and priors of the thermal structure are conservative and flexible enough to accommodate a wide range of Bond albedos (see Figs. 2 and 5). Morel et al. (2025) constrain the Bond albedo to AB = 0.15–0.40 at 1σ. This interval could potentially further constrain the thermal structure in our fiducial joint retrieval. Thus, the bulk composition obtained from joint retrievals that include reflected light would lie within the confidence intervals reported in Sect. 7. Although the analysis of reflected light data is beyond the scope of this work, our future efforts will focus on incorporating the NIRISS/SOSS dataset into our joint interior–atmosphere framework. Such an analysis could further constrain the retrieved thermal structure profile if the reflected light data is combined with a grid of self-consistent cloudy P–T profiles (Charnay et al. 2018; Lacy & Burrows 2023; Morley et al. 2024) and condensation curves (Rooney et al. 2022). These condensation curves can determine the location and composition of the condensate layer instead of assuming free cloud parameters in our retrievals.
8.4 Non-adiabatic interiors and heating mechanisms
A key assumption in our analysis is that the deep interior of WASP-80 b is adiabatic. Several mechanisms can raise the temperature above that of an adiabatic interior, such as compositional gradients (i.e., an inhomogeneous interior), tidal heating or Ohmic dissipation. Super-adiabatic interior models could accommodate more metals in the bulk composition of WASP-80 b. For instance, in Sect. 6, we noted that WASP-80 b's density and age could be compatible with a super-solar atmospheric metallicity of M/H > 30× solar, if its interior is warmer than our fiducial, interior-only model. In this section we assess the extent to which these processes could affect the inference of WASP-80 b's bulk composition.
Compositional gradients induce hotter, non-adiabatic interior temperature profiles (Vazan et al. 2018), resulting in larger planetary radii than homogeneous envelope models. This raises the question of whether WASP-80 b could have an inhomoge-neous interior, thereby affecting the bulk metal mass fraction inferred by our homogeneous model. Inhomogeneous envelopes have been confirmed in Jupiter and Saturn (Wahl et al. 2017; Nettelmann et al. 2021; Mankovich & Fuller 2021; Miguel et al. 2022), and are a natural outcome of planet formation in both the Solar System (Helled & Stevenson 2017; Lozovsky et al. 2017; Valletta & Helled 2020; Stevenson et al. 2022) and exoplanets (Bodenheimer et al. 2018; Ormel et al. 2021; Brouwers & Ormel 2020). Knierim & Helled (2024) conducted a parameter study to explore the planet masses and primordial entropies (S0) at which compositional gradients are expected. They find that at WASP-80 b's mass, fast mixing in the deep envelope is efficient enough to erase any compositional gradients from formation, regardless of the initial entropy (see their Figures 4 and 6). Thus, a planet with WASP-80 b's mass and age would be expected to have a homogeneous interior.
Moreover, helium rain could also affect the inference of the bulk metal mass fraction in extrasolar gas giants. Knierim & Helled (2025) included the effect of helium rain in interior models with equilibrium temperatures relevant to that of WASP-80 b (Teq = 500 K). Helium rain is predicted to have a negligible effect on the planetary radius at WASP-80 b's equilibrium temperature and mass, with ΔRplanet < 0.01 RJup (see Figure B.1 in Knierim & Helled 2025). Consequently, the omission of compositional gradients and helium rain in our modeling is unlikely to affect our inferred atmospheric and bulk composition of WASP-80 b.
Warm gas giants can experience internal heating due to external sources (Millholland et al. 2020; Vissapragada et al. 2024). This has been confirmed in WASP-107 b via disequilibrium chemistry, which shows its internal temperature rising from Tint ~100 K to Tint > 460 K (Sing et al. 2024; Welbanks et al. 2024). It is currently under debate whether WASP-107 b is inflated due to tidal heating or Ohmic dissipation (Batygin 2025). Triaud et al. (2015) estimate an eccentricity for WASP-80 b of 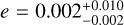 . We use the tidal heating model in Leconte et al. (2010) to estimate the internal temperature induced by tidal heating in WASP-80 b, assuming its mean eccentricity. For Q′ > 2.7 × 105 – Jupiter's minimum value – WASP-80 b's internal temperature is Tint = 200 K for a Love number and time lag factor of k2 × Δt = 0.02 s. Since internal temperature increases for lower tidal dissipation factor values, we adopted 200 K as a conservative upper limit on the internal temperature induced by tidal heating. Thus, we conclude that tidal heating is unlikely to be inflating the interior of WASP-80 b.
. We use the tidal heating model in Leconte et al. (2010) to estimate the internal temperature induced by tidal heating in WASP-80 b, assuming its mean eccentricity. For Q′ > 2.7 × 105 – Jupiter's minimum value – WASP-80 b's internal temperature is Tint = 200 K for a Love number and time lag factor of k2 × Δt = 0.02 s. Since internal temperature increases for lower tidal dissipation factor values, we adopted 200 K as a conservative upper limit on the internal temperature induced by tidal heating. Thus, we conclude that tidal heating is unlikely to be inflating the interior of WASP-80 b.
Ohmic dissipation may also play an important role in the interior structure of warm Jupiters. This mechanism results from the interaction between the planetary magnetic field and atmospheric winds. It has been studied in detail for hot Jupiters and is a leading explanation for radius inflation at Teq > 1000 K (Perna et al. 2010; Batygin & Stevenson 2010; Thorngren & Fortney 2018). More recently, it has also been proposed as a source of inflation for smaller, cooler planets, including WASP-107b and sub-Neptunes Batygin (2025); Pu & Valencia (2017). WASP-80 b lies between these two regimes in both mass and equilibrium temperature, so Ohmic dissipation may be relevant. Furthermore, for a fixed mass and equilibrium temperature, the extent of heating depends on wind depth, wind velocity, and magnetic field intensity (Ginzburg & Sari 2016; Komacek & Youdin 2017; Knierim et al. 2022). Magnetic fields and winds can be probed using ground-based, high-resolution spectroscopy (Ehrenreich et al. 2020; Keles 2021) and spectropolarimetry (Oklopčić et al. 2020). Ultra-hot and hot Jupiters are currently the only class of planets accessible to these techniques.
Although wind and magnetic field properties remain unconstrained for warm gas giants, the effect of magnetic fields in this temperature and mass regime can be suggested via other observational methods. A non-detection of the metastable-helium triplet (1083 nm) signature in transit was reported for WASP-80 b, despite hydrodynamical escape models predicting such a signal due to the low planetary density (Fossati et al. 2022; Vissapragada et al. 2022). One hypothesis to explain this lack of helium absorption states that planetary magnetic fields can disrupt the ideal assumption of the neutral gas forming a symmetric shell or extended tail around the planet disk. Instead, a strong magnetic field can channel ionized outflows along the open field lines near the poles. This scenario is termed magnetic confinement, as the magnetic pressure is high enough to prevent the outflow from expanding isotropically (Adams 2011; Trammell et al. 2011). In addition, an intense planetary magnetic field can also act as a bottleneck to the flow at the Alfvén surface, suppressing the mass flux escaping the planet due to photoevaporation (Owen & Adams 2014). Yadav & Thorngren (2017) estimate the magnetic field strength for the hot Jupiter sub-population based on their observed inflation and a luminosity-dynamo scaling model. Jupiter's field strength corresponds to 10 G (Moore et al. 2017), while hot Jupiter-mass planets can have field strengths ranging from 10 to 100 G. Their model suggests that at constant mass, a higher equilibrium temperature increases the field strength by a factor of 10. This behavior could be conserved in Saturn-mass planets, closer to WASP-80 b's mass. Saturn's magnetic field strength is 0.2 G at Teq < 100 K (Russell 1993; Belenkaya et al. 2006). For WASP-80 b at Teq = 825 K, the field strength could be has high as 2 G. This field strength would be sufficient to magnetically confine or suppress the outflow at the Alfvén surface (Fossati et al. 2023). Thus, the scenario we propose in our analysis where WASP-80 b has a super-solar envelope and is inflated by a heating mechanism could be explained, together with independent He triple transit observations, by Ohmic dissipation.
8.5 Effects of disequilibrium chemistry
In our fiducial retrieval, we assume equilibrium chemistry; however a high internal temperature combined with strong vertical mixing could drive the chemistry out of equilibrium. Methane is expected to be the dominant absorber in cold exoplanet atmospheres under chemical equilibrium (Fortney et al. 2020; Blain et al. 2021). Although our retrieved chemical abundances agree well with expectations for chemical equilibrium, the abundances of key absorbers (e.g., CH4) may be sensitive to the temperature in the deep layers of the atmosphere (Fortney et al. 2020; Ohno & Fortney 2023). Warm temperatures in these deep layers of the atmosphere can reduce the abundance of CH4 by several orders of magnitude, regardless of the vertical diffusion coefficient, Kzz (Mukherjee et al. 2025). Thus, there is a degeneracy between Kzz, Tint and C/O. If the deep atmosphere of WASP-80 b is heated (e.g., by Ohmic dissipation), the C/O ratio could be higher than the value we infer under equilibrium assumptions. Given the potential impact of disequilibrium chemistry, our future work will focus on incorporating it into our retrieval framework.
8.6 Model uncertainties and caveats
The standard deviation of the CMF posterior in the joint retrieval JR6 (ΔCMF = 0.02) is smaller than the spacing of the interior model grid (ΔCMF = 0.10). This could potentially lead to artificial precision if the assumption of linear interpolation between grid points – considered by the Python function we use – were inaccurate. This could be the case in the regime of vanishingly small cores, where the planet radius could vary non-linearly with CMF. To assess this, we evaluated the accuracy of our linear interpolation method (```scipy.RegularGridlnterpolator``) for the interpolated parameters: planetary radius and entropy at 1000 bar, and the 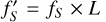 parameter (see Sect. 3.1.2). Using models computed specifically for this test over the CMF = 0–0.10 range, we find that the maximum interpolation errors are ~0.5% for radius and ~0.9% for
parameter (see Sect. 3.1.2). Using models computed specifically for this test over the CMF = 0–0.10 range, we find that the maximum interpolation errors are ~0.5% for radius and ~0.9% for  – well below the variations induced by ΔCMF = 0.02, which corresponds to the uncertainty of the retrieved CMF. The entropy remains constant with CMF, and its interpolation error is negligible (~10−6%). These results confirm that the interpolation introduces errors significantly smaller than the posterior uncertainty, validating the robustness of our retrieval in the low-CMF regime. For analyzes that use a similar joint retrieval approach, we recommend using a smaller step in the grid of forward models for less massive exoplanets (M < 0.50 MJup).
– well below the variations induced by ΔCMF = 0.02, which corresponds to the uncertainty of the retrieved CMF. The entropy remains constant with CMF, and its interpolation error is negligible (~10−6%). These results confirm that the interpolation introduces errors significantly smaller than the posterior uncertainty, validating the robustness of our retrieval in the low-CMF regime. For analyzes that use a similar joint retrieval approach, we recommend using a smaller step in the grid of forward models for less massive exoplanets (M < 0.50 MJup).
The formation of deep radiative and double-diffusive layers can impact the inferred bulk composition in gas giants. In the following, we assess the likelihood of exhibiting these in WASP-80 b. In the joint retrievals, we couple the Guillot (2010) temperature-pressure profile to the interior model at 1000 bar. While this analytical prescription of the atmospheric thermal structure enables the formation of radiative layers, GASTLI assumes that the interior is fully convective. This means that our framework cannot form radiative layers at pressures P > 1000 bar. The interior-only retrievals use self-consistent atmospheric models to compute the boundary condition for our forward models. These atmospheric models were obtained using petitCODE, which applies the Schwarzschild criterion to determine whether a layer is convective or radiative (see Sect. 3.1.1). The pressure-temperature profiles of two of these atmospheric models are shown in Fig. 5 for a solar composition and internal temperatures of Tint = 100 K and Tint = 500 K. The most favorable conditions for the formation of radiative layers are (1) low envelope metallicities and (2) low internal temperatures. From the two fiducial retrievals, the lowest atmospheric metallicity and internal temperature inferred for WASP-80 b are approximately ~2× solar and ~100 K, respectively. The petitCODE model at solar composition and Tint = 100 K (Fig. 5) already shows a convective zone extending from 100 bar to higher pressures, placing the radiative-convective boundary (RCB) of WASP-80 b at 100 bar. Increasing the internal temperature and atmospheric metallicity shifts the RCB upward (to lower pressures), as demonstrated by the model at Tint = 500 K. Moreover, the presence of clouds – which are likely in WASP-80 b (see Sect. 8.3) – would further shift the RCB to lower pressures. Therefore, maintaining the RCB at pressures higher than 100 bar, as we do in our joint retrievals at 1000 bar, represents a conservative choice for the case of WASP-80 b and does not impact its inferred bulk composition.
If our framework were applied to a colder planet with a lower internal temperature or lower atmospheric metal content, fixing the RCB (i.e., the interior-atmosphere interface) at 1000 bar would indeed introduce a significant source of uncertainty in the inferred interior structure. For example, Siebenaler et al. (2025) find that Jupiter (Teq = 122 K) could develop radiative layers at pressures between 1000 and 50 000 bar if its sodium (Na) and potassium (K) abundances were below 10−3× solar. As shown in their figure 8, the formation of radiative zones leads to colder interiors as the temperature profile becomes nearly isothermal compared to the dry adiabat. Therefore, implementing the Schwarzschild criterion in the interior structure model, GASTLI, will be within the scope of future work to extend its applicability to colder (Teq < 800 K) exoplanets.
Double diffusion (also referred to as semiconvection) could be relevant for WASP-80 b, as strong magnetic fields can inhibit large-scale, ideal convection, which is assumed in our interior model (Chabrier et al. 2007). This effect could lead to imperfect mixing of heavy elements within the envelope. This process produces a superadiabatic temperature gradient, increasing the interior temperature relative to the ideal convective assumption (Leconte & Chabrier 2012). Not treating double diffusion in our interior model may introduce a model uncertainty. Consequently, the statistical errors reported in Table 5 should be regarded as lower limits on the total uncertainty.
Finally, we discuss how the treatment of the He mass fraction in the envelope does not impact our results. GASTLI assumes a cosmogonic He mass fraction in the H-He mixture of the envelope of Y = 0.275 (see Sect. 2.3.1 in Acuña et al. 2024). Given this assumption, the He mass fraction is treated consistently between the interior and the atmosphere in the free-chemistry joint retrieval. In the equilibrium-chemistry joint retrievals, the abundances of hydrogen and helium computed by easyCHEM are summed to calculate the total mass fraction of the H-He mixture. This approximation can lead to deviations at high atmospheric metallicities (>250× solar), where the He abundance tends to exceed the cosmogonic value. However, for WASP-80 b, the atmospheric metallicity retrieved in the fiducial equilibrium-chemistry joint retrieval (JR6) is 2–5× solarand the corresponding helium abundance remains close to Y = 0.275 in the H–He mixture. Therefore, this approximation does not affect our bulk composition estimates for WASP-80 b. We will implement a more self-consistent coupling between the helium abundance in the interior and the atmosphere in future work, particularly when applying our framework to exoplanets with highly metal-rich envelopes and observational constraints on helium.
Our model does not include conduction as a heat transport mechanism in the core. Given the available observables, the effect of conduction on the core's thermal structure would have a negligible impact on the total planetary radius. Nonetheless, conduction should be considered if magnetic field data are incorporated into an interior-atmosphere framework such as the one presented in this paper.
Atmospheric and bulk interior composition of WASP-80 b under the two fiducial scenarios.
8.7 Bulk composition and formation of WASP-80 b
The formation history of a planet shapes both its atmospheric and bulk composition. Accordingly, four of the parameters obtained in this work - atmospheric M/H, C/O ratio, core mass (Mcore) and bulk metal mass fraction (Zplanet) – allow us to explore potential formation and evolutionary pathways for WASP-80 b. Calculating the planet-to-star bulk metal mass fraction ratio, Zplanet/Zstar, requires an estimate of the stellar bulk metal mass fraction. We estimated WASP-80's stellar bulk metal mass fraction using the approximation ![${Z_{{\rm{star}}}} = 0.014 \times {10^{{{\left[ {{\rm{Fe/H}}} \right]}_*}}}$](/articles/aa/full_html/2026/02/aa56519-25/aa56519-25-eq111.png) (after Thorngren et al. 2016), where
(after Thorngren et al. 2016), where ![${\left[ {{\rm{Fe/H}}} \right]_*} = - 0.13_{ - 0.17}^{ + 0.15}$](/articles/aa/full_html/2026/02/aa56519-25/aa56519-25-eq112.png) (Triaud et al. 2015).
(Triaud et al. 2015).
We consider two scenarios: one in which heating mechanisms are absent, and another in which high temperatures in the deep atmosphere are induced by such mechanisms. In the former, thermal evolution is driven by secular cooling. Under this assumption, the planet's age constrains its internal temperature, which is the approach adopted in retrieval JR6. We adopted JR6 as our fiducial joint retrieval for this scenario because it consistently fits all available data - mass, age, transmission, and emission spectra. For the second scenario, the potential impact of heating sources on the inferred bulk and atmospheric composition is captured by our free-chemistry joint retrieval JR5*. This retrieval is similar to JR6, but excludes the age constraint and does not assume chemical equilibrium. By omitting age as an observable, we removed the coupling between the planet's thermal cooling history and its internal temperature. This allowed the model to explore thermal states that are hotter than those expected in the absence of heating mechanisms.
Table 6 summarizes the atmospheric and bulk composition of WASP-80 b under our two fiducial scenarios. In the first scenario (no heating, JR6), we obtain a core mass of 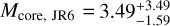 . Core accretion typically produces cores with masses of ~ 10 M⊕ (Pollack et al. 1996), which is within the 3σ upper limit of our estimate in the secular cooling scenario. Thus, the secular cooling scenario is marginally compatible with core accretion under highly favorable conditions. For example, Piso et al. (2015) estimate that cores of masses as low as 3.5–5 M⊕ can be formed if core accretion occurs at long orbital distances (100 AU) and the disk opacity is low due to grain coagulation (see also Hubickyj et al. 2005; Hori & Ikoma 2010). Classic gravitational instability models can more easily reproduce such low-mass cores and even a core-less interior, as it is suggested by our first scenario within 2σ.
. Core accretion typically produces cores with masses of ~ 10 M⊕ (Pollack et al. 1996), which is within the 3σ upper limit of our estimate in the secular cooling scenario. Thus, the secular cooling scenario is marginally compatible with core accretion under highly favorable conditions. For example, Piso et al. (2015) estimate that cores of masses as low as 3.5–5 M⊕ can be formed if core accretion occurs at long orbital distances (100 AU) and the disk opacity is low due to grain coagulation (see also Hubickyj et al. 2005; Hori & Ikoma 2010). Classic gravitational instability models can more easily reproduce such low-mass cores and even a core-less interior, as it is suggested by our first scenario within 2σ.
In contrast, if a heating mechanism (e.g., Ohmic dissipation) raises the temperature in the deep envelope of WASP-80 b, its formation would be consistent with the core accretion paradigm within 1 r . Under our additional heating scenario, we estimate 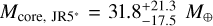 . This core mass is ~10 times higher than that obtained in the first scenario with no additional heating sources, JR6. A core as massive as ~30 M⊕ can be produced in core accretion models. For example, pure pebble accretion models without planetesimal formation can reproduce a bulk metal mass fraction consistent with our JR5* estimate within 1σ if the dust-to-gas ratio is high (2%; see Fig. 3 in Danti et al. 2023).
. This core mass is ~10 times higher than that obtained in the first scenario with no additional heating sources, JR6. A core as massive as ~30 M⊕ can be produced in core accretion models. For example, pure pebble accretion models without planetesimal formation can reproduce a bulk metal mass fraction consistent with our JR5* estimate within 1σ if the dust-to-gas ratio is high (2%; see Fig. 3 in Danti et al. 2023).
Exoplanets continue to accrete solids and gas into their envelope after reaching the pebble isolation mass (Pollack et al. 1996; Turrini et al. 2015; Emsenhuber et al. 2021). The atmospheric metallicity and C/O ratio therefore contain information about the composition of the accreted gas, its location, and the dominant accretion mechanism (pebbles vs planetesimals). In our first scenario JR6, we retrieve an atmospheric metallicity of 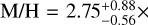 solar and a C/O ratio of
solar and a C/O ratio of 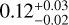 . Although the C/O ratio retrieved in JR5* – which represents a scenario with additional heating and no age constraint – is slightly higher, it remains sub-solar (C/OJR5* = 0.24±0.09). A sub-solar C/O ratio suggests that WASP-80 b accreted oxygen-rich material. This material could be H2O ice accreted outside the water snowline via planetesimal accretion. Alternatively, WASP-80 b may have accreted gas enriched in water vapor inside the snowline, especially in our heating scenario, where the atmospheric metallicity is as high as 10–20× solar. Pebbles outside the water ice line can drift inwards and evaporate as they cross this line.
. Although the C/O ratio retrieved in JR5* – which represents a scenario with additional heating and no age constraint – is slightly higher, it remains sub-solar (C/OJR5* = 0.24±0.09). A sub-solar C/O ratio suggests that WASP-80 b accreted oxygen-rich material. This material could be H2O ice accreted outside the water snowline via planetesimal accretion. Alternatively, WASP-80 b may have accreted gas enriched in water vapor inside the snowline, especially in our heating scenario, where the atmospheric metallicity is as high as 10–20× solar. Pebbles outside the water ice line can drift inwards and evaporate as they cross this line.
Inward-drifting pebbles from beyond the snowline can evaporate upon crossing it, enriching the inner disk gas with water vapor. Low C/O ratios are particularly favored if inward migration is rapid, a condition facilitated by high-viscosity disks (Schneider & Bitsch 2021).
Finally, in Fig. 6 we compare the planet-to-star bulk metal mass fraction ratio and atmospheric metalliticy for our two fiducial scenarios with the population trends derived by Thorngren et al. (2016) and Wakeford et al. (2018). Our two scenarios are consistent within 1σ with the atmospheric metallicity of the general exoplanet population. The mean bulk metal content agrees extremely well with the population trend in our secular cooling scenario, whereas the heating scenario estimate agrees within its 1c uncertainty. Thorngren et al. (2016) discuss the fact that this mass-bulk metal mass fraction trend is the result of core accretion as the dominant formation mechanism in the exoplanet population. However, a recent work by Chachan et al. (2025) revisited this trend with a larger sample (150 planets) and found that the trend flattens at high masses (> 1 MJup. This indicates that gravitational instability could play a more prominent role in the formation of the exoplanet population than previously suggested or that significant heavy-element enrichment continues after the runaway accretion stage via accretion of pebbles and planetesimals. Our two interior scenarios are compatible with this late heavy-element enrichment, while our secular cooling scenario is consistent with gravitational instability.
 |
Fig. 6 Planet mass-bulk metal mass fraction diagram (top panel) and mass-atmospheric metallicity diagram (bottom panel) for WASP-80 b. We show the estimates of WASP-80 b's for our two fiducial retrievals: JR6 (black; consistent with all data and no heating mechanism) and its heating counterpart, JR5* (orange; free chemistry and no age constraint). The bulk and atmospheric metallicity trend fits are adopted from Thorngren et al. (2016) and Wakeford et al. (2018), respectively. We compare with estimates for Jupiter (Howard & Guillot 2023b), Saturn (Militzer et al. 2019; Miguel & Vazan 2023) and Neptune (Helled etal. 2011; Karkoschka & Tomasko 2011). |
9 Conclusions
In this work, we carried out a suite of interior, atmosphere and joint interior-atmosphere retrievals for the warm gas giant WASP-80 b. Joint retrievals combine a coupled, self-consistent interior-atmosphere model with Bayesian inference, in which the log-likelihood incorporates information from both the spectrum and bulk density observables (i.e., mass, radius, age). The unique combination of transmission and emission spectra across a broad wavelength range, together with precise mass and age, allowed us to constrain the planet's bulk metal content, atmospheric composition, and thermal structure with unprecedented precision.
Based on atmospheric data alone, we found that transmission-only retrievals favor sub-solar to solar atmospheric metallicities with a C/O ratio consistent with solar, under the assumptions of chemical equilibrium and a wavelength-dependent cloud model. In contrast, free-chemistry retrievals and those employing simpler (e.g., gray cloud) models yield super-solar metallicities and low C/O ratios, consistent with previous works (Wong et al. 2022; Bell et al. 2023). We demonstrated that cloud treatment significantly affects the inferred atmospheric composition (particularly, the metallicity and C/O ratio) and that equilibrium chemistry retrievals with wavelength-dependent clouds offer the best fit to the data based on Bayesian evidence. Retrievals based on emission data alone also support a super-solar metallicity and a sub-solar C/O ratio. Additionally, they constrained the thermal structure at pressures of P = 1–10−3 bar to temperatures of T = 700–1000 K at 1σ.
Traditional interior-only retrievals treat mass, radius, age, and atmospheric metallicity as observables. For WASP-80 b, we find that interior retrievals that are consistent with the planet's age in the absence of additional heating sources favor a low envelope metallicity (M/H < 10× solar at 1σ). The higher metallicities suggested by the free transmission retrievals require extreme, high internal temperatures that are inconsistent with the age constraint. This implies that the highly enriched atmospheric metallicities inferred in previous atmospheric studies (and in our transmission free-chemistry retrievals) are only compatible with WASP-80 b's bulk density if there are additional heating mechanisms (e.g., Ohmic dissipation) and/or an interior that is not fully dominated by convection (non-adiabatic).
Thus, we adopted two fiducial joint interior-atmosphere retrievals that encapsulate different scenarios. The retrieval JR6 takes into account all available data (i.e., mass, age, and transmission and emission spectra) and represents a scenario where the planet's internal temperature is driven by secular cooling without additional heating sources. Under this scenario, WASP-80 b has an atmospheric metallicity of 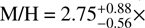 solar, a sub-solar
solar, a sub-solar 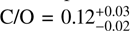 , a bulk metal mass fraction Zplanet = 0.12 ± 0.02, and a core mass of
, a bulk metal mass fraction Zplanet = 0.12 ± 0.02, and a core mass of 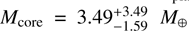 . On the other hand, the retrieval JR5* represents a second scenario where additional heating sources warm the deep envelope by decoupling the internal temperature from secular cooling and the assumption of equilibrium chemistry. In this inflated scenario, WASP-80 b has an atmospheric metallicity of
. On the other hand, the retrieval JR5* represents a second scenario where additional heating sources warm the deep envelope by decoupling the internal temperature from secular cooling and the assumption of equilibrium chemistry. In this inflated scenario, WASP-80 b has an atmospheric metallicity of 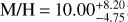 × solar; C/O = 0.24±0.09; a bulk metal mass fraction ratio of
× solar; C/O = 0.24±0.09; a bulk metal mass fraction ratio of 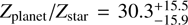 ; and a core mass,
; and a core mass, 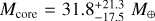 . In addition, our findings can be summarized as follows:
. In addition, our findings can be summarized as follows:
We demonstrate that joint retrievals reveal degeneracies between envelope composition, chemistry and thermal state. The comparison between the joint retrievals JR1 and JR1* indicates the degeneracy between composition and chemistry, where WASP-80 b could have: (1) a super-solar envelope and very low C/O ratio; or (2) a sub-solar envelope in chemical equilibrium and C/O~0.40. Similarly, the contrast between retrievals JR5 and JR5* show the degeneracy between chemistry and thermal state (see Fig. 5, right panel), where the equilibrium chemistry requires higher internal temperatures to fit the spectral data and bulk density simultaneously;
For planets older than 1 Gyr, the inclusion of age in interior-only retrievals does not significantly improve the estimate of the bulk metal mass fraction. However, in joint retrievals that include both emission and transmission spectra, treating the age as an observable reduces the uncertainties in the inferred CMF and bulk metal mass fraction by a factor of two;
The addition of the panchromatic emission spectrum (1–12 μm) to the joint retrievals allows us to constrain the chemical abundances and the temperature at P = 1–10−3 bar with high precision. This information, when combined with equilibrium chemistry models, allows us to break the degeneracy between temperature and envelope metal content;
If the assumption of equilibrium chemistry is relaxed by adopting free chemistry, the uncertainty in the bulk metal mass fraction increases from ΔZplaner, JR5 = 0.02 (16% precision) to ΔZplane, JR5* = 0.11 (40% precision). Thus, the degeneracy between atmospheric chemistry (equilibrium vs. free) and internal temperature can increase the uncertainty in derived bulk metal mass fraction and core mass if the age is unconstrained or the planet is exposed to additional heating sources (i.e., tidal heating, Ohmic dissipation).
We also caution against biases in joint retrievals. Specifically, we advise against assuming clear-atmospheric forward models (see Sect. 8.1) and using weighting factors in the likelihood function to give more importance to bulk properties (see Sect. 8.2). The former eliminates the degeneracy between cloud location and envelope metal content while the latter can spuriously reduce the uncertainties in mass, radius, and age. Both effects lead to an underestimation of the uncertainties in the bulk metal mass fraction and CMF.
Finally, we explore possible caveats in our model assumptions about the interior and atmosphere. For the interior model, we assume that the deep interior follows an adiabat. Although WASP-80 b is unlikely to have compositional gradients or tidal heating, Ohmic dissipation could further heat its interior. This mechanism and its implications for the interior and atmosphere of sub-Saturn exoplanets at intermediate equilibrium temperatures should be explored in future work. Similarly, in our fiducial joint retrievals, we adopted either equilibrium or free chemistry. These two assumptions fit the spectra well, but we note a degeneracy between atmospheric composition and the extent of vertical mixing, Kzz. In a future work, we will incorporate the effects of vertical mixing with self-consistent chemistry grids, as well as constraints from reflected light and Bond albedo.
We find that WASP-80 b has an atmospheric and bulk composition consistent with the general exoplanet population within 1σ in our two fiducial scenarios. The very low core mass derived in the first scenario (secular cooling) is consistent with gravitational instability and it could marginally be produced by core accretion under very favorable conditions. In contrast, the second scenario (additional heating) agrees very well with the classical core accretion paradigm. Super-solar atmospheric metallicities (~2 and ~10× solar in the secular and additional heating scenario, respectively) and sub-solar C/O ratios suggests that WASP-80 b not only accreted solids during core formation but also continued to do so afterward. This envelope enrichment is likely produced by planetesimal-dominated accretion beyond the water snowline or pure pebble accretion within the water ice line.
Our study highlights that for WASP-80 b, joint interior-atmosphere retrievals have degeneracies between atmospheric and interior processes, as well as robust inferences of atmospheric metallicity, C/O ratio and bulk metal mass fraction require precise measurements of the mass, radius, age, and atmospheric spectra combined with this approach. Future observations combining transmission, emission, and reflected light spectroscopy – especially with JWST and upcoming missions such as Ariel – will enable comprehensive interior-atmosphere modeling for a broader sample of exoplanets. This will be essential for understanding the connection between planet formation and composition at the population level.
Acknowledgements
L.A.A. thanks Bertram Bitsch, Eva-Maria Ahrer and Shreyas Vissapragada for insightful discussions on planet formation, atmospheric data analysis and exoplanet magnetic fields during the scope of this work. This research is based on observations made with NASA/ESA Hubble Space Telescope obtained from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5–26555. These observations are associated with programs GO-12473, GO-14767, GO-15131 and AR-17050. This work is based in part on observations made with the NASA/ESA/CSA JWST. These observations are associated with programs GTO-1185, GTO-1177 and ERS-01366. We also thank the anonymous referee for comments that helped improve the manuscript.
References
- Acuña, L., Deleuil, M., Mousis, O., et al. 2021, A&A, 647, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acuña, L., Kreidberg, L., Zhai, M., & Mollière, P. 2024, A&A, 688, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acuña, L., Kreidberg, L., Zhai, M., Mollière, P., & Fouesneau, M. 2025, J. Open Source Softw., 10, 7288 [Google Scholar]
- Adams, F. C. 2011, ApJ, 730, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Ahrer, E.-M., Stevenson, K. B., Mansfield, M., et al. 2023, Nature, 614, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Akinsanmi, B., Barros, S. C. C., Santos, N. C., Oshagh, M., & Serrano, L. M. 2020, MNRAS, 497, 3484 [NASA ADS] [CrossRef] [Google Scholar]
- Alderson, L., Wakeford, H. R., Alam, M. K., et al. 2023, Nature, 614, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, N. F., Spiegelman, F., Leininger, T., & Molliere, P. 2019, A&A, 628, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, D. R., Collier Cameron, A., Delrez, L., et al. 2014, MNRAS, 445, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barber, R. J., Strange, J. K., Hill, C., et al. 2014, MNRAS, 437, 1828 [CrossRef] [Google Scholar]
- Barros, S. C. C., Akinsanmi, B., Boué, G., et al. 2022, A&A, 657, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batygin, K. 2025, ApJ, 985, 87 [Google Scholar]
- Batygin, K., & Stevenson, D. J. 2010, ApJ, 714, L238 [NASA ADS] [CrossRef] [Google Scholar]
- Baumeister, P., & Tosi, N. 2023, A&A, 676, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belenkaya, E. S., Alexeev, I. I., Kalegaev, V. V., & Blokhina, M. S. 2006, Ann. Geophys., 24, 1145 [Google Scholar]
- Bell, T. J., Welbanks, L., Schlawin, E., et al. 2023, Nature, 623, 709 [Google Scholar]
- Benneke, B., & Seager, S. 2012, ApJ, 753, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Bernabò, L. M., Csizmadia, S., Smith, A. M. S., et al. 2024, A&A, 684, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bézard, B., Charnay, B., & Blain, D. 2022, Nat. Astron., 6, 537 [CrossRef] [Google Scholar]
- Blain, D., Charnay, B., & Bézard, B. 2021, A&A, 646, A15 [EDP Sciences] [Google Scholar]
- Bloot, S., Miguel, Y., Bazot, M., & Howard, S. 2023, MNRAS, 523, 6282 [NASA ADS] [CrossRef] [Google Scholar]
- Bodenheimer, P., Stevenson, D. J., Lissauer, J. J., & D'Angelo, G. 2018, ApJ, 868, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Boley, A. C., Helled, R., & Payne, M. J. 2011, ApJ, 735, 30 [Google Scholar]
- Brouwers, M. G., & Ormel, C. W. 2020, A&A, 634, A15 [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buhler, P. B., Knutson, H. A., Batygin, K., et al. 2016, ApJ, 821, 26 [CrossRef] [Google Scholar]
- Burrows, A., Hubeny, I., Hubbard, W. B., Sudarsky, D., & Fortney, J. J. 2004, ApJ, 610, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Carleo, I., Giacobbe, P., Guilluy, G., et al. 2022, AJ, 164, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Debras, F. 2021, ApJ, 917, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Gallardo, J., & Baraffe, I. 2007, A&A, 472, L17 [CrossRef] [EDP Sciences] [Google Scholar]
- Chachan, Y., Fortney, J. J., Ohno, K., Thorngren, D., & Murray-Clay, R. 2025, ApJ, 994, 43 [Google Scholar]
- Charnay, B., Bézard, B., Baudino, J. L., et al. 2018, ApJ, 854, 172 [Google Scholar]
- Coles, P. A., Yurchenko, S. N., & Tennyson, J. 2019, MNRAS, 490, 4638 [CrossRef] [Google Scholar]
- Csizmadia, S., Hellard, H., & Smith, A. M. S. 2019, A&A, 623, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danti, C., Bitsch, B., & Mah, J. 2023, A&A, 679, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorn, C., Khan, A., Heng, K., et al. 2015, A&A, 577, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dyrek, A., Min, M., Decin, L., et al. 2024, Nature, 625, 51 [Google Scholar]
- Ehrenreich, D., Lovis, C., Allart, R., et al. 2020, Nature, 580, 597 [Google Scholar]
- Emsenhuber, A., Mordasini, C., Burn, R., et al. 2021, A&A, 656, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faedi, F., Barros, S. C. C., Anderson, D. R., et al. 2011, A&A, 531, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fairman, C., Wakeford, H. R., & MacDonald, R. J. 2024, AJ, 167, 240 [Google Scholar]
- Feinstein, A. D., Radica, M., Welbanks, L., et al. 2023, Nature, 614, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., & Hobson, M. P. 2008, MNRAS, 384, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, C., & Heng, K. 2018, MNRAS, 481, 4698 [Google Scholar]
- Fisher, C., Taylor, J., Parmentier, V., et al. 2024, MNRAS, 535, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [Google Scholar]
- Fortney, J. J., Visscher, C., Marley, M. S., et al. 2020, AJ, 160, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Guilluy, G., Shaikhislamov, I. F., et al. 2022, A&A, 658, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fossati, L., Pillitteri, I., Shaikhislamov, I. F., et al. 2023, A&A, 673, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F. 2020, A&A, 641, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginzburg, S., & Sari, R. 2016, ApJ, 819, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, S. 1994, Tech. rep. NASA Lewis Research Center. [Google Scholar]
- Guillot, T. 2010, A&A, 520, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hardy, R. A., Harrington, J., Hardin, M. R., et al. 2017, ApJ, 836, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Hargreaves, R. J., Gordon, I. E., Rey, M., et al. 2020, ApJS, 247, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2009, ApJ, 706, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Sato, B., et al. 2011, ApJ, 726, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Hellard, H., Csizmadia, S., Padovan, S., et al. 2019, ApJ, 878, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Hellard, H., Csizmadia, S., Padovan, S., Sohl, F., & Rauer, H. 2020, ApJ, 889, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Helled, R. 2023, A&A, 675, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helled, R., & Stevenson, D. 2017, ApJ, 840, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Helled, R., & Schubert, G. 2008, Icarus, 198, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Helled, R., & Morbidelli, A. 2021, in ExoFrontiers; Big Questions in Exoplanetary Science, ed. N. Madhusudhan, 12 [Google Scholar]
- Helled, R., Anderson, J. D., Podolak, M., & Schubert, G. 2011, ApJ, 726, 15 [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2010, ApJ, 723, L60 [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2012, MNRAS, 426, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Hori, Y., & Ikoma, M. 2010, ApJ, 714, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, S., & Guillot, T. 2023a, A&A, 672, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, S., & Guillot, T. 2023b, A&A, 672, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2005, Icarus, 179, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jacobs, B., Désert, J.-M., Gao, P., et al. 2023, ApJ, 956, L43 [Google Scholar]
- Jiang, H., & Ormel, C. W. 2023, MNRAS, 518, 3877 [Google Scholar]
- Karkoschka, E., & Tomasko, M. G. 2011, Icarus, 211, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Keles, E. 2021, MNRAS, 502, 1456 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D., & Benneke, B. 2025, arXiv e-prints [arXiv:506.05392] [Google Scholar]
- Knierim, H., & Helled, R. 2024, ApJ, 977, 227 [Google Scholar]
- Knierim, H., & Helled, R. 2025, A&A, 698, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knierim, H., Batygin, K., & Bitsch, B. 2022, A&A, 658, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Komacek, T. D., & Youdin, A. N. 2017, ApJ, 844, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Kramm, U., Nettelmann, N., Redmer, R., & Stevenson, D. J. 2011, A&A, 528, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramm, U., Nettelmann, N., Fortney, J. J., Neuhäuser, R., & Redmer, R. 2012, A&A, 538, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacy, B., & Burrows, A. 2023, ApJ, 950, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Leconte, J., & Chabrier, G. 2012, A&A, 540, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leconte, J., Chabrier, G., Baraffe, I., & Levrard, B. 2010, A&A, 516, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lei, E., & Mollière, P. 2025, J. Open Source Softw., 10, 7712 [Google Scholar]
- Line, M. R., & Parmentier, V. 2016, ApJ, 820, 78 [Google Scholar]
- Lothringer, J. D., Bennett, K. A., Sing, D. K., et al. 2025, AJ, 169, 274 [Google Scholar]
- Love, A. E. H. 1911, Some Problems of Geodynamics [Google Scholar]
- Lozovsky, M., Helled, R., Rosenberg, E. D., & Bodenheimer, P. 2017, ApJ, 836, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Lueber, A., Novais, A., Fisher, C., & Heng, K. 2024, A&A, 687, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyon, S. P. 1992, Los Alamos National Laboratory report LA-UR-92-3407 [Google Scholar]
- MacDonald, R. J., & Madhusudhan, N. 2017, MNRAS, 469, 1979 [Google Scholar]
- Mancini, L., Southworth, J., Ciceri, S., et al. 2014, A&A, 562, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mankovich, C. R., & Fuller, J. 2021, Nat. Astron., 5, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Mazevet, S., Licari, A., Chabrier, G., & Potekhin, A. Y. 2019, A&A, 621, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McBride, B. J. G. 1996, Tech. rep. NASA Lewis Research Center [Google Scholar]
- Miguel, Y., & Vazan, A. 2023, Remote Sensing, 15, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Miguel, Y., Bazot, M., Guillot, T., et al. 2022, A&A, 662, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Militzer, B., Wahl, S., & Hubbard, W. B. 2019, ApJ, 879, 78 [Google Scholar]
- Millholland, S., Petigura, E., & Batygin, K. 2020, ApJ, 897, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Mollière, P., van Boekel, R., Bouwman, J., et al. 2017, A&A, 600, A10 [Google Scholar]
- Mollière, P., van Boekel, R., Dullemond, C., Henning, T., & Mordasini, C. 2015, ApJ, 813, 47 [Google Scholar]
- Mollière, P., Wardenier, J. P., van Boekel, R., et al. 2019, A&A, 627, A67 [Google Scholar]
- Moore, K. M., Bloxham, J., Connerney, J. E. P., Jørgensen, J. L., & Merayo, J. M. G. 2017, Geophys. Res. Lett., 44, 4687 [Google Scholar]
- Morel, K., Coulombe, L.-P., Rowe, J. F., et al. 2025, AJ, 169, 277 [Google Scholar]
- Morley, C. V., Fortney, J. J., Marley, M. S., et al. 2015, ApJ, 815, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Morley, C. V., Mukherjee, S., Marley, M. S., et al. 2024, ApJ, 975, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Mukherjee, S., Fortney, J. J., Wogan, N. F., Sing, D. K., & Ohno, K. 2025, ApJ, 985, 209 [Google Scholar]
- Müller, S., & Helled, R. 2021, MNRAS, 507, 2094 [CrossRef] [Google Scholar]
- Müller, S., & Helled, R. 2023, A&A, 669, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, S., & Helled, R. 2025, A&A, 693, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nasedkin, E., Mollière, P., & Blain, D. 2024, J. Open Source Softw., 9, 5875 [CrossRef] [Google Scholar]
- Nettelmann, N., Püstow, R., & Redmer, R. 2013, Icarus, 225, 548 [Google Scholar]
- Nettelmann, N., Wang, K., Fortney, J. J., et al. 2016, Icarus, 275, 107 [Google Scholar]
- Nettelmann, N., Movshovitz, N., Ni, D., et al. 2021, PSJ, 2, 241 [Google Scholar]
- Nixon, M. C., Piette, A. A. A., Kempton, E. M. R., et al. 2024, ApJ, 970, L28 [Google Scholar]
- Nowak, M., Lacour, S., Lagrange, A. M., et al. 2020, A&A, 642, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohno, K., & Fortney, J. J. 2023, ApJ, 946, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Oklopčić, A., Silva, M., Montero-Camacho, P., & Hirata, C. M. 2020, ApJ, 890, 88 [CrossRef] [Google Scholar]
- Ormel, C. W., Vazan, A., & Brouwers, M. G. 2021, A&A, 647, A175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Otegi, J. F., Dorn, C., Helled, R., et al. 2020, A&A, 640, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., & Adams, F. C. 2014, MNRAS, 444, 3761 [Google Scholar]
- Perna, R., Menou, K., & Rauscher, E. 2010, ApJ, 724, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Pinhas, A., Madhusudhan, N., Gandhi, S., & MacDonald, R. 2019, MNRAS, 482, 1485 [Google Scholar]
- Piso, A.-M. A., Youdin, A. N., & Murray-Clay, R. A. 2015, ApJ, 800, 82 [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Polyansky, O. L., Kyuberis, A. A., Zobov, N. F., et al. 2018, MNRAS, 480, 2597 [NASA ADS] [CrossRef] [Google Scholar]
- Poser, A. J., Nettelmann, N., & Redmer, R. 2019, Atmosphere, 10, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Poser, A. J., & Redmer, R. 2024, MNRAS, 529, 2242 [NASA ADS] [CrossRef] [Google Scholar]
- Pu, B., & Valencia, D. 2017, ApJ, 846, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, K., Baehr, H., Young, A. K., et al. 2025, MNRAS, 539, 3421 [Google Scholar]
- Rooney, C. M., Batalha, N. E., Gao, P., & Marley, M. S. 2022, ApJ, 925, 33 [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barber, R. J., et al. 2010, J. Quant. Spec. Radiat. Transf., 111, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Roy-Perez, J., Pérez-Hoyos, S., Barrado-Izagirre, N., & Chen-Chen, H. 2025, A&A, 694, A249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russell, C. T. 1993, Rep. Progr. Phys., 56, 687 [CrossRef] [Google Scholar]
- Rustamkulov, Z., Sing, D. K., Mukherjee, S., et al. 2023, Nature, 614, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, S. P., MacDonald, R. J., Tsai, S.-M., et al. 2025, AJ, 170, 298 [Google Scholar]
- Schneider, A. D., & Bitsch, B. 2021, A&A, 654, A71 [Google Scholar]
- Siebenaler, L., Miguel, Y., de Regt, S., & Guillot, T. 2025, A&A, 693, A308 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sing, D. K., Rustamkulov, Z., Thorngren, D. P., et al. 2024, Nature, 630, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, D. S., & Burrows, A. 2012, ApJ, 745, 174 [Google Scholar]
- Stevenson, D. J., Bodenheimer, P., Lissauer, J. J., & D'Angelo, G. 2022, PSJ, 3, 74 [NASA ADS] [Google Scholar]
- Thorngren, D. P., & Fortney, J. J. 2018, AJ, 155, 214 [Google Scholar]
- Thorngren, D. P., Fortney, J. J., Murray-Clay, R. A., & Lopez, E. D. 2016, ApJ, 831, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Trammell, G. B., Arras, P., & Li, Z.-Y. 2011, ApJ, 728, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Trevascus, D., Blunt, S., Christiaens, V., et al. 2025, A&A, 698, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Triaud, A. H. M. J., Anderson, D. R., Collier Cameron, A., et al. 2013, A&A, 551, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Triaud, A. H. M. J., Gillon, M., Ehrenreich, D., et al. 2015, MNRAS, 450, 2279 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R. 2008, Contemp. Phys., 49, 71 [Google Scholar]
- Tsiaras, A., Waldmann, I. P., Zingales, T., et al. 2018, AJ, 155, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Turrini, D., Nelson, R. P., & Barbieri, M. 2015, Exp. Astron., 40, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Valletta, C., & Helled, R. 2020, ApJ, 900, 133 [NASA ADS] [CrossRef] [Google Scholar]
- van Boekel, R., Benneke, B., Heng, K., et al. 2012, SPIE Conf. Ser., 8442, 84421F [Google Scholar]
- van Dijk, E. A. & Miguel, Y. 2025, MNRAS, 540, 1544 [Google Scholar]
- Vazan, A., Helled, R., & Guillot, T. 2018, A&A, 610, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vissapragada, S., Knutson, H. A., Greklek-McKeon, M., et al. 2022, AJ, 164, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Vissapragada, S., Greklek-McKeon, M., Linssen, D., et al. 2024, AJ, 167, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Wahl, S. M., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [CrossRef] [Google Scholar]
- Wakeford, H. R., Sing, D. K., Deming, D., et al. 2018, AJ, 155, 29 [Google Scholar]
- Welbanks, L., & Madhusudhan, N. 2019, AJ, 157, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Welbanks, L., Bell, T. J., Beatty, T. G., et al. 2024, Nature, 630, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkinson, C., Charnay, B., Mazevet, S., et al. 2024, A&A, 692, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiser, L. S., Bell, T. J., Line, M. R., et al. 2025, arXiv e-prints [arXiv:2506.01800] [Google Scholar]
- Wong, I., Chachan, Y., Knutson, H. A., et al. 2022, AJ, 164, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R. K., & Thorngren, D. P. 2017, ApJ, 849, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S. N., Mellor, T. M., Freedman, R. S., & Tennyson, J. 2020, MNRAS, 496, 5282 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A Forward models for traditional interior retrievals
Figure A.1 shows four thermal evolution curves (radius-age relations) evaluated at WASP-80 b's mean mass and equilibrium temperature. These thermal evolution curves constitute the forward model in the traditional interior retrievals (Sect. 6). These forward models suggest that the mass, radius and age of WASP-80 b are compatible with a 10× solar composition envelope with no core or a 10% core mass with a solar envelope. Compositions greater than 30× are ruled out by more than 4σ.
 |
Fig. A.1 Radius-age relations of WASP-80 b. These were obtained from the grid of GASTLI models described in Sect. 3.1.1 |
Appendix B Interior-atmosphere coupling for joint retrievals
 |
Fig. B.1 Interior planet radius (Rint, defined at a pressure of 1000 bar) as a function of envelope metal mass fraction Zenv and surface temperature (Tsurf, also defined at 1000 bar). These models assume a constant mass M = 0.55 MJup and CMF = 0.10. Solid and dashed black lines indicate the mean and 1er range of WASP-80 b's measured radius (Table 1). |
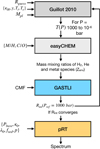 |
Fig. B.2 Modified coupling algorithm. Mpl is the planetary mass, while Rint is the radius from the planetary center up to the interior-atmosphere interface, located at P = 1000 bar. Rguess is the initial guess value for the radius, Rint. The remaining 10 parameters correspond to the P–T analytical model (Guillot 2010; κIR, γ, Ti, Te), the chemical equilibrium grid (easyChem; M/H, C/O), GASTLI's interior structure module (CMF); and pRT cloud opacity parameterization (Pbase, κ0, λ0, fsed, p). |
In Sect. 3.1.1 we recapitulate our approach to couple self-consistently GASTLI's interior model to a grid of ID atmospheric models consisting of temperature (P–T) and metal mass fraction (P-Zenv) profiles. Nonetheless, this coupling algorithm must be adapted when coupling the new interior model grid dedicated to joint retrievals (see Sect. 3.1.2) to pRT due to the new set of input parameters.
Figure B.2 illustrates the modified coupling algorithm used in the joint atmosphere-interior retrievals. The planet mass Mpl and the other 10 free parameters (see caption) are constant across one instance of the coupled model. The internal planet radius (center to 1000 bar), Rint is updated after the grid of GASTLI's interior structure models is interpolated. The condition for radius convergence is similar to that presented in Acuña et al. (2021): the difference between successive radius calculations is lower than a specified tolerance, Δtol = 10−3 × Rint. GASTLI's grid not only requires the envelope metal mass fraction estimated by the chemical equilibrium grid, Zenv, but also the temperature at 1000 bar, Tsurf, computed in the first step by the analytical P–T profile. Thus, in the last step where the transmission spectrum is computed by pRT, the reference radius is equal to the converged Rint value, specified at a reference pressure of 1000 bar.
Figure B.1 shows a slice of the multidimensional grid evaluated at the mean mass of WASP-80 b and a CMF = 0.10. The radius is a smooth function of surface temperature and envelope metal mass fraction, demonstrating that our grid is sufficiently finely sampled. This fine sampling allows us to interpolate the radius and entropy with relative errors of < 1% with respect to GASTLI computed models, which is well under the observational errors of 3%. WASP-80 b's measured radius (solid black line) is slightly larger than the interior radius (Rint) as the atmosphere contributes to the total radius from 1000 bar to ~20 mbar. Three models at low temperatures (T = 700 K) and low envelope metal mass fractions did not converge (white). This does not impact our grid interpolation and retrieval framework, as this is well below the equilibrium temperature of WASP-80 b (825 K).
Appendix C Best-fit models and corner plots
 |
Fig. C.1 Top row: Best-fit model for our transmission spectrum retrievals of WASP-80 b with equilibrium (left panel) and free (right panel) chemistry. Bottom row: Best-fit model for our emission spectrum retrievals of WASP-80 b with equilibrium (left panel) and free (right panel) chemistry. |
 |
Fig. C.2 First row: Best-fit models for our joint retrievals of WASP-80 b JR1 (equilibrium chemistry; left panel) and JR1* (free chemistry; right panel). Second row: Posterior distribution function (PDF) of the retrieved masses for JR1 and JR1*. Dashed and dotted lines indicate the mean and standard deviations of the PDFs. White circles indicate the observed data with their respective uncertainties in all four panels. Third and fourth rows: Best-fit model for our joint retrieval JR6. |
 |
Fig. C.3 Corner plot for joint retrieval JR6. The atmospheric metallicity, log(M/H) is indicated in × solar units. The planet radius, Rpl is evaluated at P = 1000 bar. The spectrum offsets, o, are shown for all instruments (WFC3, STIS, NIRCam, LRS) and both geometries (emission: E; transmission: T). The units of the offsets are parts per million (ppm). |
 |
Fig. C.4 Corner plot for joint retrieval JR5*. The atmospheric abundances of H2O, CO, CO2, CH4 and NH3 are mass fractions. The planet radius, Rvl is evaluated at P = 1000 bar. The spectrum offsets, o, are shown for all instruments (WFC3, STIS, NIRCam, LRS) and both geometries (emission: E; transmission: T). The units of the offsets are parts per million (ppm). |
All Tables
Mean and uncertainties of retrieved compositional parameters in the interior-only retrievals.
Atmospheric and bulk interior composition of WASP-80 b under the two fiducial scenarios.
All Figures
 |
Fig. 1 Comparison between our atmospheric composition estimates and previous work from transmission-only (upper panel) and emission-only (lower panel) retrievals. Previous work include Bell et al. (2023, B23, orange), Wong et al. (2022, W22, dark gold), and Wiser et al. (2025, Wi25, violet). The shaded area indicates the region forbidden by our interior-only retrievals at 4σ (see Sect. 6). |
| In the text | |
 |
Fig. 2 P–T profile of WASP-80 b as constrained by our two emission-only retrievals. The shaded region indicates the 1σ area of the retrieval, while solid lines correspond to the mean. We show self-consistent 1D models from Mollière et al. (2017) for comparison, including cloudy model 1 in their Table 2 (see text). The dotted gray line shows the contribution function from our emission-only retrievals. |
| In the text | |
 |
Fig. 3 Mean forward model from one of our two fiducial interior-atmosphere joint retrievals, JR6, of WASP-80 b. This model corresponds to a core mass fraction (CMF) of 0.02, an atmospheric metallicity of M/H = 2.75 × solar, C/O = 0.12, and Tint = 134 K. Panel a: schematic cross section of the planet; layer thicknesses are to scale. The atmosphere corresponds to pressures below 1000 bar. Panel b: P–T profile of the atmosphere (light blue) and interior (blue and teal). Panel c: transmission spectrum for this model, with the three observed transmission datasets shown for comparison. Panel d: emission spectrum for this model, compared against the four observed emission datasets. Panel e: interior metal mass fraction profile (Z; black) and H/He mass fraction as functions of normalized radius. The atmospheric region (P < 1000 bar) is indicated in light blue. Panel f: atmospheric mass mixing ratios of the molecular species comprising the metals (P < 1000 bar). The region highlighted in orange indicates the pressure range probed by emission spectra, as calculated from the contribution function. |
| In the text | |
 |
Fig. 4 Top panel: core and bulk metal mass fraction 1σ estimates obtained by our joint retrievals (JR1-JR6). Joint retrievals that take into account the age have triangle markers. Interior-only retrievals (R1–R3 and R5) are shown as colored boxes for comparison. Bottom panel: atmospheric metallicity and C/O ratio estimates from our suite of joint retrievals. Spectra-only estimates are displayed as colored boxes for comparison. |
| In the text | |
 |
Fig. 5 P–T proflies of WASP-80 b as constrained by four of our joint retrievals. The shaded regions indicate the 1, 2, and 3σ regions of the retrieval, while solid lines correspond to the mean. Black lines highlight self-consistent models from Mollière et al. (2017); Acuña et al. (2024) of a clear atmosphere with solar composition at Tim = 100 (dashed) and 500 K (dotted) for comparison. Left: the difference between JR3 and JR5 shows the effect of adding the transmission spectrum to JR3, which incorporates emission spectra plus the mass and radius. The transmission spectrum reduces significantly the uncertainties in thermal structure. Center, comparing JR6 and JR5 allows us to study the effect of including the age to the retrieval. JR6 is the most data-complete of the joint retrievals, since it incorporates both transmission and emission, plus the mass and age. If the age is removed (JR5), the temperature in the deep atmosphere increases. Right: comparison between JR5 and JR5*, which illustrates the effect of assuming equilibrium chemistry in the joint retrieval. If we relax the assumption of equilibrium chemistry in JR5 by changing to a free chemistry model (JR5*), the temperature decreases in the deep interior. |
| In the text | |
 |
Fig. 6 Planet mass-bulk metal mass fraction diagram (top panel) and mass-atmospheric metallicity diagram (bottom panel) for WASP-80 b. We show the estimates of WASP-80 b's for our two fiducial retrievals: JR6 (black; consistent with all data and no heating mechanism) and its heating counterpart, JR5* (orange; free chemistry and no age constraint). The bulk and atmospheric metallicity trend fits are adopted from Thorngren et al. (2016) and Wakeford et al. (2018), respectively. We compare with estimates for Jupiter (Howard & Guillot 2023b), Saturn (Militzer et al. 2019; Miguel & Vazan 2023) and Neptune (Helled etal. 2011; Karkoschka & Tomasko 2011). |
| In the text | |
 |
Fig. A.1 Radius-age relations of WASP-80 b. These were obtained from the grid of GASTLI models described in Sect. 3.1.1 |
| In the text | |
 |
Fig. B.1 Interior planet radius (Rint, defined at a pressure of 1000 bar) as a function of envelope metal mass fraction Zenv and surface temperature (Tsurf, also defined at 1000 bar). These models assume a constant mass M = 0.55 MJup and CMF = 0.10. Solid and dashed black lines indicate the mean and 1er range of WASP-80 b's measured radius (Table 1). |
| In the text | |
 |
Fig. B.2 Modified coupling algorithm. Mpl is the planetary mass, while Rint is the radius from the planetary center up to the interior-atmosphere interface, located at P = 1000 bar. Rguess is the initial guess value for the radius, Rint. The remaining 10 parameters correspond to the P–T analytical model (Guillot 2010; κIR, γ, Ti, Te), the chemical equilibrium grid (easyChem; M/H, C/O), GASTLI's interior structure module (CMF); and pRT cloud opacity parameterization (Pbase, κ0, λ0, fsed, p). |
| In the text | |
 |
Fig. C.1 Top row: Best-fit model for our transmission spectrum retrievals of WASP-80 b with equilibrium (left panel) and free (right panel) chemistry. Bottom row: Best-fit model for our emission spectrum retrievals of WASP-80 b with equilibrium (left panel) and free (right panel) chemistry. |
| In the text | |
 |
Fig. C.2 First row: Best-fit models for our joint retrievals of WASP-80 b JR1 (equilibrium chemistry; left panel) and JR1* (free chemistry; right panel). Second row: Posterior distribution function (PDF) of the retrieved masses for JR1 and JR1*. Dashed and dotted lines indicate the mean and standard deviations of the PDFs. White circles indicate the observed data with their respective uncertainties in all four panels. Third and fourth rows: Best-fit model for our joint retrieval JR6. |
| In the text | |
 |
Fig. C.3 Corner plot for joint retrieval JR6. The atmospheric metallicity, log(M/H) is indicated in × solar units. The planet radius, Rpl is evaluated at P = 1000 bar. The spectrum offsets, o, are shown for all instruments (WFC3, STIS, NIRCam, LRS) and both geometries (emission: E; transmission: T). The units of the offsets are parts per million (ppm). |
| In the text | |
 |
Fig. C.4 Corner plot for joint retrieval JR5*. The atmospheric abundances of H2O, CO, CO2, CH4 and NH3 are mass fractions. The planet radius, Rvl is evaluated at P = 1000 bar. The spectrum offsets, o, are shown for all instruments (WFC3, STIS, NIRCam, LRS) and both geometries (emission: E; transmission: T). The units of the offsets are parts per million (ppm). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


