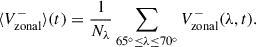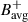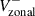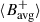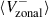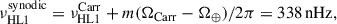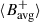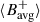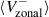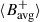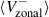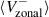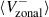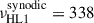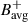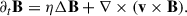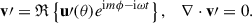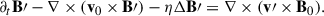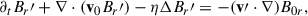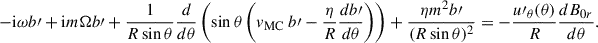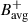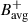| Issue |
A&A
Volume 703, November 2025
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202557360 | |
| Published online | 07 November 2025 | |
Oscillations of the solar photospheric magnetic field caused by the m = 1 high-latitude inertial mode
1
Institute of Physics, University of Graz, Universitätsplatz 5, 8010 Graz, Austria
2
Max-Planck-Institut für Sonnensystemforschung, 37077 Göttingen, Germany
3
Department of Physics, University of Helsinki, 00014 Helsinki, Finland
4
Institut für Astrophysik und Geophysik, Georg-August-Universität Göttingen, 37077 Göttingen, Germany
5
Center for Astrophysics and Space Science, NYUAD Institute, New York University Abu Dhabi, Abu Dhabi, UAE
⋆ Corresponding authors: This email address is being protected from spambots. You need JavaScript enabled to view it.
; This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
22
September
2025
Accepted:
19
October
2025
Periodic oscillations at 338 nHz in the Earth frame are observed at high latitudes in direct Doppler velocity measurements. These oscillations correspond to the m = 1 high-latitude global mode of inertial oscillation. In this study, we investigate the signature of this mode in the photospheric magnetic field using long-term series of line-of-sight magnetograms from the Helioseismic and Magnetic Imager (HMI) and the Global Oscillation Network Group (GONG). Through direct observations and spectral analysis, we detect periodic magnetic field oscillations at high latitudes (65° −70°) with a frequency of 338 nHz in the Earth frame, which match the known frequency of the m = 1 high-latitude inertial mode. The observed line-of-sight magnetic field oscillations are predominantly symmetric across the equator. We find a peak magnetic oscillation amplitude of up to 0.2 gauss and a distinct spatial pattern, both consistent with simplified model calculations in which the radial component of the magnetic field is advected by the mode’s horizontal flow field.
Key words: Sun: activity / Sun: interior / Sun: magnetic fields / Sun: oscillations / Sun: photosphere / Sun: rotation
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1. Introduction
The Sun supports periodic and quasiperiodic oscillations over a wide range of spatial and temporal scales. In addition to the well-known five-minute acoustic modes of oscillation, it also exhibits quasi-toroidal modes in the inertial frequency range, with frequencies comparable to the solar rotation frequency. Solar equatorial Rossby modes were first detected by Löptien et al. (2018) and later confirmed by Liang et al. (2019) and Hanasoge & Mandal (2019). A rich spectrum of additional inertial modes, all retrograde in the Carrington frame, were identified in frequency-latitude space by Gizon et al. (2021). Of these, the mode with the largest amplitude is an m = 1 high-latitude mode with a north-south symmetric radial vorticity. The amplitude of this mode can be as high as 20 m/s at times. It is believed to be baroclinically unstable (Bekki et al. 2022) and saturates via a nonlinear interaction with the Sun’s latitudinal differential rotation (Bekki et al. 2024). The velocity features associated with this mode had been noticed at high latitudes by various authors; however, it was not then identified as a global mode of oscillation (Ulrich 1993, 2001; Hathaway et al. 2013; Bogart et al. 2015). For a recent review of solar inertial modes, we refer to Gizon et al. (2024).
The high-latitude modes were initially identified in long time series of near-surface flows in the longitudinal (uϕ) and colatitudinal (uθ) directions. In particular, two modes with m = 1 and north-south symmetries were observed within 3 nHz of each other (Gizon et al. 2021). The mode with the significantly larger amplitude was antisymmetric in uϕ (symmetric in radial vorticity) and had a frequency  nHz in the Carrington frame, with a linewidth of 7.8 ± 0.2 nHz and a mean amplitude of 9.8 m/s, over the period 2010−2020 (Gizon et al. 2021). The latitude at maximum amplitude was determined to be close to 67.5°. In a recent paper, Liang & Gizon (2025, hereafter LG25) measured the mode amplitude in direct Doppler data and found that the mode has remained visible above 60° latitude throughout the last five solar cycles, i.e., since 1967. LG25 report that the mode amplitude exhibits a negative correlation of −0.50 with the sunspot number and a strong negative correlation of −0.82 with the differential rotation rate near the mode’s critical latitude (the latitude at which its phase speed equals the rotational velocity).
nHz in the Carrington frame, with a linewidth of 7.8 ± 0.2 nHz and a mean amplitude of 9.8 m/s, over the period 2010−2020 (Gizon et al. 2021). The latitude at maximum amplitude was determined to be close to 67.5°. In a recent paper, Liang & Gizon (2025, hereafter LG25) measured the mode amplitude in direct Doppler data and found that the mode has remained visible above 60° latitude throughout the last five solar cycles, i.e., since 1967. LG25 report that the mode amplitude exhibits a negative correlation of −0.50 with the sunspot number and a strong negative correlation of −0.82 with the differential rotation rate near the mode’s critical latitude (the latitude at which its phase speed equals the rotational velocity).
In this Letter we show that the m = 1 high-latitude inertial mode is detectable in the line-of-sight (LOS) photospheric magnetic field, and we study the temporal evolution of its amplitude over a period of 17 years (2007 to 2024). In Sect. 2 we describe the datasets used. We detect and characterize the magnetic field oscillations in Sect. 3 and compare them to the velocity oscillations in Sect. 4. The results are discussed in Sect. 5.
2. Observational datasets
To investigate oscillations in the photospheric LOS magnetic field (Blos) in the inertial frequency range, we analyzed two long-term datasets. We used 720 s cadence LOS magnetograms taken by the Helioseismic and Magnetic Imager (HMI; Schou et al. 2012) on board the Solar Dynamics Observatory (SDO; Pesnell et al. 2012) over a time period of more than 14 years (2010−2024), as well as daily merged magnetograms from the Global Oscillation Network Group (GONG; Harvey et al. 1996) spanning 17 years (2007−2024). We compiled the datasets at a one-day cadence by computing daily averages when multiple images were available for a given day. The duty cycle of the daily averages is nearly 100% for both the HMI and GONG datasets. The original magnetograms have 4096 × 4096 pixels for HMI and 839 × 839 pixels for GONG. Unlike LG25, we did not use the Mount Wilson data because their signal-to-noise ratio is significantly lower.
The data reduction procedure, which was the same for both datasets, is as follows. Daily magnetograms were binned down to 256 × 256 pixels and remapped onto a uniform grid in Stonyhurst longitude (ϕ) and latitude (λ) with a grid spacing of 1° in both coordinates. We then computed the latitudinally symmetric component of the magnetic field as
We also computed the antisymmetric component of Blos but found no significant signal in the neighborhood of the m = 1 mode frequency.
To further increase the signal-to-noise ratio, we considered averages of  in longitude at every time step:
in longitude at every time step:
where Nϕ = 61 is the number of longitude bins in the sum. To detect a perturbation in the magnetic field that may be associated with the high-latitude mode, we investigated the evolution of the magnetic field in the latitude range where the mode’s amplitude is most prominent (around or beyond 67.5°; see Gizon et al. 2021). We defined the latitudinal average of  over the latitude band 65° ≤λ ≤ 70°:
over the latitude band 65° ≤λ ≤ 70°:
where the Nλ = 6 is the number of latitude bins in the sum.
To compare the magnetic field signal with the mode characteristics derived from the reduced LOS Doppler velocity (Vlos), we also computed the following quantities from the HMI and GONG Dopplergrams (see LG25 for details):
The zonal velocity, Vzonal, serves as a proxy for the longitudinal component of surface velocity (Ulrich 2001).
3. Detection of the m = 1 mode in magnetograms
Figure 1 shows super-synoptic maps of  and
and  at high latitudes. An oscillating pattern is evident in both quantities with a temporal cadence of approximately 34 days. The oscillation is also clearly visible in the spatially averaged
at high latitudes. An oscillating pattern is evident in both quantities with a temporal cadence of approximately 34 days. The oscillation is also clearly visible in the spatially averaged  and
and 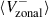 data in Fig. 2. We find an amplitude of up to 0.5 G for
data in Fig. 2. We find an amplitude of up to 0.5 G for 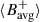 , which is associated with the already known amplitude of 10−20 m/s for
, which is associated with the already known amplitude of 10−20 m/s for  in the latitude range 65° −70°. Since the magnetic field evolution appears to be tightly related to that of the m = 1 mode observed in the Doppler data (LG25), this strongly suggests the presence of the m = 1 mode in the magnetograms; however, this still needs to be verified through spectral analysis.
in the latitude range 65° −70°. Since the magnetic field evolution appears to be tightly related to that of the m = 1 mode observed in the Doppler data (LG25), this strongly suggests the presence of the m = 1 mode in the magnetograms; however, this still needs to be verified through spectral analysis.
 |
Fig. 1. Super-synoptic maps in the Earth frame of |
 |
Fig. 2. Oscillations of |
3.1. Power spectra
We examined  in the frequency domain by performing a Fourier transform over the full time period available in each dataset. The power spectra were rescaled to account for the missing data in the time series. In the bottom row of Fig. 3, we show the power spectra of
in the frequency domain by performing a Fourier transform over the full time period available in each dataset. The power spectra were rescaled to account for the missing data in the time series. In the bottom row of Fig. 3, we show the power spectra of  for the full HMI and GONG datasets. In both spectra, we find a great deal of excess power around 338 nHz, with a full width at half maximum of approximately 11 − 16 nHz (corresponding to an e-folding lifetime of ≈8 − 11 months). We recall that the frequency of the m = 1 mode was reported by Gizon et al. (2021) to be
for the full HMI and GONG datasets. In both spectra, we find a great deal of excess power around 338 nHz, with a full width at half maximum of approximately 11 − 16 nHz (corresponding to an e-folding lifetime of ≈8 − 11 months). We recall that the frequency of the m = 1 mode was reported by Gizon et al. (2021) to be  nHz in the Carrington frame. In the Earth frame the mode frequency is
nHz in the Carrington frame. In the Earth frame the mode frequency is
 |
Fig. 3. Power spectra of magnetic fluctuations |
where ΩCarr/2π = 456 nHz is the Carrington rotation rate and Ω⊕/2π = 31.7 nHz is the Earth’s mean orbital frequency around the Sun.
Figure 3 further shows changes in the power spectra of  in three-year intervals for GONG and HMI data. It is evident that the signal is not uniformly strong over the entire time period, nor is it persistently present (i.e., significant); instead, it rises and wanes over cycle 24. The strongest and clearest signal is observed during the solar minimum interval of 2019−2021 with a peak amplitude of ≈4 × 10−4 G2 nHz−1, while no significant signal is observed in the period 2016−2018. We also find a clear signal from 2010−2015 with a peak amplitude of ≈3 × 10−4 G2 nHz−1. The GONG and HMI results are in very good agreement.
in three-year intervals for GONG and HMI data. It is evident that the signal is not uniformly strong over the entire time period, nor is it persistently present (i.e., significant); instead, it rises and wanes over cycle 24. The strongest and clearest signal is observed during the solar minimum interval of 2019−2021 with a peak amplitude of ≈4 × 10−4 G2 nHz−1, while no significant signal is observed in the period 2016−2018. We also find a clear signal from 2010−2015 with a peak amplitude of ≈3 × 10−4 G2 nHz−1. The GONG and HMI results are in very good agreement.
3.2. Latitudinal variation of the phase
We calculated the average phase of 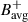 as a function of latitude using a temporal Fourier transform. Phase shifts relative to 67.5° latitude were extracted within a narrow band centered at 338 nHz (±10 nHz) and then averaged. The resulting phase, wrapped to the interval [−π, π], varies smoothly between 55° and 80° latitude (see Fig. A.1). The smooth variation suggests that the excess power at higher latitudes reflects a genuine mode signal rather than stochastic fluctuations. The phase becomes irregular at lower latitudes, where the mode power is not significant.
as a function of latitude using a temporal Fourier transform. Phase shifts relative to 67.5° latitude were extracted within a narrow band centered at 338 nHz (±10 nHz) and then averaged. The resulting phase, wrapped to the interval [−π, π], varies smoothly between 55° and 80° latitude (see Fig. A.1). The smooth variation suggests that the excess power at higher latitudes reflects a genuine mode signal rather than stochastic fluctuations. The phase becomes irregular at lower latitudes, where the mode power is not significant.
4. Comparison of Blos and Vlos
We next compared the excess power around 338 nHz in the  and
and  spectra. Following the procedure described by LG25 (their Sect. 5.2), we estimated the total power around the mode frequency by fitting a Lorentzian function. Figure 4 shows the temporal variations in the mode amplitude measured from overlapping 3-year time series, with central times spaced one year apart, starting in 2007 for
spectra. Following the procedure described by LG25 (their Sect. 5.2), we estimated the total power around the mode frequency by fitting a Lorentzian function. Figure 4 shows the temporal variations in the mode amplitude measured from overlapping 3-year time series, with central times spaced one year apart, starting in 2007 for  and in 2003 for
and in 2003 for  .
.
 |
Fig. 4. Top and middle panels: Temporal variations of the m = 1 mode amplitude extracted from Blos and Vlos data, respectively. The red, orange, green, and blue curves correspond to results from the HMI |
We find very good agreement between the GONG and HMI results for each respective quantity. The mode amplitudes seen in 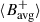 and
and  are positively correlated, but there is a time lag between the magnetic field and velocity perturbations. The maximum amplitude in
are positively correlated, but there is a time lag between the magnetic field and velocity perturbations. The maximum amplitude in 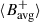 is about 0.2 G in 2012 and again around 2020−2023. Both
is about 0.2 G in 2012 and again around 2020−2023. Both  and
and 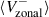 are moderately anticorrelated with the sunspot number, but the mode amplitudes measured in
are moderately anticorrelated with the sunspot number, but the mode amplitudes measured in  appear to reach a maximum during rising phases of the sunspot cycle.
appear to reach a maximum during rising phases of the sunspot cycle.
Figure 5 shows frequency-filtered images of the LOS Doppler velocity, Vlos, and the LOS magnetic field, Blos, derived from HMI observations. A bandpass filter centered at 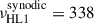 nHz with a full width of 30 nHz was applied to retain the m = 1 mode. We emphasize that no spatial Fourier transform was applied. For Vlos, the structure of the mode is clearly visible at high latitudes, while little to no signal is present at lower latitudes. The Blos data also show the mode at high latitudes, but the lower latitudes display a plethora of signals associated with residual magnetic activity and not related to the mode. The bottom panels of Fig. 5 show synoptic maps of Vlos and Blos, constructed by stacking the central meridian from bandpass-filtered images over time. The m = 1 mode appears as inclined stripes in time-latitude space. A similar pattern was already visible in the synoptic maps of Fig. 1 in the absence of a frequency filter.
nHz with a full width of 30 nHz was applied to retain the m = 1 mode. We emphasize that no spatial Fourier transform was applied. For Vlos, the structure of the mode is clearly visible at high latitudes, while little to no signal is present at lower latitudes. The Blos data also show the mode at high latitudes, but the lower latitudes display a plethora of signals associated with residual magnetic activity and not related to the mode. The bottom panels of Fig. 5 show synoptic maps of Vlos and Blos, constructed by stacking the central meridian from bandpass-filtered images over time. The m = 1 mode appears as inclined stripes in time-latitude space. A similar pattern was already visible in the synoptic maps of Fig. 1 in the absence of a frequency filter.
 |
Fig. 5. Bandpass-filtered images of the LOS Doppler velocity, Vlos, and LOS magnetic field, Blos, derived from HMI data. Top left: Filtered Vlos image from 14 June 2020. Bottom left: Central-meridian Vlos values stacked over time and plotted as a function of time and latitude. Right panels: Corresponding Blos data, with low-latitude regions (< 45°) shaded out. The filtering was performed using a bandpass filter centered at |
5. Discussion
We identified a coherent magnetic field oscillation at a frequency of 338 nHz (with a frequency resolution of 10.5 nHz) and a peak amplitude of about 0.2 G in Blos. This oscillation is associated with the high-latitude m = 1 global inertial mode previously characterized in the velocity data. The Blos perturbations are predominantly symmetric across the equator, in contrast to the Vlos perturbations, which are primarily north-south antisymmetric. The magnetic field oscillations are most clearly observed at latitudes above 60° during the recent solar minimum (2018−2022). The mode amplitude in  peaks around 2012, during the rising phase of cycle 24, and again in 2020−2023, the rising phase of cycle 25. A time lag of approximately two years is observed between the trends in the magnetic and velocity perturbations.
peaks around 2012, during the rising phase of cycle 24, and again in 2020−2023, the rising phase of cycle 25. A time lag of approximately two years is observed between the trends in the magnetic and velocity perturbations.
As outlined in a simple model in Appendix B, the amplitude of the magnetic oscillation during solar cycle minimum may be understood via the linearized induction equation, Eq. (B.3), whereby the radial magnetic field is advected by the hydrodynamic high-latitude mode. This simple model approximately reproduces the symmetric pattern at high latitudes with a maximum amplitude of ≈0.2 G. The calculation assumes a dipolar background field magnetic field during solar minimum (Fig. B.1). It would be interesting to repeat these calculations over different phases of the solar cycle using, for example, a background magnetic field from a dynamo model.
Data availability
Movie associated with Fig. 5 is available at https://www.aanda.org
Acknowledgments
The observations were analyzed by SGH and Z-CL. The analytical model was derived by LG and Z-CL. This research was funded in whole, or in part, by the Austrian Science Fund (FWF) [10.55776/J4560]. For the purpose of open access, the author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission. SGH acknowledges funding from the Research Council of Finland (RCF) Academy Fellowship [370747: RIB-Wind]. We thank B. Proxauf and S. Good for valuable discussions. This work utilizes GONG data from NSO, which is operated by AURA under a cooperative agreement with NSF and with additional financial support from NOAA, NASA, and USAF. The HMI data used are courtesy of NASA/SDO and the HMI science team.
References
- Bekki, Y., Cameron, R. H., & Gizon, L. 2022, A&A, 662, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bekki, Y., Cameron, R. H., & Gizon, L. 2024, Sci. Adv., 10, eadk5643 [NASA ADS] [CrossRef] [Google Scholar]
- Bogart, R. S., Baldner, C. S., & Basu, S. 2015, ApJ, 807, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., Cameron, R. H., Bekki, Y., et al. 2021, A&A, 652, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gizon, L., Bekki, Y., Birch, A. C., et al. 2024, IAU Symp., 365, 207 [Google Scholar]
- Hanasoge, S., & Mandal, K. 2019, ApJ, 871, L32 [Google Scholar]
- Harvey, J. W., Hill, F., Hubbard, R. P., et al. 1996, Science, 272, 1284 [Google Scholar]
- Hathaway, D. H., Upton, L., & Colegrove, O. 2013, Science, 342, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, Z.-C., & Gizon, L. 2025, A&A, 695, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, Z.-C., Gizon, L., Birch, A. C., & Duvall, T. L. 2019, A&A, 626, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Y., Hoeksema, J. T., Sun, X., & Hayashi, K. 2017, Sol. Phys., 292, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Löptien, B., Gizon, L., Birch, A. C., et al. 2018, Nat. Astron., 2, 568 [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Snodgrass, H. B. 1984, Sol. Phys., 94, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, R. K. 1993, ASP Conf. Ser., 40, 25 [NASA ADS] [Google Scholar]
- Ulrich, R. K. 2001, ApJ, 560, 466 [CrossRef] [Google Scholar]
Appendix A: Phase of magnetic oscillations as a function of latitude
 |
Fig. A.1. Latitudinal dependence of the phase of |
Appendix B: Simplified model for magnetic field perturbations during cycle minimum
Let us consider the induction equation in an inertial frame,
Assuming background values of the magnetic field (B0) and of the axisymmetric flow (v0) during solar minimum, we wished to compute the perturbations to the magnetic field at the surface (B′) caused by the fluctuating flow (v′) associated with a mode of oscillation. In the near-surface layers, the velocity field of a quasi-toroidal mode of oscillation is approximately horizontal and divergence-free,
The magnetic field was assumed to be purely radial at the surface. We linearized the induction equation to obtain an equation for the magnetic field perturbation (B′):
Taking the radial component of this equation, we have
where we used ∇ ⋅ B0 = 0 and ∇ ⋅ v′ = 0.
During solar minimum, the background field at the surface is approximately radial at the surface and independent of longitude, that is,  . As shown in Fig. B.1, a reasonable model for the field is B0r ≈ b0(cos θ)n with b0 = 10 G and n = 7. The background flow consists of rotation and the meridional flow, that is,
. As shown in Fig. B.1, a reasonable model for the field is B0r ≈ b0(cos θ)n with b0 = 10 G and n = 7. The background flow consists of rotation and the meridional flow, that is,  . We used the surface angular velocity profile Ω(θ) from Snodgrass (1984) and the meridional flow profile vMC(θ) = − 15 sin(2θ) sin θ m/s.
. We used the surface angular velocity profile Ω(θ) from Snodgrass (1984) and the meridional flow profile vMC(θ) = − 15 sin(2θ) sin θ m/s.
Next, we plugged perturbations to the magnetic field of the form Br′=ℜ{b′(θ)eimϕ − iωt} into Eq. (B.4) to obtain
We adopted a surface diffusivity of η = 250 km2/s, consistent with the supergranulation. The right-hand side (RHS) of the equation depends on the co-latitudinal component of the m = 1 high-latitude (HL1) mode velocity, u′θ(θ), which we extracted from HMI ring-diagram flow maps along the central meridian at the HL1 mode frequency. As a sanity check, we separately computed the left-hand side (LHS) of the equation using the observed b′ as input, and the RHS of the equation using the observed u′θ. At latitudes above 60° (i.e., above the critical latitude of the HL1 mode), we find that the two sides of the equation have comparable amplitudes. We also find that the diffusion and meridional flow terms on the LHS of Eq. (B.5) are negligible. This implies that a rough estimate for b′ is
where θc = 32° is the critical colatitude given by Ω(θc) = ω/m. Figure B.2 compares the LOS projection of the fluctuating magnetic field derived from Eq. (B.6) to the observed 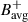 during cycle minimum (also see Fig. 1). Although the approximate model does not perfectly reproduce the observations (especially the phase), it provides the correct order-of-magnitude estimate for the observed
during cycle minimum (also see Fig. 1). Although the approximate model does not perfectly reproduce the observations (especially the phase), it provides the correct order-of-magnitude estimate for the observed 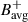 . We therefore conclude that the observed magnetic field perturbations at the surface are largely caused by the passive advection of the radial field (Br′) by the HL1 mode (velocity v′θ).
. We therefore conclude that the observed magnetic field perturbations at the surface are largely caused by the passive advection of the radial field (Br′) by the HL1 mode (velocity v′θ).
 |
Fig. B.1. Background radial magnetic field during solar minimum estimated from the data series hmi.b_synoptic (Liu et al. 2017). The synoptic maps for the radial component of the magnetic field were stacked in time and then Gaussian-smoothed with a full width of 27 days. The red curve shows the data in the northern hemisphere on 15 September 2019, when the Sun was quiet and its north pole was tilted toward the Earth. The black curve shows the approximation B0r(θ) = 10 × (cos θ)7 G, which we use in Eqs. (B.5) and (B.6). |
 |
Fig. B.2. Top: Observed |
All Figures
 |
Fig. 1. Super-synoptic maps in the Earth frame of |
| In the text | |
 |
Fig. 2. Oscillations of |
| In the text | |
 |
Fig. 3. Power spectra of magnetic fluctuations |
| In the text | |
 |
Fig. 4. Top and middle panels: Temporal variations of the m = 1 mode amplitude extracted from Blos and Vlos data, respectively. The red, orange, green, and blue curves correspond to results from the HMI |
| In the text | |
 |
Fig. 5. Bandpass-filtered images of the LOS Doppler velocity, Vlos, and LOS magnetic field, Blos, derived from HMI data. Top left: Filtered Vlos image from 14 June 2020. Bottom left: Central-meridian Vlos values stacked over time and plotted as a function of time and latitude. Right panels: Corresponding Blos data, with low-latitude regions (< 45°) shaded out. The filtering was performed using a bandpass filter centered at |
| In the text | |
 |
Fig. A.1. Latitudinal dependence of the phase of |
| In the text | |
 |
Fig. B.1. Background radial magnetic field during solar minimum estimated from the data series hmi.b_synoptic (Liu et al. 2017). The synoptic maps for the radial component of the magnetic field were stacked in time and then Gaussian-smoothed with a full width of 27 days. The red curve shows the data in the northern hemisphere on 15 September 2019, when the Sun was quiet and its north pole was tilted toward the Earth. The black curve shows the approximation B0r(θ) = 10 × (cos θ)7 G, which we use in Eqs. (B.5) and (B.6). |
| In the text | |
 |
Fig. B.2. Top: Observed |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} B_{\rm los}^{+} (\lambda , \phi , t) = \frac{1}{2} \left[B_{\rm los}(\lambda , \phi , t) + B_{\rm los}(-\lambda , \phi , t)\right]. \end{aligned} $$](/articles/aa/full_html/2025/11/aa57360-25/aa57360-25-eq2.gif)
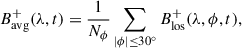
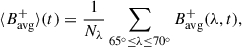
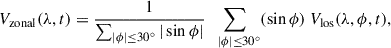
![$$ \begin{aligned} V_{\rm zonal}^{-} (\lambda ,t)&= \frac{1}{2} \left[V_{\rm zonal}(\lambda ,t) - V_{\rm zonal}(-\lambda ,t) \right],\end{aligned} $$](/articles/aa/full_html/2025/11/aa57360-25/aa57360-25-eq8.gif)