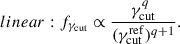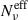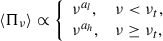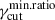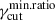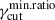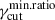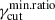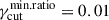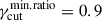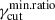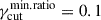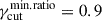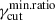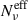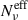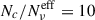| Issue |
A&A
Volume 704, December 2025
|
|
|---|---|---|
| Article Number | A199 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202556802 | |
| Published online | 09 December 2025 | |
Modeling and statistical characterization of synchrotron multi-zone polarization in blazars
Department of Astronomy, University of Geneva, Ch. d’Ecogia 16, 1290 Versoix, Switzerland
★ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.
Received:
9
August
2025
Accepted:
5
October
2025
Context. Multiwavelength polarimetric observations of blazars reveal complex energy-dependent polarization behavior, with a decrease in the polarization fraction from X-ray to millimeter bands and significant variability in the electric vector position angle (EVPA). These trends challenge simple single-zone synchrotron models and suggest a more intricate turbulent jet structure with multiple emission zones.
Aims. This work aims to develop a statistical framework to model the energy-dependent polarization patterns observed in blazars, particularly focusing on the behavior captured by IXPE in the X-ray and RoboPol in the optical. The goal is to determine the statistical characterization of multi-zone models, in terms of the cell size distribution, and of the distribution of the physical parameters of the electron energy distribution (EED).
Methods. A Monte Carlo simulation approach was employed to generate synthetic multi-zone synchrotron emission, using the JetSeT code, from a spherical region populated by turbulent cells with randomly distributed physical properties. Simulations were run across various scenarios: from identical cells to power-law-distributed cell sizes and EEDs with different cutoff and low-energy slope distributions. The simulation results were compared with the observed IXPE and RoboPol polarization trends.
Results. Our analysis demonstrates that a purely turbulent, multi-zone model can explain the observed energy-dependent polarization patterns without requiring a correlation between the cell size and the EED parameters. The key determinant of polarization is the effective number (flux-weighted) of emitting cells, which is significantly modulated by the dispersion in cell properties, especially the EED cutoff energy, at higher frequencies, and the dispersion in the EED low-energy spectral index, at lower frequencies.
Conclusions. Using a fractional dispersion on the EED cutoff on the order of 90%, and a dispersion of the EED low-energy spectral index between ≈0.5 and ≈1.5, our model reproduces both the chromaticity of the millimiter-to-X-ray polarization trends observed in IXPE multiwavelength campaigns for high synchrotron-peaked blazars, and the optical polarization limiting envelope, observed in the RoboPol dataset.
Key words: polarization / radiation mechanisms: non-thermal / galaxies: active / BL Lacertae objects: general / galaxies: jets
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. This email address is being protected from spambots. You need JavaScript enabled to view it. to support open access publication.
1. Introduction
Blazars are a subclass of active galactic nuclei (AGNs) in which a relativistic jet, launched by the central engine, is oriented close to the observer’s line of sight (Blandford & Rees 1978), resulting in highly beamed, rapidly variable, and strongly polarized emission across the entire electromagnetic spectrum (Urry & Padovani 1995). Their spectral energy distributions (SEDs) exhibit two principal components: a low-energy component, with power peaking from the infrared (IR) to the X-ray band, and a high-energy component, which peaks in the γ-rays. In the most widely accepted scenario, the low-energy component is interpreted as synchrotron (S) radiation emitted by ultrarelativistic electrons, while the high-energy bump is attributed either to inverse Compton (IC) emission in purely leptonic models (Blandford & Königl 1979) or to high-energy emission from ultrarelativistic protons in hadronic models (Böttcher et al. 2013). These sources are traditionally classified based on their synchrotron peak frequency (νpS), ranging from low synchrotron-peaked (LSP, νpS < 1014 Hz) through intermediate synchrotron-peaked (ISP, 1014 Hz < νpS < 1015 Hz) to high synchrotron-peaked (HSP, νpS > 1015 Hz) blazars (Abdo et al. 2010).
The radiation in the S bump is linearly polarized, and the level of the fractional polarization is very low (close to zero) in the low-energy branch, at millimiter frequencies, and reaches a level of tens of percent above the peak of the S bump (Marscher & Jorstad 2022). Moreover, Angelakis et al. (2016), using data from the RoboPol high-cadence polarization-monitoring program (King et al. 2014; Pavlidou et al. 2014), found that for a large sample of γ-ray-loud blazars, the fractional optical polarization depends on νpS showing a limiting envelope, with both the polarization and its dispersion higher in LSP sources than in HSP ones. They also demonstrated that the randomness of the optical electric vector position angle (EVPA) is higher in LSP sources compared to HSP ones.
The synchrotron emission from these sources, extending from radio to X-ray frequencies, provides a unique window into the physical conditions within relativistic jets, including magnetic field structure, particle acceleration mechanisms, and jet dynamics (Marscher 2014). Recent observational advances have dramatically enhanced our ability to probe these phenomena through polarimetric studies spanning from millimeter to X-ray wavelengths. In particular, the launch of the Imaging X-ray Polarimetry Explorer (IXPE) has enabled the first systematic measurements of X-ray polarization in blazars (Weisskopf et al. 2022). IXPE observations of HSP blazars (Liodakis et al. 2022; Di Gesu et al. 2023; Kouch et al. 2024) have revealed X-ray polarization degrees ranging from 10% to 20%, showing a systematic decrease at lower frequencies, with the optical polarization degree systematically larger than the millimiter one. This phenomenology, and the one observed in the RoboPol sample, has been explained by energy stratification of emission regions as electrons lose energy via radiation (Liodakis et al. 2022), providing strong support for shock acceleration models (Kirk et al. 2000) and suggesting a complex multi-zone structure within blazar jets where different energy bands probe distinct physical regions. However, IXPE observations have also revealed EVPA rotations in several blazars (Middei et al. 2023), which present a challenge to simple energy-stratified models that would predict stable, frequency-independent EVPAs if magnetic field configurations remain coherent across emission zones. This discrepancy suggests either that the magnetic field geometry varies significantly between different emission regions or that additional physical processes, such as Faraday rotation or turbulent magnetic field fluctuations, play important roles in determining the observed polarization characteristics.
In this work, we present a comprehensive Monte Carlo framework for modeling multi-zone synchrotron emission in blazar jets, specifically designed to reproduce the energy-dependent polarization characteristics observed from millimeter to X-ray wavelengths. Our approach incorporates spatially resolved emission regions with distinct physical properties, in a purely turbulent framework, that is, we do not assume any correlation between magnetic field and cell size and/or position; we only assume a power-law distribution for the cell size, and we tested different levels of correlation between the size of the cells and cutoff in the electron distribution. This minimal approach aims to provide the most likely statistical characterization of the cell distributions, in terms of size and energy of the electrons, able to reproduce the energy-dependent polarization patterns observed in the millimiter-to-X-ray data for IXPE HPS, and in the optical for the RoboPol dataset. The paper is organized as follows: in Sect. 2.1 we discuss the single-cell S emission, and we provide some useful δ approximations both for the S SED emission and for the fraction polarization. In Sect. 2.2 we investigate analytical trends for the fractional polarization, for the case of a multi-zone scenario, without flux dispersions. In Sect. 2.3, we extend the results of Sect. 2.2 to the case of dispersion of cells flux, and we introduce the concept of flux-weighted effective number of cells contributing to the observed polarization. In Sect. 3.2 we describe the setup for our Monte Carlo (MC) simulation workflow. In Sect. 4 we analyze our MC results for the case of no dispersion on cells’ flux and same cells size (Sect. 4.1), and the case of dispersions on cells’ flux and power-law-distributed cells’ size (Sect. 4.2), presenting the predicted trends for the patterns of the multiwavelength fractional polarization. In Sect. 5 we compare our trends to the multiwavelength trends observed, for a sample of HSP, by IXPE, and to the optical trends observed by RoboPol for a large sample of γ-ray-loud blazars. Finally, in Sect. 6 we discuss our results and present our conclusions.
2. Synchrotron polarization
2.1. Single cell
Let us consider a single spherical emitting region, with an ordered magnetic field B, and a population of relativistic electrons, described by energy distribution (EED) n(γ). According to the standard synchrotron (S) theory (Westfold 1959; Rybicki & Lightman 1986), the degree of linear polarization is given by the flux emitted in the directions parallel (Fν, ∥) and perpendicular (Fν, ⊥) to the projection of the magnetic field on the plane of the sky,
where νc is the S critical frequency, and the functions F(x)≡x∫K5/3(ξ)dξ and G(x)≡xK2/3(x), are defined in terms of modified Bessel functions of the second kind and fractional order. The S numerical computation, both for the SED and polarization, is performed using the JetSeT12 code v1.3.1 (Tramacere et al. 2009, 2011; Tramacere 2020). If we assume a reference direction on the sky plane, and χ is the angle between this direction and the projection of the magnetic field on the plane of the sky, then Πνord can be expressed in terms of Stokes’ parameters:
For a power-law EED, with a spectral index p,
The relation above is valid only for a pure power law, or as long as the S emission is dominated by the power-law branch of the underlying EED. We can obtain a more generic trend, for Eq. (3), by deriving an approximate expression of Πν(p) using the standard S theory in δ−function approximation,
where z is the cosmological redshift, and δ the beaming factor, V is the volume of the emitting source, and dL is the luminosity distance. These relations link the flux emitted at a given frequency to the corresponding shape of the electron distribution at γ(ν). The peak frequency of the SED,νp, will be at
Assuming that EED is a power-law with an exponential cutoff,
By using the δ−function approximation, the energy-dependent slope, 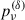 , can be evaluated as the log-derivative of n(γ) at γ(ν),
, can be evaluated as the log-derivative of n(γ) at γ(ν),
or, conversely, 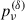 can be estimated from Fν as
can be estimated from Fν as
Finally, the δ−function approximation for the fractional polarization can be obtained from Eq. (3):
In Figure 1, we show a comparison for Πνord using the different methods described above. The row-a panel shows the S SED, and the row-b panel the corresponding fractional polarization as a function of the frequency, for a power-law cutoff EED, for γcut = 5 × 104, γmin = 2, and p = [1.5, 2.0, 2.5]. We notice that the exact calculation of Πνord, evaluated using Eq. (1), and marked by solid lines, is well approximated by the δ−approximation from Eq. (9), both using 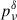 from Eq. (7) (solid circles), and using
from Eq. (7) (solid circles), and using 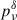 from Eq. (8) (crosses). The fractional deviation of the two δ-approximation methods, reported in the c-row panel of Figure 1, reaches a maximum value of a few percents, with the method using
from Eq. (8) (crosses). The fractional deviation of the two δ-approximation methods, reported in the c-row panel of Figure 1, reaches a maximum value of a few percents, with the method using 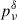 from Eq. (8) providing a better performance compared to
from Eq. (8) providing a better performance compared to 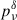 from Eq. (7). We also notice the asymptotic behavior of Πνord: below νpΠνord asymptotically approaches the value dictated by Eq. (3) (horizontal dashed lines), whilst, above νp it deviates significantly from the Eq. (3), asymptotically approaching the maximal polarization limit of 1.0, for ν/νp > > 1. More in detail, if we define the polarization slope, a, as the log-derivative:
from Eq. (7). We also notice the asymptotic behavior of Πνord: below νpΠνord asymptotically approaches the value dictated by Eq. (3) (horizontal dashed lines), whilst, above νp it deviates significantly from the Eq. (3), asymptotically approaching the maximal polarization limit of 1.0, for ν/νp > > 1. More in detail, if we define the polarization slope, a, as the log-derivative:
 |
Fig. 1. Left panels: The S SED (row a), and the corresponding fractional polarization (row b) as a function of the frequency, for a power-law cutoff EED, γcut = 5 × 104, and p = [1.5, 2.0, 2.5]. The solid lines in the row b panel mark the Πνord evaluated using Eq. (1), the circles mark the δ approximation from Eq. (9) using |
and we fit Πνord by means of a broken power-law, we notice that Πνord, below νp, asymptotically approaches a value of al ≈ 0, above νp reaches a value of ah ≈ [0.02, 0.03]. The maximum value of a is limited by the log-ratio of the maximum excursion of polarization (typically [0.75 − 1]) to the maximum SED excursion in frequency above νp (typically a few decades, depending on the EED).
2.2. Synchrotron polarization: case of N cells with no dispersion on flux
Now, let’s consider a system of Nc cells, with Nν ≤ Nc indicating the number of cells emitting at the frequency ν. In each cell, the magnetic field is ordered, but the single-cell position angle, χir, is randomly oriented, and Fν, i is the single-cell flux. We assume that the pitch angle (the angle between an electron’s velocity vector and the direction of the magnetic field), in each cell, it can be either fixed or distributed uniformly, without any loss of generality, since in the former case the term in sin(α) can be factored out in Eq. 1, and in the latter, the average of a uniform distribution of α, does not change the results compared to the fixed angle case. For the specific case of almost identical cells, that is, 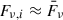 , and
, and 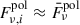 , the average degree of the linear S polarization (⟨Πν⟩), at a given frequency, can be evaluated as in Marscher & Jorstad (2022):
, the average degree of the linear S polarization (⟨Πν⟩), at a given frequency, can be evaluated as in Marscher & Jorstad (2022):
We can also define a polarization factor, as in Marscher & Jorstad (2022):
where ford is the fraction of coherent magnetic field in the system, which reduces to 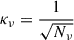 , for ford = 0. In the following, we investigate the case of ford = 0, hence, all the results presented in the following can be easily rescaled to the case of 0 < ford ≤ 1.
, for ford = 0. In the following, we investigate the case of ford = 0, hence, all the results presented in the following can be easily rescaled to the case of 0 < ford ≤ 1.
2.3. Synchrotron polarization: Case of N cells with dispersion on flux
In a more general and realistic scenario, the flux of each cell, Fν, i, depends on the physical properties of each cell, that is, 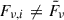 , preventing the Fν term from being factored out in Eq. 11 :
, preventing the Fν term from being factored out in Eq. 11 :
This implies that the effective number of emitting cells at a given frequency will depend on the statistical distribution of the physical parameters of the cells in the system. From a statistical standpoint, the effective number of emitting cells can be interpreted as the effective sample size (ESS) in a sample with weights (wi), using the approach of Shook-Sa & Hudgens (2022):
where the cell weights, for Eq. (13), are defined as:
hence, the effective number of cells contributing to a given frequency, 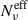 , will read:
, will read:
and the average frequency-dependent fraction polarization will read:
We stress that our definition of 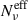 provides a more robust estimate of the flux-weighted cell contribution to the total fractional polarization compared to that presented in Peirson & Romani (2019), being the latter defined as the number of zones contributing half of the integrated flux.
provides a more robust estimate of the flux-weighted cell contribution to the total fractional polarization compared to that presented in Peirson & Romani (2019), being the latter defined as the number of zones contributing half of the integrated flux.
The relevant result here is that the observed fractional polarization, in general, will not depend on Nν, but on 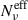 . As a consequence, the estimate of Nν (or Nc), from (Πνord/⟨Πν⟩)2 will lead to an underestimation of the actual number of cells in the system.
. As a consequence, the estimate of Nν (or Nc), from (Πνord/⟨Πν⟩)2 will lead to an underestimation of the actual number of cells in the system.
3. Simulation setup and workflow
3.1. MC simulations setup
In a turbulent medium, even though we might have similar cell sizes, the EED, the beaming factor, and other parameters can change. We need to accurately compute the S emission and polarization for each cell and generate the individual cell properties via a Monte Carlo approach. We assume that our system has a spherical geometry, with a characteristic radius, RS, and that the single-cell radius, Rc, is distributed as a power-law, with index q, via the scaling factor r, according to:
we set RS = 1016 cm. The cell values of the magnetic field intensity, Bc, and of the beaming factor, δc, are distributed as a flat PDF or have a fixed value:
The position angle of the magnetic field, in a single cell, χcr, is randomly oriented: fχcr = 𝒰[0, 2π].
The EED is assumed to be a power-law with an exponential cutoff:
the cell values of the index EED index, pc, are distributed as a uniform distribution, or have a fixed value:
We investigated four different scenarios for the PDF of γcut, fγcut: a scenario with a fixed value of γcut:
and a scenario with dispersion on γcut. For the latter scenario, two distributions have no correlation between cell size and γcut:
and the third one establishes a linear relationship between Rc and γcut, setting 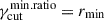 and
and 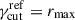 , and applying the transformation
, and applying the transformation 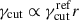 , leading to:
, leading to:
The dispersion on γcut is controlled by the value of the lower bound defined as 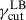 , as
, as 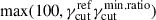 , implying that lower values of
, implying that lower values of 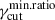 lead to a larger dispersion. The linear distribution is motivated by results from magnetic reconnection Particle-in-Cell (PIC) simulations (Li et al. 2023; Sironi et al. 2016), finding the EED high-energy cutoff scaling linearly with the plasmoids’ width. We notice that for q < 0 both the log-uniform and linear cases result in fγcut being a decreasing function of γcut, with the relevant difference that the linear case introduces a positive correlation between the cell size and the value of fγcut.
lead to a larger dispersion. The linear distribution is motivated by results from magnetic reconnection Particle-in-Cell (PIC) simulations (Li et al. 2023; Sironi et al. 2016), finding the EED high-energy cutoff scaling linearly with the plasmoids’ width. We notice that for q < 0 both the log-uniform and linear cases result in fγcut being a decreasing function of γcut, with the relevant difference that the linear case introduces a positive correlation between the cell size and the value of fγcut.
3.2. MC simulations workflow
For each combination of the input parameters described in Sect. 3.1, we first perform a calibration stage, that is, we calibrate Nc and 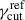 , to obtain a trial-averaged optical polarization fraction, ⟨Πνopt⟩, within [0.4 − 0.5]%, and a trial-averaged value of νpS within=[0.8 − 1.2]×1017 Hz. As a reference value for the optical frequency, we use the value of 5 × 1014 Hz. Details of the calibration stage are reported in Sect. A. At the end of the calibration stage, the calibrated values of Nc and
, to obtain a trial-averaged optical polarization fraction, ⟨Πνopt⟩, within [0.4 − 0.5]%, and a trial-averaged value of νpS within=[0.8 − 1.2]×1017 Hz. As a reference value for the optical frequency, we use the value of 5 × 1014 Hz. Details of the calibration stage are reported in Sect. A. At the end of the calibration stage, the calibrated values of Nc and 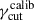 are used for the full MC simulations as follows:
are used for the full MC simulations as follows:
-
we define six bins for νpS, evenly spaced in the logarithm, over the range [
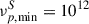 ,
, 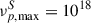 ] Hz. Each value of νp, iS is mapped to a corresponding bin for the EED cutoff energy of
] Hz. Each value of νp, iS is mapped to a corresponding bin for the EED cutoff energy of 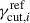 , by scaling the calibrated value of
, by scaling the calibrated value of 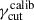 according to the third of Eq. (6).
according to the third of Eq. (6). -
For each bin of γcut, i we run 1000 trials using always the same value of Nc, and drawing
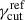 from
from ![$ \mathcal{U}[\gamma_{\mathrm{cut},i}^{\mathrm{ref}},\gamma_{\mathrm{cut, i+1}}^{\mathrm{ref}}] $](/articles/aa/full_html/2025/12/aa56802-25/aa56802-25-eq53.gif) .
. -
For each run, we verify that the sample variance converges according to Stein’s two-stage scheme (Stein 1945) as implemented in Wübbeler et al. (2010). In detail, we have verified, for each run, that the interval, [⟨Πν⟩(1 − εMC),⟨Πν⟩(1 + εMC)], for εMC ≤ 0.15, provides confidence interval for the true value of Πν, at a confidence level of 0.95, up to ν ≤ 1000 × νp.
At the end of the MC, we have 1000 realizations for each of the six νpS bins, where the only changed parameter per bin is 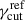 , that is, each trial and each bin of νpS, has the same value of Nc and the same PDFs fRc, fδc, fBc, and fχr. The trials are eventually binned according to the
, that is, each trial and each bin of νpS, has the same value of Nc and the same PDFs fRc, fδc, fBc, and fχr. The trials are eventually binned according to the 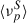 value in the νp, iS bins, and the relevant statistics of the parameters are extracted.
value in the νp, iS bins, and the relevant statistics of the parameters are extracted.
4. Simulation trends
In this section, we provide a statistical description of the ⟨Πν⟩ trends, for two different scenarios: the case of cells with the equal size (Sect. 4.1) and the case of power-law-distributed cell sizes (Sect. 4.2). We aim to do the following:
-
verify the ⟨Πν⟩ trend provide by Eq. (17) and in particular the connection between the polarization factor κνeff and
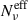 .
. -
characterize the ⟨Πν⟩ trends as a function of ν/νp.
-
identify how the different PDFs for fRc, fδc, fBc, and fγcut impact the trends.
4.1. Case of equal-size cells
We start by investigating the case of equal-size (ES) cells with three different configurations, whose parameters are summarized in Table 1. In Figure 2 we show the impact, on the frequency-dependent polarization pattern ⟨Πν⟩, of different levels of randomization, from configuration ES1 to ES3. The left column panels refer to the case of identical cells, i.e., the configuration ES1 of Table 1. The middle column panels refer to the configuration ES2, i.e. same as ES1 but using for fγcut the log-uniform PDF and, finally, the right column panels refer to the ES3 case, with the same configuration as for the ES2 case, but adding a uniform PDF, for p, fp ∼ 𝒰[1.8, 2.8]. For all the cases, we use 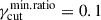 .
.
MC parameter space for equal-size distributed cells.
 |
Fig. 2. Different colors identifying the corresponding νp bins, which are the same for all the panels. Top panels: Left column: case of identical cells (configuration ES1 in Table 1). Middle column: case of configuration ES2 in Table 1, i.e. using fγcut = log-uniform. Right column: panel, case of configuration ES3, same as ES2 but adding a flat PDF, for p : fp ∼ 𝒰[1.8, 2.8]. All the trends are reported versus ν/νp. Solid lines mark the MC 0.5 quantiles and shaded areas mark the 1-σ quantiles dispersion, for the MC trials. Row a: the trend of the ratio of ⟨Πν⟩. Row b: same as for Row 1, but for trials-averaged trends for ⟨Πν⟩/⟨Πνord⟩. Row c: trials-averaged trends for Nν (dashed lines) and |
The trends for the ratio of ⟨Πν⟩ and ⟨Πν⟩/⟨Πνord⟩ are shown in the panels of row a and b, respectively, where the shaded area represents the 1-σ quantiles dispersion for the MC trials, and the solid line represents the median value. The different colors identify the corresponding νp bins, and are the same for all the panels. The c-row panels show the trends for the trials-averaged value of 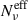 , and the d-row panels the trials-averaged trends for the polarization factor κν (dashed line) and κνeff (solid lines). The SEDs for the case νp bin = [1016 − 1017] Hz are represented in the e-row panels, where the shaded area encompasses the entire MC range. The dot-dashed vertical lines mark the SED peak value for the lowest flux cell,ν = νpmin, and the dashed vertical lines the ν/νp value above which not all the cells contribute to the SED flux. It is clear that for the case of identical cells (ES1), Nν and
, and the d-row panels the trials-averaged trends for the polarization factor κν (dashed line) and κνeff (solid lines). The SEDs for the case νp bin = [1016 − 1017] Hz are represented in the e-row panels, where the shaded area encompasses the entire MC range. The dot-dashed vertical lines mark the SED peak value for the lowest flux cell,ν = νpmin, and the dashed vertical lines the ν/νp value above which not all the cells contribute to the SED flux. It is clear that for the case of identical cells (ES1), Nν and 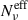 coincide, and this translates to κν = κνeff. In contrast, by adding a randomization on γcut (middle column,ES2), we start to introduce a modulation on
coincide, and this translates to κν = κνeff. In contrast, by adding a randomization on γcut (middle column,ES2), we start to introduce a modulation on 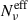 , with
, with 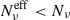 for ν ≥ νpmin, leading to a difference between the polarization factor, with κνeff > κν, for ν ≥ νpmin. This modulation is not only related to the fact that above a given γcut only a few cells are contributing, as demonstrated by the dashed lines trends related to κν, but mostly to the impact of the different cell flux contribution, which is shown by the κνeff trend. This modulation introduces a turnover in
for ν ≥ νpmin, leading to a difference between the polarization factor, with κνeff > κν, for ν ≥ νpmin. This modulation is not only related to the fact that above a given γcut only a few cells are contributing, as demonstrated by the dashed lines trends related to κν, but mostly to the impact of the different cell flux contribution, which is shown by the κνeff trend. This modulation introduces a turnover in 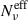 and consequently in κνeff and ⟨Πν⟩, located around ν ≳ νpmin. The turnover still persists when we introduce a randomization on p (left column, ES3). We model the ⟨Πν⟩ trend by means of a broken power-law function:
and consequently in κνeff and ⟨Πν⟩, located around ν ≳ νpmin. The turnover still persists when we introduce a randomization on p (left column, ES3). We model the ⟨Πν⟩ trend by means of a broken power-law function:
with al and ah, indicating the low and high-energy indices, respectively, and νt the turnover frequency, capturing the νpmin position. In the following, we analyze the trends of al and ah, focusing on the νp bin = [1016 − 1017] Hz (rows e and f of Figure 2), and we find:
-
For the ES1 configuration, since
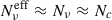 , the value of the two power-law indices, al ≈ 0 and ah ≈ 0.03 reflect the single-cell polarization trend, as reported in the bottom panel of Figure 1, i.e. asymptotically equal to the value from Equation (3), for ν < νpmin (γ < γ3p) and mildly increasing for ν > νpmin (γ > γ3p).
, the value of the two power-law indices, al ≈ 0 and ah ≈ 0.03 reflect the single-cell polarization trend, as reported in the bottom panel of Figure 1, i.e. asymptotically equal to the value from Equation (3), for ν < νpmin (γ < γ3p) and mildly increasing for ν > νpmin (γ > γ3p). -
For the ES2 configuration, the trend below νpmin is the same as for ES1, since there is no modulation on
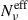 below νp, on the contrary, above νpmin the modulation on
below νp, on the contrary, above νpmin the modulation on 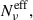 introduced by the dispersion on γcut, leads to a significant hardening of ah ≈ 0.15. We notice that such a large value of ah is incompatible with the low value obtained for the single-cell configuration (ah ≲ 0.03), which hints that a significant dispersion is required in γcut (and consequently on γ3p and νp), to reproduce it.
introduced by the dispersion on γcut, leads to a significant hardening of ah ≈ 0.15. We notice that such a large value of ah is incompatible with the low value obtained for the single-cell configuration (ah ≲ 0.03), which hints that a significant dispersion is required in γcut (and consequently on γ3p and νp), to reproduce it. -
For the ES3 configuration, the trends above νpmin are similar to the case of ES2, with ah ≈ 0.17, on the contrary, below νpmin, the dispersion on p introduces a low-energy slope al ≈ 0.05, which is significantly larger than the value of al ≈ 0.01 observed for the case of no dispersion on p (ES1 and ES2). The value of the slope al relates to the dispersion of p, and will be investigated in more detail in the next subsection.
In conclusion, the results of the ES scenario indicate that the slope of the high-frequency polarization is mainly influenced by the modulation of 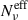 above νpmin, driven by the dispersion in γcut. On the other hand, the low-frequency slope al is significantly affected by the dispersion on p. This behavior highlights the interplay between the EED parameters and the resulting polarization patterns, emphasizing the importance of accurately modeling the underlying physical properties of the emitting cells to interpret observational data effectively.
above νpmin, driven by the dispersion in γcut. On the other hand, the low-frequency slope al is significantly affected by the dispersion on p. This behavior highlights the interplay between the EED parameters and the resulting polarization patterns, emphasizing the importance of accurately modeling the underlying physical properties of the emitting cells to interpret observational data effectively.
4.2. Case of power-law-distributed cell sizes
In this section, we extend the parameter space investigated in the previous section by considering the case of cells distributed according to a power law, testing different fγcut distributions and different levels of dispersion on fpc. In total, the power-law (PL) scenario counts 780 different configurations, obtained by combining the different PDF configurations listed in Table 2. Our goal is to investigate the impact of fRc, fγcut, and fpc on the values of al and ah. We fit the 0.5 quantiles of the ⟨Πν⟩ obtained for each run using Eq. (25) and leaving all the parameters free. In Figure 3, we show the resulting trends of al (left panels) and ah (right panels), as functions of Δp (top panels), rmin (middle panels), and 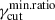 (bottom panels). Our findings on the values of ah and al are summarized as follows:
(bottom panels). Our findings on the values of ah and al are summarized as follows:
-
al: Consistent with the ES configuration, we find that the average value of al increases with the dispersion in p, and is largely independent of rmin and
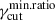 . However, for the case of log-uniformfγcut, al decreases as
. However, for the case of log-uniformfγcut, al decreases as 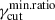 increases. This is expected since
increases. This is expected since 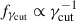 and the cell size is uncorrelated with γcut; thus, lower values of
and the cell size is uncorrelated with γcut; thus, lower values of 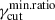 lead to a larger dispersion in cell flux weights at low frequencies, increasing
lead to a larger dispersion in cell flux weights at low frequencies, increasing 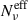 , with a consequent hardening of the slope of the polarization factor below νp. In contrast, for the linear case, the positive correlation between r and γcut compensates for the decreasing probability of cells with large γcut with the larger size of the same cells, mitigating the flux weight dispersion at low frequencies, and making the al slope of the polarization factor insensitive to
, with a consequent hardening of the slope of the polarization factor below νp. In contrast, for the linear case, the positive correlation between r and γcut compensates for the decreasing probability of cells with large γcut with the larger size of the same cells, mitigating the flux weight dispersion at low frequencies, and making the al slope of the polarization factor insensitive to 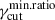 .
. -
ah: The high-energy slope of the polarization factor, unlike al, is independent of Δp, and generally also of rmin, since these parameters do not affect the modulation of
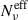 above the turnover frequency. Also
above the turnover frequency. Also 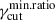 does not impact the trends, since its impact on νpmin is captured by the νt free parameter.
does not impact the trends, since its impact on νpmin is captured by the νt free parameter.
MC parameter space for power-law-distributed cell sizes.
 |
Fig. 3. Summary of the polarization slope trends for the PL-distributed parameter space reported in Table 2. Each subpanel refers to the three different values of q = [0, −1.0, −1.5], as reported in the subpanel title. Top panels: Low-energy (al, left panels) and high-energy (ah, right panels) polarization slopes as a function of the dispersion in the electron energy distribution index, Δp. Middle panels: al and ah as a function of the minimum cell size ratio, rmin. Bottom panels: al and ah as a function of the minimum cutoff ratio, |
Finally, in the left panel of B.1 we show the trend of the effective flux-averaged, 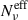 , at the reference frequencies used for the millimiter (2 × 1011 Hz), optical (5 × 1014 Hz), and X-ray (1 × 1018 Hz) frequencies, and in the top panel of Figure B.2, we show how the number of Nc exceeds, at least by a factor of 10, the value of
, at the reference frequencies used for the millimiter (2 × 1011 Hz), optical (5 × 1014 Hz), and X-ray (1 × 1018 Hz) frequencies, and in the top panel of Figure B.2, we show how the number of Nc exceeds, at least by a factor of 10, the value of 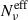 . The upper value of
. The upper value of 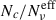 reaches up to a few thousand, for the X-ray frequency, and decrease to a few hundred for the optical frequency, and up to a few tens for millimiter frequency. The effect is larger for steeper values of q.
reaches up to a few thousand, for the X-ray frequency, and decrease to a few hundred for the optical frequency, and up to a few tens for millimiter frequency. The effect is larger for steeper values of q.
In summary, the low-frequency polarization slope al is most sensitive to the dispersion in p, while the high-frequency slope ah is mainly set by the decrease in the effective number of emitting cells above the SED peak, driven by the dispersion ob γcut, and is less sensitive to the parameters related to the low-energy branch of the EED.
5. Comparison with observed data
In this section, we compare the results of our simulations for the case of PL-distributed cell size, discussed in the previous section, with the observed data. We test the following features, observed in the phenomenology:
-
The Πν trend observed by IXPE for HPS objects, resulting in the X-ray polarization degrees on the order of 10–20%, with a systematic decrease at lower frequencies, with the optical polarization degree systematically larger than the millimiter one. This trend is shown in the right panel of Figure 4. The sample refers to the millimiter-to-X-ray Πν trends (dashed lines) for Mrk 421, Mrk 501, PKS2155-304, 1ES0229+200, and 1ES1959+650, collected from recent IXPE multiwavelength campaigns (Liodakis et al. 2022; Di Gesu et al. 2023; Kouch et al. 2024; Middei et al. 2023). The solid blue line represents a broken-power-law fit to the data, returning a millimiter-to-optical polarization index of amm − o ≈ 0.1, and an optical-to-X-ray index of ao − X ≈ 0.17.

Fig. 4. Left panel: The limiting envelope, found by RoboPol (Angelakis et al. 2016), for a large sample of γ-ray-loud blazars between νpS and both the average fractional optical polarization and its dispersion. Right panel: The Πν trend observed in by IXPE for the HPS Mrk 501, Mrk 421, PKS2155-304, 1ES0229+200, and 1ES1959+650 collected from recent IXPE multiwavelength campaigns (Liodakis et al. 2022; Di Gesu et al. 2023; Kouch et al. 2024; Middei et al. 2023).
-
The limiting envelope, found by RoboPol (Angelakis et al. 2016) for a large sample of γ-ray-loud blazars, between νpS and both the average fractional optical polarization and its dispersion (left panel of 4), and between νpS and the EVPA.
5.1. IXPE HPS ⟨Πν⟩ trends
To compare the HSP Πν trends observed by IXPE with our simulations, we perform the same analysis as in Sect. 4.2, but we select only the MC runs for 10 × 15 Hz ≤ νpS ≤ 10 × 18 Hz, and in place of estimating al and ah using the best-fit values returned by Eq. (25) with all the parameters free, we compute directly the indices amillimiter − o and ao − X using the reference values for the millimiter, optical, and X-ray frequencies, of 2 × 1011 Hz, 5 × 1014 Hz, and 1 × 1018 Hz, respectively.
The shaded areas in Figure 5, represent the ±20% boundary for the observed values of amm − o and of ao − X, and the solid lines represent the results of our MC simulations, with the error bar indicating the 2-σ confidence quantiles.
 |
Fig. 5. Summary of polarization slope trends for the PL-distributed parameter space reported in Table 2, for the HSP objects, selecting MC runs with (10 × 15 Hz ≤ νpS ≤ 10 × 18 Hz). Top panels: Low-energy (amm − o, left panels) and high-energy (ao − X, right panels) polarization slopes as a function of the dispersion in the electron energy distribution index, Δp. Middle panels: al and ah as a function of the minimum cell size ratio, rmin. Bottom panels: al and ah as a function of the minimum cutoff ratio, |
Although the amm − o index samples ⟨Πν⟩ below the optical frequency, which is typically below the peak frequency of the HSP objects, the pattern is similar to the one obtained for al, since the modulation in 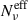 does not change below νpS. Consistent with al, we find that the most relevant parameters for the amm − o index are the dispersion on p, which is positively correlated with amm − o, and the value of
does not change below νpS. Consistent with al, we find that the most relevant parameters for the amm − o index are the dispersion on p, which is positively correlated with amm − o, and the value of 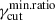 , which has a negative correlation, for fγcut = log-uniform. In general, the observed data favor a dispersion Δp ⪆ 1, and values of
, which has a negative correlation, for fγcut = log-uniform. In general, the observed data favor a dispersion Δp ⪆ 1, and values of 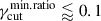 for the case of fγcut = log-uniform. We also notice that the log-uniform distribution provides the best match with the data.
for the case of fγcut = log-uniform. We also notice that the log-uniform distribution provides the best match with the data.
The ao − X index shows a different trend compared to ah, for rmin ≈ 1, for the case of linearfγcut, and for values of 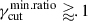 , for all the fγcut distributions. The different behavior between ah and ao − X comes from the fact that ah depends on the modulation of
, for all the fγcut distributions. The different behavior between ah and ao − X comes from the fact that ah depends on the modulation of 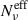 above νpmin. For the al case, the modulation on νpmin, driven by the dispersion on γcut, is captured by the νt free parameter. In contrast, in the case of ao − X, the value of νt is fixed to the value of 5 × 1014 Hz. As a consequence, the modulation on νpmin, driven by
above νpmin. For the al case, the modulation on νpmin, driven by the dispersion on γcut, is captured by the νt free parameter. In contrast, in the case of ao − X, the value of νt is fixed to the value of 5 × 1014 Hz. As a consequence, the modulation on νpmin, driven by 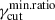 , places the optical frequency below the actual value of νt, leading to a softening of ao − X, compared to ah. This effect increases for lower values of
, places the optical frequency below the actual value of νt, leading to a softening of ao − X, compared to ah. This effect increases for lower values of 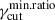 . This results in a significant tension with the data for rmin ≈ 1, for the case of linearfγcut, and for values of
. This results in a significant tension with the data for rmin ≈ 1, for the case of linearfγcut, and for values of 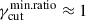 , for all the fγcut distributions, improving the constraining power of ao − X.
, for all the fγcut distributions, improving the constraining power of ao − X.
5.2. RoboPol limiting envelope
To test whether the samples generated in our MC are statistically compatible with the RoboPol observed trend, we use a two-dimensional two-sample Kolmogorov–Smirnov (KS) test, where the two independent variables are νpS and Πopt (evaluated at 5 × 1014 Hz). The KS test is performed using the public code NDTEST3, and crosschecked against the public code 2DKS4. In Figure 6 we show the trends of the KS test p-value as a function of Δp (top panels), rmin (middle panels) and 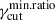 (bottom panels).
(bottom panels).
 |
Fig. 6. Trends of the KS test p value for the Πopt-versus-νpS limiting envelope, for the PL-distributed parameter space reported in Table 2. We report the KS trends as a function of Δp (top panels), rmin (middle panels), and |
We notice that consistently with the HSPs IXPE trends, the RoboPol Πopt-versus-νpS limiting envelope rules out the fγcut = fixed PDF, and disfavor values of 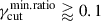 , for all the fγcut PDFs, and values of rmin ⪆ 0.1 for the linearfγcut. Anyhow, the Πopt-versus-νpS limiting envelope does not constrain the dispersion on Δp. The reason for this behavior stems from the fact that the observed RoboPol Πopt-versus-νpS envelope depends mostly on the ‘distance’ between the optical frequency and νpS, and in particular on the modulation of Nνeff, that is, the polarization factor κνeff below νpS. This effect is shown in Figures 7 and 8. In Figure 7 we plot the trial-averaged trends for Nνeff and for the polarization factor, κνeff for the PL scenario with fpc = 𝒰[1.5, 2.5], q = −1.0, rmin = 0.1, and fγcut = log-uniform. The different values of
, for all the fγcut PDFs, and values of rmin ⪆ 0.1 for the linearfγcut. Anyhow, the Πopt-versus-νpS limiting envelope does not constrain the dispersion on Δp. The reason for this behavior stems from the fact that the observed RoboPol Πopt-versus-νpS envelope depends mostly on the ‘distance’ between the optical frequency and νpS, and in particular on the modulation of Nνeff, that is, the polarization factor κνeff below νpS. This effect is shown in Figures 7 and 8. In Figure 7 we plot the trial-averaged trends for Nνeff and for the polarization factor, κνeff for the PL scenario with fpc = 𝒰[1.5, 2.5], q = −1.0, rmin = 0.1, and fγcut = log-uniform. The different values of 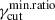 are reported in the panel title, and the dashed vertical line marks the reference value for the optical frequency. We notice how increasing
are reported in the panel title, and the dashed vertical line marks the reference value for the optical frequency. We notice how increasing 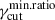 from 0.1 to 0.9, the optical excursion across the νp range, of both Nνeff and κνeff, decreases. This leads to a different trend in the Πopt-versus-νpS plane, as shown in Figure 8, where we notice the increase of
from 0.1 to 0.9, the optical excursion across the νp range, of both Nνeff and κνeff, decreases. This leads to a different trend in the Πopt-versus-νpS plane, as shown in Figure 8, where we notice the increase of 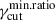 from 0.1 to 0.9 leads to a flattening of the limiting envelope, with the KS p-value decreasing from ≈0.14, for the case of
from 0.1 to 0.9 leads to a flattening of the limiting envelope, with the KS p-value decreasing from ≈0.14, for the case of 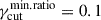 , to a p-value ≈0.015, for the case of
, to a p-value ≈0.015, for the case of 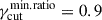 . Finally, in Figure 9 we plot the best runs for fγcut = uniform (top panels), fγcut = log-uniform (middle panels), and fγcut = linear (bottom panels). The left panels show the Πopt-versus-νpS limiting envelopes for both the MC simulations and the observed RoboPol data, the center panels show the dispersion trends of the MC optical EVPA angle,
. Finally, in Figure 9 we plot the best runs for fγcut = uniform (top panels), fγcut = log-uniform (middle panels), and fγcut = linear (bottom panels). The left panels show the Πopt-versus-νpS limiting envelopes for both the MC simulations and the observed RoboPol data, the center panels show the dispersion trends of the MC optical EVPA angle, 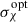 vs νpS, and the right panels show the IXPE HSP observed ⟨Πν⟩ trends compared to the MC results, extracted from the same runs used for the RoboPol panels. The decreasing trend of the optical EVPA angle dispersion has the same root as the Πopt-versus-νpS. i.e. the modulation of Nνeff below νpS. For lower values of νpS, the optical Nνeff decreases; hence, the dispersion on the optical EVPA angle increases.
vs νpS, and the right panels show the IXPE HSP observed ⟨Πν⟩ trends compared to the MC results, extracted from the same runs used for the RoboPol panels. The decreasing trend of the optical EVPA angle dispersion has the same root as the Πopt-versus-νpS. i.e. the modulation of Nνeff below νpS. For lower values of νpS, the optical Nνeff decreases; hence, the dispersion on the optical EVPA angle increases.
 |
Fig. 7. Trial-averaged trends for Nνeff and for the polarization factor, κνeff, for the PL scenario with fpc = 𝒰[1.5, 2.5], q = −1.0, rmin = 0.1, and fγcut = log-uniform. The different values of |
 |
Fig. 8. MC Πopt-versus-νpS trend, compared to the RoboPol observed one, for the same MC run configuration as reported in Figure 7. The panels from top to bottom show the trend for increasing values of |
 |
Fig. 9. Best runs for fγcut = uniform (top panels), fγcut = log-uniform (middle panels), and fγcut = linear (bottom panels). The left panels show the Πopt-versus-νpS limiting envelopes for both the MC simulations and the observed RoboPol data, the center panels show the trends of the MC-averaged dispersion of the MC optical EVPA angle vs νpS, and in the right panels, the IXPE HPS observed trends compared to the MC results extracted from the same runs used for the RoboPol panels. |
5.3. Phenomenology constraint on the MC parameter space
The two tests against IXPE and RoboPol data have provided an interesting constraint on the MC parameter space. We define our best sample by selecting runs resulting in a RoboPol KS p-value > 0.1, and a 20% maximal relative difference between the IXPE and MC for both the amm − o and ao − X. The selection reduces the volume of the parameter space, from 780 (for the total MC volume) to 79, for the best selection volume. In Figure 11 we show the statistical outcome of the selection. In the top panels, we report the Δp-versus-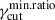 , and in the bottom panels the Δp-versus-rmin parameter space. The three columns refer to the selected fγcut PDF. The blue crosses mark the total MC parameter space, and the filled circles the best sample parameter space. The color scale marks the ratio of the volume of best parameter space, at the coordinate reported on the x and y axes, to the total MC parameter space; both the volume sizes refer to the given fγcut PDF. The plots confirm the results discussed in the previous section, i.e., the observed and combined RoboPol/IXPE phenomenology constrain Δp ⪆ 0.6, and
, and in the bottom panels the Δp-versus-rmin parameter space. The three columns refer to the selected fγcut PDF. The blue crosses mark the total MC parameter space, and the filled circles the best sample parameter space. The color scale marks the ratio of the volume of best parameter space, at the coordinate reported on the x and y axes, to the total MC parameter space; both the volume sizes refer to the given fγcut PDF. The plots confirm the results discussed in the previous section, i.e., the observed and combined RoboPol/IXPE phenomenology constrain Δp ⪆ 0.6, and 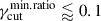 . The log-uniformfγcut PDF covers a larger volume of the parameter space, and reaches the peak value of the fractional acceptance, at almost 0.05. We find it quite promising that by only imposing the MC calibration condition of Πopt ≈ 0.045, for HSP sources, our model was able to reproduce simultaneously both the IXPE and RoboPol observed phenomenology. Finally, we test our MC-predicted Πν trends against the data of Mrk 421, showing pronounced chromaticity in Πν. To this end, we restrict the νpS bin to [1016, 1018] Hz (consistent with the source SED) and select the runs that best match the observed values of amm − o and ao − X, ranking them by the χ2 computed from each run’s median (0.5-quantile) predictions. In Figure 10 we show the top-ranked runs for fγcut = uniform (top panel), log-uniform (middle panel), and linear (bottom panel). The MC Πν trends reproduce the observed chromaticity of Mrk 421 with good accuracy. This contrasts with Liodakis et al. (2022), who argued that multi-zone models can reproduce only a mild level of chromaticity in Πν.
. The log-uniformfγcut PDF covers a larger volume of the parameter space, and reaches the peak value of the fractional acceptance, at almost 0.05. We find it quite promising that by only imposing the MC calibration condition of Πopt ≈ 0.045, for HSP sources, our model was able to reproduce simultaneously both the IXPE and RoboPol observed phenomenology. Finally, we test our MC-predicted Πν trends against the data of Mrk 421, showing pronounced chromaticity in Πν. To this end, we restrict the νpS bin to [1016, 1018] Hz (consistent with the source SED) and select the runs that best match the observed values of amm − o and ao − X, ranking them by the χ2 computed from each run’s median (0.5-quantile) predictions. In Figure 10 we show the top-ranked runs for fγcut = uniform (top panel), log-uniform (middle panel), and linear (bottom panel). The MC Πν trends reproduce the observed chromaticity of Mrk 421 with good accuracy. This contrasts with Liodakis et al. (2022), who argued that multi-zone models can reproduce only a mild level of chromaticity in Πν.
 |
Fig. 10. Πν trends for the top-ranked MC runs tested against the observed data of Mrk 421 for the case of fγcut = uniform (top panel), fγcut = log-uniform (middle panel), and fγcut = linear (bottom panel). |
 |
Fig. 11. Statistical outcome of the PL-distributed MC parameter space selection. The Δp-versus- |
6. Discussion and conclusions
We have presented an analysis of the multiwavelength pattern in the Πν of blazars, based on a comprehensive Monte Carlo framework modeling multi-zone synchrotron emission, able to reproduce the energy-dependent polarization characteristics observed from millimeter to X-ray wavelengths. Our approach implements spatially resolved emitting regions, with distinct physical properties, in a purely turbulent framework, that is, we do not assume any correlation between magnetic field and cell size and/or position; we only assume a power-law distribution for the cell size, and we test different levels of correlation between the size of the cells, and cutoff in the electron distribution. This minimal approach aims to provide the most likely statistical characterization of the cell distributions, in terms of size and energy of the electrons, capable to reproduce the energy-dependent polarization patterns observed in the millimiter-to-X-ray data for IXPE HPS, and in the optical for the RoboPol dataset. Our main findings are summarized below:
-
The frequency-dependent polarization fraction, Πν does not actually depend on the number of emitting cells contributing to a given frequency, Nν, but on the flux-weighted average effective number
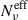 , which gives the actual contribution from each cell. This effect plays a relevant role when the size of the cells and the EED have significant dispersions. According to the distributions of the cell size, and/or of the EED parameters, the difference between Nν and
, which gives the actual contribution from each cell. This effect plays a relevant role when the size of the cells and the EED have significant dispersions. According to the distributions of the cell size, and/or of the EED parameters, the difference between Nν and 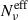 can be of a few orders of magnitude, with
can be of a few orders of magnitude, with 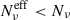 . Hence, using the estimate of Nν, for example, from X-ray measurements of Πν, leads to an underestimation of the actual number, Nc, of cells populating the region, and in the number of cells radiating at lower frequencies. This effect is significant both for the total and the best MC parameter space (see Figure B.2).
. Hence, using the estimate of Nν, for example, from X-ray measurements of Πν, leads to an underestimation of the actual number, Nc, of cells populating the region, and in the number of cells radiating at lower frequencies. This effect is significant both for the total and the best MC parameter space (see Figure B.2). -
In general, Πν shows a broken power-law shape, with the turnover frequency around νpS. For the case of no dispersion on the low-energy index of the EED, Δp = 0, the low energy spectral index al ≈ 0, whilst it increases as Δp increases, up to a value of al ≈ 0.1 for Δp = 1.5. al results to be in general independent on q, rmin, and
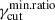 . The only fγcut distribution showing a dependence on
. The only fγcut distribution showing a dependence on 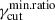 is the log-uniform, with al decreasing as
is the log-uniform, with al decreasing as 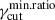 increases. This is expected since
increases. This is expected since 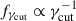 and the cell size is uncorrelated with γcut; thus, lower values of
and the cell size is uncorrelated with γcut; thus, lower values of 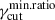 lead to a larger dispersion in the cell flux weights at low frequencies, increasing
lead to a larger dispersion in the cell flux weights at low frequencies, increasing 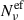 , with a consequent hardening in the slope of the polarization factor below νpS. The high-energy slope, ah, of the polarization fraction, unlike al, is independent of Δp, and generally also of rmin and
, with a consequent hardening in the slope of the polarization factor below νpS. The high-energy slope, ah, of the polarization fraction, unlike al, is independent of Δp, and generally also of rmin and 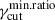 , since the modulation of
, since the modulation of 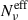 is mainly dictated by the cell flux contributions above νp, which depends on the dispersion above γcut.
is mainly dictated by the cell flux contributions above νp, which depends on the dispersion above γcut. -
We have tested our MC Πν trends against the IXPE HPS multiwavelength datasets. We find that the observed amm − o index significantly constrains the dispersion on p, favoring a dispersion Δp ⪆ 1, and values of
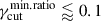 for the log-uniform distribution. We also noticed that log-uniform distribution provides the best match with the data, and that the scenario with a fixed cutoff in the EED is ruled out. The high-energy index, ao − X, provides a lower constraining power, anyhow, a significant tension with the data is observed for rmin ≈ 1, for the case of linearfγcut, and for values of
for the log-uniform distribution. We also noticed that log-uniform distribution provides the best match with the data, and that the scenario with a fixed cutoff in the EED is ruled out. The high-energy index, ao − X, provides a lower constraining power, anyhow, a significant tension with the data is observed for rmin ≈ 1, for the case of linearfγcut, and for values of 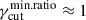 , for all the fγcut distributions.
, for all the fγcut distributions. -
The result from the test of the MC Πopt-versus-νpS limiting envelope against the observed RoboPol one is consistent with the outcome of the test against the IXPE HPS multiwavelength datasets. RoboPol data rules of the scenario with a fixed cutoff in the EED. Values of
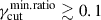 are disfavored for all tested fγcut PDFs. The trend is primarily sensitive to the modulation of the effective number of emitting cells at optical frequencies, which depends on the distance between the optical band and the synchrotron peak. The observed limiting envelope between optical polarization and νpS is well reproduced for models with a broad distribution of cutoff energies and a sufficiently large dispersion in the EED index p. Interestingly, we find that the same driver of the Πopt-versus-νpS leads to a similar trend for the dispersion of the MC optical EVPA angle,
are disfavored for all tested fγcut PDFs. The trend is primarily sensitive to the modulation of the effective number of emitting cells at optical frequencies, which depends on the distance between the optical band and the synchrotron peak. The observed limiting envelope between optical polarization and νpS is well reproduced for models with a broad distribution of cutoff energies and a sufficiently large dispersion in the EED index p. Interestingly, we find that the same driver of the Πopt-versus-νpS leads to a similar trend for the dispersion of the MC optical EVPA angle, 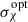 vs νpS, that is, an anticorrelation with νpS, in agreement with the observed RoboPol one.
vs νpS, that is, an anticorrelation with νpS, in agreement with the observed RoboPol one. -
The test of our simulations against combined IXPE and RoboPol observational data has provided a further constraint on model parameter space. By selecting MC runs that simultaneously match the RoboPol limiting envelope (KS p-value > 0.1) and reproduce the IXPE millimiter-to-optical and optical-to-X-ray polarization slopes within 20% of the observed values, the allowed parameter space (reported in Figure 11) is reduced by a factor of ten, compared to the full MC parameter space. The analysis shows that the best agreement is obtained for models with a broad dispersion in the EED index (Δp ≳ 0.6) and values of
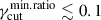 (that is, a large dispersion on γcut), with the log-uniformfγcut distribution providing the best agreement.
(that is, a large dispersion on γcut), with the log-uniformfγcut distribution providing the best agreement.
The constraints discussed above hint to both a wide range of single-cell electron spectral indices and a broad distribution of single-cell cutoff energies to reproduce the observed S multiwavelength polarization properties of blazars. The results demonstrate that a minimal, turbulence-driven multi-zone scenario can account for the key features seen in both IXPE and RoboPol datasets. We also notice that the linear model does not provide statistical improvement compared to the log-uniform, hence, the current dataset and analysis are not able to find significant evidence for this model, which mimics statistically the magnetic reconnection scenario. Nevertheless, this scenario is not ruled out.
Our results regarding the IXPE Πν trends are consistent with those presented in Peirson & Romani (2019); however, we have investigated a broader parameter space and presented a quantitative prediction of the related phenomenology, validated by a test against recent observational data from millimiter to X-ray frequencies. Moreover, we notice that contrary to what is reported in Liodakis et al. (2022), the multi-zone scenario is capable of reproducing the observed chromaticity of the Πν trends. We stress that our model does not test the presence or not of a shock, and that the investigation on the dispersion of the optical EVPA is mostly limited to the multi-zone scenario, with any implication on observed systematic rotations at different wavelengths. Hence, our analysis can fit a purely stochastic scenario or a scenario where the turbulent medium develops within the shock. In this regard, we notice how HSP objects, such as Mrk 421, have shown in their spectral shapes evidence for the coexistence of both first-order shock acceleration and stochastic acceleration (Tramacere et al. 2009, 2011). The presence of a shock is supported by recent population studies of IXPE results (Chen et al. 2024; Capecchiacci et al. 2025) providing an important observational constraint: they report EVPA–jet alignment in X-rays with a dispersion on the order of 20°(except for the larger rotations seen in Mrk 421 (Di Gesu et al. 2023)). If the EVPA–jet stable alignment reflects shock acceleration with in-shock turbulence, the MC EVPA should exhibit low dispersion, particularly in X-rays, in agreement with the IXPE results. For this purpose, in Figure 11 we marked with red boxes the points in our MC best parameter space that yield, on average, a 1-σ dispersion of the X-ray EVPA below 25°. This selection restricts the best parameter space to fγcut distributed uniformly or log-uniformly, with Δp = 1.5. In particular, for the fγcut = uniform case we obtain constraints rmin = 0.9 and 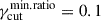 , while for the fγcut = emphlog-uniform case the constraints are rmin = 0.01 and
, while for the fγcut = emphlog-uniform case the constraints are rmin = 0.01 and 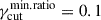 . Across the MC parameter space, the MC-averaged 1-σ dispersion of the X-ray EVPA is < 40°, and roughly 75% of the best region is compatible with a dispersion < 35°. These constraints can help to clarify the turbulence structure developed in the jet, during states when jet-axis/EVPA alignment is observed, but stronger conclusions will require more comprehensive shock-plus-turbulence modeling and longer, more densely sampled X-ray polarimetric observations of the sources.
. Across the MC parameter space, the MC-averaged 1-σ dispersion of the X-ray EVPA is < 40°, and roughly 75% of the best region is compatible with a dispersion < 35°. These constraints can help to clarify the turbulence structure developed in the jet, during states when jet-axis/EVPA alignment is observed, but stronger conclusions will require more comprehensive shock-plus-turbulence modeling and longer, more densely sampled X-ray polarimetric observations of the sources.
Written by Zhaozhou Li, https://github.com/syrte/ndtest
Written by Gabriel Taillon, https://github.com/Gabinou/2DKS, (Peacock 1983; Fasano & Franceschini 1987; Press et al. 2007).
Acknowledgments
A.T. would like to thank the anonymous referee for carefully reading the manuscript and for giving constructive comments, which helped to improve the quality of the paper, and Enrico Massaro for fruitful discussions.
References
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010, ApJ, 716, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Angelakis, E., Hovatta, T., Blinov, D., et al. 2016, MNRAS, 463, 3365 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [Google Scholar]
- Blandford, R. D., & Rees, M. J. 1978, Proceedings of the Pittsburgh Conference on BL Lac Objects (University of Pittsburgh), 328 [Google Scholar]
- Böttcher, M., Reimer, A., Sweeney, K., & Prakash, A. 2013, ApJ, 768, 54 [Google Scholar]
- Capecchiacci, S., Liodakis, I., Middei, R., et al. 2025, A&A, 703, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, C.-T. J., Liodakis, I., Middei, R., et al. 2024, ApJ, 974, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Di Gesu, L., Marshall, H. L., Ehlert, S. R., et al. 2023, ApJ, 949, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Fasano, G., & Franceschini, A. 1987, MNRAS, 225, 155 [NASA ADS] [CrossRef] [Google Scholar]
- King, O. G., Angelakis, E., Hovatta, T., et al. 2014, MNRAS, 442, 1706 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Rieger, F. M., & Mastichiadis, A. 2000, A&A, 333, 452 [Google Scholar]
- Kouch, P. M., Liodakis, I., Middei, R., et al. 2024, A&A, 689, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, X., Guo, F., Liu, Y.-H., & Li, H. 2023, ApJ, 954, L37 [NASA ADS] [Google Scholar]
- Liodakis, I., Marscher, A. P., Agudo, I., et al. 2022, Nature, 611, 677 [CrossRef] [Google Scholar]
- Marscher, A. P. 2014, ApJ, 780, 87 [Google Scholar]
- Marscher, A. P., & Jorstad, S. G. 2022, Universe, 8, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Middei, R., Liodakis, I., Perri, M., et al. 2023, ApJ, 942, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlidou, V., Blinov, D., Angelakis, E., et al. 2014, MNRAS, 442, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A. 1983, MNRAS, 202, 615 [NASA ADS] [Google Scholar]
- Peirson, A. L., & Romani, R. W. 2019, ApJ, 885, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical Recipes: The Art of Scientific Computing, 3rd edn. (Cambridge University Press), see Section 14.8 [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Wiley-VCH), 400 [Google Scholar]
- Shook-Sa, B. E., & Hudgens, M. G. 2022, Biometrics, 78, 388 [Google Scholar]
- Sironi, L., Giannios, D., & Petropoulou, M. 2016, MNRAS, 462, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, C. 1945, AnnMathStat, 16, 243 [Google Scholar]
- Tramacere, A. 2020, Astrophysics Source Code Library [record ascl:2009.001] [Google Scholar]
- Tramacere, A., Giommi, P., Perri, M., Verrecchia, F., & Tosti, G. 2009, A&A, 501, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tramacere, A., Massaro, E., & Taylor, A. M. 2011, ApJ, 739, 66 [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Ramsey, B., O’Dell, S., et al. 2022, JATIS, 8, 026002 [NASA ADS] [Google Scholar]
- Westfold, K. C. 1959, ApJ, 130, 241 [Google Scholar]
- Wübbeler, G., Harris, P. M., Cox, M. G., & Elster, C. 2010, Metrologia, 47, 317 [Google Scholar]
Appendix A: MC calibration stage
The calibration stage, performed for each run, calibrates Nc and 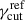 , to obtain a trial-averaged optical polarization fraction,
, to obtain a trial-averaged optical polarization fraction, 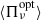 , within [0.4 − 0.5]%, and a trial-averaged value of
, within [0.4 − 0.5]%, and a trial-averaged value of 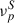 within=[0.8 − 1.2]×1017 Hz. As a reference value for the optical frequency, we use the value of 5 × 1014 Hz. The calibration stage proceeds as follows:
within=[0.8 − 1.2]×1017 Hz. As a reference value for the optical frequency, we use the value of 5 × 1014 Hz. The calibration stage proceeds as follows:
-
Initially, we set Nc = 1000, and we set
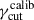 by a numerical sampling. In detail, we define a range of 100
by a numerical sampling. In detail, we define a range of 100 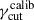 values, evenly spaced in the logarithm, in the range [10, 108], and for each value we estimate the value of νpS, according to the third of Eq.6, plugging the expectation values of
values, evenly spaced in the logarithm, in the range [10, 108], and for each value we estimate the value of νpS, according to the third of Eq.6, plugging the expectation values of 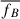 ,
, 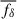 , and
, and 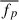 . The value of
. The value of 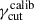 resulting in the best match to νpS = 1 × 1017 Hz is chosen.
resulting in the best match to νpS = 1 × 1017 Hz is chosen. -
A first 10-trial run is performed with the value of
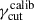 obtained at the previous step. The resulting trials-averaged values of
obtained at the previous step. The resulting trials-averaged values of 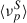 and the ⟨Πνopt⟩ are tested against the reference values, within a relative tolerance of 0.02. If the difference exceeds the tolerance, the previous step is repeated updating the value of Nc according to equation 11, and the value of
and the ⟨Πνopt⟩ are tested against the reference values, within a relative tolerance of 0.02. If the difference exceeds the tolerance, the previous step is repeated updating the value of Nc according to equation 11, and the value of 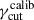 is updated compensating the relative offset on
is updated compensating the relative offset on 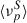 according to the proportionality established by the third of, Eq.6.
according to the proportionality established by the third of, Eq.6.
Appendix B: N cells versus N eff
We investigate the dependence of 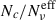 for different values of q. In Figure B.1 we show the MC trends for the effective flux-averaged,
for different values of q. In Figure B.1 we show the MC trends for the effective flux-averaged, 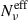 , at the reference frequencies used for the millimiter (2 × 1011 Hz), optical (5 × 1014 Hz), and X-ray (1 × 1018 Hz) frequencies. The dependence of
, at the reference frequencies used for the millimiter (2 × 1011 Hz), optical (5 × 1014 Hz), and X-ray (1 × 1018 Hz) frequencies. The dependence of  for difference values of q is reported in B.2, where the top panels refer to the full PL MC parameter space, and the bottom panels to the best sample parameter space. We notice how the number of Nc exceeds by at least a factor of 10 the value of
for difference values of q is reported in B.2, where the top panels refer to the full PL MC parameter space, and the bottom panels to the best sample parameter space. We notice how the number of Nc exceeds by at least a factor of 10 the value of 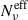 . The upper value of
. The upper value of 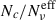 reaches up to a few thousands, for the X-ray (ν = 1018 Hz) frequency, and decrease to a few hundreds for the optical frequency (ν = 5 × 1014 Hz), and up to a few tens for millimiter frequency (ν = 2 × 101 Hz). The effect is larger for steeper values of q, meaning that a larger dispersion on the cell size amplifies the difference between Nc and
reaches up to a few thousands, for the X-ray (ν = 1018 Hz) frequency, and decrease to a few hundreds for the optical frequency (ν = 5 × 1014 Hz), and up to a few tens for millimiter frequency (ν = 2 × 101 Hz). The effect is larger for steeper values of q, meaning that a larger dispersion on the cell size amplifies the difference between Nc and 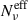 , due to the higher impact on the flux-weighted average effective number
, due to the higher impact on the flux-weighted average effective number 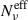 .
.
 |
Fig. B.1. The trend of the effective flux-averaged, |
 |
Fig. B.2. The cumulative distribution function (CDF) for the ratio of the total number of cells, Nc, to the value of the effective flux-averaged, |
All Tables
All Figures
 |
Fig. 1. Left panels: The S SED (row a), and the corresponding fractional polarization (row b) as a function of the frequency, for a power-law cutoff EED, γcut = 5 × 104, and p = [1.5, 2.0, 2.5]. The solid lines in the row b panel mark the Πνord evaluated using Eq. (1), the circles mark the δ approximation from Eq. (9) using |
| In the text | |
 |
Fig. 2. Different colors identifying the corresponding νp bins, which are the same for all the panels. Top panels: Left column: case of identical cells (configuration ES1 in Table 1). Middle column: case of configuration ES2 in Table 1, i.e. using fγcut = log-uniform. Right column: panel, case of configuration ES3, same as ES2 but adding a flat PDF, for p : fp ∼ 𝒰[1.8, 2.8]. All the trends are reported versus ν/νp. Solid lines mark the MC 0.5 quantiles and shaded areas mark the 1-σ quantiles dispersion, for the MC trials. Row a: the trend of the ratio of ⟨Πν⟩. Row b: same as for Row 1, but for trials-averaged trends for ⟨Πν⟩/⟨Πνord⟩. Row c: trials-averaged trends for Nν (dashed lines) and |
| In the text | |
 |
Fig. 3. Summary of the polarization slope trends for the PL-distributed parameter space reported in Table 2. Each subpanel refers to the three different values of q = [0, −1.0, −1.5], as reported in the subpanel title. Top panels: Low-energy (al, left panels) and high-energy (ah, right panels) polarization slopes as a function of the dispersion in the electron energy distribution index, Δp. Middle panels: al and ah as a function of the minimum cell size ratio, rmin. Bottom panels: al and ah as a function of the minimum cutoff ratio, |
| In the text | |
 |
Fig. 4. Left panel: The limiting envelope, found by RoboPol (Angelakis et al. 2016), for a large sample of γ-ray-loud blazars between νpS and both the average fractional optical polarization and its dispersion. Right panel: The Πν trend observed in by IXPE for the HPS Mrk 501, Mrk 421, PKS2155-304, 1ES0229+200, and 1ES1959+650 collected from recent IXPE multiwavelength campaigns (Liodakis et al. 2022; Di Gesu et al. 2023; Kouch et al. 2024; Middei et al. 2023). |
| In the text | |
 |
Fig. 5. Summary of polarization slope trends for the PL-distributed parameter space reported in Table 2, for the HSP objects, selecting MC runs with (10 × 15 Hz ≤ νpS ≤ 10 × 18 Hz). Top panels: Low-energy (amm − o, left panels) and high-energy (ao − X, right panels) polarization slopes as a function of the dispersion in the electron energy distribution index, Δp. Middle panels: al and ah as a function of the minimum cell size ratio, rmin. Bottom panels: al and ah as a function of the minimum cutoff ratio, |
| In the text | |
 |
Fig. 6. Trends of the KS test p value for the Πopt-versus-νpS limiting envelope, for the PL-distributed parameter space reported in Table 2. We report the KS trends as a function of Δp (top panels), rmin (middle panels), and |
| In the text | |
 |
Fig. 7. Trial-averaged trends for Nνeff and for the polarization factor, κνeff, for the PL scenario with fpc = 𝒰[1.5, 2.5], q = −1.0, rmin = 0.1, and fγcut = log-uniform. The different values of |
| In the text | |
 |
Fig. 8. MC Πopt-versus-νpS trend, compared to the RoboPol observed one, for the same MC run configuration as reported in Figure 7. The panels from top to bottom show the trend for increasing values of |
| In the text | |
 |
Fig. 9. Best runs for fγcut = uniform (top panels), fγcut = log-uniform (middle panels), and fγcut = linear (bottom panels). The left panels show the Πopt-versus-νpS limiting envelopes for both the MC simulations and the observed RoboPol data, the center panels show the trends of the MC-averaged dispersion of the MC optical EVPA angle vs νpS, and in the right panels, the IXPE HPS observed trends compared to the MC results extracted from the same runs used for the RoboPol panels. |
| In the text | |
 |
Fig. 10. Πν trends for the top-ranked MC runs tested against the observed data of Mrk 421 for the case of fγcut = uniform (top panel), fγcut = log-uniform (middle panel), and fγcut = linear (bottom panel). |
| In the text | |
 |
Fig. 11. Statistical outcome of the PL-distributed MC parameter space selection. The Δp-versus- |
| In the text | |
 |
Fig. B.1. The trend of the effective flux-averaged, |
| In the text | |
 |
Fig. B.2. The cumulative distribution function (CDF) for the ratio of the total number of cells, Nc, to the value of the effective flux-averaged, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



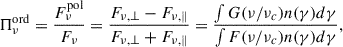
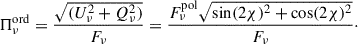
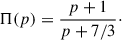
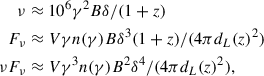
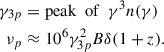
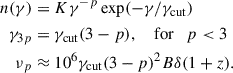
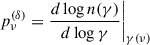
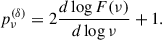
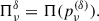
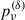
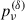
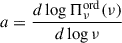
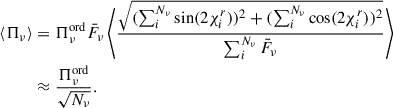
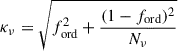
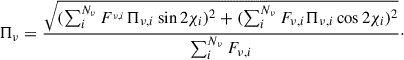
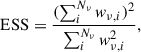
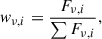
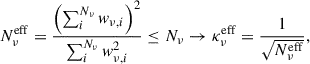
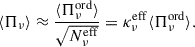
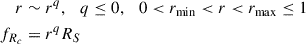
![$$ \begin{aligned} \begin{aligned} f_{\delta _c}&= \mathcal{U} [\delta _{\rm min},\delta _{\rm max}],\ \mathrm {or}\quad f_{\delta _c} =\delta _0\\ f_{B_c}&= \mathcal{U} {[B_{\rm min}},B_{\rm max}],\ \mathrm{or} \quad f_{B_c} =B_0. \end{aligned} \end{aligned} $$](/articles/aa/full_html/2025/12/aa56802-25/aa56802-25-eq34.gif)
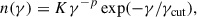
![$$ \begin{aligned} f_{p_c} = \mathcal{U} [p_0,p_0+\Delta p], \mathrm{\ or\ } f_{p_c} =p_0. \end{aligned} $$](/articles/aa/full_html/2025/12/aa56802-25/aa56802-25-eq36.gif)
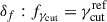
![$$ \begin{aligned} \begin{aligned} {uniform}:\ {f_{\gamma _{\rm cut}}}&=\mathcal{U} [\gamma _{\rm cut}^\mathrm{LB},{\gamma _{\mathrm{cut}}^\mathrm{ref}}]\\ {log-uniform}:\ {f_{\gamma _{\rm cut}}}&=\mathcal{U} [\log (\gamma _{\rm cut}^\mathrm{LB}),\log ({\gamma _{\mathrm{cut}}^\mathrm{ref}})] \\&=\frac{1}{\gamma _{\rm cut}\log ({\gamma _{\mathrm{cut}}^\mathrm{ref}}/\gamma _{\rm cut}^\mathrm{LB})}\propto \gamma _{\rm cut}^{-1} \end{aligned} \end{aligned} $$](/articles/aa/full_html/2025/12/aa56802-25/aa56802-25-eq38.gif)