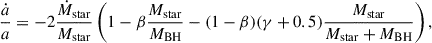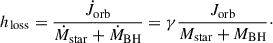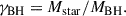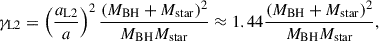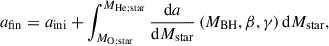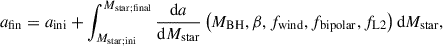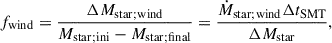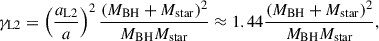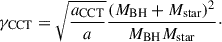Comfort zones of stars: A limit on orbital tightening via stable mass transfer shapes the properties of binary black hole mergers

Jakub Klencki; Philipp Podsiadlowski; Norbert Langer; Aleksandra Olejak; Stephen Justham; Alejandro Vigna-Gómez; Selma E. de Mink

doi:10.1051/0004-6361/202555500

Home

All issues

Volume 706 (February 2026)

A&A, 706 (2026) A296

Full HTML

Open Access

Issue		A&A Volume 706, February 2026


Article Number		A296
Number of page(s)		27
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/202555500
Published online		18 February 2026

A&A, 706, A296 (2026)

Comfort zones of stars: A limit on orbital tightening via stable mass transfer shapes the properties of binary black hole mergers

Jakub Klencki¹^,2^★, Philipp Podsiadlowski³^,4, Norbert Langer⁵^,6, Aleksandra Olejak¹, Stephen Justham¹, Alejandro Vigna-Gómez¹ and Selma E. de Mink¹

¹ Max Planck Institute for Astrophysics Karl-Schwarzschild-Strasse 1 85748 Garching, Germany
² European Southern Observatory Karl-Schwarzschild-Strasse 2 85748 Garching bei München, Germany
³ London Centre for Stellar Astrophysics Vauxhall London, UK
⁴ University of Oxford St Edmund Hall Oxford OX1 4AR, UK
⁵ Argelander Institut für Astronomie Auf dem Hügel 71 53121 Bonn, Germany
⁶ Max-Planck-Institut für Radioastronomie Auf dem Hügel 69 53121 Bonn, Germany

^★ Corresponding author: This email address is being protected from spambots. You need JavaScript enabled to view it.

Received: 13 May 2025
Accepted: 26 September 2025

Abstract

Mass transfer in binary systems is the key process in the formation of various classes of objects, including merging binary black holes (BBHs) and neutron stars. The orbital evolution that occurs during mass transfer depends on how much mass is accreted and how much angular momentum is lost – two of the main uncertainties in binary evolution. This poses a challenge for obtaining reliable predictions from binary channels. Here, we demonstrate that despite these unknowns, a fundamental limit exists to how close binary systems can become via stable mass transfer (SMT) that is robust against uncertainties in orbital evolution. Based on detailed evolutionary models of interacting systems with a BH accretor and a massive-star companion, we show that the post-interaction orbit is always wider than ∼10 R_⊙, even when extreme shrinkage due to L2 outflows is assumed. Systems evolving toward tighter orbits become dynamically unstable and result in stellar mergers. This separation limit has direct implications for the properties of BBH mergers, including long delay times (≳1 Gyr) and an absence of high BH spins from the tidal spin-up of helium stars. At high metallicity, the SMT channel may be severely quenched due to Wolf-Rayet winds. We predict BBH mergers from ∼10 M_⊙ to 90 M_⊙, with case A mass transfer dominating above 40 M_⊙. The reason for the separation limit lies in the stellar structure, not in binary physics. If the orbit becomes too narrow during mass transfer, a dynamical instability is triggered by a rapid expansion of the remaining donor envelope due to its near-flat entropy profile. The closest separations can be achieved from core-He burning (∼8−15 R_⊙) and Main Sequence donors (∼15−30 R_⊙), while Hertzsprung gap donors lead to wider orbits (≳30−50 R_⊙) and non-merging BBHs. These outcomes and mass transfer stability are determined by the entropy structures, which are governed by internal composition profiles. Consequently, the formation of BBH mergers and other compact binaries via SMT is a sensitive probe of chemical mixing in stars, and it may help address open questions of stellar astrophysics, such as the blue supergiant problem. Finally, we propose a new simplified treatment of mass transfer stability that more accurately reproduces detailed results and remains flexible under varying assumptions for orbital evolution.

Key words: gravitational waves / binaries: general / stars: black holes / stars: evolution / stars: interiors / stars: massive

© The Authors 2026

Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open access funding provided by Max Planck Society.

1. Introduction

We are at the brink of the data-driven era of gravitational-wave (GW) astrophysics. With the three observing runs concluded and the fourth run O4 currently underway, the LIGO-Virgo-Kagra collaboration has reported detections of about 100 compact binary coalescences, most of which are binary black hole (BBH) mergers (Abbott et al. 2021, 2023). In the next few years, the number of GW detections will increase to thousands and eventually many millions with the increasing sensitivity of the current detectors (O4-O5, AdV+ Abbott et al. 2020) and the next-generation instruments, such as the Einstein Telescope (Maggiore et al. 2020) and Cosmic Explorer (Reitze et al. 2019). With millions of compact binary coalescences detected every year, merging pairs of black holes (BH) and neutron stars (NSs) will arguably become the best measured state in the evolution of massive stars across the Universe.

Gravitational-wave astronomy has an enormous potential for probing massive-star formation and evolution across all environments and redshifts. The key to unlocking this treasure chest are population models exploring formation scenarios for GW sources that allow for a confrontation between theory and observation. However, this undertaking is currently hindered by the “Interpretation Challenge”: due to severe uncertainties and multiple free parameters in the formation scenarios, we are unable to robustly interpret the observed population and link the GW sources with their progenitor stars (Broekgaarden et al. 2022a; Mandel & Broekgaarden 2022; Chruślińska 2024). The task is not made easier by the fact that multiple diverse formation channels may simultaneously be at play (Zevin et al. 2021), such as isolated evolution of stellar multiples (Belczynski et al. 2016; Tauris et al. 2017; Stevenson et al. 2017; Antonini et al. 2017; Kruckow et al. 2018; Mapelli & Giacobbo 2018; Belczynski et al. 2020; Vynatheya & Hamers 2022), dynamical evolution in dense stellar clusters (Rodriguez et al. 2016; Askar et al. 2017; Samsing 2018; Rodriguez et al. 2019; Mapelli et al. 2021, 2022), evolution in gas-rich environments such as active galactic nucleus disks (Antonini & Rasio 2016; Stone et al. 2017; McKernan et al. 2018; Samsing et al. 2022), or channels involving the existence of primordial BHs formed shortly after the Big Bang (Sasaki et al. 2018; Papanikolaou et al. 2021).

Fig. 1.

Schematic comparison of orbital shrinkage via common envelope and stable mass transfer in a BBH merger progenitor (here a binary with a 35 M_⊙ stellar donor and 10 M_⊙ BH accretor), based on a simple analytical model (Sect. 2.3) rather than a detailed evolutionary calculation. The SMT lines follow assumptions typically used in population synthesis of GW sources, naively suggesting that mass transfer with enhanced AM loss (blue) can produce separation as small as CE evolution. In this paper, we use detailed binary evolution calculations to show why this is not the case (Fig. 3).

All the formation scenarios necessarily need a way to bring two BHs or NSs close together such that they spiral inward due to GW emission and merge within the age of the Universe. In isolated binaries, with the exception of chemically homogeneous evolution (Mandel & de Mink 2016; de Mink & Mandel 2016; Marchant et al. 2016; Riley et al. 2021), this is achieved through mass transfer interactions between the binary components. Classically, the key stage in the binary channel has been a phase of dynamically unstable mass transfer, leading to common envelope (CE) inspiral (Tutukov & Yungelson 1993; van den Heuvel 1994; Tauris & van den Heuvel 2006). This view emerged quite naturally. The dramatic shrinkage of the orbit during a CE phase is thought to produce a very short period binary (Ivanova et al. 2013, 2020) that comfortably falls into the separation range required for GW-induced mergers (Fig. 1). In comparison, stable mass transfer (SMT) evolution can lead to all sorts of different outcomes, from moderate orbital shrinkage to orbital expansion and wide post-interaction systems (Tauris & van den Heuvel 2023, and references therein).

In recent years, the CE-focused picture has been undergoing a revision, driven by the emergence of systematic studies with detailed stellar and binary evolutionary models dedicated to the formation of GW sources (Mennekens & Vanbeveren 2014; Kruckow et al. 2016; Eldridge & Stanway 2016; Fragos et al. 2019; Klencki et al. 2020, 2021; Marchant et al. 2021; García et al. 2021). The argument is that the survival of a CE event from a massive BH progenitor may be a much rarer and fine-tuned event than previously thought, putting in question the efficiency of the CE channel for the formation of massive BBH mergers. At the same time, it has been pointed out that even though the orbital shrinkage from SMT evolution is not as substantial as during a CE phace, it can also produce sufficiently short-period orbits for BBH mergers if the interaction begins in a relatively narrow orbit to begin with (see Fig. 1 van den Heuvel et al. 2017; Neijssel et al. 2019; Marchant et al. 2021; Gallegos-Garcia et al. 2021; Picco et al. 2024). This realization came in part following arguments that mass transfer stability increases with the stellar mass (Ge et al. 2015, 2020; Pavlovskii et al. 2017; Olejak et al. 2021). The SMT channel for BBH mergers was established, with the SMT phase in question taking place after the first BH has already been formed, at the BH+Star binary stage.

A key question for any formation scenario is what are the orbital separations or periods of the double compact objects (DCOs) it predicts. This is because the size of the orbit is the primary factor determining the time it takes for a DCO to merge (t_merge ∝ a⁴), and it dictates whether GW sources preferably trace star-forming galaxies (t_merge ≲ 100 Myr) or whether they are remnants of massive stars formed in high-redshift environments (t_merge ≳ 1 − 10 Gyr; Chruslinska et al. 2019; Chruslinska & Nelemans 2019; van Son et al. 2022a). The orbital separation at the BH–Wolf-Rayet stage (i.e., just prior to the formation of the second BH) has a strong effect on the tidal torque (∝a⁻⁶ Zahn 2008) and therefore the amount of angular momentum (AM) in the Wolf-Rayet star at core-collapse (Ma & Fuller 2023). This directly affects the amount of AM in the BH progenitor at the point of core-collapse, which likely determines the BH spin. Tidally locked BH–Wolf-Rayet systems with orbital periods as short as ≲0.5 − 1 day may be required to explain the observed non-zero effective spins of BBH mergers as products of binary evolution (Detmers et al. 2008; Kushnir et al. 2016; Zaldarriaga et al. 2018; Belczynski et al. 2020; Bavera et al. 2020, 2021; Ma & Fuller 2023).

Despite their importance, the orbital separations of massive DCO systems are difficult to predict in binary channels. In the case of CE evolution, 3D hydrodynamic simulations cannot yet resolve the innermost region of the envelope and model the final stages of the inspiral to find the resulting orbit (e.g., Moreno et al. 2022, although see Law-Smith et al. 2020). Following CE ejection, the orbit may further be altered due to an interaction with the substantial amount of circumbinary material that has not become fully unbound (possibly of a disk-like structure Wei et al. 2023; Gagnier & Pejcha 2023) or an additional mass-transfer phase (Vigna-Gómez et al. 2022; Hirai & Mandel 2022). With no unambiguous massive post-CE systems discovered to date (Kruckow et al. 2021), there are few observational constraints to guide the models. Most GW-source population models predict post-CE separations according to the energy budget criteria (van den Heuvel 1976; Webbink 1984; Livio & Soker 1988), with no lower limit other than the crude requirement that the naked He core must fit into its Roche lobe in the post-CE orbit.

In the case of SMT evolution, the main source of uncertainty for orbital shrinkage is the assumption of how much orbital AM is lost with the non-accreted matter (the more AM that is lost, the more the separation decreases). The key mass transfer phase takes place at a high-mass X-ray binary stage. The mass transfer rates are typically highly super-Eddington (King & Ritter 1999; Podsiadlowski & Rappaport 2000; Podsiadlowski et al. 2002), leading to supercritical accretion disks and, depending on the viewing angle, the appearance of an ultraluminous X-ray source (ULX; Shakura & Sunyaev 1973; King et al. 2000; Poutanen et al. 2007; Lasota et al. 2016). Most of the transferred mass likely never reaches the BH but is instead ejected from the disk in the form of jets and bipolar outflows or disk winds or as a slow ejecta concentrated in the equatorial plane (Lipunova 1999; McKinney et al. 2014; Sądowski et al. 2014; Sądowski & Narayan 2015; Sądowski & Narayan 2016). All of those components have been observed in the Galactic X-ray system SS433, the prototype for these so-called microquasars (Fabrika 2004; Cherepashchuk et al. 2005; Begelman et al. 2006; Blundell et al. 2008; Middleton et al. 2021). Indirectly, they have been proposed to give rise to the observed diversity in the X-ray spectra of ULXs as a result of the viewing angle effect (Kaaret et al. 2017; King et al. 2023). Whereas this general pictures holds fairly well qualitatively, we know very little about how much mass and AM is lost with each of the ejecta. Most GW-source population studies assume that all the non-accreted matter is lost through a bipolar outflow or fast wind launched close to the BH, i.e., the isotropic reemission model. This can be viewed as a lower limit on the AM loss¹. However, having a fraction of the mass leave the system as an outflow launched far away from the BH (e.g., through the L2 or L3 outer Lagrangian point) would significantly enhance the loss of AM and the degree of orbital shrinkage (Lu et al. 2023). We illustrate this in Fig. 1 as a comparison between the yellow and blue lines². The blue model ejects 25% of the non-accreted mass through L2 outflows. As a result, it produces a BBH merger with a delay time that is ∼100 times shorter and comparable to the fast-merging BBH systems that would otherwise originate only from CE evolution. The importance of AM loss for the SMT evolution channel has been emphasized and discussed in several recent studies (van Son et al. 2022b; Willcox et al. 2023; Picco et al. 2024; Olejak et al. 2024; Gallegos-Garcia et al. 2024).

The idealized example in Fig. 1, however, does not model the donor star and its reaction to mass loss, which is the necessary step to gauge how much mass is transferred and on what timescale and whether the interaction remains stable. This can be achieved with detailed stellar models of BH+Star systems (e.g., Podsiadlowski et al. 2003; Detmers et al. 2008; Marchant et al. 2021; Gallegos-Garcia et al. 2021; Klencki et al. 2021, 2022; Fragos et al. 2023; Misra et al. 2024). Although numerically more expensive than rapid binary evolution simulations, binary models involving a 1D stellar structure are crucial for realistic predictions from binary channels as, at the moment, these detailed results are not at all well reproduced by rapid GW-source population models (Marchant et al. 2021; Gallegos-Garcia et al. 2021; Klencki et al. 2022).

Previous studies of the SMT channel using detailed binary evolution models of BH+Star systems explored only a limited number of cases and did not investigate the impact of the AM budget uncertainty on the properties of BBH mergers (Marchant et al. 2021; Gallegos-Garcia et al. 2021). Here, we fill this gap by modeling BH+Star systems with the 1D stellar evolution code MESA (Sect. 2.4) in the entire parameter space of masses, periods, and mass ratios in which the SMT channel operates at low metallicity. We explore different assumptions on the orbital AM loss and the resulting shrinkage during mass transfer.

We find that there is a fundamental limit to how tight binary systems can become via stable mass transfer that is robust against uncertainties in binary physics (contrary to expectations outlined in Fig. 1; Sects. 3.1 and 3.2). This orbital separation limit has direct implications for the properties of BBH mergers, in particular delay times and spins (Sects. 3.4 and 4.4). The reason for the limit lies in the stellar structure of the donor star (as opposed to in binary processes), which dictates when the mass transfer becomes unstable (Sects. 3.3 and 4.1). We discuss which types of donor stars can lead to BBH mergers (Sect. 4.2) and how GW astronomy could yield clues into stellar interiors (Sect. 4.3). The results from our detailed models can be applied in rapid binary codes (Sect. 4.5). We conclude our work with a summary in Sect. 5.

2. Methods

2.1. Overview of model grids

We compute detailed binary evolution models of BH+O-star systems, i.e., binaries comprised of a BH and a massive hydrogen-rich star. We calculate two types of model grids: (a) given the mass of the first-formed BH (M_BH; 1), grids covering different initial periods and mass ratios of BH+O-star systems; (b) given the mass and radius of a donor star, grids exploring different mass ratios to determine the critical mass ratio for SMT of the donor. For the first type of grids, we explored BH masses M_BH; 1 = 4, 7, 10, 13, 16, 20, 24, 28, 32, 36, and 40 M_⊙. For each M_BH; 1, we considered periods and mass ratios from a wide enough range to capture the entire parameter space for the formation of BBH mergers through SMT. As the range is not known a priori, for the first few M_BH; 1 masses we evolved BH+O-star systems for all the initial periods that lead to mass transfer (from ∼1 to 1000 days). Most of the grids were computed at metallicity Z = 0.1 Z_⊙ = 0.0017. In addition, for M_BH; 1 = 10 M_⊙ we explored several different metallicities from Z = 0.4 Z_⊙ to Z = 0.01 Z_⊙. The BH+O-star grids are summarized in Figs. D.1 and D.2. For the second type of grids, we explored donor masses from 10 to 100 M_⊙ and two assumptions on the efficiency of semiconvection: α_sc = 33 (the same as in the BH+O-star grids) and α_SC = 0.01. The choice of semiconvection affects the evolutionary stage of donors (see Sect. 2.4), which has an impact on the mass transfer evolution and BBH merger formation (Sect. 3.3). In addition, for both types of grids we considered two variations (three for M_BH; 1 = 10 M_⊙) on how much AM is carried away with the non-accreted matter during mass transfer, introduced in Sect. 2.2. To better understand the results of these detailed binary models and compare with rapid binary-evolution methods, in Sect. 2.3 we introduce a semi-analytical model to estimate the outcome of mass transfer evolution. Our stellar evolution computations terminate at central-carbon depletion (Sect. 2.4). In Sect. 2.5 we detail our assumptions on further evolution until the core-collapse and the formation of the secondary BH.

2.2. Orbital evolution during stable mass transfer

Through considerations of the orbital AM in an interacting BH+Star system with a circular orbit³, one can express the rate of the separation change as

$\begin{matrix} \frac{\dot{a}}{a} = - 2 \frac{{\dot{M}}_{star}}{M_{star}} (1 - β \frac{M_{star}}{M_{BH}} - (1 - β) (γ + 0.5) \frac{M_{star}}{M_{star} + M_{BH}}), \end{matrix}$ $\begin{aligned} \frac{\dot{a}}{a} = -2 \frac{\dot{M}_{\rm star}}{M_{\rm star}} \left(1-\beta \frac{M_{\rm star}}{M_{\rm BH}} - (1-\beta )(\gamma +0.5) \frac{M_{\rm star}}{M_{\rm star}+M_{\rm BH}}\right), \end{aligned}$ (1)

where a is the semi-major axis (separation), M_star is mass of the mass-losing star (the donor), M_BH is mass of the accreting BH (the accretor), β is the fraction of the transferred mass that is accreted, and γ parametrizes the specific AM of the non-accreted matter, h_loss, in units of the orbital AM J_orb:

$\begin{matrix} h_{loss} = \frac{{\dot{J}}_{orb}}{{\dot{M}}_{star} + {\dot{M}}_{BH}} = γ \frac{J_{orb}}{M_{star} + M_{BH}} \cdot \end{matrix}$ $\begin{aligned} h_{\rm loss} = \frac{\dot{J}_{\rm orb}}{\dot{M}_{\rm star}+\dot{M}_{\rm BH}} = \gamma \frac{J_{\rm orb}}{M_{\rm star}+M_{\rm BH}}\cdot \end{aligned}$ (2)

For a circular orbit, 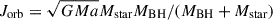$J_{orb} = \sqrt{GMa} M_{star} M_{BH} / (M_{BH} + M_{star})$ $J_{\mathrm{orb}} = \sqrt{GMa} M_{\mathrm{star}} M_{\mathrm{BH}}/(M_{\mathrm{BH}}+M_{\mathrm{star}})$ . The value of γ depends on how the non-accreted matter is lost from the system. The assumption that it is ejected from the close proximity of the BH, carrying its orbital AM, gives

$\begin{matrix} γ_{BH} = M_{star} / M_{BH} . \end{matrix}$ $\begin{aligned} \gamma _{\rm BH} = M_{\rm star}/M_{\rm BH}. \end{aligned}$ (3)

The assumption that the mass is lost through the outer Lagrangian point L2 can be approximated with

$\begin{matrix} γ_{L 2} = {(\frac{a_{L 2}}{a})}^{2} \frac{{(M_{BH} + M_{star})}^{2}}{M_{BH} M_{star}} \approx 1.44 \frac{{(M_{BH} + M_{star})}^{2}}{M_{BH} M_{star}}, \end{matrix}$ $\begin{aligned} \gamma _{\rm L2} = \left(\frac{a_{\rm L2}}{a}\right)^2 \frac{(M_{\rm BH}+M_{\rm star})^2}{M_{\rm BH}M_{\rm star}} \approx 1.44 \frac{(M_{\rm BH}+M_{\rm star})^2}{M_{\rm BH}M_{\rm star}}, \end{aligned}$ (4)

where a_L2 is the distance from the L2 to the center of mass. Its value slowly depends on the mass ratio and can be approximated as a_L2 ≈ 1.2a (Pribulla 1998). The L2 point is located on the outer side of the BH for mass ratios M_star > M_BH (the usual case throughout the paper), with the L3 point then located on the outer side of the donor. For mass ratios M_star < M_BH, the location of the L2 and L3 points becomes swapped. Here, for simplicity, we only consider the mass loss through L2, regardless of the mass ratio. This is justified because, as we show, in BBH merger progenitors the mass ratio M_star/M_BH never becomes lower than ∼1/3, in which case γ_L2 does not deviate from γ_L3 by more than 25%.

Finally, mass lost with the wind of the donor corresponds to γ_star = M_BH/M_star. Mass loss with the specific AM of the entire orbit would correspond to γ_orbit = 1.0. Equation (1) only considers the AM associated with the orbit, neglecting the internal AM from the spin of the star or the BH because typically J_spin; BH ≪ J_spin; star ≪ J_orb⁴. The J_spin; star term is accounted for in our detailed binary models (Sect. 2.4).

As the orbit is expected to stay (nearly) circular during an SMT phase, the loss of orbital AM directly affects the orbital separation (J_orb² ∝ a) and the larger the γ, the more the orbit shrinks or the less it expands. For BH-star systems with M_star > M_BH we have γ_star < γ_orbit < γ_BH < γ_L2. This is why mass loss through stellar winds (γ_star) expands the orbit, non-conservative mass transfer with mass loss from the proximity of the BH (γ_BH) shrinks the orbit⁵, and any L2 outflows (γ_L2) enhance the orbital shrinkage even more.

Throughout the paper, we consider the case where γ can be divided into three components:

$\begin{matrix} γ = f_{wind} γ_{star} + f_{bipolar} γ_{BH} + f_{L 2} γ_{L 2}, \end{matrix}$ $\begin{aligned} \gamma = f_{\rm wind} \gamma _{\rm star} + f_{\rm bipolar} \gamma _{\rm BH} + f_{\rm L2} \gamma _{\rm L2}, \end{aligned}$ (5)

where f_wind + f_bipolar + f_L2 = 1. In this case a fraction f_bipolar of the non-accreted mass is ejected from near the BH (as a bipolar outflow/jet or via fast disk wind), fraction f_L2 is lost from near the L2 point, and fraction f_wind is lost from the system with the wind of the donor star. Most of the time, we have f_wind ≪ 1 (i.e., the wind is negligible). We explore three scenarios:

Fiducial treatment: γ ≈ γ_BH. Here, the mass is ejected from the proximity of the BH with no L2 outflows.
Enhanced orbital shrinkage: γ ≈ 0.8γ_BH + 0.2γ_L2. In this case, ∼20% of the mass is ejected through L2.
Extreme orbital shrinkage: γ ≈ 0.45γ_BH + 0.55γ_L2. For this case, ∼55% of the mass is ejected through L2.

The exact fractions of mass lost through L2 in the medium or high AM loss models depend on the mass ratio of the binary, as described in detail in Appendix C.

2.3. Semi-analytical model for a mass transfer phase

To better understand the results obtained in detailed binary models, we develop a semi-analytical model to calculate the outcome of an SMT phase. This method is similar to the way in which the SMT is treated in rapid binary-evolution codes widely used for GW-source population synthesis. The main two differences with respect to MESA binary models are: (a) mass transfer stability, which in MESA is obtained self-consistently for each individual binary while rapid codes rely on prescriptions, and (b) the effect of mass transfer on the donor’s core mass (Schürmann et al. 2024; Shikauchi et al. 2025).

We consider a binary comprised of a BH and a massive hydrogen-rich star (M_O; Star), which we refer to as a BH+O-star system. The star initiates an SMT phase when the orbital separation is a_ini. For simplicity, we assume circular orbits. The product of this interaction in a binary with a BH and a massive He-rich star (M_He; Star): a BH+He-star system. The final separation is

$\begin{matrix} a_{fin} = a_{ini} + \int_{M_{O ; star}}^{M_{He ; star}} \frac{d a}{d M_{star}} (M_{BH}, β, γ) d M_{star}, \end{matrix}$ $\begin{aligned} a_{\rm fin} = a_{\rm ini} + \int _{M_{\rm O;star}}^{M_{\rm He;star}} \frac{\mathrm{d}a}{\mathrm{d}M_{\rm star}} \left(M_{\rm BH}, \beta , \gamma \right) \mathrm{d}M_{\rm star}, \end{aligned}$ (6)

where the expression for da/dM_star can be found by combining Eqs. (1) and (5). To compute the integral in Eq. (6), one needs to know how much mass was lost from the star (M_He; star), whether via wind or mass transfer, as well as what were the accretion efficiency (β) and the specific AM of the non-accreted matter (γ). Briefly, to obtain M_He; star at the end of the mass transfer, we assume that the donor has lost 90% of its H-rich envelope. After the SMT phase, the He-star will continue to lose mass via winds, which we estimate knowing its approximate luminosity and the remaining lifetime (typically ∼core-He burning) based on single stellar tracks. We describe our set of assumptions and methodology further in Appendix A.

2.4. Detailed MESA binary models

We employed the MESA stellar evolution code (Paxton et al. 2011, 2013, 2015, 2018, 2019; Jermyn et al. 2023)⁶. We modeled the evolution of BH+O-star systems and begin our simulations at the zero-age MS (ZAMS) of the stellar component. We thus assumed that the companion evolves as a normal, single star (in reality it had most likely been a mass gainer in a past mass transfer prior the first BH formation). The evolution was followed throughout the entire mass transfer phase (or until the mass transfer becomes unstable) and later until the central carbon depletion.

We applied the mixing-length theory (Böhm-Vitense 1958) with mixing length α = 1.5, the Ledoux criterion for convection, and semiconvective mixing with an efficiency of α_SC = 33 (Schootemeijer et al. 2019)⁷. We accounted for convective core-overshooting during H- and He-burning with a step overshooting length of σ_ov = 0.33 in the fiducial model (as calibrated by Brott et al. 2011). In addition, in Sect. 3.3 we considered a variation with a severely reduced efficiency of semiconvection α_SC = 0.01. The choice of semiconvection affects whether the transition to the core-He burning phase occurs in the blue (high semiconvection) or in the red part of the HR diagram (low semiconvection; see Stothers & Chin 1992; Georgy et al. 2013; Schootemeijer et al. 2019; Klencki et al. 2020). The variation with α_SC = 0.01 allows us to explore a case in which blue supergiant donor stars are less evolved (pre-core He burning) compared to our default assumption of α_SC = 33. While it is convenient to vary α_SC to explore this effect, there are other uncertain factors that affect the radial expansion of massive stars (rotational-mixing, convective-boundary mixing, mass loss) and the transition from blue to red supergiants is an open problem of stellar astrophysics (see Sect. 4.3 and references therein). To help converge models approaching the Eddington limit, we applied a reduction of superadiabacity in radiation-dominated regions using the new implicit method from Jermyn et al. (2023)⁸. Stellar winds were modeled following the approach of Klencki et al. (2022), comprised of various recipes for H-rich stars (Nieuwenhuijzen & de Jager 1990; Vink et al. 2001) and He-rich stars (Nugis & Lamers 2000; Hainich et al. 2014; Tramper et al. 2016; Yoon 2017). In addition, based on Gräfener & Hamann (2008), we enhanced the mass loss rates for H-rich stars from Vink et al. (2001)⁹ for stars approaching the Eddington limit to account for the transition to optically thick winds (Vink et al. 2011; Bestenlehner et al. 2014; Sander et al. 2020, see also). We modeled rotationally induced mixing and internal angular-momentum transport via Taylor-Spruit dynamo, Eddington-Sweet circulation, secular shear instabilities, and the Goldreich-Schubert-Fricke instability, with a combined efficiency factor f_c = 1/30 (Heger et al. 2000; Brott et al. 2011). We included rotationally enhanced mass loss as in Langer (1998). Tidal interactions follow the synchronization timescale for radiative envelopes from Hurley et al. (2002). The mass transfer rate was calculated following the scheme by Marchant et al. (2021) and the accretion rate was Eddington-limitted. The scheme self-consistently accounts for L2 and L3 outflows when the size of the donor reaches the L2 or L3 equipotential. In practice, this happens only briefly during instances of very rapid mass transfer and the amount of mass lost via L2 or L3 this way is very small (≪1%). Here, we model the fraction of mass ejected through L2 (f_L2) as possibly being much higher, with f_L2 = 0.0, ∼0.2, or ∼0.55 (following the three AM loss models introduced in Sect. 2.2; see also Appendix C for exact f_L2 values). The higher f_L2 values account for the possibility of a substantial amount of mass and AM leaving the accretor’s Roche lobe in the form of slow and mostly equatorial outflows, rather than as fast bipolar disk winds or jets. This become especially important at the highly super-Eddington mass transfer rates of BH-OB systems (Ṁ/Ṁ_Edd ∼ 10⁴; e.g., Lu et al. 2023). Apart from L2 outflows, the rest of the non-accreted matter is ejected with the specific AM of the BH (γ_BH; Sect. 2.2). Mass lost in stellar winds is lost with the specific AM of the star (γ_star).

We assumed a maximum mass transfer rate Ṁ_max = 10^−0.5 M_⊙ yr⁻¹, above which the mass transfer is deemed to become unstable and to soon enter a CE phase. Although somewhat arbitrary, the choice of Ṁ_max does not strongly affect our results, as we discuss in Sect. 4.1. We let the MESA calculations continue above the Ṁ_max threshold and find that in most of the cases that surpass this critical rate, the value of Ṁ keeps increasing rapidly to ≳1 − 10 M_⊙ yr⁻¹, at which point the models crash. The physical justification for determining stability based on a threshold mass transfer rate is that once a certain Ṁ_th;crit is reached, the timescale of mass loss is shorter than the timescale needed to thermally re-adjust the surface layers and rebuild a stabilizing entropy gradient, which facilitates an even more rapid further increase in Ṁ that is found in 1D stellar models (Temmink et al. 2023). The value of Ṁ_th;crit varies across donors of different mass and radius, typically exceeding ≳0.1 M_⊙ yr⁻¹ for massive donors, which is ∼10 − 100 times larger than their thermal-timescale mass-transfer rate (see Fig. 4 in Temmink et al. 2023). A different stability criteria adopted in the literature is based on a critical relative rate of change A_dyn of the orbital separation or the mass transfer rate over a single orbital period P, i.e., unstable if max(|Ṁ/M|,|ȧ/a|)P > A_dyn, with A_dyn = 0.02 (Pavlovskii & Ivanova 2015; Pavlovskii et al. 2017) or A_dyn = 0.05 (Temmink et al. 2023). Our criteria of Ṁ_max = 10^−0.5 M_⊙ yr⁻¹ corresponds to A_dyn ranging from ∼0.0001 for P ≈ 1 day to ∼0.1 for P ≈ 1000 days, meaning that we may be optimistic in assessing stability in wide orbits (P ≳ 200 days). For systems assumed to enter a CE phase, we calculated the envelope binding energy of the donor and estimate the CE survival based on the energy budget formalism, assuming α_CE = 1.0 (similarly to Klencki et al. 2021).

2.5. From the end point of MESA to BBH mergers

To put the BH+He-star systems obtained in our binary models in the context of BBH mergers, we assume that the massive He-star always collapses to form a second BH. To illustrate how the final orbital separations relate to BBH delay times, we make a simplifying assumption that the secondary BH forms in direct collapse, with no natal kick or mass loss (whether in baryons or in neutrinos). The only exception is that we account for pair-instability induced mass loss for the most massive stars (carbon-oxygen cores M_CO > 38 M_⊙) using fits from Renzo et al. (2022), based on models by Farmer et al. (2019). This results in the most massive BHs of around ∼43 M_⊙ (but see Farag et al. 2022). The presence of non-zero kicks of BHs or mass loss at BH formation would affect the predicted merger times, potentially allowing for a small population of fast merging BBH even from relative wide but eccentric orbits (see our Appendix B, Vigna-Gómez 2025, and the Appendix in Marchant et al. 2016). To calculate the merger time of a DCO system we follow the analytical fit from Mandel (2021), based on Peters (1964).

2.6. Determining critical mass ratios and minimum orbital separations

Using the numerical MESA setup and mass transfer stability criteria described in Sect. 2.4, we determine critical mass ratios for donor stars with masses from 10 to 100 M_⊙. To this end, we first simulated a grid of 15 single-star evolutionary tracks from 10 to 100 M_⊙, at Z = 0.1 Z_⊙ metallicity (see Fig. D.3 for the HR diagram). For each stellar track, we consider the entire range of its radial expansion as the possible donor stars for mass transfer in binaries. Every 0.1 dex in radius of the single-star track (i.e., ∼20 − 25 times for each mass), we copy the exact stellar structure into a binary MESA model to examine its behavior as a donor. The companion is set to be a point mass and the initial orbit is set to be circular with a separation such that the copied star is about to fill its Roche lobe. We explore many different mass ratios M_donor/M_accretor, ranging from 1 to 12, with the goal of finding the critical mass ratio q_crit: the largest q for which the mass transfer remains stable. We did so in an iterative way: We began with a sparse grid of mass ratios with Δq = 2, found the largest q (lowest q) for which the mass transfer remains stable (becomes unstable), narrowed down the search to mass ratios between those two values, and decreased Δq. After three to four such iterations, we steadily converged to q_crit. We followed this procedure and employed three variations: a fiducial SMT model with γ = γ_BH, a model with enhanced AM loss due to L2 outflows (γ ≈ 0.8γ_BH + 0.2γ_L2), and a model with γ = γ_BH and low efficiency of semiconvection, α_SC = 0.01 (as opposed to α_SC = 33 in all the other grids). Ultimately, for each initial mass-radius of the donor, we determined q_crit with accuracy Δq ± 0.02 for the fiducial model and Δq ± 0.1 for the variations with L2 outflows and low efficiency of semiconvection. We computed about 30−40 models with different q values for each mass-radius pair, making it about 20 000 MESA binary models for both variations, with the results presented in Figs. 5 and 6.

Fig. 6.

Formation of BBH mergers is a probe of internal chemical mixing in stars and of the stellar structure. We plot the minimum BBH delay times from SMT evolution given the donor mass (at ZAMS) and radius (at RLOF) for two variations in the efficiency of semiconvective mixing in stars (α_semiconv.). Only cases with the BBH delay time below ≲13.7 Gyr (yellow-brown regions) are potential GW sources. The range of donors that may lead to BBH mergers is severely reduced in the variation with low efficiency of semiconvection (right panel) and it shows a preference for high-mass donors (≳40 M_⊙). This is because the chemical structure of donor stars determines the conditions for delayed-dynamical instability and therefore affects the critical mass ratios, the minimum post-SMT separations, and BBH delay times (Sect. 4.2). This is different from the assumptions on the orbital AM loss that only affects the q_crit (Fig. 5). The difference between stellar models in both panels is closely connected to the blue supergiant problem (Sect. 4.3). The thick blue line shows the transition from MS to post-MS donors. Several main types of donors are labeled (Hertzsprung gap, core-He burning, convective envelopes, He-rich envelopers); see text. Based on MESA models of BH+O-star binaries evolving through SMT at the critical mass ratio q = q_crit. See Fig. D.2 for post-SMT separations.

3. Results

3.1. From BH+O-star systems to BBH mergers: Semi-analytical and detailed binary evolution models

Here, we analyze the evolution of BH+O-star systems with different initial orbital periods and mass ratios to investigate which of them form BBH mergers. To develop intuition, we begin with the rapid semi-analytical method for mass transfer evolution (Sect. 2.3) in the left panel of Fig. 2, before moving to results from detailed MESA binary models. We consider BH+O-star systems with initial periods from ∼1 to 1000 days (Y axis; wider orbits would be non-interacting systems) and mass ratios M_BH; 1/M_O; Star from 0.1 to 0.5 (X axis). The initial BH mass is always M_BH; 1 = 10 M_⊙, meaning the initial O-star mass ranges from 20 to 100 M_⊙. In each binary, as the O-star evolves and expands, it will eventually initiate mass transfer onto the BH. By that point, the period and mass ratio have changed slightly from the initial values due to winds. For the purpose of the semi-analytical exercise, we consider the mass transfer to be always stable and simply mark the potential stability criteria at critical mass ratio q_crit = ≈0.28 (dashed vertical line, after Riley et al. 2022 who follow Ge et al. 2015). For simplicity, we assume fully non-conservative mass transfer (β = 0) as the mass transfer rates expected in BH binaries with massive donors are generally highly super-Eddington (Podsiadlowski et al. 2003; Rappaport et al. 2005). Indeed, in our MESA models with Eddington-limited accretion we find β ≲ 0.1. We assumed that the non-accreted matter is ejected from near the BH (γ = γ_BH). For each BH+O-star system, we calculate the final post-SMT separations a_fin according to Eq. (6). Assuming the secondary collapses to form the second BH (Sect. 2.5), we obtain the corresponding BBH merger delay times. The results are in the left panel of Fig. 2, where we color-code the parameter space of BH+O-star binaries according to the final outcome of SMT evolution. The two solid blue lines mark which BH+O-star binaries would reach the final separation a_fin = 2 R_⊙ or 25 R_⊙, which is approximately the range of orbits required for BBH systems to merge within the Hubble time. Importantly, both the a_fin values and the final outcomes in the left panel assume that the mass transfer is always stable, which in reality is not case. In most rapid binary codes, the stability criteria is comprised of a set of critical mass ratio values (or their corresponding critical ζ_crit = d log R_RL/d log M_star exponents); see also Sect. 4.5. A fixed critical mass ratio for stability would mean excluding systems to the left of a vertical line in Fig. 2, as illustrated by a dashed red line example at q_crit = 0.286 ≈ 1/3.5 in the left panel. This choice of q_crit corresponds to the stability criteria for radiative giants in the COMPAS code (assuming non-conservative mass transfer, γ = γ_BH, and their ζ_crit = 6.5, Vigna-Gómez et al. 2018; Riley et al. 2022).

Fig. 2.

Window for the formation of BBH mergers as predicted by semi-analytical and detailed binary models. Colors mark the evolutionary outcomes of interacting BH+O-star systems across different initial periods and mass ratios, calculated with our semi-analytical rapid model of SMT evolution (left panel; Sect. 2.3) and compared with MESA binary models for two different assumptions on orbital shrinkage during mass transfer: fiducial (γ = γ_BH, center) and enhanced shrinkage due to L2 outflows (right). The initial BH mass is always M_BH; 1 = 10 M_⊙ and metallicity is Z = 0.1 Z_⊙ (see Fig. D.1 for other BH masses). Wide-non interacting systems are not shown. Solid blue lines mark systems in which the SMT evolution would lead to final orbital separation a_fin = 2 R_⊙ or 25 R_⊙, according to the semi-analytical model, which is approximately the range of separations needed for BBH mergers. The dashed red line is the boundary between stable and unstable mass transfer. The outcomes of the semi-analytical model are only applicable if the mass transfer is stable. In rapid codes, it is typically assumed to be related to a critical mass ratio (the vertical line at q_crit ≈ 0.28, left panel). In the MESA models, the stability is determined self-consistently at every timestep, and it is found to be entirely different. The mass transfer only remains stable in systems where the final separation is a_fin ≳ 10 R_⊙. This conclusion is robust against uncertainties of SMT evolution and holds even if enhanced orbital shrinkage is assumed (right), leading to BBH mergers with long delay times ≳1 Gyr (Sect. 3.4).

The area between the a_fin = 2 R_⊙ and 25 R_⊙ lines in the left panel of Fig. 2 marks the potential parameter window for the formation of BBH mergers, colored by the BBH delay time. The dark dotted area on the left are systems that would technically produce BH+He-star systems with separations < 2 R_⊙. In such orbits, even the naked He-star would overflow its Roche lobe, potentially leading to a merger and a transient (Metzger 2022; Klencki & Metzger 2025) or reducing the He-core mass so substantially that it never forms a BH, unless the interaction can be cut short (e.g., by core collapse or the orbit widening). Finally, the light yellow region are systems in which the SMT evolution would lead to the formation of wide non-merging BBH systems. The stability requirement of q > q_crit reduces the parameter space for BBH merger formation to initially short-period systems (≲10 day) that interact on the MS, i.e., case A mass transfer. Coincidentally, the treatment of case A evolution in rapid codes has been shown to suffer particularly significantly from the necessary simplifications of the rapid method, under-predicting the final core mass and over-predicting the amount of mass transferred (Belczynski et al. 2022; Romero-Shaw et al. 2023; Shikauchi et al. 2025; Schürmann et al. 2024).

The results from MESA binary models are presented in the other two panels of Fig. 2, for both the assumption of low AM loss during SMT (fiducial model, γ = γ_BH) as well as the enhanced AM loss due to L2 outflows (γ ≈ 0.8γ_BH + 0.2γ_L2). Here, we focus mainly on the final evolutionary outcomes of these models and the question whether the mass transfer has remained stable and the final separation is close enough to form a merging BBH system. We refer to Marchant et al. (2021) for a detailed overview of the evolutionary pathway from BH+O-star systems to BBH binaries, and to Podsiadlowski et al. (2002, 2003) for a general discussion of mass transfer rates and interaction timescales in BH binaries. Each rectangle in Fig. 2 represents one MESA binary model. Non-interacting wide systems are not shown. Models in which the mass transfer remains stable and the second BH forms are color-coded according to the BBH delay time, with non-merging wide BBHs shown in yellow. Models in which the mass transfer becomes unstable are labeled either as “common envelope” (for convective-envelope donors, P_ini ≳ 700 day) or as “BH and Star merger” (for radiative-envelope donors, P_ini ≲ 700 day). This choice is based on the expectation that unstable mass transfer and CE evolution with radiative donors lead to stellar mergers (Kruckow et al. 2016; Ivanova et al. 2020; Klencki et al. 2021; Marchant et al. 2021)¹⁰. The two blue solid lines mark the parameter space for BBH merger formation found in the semi-analytical model (a_fin = 2 and 25 R_⊙ in the left panel), adjusted for the value of γ. Notably, the upper boundary coincides with the widest MESA models that form BBH mergers. This indicates that the orbital evolution in the semi-analytical model generally agrees well with the orbital evolution in MESA, with the exception of mass ratios q ≳ 0.15 and initial periods P ≲ 3 day (for γ = γ_BH). The first case is mass transfer from very massive donors (> 70 M_⊙), which in MESA transfer a lower amount of mass before detaching compared to ΔM_star = 0.9 M_env assumed in the rapid method, such that the orbit does not shrink as significantly. The second case, i.e., short-period systems, are binaries following early case A mass transfer evolution, which in MESA produce lower secondary BH masses compared to our rapid method due to the core mass reduction (Schürmann et al. 2024).

The striking difference between the rapid and detailed binary models is in the mass transfer stability (red dashed lines in Fig. 2). In MESA calculations, the stability threshold for radiative-envelope donors (P ≲ 700^d) is not at all a vertical line that would correspond to any critical mass ratio q_crit, or even a combination of several q_crit values. Instead, the stability line spans a wide range of mass ratios and depends on the size of the orbit: The longer the orbital period, the more stable the mass transfer in BH+Star systems (see also Marchant et al. 2021; Gallegos-Garcia et al. 2021). This result agrees with the findings of Ge et al. (2015, 2020, 2024) who have found that critical mass ratios vary significantly as massive stars expand such that interactions in wider orbits (with more expanded radiative giants) are more stable.

The mass transfer (in)stability found in detailed models directly affects the properties of BBH mergers. Most of the potential parameter space for BBH merger formation is excluded due to instability (BH + Star merge). The BBH mergers that do form in MESA have relatively wide final separations a_fin between ∼10 and 25 R_⊙ (for M_BH; 1 = 10 M_⊙), leading to long delay times ≳1 Gyr. Surprisingly, this is also the case in the variation with enhanced AM loss due to L2 outflows (right panel). Even though the orbits shrink significantly more and BBH mergers may originate from initially wider BH+O-star systems, no BBH mergers with a_fin ≲ 10 R_⊙ and short delay times are produced. In the following sections we explain this as the fundamental separation limit of the SMT evolution.

3.2. There is a limit: Minimum orbital size from SMT evolution

We find that there is limit on how close binary systems can become via mass transfer without triggering dynamical instability, as illustrated in Fig. 3. The figure is based on a grid of detailed MESA binary models of BH+O-star systems with M_BH; 1 = 10 M_⊙ (same as the right-hand panel of Fig. 2), with similar results found for other BH masses. The hatched region marks the range of separations that we find to be excluded in the SMT channel due to mass transfer instability, with the densely hatched region also excluded in the CE channel. Figure 3 demonstrates that the minimum orbital size of BH+He-star systems from SMT evolution is around ∼8 − 10 R_⊙ (periods ∼0.8 day). This has consequences for the properties of BBH mergers: long delay times (≳1 Gyr) and inefficient tidal spin-up at the BH+He-star stage (Sects. 3.4 and 4.4). More broadly, the separation limit from SMT evolution depends on the type of the donor star (Sect. 3.3).We note a trend between the minimum separation of BH+He-star systems and their mass ratio q_{BH − He; Star} = M_BH; 1/M_He; Star in Fig. 3. This is because systems with lower q_{BH − He; Star} (i.e., more massive He stars) originate from wider BH+O-star systems, which undergo case B/C mass transfer with donors that are core-He burning stars. We find that mass transfer from such donors may remain stable in tighter orbits than case A interaction.

Fig. 3.

Fundamental orbital separation limit from stable mass transfer (red dashed line) seen in the population of BH+He-star systems formed in MESA binary models. Separations below ∼8−10 R_⊙ are excluded in the SMT channel due to mass transfer instability (dashed region, physical origin in Sect. 4.1). As a result, BBH mergers from SMT evolution have long delay times of ≳1 Gyr, and their BH+He-star progenitors tend to be outside the regime of tidal spin-up (P ≳ 0.8 day). Here, the orbital evolution during SMT assumes enhanced AM loss due to L2 outflows with γ ≈ 0.8γ_BH + 0.2γ_L2. However, models assuming a different γ yield a similar range of BH+He-star separations (Fig. 4). The solid red line indicates a hard lower limit for the separation of BH+He-star systems in the CE channel, set by the size of a naked helium star. The figure is based on a grid of BH+O-star models with M_BH; 1 = 10 M_⊙ and Z = 0.1 Z_⊙ metallicity, with similar results found also for larger BH masses (Sect. 3.4).

Fig. 4.

Narrow window in the parameter space for the SMT channel converging to a well-defined narrow range of final orbits regardless of uncertainties in binary physics. We plot the orbital periods of BBH merger progenitors from before the mass transfer (BH+O-star stage, left) and after the SMT phase has taken place (BH+He-star stage, right). The figure is based on grids of detailed binary models with M_BH; 1 = 10 M_⊙ and varying assumptions on the orbital shrinkage during mass transfer (i.e., γ values, shown in different colors). Changing the assumption on γ significantly shifts the pre-SMT periods of BBH merger progenitors, but has little effect on the post-interaction orbits at the BH+He-star stage (or the properties of BBH mergers). The dashed red line shows the lower limit on the period of a BH+He-star systems, such that the naked helium star does not overflow its Roche lobe. We mark the periods and mass ratios of the known BH+OB-star systems (left panel, including supergiant high mass X-ray binaries) and of BH+Wolf-Rayet X-ray binaries (right). Cyg X-3 cannot be reproduced by SMT in our models, suggesting its origin in CE evolution.

Counter-intuitively, the separations of BH+He-star systems from SMT evolution only weakly depend on the degree of orbital shrinkage and the choice of γ. In Fig. 4, we compare the range of periods of BBH merger progenitors before the SMT phase (BH+O-star) and after the interaction (BH+He-star) for three different assumptions on the amount of L2 outflows and the corresponding AM loss. The more mass is lost through L2, the more the orbit shrinks during SMT, meaning that wider BH+O-star systems evolve to become BBH mergers (left panel). This difference can be quite dramatic, shifting BBH merger progenitors from BH+O-star systems on orbits of a few days (case A mass transfer) to wide dormant BH binaries with periods of hundreds of days, essentially covering the entire parameter space for interaction with radiative stars (Klencki et al. 2020). The uncertainty in γ causes a difficulty in predicting which of the observed BH-Star systems are progenitors of GW sources. For comparison, we mark the sample of BH high-mass X-ray binaries and X-ray quiet massive BH-Star systems with known periods and mass ratios: Cyg X-1 (Miller-Jones et al. 2021), LMC X-1 (Orosz et al. 2009), M33 X-7 (Orosz et al. 2007, although see Ramachandran et al. 2022), HD 130298 (Mahy et al. 2022), VFTS 243 (Shenar et al. 2022), HD 96670 (Gomez & Grindlay 2021), and HD 215227 (Casares et al. 2014), although see (Janssens et al. 2023).

At the BH+He-star stage, on the other hand, the orbits are similar across all the variations (right panel). Even with extreme orbital shrinkage, the SMT evolution does not lead to periods below ∼0.6 day, with most BH+He-star systems at P ≳ 1 day. As in Fig. 3, shorter periods (closer separations) are excluded by mass transfer instability. The small differences in BH+He-stars systems in the three variations in Fig. 4 are due to differences in the structure of donor stars interacting at different P_{BH − O; Star} periods, rather than due to the mechanism of orbital shrinkage or the amount of AM loss. As we discuss in the following: it is the star that matters.

3.3. The inside matters: Determining which donor stars lead to short-period systems and BBH mergers

It is not a coincidence that mass transfer becomes unstable in systems heading to orbital separations below ∼8 R_⊙. By examining individual cases (Sect. 4.1), we find that in such binaries, a delayed dynamical instability is triggered when the near-core envelope layers of the donor star are being transferred. These layers are located at radial coordinates ∼3 − 10 R_⊙ inside the radiative envelope, depending the stellar mass and evolutionary stage. They are characterized by a particularly fast rate of expansion in response to mass loss compared to the rest of the envelope due to their near-flat entropy profile. To keep the mass transfer stable, the orbit cannot continue to shrink significantly anymore when the flat-entropy layers are being stripped. This prevents the formation of BH+He-star systems with separations ≲8 − 10 R_⊙ via SMT evolution, regardless of the overall degree of orbital shrinkage from the moment of Roche-lobe overflow (RLOF) and the choice of γ. We discuss the mechanism of near-core instability in more detail in Sect. 4.1.

This signals an important point: orbits of BH+He-star systems formed in the SMT channel depend primarily on the donor stars and their inner entropy profiles rather than on the AM loss or accretion efficiency during the SMT phase. The internal structure of stars, on the other hand, can vary greatly depending on the stellar mass and radius, evolutionary stage, and chemical mixing. To examine which types of donors favor the formation of close BH+He-star systems and BBH mergers, we systematically compute mass transfer evolution from stars of different mass (from 10 to 100 M_⊙) and size (the entire range of radial expansion) at Z = 0.1 Z_⊙. For each mass-radius pair of the donor, we determine the critical mass ratio for SMT evolution q_crit following methodology described in Sect. 2.6. The result is shown in the upper panels of Fig. 5 for two variations: with fiducial SMT treatment (γ = γ_BH, left panel) and with enhanced AM loss (γ ≈ 0.8γ_BH + 0.2γ_L2, right panel).

Fig. 5.

Minimum orbital size from SMT evolution is primarily determined by the donor star, rather than by binary physics. Here, we report the critical mass ratios q_crit for BH+O-star systems (top panels), final orbital separations in binaries with q_RLOF = q_crit (middle panels), and their corresponding BBH delay times (bottom panels), calculated with MESA for a grid of donor stars of different mass (at ZAMS) and radius (at the onset of RLOF) at Z = 0.1 Z_⊙. The separations and BBH delay times shown here can be viewed as the minimum values achievable from SMT evolution given the donor mass and radius. Left panels follow the fiducial SMT treatment with γ = γ_BH, right panels assume enhanced orbital shrinkage due to L2 outflows. While enhancing the orbital shrinkage (left vs right) affects the critical mass ratios, the post-SMT orbits and their corresponding BBH delay times remain nearly unchanged. This is because these final outcomes are primarily determined by the stellar structure of the donor, which is the same in both variations. For illustrative purposes, the BBH delay times assume that each donor collapses to form the second BH, no matter its final core mass. Only the systems with delay times below ∼13.7 Gyr (i.e., brown in the bottom panels) are potential BBH mergers and GW sources for the LIGO/Virgo/Kagra detectors. The scatter points indicate the explored grid of donor masses and radii. For each pair, the q_crit value was found iteratively via binary MESA models down to at least ±0.1 accuracy.

The q_crit values we find in Fig. 5 have several characteristics. For a given donor mass, q_crit increases as a function of the donor radius all the way until the donor develops an outer convective envelopes (≳200 − 700 R_⊙, depending on the mass). At that point, q_crit rapidly decreases. We also see a slow trend with mass: the more massive a donor, the larger its q_crit values. This is consistent with the prior large-scale studies of mass transfer stability, which also discuss the origin of those trends in detail (Ge et al. 2015, 2020, 2024). Notably, both these past as well as our results indicate that an assumption of a single q_crit value for radiative or convective donors is an oversimplification, as the trend with radius is strong. Finally, we observe that all the q_crit values decrease when enhanced AM loss is assumed (right vs left in Fig. 5). This is fully expected, as the more AM that is lost, the more rapidly the orbit shrinks, and therefore the more unstable the mass transfer is. While it is possible to analytically compute correcting factors to q_crit given any chosen γ such that the rate of shrinkage at the onset of RLOF is the same¹¹, these values would not be correct because the instability is not determined at the moment of RLOF but at some later stage, a priori unknown.

In the central panels of Fig. 5, we show the orbital separations at the end of SMT in binary models with q = q_crit as a function of the initial donor mass and its radius at RLOF. These can be viewed as the minimum orbital size of BH+He-star system that may be formed as a result of SMT evolution, given the donor star¹². As we are interested in close-orbit BH+He-star systems, we focus the color-scale on the range of separation from 8 to 100 R_⊙, without resolving the wider orbits of systems that underwent SMT with convective donors. Assuming that all the He-stars collapse to form the secondary BHs (Sect. 2.5), we further compute the delay times of the resulting BBH systems and color-code the result in the bottom panels of Fig. 5. Delay times ≲13.7 Gyr (brown) are BBH systems that merge within the age of the Universe. We find that donors with masses ≲20 M_⊙ do not lead to BBH mergers, which may set the lower mass limit for the SMT channel.

Figure 5 reveals a surprising result: whereas the critical mass ratios change significantly when varying the assumption on γ (left vs right), the minimum orbital separations and BBH delay times from SMT evolution remain virtually unchanged. In other words, BH+He-star orbits in the SMT channel appear to be robust against the major uncertainties of orbital evolution during SMT, which is a rare case in binary astrophysics. It also suggest that for radiative donors, the physical origin of instability is more closely related to the orbital evolution at advanced stages of mass transfer (and therefore the final orbit), rather than to the initial rate of orbital shrinkage at RLOF. We discuss this in the context of delayed-dynamical instability and stability criteria in Sect. 4.1.

In addition, the post-SMT orbital separations in Fig. 5 show a complex behavior rather than a simple trend with mass or radius. The corresponding BBH delay times indicate that for some donor stars, the SMT channel cannot lead to sufficiently close orbits to produce BBH mergers (i.e., t_delay > 14 Gyr), even for the most favorable case of q = q_crit. It turns out that the donors that “do not work” in the SMT channel can be identified as several distinct types of stars and linked to evolutionary stages and envelope characteristics. We do so in Fig. 6, where we re-plot in more detail the minimum BBH delay times (for q = q_crit) obtained from different donors in our Fiducial model (left panel) and compare with a model variation with a severely reduced efficiency of semiconvective mixing α_semiconv. = 0.01 (right panel). We choose to vary semiconvection as it is a known factor to affect the evolutionary types of giant donors in 1D stellar models (Schootemeijer et al. 2019; Klencki et al. 2020; Kaiser et al. 2020)¹³. The thick blue line in Fig. 6 marks the boundary between MS and post-MS donors.

The largest donors with R ≳ 500 − 700 R_⊙ are red supergiants with outer convective envelopes. They are the most prone to unstable mass transfer, with low q_crit values. The SMT evolution in their case leads to wide BH+He-star orbits of hundreds of R_⊙ and delay times ≫14 Gyr. Instead of SMT, these donors may lead to NS or BH mergers via CE evolution (Kruckow et al. 2016; Klencki et al. 2021).

The other post-MS stars are radiative-envelope giants. They can be split into two categories (Klencki et al. 2020): Hertzsprung gap (HG) donors that engage into mass transfer right after the end of MS, as a result of a rapid envelope expansion when the core contracts, and Core-He burning (CHeB) donors that initiate mass transfer at a more advanced evolutionary stage, as a result of a slow nuclear-timescale expansion during the core-He burning phase. We find that this distinction plays a crucial role in the SMT channel. As it turns out, all the post-MS donors that cannot produce BBH mergers (t_merge > 14 Gyr in Fig. 6) are HG donors. On the other hand, CHeB donors lead to delay times as short as ∼300 Myr. As we discuss in Sect. 4.1, the reason lies in the different inner entropy structure of HG and CHeB stars. As a result, the mass transfer from HG donors leads to higher mass transfer rates and is less stable than from CHeB donors. Even the smallest orbital separations of BH+He-star systems from HG donors are comparatively quite large (≳20 − 30 R_⊙), whereas CHeB donors may lead to systems with ∼8 R_⊙ orbits (Fig. 5).

The significance of the HG vs CHeB distinction becomes apparent when comparing both panels of Fig. 6. In the variation with reduced efficiency of semiconvection (right), all massive stars expand rapidly at the end of the MS and consequently all the radiative post-MS donors are of the HG type (Schootemeijer et al. 2019; Klencki et al. 2020). They do not lead to the formation of BBH mergers via the SMT channel, nearly completely quenching the role of post-MS mass transfer. It is not a surprise that a variation in assumptions behind 1D stellar models lead to somewhat different outcomes, but it is rare for an uncertainty in the inner structure of stars to have such a strong effect on GW-source predictions. Whether massive stars interact as HG or CHeB donors is closely related to the long-standing debate on the nature of blue supergiants, as we discuss in Sect. 4.3.

The MS donors are weakly affected by the change in semiconvective mixing (Fig. 6) or the γ variation (Fig. 5). We find that most MS donors with M ≳ 20 M_⊙ and R > 10 R_⊙ can lead to BBH mergers via SMT evolution (at Z = 0.1 Z_⊙ here), although with long delay times of a few gigayears. In fact, case A mass transfer may be the dominant mode of formation of BBH mergers in SMT evolution, especially above the total BBH mass of 40 − 50 M_⊙ (Fig. 7). While the BBH delay times from MS donors are generally ≳2 Gyr, the delay times from CHeB donors may be as short as ∼300 Myr. That means that counter-intuitively, the most narrow BH+He-star orbits may be formed from initially the widest BH+O-star binaries with M_O; Star > M_BH (Fig. D.4)¹⁴.

Fig. 7.

BBH mergers from the SMT channel have long delay times (≳1 Gyr) as a consequence of the fundamental separation limit, regardless of the uncertainties in binary orbit evolution (left vs. right). Here, we plot the delay times of merging BBHs from SMT evolution (t_merge ≲ 13.7 Gyr) from all our binary MESA grids, as a function of the total BBH mass. We distinguish between BBH mergers formed via SMT evolution from MS donors (case A mass transfer) and post-MS donors (case B or C). Notably, case A evolution dominates for massive BBH mergers (≳40 M_⊙). Two variations are considered: non-accreted mass ejected with the specific AM of the BH (γ = γ_BH) and enhanced AM loss due to L2 outflows (γ ≈ 0.8γ_BH + 0.2γ_L2). The BBH delay times are unaffected by the choice of γ. The green shading indicates the approximate range of delay times and masses where we expect the CE channel to contribute. The figure is based on MESA binary grids of BH+O-star systems with the firstly formed BH initial mass of M_BH; 1 = 4, 7, 10, 13, 16, 20, 24, 28, 32, 36 M_⊙, and 40 M_⊙ (see Fig. 2 for details and Appendix D for other masses).

We find that there are two types of MS donors that do not lead to BBH mergers (Fig. 6). The first are O-type stars in very close BH binaries that overflow their Roche lobes with R_RLOF ≲ 10 R_⊙ (periods ≲2 days). These donors generally engage into mass transfer when they are still early during their MS evolution. As a result, their He-core mass decreases with respect to a single star or a post-MS donor (Schürmann et al. 2024). This leads to the orbit reexpanding in the later half of the case A mass transfer due to the mass ratio reversal (see also the left panel of Fig. D.4), and BBH delay times significantly above 14 Gyr. We note that this late reexpansion of the orbit can be reduced with enhanced orbital AM loss, for example due to L2 outflow (comparing left and right of Fig. 5). While the regime of ∼1 day orbits may not be the most suited for the SMT channel, it could be where the CHE channel for BBH mergers takes over (de Mink & Mandel 2016; Mandel & de Mink 2016; Marchant et al. 2016).

Finally, we find that very massive stars (≳80 M_⊙) may not be suitable as donors for the SMT channel once they expand beyond ∼50 − 100 R_⊙. This comes as a surprise, given that these stars are characterized by the most extreme critical mass ratios of even up to 9 (top of Fig. 5). In principle, they should thus be the ideal candidates for enormous orbital shrinkage during the SMT phase and the formation of BBH mergers (as also found in our semi-analytical model). However, what detailed MESA models reveal is that the very massive stars do not transfer much mass before detaching from the SMT phase, never allowing the orbit to shrink significantly. This is because their envelopes are already He-enriched even without any mass transfer due to more extended MS convection and stronger mass loss. As a result, stars of ≳80 M_⊙ transfer only ∼20 − 30% of their mass before contracting to ≲20 R_⊙, which in wider orbits leads to an early detachment from mass transfer. This amount of transferred mass is far less than what is assumed is any rapid binary evolution model. After detachment, the partially stripped He-enriched star is a hybrid between a normal single star and a fully stripped helium core, making it extremely difficult to model without detailed 1D stellar computations. This phenomena of the mass transfer stopping early was discovered by Sen et al. (2023) as a scenario to form reverse Algol systems, i.e., post-interaction binaries in which the mass-loser remains more massive than the mass gainer. Observationally, such stars would likely appear as H-rich Wolf-Rayet stars of the WN type (Pauli et al. 2022). In the context of binary evolution scenarios, an early detachment from mass transfer would have significant consequences. It may indicate that binary interactions do not have as strong an effect on the properties and orbits of very massive stars in ≳100 day systems as they do on normal massive stars systems even up to ∼1000 days. Binary channels, such as the SMT pathways to BBH mergers, may become less effective in the regime of very massive stars. Without a better understanding of internal chemical mixing and stellar winds of very massive stars it may be impossible to arrive at robust predictions for GW sources from binary channels (for a discussion of these challenges in the CE channel see Romagnolo et al. 2025).

3.4. Consequences for the properties of BBH mergers

So far in Sect. 3.1, we examined the formation of BBH mergers from BH+O-star MESA models with M_BH; 1 = 10 M_⊙. We found BBH delay times of ≳1 Gyr, regardless of the degree of orbital shrinkage during SMT and the assumption on γ (Sect. 3.2). We argued that the key factors determining BBH orbits in the SMT channel are instead the evolutionary stage and envelope structure of donor stars (Sect. 3.3). Here, we combine results from MESA grids of BH+O-star systems with other BH masses: M_BH; 1 = 4, 7, 10, 13, 16, 20, 24, 28, 32, 36 M_⊙, and 40 M_⊙ (see Fig. D.1 for a collection of grid figures, all at Z = 0.1 Z_⊙ metallicity). For each M_BH; 1 case, we simulated a range of periods and mass ratios that is large enough to capture the entire parameter space for the formation of BBH mergers (notably, the range changes with mass, Fig. D.1). Two variations were explored: the fiducial SMT treatment with γ = γ_BH, and variation with enhanced orbital shrinkage due to AM loss through L2 outflows (γ ≈ 0.8γ_BH + 0.2γ_L2). As we do not model the prior distribution of BH + O-type systems formed in Nature, we do not make predictions for the formation rate or the mass distribution of the observable population of BBH sources (however, see the discussion in Sect. 4.4). Instead, in Figs. 7 and 8, we demonstrate what is the entire possible range of BBH masses, delay times, and mass ratios that may be realized in the SMT channel given our assumption of direct collapse with no natal kick (in Appendix B and Vigna-Gómez 2025 we discuss how BH kicks may affect our results).

Fig. 8.

Mass ratios of BBH mergers from SMT evolution are confined to the range from ∼0.3 to ∼3, determined by the physics of stable binary interactions. We plot the BBH mass ratios q_{BH − BH} as a function of the BBH mass from our binary MESA grids, where q_{BH − BH} is defined as M_BH; 1/M_BH; 2 and with M_BH; 1 (M_BH; 2) as the mass of the first (second) born BH. Hatched regions indicate the combinations of BBH masses and mass ratios that cannot be produced via SMT evolution (see text). This results in a positive trend between q_{BH − BH} and M_tot. Circles indicate models in which the SMT interaction was initiated by a MS donor (case A) and diamonds mark SMT evolution from a post-MS donor (case B or C). The color indicates the orbital period at the BH+O-star stage (i.e., before the SMT). Based on binary grids of BH+O-star systems with M_BH; 1 = 4, 7, 10, 13, 16, 20, 24, 28, 32, 36 M_⊙, and 40 M_⊙.

In Fig. 7, we show the BBH delay times as a function of the total BBH mass for all the BBH mergers formed across our MESA binary grids. In two panels we compare both γ variations, confirming that the enhanced orbital shrinkage from L2 outflows does not lead to shorter delay times across all the BBH masses. We distinguish between BBH mergers formed via SMT evolution from MS donors (case A mass transfer) and post-MS donors (case B or C). Green shading indicates where we expect the CE channel to contribute, assuming that it falls off at the high-mass end as indicated by the empirical lack of red supergiants with masses ≳40 M_⊙ (Davies et al. 2018); see also Klencki et al. (2021). For the SMT channel, we find that MS donors always leads to long BBH delay times of ≳2 Gyr, whereas post-MS donors (specifically CHeB giants) may lead to tighter BBH systems and shorter delay times of a few hundred megayears. This is in line with our investigation of different donor types and structures (Sect. 3.3; see also the discussion in Sect. 4.1). In addition, we find that BBH mergers with the total mass above ∼40 M_⊙ form predominantly from case A mass transfer. This is because of the large radii of MS stars above the mass of ∼50 − 60 M_⊙ in our models, such that the case A interaction occurs even in wider orbits of hundreds of R_⊙ (Fig. 6). While the radii of these massive MS stars are likely overly inflated in 1D stellar models (Sanyal et al. 2015, 2017; Klencki et al. 2020; Agrawal et al. 2020; Romagnolo et al. 2023), we find that very massive stars in wider binaries (i.e., typical case B/C range) are not efficient in forming BBH mergers via the SMT channel due to their He-rich envelopes causing an early detachment (Fig. 6). Our results suggest that case A evolution may be the dominant formation channel of massive BBH mergers via SMT evolution. This poses a challenge for the SMT treatment in rapid binary evolution codes to accurately predict the cores and final masses of case A donor stars (Belczynski et al. 2022; Romero-Shaw et al. 2023; Schürmann et al. 2024; Shikauchi et al. 2025).

In Fig. 8, we examine the mass ratios of BBH mergers as a function of their total mass. We define the mass ratio q_{BH − BH} as M_BH; 1/M_BH; 2, meaning that q_{BH − BH} > 1 are systems in which the firstly formed BH is the more massive, and vice versa. Similarly to Fig. 7, we include BBH mergers formed across all our BH+O-star grids. They are arranged along several discrete curves, each corresponding to a different M_BH; 1, ranging from 4 to 40 M_⊙. In black, we mark BBH systems in which one of the BHs would exceed the pair-instability limit (Farmer et al. 2019; Renzo et al. 2022, although see Farag et al. 2022), while red is the regime of BH + NS mergers assuming an upper NS mass limit at 3 M_⊙. Hatched regions indicate the combinations of BBH masses and mass ratios that are not produced by SMT evolution according to our models. We find that the exclusion of high q_{BH − BH} systems (i.e., the secondary-formed BH being notably less massive) is due to insufficient orbital shrinkage during SMT. For BBH mergers to form with such mass ratios, the companion stars at the BH+O-star stage could not be too massive with respect to the BH, which prevents the orbit from shrinking during SMT. This limitation is partly alleviated if enhanced AM loss is assumed (the right panel), though even in this case none of the BBH mergers exceed q_{BH − BH} ≈ 3. More extreme BBH mass ratios could potentially be obtained if a substantial amount of mass is lost during the formation of the BH (i.e., non-direct collapse), although the resulting Blaauw kick would further increase the already long delay times that we find (see Appendix B). On the other end of the spectrum, BBH mergers with very low q_{BH − BH} would require BH+O-star systems in which the stellar companion is substantially more massive than the BH, leading to significant orbital shrinkage during the SMT phase and a wide pre-SMT orbit. We find that such BBHs do not form in the SMT channel, particularly at high masses, because interactions with very massive donors (≳75 M_⊙) in wide orbits do not lead to close post-SMT orbits (see Fig. 6 and donors with He-enriched envelopes).

Figure 8 reveals a positive trend between q_{BH − BH} and M_tot. However, it is unclear to what extend this effect might be realized in the measured population of BBH merges. Observationally, it is impossible to infer which BH was formed first, meaning that the q_{BH − BH} > 1 values would instead be measured as 1.0/q_{BH − BH}, negating the existence of any trends.

4. Discussion

4.1. The physical reason behind the limit on orbital tightening via SMT

In this section we discuss the following questions: (a) Why is there a limit on how close the post-SMT orbital separation can be, and what determines the ∼8 R_⊙ value? (b) Why does the limit remain unchanged even if enhanced orbital shrinkage due to strong AM loss through L2 is assumed?

In Fig. 9 we examine mass transfer evolution from a 30 M_⊙ donor interacting in systems with BH companions of different masses. The mass ratio at RLOF q_RLOF = M_donor/M_BH varies from q_min = 1.5 to q_max = 12. The donor is the same for each q_RLOF: a core-He burning giant of 252 R_⊙ at 0.1 Z_⊙ metallicity with a ∼17 M_⊙ envelope and a ∼13 M_⊙ core¹⁵. We chose this particular donor as it leads to the smallest post-SMT orbit of ∼8 R_⊙. The top panel in Fig. 9 shows the mass transfer rate evolution as a function of the decreasing envelope mass. Models reaching log(Ṁ/M_⊙ yr⁻¹) > 0.5 are assumed to become unstable. The model with q_RLOF = q_crit = 6.06 (shown in bold) is the critical one, i.e., at the threshold between stable and unstable mass transfer evolution, leading to the smallest post-SMT orbital separation. In the remaining two panels of Fig. 9, we show the internal entropy profiles of the donor star from the critical model, plotted every 1.5 M_⊙ from the onset of RLOF (dark red, left) to near the end of the mass transfer (dark blue, right).

Fig. 9.

Origin of the separation limit lies in delayed dynamical instability. Top: Mass transfer rate (Ṁ) in systems with a 30 M_⊙ donor and a varying mass ratio at RLOF, shown as a function of the decreasing envelope mass. The donor is the same for each mass ratio at the onset of RLOF: ∼250 R_⊙ core-He burning giant with a ∼17 M_⊙ envelope and ∼13 M_⊙ core. Models reaching log(Ṁ/M_⊙ yr⁻¹) > 0.5 become unstable (Sect. 2.4), as indicated by the dashed horizontal line. The critical mass ratio for stability is q_crit = 6.06 (marked in bold). The threshold between stable and unstable models is determined by the Ṁ peak at M_env ≈ 2.5 M_⊙. Middle: Internal entropy profiles of the donor in the q = q_crit model, ranging from the onset of RLOF (light, left) to the end of mass transfer (dark, right). The Ṁ peak seen in the top panel is caused by stripping off the layers where the entropy profile is nearly flat. Bottom: The same entropy profiles but as a function of the radius coordinate. The flat entropy layers are within the inner 3 R_⊙ of the donor (6 R_⊙ during the Ṁ peak), causing instability in models in which the mass transfer would shrink the orbit below a ≲ 8 R_⊙.

We analyze how the mass transfer rate Ṁ evolves across models of different mass ratios. Systems with q_RLOF ≤ 6.06 remain stable. For most stable mass ratios (q_RLOF < 5.5), the Ṁ peaks once about 30% of the envelope has been transferred (here at the envelope mass ∼12 M_⊙). In the remainder of the mass transfer phase, the rate is smaller and may even drop to the nuclear-timescale Ṁ ≈ 10^−0.5 M_⊙ yr⁻¹. This is consistent with prior models of stable mass transfer evolution (e.g., Podsiadlowski et al. 2002; Rappaport et al. 2005; Pavlovskii et al. 2017; Klencki et al. 2022). However, as the mass ratio of the model increases (q_RLOF > 5.5), we begin to observe a delayed Ṁ peak appear at late stages of the interaction, when the final ∼5 M_⊙ of the envelope are being transferred. The delayed Ṁ peak rises in magnitude the higher the mass ratio and eventually triggers instability for q_crit = 6.08. Notably, among models with q_RLOF near the q_crit value, the peak mass transfer rate varies strongly as a function of q_RLOF. For example, comparison models with q_RLOF = 5.98, 6.08 (critical), and 6.12, their maximum reached Ṁ values are ≈0.025, 0.34, and 1.1 M_⊙ yr⁻¹, respectively. This indicates that our choice to set the critical rate Ṁ_crit at 10^−0.5 M_⊙ yr⁻¹ has a small effect on q_crit, at least for post-MS donors. For the MS donors the uncertainty on q_crit due to instability criteria is larger.

Figure 9 illustrates that it is the delayed Ṁ peak at M_env ≈ 2.5 M_⊙ that determines the transition from stable to unstable MT evolution and the critical mass ratio. Internal entropy profiles of the donor (middle panel) reveal that this Ṁ peak is associated with deep envelope layers in which the entropy profile is nearly flat. This is a well-known effect: the flatter the entropy profile, the more the donor star expands in response to mass loss, leading to higher mass transfer rates (for a perfectly constant entropy, the donor would react as dlnR/dlnM = −1/3, Paczyński et al. 1969; Paczyński & Sienkiewicz 1972; Webbink 1985). Mass transfer instability caused by a flattening entropy profile in deep stellar interiors has been identified as delayed dynamical instability already by Hjellming & Webbink (1987).

The near-flat entropy layers are present in the inner ∼5 M_⊙ of the donor’s envelope already at the moment of RLOF (dark red profile), enclosed within just the inner ∼3 R_⊙ of the 252 R_⊙ giant (the bottom panel). These layers remained nearly unchanged through most of the interaction and hidden deep inside the Roche lobe: as the mass transfer progresses (profiles from left to right), the entropy adjusts in the outer layers of the donor such that the near-surface entropy peak, characteristic of radiative envelopes, is rebuilt¹⁶. If the orbit was to remain wide throughout the entire mass transfer (e.g., more equal mass systems), the entropy structure of the inner few R_⊙ would have relatively little effect on the overall response of the donor and on the mass transfer rate. However, as the orbital separation decreases down to tens of R_⊙ in the q = q_crit model examined here (see also Fig. 10), the deep flat entropy layers come close to the surface. Eventually, once the orbit has shrunk enough and the flat entropy layers occupy a substantial volume of the Roche lobe, they cause the delayed Ṁ rise. Its peak value Ṁ ≈ 0.1 M_⊙ yr⁻¹ at M_env ≈ 2.5 M_⊙ corresponds to the penultimate profile in the middle panel (indicated by the arrow). For such a high transfer rate, the donor loses mass on a timescale that is shorter than the thermal-timescale of even its outermost envelope, such that the response becomes nearly adiabatic and the subsurface entropy peak is no longer rebuilt (Temmink et al. 2023). At that point, the size of the donor is about 6 R_⊙ (orbital separation ≈12 R_⊙) and its entropy profile is nearly flat all the way to the surface (bottom panel). This is the critical bottleneck that determines how tight the post-SMT orbit can be. To avoid instability, the orbit cannot shrink significantly while the flat entropy layers are being transferred. For the donor in Fig. 9, the Roche-lobe exponent must remain ζ_RL ≲ 4 or dR_RL/dM_don ≲ 1.5 during the delayed Ṁ peak. As a result, from that point on, the orbital size only slightly decreases from ∼12 R_⊙ down to ∼8 R_⊙ at the end of the interaction. Importantly, the properties of the donor (mass, radius) at the critical point of max Ṁ, and consequently the orbital separation, are the same no matter what is the assumption on the AM budget of the SMT phase (γ): see Fig. 10. This is why throughout the paper we find that the minimum post-SMT separations and the BBH orbits are independent of γ. The same considerations imply that they are also independent of how much matter is accreted (β)¹⁷. Our results are qualitatively similar to those of Ge et al. (2015) who describe that the critical mass ratios for radiative donors are set by a delayed dynamical instability triggered in layers where the entropy is nearly constant. This does not imply that in all unstable systems the instability occurs precisely when these layers are being stripped: for larger mass ratios q_RLOF > q_crit the instability may be triggered much sooner, still within the layers with an entropy gradient (e.g., yellow models in the top panel of Fig. 9). While these layers are characterized by a comparatively larger dlnR/dlnM_don (i.e., more stable), the instability still occurs if the orbit is shrinking sufficiently quickly.

Fig. 10.

Path to delayed dynamical instability and the resulting minimum post-SMT separation do not depend on the assumption on orbital shrinkage (γ value). Here, we plot the evolution of the mass transfer rate (top) and orbital separation (bottom) in binaries interacting at the critical mass ratio for the fiducial SMT treatment (γ = γ_BH) and assuming enhanced shrinkage due to L2 outflows (γ ≈ 0.8γ_BH + 0.2γ_L2). The donor is the same 30 M_⊙ CHeB giant as in Fig. 9, the companion is a BH accreting at the Eddington limit, with its mass determined by the q_crit value: ≈5 M_⊙ in the fiducial model, ≈6 M_⊙ in the case with enhanced shrinkage. Regardless of the assumed γ, the critical Ṁ peak that determines stability occurs at the same moment of the interaction. As a result, the mass and the radius of the donor at this critical point do not depend on γ, leading to the same final orbital separation.

The discussion of Fig. 9 suggests that it is the presence of flat entropy layers at the bottom of the radiative envelope of CHeB giants that prevents the formation of ∼2−8 R_⊙ orbits via SMT evolution, which consequently lead to long BBH delay times. A question arises how robust is the presence of such layers in the envelope and whether they could be avoided. In Sect. 4.2 we compare the internal structures of CHeB giants with other main donor types in our grids, finding that layers of flat entropy are always present and that the case explored in Fig. 9 is the most favorable for the formation of short-period orbits, as well as discuss whether hypothetical “ultra-stable” donor stars could exist in Nature.

4.2. Why are some donor types favorable for the SMT channel? The role of chemical mixing for stability

In Sect. 3.3 we found that the minimum size of the post-SMT orbit depends on the type of donor star, with smallest separations achievable from CHeB giants (∼8−15 R_⊙) and MS donors (∼15−30 R_⊙), and wider orbits from HG giants and convective-envelope stars. Here, we discuss whether those findings can be understood as a result of differences in the internal structure of different donors.

In the top left panel of Fig. 11, we examine the evolution of the mass transfer rate Ṁ as a function of the decreasing binary separation for four main donor types, comparing the evolution at q = q_crit (solid lines, stable MT) and at q slightly larger than q_crit (dashed lines, unstable MT). The donor mass is 30 M_⊙, with a core mass of ∼13 M_⊙ (for post-MS donors), or 26 M_⊙ with the core of ∼10 M_⊙ for the convective-envelope donor (to avoid lines in other panels overlapping). The CHeB donor is the same ∼250 R_⊙ giant as in Fig. 9, while the HG donor is taken from the grid variation with low semiconvection (α_SC = 0.01; see Fig. 6). For each donor, we label the final orbital separation from SMT evolution at q = q_crit. The figure illustrates that, depending on the donor type, the critical mass transfer rate peak that may lead to instability (star symbols) occurs at different stages of the interaction. For example, for convective donors the instability is triggered shortly after the onset of RLOF, whereas for CHeB donors it is substantially delayed, as the Ṁ peaks when the separation as well as the donor are much smaller than at the start of the mass transfer.

Fig. 11.

Minimum orbital separation from SMT evolution is different for different types of donor stars. Top left: Evolution of the mass transfer rate (Ṁ) as a function of the decreasing binary separation in interacting systems with a BH accretor and a 30 M_⊙ donor of different donor types. The CHeB donor is the same ∼250 R_⊙ giant as in Fig. 9, whereas its HG variant comes from the grid with low semiconvection. The solid lines are models at q = q_crit, dashed lines are at q slightly larger than q_crit, such that the MT becomes unstable (star symbols). Right: Internal entropy and H abundance profiles of different donors from the onset of RLOF, plotted as a function of the internal mass coordinate m. The He-core in post-MS donors is at m ≲ 13 M_⊙. The layers that cause the Ṁ peak and dynamical instability (star symbols) are where the entropy profile is nearly flat. Bottom left: Same entropy profiles but as a function of the radial coordinate. The difference in the location of the constant entropy regions in the envelopes of different donors is primarily responsible for different minimum orbital separations a_min that may be reached via SMT.

It turns out that for each donor type, the point when the mass transfer becomes unstable is related to where in the envelope of the donor the entropy profile becomes nearly flat. We see this in the other panels of Fig. 11, which show the entropy profiles of different donors at the onset of RLOF, plotted as a function of the mass coordinate (top right) or the radius coordinate (bottom left). The star symbols indicate precisely which layers are being transferred at the moment when the MT becomes unstable. In the bottom right panel we show the internal H abundance profiles for comparison, as it is the chemical composition structure that determines the entropy structure of a radiative envelope.

For the MS donor in Fig. 11, the instability occurs at m ≈ 20 M_⊙, at the bottom of the outer part of the star with the pristine H abundance. This is where the entropy profile is the flattest, besides the inner convective core (m < 15 M_⊙). The region with 15 < m/M_⊙ < 20 is characterized by an entropy slope, which stabilizes the mass transfer and leads to lower Ṁ rates compared to the peak at m ≈ 20 M_⊙. This entropy slope is a direct consequence of the H abundance slope that was created by the convective core decreasing in size during the prior MS evolution. The gradient in the H abundance introduces a gradient in the mean molecular weight, which in turn causes a gradient in the specific entropy: the most relevant quantity for how the donor star responses to mass loss. In that way, the abundance gradients in stars have a stabilizing effect on the mass transfer. The entropy and the abundance profiles of the HG donor are similar to the MS donor, with the same H abundance gradient present on top of the now fully H-depleted helium core. As a result, the instability occurs at the similar layer of m ≈ 21 M_⊙. The striking difference, however, is in the radial coordinate at which the flat entropy layers are located (bottom left in Fig. 11). The envelopes of HG stars have undergone a phase of substantial expansion following the end of the MS. As a result, the near-constant entropy region extends out to the radius of ≈30 − 40 R_⊙, compared to ≈3 − 4 R_⊙ in the MS donor. For the HG donor, the Ṁ peaks when the binary separation is still quite large (∼100 R_⊙). To avoid instability, the orbit cannot shrink too quickly at this point, which limits the final separation at a few tens of R_⊙. This is also where the difference between HG and CHeB donors becomes apparent. First, the H abundance profile of the CHeB giant has been more significantly altered compared to the MS star due to more extensive mixing via (semi)convection in the envelope layers above the H-burning shell (Schootemeijer et al. 2019; Klencki et al. 2020; Kaiser et al. 2020). This has extended the He-enriched layers up to m ≈ 25 M_⊙, inducing a mean molecular weight gradient and consequently an entropy gradient that decreases the Ṁ rate compared to the HG donor case and stabilizes the mass transfer. On the other hand, the CHeB giant developed an intermediate convective zone at the bottom of the envelope, which flattened the H abundance and the entropy profiles in layers 14 < m/M_⊙ < 18. These are the envelope layers responsible for the delayed Ṁ peak observed in the top left panel (and in Fig. 9) that determines the critical mass ratio and the minimum post-SMT separation. Notably, they are located far closer to the core than in the HG giant case, at radial coordinates of ∼3 R_⊙, resulting in the peak of Ṁ occurring when the binary separation is already small (∼10 − 15 R_⊙). This is why CHeB donors may lead to far tighter orbits via SMT evolution compared to HG donors. In the case of MS donors, the Ṁ peak also occurs when the orbit is quite small. However, what follows is the mass ratio reversal and orbital expansion, which is why MS donor lead to somewhat wider orbits than CHeB donors.

The above analysis reveals an intriguing effect: chemical composition gradients induce mean molecular weight gradient, which in turn introduce specific entropy gradients that have a stabilizing effect on the mass transfer. This means that a hypothetical ultra-stable type of a donor star would be a radiative-envelope post-MS giant with no intermediate convective zone and with a He/H composition gradient extending throughout most of its envelope.

4.3. Whether GW astronomy can teach us about stellar interiors and solve the blue supergiant problem

Figure 6 suggests that different assumptions on the efficiency of internal mixing in stars may have a dramatic impact on the formation of BBH mergers via SMT evolution. This is because the ability of SMT to form a close-orbit system is fundamentally related to the internal structure of the donor star (Sect. 4.1) and is robust against uncertainties in mass transfer (AM loss, accretion efficiency). This leads to a question whether the population of GW sources can teach us about stellar interiors. Indeed, while any prediction from stellar evolution (e.g., tracks, isochrones, and metal yields) is always subject to uncertainties in the stellar physics (e.g., internal mixing and transport, nuclear reaction rates, mass loss), the effect illustrated in Fig. 6 is exceptionally significant. Assuming low efficiency of semiconvection (the right panel), makes half the parameter space disappear (all post-MS donors), excludes most of 20 − 40 M_⊙ stellar progenitors, and likely shifts the predicted BH mass distribution to higher masses by a considerable amount.

Interestingly, the two variations of stellar evolution in Fig. 6 are not arbitrary but are closely related to a long-standing puzzle of the nature of blue supergiants (Langer et al. 1985, 1989; Stothers & Chin 1992; Schootemeijer et al. 2019; Klencki et al. 2020; Bellinger et al. 2024). For stellar models in the left panel, most massive stars spend a substantial fraction of their core-He burning lifetime as blue supergiants, which could explain the large number of blue supergiants found in spectroscopic surveys (Humphreys & McElroy 1984; Casares & Jonker 2014; Castro et al. 2018; de Burgos et al. 2023; Patrick et al. 2025). We find that SMT evolution from such core-He burning blue supergiants may lead to BBH mergers. For stellar models in the right panel, massive stars tend to rapidly expand at the end of MS and spend most of their core-He burning as red supergiants, in which case the observed population of blue supergiants would be a manifestation of a more unique evolutionary scenario, possibly of stellar mergers or past mass accretors (Vanbeveren et al. 2013; Justham et al. 2014; Bellinger et al. 2024; Menon et al. 2024; Schneider et al. 2024). We find that SMT evolution from such rapidly expanding donors does not lead to BBH mergers. This suggests that in the future, a well characterized population of BBH mergers could help resolve the blue supergiants problem¹⁸.

While this is an exciting outlook, it should be noted that our study if just the first step. An important caveat is that, at the moment, we are dealing with single star models rather than models of past mass-gainer stars, in which the chemical abundance and entropy profiles will be different (Renzo & Götberg 2021; Renzo et al. 2023; Schneider et al. 2024). Another relevant factor is metallicity: whereas large spectroscopic surveys of blue supergiants and massive binaries are mostly confined to metallicities ≳0.1 − 0.2 Z_⊙ (Shenar et al. 2024), a significant fraction of detectable BBH mergers may well originate from more distant and metal-poor environments (Chruślińska et al. 2021; Chruślińska 2024). Meanwhile, single stellar models suggest that the blue versus red supergiant evolution is metallicity-dependent, with low metallicity favoring core-He burning in the blue (see Klencki et al. 2020, and references therein). It is therefore possible that the red supergiant evolution is the most common in the nearby Universe (and observable stellar populations), whereas the blue supergiant evolution dominates the formation of BBH mergers at metallicities ≲0.1 Z_⊙.

4.4. Implications for BBH mergers: Delay times, masses, mass ratios, spins, and metallicity

Here, we discuss the main implications of our findings for the properties of BBH mergers from the SMT channel.

4.4.1. Delay times.

We find that because of the fundamental separation limit from SMT evolution, the BBH systems formed have preferentially long delay times (≳2 Gyr), independently of how much AM is lost during SMT (Fig. 7). This means that the contribution from the SMT channel is expected to fall off with redshift more quickly than in channels with shorter delay times, especially at z > 2 − 3 (lookback time ∼10 Gyr). We find that shorter delay times of a few hundred megayears are possible for BBH mergers with masses ≲40 M_⊙. This could be the regime where the CE channel is the strongest due to the prevalence of red supergiants (Klencki et al. 2021). If the CE channel can produce shorter delay times of ∼10 − 100 Myr than there may be an overall trend in binary channels: the more massive the BBH, the longer the delay time.

4.4.2. BBH masses.

We find that the SMT channel can operate in the entire explored range of BH masses from ∼4 M_⊙ up to the pair-instability mass gap at ∼45 M_⊙ (BBH total masses from ∼10 M_⊙ to ∼90 M_⊙, Fig. D.1). The size of the parameter space is comparable for all BH masses above ≳10 M_⊙. This means that assuming a flat prior on mass ratios and log periods of BH+O-star systems, our models would likely favor the low-mass BH end (due to the initial-mass function), rather than the ≳20 M_⊙ range as found in some population models (Olejak et al. 2022; van Son et al. 2022a). On the other hand, we show that the range of donor masses that facilitate the SMT channel depends on the assumed stellar physics of internal mixing (Fig. 6): different assumptions on the structure of stars may affect the mass distribution considerably. Regardless, we find that case A mass transfer at the BH+O-star stage dominates the formation of BBH mergers with masses ≳40 M_⊙. It is also worth pointing out that the parameter space for BBH mergers shifts to more equal mass ratios at the BH+O-star stage the higher the BH mass (Fig. D.1); see also Picco et al. (2024).

4.4.3. BBH mass ratios.

We find BBH mergers formed with mass ratios from 0.3 to 1.0 (Fig. 8). These limits are determined by the requirement that SMT evolution in BH+O-star systems leads to short-period orbits. To form the secondary BH with mass more than 3 times the mass of the primary BH would require very wide BH+O-star systems, which do not follow the SMT evolution (convective donors). To form the secondary BH with mass less than 0.3 times the mass of the primary BH would mean that the SMT phase leads to orbits that are too wide. On the other hand, these conclusions are based on the assumption that the secondary BH forms in direct collapse with no mass loss. Taking uncertainty in the BH formation process into account, it is hard to put a robust lower limit on the mass ratios of BBH systems from the SMT channel. Nevertheless, we do not find any particular reason for a preference of BBH mass ratios between ∼0.6 − 0.8, as found for the SMT channel in some population models (Olejak et al. 2022; van Son et al. 2022a). However, this likely depends on the assumptions on the first mass transfer and possibly the metallicity-weighted cosmic star formation rate that we do not explore here (van Son et al. 2022a,b; Zevin & Bavera 2022; Banerjee & Olejak 2024; Dorozsmai & Toonen 2024).

4.4.4. BH spins.

Due to the separation limit, we find that BBH mergers from the SMT channel have orbital periods predominantly ≳0.8 days at the BH+He-star stage. These systems are generally too wide for an efficient tidal spin-up of the He-star, which has been the primary scenario explaining the origin of BH spins in the CE channel (Kushnir et al. 2016; Qin et al. 2018; Bavera et al. 2020). Even if tides were strong enough to fully synchronize the He-star with the orbit, for a period of 0.8 day Belczynski et al. (2020) fit the secondary BH spin of only ∼0.2. Therefore, our results suggest a limit on the maximum spin achievable in the SMT channel, which would impact the mass ratio reversal scenarios as an explanation for the reported anticorrelation between the effective spin (χ_eff) and mass ratio (Broekgaarden et al. 2022b; Olejak et al. 2024; Banerjee & Olejak 2024). On the other hand, the closest separation BH+He-star systems we find are preferentially of unequal mass ratio with M_He; star > M_BH; 1 (Fig. 3), originating from relatively wide pre-SMT orbits and CHeB donors (Fig. D.4). In some borderline cases their periods may extend down to ∼0.4 day (Fig. 4), which would correspond to a_BH; 2 ∼ 0.5 and BBH mergers with χ_eff ∼ 0.3 − 0.4 and q_BBH down to 0.3. More generally, however, without strong tides at the BH+He-star stage, the rotation of the second BH progenitor may predominantly be determined by the SMT phase itself (Qin et al. 2019), potentially leading to notable spins even in > 1 day orbits. A more in-depth analysis of BH spins in the SMT channel is beyond the scope of this paper.

4.4.5. Metallicity dependence.

We found long delay times of BBH mergers at the favorable, low metallicity of Z = 0.1 Z_⊙. At higher metallicity, the winds of (He-)stars will be stronger, likely leading to more significant orbital expansion at the BH+He-star stage and even longer delay times. Our limited exploration of the metallicity effects suggests that this may quench the SMT channel completely at Z ≳ 0.4 Z_⊙ (Fig. D.2). This, however, is sensitive to the uncertain strength of winds, particularly from He-rich stars (Vink 2017; Sander et al. 2020; Sander & Vink 2020; Vink 2022; Dorozsmai & Toonen 2024), as well as the orbital evolution due to wind-mass loss (e.g., Schrøder et al. 2021). In addition, we found that while CHeB donors may lead to BBH mergers via the SMT channel, HG donors do not (Fig. 6). The ratio between these two donors types is metallicity-dependent, with lower metallicity favoring CHeB donors (e.g., Belczynski et al. 2010; Romagnolo et al. 2025), which likely further increases the preference for low-metallicity progenitors.

4.4.6. Rate calculation.

Our results suggest that the parameter space for the formation of BBH mergers from BH+O-star systems is only weakly affected by mass transfer uncertainties (Fig. 4). This means that by knowing how many BH+O-star systems form in the Universe, it may be relatively straightforward (compared to many other formation scenarios Mandel & Broekgaarden 2022) to accurately obtain the rate of BBH mergers from SMT evolution. While so far only a few BH+O-star systems are known, this number is set to increase substantially in the following years thanks to large-scale astrometric, spectroscopic, and microlensing surveys of tens of thousands of massive stars (Shenar et al. 2024; El-Badry 2024; Abrams et al. 2025), predicted to yield tens to hundreds of BH binary detections (Wiktorowicz et al. 2020; Langer et al. 2020; Janssens et al. 2022).

4.5. Importance of mass transfer stability for the SMT channel and how to model it in rapid binary codes

Criteria for mass transfer stability are, arguably, the single most important assumption to make when modeling the formation of compact binary systems, such as merging BBHs, through SMT evolution. This is because close orbital separations are reached via SMT only in systems that evolve near the threshold between stable and unstable MT evolution (e.g., Fig. 2). As a result, it is the stability criteria that determine the parameter space for the formation of BBH merges via SMT and consequently the BBH merger properties (masses, mass rations, rates). For example, because the critical mass ratio for stability increases with the radius of the radiative donor (Fig. 5), the mass ratios of BBH mergers correlate with the orbital period at the BH+Star progenitor stage (Fig. 8). Another direct manifestation of mass transfer (in)stability is the fundamental limit to how close the orbit may become via SMT evolution (Fig. 3), i.e., the main finding of this work. This minimum post-SMT separation is different for different types of donor stars, which can be understood via their internal structure that sets conditions for delayed dynamical instability (Fig. 11). Only for some donor stars the minimum post-SMT separation is sufficiently small to produce BBH mergers, and this favorable donor mass range depends on stellar physics such as internal mixing (Fig. 6). Modeling stability in a way that reproduces the minimum post-SMT separations is therefore critical for population predictions of BBH mergers, in particular their masses and delay times. The few cases of population synthesis studies that have explored different assumptions on stability have indeed found a substantial effect on predictions from the SMT channel (Olejak et al. 2021; Shao & Li 2021; van Son et al. 2022b; Dorozsmai & Toonen 2024).

The question arises how to best model mass transfer stability in rapid binary codes to capture the results and trends found in detailed models. A common approach (e.g., Hurley et al. 2002; Claeys et al. 2014; Breivik et al. 2020; Riley et al. 2022) is to determine stability based on several fixed critical mass ratio values (or equivalent mass-radius exponents) for stars at different evolutionary stages, with a possible variation as a function of the core mass fraction in convective giants (Webbink 1985; Hjellming & Webbink 1987). We find that this is strongly inconsistent with stability in detailed stellar models, which indicate a clear trend of q_crit increasing with radius for radiative donors (e.g., q_crit ranging from 2 to 7 for a 30 M_⊙ donor depending on its radius; see Fig. 5). While here we show it with full 1D stellar models, this point was made and discussed already by Ge et al. (2015) and later Ge et al. (2020), using their adiabatic mass-loss model (Ge et al. 2010).

Here, we propose a revised approach for the treatment of mass transfer stability in population synthesis, motivated by the results in Sect. 3.3. Rather than deciding based on the mass ratio at RLOF, we suggest to determine stability based on the minimum orbital separation that may be reached via SMT evolution. Namely, if at the end of an SMT phase the orbit was to become smaller than the separation limit of the donor, the mass transfer becomes unstable. This approach is attractive for several reasons: (a) the minimum separations achievable from SMT evolution for different donors are robust against uncertainties of mass transfer (accretion efficiency, AM loss), whereas critical mass ratios are not (Fig. 5); (b) for radiative donors, it is the orbital separation near the end of the SMT phase that is directly connected to the physical origin of instability (Sect. 4.1); (c) for a given donor type, the minimum separation from SMT varies more slowly with the donor radius than the critical mass ratio; (d) final orbital separation after mass transfer is often the most relevant quantity for an evolutionary channel (e.g., formation of BBH mergers). Furthermore, in Sect. 4.2 we discuss how the minimum separation from SMT evolution can be related to the internal structure of the donor star. This opens an exciting new avenue of using the population of GW sources to constrain models of stellar interiors and solve puzzles such as the blue supergiant problem (Sect. 4.3). However, this only becomes possible if the separation limit is self-consistently implemented in the treatment of SMT evolution. Even having the most precise mapping of critical mass ratios for donors of different mass and radius will result in altered post-SMT separations when used across different binary evolution codes (e.g., due to the amount of mass transfer code-different).

The minimum orbital separation from SMT evolution obtained in this work are available on Zenodo. As a rule of thumb, minimum separation from MS donors are between ∼15 and 30 R_⊙, for HG donors are between ∼30 and 50 R_⊙, and for CHeB donors are between ∼8 and 15 R_⊙ (all for radiative-envelope donors). For convective-envelope donors, the stability is better described with critical mass ratios or mass-radius exponents.

5. Summary

At the advent of a rapid increase in the number of detections of compact binary mergers, theoretical predictions of the population of GW sources are highly needed, and yet they are still highly uncertain. A promising formation scenario, particularly for binary BH mergers, is stable mass transfer evolution in massive binary systems. Its main open questions have to do with how the binary orbit evolves during mass transfer under the influence of complex gas dynamics of high-mass X-ray binaries. Here, we studied the SMT channel through detailed binary evolution computations of interacting systems with a BH accretor and a massive star companion (BH+O-star), complemented with analytical results for interpretation. Our work yielded the following results.

(a) There is a fundamental limit to how close binary systems can get via SMT evolution that is robust against the uncertainties in binary physics of orbital evolution. Even under the assumption of very efficient orbital shrinkage due to AM loss through L2 outflows, the final size of the orbit is always ≳10 R_⊙. Systems evolving toward tighter orbits become dynamically unstable and result in stellar mergers instead (Fig. 3). While it remains uncertain which BH+Star systems evolve to become GW sources due to mass transfer unknowns, the outcomes of the SMT channel all converge to the same narrow window of final orbits of merging BBH systems across different model variations (Fig. 4), which facilitates confident predictions for the properties of BBH mergers.

(b) The orbital separation limit has direct implications for the properties of BBH mergers in the SMT channel: long delay times (≳1−2 Gyr) and a lack of a high BH spins from the tidal spin-up of their helium star progenitors (Fig. 7 and Sect. 4.4). At high metallicity, where the post-mass transfer orbits are expected to further expand due to strong Wolf-Rayet winds, the SMT channel may become severely quenched. (Fig. D.2). We find BBH mergers with masses from 10 M_⊙ to 90 M_⊙ and mass ratios from 0.3 to 1 (Fig. 8). Case A mass transfer dominates the formation of massive BBH mergers (≳40 M_⊙).

(c) The reason for the separation limit lies in the properties of the stellar structure (as opposed to in binary physics), which dictates when a system will become unstable. If the orbit becomes too narrow during mass transfer, a delayed dynamical instability is triggered by a rapid expansion of the remaining donor envelope due to its near-flat entropy profile (Fig. 9 and Sect. 4.1). The orbital size when this may occur depends on the entropy structure of the donor, which varies across evolutionary types. The closest separation from SMT evolution can be achieved from core-He burning donors (∼8−15 R_⊙) and late main sequence donors (∼15−30 R_⊙), while HG donors lead to wider orbits (≳30−50 R_⊙) and wide non-merging BBHs (Fig. 11).

(d) Close-orbit binaries from the SMT channel (such as BBH mergers or stripped-star systems) can be a unique probe of chemical mixing in stars. This is because any chemical abundance gradient in a radiative envelope of the donor introduces an entropy gradient, which stabilizes the mass transfer and allows for a tighter final orbit. Extended regions of constant composition (e.g., inner convective zones) have the opposite effect. The same internal mixing in stars that is important for the blue supergiant problem may have a substantial effect on the formation of BBH mergers (Fig. 6 and Sect. 4.3).

Our findings help identify the fundamental predictions of the SMT channel that may be used to discriminate which formation scenarios contribute to the observed population of GW sources. This will become particularly important in the near future, when the growing dataset of GW sources allows for the measurement of trends with redshift and spin. To incorporate our results into population models of GW sources, we propose a new treatment of mass transfer stability for rapid binary codes (Sect. 4.5).

Data availability

All the files needed to reproduce the MESA simulations performed in this study are available on Zenodo under https://zenodo.org/records/18198079. We also provide tables with minimum orbital separations from SMT evolution derived for donor stars of different mass radius, as well as the corresponding critical mass ratios, with application to rapid binary evolution codes (Sect. 4.5).

Acknowledgments

We thank the anonymous referee for useful comments and suggestions that helped to improve the paper. This research was supported by the Munich Institute for Astro-, Particle and BioPhysics (MIAPbP) which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. This research was supported by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project #512 (“Multiwavelength View on Massive Stars in the Era of Multimessanger Astronomy”). This work was performed in part at Aspen Center for Physics, which is supported by National Science Foundation grant PHY-2210452. AO acknowledge funding from the Netherlands 732 Organization for Scientific Research (NWO), as part of 733 the Vidi research program BinWaves (project number 734 639.042.728, PI: de Mink).

References

Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2020, Liv. Rev. Relat., 23, 3 [NASA ADS] [Google Scholar]
Abbott, R., Abbott, T. D., Abraham, S., et al. 2021, Phys. Rev. X, 11, 021053 [Google Scholar]
Abbott, R., Abbott, T. D., Acernese, F., et al. 2023, Phys. Rev. X, 13, 041039 [Google Scholar]
Abrams, N. S., Hundertmark, M. P. G., Khakpash, S., et al. 2025, ApJS, 276, 10 [Google Scholar]
Agrawal, P., Hurley, J., Stevenson, S., Szécsi, D., & Flynn, C. 2020, MNRAS, 497, 4549 [NASA ADS] [CrossRef] [Google Scholar]
Antonini, F., & Rasio, F. A. 2016, ApJ, 831, 187 [Google Scholar]
Antonini, F., Toonen, S., & Hamers, A. S. 2017, ApJ, 841, 77 [NASA ADS] [CrossRef] [Google Scholar]
Askar, A., Szkudlarek, M., Gondek-Rosińska, D., Giersz, M., & Bulik, T. 2017, MNRAS, 464, L36 [CrossRef] [Google Scholar]
Banerjee, S., & Olejak, A. 2024, ArXiv e-prints [arXiv:2411.15112] [Google Scholar]
Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, A&A, 635, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bavera, S. S., Fragos, T., Zevin, M., et al. 2021, A&A, 647, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Begelman, M. C., King, A. R., & Pringle, J. E. 2006, MNRAS, 370, 399 [Google Scholar]
Belczynski, K., Dominik, M., Bulik, T., et al. 2010, ApJ, 715, L138 [Google Scholar]
Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]
Belczynski, K., Klencki, J., Fields, C. E., et al. 2020, A&A, 636, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Belczynski, K., Romagnolo, A., Olejak, A., et al. 2022, ApJ, 925, 69 [NASA ADS] [CrossRef] [Google Scholar]
Bellinger, E. P., de Mink, S. E., van Rossem, W. E., & Justham, S. 2024, ApJ, 967, L39 [NASA ADS] [CrossRef] [Google Scholar]
Bestenlehner, J. M., Gräfener, G., Vink, J. S., et al. 2014, A&A, 570, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Blaauw, A. 1961, Bull. Astron. Inst. Nether., 15, 265 [Google Scholar]
Blundell, K. M., Bowler, M. G., & Schmidtobreick, L. 2008, ApJ, 678, L47 [NASA ADS] [CrossRef] [Google Scholar]
Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
Brandt, N., & Podsiadlowski, P. 1995, MNRAS, 274, 461 [NASA ADS] [CrossRef] [Google Scholar]
Breivik, K., Coughlin, S., Zevin, M., et al. 2020, ApJ, 898, 71 [Google Scholar]
Broekgaarden, F. S., Berger, E., Stevenson, S., et al. 2022a, MNRAS, 516, 5737 [NASA ADS] [CrossRef] [Google Scholar]
Broekgaarden, F. S., Stevenson, S., & Thrane, E. 2022b, ApJ, 938, 45 [CrossRef] [Google Scholar]
Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Casares, J., & Jonker, P. G. 2014, Space Sci. Rev., 183, 223 [NASA ADS] [CrossRef] [Google Scholar]
Casares, J., Negueruela, I., Ribó, M., et al. 2014, Nature, 505, 378 [Google Scholar]
Castro, N., Oey, M. S., Fossati, L., & Langer, N. 2018, ApJ, 868, 57 [NASA ADS] [CrossRef] [Google Scholar]
Cherepashchuk, A. M., Sunyaev, R. A., Fabrika, S. N., et al. 2005, A&A, 437, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Chruślińska, M. 2024, Ann. Phys., 536, 2200170 [CrossRef] [Google Scholar]
Chruslinska, M., & Nelemans, G. 2019, MNRAS, 488, 5300 [NASA ADS] [Google Scholar]
Chruslinska, M., Nelemans, G., & Belczynski, K. 2019, MNRAS, 482, 5012 [Google Scholar]
Chruślińska, M., Nelemans, G., Boco, L., & Lapi, A. 2021, MNRAS, 508, 4994 [CrossRef] [Google Scholar]
Claeys, J. S. W., Pols, O. R., Izzard, R. G., Vink, J., & Verbunt, F. W. M. 2014, A&A, 563, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Davies, B., Crowther, P. A., & Beasor, E. R. 2018, MNRAS, 478, 3138 [NASA ADS] [CrossRef] [Google Scholar]
de Burgos, A., Simón-Díaz, S., Urbaneja, M. A., & Negueruela, I. 2023, A&A, 674, A212 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
de Mink, S. E., & Mandel, I. 2016, MNRAS, 460, 3545 [NASA ADS] [CrossRef] [Google Scholar]
Detmers, R. G., Langer, N., Podsiadlowski, P., & Izzard, R. G. 2008, A&A, 484, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dorozsmai, A., & Toonen, S. 2024, MNRAS, 530, 3706 [NASA ADS] [CrossRef] [Google Scholar]
El-Badry, K. 2024, New Astron. Rev., 98, 101694 [NASA ADS] [CrossRef] [Google Scholar]
Eldridge, J. J., & Stanway, E. R. 2016, MNRAS, 462, 3302 [Google Scholar]
Fabrika, S. 2004, Astrophys. Space Phys. Res., 12, 1 [NASA ADS] [Google Scholar]
Farag, E., Renzo, M., Farmer, R., Chidester, M. T., & Timmes, F. X. 2022, ApJ, 937, 112 [NASA ADS] [CrossRef] [Google Scholar]
Farmer, R., Renzo, M., de Mink, S. E., Marchant, P., & Justham, S. 2019, ApJ, 887, 53 [Google Scholar]
Farrell, E., Groh, J. H., Meynet, G., & Eldridge, J. J. 2022, MNRAS, 512, 4116 [NASA ADS] [CrossRef] [Google Scholar]
Fragos, T., Andrews, J. J., Ramirez-Ruiz, E., et al. 2019, ApJ, 883, L45 [Google Scholar]
Fragos, T., Andrews, J. J., Bavera, S. S., et al. 2023, ApJS, 264, 45 [NASA ADS] [CrossRef] [Google Scholar]
Gagnier, D., & Pejcha, O. 2023, A&A, 674, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gallegos-Garcia, M., Berry, C. P. L., Marchant, P., & Kalogera, V. 2021, ApJ, 922, 110 [NASA ADS] [CrossRef] [Google Scholar]
Gallegos-Garcia, M., Jacquemin-Ide, J., & Kalogera, V. 2024, ApJ, 973, 168 [NASA ADS] [CrossRef] [Google Scholar]
García, F., Simaz Bunzel, A., Chaty, S., Porter, E., & Chassande-Mottin, E. 2021, A&A, 649, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ge, H., Hjellming, M. S., Webbink, R. F., Chen, X., & Han, Z. 2010, ApJ, 717, 724 [NASA ADS] [CrossRef] [Google Scholar]
Ge, H., Webbink, R. F., Chen, X., & Han, Z. 2015, ApJ, 812, 40 [Google Scholar]
Ge, H., Webbink, R. F., & Han, Z. 2020, ApJS, 249, 9 [NASA ADS] [CrossRef] [Google Scholar]
Ge, H., Tout, C. A., Chen, X., et al. 2024, ApJ, 975, 254 [NASA ADS] [CrossRef] [Google Scholar]
Georgy, C., Ekström, S., Eggenberger, P., et al. 2013, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gomez, S., & Grindlay, J. E. 2021, ApJ, 913, 48 [NASA ADS] [CrossRef] [Google Scholar]
Gräfener, G., & Hamann, W. R. 2008, A&A, 482, 945 [Google Scholar]
Hainich, R., Rühling, U., Todt, H., et al. 2014, A&A, 565, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Hamann, W. R., Koesterke, L., & Wessolowski, U. 1995, A&A, 299, 151 [Google Scholar]
Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
Hirai, R., & Mandel, I. 2022, ApJ, 937, L42 [NASA ADS] [CrossRef] [Google Scholar]
Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [Google Scholar]
Humphreys, R. M., & McElroy, D. B. 1984, ApJ, 284, 565 [NASA ADS] [CrossRef] [Google Scholar]
Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [Google Scholar]
Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
Ivanova, N., Justham, S., & Ricker, P. 2020, Common Envelope Evolution (IOP Publishing) [Google Scholar]
Janka, H.-T., & Kresse, D. 2024, Ap&SS, 369, 80 [NASA ADS] [CrossRef] [Google Scholar]
Janssens, S., Shenar, T., Sana, H., et al. 2022, A&A, 658, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Janssens, S., Shenar, T., Degenaar, N., et al. 2023, A&A, 677, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Jermyn, A. S., Bauer, E. B., Schwab, J., et al. 2023, ApJS, 265, 15 [NASA ADS] [CrossRef] [Google Scholar]
Justham, S., Podsiadlowski, P., & Vink, J. S. 2014, ApJ, 796, 121 [NASA ADS] [CrossRef] [Google Scholar]
Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
Kaiser, E. A., Hirschi, R., Arnett, W. D., et al. 2020, MNRAS, 496, 1967 [Google Scholar]
King, A. R., & Ritter, H. 1999, MNRAS, 309, 253 [Google Scholar]
King, A. R., Taam, R. E., & Begelman, M. C. 2000, ApJ, 530, L25 [NASA ADS] [CrossRef] [Google Scholar]
King, A., Lasota, J.-P., & Middleton, M. 2023, New Astron. Rev., 96, 101672 [CrossRef] [Google Scholar]
Kippenhahn, R., & Weigert, A. 1967, ZAp, 65, 251 [Google Scholar]
Klencki, J., & Metzger, B. D. 2025, ArXiv e-prints [arXiv:2510.09745] [Google Scholar]
Klencki, J., & Nelemans, G. 2019, IAU Symp., 346, 417 [Google Scholar]
Klencki, J., Nelemans, G., Istrate, A. G., & Pols, O. 2020, A&A, 638, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Klencki, J., Nelemans, G., Istrate, A. G., & Chruslinska, M. 2021, A&A, 645, A54 [EDP Sciences] [Google Scholar]
Klencki, J., Istrate, A., Nelemans, G., & Pols, O. 2022, A&A, 662, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kresse, D., Ertl, T., & Janka, H.-T. 2021, ApJ, 909, 169 [NASA ADS] [CrossRef] [Google Scholar]
Kruckow, M. U., Tauris, T. M., Langer, N., et al. 2016, A&A, 596, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kruckow, M. U., Tauris, T. M., Langer, N., Kramer, M., & Izzard, R. G. 2018, MNRAS, 481, 1908 [CrossRef] [Google Scholar]
Kruckow, M. U., Neunteufel, P. G., Di Stefano, R., Gao, Y., & Kobayashi, C. 2021, ApJ, 920, 86 [NASA ADS] [CrossRef] [Google Scholar]
Kushnir, D., Zaldarriaga, M., Kollmeier, J. A., & Waldman, R. 2016, MNRAS, 462, 844 [NASA ADS] [CrossRef] [Google Scholar]
Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
Langer, N., El Eid, M. F., & Fricke, K. J. 1985, A&A, 145, 179 [NASA ADS] [Google Scholar]
Langer, N., El Eid, M. F., & Baraffe, I. 1989, A&A, 224, L17 [NASA ADS] [Google Scholar]
Langer, N., Schürmann, C., Stoll, K., et al. 2020, A&A, 638, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lasota, J.-P., Vieira, R. S. S., Sadowski, A., Narayan, R., & Abramowicz, M. A. 2016, A&A, 587, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Law-Smith, J. A. P., Everson, R. W., Ramirez-Ruiz, E., et al. 2020, ArXiv e-prints [arXiv:2011.06630] [Google Scholar]
Lipunova, G. V. 1999, Astron. Lett., 25, 508 [NASA ADS] [Google Scholar]
Livio, M., & Soker, N. 1988, ApJ, 329, 764 [Google Scholar]
Lu, W., Fuller, J., Quataert, E., & Bonnerot, C. 2023, MNRAS, 519, 1409 [Google Scholar]
Ma, L., & Fuller, J. 2023, ApJ, 952, 53 [CrossRef] [Google Scholar]
Maggiore, M., Van Den Broeck, C., Bartolo, N., et al. 2020, JCAP, 2020, 050 [CrossRef] [Google Scholar]
Mahy, L., Sana, H., Shenar, T., et al. 2022, A&A, 664, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mandel, I. 2021, Res. Notes Am. Astron. Soc., 5, 223 [Google Scholar]
Mandel, I., & Broekgaarden, F. S. 2022, Liv. Rev. Relat., 25, 1 [Google Scholar]
Mandel, I., & de Mink, S. E. 2016, MNRAS, 458, 2634 [NASA ADS] [CrossRef] [Google Scholar]
Mapelli, M., & Giacobbo, N. 2018, MNRAS, 479, 4391 [NASA ADS] [CrossRef] [Google Scholar]
Mapelli, M., Dall’Amico, M., Bouffanais, Y., et al. 2021, MNRAS, 505, 339 [CrossRef] [Google Scholar]
Mapelli, M., Bouffanais, Y., Santoliquido, F., Arca Sedda, M., & Artale, M. C. 2022, MNRAS, 511, 5797 [NASA ADS] [CrossRef] [Google Scholar]
Marchant, P., & Bodensteiner, J. 2024, ARA&A, 62, 21 [NASA ADS] [CrossRef] [Google Scholar]
Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Marchant, P., Pappas, K. M. W., Gallegos-Garcia, M., et al. 2021, A&A, 650, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
McKernan, B., Ford, K. E. S., Bellovary, J., et al. 2018, ApJ, 866, 66 [Google Scholar]
McKinney, J. C., Tchekhovskoy, A., Sadowski, A., & Narayan, R. 2014, MNRAS, 441, 3177 [NASA ADS] [CrossRef] [Google Scholar]
Mennekens, N., & Vanbeveren, D. 2014, A&A, 564, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Menon, A., Ercolino, A., Urbaneja, M. A., et al. 2024, ApJ, 963, L42 [NASA ADS] [CrossRef] [Google Scholar]
Metzger, B. D. 2022, ApJ, 932, 84 [NASA ADS] [CrossRef] [Google Scholar]
Middleton, M. J., Walton, D. J., Alston, W., et al. 2021, MNRAS, 506, 1045 [NASA ADS] [CrossRef] [Google Scholar]
Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]
Mirabel, I. F., & Rodrigues, I. 2003, Science, 300, 1119 [Google Scholar]
Misra, D., Kovlakas, K., Fragos, T., et al. 2024, A&A, 682, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Moreno, M. M., Schneider, F. R. N., Röpke, F. K., et al. 2022, A&A, 667, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Neijssel, C. J., Vigna-Gómez, A., Stevenson, S., et al. 2019, MNRAS, 490, 3740 [Google Scholar]
Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
Olejak, A., Belczynski, K., & Ivanova, N. 2021, A&A, 651, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Olejak, A., Fryer, C. L., Belczynski, K., & Baibhav, V. 2022, MNRAS, 516, 2252 [NASA ADS] [CrossRef] [Google Scholar]
Olejak, A., Klencki, J., Xu, X.-T., et al. 2024, A&A, 689, A305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Orosz, J. A., McClintock, J. E., Narayan, R., et al. 2007, Nature, 449, 872 [NASA ADS] [CrossRef] [Google Scholar]
Orosz, J. A., Steeghs, D., McClintock, J. E., et al. 2009, ApJ, 697, 573 [NASA ADS] [CrossRef] [Google Scholar]
Paczyński, B., & Sienkiewicz, R. 1972, Acta Astron., 22, 73 [NASA ADS] [Google Scholar]
Paczyński, B., Ziólkowski, J., & Zytkow, A. 1969, Astrophys. Space Sci. Lib., 13, 237 [Google Scholar]
Papanikolaou, T., Vennin, V., & Langlois, D. 2021, JCAP, 2021, 053 [CrossRef] [Google Scholar]
Patrick, L. R., Lennon, D. J., Najarro, F., et al. 2025, A&A, 698, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pauli, D., Langer, N., Aguilera-Dena, D. R., Wang, C., & Marchant, P. 2022, A&A, 667, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pavlovskii, K., & Ivanova, N. 2015, MNRAS, 449, 4415 [Google Scholar]
Pavlovskii, K., Ivanova, N., Belczynski, K., & Van, K. X. 2017, MNRAS, 465, 2092 [Google Scholar]
Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
Picco, A., Marchant, P., Sana, H., & Nelemans, G. 2024, A&A, 681, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Podsiadlowski, P., & Rappaport, S. 2000, ApJ, 529, 946 [Google Scholar]
Podsiadlowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
Podsiadlowski, P., Rappaport, S., & Han, Z. 2003, MNRAS, 341, 385 [NASA ADS] [CrossRef] [Google Scholar]
Pols, O. R. 1994, A&A, 290, 119 [Google Scholar]
Poutanen, J., Lipunova, G., Fabrika, S., Butkevich, A. G., & Abolmasov, P. 2007, MNRAS, 377, 1187 [NASA ADS] [CrossRef] [Google Scholar]
Pribulla, T. 1998, Contrib. Astron. Obs. Skaln. Pleso, 28, 101 [NASA ADS] [Google Scholar]
Qin, Y., Fragos, T., Meynet, G., et al. 2018, A&A, 616, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Qin, Y., Marchant, P., Fragos, T., Meynet, G., & Kalogera, V. 2019, ApJ, 870, L18 [Google Scholar]
Ramachandran, V., Oskinova, L. M., Hamann, W. R., et al. 2022, A&A, 667, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rappaport, S. A., Podsiadlowski, P., & Pfahl, E. 2005, MNRAS, 356, 401 [NASA ADS] [CrossRef] [Google Scholar]
Reitze, D., Adhikari, R. X., Ballmer, S., et al. 2019, BAAS, 51, 35 [NASA ADS] [Google Scholar]
Renzo, M., & Götberg, Y. 2021, ApJ, 923, 277 [NASA ADS] [CrossRef] [Google Scholar]
Renzo, M., Hendriks, D. D., van Son, L. A. C., & Farmer, R. 2022, Res. Notes Am. Astron. Soc., 6, 25 [Google Scholar]
Renzo, M., Zapartas, E., Justham, S., et al. 2023, ApJ, 942, L32 [NASA ADS] [CrossRef] [Google Scholar]
Repetto, S., & Nelemans, G. 2015, MNRAS, 453, 3341 [Google Scholar]
Repetto, S., Davies, M. B., & Sigurdsson, S. 2012, MNRAS, 425, 2799 [Google Scholar]
Riley, J., Mandel, I., Marchant, P., et al. 2021, MNRAS, 505, 663 [Google Scholar]
Riley, J., Agrawal, P., Barrett, J. W., et al. 2022, ApJS, 258, 34 [NASA ADS] [CrossRef] [Google Scholar]
Rodriguez, C. L., Haster, C.-J., Chatterjee, S., Kalogera, V., & Rasio, F. A. 2016, ApJ, 824, L8 [NASA ADS] [CrossRef] [Google Scholar]
Rodriguez, C. L., Zevin, M., Amaro-Seoane, P., et al. 2019, Phys. Rev. D, 100, 043027 [Google Scholar]
Romagnolo, A., Belczynski, K., Klencki, J., et al. 2023, MNRAS, 525, 706 [NASA ADS] [CrossRef] [Google Scholar]
Romagnolo, A., Klencki, J., Vigna-Gómez, A., & Belczynski, K. 2025, A&A, 693, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Romero-Shaw, I., Hirai, R., Bahramian, A., Willcox, R., & Mandel, I. 2023, MNRAS, 524, 245 [NASA ADS] [CrossRef] [Google Scholar]
Sądowski, A., & Narayan, R. 2015, MNRAS, 453, 3213 [Google Scholar]
Sądowski, A., & Narayan, R. 2016, MNRAS, 456, 3929 [CrossRef] [Google Scholar]
Sądowski, A., Narayan, R., McKinney, J. C., & Tchekhovskoy, A. 2014, MNRAS, 439, 503 [CrossRef] [Google Scholar]
Samsing, J. 2018, Phys. Rev. D, 97, 103014 [CrossRef] [Google Scholar]
Samsing, J., Bartos, I., D’Orazio, D. J., et al. 2022, Nature, 603, 237 [NASA ADS] [CrossRef] [Google Scholar]
Sander, A. A. C., & Vink, J. S. 2020, MNRAS, 499, 873 [Google Scholar]
Sander, A. A. C., Vink, J. S., & Hamann, W. R. 2020, MNRAS, 491, 4406 [Google Scholar]
Sanyal, D., Grassitelli, L., Langer, N., & Bestenlehner, J. M. 2015, A&A, 580, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sanyal, D., Langer, N., Szécsi, D., Yoon, S.-C., & Grassitelli, L. 2017, A&A, 597, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sasaki, M., Suyama, T., Tanaka, T., & Yokoyama, S. 2018, Class. Quant. Grav., 35, 063001 [NASA ADS] [CrossRef] [Google Scholar]
Schneider, F. R. N., Podsiadlowski, P., & Laplace, E. 2024, A&A, 686, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Schootemeijer, A., Langer, N., Grin, N. J., & Wang, C. 2019, A&A, 625, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Schrøder, S. L., MacLeod, M., Ramirez-Ruiz, E., et al. 2021, ArXiv e-prints [arXiv:2107.09675] [Google Scholar]
Schürmann, C., Langer, N., Kramer, J. A., et al. 2024, A&A, 690, A282 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sen, K., Langer, N., Pauli, D., et al. 2023, A&A, 672, A198 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]
Shao, Y., & Li, X.-D. 2021, ApJ, 920, 81 [NASA ADS] [CrossRef] [Google Scholar]
Shenar, T., Sana, H., Mahy, L., et al. 2022, Nat. Astron., 6, 1085 [NASA ADS] [CrossRef] [Google Scholar]
Shenar, T., Bodensteiner, J., Sana, H., et al. 2024, A&A, 690, A289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Shikauchi, M., Hirai, R., & Mandel, I. 2025, ApJ, 984, 149 [Google Scholar]
Stevenson, S., Vigna-Gómez, A., Mandel, I., et al. 2017, Nat. Commun., 8, 14906 [Google Scholar]
Stone, N. C., Metzger, B. D., & Haiman, Z. 2017, MNRAS, 464, 946 [Google Scholar]
Stothers, R. B., & Chin, C.-W. 1992, ApJ, 390, 136 [NASA ADS] [CrossRef] [Google Scholar]
Tauris, T. M., & van den Heuvel, E. P. J. 2006, Formation and Evolution Of Compact Stellar X-ray Sources (Cambridge: Cambridge University Press) [Google Scholar]
Tauris, T. M., & van den Heuvel, E. P. J. 2023, Physics of Binary Star Evolution. From Stars to X-ray Binaries and Gravitational Wave Sources (Princeton University Press) [Google Scholar]
Tauris, T. M., Kramer, M., Freire, P. C. C., et al. 2017, ApJ, 846, 170 [Google Scholar]
Temmink, K. D., Pols, O. R., Justham, S., Istrate, A. G., & Toonen, S. 2023, A&A, 669, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Tramper, F., Sana, H., & de Koter, A. 2016, ApJ, 833, 133 [CrossRef] [Google Scholar]
Tutukov, A. V., & Yungelson, L. R. 1993, MNRAS, 260, 675 [Google Scholar]
van den Heuvel, E. P. J. 1976, IAU Symp., 73, 35 [Google Scholar]
van den Heuvel, E. P. J. 1994, A&A, 291, L39 [NASA ADS] [Google Scholar]
van den Heuvel, E. P. J., Portegies Zwart, S. F., & de Mink, S. E. 2017, MNRAS, 471, 4256 [Google Scholar]
van Son, L. A. C., de Mink, S. E., Callister, T., et al. 2022a, ApJ, 931, 17 [NASA ADS] [CrossRef] [Google Scholar]
van Son, L. A. C., de Mink, S. E., Renzo, M., et al. 2022b, ApJ, 940, 184 [NASA ADS] [CrossRef] [Google Scholar]
Vanbeveren, D., Mennekens, N., Van Rensbergen, W., & De Loore, C. 2013, A&A, 552, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Vigna-Gómez, A. 2025, A&A, 701, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Vigna-Gómez, A., Neijssel, C. J., Stevenson, S., et al. 2018, MNRAS, 481, 4009 [Google Scholar]
Vigna-Gómez, A., Wassink, M., Klencki, J., et al. 2022, MNRAS, 511, 2326 [CrossRef] [Google Scholar]
Vigna-Gómez, A., Willcox, R., Tamborra, I., et al. 2024, Phys. Rev. Lett., 132, 191403 [CrossRef] [Google Scholar]
Vink, J. S. 2017, A&A, 607, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Vink, J. S. 2022, ARA&A, 60, 203 [NASA ADS] [CrossRef] [Google Scholar]
Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Vink, J. S., Muijres, L. E., Anthonisse, B., et al. 2011, A&A, 531, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Vynatheya, P., & Hamers, A. S. 2022, ApJ, 926, 195 [NASA ADS] [CrossRef] [Google Scholar]
Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
Webbink, R. F. 1985, in Interacting Binary Stars, eds. J. E. Pringle, & R. A. Wade, 39 [Google Scholar]
Wei, D., Schneider, F. R. N., Podsiadlowski, P., et al. 2023, ArXiv e-prints [arXiv:2311.07278] [Google Scholar]
Wellstein, S., Langer, N., & Braun, H. 2001, A&A, 369, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Wiktorowicz, G., Lu, Y., Wyrzykowski, Ł., et al. 2020, ApJ, 905, 134 [NASA ADS] [CrossRef] [Google Scholar]
Willcox, R., MacLeod, M., Mandel, I., & Hirai, R. 2023, ApJ, 958, 138 [NASA ADS] [CrossRef] [Google Scholar]
Woods, T. E., & Ivanova, N. 2011, ApJ, 739, L48 [NASA ADS] [CrossRef] [Google Scholar]
Yoon, S.-C. 2017, MNRAS, 470, 3970 [NASA ADS] [CrossRef] [Google Scholar]
Yoon, S. C., Langer, N., & Norman, C. 2006, A&A, 460, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Zahn, J. P. 2008, EAS Publi. Ser., 29, 67 [Google Scholar]
Zaldarriaga, M., Kushnir, D., & Kollmeier, J. A. 2018, MNRAS, 473, 4174 [Google Scholar]
Zevin, M., & Bavera, S. S. 2022, ApJ, 933, 86 [NASA ADS] [CrossRef] [Google Scholar]
Zevin, M., Bavera, S. S., Berry, C. P. L., et al. 2021, ApJ, 910, 152 [Google Scholar]

¹

Unless the stellar wind of the donor is comparable to the highly super-Eddington mass transfer rate through L1 of ∼10⁻³ M_⊙ yr⁻¹.

²

Both examples of SMT evolution in Fig. 1 would satisfy the mass transfer stability criteria often used in population synthesis (ζ_RL < 6.5).

³

See Chapter 7 of the lecture notes by Onno Pols https://www.astro.ru.nl/~onnop/education/binaries_utrecht_notes/

⁴

This is because massive stars are centrally condensed and have low moments of inertia. An exception are early MS stars interacting in short-period orbits, in which case J_spin; star may be of the order of ∼0.1J_orb.

⁵

What is meant here is mass ejected at distance r ≪ a from the BH, with velocity V ≫ V_orb. This includes winds launched at the spherization radius of a supercritical disk (Shakura & Sunyaev 1973).

⁶

MESA version r15140, http://mesa.sourceforge.net/

⁷

We did not apply the convective premixing scheme introduced in Paxton et al. (2019).

⁸

Notably, this does not affect the evolution of stellar radii nearly as much as the previous MLT++ treatment; see Sect. 7.2 in Jermyn et al. (2023) for a comparison.

⁹

On the hot side of the bi-stability jump.

¹⁰

Other outcomes may be possible if, despite the mass transfer instability, a dynamical in-spiral and a classical CE phase are avoided.

¹¹

Meaning the ζ exponent stays the same, where ζ = d log R_RL/d log M_donor.

¹²

In a system with q smaller than q_crit, the orbit would shrink less during the phase when M_donor > M_accretor and it would expand more once/if the mass ratio becomes reversed (M_accretor > M_donor).

¹³

The critical mass ratios q_crit in the α_semiconv. = 0.01 variation were computed in the same as in the other variations.

¹⁴

This is the reason for the trend in orbital separations of BH+He-star systems in Fig. 3.

¹⁵

These models are a small subset of the grid with a varying q_RLOF that was computed to determine the critical mass ratio q_crit for the donors of different masses and radii in Fig. 5.

¹⁶

As pointed out already by Paczyński & Sienkiewicz (1972) and more recently discussed by Podsiadlowski et al. (2002), Woods & Ivanova (2011), Pavlovskii & Ivanova (2015), the entropy adjustment in the outermost layers of the donor plays a meaningful role in how the donor responses to mass loss, decreasing Ṁ and stabilizing the mass transfer, which is neglected in the classical adiabatic results such as Hjellming & Webbink (1987).

¹⁷

The only hypothetical way to have these uncertainties play a role is if γ was not constant but would increase only after the flat entropy layers have been stripped, in which case the transfer of the remaining envelope could lead to stronger orbital shrinkage at late SMT stages. This would require the specific AM loss increasing with the decreasing mass transfer rate.

¹⁸

While we chose to vary semiconvection in Fig. 6, various mixing processes simultaneously play a role in establishing the chemical structure of a radiative envelope, which in turn determines the transition from blue to red supergiants (e.g., Georgy et al. 2013; Kaiser et al. 2020; Farrell et al. 2022) and the minimum separation from SMT (Sect. 4.2).

¹⁹

One key additional component is the criteria for mass transfer stability, which greatly vary across different codes and their iterations.

Appendix A: Semi-analytical model for stable-mass transfer evolution

Here we describe our method to estimate the outcome of an SMT phase in a BH+Star binary (used, for instance, to obtain the orbital evolution in Fig. 1). The goal is not have a fully accurate model but rather a simple tool to compare our expectations with the results from detailed binary simulations.

We consider a binary with a BH M_BH and a star M_star; ini that initiates mass transfer when the orbital separation is a_ini (and the eccentricity is zero). The change of separation as a result of an SMT phase can be written as

$\begin{matrix} a_{fin} = a_{ini} + \int_{M_{star ; ini}}^{M_{star ; final}} \frac{d a}{d M_{star}} (M_{BH}, β, f_{wind}, f_{bipolar}, f_{L 2}) d M_{star}, \end{matrix}$ $\begin{aligned} a_{\rm fin} = a_{\rm ini} + \int _{M_{\rm star;ini}}^{M_{\rm star;final}} \frac{\mathrm{d}a}{\mathrm{d}M_{\rm star}} \left(M_{\rm BH}, \beta , f_{\rm wind}, f_{\rm bipolar}, f_{\rm L2}\right) \mathrm{d}M_{\rm star}, \end{aligned}$ (A.1)

where the expression for da/dM_star can be found by combining Eqn. 1 and Eqn. 5. Here, M_{star; final} is the mass at the end of the SMT phase, which may further decrease before the core collapse due to post-SMT wind mass loss. To compute the integral in Eqn. 6, we need to know M_BH, β, f_wind, f_bipolar, f_L2, and M_{star; final}. The BH mass M_BH is given by the initial conditions, alongside a_ini and M_star; ini. We assume that the accretion rate onto the BH is Eddington-limited, which in the case of BH+Star systems with massive star donors leads to nearly fully non-conservative mass transfer with β ≈ 0 and M_BH ≈ const (e.g., Klencki & Nelemans 2019). Furthermore, the fraction of the mass lost via wind is

$\begin{matrix} f_{wind} = \frac{Δ M_{star ; wind}}{M_{star ; ini} - M_{star ; final}} = \frac{{\dot{M}}_{star ; wind} Δ t_{SMT}}{Δ M_{star}}, \end{matrix}$ $\begin{aligned} f_{\rm wind} = \frac{\Delta M_{\rm star;wind}}{M_{\rm star;ini}-M_{\rm star;final}} = \frac{\dot{M}_{\rm star;wind}\Delta t_{\rm SMT}}{\Delta M_{\rm star}}, \end{aligned}$ (A.2)

where Ṁ_star;wind is the average mass-loss rate via stellar wind and Δt_SMT is the duration of the SMT phase. Fractions f_bipolar and f_L2 are free parameters that need to satisfy f_bipolar + f_L2 = 1 − f_wind.

To gauge how much mass is lost from the donor (ΔM_star) and on what timescale (Δt_SMT), we take a look at the evolutionary stage of the donor star. The first possibility is that the donor is a post-main sequence (post-MS) giant star, with a helium core M_core and a hydrogen envelope M_env, i.e., case B or case C mass transfer (Kippenhahn & Weigert 1967). In that case, we assume ΔM_star = 0.9M_env, i.e., the mass transfer strips nearly the entire envelope (90%). The exact choice of 90% is somewhat arbitrary but it is motivated by our detailed binary models of BBH merger progenitors in which the remaining unstripped envelope fraction is typically between 5% and 10% (in SMT leading to wide orbit BBH systems, the amount of envelope left unstripped can be much larger, Klencki et al. 2022). We further assumed a thermal timescale mass transfer rate of Ṁ_star = 10⁻³ M_⊙ yr⁻¹ so that the duration Δt_SMT = ΔM_star/Ṁ_star is typically of the order of 10⁴ yr.

In the case of a donor that is a MS star (case A interaction), there is no distinct core-envelope structure yet to estimate the amount of mass that is transferred. In general, ΔM_star will depend on the parameters of each individual system such as the orbital period, mass ratio, and the donor mass (see the analytical fits and the methods by Schürmann et al. 2024; Shikauchi et al. 2025). Case A mass transfer is also typically not a single short-lived event but rather a series of two or more separate interaction phases, some happening on the nuclear timescale, taking place all the way until the end of the MS (Pols 1994; Wellstein et al. 2001; Marchant & Bodensteiner 2024). Right afterward, the post-MS expansion of the remaining donor leads to another interaction referred to as case AB mass transfer, that further strips the star of mass. Here, for simplicity, we model this entire sequence of interactions (case A + AB) as a single SMT phase with the duration Δt_SMT equal to remaining MS lifetime from the onset of RLOF. We further assume that the mass of the donor after the mass transfer is M_{star; final} = M_star; TAMS − 0.9M_env; TAMS, where M_star; TAMS and M_env; TAMS are respectively the mass of the donor and the mass of its envelope at terminal-age MS (TAMS) if the donor was to continue its evolution without ever engaging into mass transfer (as a single star). This approach is quite accurate for case A mass transfer initiated during an advanced MS stage (X_center ≲ 0.2 − 0.3) but it underestimates the amount of mass that is transferred in very-close binaries that interact earlier.

To obtain M_{star; final} and f_wind, we thus need to know several parameters of the donor star: its evolutionary stage, core mass, remaining MS lifetime (for MS stars), and the wind mass-loss rate. Those could be derived from analytical fits to stellar tracks by Hurley et al. (2002), as done in various population synthesis codes. Here, we use our custom and publicly available massive star models from Klencki et al. (2020), with more up-to-date treatment of mixing and mass loss.

Finally, we account from the post-SMT wind mass loss from the donor star, now a massive He star. We assume optically thick He-star winds from Hamann et al. (1995) divided by 10 (Yoon et al. 2006). The wind prescription depends on the luminosity of the He-star L_He; star and its surface X fraction X_surf. We approximate L_He; star as the average core-He burning luminosity of a single stellar model with the TAMS He core mass equal to M_{star; final}. For X_surf, we assume 0.1. For the assumed metallicity Z = 0.1 Z_⊙, the mass loss through He-star winds is generally small.

Although simplistic, the mass-transfer model presented above is similar to how SMT evolution (in particular case B/C interaction) is treated in rapid binary-evolution codes widely used for GW-source population synthesis.¹⁹

Appendix B: Uncertainty: BH natal kicks

Throughout the paper, we have assumed that the secondary BH forms via direct collapse with no natal kick. While tentative evidence suggests that complete collapse may occur in stellar-mass BHs (Mirabel & Rodrigues 2003; Shenar et al. 2022; Vigna-Gómez et al. 2024), the conditions required are not fully understood. Moreover, even in a complete collapse scenario, uncertainties remain regarding the amount of mass radiated in neutrinos and the natal kick they impart. From simulations, the mass decrement from neutrino emission is less than 0.6 M_⊙ (e.g., Kresse et al. 2021) and the neutrino natal kick magnitude is likely around a few or a few tens of kilometers per second (see Janka & Kresse 2024, and references therein). Recently, Vigna-Gómez et al. (2024) used VFTS 243 to constrain the neutrino natal kick magnitude to ≲10 km/s, corresponding to neutrino emission asymmetries of ≲4%. On the other hand, space distribution and proper motions of Galactic BH low-mass X-ray binaries point toward BH kicks with magnitudes up to ∼100 km/s (Repetto et al. 2012; Repetto & Nelemans 2015; Mandel & de Mink 2016).

Altogether, these findings suggest that while the natal kicks of BHs are likely not as strong as in the case of NSs, our default assumption of a zero kick and no mass loss may be too simplistic. The main question is how much may it affect the delay times of BBH mergers obtained in our study. This is addressed in depth in the recent Vigna-Gómez (2025). Briefly, in the case of mass loss with no additional kick, a spherically symmetric mass ejection would make the orbit wider everywhere except at the periastron (Blaauw 1961), thus weakening the GW emission and always leading to longer delay times. If the newly formed BH receives an additional velocity kick, the impact on its orbit will depend on the direction of the kick. This has been discussed in the literature in the context of X-ray binaries (Brandt & Podsiadlowski 1995), BBH mergers (Marchant et al. 2016), and recently in the context of BBHs formed via the complete collapse scenario (Vigna-Gómez 2025). Broadly, the resulting BBH delay time becomes notably shorter only if the kick is directed in the opposed direction to the orbital movement and its magnitude is comparable to the orbital velocity, which in the case of BH + massive He stars systems are of the order 200-400 km/s. For example, for isotropic BH kicks with the magnitude equal to half the orbital velocity (i.e., 100-200 km/s), in 20% of cases the BBH delay time would become shorter by a factor of at least ten (Vigna-Gómez 2025). BH kicks of a few tens of kilometers per second or less would have a negligible effect on the resulting BBH delay times.

Appendix C: Typo in the angular momentum loss through L2 in MESA models

Fig. C.1.

Comparison of the intended versus the actual effective fraction of the mass lost through L2 in our MESA models (see text for explanation of the discrepancy). The analytical predictions of the orbital separation during SMT in Fig. 2 follow the actual mass loss fractions, i.e., the solid lines, so that they can be directly compared with the MESA models.

Throughout the paper, we consider three modes of ejection of the non-accreted matter in an interacting BH + Star binary: with the wind of the donor, as a bipolar outflow or fast wind launched close to the BH accretor, or as mass ejected from the proximity of the L2 point. Each case corresponds to different specific amount of AM that is lost, parametrized by γ (see Sect. 2.2 for details). In particular, for the mass loss through the L2 point, we recall

$\begin{matrix} γ_{L 2} = {(\frac{a_{L 2}}{a})}^{2} \frac{{(M_{BH} + M_{star})}^{2}}{M_{BH} M_{star}} \approx 1.44 \frac{{(M_{BH} + M_{star})}^{2}}{M_{BH} M_{star}}, \end{matrix}$ $\begin{aligned} \gamma _{\rm L2} = \left(\frac{a_{\rm L2}}{a}\right)^2 \frac{(M_{\rm BH}+M_{\rm star})^2}{M_{\rm BH}M_{\rm star}} \approx 1.44 \frac{(M_{\rm BH}+M_{\rm star})^2}{M_{\rm BH}M_{\rm star}}, \end{aligned}$ (C.1)

where a_L2 is the distance from the L2 to the center of mass that for most mass ratios can be approximates as a_L2 ≈ 1.2a (Pribulla 1998). The above equation assumes that at the location of L2 the ejected mass co-rotates with the binary.

In the binary module of MESA (Paxton et al. 2015), the treatment of the non-accreted matter is set up with several mass_transfer controls. In particular, mass_transfer_delta defines the fraction of mass that is lost via a circumbinary coplanar toroid. The radius of the toroid a_cct is set by the mass_transfer_gamma parameter, such that (a_cct/a)^0.5 = mass_transfer_gamma. Crucially, the toroid is assumed to rotate with its own period of a Keplerian orbit, rather than to corotate with the binary. As a result, the specific AM of the mass lost from the toroid can be characterized by γ_CCT:

$\begin{matrix} γ_{CCT} = \sqrt{\frac{a_{CCT}}{a}} \frac{{(M_{BH} + M_{star})}^{2}}{M_{BH} M_{star}} \cdot \end{matrix}$ $\begin{aligned} \gamma _{\rm CCT} = \sqrt{\frac{a_{\rm CCT}}{a}} \frac{(M_{\rm BH}+M_{\rm star})^2}{M_{\rm BH}M_{\rm star}}\cdot \end{aligned}$ (C.2)

That means to obtain γ_CCT = γ_L2 and model mass loss through the L2 point in MESA, one needs to set mass_transfer_gamma = 1.44 and mass_transfer_delta to the intended fraction of mass lost through L2. In our case, we have set mass_transfer_delta = 0, 0.25, and 0.75 (depending on the model variation) and, unfortunately, mass_transfer_gamma = 1.2 instead of 1.44. This means that the amount of AM lost with L2 outflows was lower than intended. Alternatively, this means that the effective fraction of mass lost through L2 in our models was lower than the intended value set with mass_transfer_delta. The correction factor depends on the mass ratio, as illustrated in Fig. C.1. Effectively, in MESA models with mass_transfer_delta = 0.25 and mass_transfer_gamma = 1.2, the actual fraction of mass lost through L2 was about ∼0.2. We refer to them as enhanced orbital shrinkage or enhanced AM loss in the main text, with γ ≈ 0.2γ_L2 + 0.8γ_BH. Similarly, in models with mass_transfer_delta = 0.75 and mass_transfer_gamma = 1.2, the actual fraction of mass lost through L2 was about ∼0.55. In the main text these are referred to as extreme orbital shrinkage with γ ≈ 0.55γ_L2 + 0.4γ_BH (Fig. 4). Figure C.1 reveals that as the mass ratio M_donor/M_accretor decreases during a mass transfer phase, the effective fraction of L2 mass loss in our models slowly increases. We do not expect this to have any effect on the conclusions presented in the paper and the predicted existence of a separation limit from SMT evolution. If anything, the enhanced L2 mass loss at late stages of an interaction (after the constant entropy layers have already been stripped, e.g., MS or HG donors) might allow for a somewhat smaller final separation compared to models with a constant AM loss.

Appendix D: Additional figures

Fig. D.1.

Parameter window for BBH mergers from SMT evolution across different BH masses. Here, we plot the outcome of binary MESA models marking BBH mergers with star symbols, assuming fiducial AM loss (γ = γ_BH) and different primary BH masses M_BH; 1. Color indicates the final fate: wide BBH system (light yellow), merging BBH system (colorscale indicating the delay time), unstable MT with a convective donor (red), unstable MT with a radiative donor, likely leading to a BH + star merger (grey), close non-interacting systems due to chemically homogeneous mixing or very strong winds (white dotted). In the top two rows, the blue line marks the boundary between MS and post-MS donors. In the bottom two rows, only a limited range of periods is computed and all the donors are on the MS. The grid is constructed based on the initial mass ratio M_BH; 1/M_star in steps of 0.02.

Fig. D.2.

SMT channel becoming ineffective at high metallicity because of the combined effect of the separation limit in SMT evolution and orbital widening via Wolf-Rayet winds. We plot the outcome of binary MESA models at different metallicities, marking BBH mergers with stars. The first BH mass is M_BH; 1 = 10 M_⊙ and we assume the fiducial AM loss for SMT (γ = γ_BH). Color indicates the final fate, same as Fig. D.1. The blue line marks the boundary between MS and post-MS donors.

Fig. D.3.

Hertzsprung-Russell diagram with single stellar tracks that were used as a basis for the computation of critical mass ratios, minimum orbital separations from SMT evolution, and the corresponding minimum BBH merger delay times (see results for stellar models with semiconvection α_semiconv. = 33 in Fig. 5 and with α_semiconv. = 0.01 in the right panel of Fig. 6). Here there tracks are of 30 different masses, logarithmically spaced from 10 to 100 M_⊙, evolved until at least the end of core-He burning. Black dots are equally spaced every 50,000 years during the post-MS evolution.

Fig. D.4.

Evolution of binary separation during the mass transfer phase in MESA models of BH+O-star systems with q = q_crit mass ratios and initial O-star masses of 35, 55, and 75 M_⊙ (the three different panels), plotted as a function of the decreasing remaining donor mass. Different lines correspond to different initial separations, colored by the initial mass ratio M_donor/M_accretor. The initially more narrow systems interact when the donor is a MS star (closed circles), whereas in wider orbits the interaction is from a post-MS donor (open squares). Because the mass ratio is critical for each mass and radius of the donor at RLOF, the models shown here lead to the smallest binary separations via SMT evolution given the donor. See Fig. 5 for a full parameter space exploration, with other initial donor masses and radii. Assuming that at the end of its evolution the donor collapses to form a BH with mass 15, 22, and 27 M_⊙ (for different panels), we mark which binary separations would be required for BBH delay times of 100, 1000, or 10000 Myr for BBH mass ratio 0.9. Counter-intuitively, the smallest separations and the shortest BBH delay times from the SMT channel may originate from initially the widest BH+O-star systems (post-MS donors in the 35 and 55 M_⊙ panels).

Fig. D.5.

Same as Fig. 6 but comparing the final orbital separations instead of the BBH delay times. In the variation with low efficiency of semiconvection (right) all the post-MS donors are of the HG type. They are characterized by wider post-SMT separations compared to core-He burning (CHeB) donors due to differences in their internal chemical / entropy structure (Fig. 11). Based on that, we propose a new mass transfer stability treatment in rapid binary codes in Sect. 4.5. The difference between stellar models in both panels is closely connected to the so-called blue supergiant problem (Sect. 4.3).

All Figures

Fig. 1.

Schematic comparison of orbital shrinkage via common envelope and stable mass transfer in a BBH merger progenitor (here a binary with a 35 M_⊙ stellar donor and 10 M_⊙ BH accretor), based on a simple analytical model (Sect. 2.3) rather than a detailed evolutionary calculation. The SMT lines follow assumptions typically used in population synthesis of GW sources, naively suggesting that mass transfer with enhanced AM loss (blue) can produce separation as small as CE evolution. In this paper, we use detailed binary evolution calculations to show why this is not the case (Fig. 3).

In the text

Fig. 6.

Formation of BBH mergers is a probe of internal chemical mixing in stars and of the stellar structure. We plot the minimum BBH delay times from SMT evolution given the donor mass (at ZAMS) and radius (at RLOF) for two variations in the efficiency of semiconvective mixing in stars (α_semiconv.). Only cases with the BBH delay time below ≲13.7 Gyr (yellow-brown regions) are potential GW sources. The range of donors that may lead to BBH mergers is severely reduced in the variation with low efficiency of semiconvection (right panel) and it shows a preference for high-mass donors (≳40 M_⊙). This is because the chemical structure of donor stars determines the conditions for delayed-dynamical instability and therefore affects the critical mass ratios, the minimum post-SMT separations, and BBH delay times (Sect. 4.2). This is different from the assumptions on the orbital AM loss that only affects the q_crit (Fig. 5). The difference between stellar models in both panels is closely connected to the blue supergiant problem (Sect. 4.3). The thick blue line shows the transition from MS to post-MS donors. Several main types of donors are labeled (Hertzsprung gap, core-He burning, convective envelopes, He-rich envelopers); see text. Based on MESA models of BH+O-star binaries evolving through SMT at the critical mass ratio q = q_crit. See Fig. D.2 for post-SMT separations.

In the text

Fig. 2.

Window for the formation of BBH mergers as predicted by semi-analytical and detailed binary models. Colors mark the evolutionary outcomes of interacting BH+O-star systems across different initial periods and mass ratios, calculated with our semi-analytical rapid model of SMT evolution (left panel; Sect. 2.3) and compared with MESA binary models for two different assumptions on orbital shrinkage during mass transfer: fiducial (γ = γ_BH, center) and enhanced shrinkage due to L2 outflows (right). The initial BH mass is always M_BH; 1 = 10 M_⊙ and metallicity is Z = 0.1 Z_⊙ (see Fig. D.1 for other BH masses). Wide-non interacting systems are not shown. Solid blue lines mark systems in which the SMT evolution would lead to final orbital separation a_fin = 2 R_⊙ or 25 R_⊙, according to the semi-analytical model, which is approximately the range of separations needed for BBH mergers. The dashed red line is the boundary between stable and unstable mass transfer. The outcomes of the semi-analytical model are only applicable if the mass transfer is stable. In rapid codes, it is typically assumed to be related to a critical mass ratio (the vertical line at q_crit ≈ 0.28, left panel). In the MESA models, the stability is determined self-consistently at every timestep, and it is found to be entirely different. The mass transfer only remains stable in systems where the final separation is a_fin ≳ 10 R_⊙. This conclusion is robust against uncertainties of SMT evolution and holds even if enhanced orbital shrinkage is assumed (right), leading to BBH mergers with long delay times ≳1 Gyr (Sect. 3.4).

In the text

Fig. 3.

Fundamental orbital separation limit from stable mass transfer (red dashed line) seen in the population of BH+He-star systems formed in MESA binary models. Separations below ∼8−10 R_⊙ are excluded in the SMT channel due to mass transfer instability (dashed region, physical origin in Sect. 4.1). As a result, BBH mergers from SMT evolution have long delay times of ≳1 Gyr, and their BH+He-star progenitors tend to be outside the regime of tidal spin-up (P ≳ 0.8 day). Here, the orbital evolution during SMT assumes enhanced AM loss due to L2 outflows with γ ≈ 0.8γ_BH + 0.2γ_L2. However, models assuming a different γ yield a similar range of BH+He-star separations (Fig. 4). The solid red line indicates a hard lower limit for the separation of BH+He-star systems in the CE channel, set by the size of a naked helium star. The figure is based on a grid of BH+O-star models with M_BH; 1 = 10 M_⊙ and Z = 0.1 Z_⊙ metallicity, with similar results found also for larger BH masses (Sect. 3.4).

Fig. 4.

Narrow window in the parameter space for the SMT channel converging to a well-defined narrow range of final orbits regardless of uncertainties in binary physics. We plot the orbital periods of BBH merger progenitors from before the mass transfer (BH+O-star stage, left) and after the SMT phase has taken place (BH+He-star stage, right). The figure is based on grids of detailed binary models with M_BH; 1 = 10 M_⊙ and varying assumptions on the orbital shrinkage during mass transfer (i.e., γ values, shown in different colors). Changing the assumption on γ significantly shifts the pre-SMT periods of BBH merger progenitors, but has little effect on the post-interaction orbits at the BH+He-star stage (or the properties of BBH mergers). The dashed red line shows the lower limit on the period of a BH+He-star systems, such that the naked helium star does not overflow its Roche lobe. We mark the periods and mass ratios of the known BH+OB-star systems (left panel, including supergiant high mass X-ray binaries) and of BH+Wolf-Rayet X-ray binaries (right). Cyg X-3 cannot be reproduced by SMT in our models, suggesting its origin in CE evolution.

In the text

Fig. 4.

Narrow window in the parameter space for the SMT channel converging to a well-defined narrow range of final orbits regardless of uncertainties in binary physics. We plot the orbital periods of BBH merger progenitors from before the mass transfer (BH+O-star stage, left) and after the SMT phase has taken place (BH+He-star stage, right). The figure is based on grids of detailed binary models with M_BH; 1 = 10 M_⊙ and varying assumptions on the orbital shrinkage during mass transfer (i.e., γ values, shown in different colors). Changing the assumption on γ significantly shifts the pre-SMT periods of BBH merger progenitors, but has little effect on the post-interaction orbits at the BH+He-star stage (or the properties of BBH mergers). The dashed red line shows the lower limit on the period of a BH+He-star systems, such that the naked helium star does not overflow its Roche lobe. We mark the periods and mass ratios of the known BH+OB-star systems (left panel, including supergiant high mass X-ray binaries) and of BH+Wolf-Rayet X-ray binaries (right). Cyg X-3 cannot be reproduced by SMT in our models, suggesting its origin in CE evolution.

In the text

Fig. 5.

Minimum orbital size from SMT evolution is primarily determined by the donor star, rather than by binary physics. Here, we report the critical mass ratios q_crit for BH+O-star systems (top panels), final orbital separations in binaries with q_RLOF = q_crit (middle panels), and their corresponding BBH delay times (bottom panels), calculated with MESA for a grid of donor stars of different mass (at ZAMS) and radius (at the onset of RLOF) at Z = 0.1 Z_⊙. The separations and BBH delay times shown here can be viewed as the minimum values achievable from SMT evolution given the donor mass and radius. Left panels follow the fiducial SMT treatment with γ = γ_BH, right panels assume enhanced orbital shrinkage due to L2 outflows. While enhancing the orbital shrinkage (left vs right) affects the critical mass ratios, the post-SMT orbits and their corresponding BBH delay times remain nearly unchanged. This is because these final outcomes are primarily determined by the stellar structure of the donor, which is the same in both variations. For illustrative purposes, the BBH delay times assume that each donor collapses to form the second BH, no matter its final core mass. Only the systems with delay times below ∼13.7 Gyr (i.e., brown in the bottom panels) are potential BBH mergers and GW sources for the LIGO/Virgo/Kagra detectors. The scatter points indicate the explored grid of donor masses and radii. For each pair, the q_crit value was found iteratively via binary MESA models down to at least ±0.1 accuracy.

In the text

Fig. 7.

BBH mergers from the SMT channel have long delay times (≳1 Gyr) as a consequence of the fundamental separation limit, regardless of the uncertainties in binary orbit evolution (left vs. right). Here, we plot the delay times of merging BBHs from SMT evolution (t_merge ≲ 13.7 Gyr) from all our binary MESA grids, as a function of the total BBH mass. We distinguish between BBH mergers formed via SMT evolution from MS donors (case A mass transfer) and post-MS donors (case B or C). Notably, case A evolution dominates for massive BBH mergers (≳40 M_⊙). Two variations are considered: non-accreted mass ejected with the specific AM of the BH (γ = γ_BH) and enhanced AM loss due to L2 outflows (γ ≈ 0.8γ_BH + 0.2γ_L2). The BBH delay times are unaffected by the choice of γ. The green shading indicates the approximate range of delay times and masses where we expect the CE channel to contribute. The figure is based on MESA binary grids of BH+O-star systems with the firstly formed BH initial mass of M_BH; 1 = 4, 7, 10, 13, 16, 20, 24, 28, 32, 36 M_⊙, and 40 M_⊙ (see Fig. 2 for details and Appendix D for other masses).

In the text

Fig. 8.

Mass ratios of BBH mergers from SMT evolution are confined to the range from ∼0.3 to ∼3, determined by the physics of stable binary interactions. We plot the BBH mass ratios q_{BH − BH} as a function of the BBH mass from our binary MESA grids, where q_{BH − BH} is defined as M_BH; 1/M_BH; 2 and with M_BH; 1 (M_BH; 2) as the mass of the first (second) born BH. Hatched regions indicate the combinations of BBH masses and mass ratios that cannot be produced via SMT evolution (see text). This results in a positive trend between q_{BH − BH} and M_tot. Circles indicate models in which the SMT interaction was initiated by a MS donor (case A) and diamonds mark SMT evolution from a post-MS donor (case B or C). The color indicates the orbital period at the BH+O-star stage (i.e., before the SMT). Based on binary grids of BH+O-star systems with M_BH; 1 = 4, 7, 10, 13, 16, 20, 24, 28, 32, 36 M_⊙, and 40 M_⊙.

In the text

Fig. 9.

Origin of the separation limit lies in delayed dynamical instability. Top: Mass transfer rate (Ṁ) in systems with a 30 M_⊙ donor and a varying mass ratio at RLOF, shown as a function of the decreasing envelope mass. The donor is the same for each mass ratio at the onset of RLOF: ∼250 R_⊙ core-He burning giant with a ∼17 M_⊙ envelope and ∼13 M_⊙ core. Models reaching log(Ṁ/M_⊙ yr⁻¹) > 0.5 become unstable (Sect. 2.4), as indicated by the dashed horizontal line. The critical mass ratio for stability is q_crit = 6.06 (marked in bold). The threshold between stable and unstable models is determined by the Ṁ peak at M_env ≈ 2.5 M_⊙. Middle: Internal entropy profiles of the donor in the q = q_crit model, ranging from the onset of RLOF (light, left) to the end of mass transfer (dark, right). The Ṁ peak seen in the top panel is caused by stripping off the layers where the entropy profile is nearly flat. Bottom: The same entropy profiles but as a function of the radius coordinate. The flat entropy layers are within the inner 3 R_⊙ of the donor (6 R_⊙ during the Ṁ peak), causing instability in models in which the mass transfer would shrink the orbit below a ≲ 8 R_⊙.

In the text

Fig. 10.

Path to delayed dynamical instability and the resulting minimum post-SMT separation do not depend on the assumption on orbital shrinkage (γ value). Here, we plot the evolution of the mass transfer rate (top) and orbital separation (bottom) in binaries interacting at the critical mass ratio for the fiducial SMT treatment (γ = γ_BH) and assuming enhanced shrinkage due to L2 outflows (γ ≈ 0.8γ_BH + 0.2γ_L2). The donor is the same 30 M_⊙ CHeB giant as in Fig. 9, the companion is a BH accreting at the Eddington limit, with its mass determined by the q_crit value: ≈5 M_⊙ in the fiducial model, ≈6 M_⊙ in the case with enhanced shrinkage. Regardless of the assumed γ, the critical Ṁ peak that determines stability occurs at the same moment of the interaction. As a result, the mass and the radius of the donor at this critical point do not depend on γ, leading to the same final orbital separation.

In the text

Fig. 11.

Minimum orbital separation from SMT evolution is different for different types of donor stars. Top left: Evolution of the mass transfer rate (Ṁ) as a function of the decreasing binary separation in interacting systems with a BH accretor and a 30 M_⊙ donor of different donor types. The CHeB donor is the same ∼250 R_⊙ giant as in Fig. 9, whereas its HG variant comes from the grid with low semiconvection. The solid lines are models at q = q_crit, dashed lines are at q slightly larger than q_crit, such that the MT becomes unstable (star symbols). Right: Internal entropy and H abundance profiles of different donors from the onset of RLOF, plotted as a function of the internal mass coordinate m. The He-core in post-MS donors is at m ≲ 13 M_⊙. The layers that cause the Ṁ peak and dynamical instability (star symbols) are where the entropy profile is nearly flat. Bottom left: Same entropy profiles but as a function of the radial coordinate. The difference in the location of the constant entropy regions in the envelopes of different donors is primarily responsible for different minimum orbital separations a_min that may be reached via SMT.

In the text

	Fig. C.1. Comparison of the intended versus the actual effective fraction of the mass lost through L2 in our MESA models (see text for explanation of the discrepancy). The analytical predictions of the orbital separation during SMT in Fig. 2 follow the actual mass loss fractions, i.e., the solid lines, so that they can be directly compared with the MESA models.
In the text

Fig. D.1.

Parameter window for BBH mergers from SMT evolution across different BH masses. Here, we plot the outcome of binary MESA models marking BBH mergers with star symbols, assuming fiducial AM loss (γ = γ_BH) and different primary BH masses M_BH; 1. Color indicates the final fate: wide BBH system (light yellow), merging BBH system (colorscale indicating the delay time), unstable MT with a convective donor (red), unstable MT with a radiative donor, likely leading to a BH + star merger (grey), close non-interacting systems due to chemically homogeneous mixing or very strong winds (white dotted). In the top two rows, the blue line marks the boundary between MS and post-MS donors. In the bottom two rows, only a limited range of periods is computed and all the donors are on the MS. The grid is constructed based on the initial mass ratio M_BH; 1/M_star in steps of 0.02.

In the text

Fig. D.2.

SMT channel becoming ineffective at high metallicity because of the combined effect of the separation limit in SMT evolution and orbital widening via Wolf-Rayet winds. We plot the outcome of binary MESA models at different metallicities, marking BBH mergers with stars. The first BH mass is M_BH; 1 = 10 M_⊙ and we assume the fiducial AM loss for SMT (γ = γ_BH). Color indicates the final fate, same as Fig. D.1. The blue line marks the boundary between MS and post-MS donors.

In the text

Fig. D.3.

Hertzsprung-Russell diagram with single stellar tracks that were used as a basis for the computation of critical mass ratios, minimum orbital separations from SMT evolution, and the corresponding minimum BBH merger delay times (see results for stellar models with semiconvection α_semiconv. = 33 in Fig. 5 and with α_semiconv. = 0.01 in the right panel of Fig. 6). Here there tracks are of 30 different masses, logarithmically spaced from 10 to 100 M_⊙, evolved until at least the end of core-He burning. Black dots are equally spaced every 50,000 years during the post-MS evolution.

In the text

Fig. D.4.

Evolution of binary separation during the mass transfer phase in MESA models of BH+O-star systems with q = q_crit mass ratios and initial O-star masses of 35, 55, and 75 M_⊙ (the three different panels), plotted as a function of the decreasing remaining donor mass. Different lines correspond to different initial separations, colored by the initial mass ratio M_donor/M_accretor. The initially more narrow systems interact when the donor is a MS star (closed circles), whereas in wider orbits the interaction is from a post-MS donor (open squares). Because the mass ratio is critical for each mass and radius of the donor at RLOF, the models shown here lead to the smallest binary separations via SMT evolution given the donor. See Fig. 5 for a full parameter space exploration, with other initial donor masses and radii. Assuming that at the end of its evolution the donor collapses to form a BH with mass 15, 22, and 27 M_⊙ (for different panels), we mark which binary separations would be required for BBH delay times of 100, 1000, or 10000 Myr for BBH mass ratio 0.9. Counter-intuitively, the smallest separations and the shortest BBH delay times from the SMT channel may originate from initially the widest BH+O-star systems (post-MS donors in the 35 and 55 M_⊙ panels).

In the text

Fig. D.5.

Same as Fig. 6 but comparing the final orbital separations instead of the BBH delay times. In the variation with low efficiency of semiconvection (right) all the post-MS donors are of the HG type. They are characterized by wider post-SMT separations compared to core-He burning (CHeB) donors due to differences in their internal chemical / entropy structure (Fig. 11). Based on that, we propose a new mass transfer stability treatment in rapid binary codes in Sect. 4.5. The difference between stellar models in both panels is closely connected to the so-called blue supergiant problem (Sect. 4.3).

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2020, Liv. Rev. Relat., 23, 3 [NASA ADS] [Google Scholar]

[2] Abbott, R., Abbott, T. D., Abraham, S., et al. 2021, Phys. Rev. X, 11, 021053 [Google Scholar]

[3] Abbott, R., Abbott, T. D., Acernese, F., et al. 2023, Phys. Rev. X, 13, 041039 [Google Scholar]

[4] Abrams, N. S., Hundertmark, M. P. G., Khakpash, S., et al. 2025, ApJS, 276, 10 [Google Scholar]

[5] Agrawal, P., Hurley, J., Stevenson, S., Szécsi, D., & Flynn, C. 2020, MNRAS, 497, 4549 [NASA ADS] [CrossRef] [Google Scholar]

[6] Antonini, F., & Rasio, F. A. 2016, ApJ, 831, 187 [Google Scholar]

[7] Antonini, F., Toonen, S., & Hamers, A. S. 2017, ApJ, 841, 77 [NASA ADS] [CrossRef] [Google Scholar]

[8] Askar, A., Szkudlarek, M., Gondek-Rosińska, D., Giersz, M., & Bulik, T. 2017, MNRAS, 464, L36 [CrossRef] [Google Scholar]

[9] Banerjee, S., & Olejak, A. 2024, ArXiv e-prints [arXiv:2411.15112] [Google Scholar]

[10] Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, A&A, 635, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[11] Bavera, S. S., Fragos, T., Zevin, M., et al. 2021, A&A, 647, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[12] Begelman, M. C., King, A. R., & Pringle, J. E. 2006, MNRAS, 370, 399 [Google Scholar]

[13] Belczynski, K., Dominik, M., Bulik, T., et al. 2010, ApJ, 715, L138 [Google Scholar]

[14] Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]

[15] Belczynski, K., Klencki, J., Fields, C. E., et al. 2020, A&A, 636, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[16] Belczynski, K., Romagnolo, A., Olejak, A., et al. 2022, ApJ, 925, 69 [NASA ADS] [CrossRef] [Google Scholar]

[17] Bellinger, E. P., de Mink, S. E., van Rossem, W. E., & Justham, S. 2024, ApJ, 967, L39 [NASA ADS] [CrossRef] [Google Scholar]

[18] Bestenlehner, J. M., Gräfener, G., Vink, J. S., et al. 2014, A&A, 570, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[19] Blaauw, A. 1961, Bull. Astron. Inst. Nether., 15, 265 [Google Scholar]

[20] Blundell, K. M., Bowler, M. G., & Schmidtobreick, L. 2008, ApJ, 678, L47 [NASA ADS] [CrossRef] [Google Scholar]

[21] Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]

[22] Brandt, N., & Podsiadlowski, P. 1995, MNRAS, 274, 461 [NASA ADS] [CrossRef] [Google Scholar]

[23] Breivik, K., Coughlin, S., Zevin, M., et al. 2020, ApJ, 898, 71 [Google Scholar]

[24] Broekgaarden, F. S., Berger, E., Stevenson, S., et al. 2022a, MNRAS, 516, 5737 [NASA ADS] [CrossRef] [Google Scholar]

[25] Broekgaarden, F. S., Stevenson, S., & Thrane, E. 2022b, ApJ, 938, 45 [CrossRef] [Google Scholar]

[26] Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[27] Casares, J., & Jonker, P. G. 2014, Space Sci. Rev., 183, 223 [NASA ADS] [CrossRef] [Google Scholar]

[28] Casares, J., Negueruela, I., Ribó, M., et al. 2014, Nature, 505, 378 [Google Scholar]

[29] Castro, N., Oey, M. S., Fossati, L., & Langer, N. 2018, ApJ, 868, 57 [NASA ADS] [CrossRef] [Google Scholar]

[30] Cherepashchuk, A. M., Sunyaev, R. A., Fabrika, S. N., et al. 2005, A&A, 437, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[31] Chruślińska, M. 2024, Ann. Phys., 536, 2200170 [CrossRef] [Google Scholar]

[32] Chruslinska, M., & Nelemans, G. 2019, MNRAS, 488, 5300 [NASA ADS] [Google Scholar]

[33] Chruslinska, M., Nelemans, G., & Belczynski, K. 2019, MNRAS, 482, 5012 [Google Scholar]

[34] Chruślińska, M., Nelemans, G., Boco, L., & Lapi, A. 2021, MNRAS, 508, 4994 [CrossRef] [Google Scholar]

[35] Claeys, J. S. W., Pols, O. R., Izzard, R. G., Vink, J., & Verbunt, F. W. M. 2014, A&A, 563, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[36] Davies, B., Crowther, P. A., & Beasor, E. R. 2018, MNRAS, 478, 3138 [NASA ADS] [CrossRef] [Google Scholar]

[37] de Burgos, A., Simón-Díaz, S., Urbaneja, M. A., & Negueruela, I. 2023, A&A, 674, A212 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[38] de Mink, S. E., & Mandel, I. 2016, MNRAS, 460, 3545 [NASA ADS] [CrossRef] [Google Scholar]

[39] Detmers, R. G., Langer, N., Podsiadlowski, P., & Izzard, R. G. 2008, A&A, 484, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[40] Dorozsmai, A., & Toonen, S. 2024, MNRAS, 530, 3706 [NASA ADS] [CrossRef] [Google Scholar]

[41] El-Badry, K. 2024, New Astron. Rev., 98, 101694 [NASA ADS] [CrossRef] [Google Scholar]

[42] Eldridge, J. J., & Stanway, E. R. 2016, MNRAS, 462, 3302 [Google Scholar]

[43] Fabrika, S. 2004, Astrophys. Space Phys. Res., 12, 1 [NASA ADS] [Google Scholar]

[44] Farag, E., Renzo, M., Farmer, R., Chidester, M. T., & Timmes, F. X. 2022, ApJ, 937, 112 [NASA ADS] [CrossRef] [Google Scholar]

[45] Farmer, R., Renzo, M., de Mink, S. E., Marchant, P., & Justham, S. 2019, ApJ, 887, 53 [Google Scholar]

[46] Farrell, E., Groh, J. H., Meynet, G., & Eldridge, J. J. 2022, MNRAS, 512, 4116 [NASA ADS] [CrossRef] [Google Scholar]

[47] Fragos, T., Andrews, J. J., Ramirez-Ruiz, E., et al. 2019, ApJ, 883, L45 [Google Scholar]

[48] Fragos, T., Andrews, J. J., Bavera, S. S., et al. 2023, ApJS, 264, 45 [NASA ADS] [CrossRef] [Google Scholar]

[49] Gagnier, D., & Pejcha, O. 2023, A&A, 674, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[50] Gallegos-Garcia, M., Berry, C. P. L., Marchant, P., & Kalogera, V. 2021, ApJ, 922, 110 [NASA ADS] [CrossRef] [Google Scholar]

[51] Gallegos-Garcia, M., Jacquemin-Ide, J., & Kalogera, V. 2024, ApJ, 973, 168 [NASA ADS] [CrossRef] [Google Scholar]

[52] García, F., Simaz Bunzel, A., Chaty, S., Porter, E., & Chassande-Mottin, E. 2021, A&A, 649, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[53] Ge, H., Hjellming, M. S., Webbink, R. F., Chen, X., & Han, Z. 2010, ApJ, 717, 724 [NASA ADS] [CrossRef] [Google Scholar]

[54] Ge, H., Webbink, R. F., Chen, X., & Han, Z. 2015, ApJ, 812, 40 [Google Scholar]

[55] Ge, H., Webbink, R. F., & Han, Z. 2020, ApJS, 249, 9 [NASA ADS] [CrossRef] [Google Scholar]

[56] Ge, H., Tout, C. A., Chen, X., et al. 2024, ApJ, 975, 254 [NASA ADS] [CrossRef] [Google Scholar]

[57] Georgy, C., Ekström, S., Eggenberger, P., et al. 2013, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[58] Gomez, S., & Grindlay, J. E. 2021, ApJ, 913, 48 [NASA ADS] [CrossRef] [Google Scholar]

[59] Gräfener, G., & Hamann, W. R. 2008, A&A, 482, 945 [Google Scholar]

[60] Hainich, R., Rühling, U., Todt, H., et al. 2014, A&A, 565, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[61] Hamann, W. R., Koesterke, L., & Wessolowski, U. 1995, A&A, 299, 151 [Google Scholar]

[62] Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]

[63] Hirai, R., & Mandel, I. 2022, ApJ, 937, L42 [NASA ADS] [CrossRef] [Google Scholar]

[64] Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [Google Scholar]

[65] Humphreys, R. M., & McElroy, D. B. 1984, ApJ, 284, 565 [NASA ADS] [CrossRef] [Google Scholar]

[66] Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [Google Scholar]

[67] Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]

[68] Ivanova, N., Justham, S., & Ricker, P. 2020, Common Envelope Evolution (IOP Publishing) [Google Scholar]

[69] Janka, H.-T., & Kresse, D. 2024, Ap&SS, 369, 80 [NASA ADS] [CrossRef] [Google Scholar]

[70] Janssens, S., Shenar, T., Sana, H., et al. 2022, A&A, 658, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[71] Janssens, S., Shenar, T., Degenaar, N., et al. 2023, A&A, 677, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[72] Jermyn, A. S., Bauer, E. B., Schwab, J., et al. 2023, ApJS, 265, 15 [NASA ADS] [CrossRef] [Google Scholar]

[73] Justham, S., Podsiadlowski, P., & Vink, J. S. 2014, ApJ, 796, 121 [NASA ADS] [CrossRef] [Google Scholar]

[74] Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]

[75] Kaiser, E. A., Hirschi, R., Arnett, W. D., et al. 2020, MNRAS, 496, 1967 [Google Scholar]

[76] King, A. R., & Ritter, H. 1999, MNRAS, 309, 253 [Google Scholar]

[77] King, A. R., Taam, R. E., & Begelman, M. C. 2000, ApJ, 530, L25 [NASA ADS] [CrossRef] [Google Scholar]

[78] King, A., Lasota, J.-P., & Middleton, M. 2023, New Astron. Rev., 96, 101672 [CrossRef] [Google Scholar]

[79] Kippenhahn, R., & Weigert, A. 1967, ZAp, 65, 251 [Google Scholar]

[80] Klencki, J., & Metzger, B. D. 2025, ArXiv e-prints [arXiv:2510.09745] [Google Scholar]

[81] Klencki, J., & Nelemans, G. 2019, IAU Symp., 346, 417 [Google Scholar]

[82] Klencki, J., Nelemans, G., Istrate, A. G., & Pols, O. 2020, A&A, 638, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[83] Klencki, J., Nelemans, G., Istrate, A. G., & Chruslinska, M. 2021, A&A, 645, A54 [EDP Sciences] [Google Scholar]

[84] Klencki, J., Istrate, A., Nelemans, G., & Pols, O. 2022, A&A, 662, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[85] Kresse, D., Ertl, T., & Janka, H.-T. 2021, ApJ, 909, 169 [NASA ADS] [CrossRef] [Google Scholar]

[86] Kruckow, M. U., Tauris, T. M., Langer, N., et al. 2016, A&A, 596, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[87] Kruckow, M. U., Tauris, T. M., Langer, N., Kramer, M., & Izzard, R. G. 2018, MNRAS, 481, 1908 [CrossRef] [Google Scholar]

[88] Kruckow, M. U., Neunteufel, P. G., Di Stefano, R., Gao, Y., & Kobayashi, C. 2021, ApJ, 920, 86 [NASA ADS] [CrossRef] [Google Scholar]

[89] Kushnir, D., Zaldarriaga, M., Kollmeier, J. A., & Waldman, R. 2016, MNRAS, 462, 844 [NASA ADS] [CrossRef] [Google Scholar]

[90] Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]

[91] Langer, N., El Eid, M. F., & Fricke, K. J. 1985, A&A, 145, 179 [NASA ADS] [Google Scholar]

[92] Langer, N., El Eid, M. F., & Baraffe, I. 1989, A&A, 224, L17 [NASA ADS] [Google Scholar]

[93] Langer, N., Schürmann, C., Stoll, K., et al. 2020, A&A, 638, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[94] Lasota, J.-P., Vieira, R. S. S., Sadowski, A., Narayan, R., & Abramowicz, M. A. 2016, A&A, 587, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[95] Law-Smith, J. A. P., Everson, R. W., Ramirez-Ruiz, E., et al. 2020, ArXiv e-prints [arXiv:2011.06630] [Google Scholar]

[96] Lipunova, G. V. 1999, Astron. Lett., 25, 508 [NASA ADS] [Google Scholar]

[97] Livio, M., & Soker, N. 1988, ApJ, 329, 764 [Google Scholar]

[98] Lu, W., Fuller, J., Quataert, E., & Bonnerot, C. 2023, MNRAS, 519, 1409 [Google Scholar]

[99] Ma, L., & Fuller, J. 2023, ApJ, 952, 53 [CrossRef] [Google Scholar]

[100] Maggiore, M., Van Den Broeck, C., Bartolo, N., et al. 2020, JCAP, 2020, 050 [CrossRef] [Google Scholar]

[101] Mahy, L., Sana, H., Shenar, T., et al. 2022, A&A, 664, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[102] Mandel, I. 2021, Res. Notes Am. Astron. Soc., 5, 223 [Google Scholar]

[103] Mandel, I., & Broekgaarden, F. S. 2022, Liv. Rev. Relat., 25, 1 [Google Scholar]

[104] Mandel, I., & de Mink, S. E. 2016, MNRAS, 458, 2634 [NASA ADS] [CrossRef] [Google Scholar]

[105] Mapelli, M., & Giacobbo, N. 2018, MNRAS, 479, 4391 [NASA ADS] [CrossRef] [Google Scholar]

[106] Mapelli, M., Dall’Amico, M., Bouffanais, Y., et al. 2021, MNRAS, 505, 339 [CrossRef] [Google Scholar]

[107] Mapelli, M., Bouffanais, Y., Santoliquido, F., Arca Sedda, M., & Artale, M. C. 2022, MNRAS, 511, 5797 [NASA ADS] [CrossRef] [Google Scholar]

[108] Marchant, P., & Bodensteiner, J. 2024, ARA&A, 62, 21 [NASA ADS] [CrossRef] [Google Scholar]

[109] Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[110] Marchant, P., Pappas, K. M. W., Gallegos-Garcia, M., et al. 2021, A&A, 650, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[111] McKernan, B., Ford, K. E. S., Bellovary, J., et al. 2018, ApJ, 866, 66 [Google Scholar]

[112] McKinney, J. C., Tchekhovskoy, A., Sadowski, A., & Narayan, R. 2014, MNRAS, 441, 3177 [NASA ADS] [CrossRef] [Google Scholar]

[113] Mennekens, N., & Vanbeveren, D. 2014, A&A, 564, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[114] Menon, A., Ercolino, A., Urbaneja, M. A., et al. 2024, ApJ, 963, L42 [NASA ADS] [CrossRef] [Google Scholar]

[115] Metzger, B. D. 2022, ApJ, 932, 84 [NASA ADS] [CrossRef] [Google Scholar]

[116] Middleton, M. J., Walton, D. J., Alston, W., et al. 2021, MNRAS, 506, 1045 [NASA ADS] [CrossRef] [Google Scholar]

[117] Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]

[118] Mirabel, I. F., & Rodrigues, I. 2003, Science, 300, 1119 [Google Scholar]

[119] Misra, D., Kovlakas, K., Fragos, T., et al. 2024, A&A, 682, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[120] Moreno, M. M., Schneider, F. R. N., Röpke, F. K., et al. 2022, A&A, 667, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[121] Neijssel, C. J., Vigna-Gómez, A., Stevenson, S., et al. 2019, MNRAS, 490, 3740 [Google Scholar]

[122] Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]

[123] Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]

[124] Olejak, A., Belczynski, K., & Ivanova, N. 2021, A&A, 651, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[125] Olejak, A., Fryer, C. L., Belczynski, K., & Baibhav, V. 2022, MNRAS, 516, 2252 [NASA ADS] [CrossRef] [Google Scholar]

[126] Olejak, A., Klencki, J., Xu, X.-T., et al. 2024, A&A, 689, A305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[127] Orosz, J. A., McClintock, J. E., Narayan, R., et al. 2007, Nature, 449, 872 [NASA ADS] [CrossRef] [Google Scholar]

[128] Orosz, J. A., Steeghs, D., McClintock, J. E., et al. 2009, ApJ, 697, 573 [NASA ADS] [CrossRef] [Google Scholar]

[129] Paczyński, B., & Sienkiewicz, R. 1972, Acta Astron., 22, 73 [NASA ADS] [Google Scholar]

[130] Paczyński, B., Ziólkowski, J., & Zytkow, A. 1969, Astrophys. Space Sci. Lib., 13, 237 [Google Scholar]

[131] Papanikolaou, T., Vennin, V., & Langlois, D. 2021, JCAP, 2021, 053 [CrossRef] [Google Scholar]

[132] Patrick, L. R., Lennon, D. J., Najarro, F., et al. 2025, A&A, 698, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[133] Pauli, D., Langer, N., Aguilera-Dena, D. R., Wang, C., & Marchant, P. 2022, A&A, 667, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[134] Pavlovskii, K., & Ivanova, N. 2015, MNRAS, 449, 4415 [Google Scholar]

[135] Pavlovskii, K., Ivanova, N., Belczynski, K., & Van, K. X. 2017, MNRAS, 465, 2092 [Google Scholar]

[136] Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]

[137] Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]

[138] Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]

[139] Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]

[140] Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]

[141] Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]

[142] Picco, A., Marchant, P., Sana, H., & Nelemans, G. 2024, A&A, 681, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[143] Podsiadlowski, P., & Rappaport, S. 2000, ApJ, 529, 946 [Google Scholar]

[144] Podsiadlowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]

[145] Podsiadlowski, P., Rappaport, S., & Han, Z. 2003, MNRAS, 341, 385 [NASA ADS] [CrossRef] [Google Scholar]

[146] Pols, O. R. 1994, A&A, 290, 119 [Google Scholar]

[147] Poutanen, J., Lipunova, G., Fabrika, S., Butkevich, A. G., & Abolmasov, P. 2007, MNRAS, 377, 1187 [NASA ADS] [CrossRef] [Google Scholar]

[148] Pribulla, T. 1998, Contrib. Astron. Obs. Skaln. Pleso, 28, 101 [NASA ADS] [Google Scholar]

[149] Qin, Y., Fragos, T., Meynet, G., et al. 2018, A&A, 616, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[150] Qin, Y., Marchant, P., Fragos, T., Meynet, G., & Kalogera, V. 2019, ApJ, 870, L18 [Google Scholar]

[151] Ramachandran, V., Oskinova, L. M., Hamann, W. R., et al. 2022, A&A, 667, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[152] Rappaport, S. A., Podsiadlowski, P., & Pfahl, E. 2005, MNRAS, 356, 401 [NASA ADS] [CrossRef] [Google Scholar]

[153] Reitze, D., Adhikari, R. X., Ballmer, S., et al. 2019, BAAS, 51, 35 [NASA ADS] [Google Scholar]

[154] Renzo, M., & Götberg, Y. 2021, ApJ, 923, 277 [NASA ADS] [CrossRef] [Google Scholar]

[155] Renzo, M., Hendriks, D. D., van Son, L. A. C., & Farmer, R. 2022, Res. Notes Am. Astron. Soc., 6, 25 [Google Scholar]

[156] Renzo, M., Zapartas, E., Justham, S., et al. 2023, ApJ, 942, L32 [NASA ADS] [CrossRef] [Google Scholar]

[157] Repetto, S., & Nelemans, G. 2015, MNRAS, 453, 3341 [Google Scholar]

[158] Repetto, S., Davies, M. B., & Sigurdsson, S. 2012, MNRAS, 425, 2799 [Google Scholar]

[159] Riley, J., Mandel, I., Marchant, P., et al. 2021, MNRAS, 505, 663 [Google Scholar]

[160] Riley, J., Agrawal, P., Barrett, J. W., et al. 2022, ApJS, 258, 34 [NASA ADS] [CrossRef] [Google Scholar]

[161] Rodriguez, C. L., Haster, C.-J., Chatterjee, S., Kalogera, V., & Rasio, F. A. 2016, ApJ, 824, L8 [NASA ADS] [CrossRef] [Google Scholar]

[162] Rodriguez, C. L., Zevin, M., Amaro-Seoane, P., et al. 2019, Phys. Rev. D, 100, 043027 [Google Scholar]

[163] Romagnolo, A., Belczynski, K., Klencki, J., et al. 2023, MNRAS, 525, 706 [NASA ADS] [CrossRef] [Google Scholar]

[164] Romagnolo, A., Klencki, J., Vigna-Gómez, A., & Belczynski, K. 2025, A&A, 693, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[165] Romero-Shaw, I., Hirai, R., Bahramian, A., Willcox, R., & Mandel, I. 2023, MNRAS, 524, 245 [NASA ADS] [CrossRef] [Google Scholar]

[166] Sądowski, A., & Narayan, R. 2015, MNRAS, 453, 3213 [Google Scholar]

[167] Sądowski, A., & Narayan, R. 2016, MNRAS, 456, 3929 [CrossRef] [Google Scholar]

[168] Sądowski, A., Narayan, R., McKinney, J. C., & Tchekhovskoy, A. 2014, MNRAS, 439, 503 [CrossRef] [Google Scholar]

[169] Samsing, J. 2018, Phys. Rev. D, 97, 103014 [CrossRef] [Google Scholar]

[170] Samsing, J., Bartos, I., D’Orazio, D. J., et al. 2022, Nature, 603, 237 [NASA ADS] [CrossRef] [Google Scholar]

[171] Sander, A. A. C., & Vink, J. S. 2020, MNRAS, 499, 873 [Google Scholar]

[172] Sander, A. A. C., Vink, J. S., & Hamann, W. R. 2020, MNRAS, 491, 4406 [Google Scholar]

[173] Sanyal, D., Grassitelli, L., Langer, N., & Bestenlehner, J. M. 2015, A&A, 580, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[174] Sanyal, D., Langer, N., Szécsi, D., Yoon, S.-C., & Grassitelli, L. 2017, A&A, 597, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[175] Sasaki, M., Suyama, T., Tanaka, T., & Yokoyama, S. 2018, Class. Quant. Grav., 35, 063001 [NASA ADS] [CrossRef] [Google Scholar]

[176] Schneider, F. R. N., Podsiadlowski, P., & Laplace, E. 2024, A&A, 686, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[177] Schootemeijer, A., Langer, N., Grin, N. J., & Wang, C. 2019, A&A, 625, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[178] Schrøder, S. L., MacLeod, M., Ramirez-Ruiz, E., et al. 2021, ArXiv e-prints [arXiv:2107.09675] [Google Scholar]

[179] Schürmann, C., Langer, N., Kramer, J. A., et al. 2024, A&A, 690, A282 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[180] Sen, K., Langer, N., Pauli, D., et al. 2023, A&A, 672, A198 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[181] Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]

[182] Shao, Y., & Li, X.-D. 2021, ApJ, 920, 81 [NASA ADS] [CrossRef] [Google Scholar]

[183] Shenar, T., Sana, H., Mahy, L., et al. 2022, Nat. Astron., 6, 1085 [NASA ADS] [CrossRef] [Google Scholar]

[184] Shenar, T., Bodensteiner, J., Sana, H., et al. 2024, A&A, 690, A289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[185] Shikauchi, M., Hirai, R., & Mandel, I. 2025, ApJ, 984, 149 [Google Scholar]

[186] Stevenson, S., Vigna-Gómez, A., Mandel, I., et al. 2017, Nat. Commun., 8, 14906 [Google Scholar]

[187] Stone, N. C., Metzger, B. D., & Haiman, Z. 2017, MNRAS, 464, 946 [Google Scholar]

[188] Stothers, R. B., & Chin, C.-W. 1992, ApJ, 390, 136 [NASA ADS] [CrossRef] [Google Scholar]

[189] Tauris, T. M., & van den Heuvel, E. P. J. 2006, Formation and Evolution Of Compact Stellar X-ray Sources (Cambridge: Cambridge University Press) [Google Scholar]

[190] Tauris, T. M., & van den Heuvel, E. P. J. 2023, Physics of Binary Star Evolution. From Stars to X-ray Binaries and Gravitational Wave Sources (Princeton University Press) [Google Scholar]

[191] Tauris, T. M., Kramer, M., Freire, P. C. C., et al. 2017, ApJ, 846, 170 [Google Scholar]

[192] Temmink, K. D., Pols, O. R., Justham, S., Istrate, A. G., & Toonen, S. 2023, A&A, 669, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[193] Tramper, F., Sana, H., & de Koter, A. 2016, ApJ, 833, 133 [CrossRef] [Google Scholar]

[194] Tutukov, A. V., & Yungelson, L. R. 1993, MNRAS, 260, 675 [Google Scholar]

[195] van den Heuvel, E. P. J. 1976, IAU Symp., 73, 35 [Google Scholar]

[196] van den Heuvel, E. P. J. 1994, A&A, 291, L39 [NASA ADS] [Google Scholar]

[197] van den Heuvel, E. P. J., Portegies Zwart, S. F., & de Mink, S. E. 2017, MNRAS, 471, 4256 [Google Scholar]

[198] van Son, L. A. C., de Mink, S. E., Callister, T., et al. 2022a, ApJ, 931, 17 [NASA ADS] [CrossRef] [Google Scholar]

[199] van Son, L. A. C., de Mink, S. E., Renzo, M., et al. 2022b, ApJ, 940, 184 [NASA ADS] [CrossRef] [Google Scholar]

[200] Vanbeveren, D., Mennekens, N., Van Rensbergen, W., & De Loore, C. 2013, A&A, 552, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[201] Vigna-Gómez, A. 2025, A&A, 701, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[202] Vigna-Gómez, A., Neijssel, C. J., Stevenson, S., et al. 2018, MNRAS, 481, 4009 [Google Scholar]

[203] Vigna-Gómez, A., Wassink, M., Klencki, J., et al. 2022, MNRAS, 511, 2326 [CrossRef] [Google Scholar]

[204] Vigna-Gómez, A., Willcox, R., Tamborra, I., et al. 2024, Phys. Rev. Lett., 132, 191403 [CrossRef] [Google Scholar]

[205] Vink, J. S. 2017, A&A, 607, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[206] Vink, J. S. 2022, ARA&A, 60, 203 [NASA ADS] [CrossRef] [Google Scholar]

[207] Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[208] Vink, J. S., Muijres, L. E., Anthonisse, B., et al. 2011, A&A, 531, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[209] Vynatheya, P., & Hamers, A. S. 2022, ApJ, 926, 195 [NASA ADS] [CrossRef] [Google Scholar]

[210] Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]

[211] Webbink, R. F. 1985, in Interacting Binary Stars, eds. J. E. Pringle, & R. A. Wade, 39 [Google Scholar]

[212] Wei, D., Schneider, F. R. N., Podsiadlowski, P., et al. 2023, ArXiv e-prints [arXiv:2311.07278] [Google Scholar]

[213] Wellstein, S., Langer, N., & Braun, H. 2001, A&A, 369, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[214] Wiktorowicz, G., Lu, Y., Wyrzykowski, Ł., et al. 2020, ApJ, 905, 134 [NASA ADS] [CrossRef] [Google Scholar]

[215] Willcox, R., MacLeod, M., Mandel, I., & Hirai, R. 2023, ApJ, 958, 138 [NASA ADS] [CrossRef] [Google Scholar]

[216] Woods, T. E., & Ivanova, N. 2011, ApJ, 739, L48 [NASA ADS] [CrossRef] [Google Scholar]

[217] Yoon, S.-C. 2017, MNRAS, 470, 3970 [NASA ADS] [CrossRef] [Google Scholar]

[218] Yoon, S. C., Langer, N., & Norman, C. 2006, A&A, 460, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[219] Zahn, J. P. 2008, EAS Publi. Ser., 29, 67 [Google Scholar]

[220] Zaldarriaga, M., Kushnir, D., & Kollmeier, J. A. 2018, MNRAS, 473, 4174 [Google Scholar]

[221] Zevin, M., & Bavera, S. S. 2022, ApJ, 933, 86 [NASA ADS] [CrossRef] [Google Scholar]

[222] Zevin, M., Bavera, S. S., Berry, C. P. L., et al. 2021, ApJ, 910, 152 [Google Scholar]